Расчет линейных электрических цепей в переходном и стационарном режимах работы
Федеральное
агентство связи
Федеральное
государственное образовательное бюджетное учреждение
высшего
профессионального образования
Сибирский
государственный университет телекоммуникаций и информатики
ФГОБУ
ВПО «СибГУТИ»
Кафедра
ТЭЦ
КУРСОВАЯ
РАБОТА
по
курсу ТОЭ
тема:
Расчет линейных электрических цепей в переходном и стационарном режимах работы
Выполнил: ст.гр.
МП-38
Лаптев С.В
Проверил: Черных
Ю.С.
Новосибирск
2014
Содержание
Введение
Часть
1. Электрические цепи постоянного тока
Часть
2. Электрические цепи при гармоническом воздействии
Часть
3. Переходные процессы в электрических цепях первого порядка
Часть
4. Определение реакции цепи на произвольное внешнее воздействие
Заключение
Список
литературы
Введение
Цель написания данной курсовой работы -
обобщение и укрепление полученных знаний в ходе курса «Теоретические основы
электротехники», полученных при изучении линейных цепей в стационарном и
переходном режимах работы, а так же при воздействии на цепь сигнала
произвольной формы.
Часть 1. Электрические цепи постоянного тока
Полный анализ работы цепи при воздействии
источников постоянного напряжения и тока
В цепях постоянного тока свойства реактивных
элементов меняются. Принято, что при протекании через емкостной элемент
постоянного тока его принято считать за холостой ход, а через индуктивность -
за короткое замыкание.
В этом случае схему можно заменить на
эквивалентную ей схему.
Исходные данные схемы:
E1=50 B;
E2=90 B;=2 кОм;=2 кОм;=2 кОм;=3 кОм;=6 кОм;=10
мА;
Расчет схемы методом наложения
(суперпозиции)
Метод основан на принципе наложения, который
применяется только к линейным системам.
Метод наложения относительно прост, и в основном
применяется для не сложных электрических цепей.
Его суть заключается в том, что токи в ветвях
определяются как алгебраическая сумма их составляющих от каждого источника. То
есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти
эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим
решение одной сложной цепи к нескольким простым (с одним источником).
Составим частичные схемы:
Токи в первой частичной схеме:
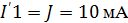
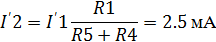
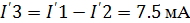
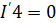
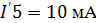
Токи во второй частичной схеме:
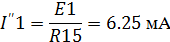
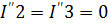
Токи в третьей частичной схеме:
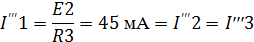
Согласно принципу суперпозиции определим
истинные токи:
Токи в ветвях исходной схемы это алгебраическая
сумма токов в соответствующих ветвях частичных схем. Частичные токи
записываются со знаком «+», если их направление совпадает с направлением тока в
исходной схеме, и со знаком «-», если не совпадают.
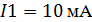
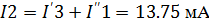
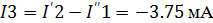

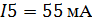
Метод узловых потенциалов
(напряжений)
Данный метод используется для расчета сложных
цепей. В основе его лежит расчет потенциалов во всех узлах цепи относительно
базисного узла, потенциал которого принимают равным нулю. Рациональнее выбирать
базисным узел, к которому подключен «минус» идеального источника ЭДС.
Примем за базисный узел 3:
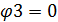
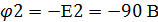
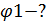
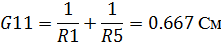
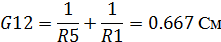
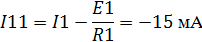
Поскольку мы имеем только один неизвестный узел,
то получаем уравнение:
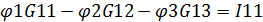
Выразим отсюда неизвестный потенциал 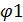 :
:
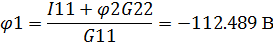
Найдем с его помощью истинные токи:
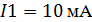
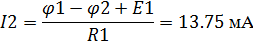

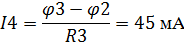
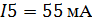
Определение напряжений на элементах цепи
=I2R1=27.5 B
UR2=I1R2=20 B=90 B =I3R5= -22.5 B
UJ= -92.5 B
Проверка правильности расчетов балансом мощности
Сущность метода баланса мощности заключается в
том, что сумма мощностей, отдаваемых независимыми источниками энергии равна
сумме можностей, потребляемых остальными элементами ЭЦ.
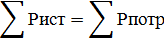
Рассчитаем мощности источников энергии и
элементов цепи:
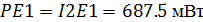
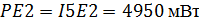
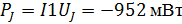
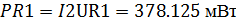
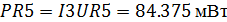

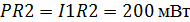


Равенство мощностей источников и потребления
свидетельствует о правильности проведенных расчетов.
Таблица 1: Результаты расчета электрической цепи
постоянного тока
|
Параметры
Элементы
|
Ток, мА
|
Напряжение, В
|
Мощность, мВт
|
|
R1
|
13.75
|
27.5
|
378.125
|
|
R2
|
10
|
20
|
200
|
|
R3
|
45
|
90
|
4050
|
|
R4
|
0
|
0
|
0
|
|
R5
|
-3.75
|
-22.5
|
84.375
|
|
L1
|
55
|
0
|
0
|
|
L2
|
55
|
0
|
0
|
|
C
|
0
|
50
|
0
|
|
E1
|
13.75
|
50
|
687.5
|
|
E2
|
55
|
90
|
4950
|
|
J
|
10
|
-92.5
|
-925
|
В ходе выполнения данной части курсовой работы я
определил токи во всех ветвях исходной схемы методами наложения(суперпозиции) и
узловых потенциалов(напряжений). Так же я определил напряжение на каждом
элементе схемы и провел проверку расчетов балансом мощности.
Часть 2. Электрические цепи при гармоническом
воздействии
Для упрощения расчета индуктивно связанных цепей
можно выполнить так называемую «развязку». Выполняется это следующим образом:
проводится так называемая развязка схемы, которая позволяет переделать для
расчета схему индуктивно связанных элементов цепью с исключенными индуктивными
связями. При этом, рассматриваются две обмотки L1 и L2, создающие взаимное
индуктивное влияние между собой.
Переходим на эквивалентную схему. Для этого, в
электрическую цепь вводим новый элемент - узел М, определяющий величину взаимоиндукции.
В новом варианте к индуктивностям L1 и L2 добавляем значение взаимоиндукции -М
(с отрицательным значением), одновременно включая ее значение в третий элемент.
Параметры схемы:
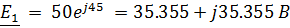

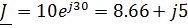
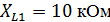
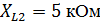
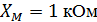
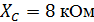
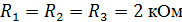


Нахождение токов в ветвях схемы методом контурных
токов
Один из методов анализа электрической цепи
является метод контурных токов. Основой для него служит второй закон Кирхгофа.
Главное его преимущество это уменьшение количества уравнений до m - n +1,
напоминаем что m - количество ветвей, а n - количество узлов в цепи. На
практике такое уменьшение существенно упрощает расчет.
Контурный ток - это величина, которая одинакова
во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными
индексами, например I11, I22 и тд.
Действительный ток в определенной ветви
определяется алгебраической суммой контурных токов, в которую эта ветвь входит.
Нахождение действительных токов и есть первоочередная задача метода контурных
токов.
Контурная ЭДС - это сумма всех ЭДС входящих в
этот контур.
Собственным сопротивлением контура называется
сумма сопротивлений всех ветвей, которые в него входят.
Общим сопротивлением контура называется
сопротивление ветви, смежное двум контурам.
В нашем случае контурный ток контура с
источником тока:
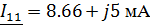
Составим систему уравнений по МКТ:
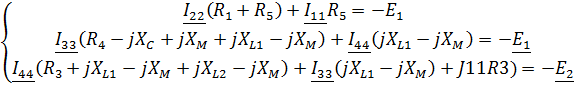
Преобразуем нашу систему уравнений, подставив
имеющиеся значения и получим первый контурный ток из числа неизвестных:
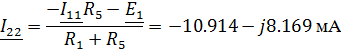
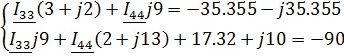
Найдем контурные токи по методу Крамера:
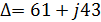
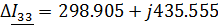
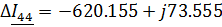
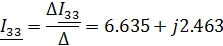
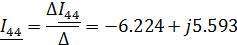
Зная контурные токи, найдем токи в ветвях цепи
используя принцип наложения:
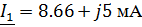
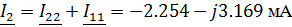
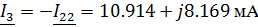
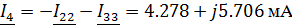
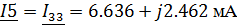
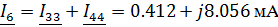
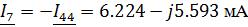
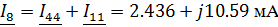
Нахождение тока в емкостном элементе методом
эквивалентного генератора
Исключим конденсатор С из ветви и рассчитаем
эквивалентное сопротивление относительно зажимов а и б:
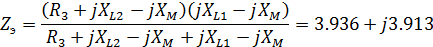
Определим Uxx по второму закону Кирхгофа:
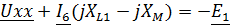
Найдем ток I6 исходя из МКТ:
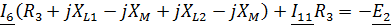
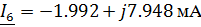
С его помощью найдем Uxx:
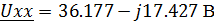
Таким образом, ток в конденсаторе С:
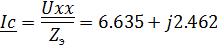
Сравнив полученный ток в конденсаторе с током
I5, полученным по МКТ, видим что они совпадают, что говорит о правильности
проведенных расчетов.
Определение напряжений на элементах цепи
Определим напряжения на активных элементах цепи:
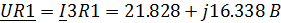
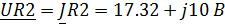
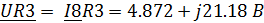
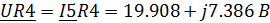
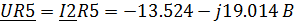
Определим напряжения на реактивных элементах
цепи(с учетом взаимоиндукции):
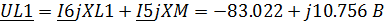
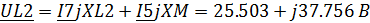
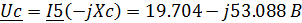
Напряжение на источнике тока определим по ЗНК:
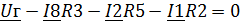
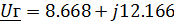
Проверим правильность полученных значений по
законам Кирхгофа:
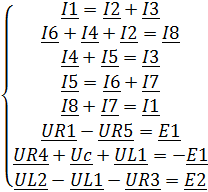
Подставив полученные значения, получим:
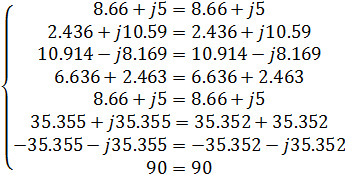
Баланс мощности
Баланс мощности в цепях переменного тока
отличается от него же в цепях постоянного тока.
В цепях постоянного тока баланс мощности
соблюдается если сумма комплексных мощностей, отдаваемых источниками энергии
равна сумме комплексных мощностей, потребляемых потреблением цепи.
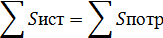
S=P+jQр - полная комплекскная мощность;активная
мощность, ВА;реактивная мощность, ВАр;
Определим комплексную мощность источников:
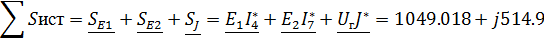
Посчитаем отдельно активную и реактивную
составляющую мощности потребления:
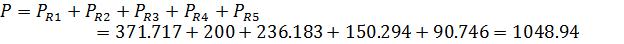

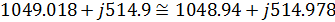
Выполнение равенства мощностей свидетельствует о
правильности проведенных расчетов.
Таблица 2. Результаты расчета электрической цепи
при воздействии переменного тока
|
Параметры
Элементы
|
Ток, мА
|
Напряжение, В
|
Мощность, мВАр
|
|
R1
|
10.914-j8.169
|
21.828-j16.338
|
371.717
|
|
R2
|
8.66+j5
|
17.32+j10
|
200
|
|
R3
|
2.436+j10.59
|
4.872+j21.18
|
236.183
|
|
R4
|
6.636+j2.463
|
19.909+j7.389
|
150.294
|
|
R5
|
-2.254-j3.169
|
-13.524-j19.014
|
90.746
|
|
L1
|
0.412+j7.996
|
-77.497-j2.516
|
585.619
|
|
L2
|
6.224-j5.593
|
30.428+j24.484
|
280.079
|
|
C
|
6.636+j2.463
|
19.704-j53.088
|
400.823
|
|
E1
|
4.278+j5.706
|
35.355+j35.355
|
352.383-j50.487
|
|
E2
|
6.224-j5.593
|
90
|
560.14+j503.37
|
|
J
|
8.66+j5
|
8.668+j12.166
|
135.895+j62.018
|
В этой части курсовой работы я определил токи в
ветвях исходной схемы методом контурных токов. Определил ток в емкостном
элементе методом эквивалентного генератора напряжения. Так же мной были
определены напряжения на элементах схемы, расчеты были проверены законами
Кирхгофа и балансом мощности.
Часть 3. Переходные процессы в электрических
цепях первого порядка
Расчет напряжения на выходе цепи
Расчет закона изменения любого параметра ЭЦ при
возникновении в ней переходного процесса базируется на законах коммутации:
В первый момент времени непосредственно после
коммутации ток в индуктивности остается таким же, каким он был в момент времени
непосредственно перед коммутацией, а затем плавно изменяется
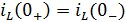
В первый момент времени непосредственно после
коммутации напряжение на емкости остается таким же, каким оно было в момент
времени непосредственно перед коммутацией, а затем плавно изменяется
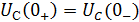
Закон изменения любого параметра в цепи первого
порядка в общем виде можно записать следующим образом:
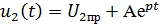
Где  -
принужденная составляющая выходного напряжения (определяется при t→∞),
В
-
принужденная составляющая выходного напряжения (определяется при t→∞),
В
А- постоянная интегрирования, В
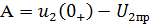
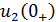 - выходное
напряжение в первый момент после коммутации ключа, р-корень характеристического
уравнения [
- выходное
напряжение в первый момент после коммутации ключа, р-корень характеристического
уравнения [ ]
]
Корень характеристического уравнения можно
найти, не составляя дифференциального уравнения. Достаточно найти сопротивление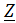 цепи, разорвав ее в любом месте, где протекает ток, и, заменив jω
на
р. Прировняв Z(p) к нулю и решив полученное уравнение относительно р, находят
корень характеристического уравнения.
цепи, разорвав ее в любом месте, где протекает ток, и, заменив jω
на
р. Прировняв Z(p) к нулю и решив полученное уравнение относительно р, находят
корень характеристического уравнения.
Для RL- цепи: 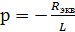
Первый случай(R* подключено):=12 B=1 мкФ=1 кОм=3
мс
В момент времени t=0- исходная схема принимает
вид(12):
Так как к схеме еще не подключен источник ЭДС,
токи в схеме отсутствуют, напряжение на элементах отсутствует, и выходное
напряжение тоже отсутствует.
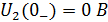
Начальное условие в цепи: Uc(0-)=Uc(0+)
Поскольку напряжение до коммутации на
конденсаторе отсутствовало, то в момент коммутации конденсатор ведет себя как
короткозамкнутый провод:
В этой схеме выходное напряжение соответствует напряжению
на резисторе R/2:
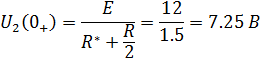
В установившемся режиме после коммутации (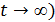 емкостной элемент ведет себя как холостой ход:
емкостной элемент ведет себя как холостой ход:
В таком случае выходное напряжение:
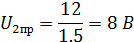
Определим корень характеристического уравнения
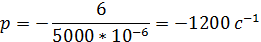
Закон изменения выходного напряжения:
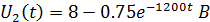
Второй случай(R* отключается):
В таком случае определим закон изменения
операторным методом. Переходный процесс возникает в следствии отключения
резистора R*(15).
Определим независимое начальное условие
(напряжение на конденсаторе до коммутации).
Такой случай уже был рассчитан в предыдущем
пункте, поэтому(16):
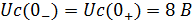
Изобразим операторную схему замещения с учетом
ННУ.
Найдем изображение выходного напряжения по ЗНК:
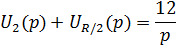
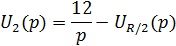
Найдем ток в ОСЗ:
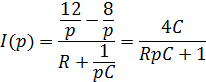
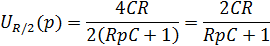
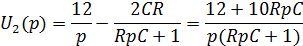
Найдем полюсы функции, приравняв знаменатель
функции выходного напряжения к нулю:
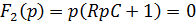
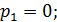
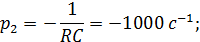
Найдем производную от знаменателя:
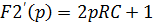
Затем подставим полученные полюсы в числитель
функции выходного напряжения и производную знаменателя:
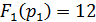
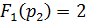
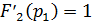
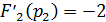
Тогда оригинал выходного напряжения согласно
теореме разложения имеет вид:
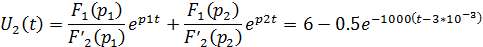
Итоговое выходное напряжение U2(t):
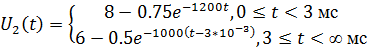
Вычислим постоянные времени 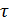 для
каждого случая:
для
каждого случая:
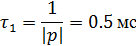
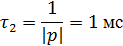
Таблица 3. Значения выходного напряжения
|
t, мс
|
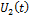 , B , B
|
t, мс
|
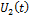 , B , B
|
|
0
|
0
|
7.25
|
3
|
3
|
5.5
|
|
0.5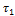
|
0.25
|
7.444
|
3+0.5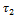
|
3.5
|
5.697
|
|
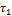
|
0.5
|
7.588
|
3+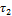
|
4
|
5.816
|
|
1.5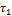
|
0.75
|
7.695
|
3+1.5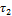
|
4.5
|
5.888
|
|
2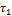
|
1
|
7.774
|
3+2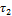
|
5
|
5.932
|
|
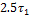
|
1.25
|
7.833
|
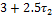
|
5.5
|
5.959
|
|
3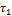
|
1.5
|
7.876
|
3+3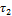
|
6
|
5.975
|
|
3.5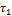
|
1.75
|
7.908
|
3+3.5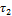
|
6.5
|
5.985
|
|
4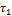
|
2
|
7.932
|
3+4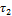
|
7
|
5.991
|
|
3
|
3
|
7.998
|
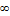
|
6
|
График выходного напряжения.
В этой части курсовой работы мной были
рассчитаны переходные процессы в электрической цепи первого порядка
классическим и операторным методами, был определен закон изменения выходного
напряжения U2(t). Был построен график выходного напряжения.
Часть 4. Определение реакции цепи на
произвольное внешнее воздействие
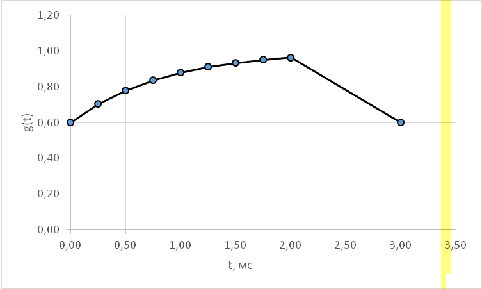
Определение переходной характеристики g(t)
Переходной характеристикой цепи называется
реакция цепи на на единичное ступенчатое воздействие 1(t):
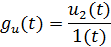
Параметры схемы(18):=12 B=1 мкФ=1 кОм
Параметры входного сигнала:и=6 мс=4 B
Для определения переходной характеристики цепи
рассмотрим процесс коммутации цепи (20) при подключении на нее единичного
источника напряжения.
В цепи в режиме до коммутации не было источников
энергии (21), по этому выходное напряжение отсутствует:
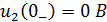
В момент коммутации при подключении единичного
источника ЭДС, согласно второму закону коммутации, емкостной элемент ведет себя
как короткозамкнутый провод (22). В таком случае выходное напряжение снимаем с
резистора 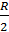 :
:
По закону Ома:
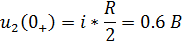
В установившемся режиме работы цепи после
коммутации (23) емкостной элемент ведет себя как холостой ход. В этом случае
выходное напряжение снимаем с холостого хода и резистора 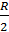 :
:
Эквивалентное сопротивление цепи:
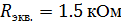
Ток в цепи:
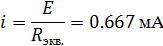
Поскольку напряжения на элементах в параллельных
ветвях схемы равны, то принужденная составляющая выходного напряжения имеет
вид:
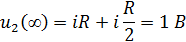
Коэффициент p был рассчитан в предыдущей
части(см. классический метод).
Таким образом, наша переходная характеристика
имеет вид:

Построим график переходной характеристики цепи:
|
t, мс
|

|
|
0
|
0
|
0.6
|
|
0.5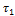
|
0.25
|
0.704
|
|
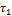
|
0.5
|
0.78
|
|
1.5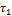
|
0.75
|
0.837
|
|
2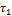
|
1
|
0.88
|
|
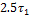
|
1.25
|
0.911
|
|
3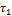
|
1.5
|
0.934
|
|
3.5
|
1.75
|
0.951
|
|
4
|
2
|
0.964
|
|
3
|
3
|
0.6
|
Определение импульсной характеристики цепи
Импульсной характеристикой цепи h(t) называется
реакция цепи на воздействие импульсной функции 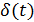 (функция
Дирака):
(функция
Дирака):
Если g(t) - непрерывная функция и имеет разрыв
при t=0 то импульсная характеристика цепи имеет вид:
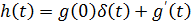
В нашем случае импульсная характеристика
принимает вид:

Определение КПФ
Комплексная передаточная функция цепи -
отношение комплексной амплитуды реакции цепи к комплексной амплитуде
воздействия:

Зная, что временные и частотные характеристики
цепи связаны между собой преобразованием Фурье, то в нашем случае для
нахождения КПФ будет рациональнее взять интеграл от импульсной функции:
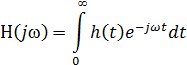
В таком случае наша КПФ примет вид:
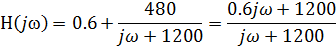
Амплитудно-частотной характеристикой цепи
называется модуль КПФ:
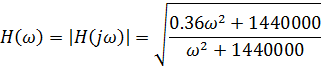
 Фазо-частотной
характеристикой называется арктангенс отношения мнимой части КПФ к
действительной:
Фазо-частотной
характеристикой называется арктангенс отношения мнимой части КПФ к
действительной:
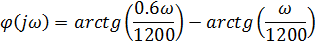
Расчет выходного напряжения(временной метод)
Зная переходную характеристику цепи, можно
вычислить реакцию цепи на воздействие любой формы, используя интеграл Дюамеля.
При расчете цепей с помощью интеграла Дюамеля
необходимо учитывать все скачки входного воздействия, а так же записывать
интеграл Дюамеля для всех временных промежутков с учетом предыдущего
воздействия.
На вход цепи подается сигнал, параметры которого
описаны выше.
Для того, чтобы определить выходной сигнал, для
начала аналитически запишем входной.
В общем виде наш входной сигнал можно разбить на
три временных промежутка, и тогда его аналитическая запись может быть
представлена в виде:
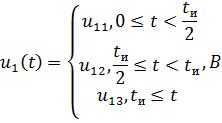
Наш входной сигнал имеет следующую аналитическую
запись:
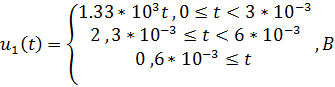
Найдем значения входного напряжения в моменты
времени 0,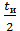 , tи:
, tи:
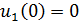
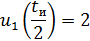
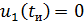
Найдем производные от составляющих входного
сигнала:
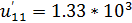
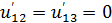
Запишем интеграл Дюамеля в первой форме для 3-х
временных промежутков:
-й временной промежуток (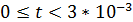 ):
):
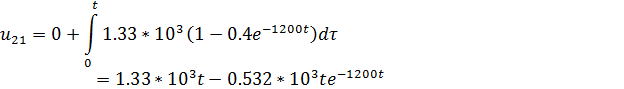
-й временной промежуток (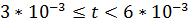 ):
):
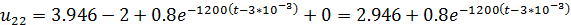
-й временной промежуток (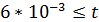 ):
):
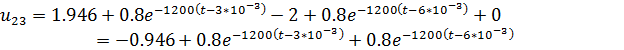
Запишем полученное аналитическое выражение
выходного сигнала
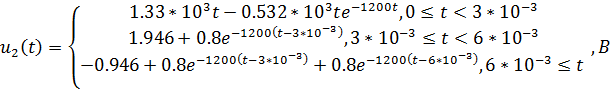
Построим график выходного напряжения:
|
t, мс
|
u2(t), B
|
|
0
|
0
|
|
0,2
|
0,182
|
|
0,4
|
0,4
|
|
0,6
|
0,643
|
|
0,8
|
0,901
|
|
1
|
1,17
|
|
1,2
|
1,445
|
|
1,4
|
1,723
|
|
1,6
|
2,003
|
|
1,8
|
2,284
|
|
2
|
2,563
|
|
2,2
|
2,842
|
|
2,4
|
3,12
|
|
2,6
|
3,397
|
|
2,8
|
3,672
|
|
3
|
3.946
|
|
3
|
2.746
|
|
3,2
|
2,575
|
|
3,4
|
2,441
|
|
3,6
|
2,335
|
|
3,8
|
2,252
|
|
4
|
2,187
|
|
4,2
|
2,136
|
|
4,4
|
2,095
|
|
4,6
|
2,063
|
|
4,8
|
2,038
|
|
5
|
2,019
|
|
5,2
|
2,003
|
|
5,4
|
1,991
|
|
5,6
|
1,981
|
|
5,8
|
1,974
|
|
6
|
-0,124
|
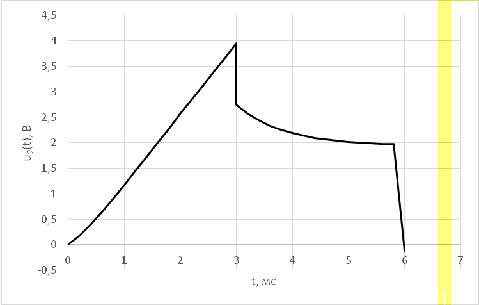
В этой части курсовой работы мной была
определены переходная и истинная характеристики цепи, комплексная передаточная
функция цепи, АЧХ и ФЧХ цепи. Мной на основе временного метода анализа
электрических цепей было рассчитано и записано аналитическое выражение
выходного сигнала, а так же был построен график выходного сигнала для времени
импульса.
Заключение
В ходе написания данной курсовой работы мной
были произведены расчеты параметров электрических цепей при воздействии
постоянного и переменного тока, были рассчитаны переходные процессы в цепи
первого порядка, определил реакцию цепи и сигнал на выходе после воздействия
сигнала произвольной формы.
Список литературы
цепь напряжение ток
Бакалов
В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. Радио и связь, 2000г.
Бакалов
В.П., Журавлева О.Б., Крук Б.И. Основы анализа цепей, Москва, Горячая линия -
Телеком, 2007г.
Курс
лекций по дисциплине «Теоретические основы электротехники». «СибГУТИ», 2014