Решение дифференциальных уравнений
Контрольная
работа №2
Вариант
4
Анастасия
Рафальская
.02.11
Задача 1
Найти общее решение дифференциальных уравнений
первого порядка с разделяющимися переменными.
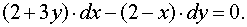
Решение. Перепишем
данное уравнение в виде
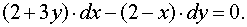
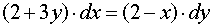
Разделяем переменные:
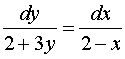
Теперь интегрируем обе части
полученного равенства:
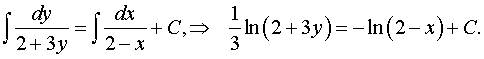
Это и есть искомое общее решение
уравнения.
Задача 2
Найти частное решение линейного
дифференциального уравнения первого порядка, удовлетворяющее указанному
начальному условию.
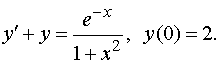
Решение. Перепишем
исходное уравнение в виде
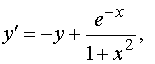
а искомую функцию 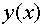 представим
в виде произведения двух других:
представим
в виде произведения двух других: 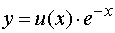 . Тогда
. Тогда
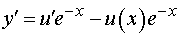
Или 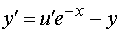
В этом случае исходное уравнение
сводится к виду
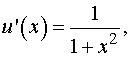
Интегрируя, получаем
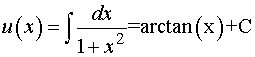
А решение исходного уравнения примет
вид:
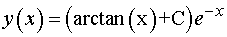 . (*)
. (*)
Выберем константу в (*) так, чтобы
выполнялось дополнительное условие 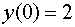 .
.
Следовательно, 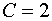 .
.
Таким образом, искомое частное
решение имеет вид:
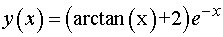
Задача 3
Вычислить определенный интеграл 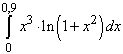 с точностью
до 0.001 путем предварительного разложения подынтегральной функции в ряд и
почленного интегрирования этого ряда.
с точностью
до 0.001 путем предварительного разложения подынтегральной функции в ряд и
почленного интегрирования этого ряда.
Решение. В разложении
функции 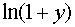 в степенной
ряд
в степенной
ряд
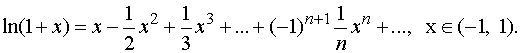
заменим x на 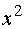 . Тогда
получим
. Тогда
получим
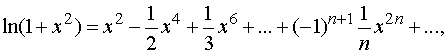
Умножая этот ряд почленно на 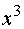 , будем
иметь
, будем
иметь
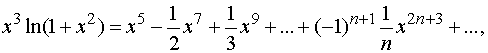
Следовательно,
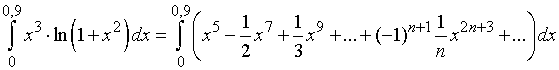
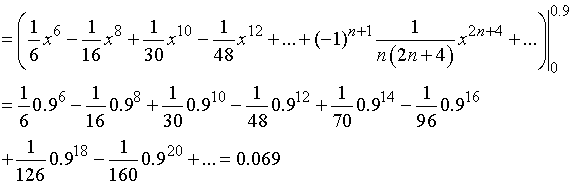
Полученный числовой
знакочередующийся ряд удовлетворяет условиям признака Лейбница. Восьмой член
этого ряда по абсолютной величине меньше 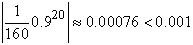 , поэтому для обеспечения требуемой
точности нужно просуммировать первые семь членов ряда и результат округлить до
0,001. Итак,
, поэтому для обеспечения требуемой
точности нужно просуммировать первые семь членов ряда и результат округлить до
0,001. Итак,
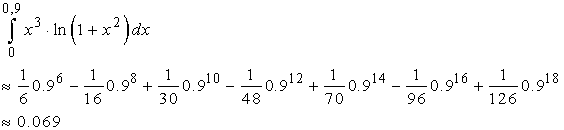
Задача 4
Студент знает ответы на 15 из 20 вопросов
программы. Какова вероятность того, что он знает ответы на все три вопроса,
предложенные экзаменатором.
Решение. Рассмотрим
события:
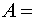 {студент знает ответ на первый
вопрос};
{студент знает ответ на первый
вопрос};
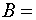 {студент знает ответ на второй
вопрос};
{студент знает ответ на второй
вопрос};
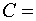 {студент знает ответ на третий
вопрос}.
{студент знает ответ на третий
вопрос}.
Тогда
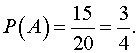
Вероятность того, что второй вопрос
окажется для студента известным, при условии, что он смог правильно ответить на
первый вопрос, т. е. условная вероятность события 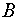 , равна
, равна
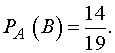
Вероятность того, что третьим будет
отобран знакомый вопрос, при условии, что уже отобраны два знакомых вопроса, т.
е. условная вероятность события 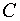 , равна
, равна
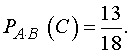
Искомая вероятность того, что все
три вопроса окажутся ответными, равна
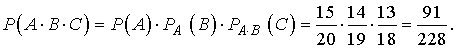
Задача 5
В группе из 18 студентов имеется 5 отличников.
Выбираются наудачу три студента. Какова вероятность того, что все они
отличники?
Решение. Рассмотрим
события:
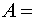 {первый студент является
отличником};
{первый студент является
отличником};
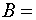 {второй студент является
отличником};
{второй студент является
отличником};
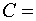 {третий студент является
отличником}.
{третий студент является
отличником}.
Тогда
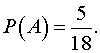
Вероятность того, что второй студент
окажется отличником, при условии, что первый студент оказался отличником, т. е.
условная вероятность события 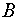 , равна
, равна
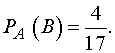
Вероятность того, что третьим будет
отобран отличник, при условии, что уже отобраны два отличника, т. е. условная
вероятность события 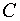 , равна
, равна
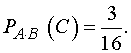
Искомая вероятность того, что все
три отобранных студента окажутся отличниками, равна
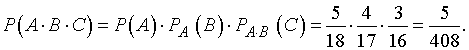
Задача 6
Дана вероятность 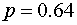 того, что
семя злака прорастет. Найти вероятность того, что
того, что
семя злака прорастет. Найти вероятность того, что
а) из 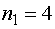 семян прорастет ровно
семян прорастет ровно 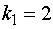 ;
;
б) из 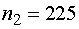 семян прорастет ровно
семян прорастет ровно 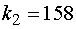 ;
;
в) из 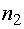 семян прорастет не менее
семян прорастет не менее 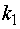 , но не
более
, но не
более 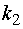 .
.
Решение.
А) Пусть событие 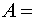 { из
{ из 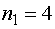 семян
прорастет ровно
семян
прорастет ровно 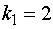 }; Вероятность
}; Вероятность
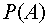 можно
определить по формуле Бернулли
можно
определить по формуле Бернулли
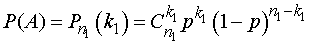
где 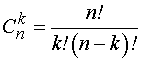 - число сочетаний из
- число сочетаний из  элементов
по
элементов
по 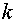 .
.
В нашем примере искомая вероятность
события A
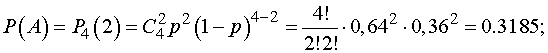
Б) Вычислить
искомую вероятность 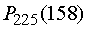 по формуле
Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим
приближенную формулу, выражающую локальную теорему Лапласа:
по формуле
Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим
приближенную формулу, выражающую локальную теорему Лапласа:
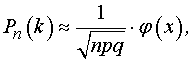
где 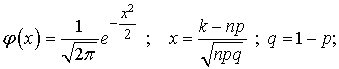 .
.
Из условия задачи
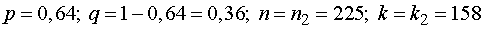 .
.
Тогда 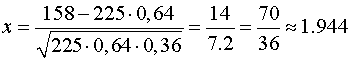 .
.
Далее находим 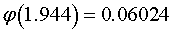 .
.
Искомая вероятность равна
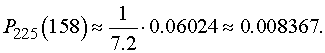
В) Вероятность 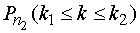 того, что
событие
того, что
событие 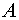 в таких
испытаниях наступит не менее
в таких
испытаниях наступит не менее 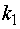 раз и не более
раз и не более 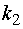 раз
определяется по интегральной теореме Лапласа следующей формулой:
раз
определяется по интегральной теореме Лапласа следующей формулой:
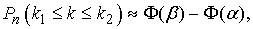
где 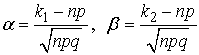 .
.
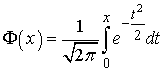
функция Лапласа.
По условию задачи 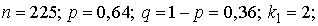
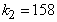 . Из
приведенных выше формул находим
. Из
приведенных выше формул находим 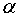 и
и 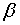 :
:
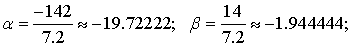
Тогда
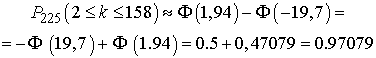
Задача 7
Задан закон распределения двух
независимых случайных величин 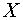 и
и 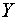 . Требуется найти математическое
ожидание и дисперсию случайной величины
. Требуется найти математическое
ожидание и дисперсию случайной величины 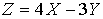 .
.
Решение. Найдем
сначала математические ожидания и дисперсии случайных величин 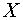 и
и 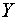 (для
вычисления дисперсий воспользуемся универсальной формулой):
(для
вычисления дисперсий воспользуемся универсальной формулой):
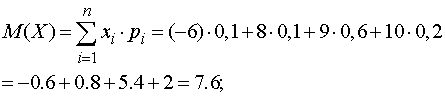
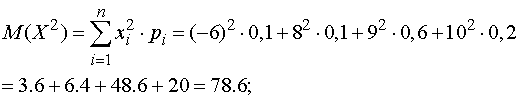
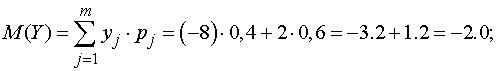
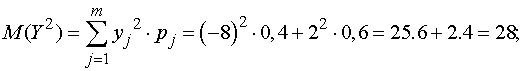
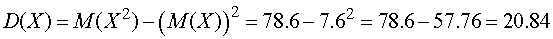
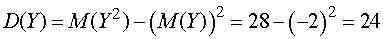
Теперь, воспользовавшись свойствами
математического ожидания и дисперсии, а также условием независимости случайных
величин 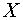 и
и 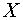 , получаем
математическое ожидание
, получаем
математическое ожидание
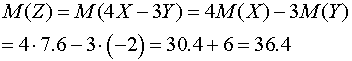
и дисперсию
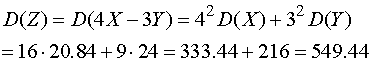
Задача 8
Непрерывная случайная величина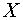 задана интегральной
функцией распределения
задана интегральной
функцией распределения
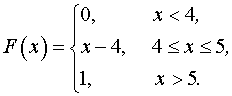 .
.
Найти:
) дифференциальную функцию
распределения (плотность вероятностей)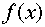 ;
;
) математическое ожидание 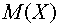 ;
;
) дисперсию 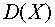 и с.к.о.
и с.к.о. 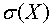 .
.
Построить графики 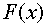 и
и 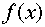 .
.
Решение.
) Дифференциальной функцией
распределения 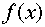 непрерывной
случайной величины
непрерывной
случайной величины 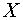 называется
производная от интегральной функции распределения
называется
производная от интегральной функции распределения 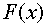 , то есть
, то есть 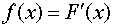 .
.
Искомая дифференциальная функция
имеет следующий вид:
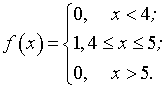
) Если непрерывная случайная
величина 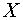 задана
плотностью вероятностей
задана
плотностью вероятностей 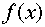 , то ее математическое ожидание
определяется формулой
, то ее математическое ожидание
определяется формулой
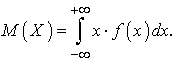
Так как в нашем случае функция 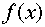 при
при 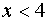 и при
и при 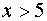 равна нулю,
то из последней формулы имеем
равна нулю,
то из последней формулы имеем
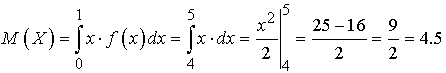
) Дисперсию 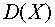 определим,
например, по формуле
определим,
например, по формуле
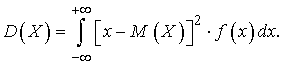
Тогда
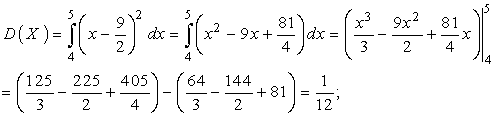
Отсюда имеем: 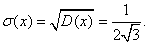
Строим графики 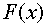
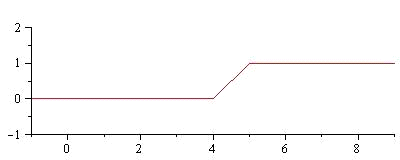
и 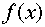
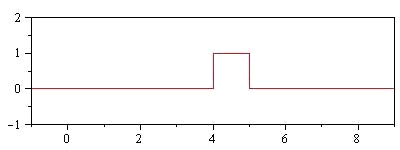
Задача 9
Контролируемый размер деталей,
выпускаемых цехом, распределен по нормальному закону. Стандартная величина
размера детали (математическое ожидание) равна 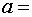 30 мм, среднее квадратичное
отклонение размера составляет
30 мм, среднее квадратичное
отклонение размера составляет 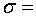 3 мм.
3 мм.
Требуется найти:
) вероятность того, что размер
наудачу взятой детали будет больше 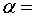 24 мм, но меньше
24 мм, но меньше 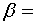 33 мм;
33 мм;
) вероятность того, что размер
детали отклонится от стандартной величины не более чем на 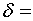 1,5 мм;
1,5 мм;
) диапазон изменения размера детали.
Решение.
1) Пусть 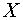 – длина
детали. Если случайная величина
– длина
детали. Если случайная величина 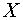 задана дифференциальной функцией
задана дифференциальной функцией 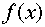 , то
вероятность того, что
, то
вероятность того, что 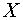 примет
значения, принадлежащие промежутку
примет
значения, принадлежащие промежутку 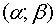 , определяется по формуле
, определяется по формуле
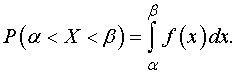
Если 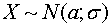 , то
, то
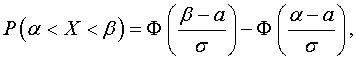
где 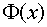 - функция
Лапласа,
- функция
Лапласа, 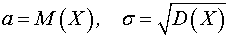 .
.
У нас 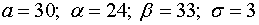 , то есть
, то есть
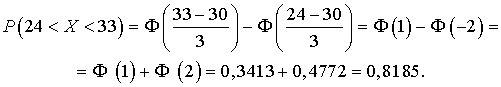
) Если 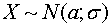 , то
, то
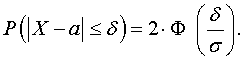
По условию задачи 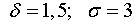 , поэтому из
последней формулы получаем
, поэтому из
последней формулы получаем
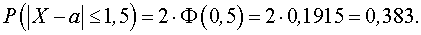
3) Для нахождения диапазона
изменения длины детали воспользуемся правилом "3s":
если 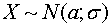 , то
, то 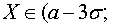
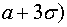 .
.
В рассматриваемом примере имеем
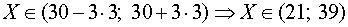 .
.
Задача 10
Признак 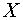 представлен
таблицей, которая является выборкой его значений, полученных в результате 100
независимых наблюдений. Требуется:
представлен
таблицей, которая является выборкой его значений, полученных в результате 100
независимых наблюдений. Требуется:
1. Составить интервальное выборочное
распределение.
. Построить гистограмму относительных частот.
. Перейти от составленного интервального к
точечному выборочному распределению, взяв при этом за значения признака
середины частичных интервалов.
. Построить полигон относительных частот.
5. Вычислить все точечные выборочные
оценки числовых характеристик признака: выборочное среднее 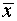 ; выборочную
дисперсию
; выборочную
дисперсию 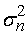 и
исправленную выборочную дисперсию
и
исправленную выборочную дисперсию 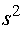 ; выборочное среднее квадратичное
отклонение
; выборочное среднее квадратичное
отклонение 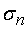 и
исправленное выборочное с.к.o.
и
исправленное выборочное с.к.o. 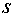 .
.
. Считая первый столбец таблицы
выборкой значений нормально распределенного признака 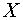 , построить
доверительные интервалы, покрывающие неизвестные математическое ожидание и
дисперсию этого признака с надежностью
, построить
доверительные интервалы, покрывающие неизвестные математическое ожидание и
дисперсию этого признака с надежностью 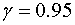 .
.
|
54.2
|
58.0
|
45.0
|
46.0
|
62.2
|
63.3
|
88.8
|
46.0
|
80.5
|
62.3
|
|
14.0
|
25.0
|
49.0
|
25.5
|
50.0
|
48.0
|
46.5
|
59.0
|
53.0
|
52.7
|
|
79.0
|
67.0
|
19.3
|
59.0
|
50.5
|
57.0
|
66.8
|
82.5
|
71.0
|
38.5
|
|
53.9
|
52.8
|
53.7
|
73.0
|
34.0
|
36.0
|
26.4
|
56.0
|
74.4
|
61.2
|
|
27.8
|
54.0
|
75.2
|
27.0
|
51.8
|
51.4
|
54.8
|
82.3
|
31.0
|
60.6
|
|
55.3
|
62.6
|
32.4
|
46.4
|
58.4
|
55.7
|
52.8
|
53.4
|
61.5
|
51.4
|
|
37.5
|
54.0
|
31.0
|
43.7
|
61.5
|
51.8
|
22.4
|
39.6
|
32.4
|
41.6
|
|
53.5
|
30.7
|
58.0
|
72.6
|
33.3
|
66.7
|
35.2
|
47.8
|
48.0
|
73.1
|
|
50.3
|
80.7
|
41.1
|
73.2
|
43.3
|
34.0
|
47.0
|
50.1
|
94.0
|
67.0
|
|
34.0
|
47.8
|
68.8
|
26.0
|
42.8
|
46.3
|
68.8
|
45.0
|
21.8
|
34.7
|
Решение.
1) Построим интервальное выборочное
распределение значений признака. Для этого сначала отметим, что у нас 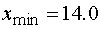 ,
, 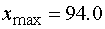 , поэтому
размах выборочных значений
, поэтому
размах выборочных значений
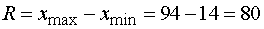 .
.
Теперь определим длину 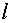 каждого
частичного интервала (их также называют классовыми интервалами),
воспользовавшись формулой Стерджеса
каждого
частичного интервала (их также называют классовыми интервалами),
воспользовавшись формулой Стерджеса
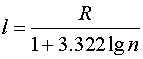 ,
,
где  – объем выборки. В рассматриваемом
примере
– объем выборки. В рассматриваемом
примере

Далее устанавливаем границы частичных
интервалов: левую границу первого интервала принимаем равной 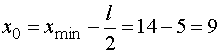 , далее
полагаем
, далее
полагаем 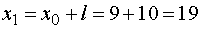 ,
, 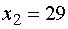 ,…,
,…, 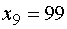 . На этом
указанная процедура заканчивается, т.к. последующие частичные интервалы не
будут содержать выборочных значений признака.
. На этом
указанная процедура заканчивается, т.к. последующие частичные интервалы не
будут содержать выборочных значений признака.
Приступаем к распределению по
частичным интервалам выборочных значений признака, ставя в соответствие
интервалу с номером 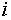 частоту
частоту 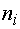 как число
выборочных значений признака, попавших в интервал. При этом договоримся, что
если некоторое из выборочных значений совпадет с границей двух соседних
интервалов, то будем относить его к предыдущему из них.
как число
выборочных значений признака, попавших в интервал. При этом договоримся, что
если некоторое из выборочных значений совпадет с границей двух соседних
интервалов, то будем относить его к предыдущему из них.
В итоге реализации данных
рекомендаций получим таблицу 2, в первых двух столбцах которой разместим
искомое интервальное распределение выборки, в третьем - относительные частоты 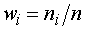 , а в
последнем четвертом - плотности
распределения относительных частот на частичных интервалах:
, а в
последнем четвертом - плотности
распределения относительных частот на частичных интервалах: 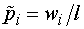 (величины
(величины 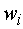 и
и 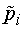 нам
потребуются в дальнейшем).
нам
потребуются в дальнейшем).
Таблица 1
|
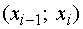 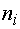 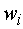 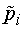
|
|
|
|
|
(9;
19)
|
1
|
0.01
|
0.001
|
|
(19;
29)
|
9
|
0.09
|
0.009
|
|
(29;
39)
|
14
|
0.14
|
0.014
|
|
(39;
49)
|
19
|
0.19
|
0.019
|
|
(49;
59)
|
29
|
0.29
|
0.029
|
|
(59;
69)
|
14
|
0.14
|
0.014
|
|
(69;
79)
|
8
|
0.08
|
0.008
|
|
(79;
89)
|
5
|
0.05
|
0.005
|
|
(89;
99)
|
1
|
0.01
|
0.001
|
|
 1001.00 1001.00
|
|
|
|
) Строим гистограмму относительных частот в
нашем примере, используя при этом первый и последний столбцы таблицы 1.
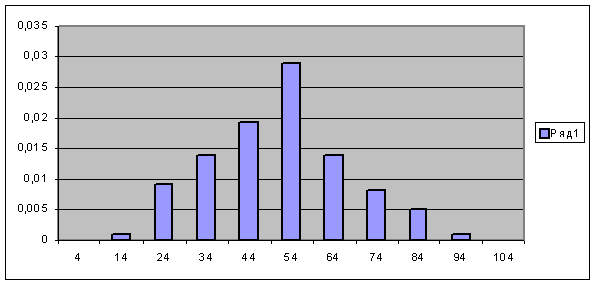
Гистограмма относительных частот
) Перейдем от интервального распределения
выборки к точечному (дискретному) распределению, взяв за новые выборочные
значения признака середины частичных интервалов. В рассматриваемом примере
такое распределение, очевидно, имеет вид следующей таблицы 2.
Таблица 2
|
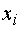 142434445464748494 142434445464748494
|
|
|
|
|
|
|
|
|
|
|
 1914192914851 1914192914851
|
|
|
|
|
|
|
|
|
|
4) По полученной таблице 2 может
быть построен полигон относительных частот, который является, как и гистограмма
относительных частот, статистической оценкой кривой распределения признака. Это
ломаная линия, вершины которой находятся в точках 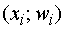 . В
рассматриваемом случае в соответствии с первой строкой таблицы 2 и третьим
столбцом таблицы 1 полигон относительных частот имеет следующий вид.
. В
рассматриваемом случае в соответствии с первой строкой таблицы 2 и третьим
столбцом таблицы 1 полигон относительных частот имеет следующий вид.
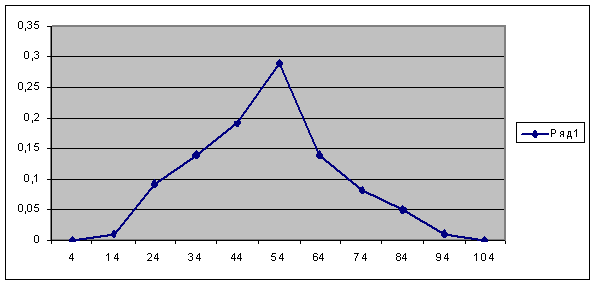
Полигон
относительных частот
5) Определим теперь основные
числовые характеристиками признака 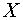 , такие как математическое ожидание,
дисперсия и среднее квадратичное отклонение (с.к.o.). Точечными выборочными
оценками этих параметров служат соответственно выборочное среднее
, такие как математическое ожидание,
дисперсия и среднее квадратичное отклонение (с.к.o.). Точечными выборочными
оценками этих параметров служат соответственно выборочное среднее 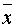 , выборочная
дисперсия
, выборочная
дисперсия 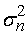 и
исправленная выборочная дисперсия
и
исправленная выборочная дисперсия 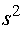 , выборочное с.к.o.
, выборочное с.к.o. 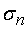 и
исправленное выборочное с.к.o.
и
исправленное выборочное с.к.o. 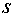 , которые вычисляются по формулам
, которые вычисляются по формулам
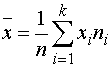 ;
;
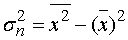 , где
, где 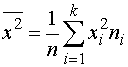 ;
;
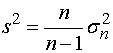 ;
;
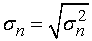 ;
; 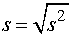 ,
,
где 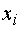 – выборочные значения признака
– выборочные значения признака 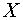 ,
, 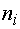 – частоты
этих значений,
– частоты
этих значений,  – объем
выборки.
– объем
выборки.
Воспользовавшись перечисленными
формулами, найдем точечные выборочные оценки генеральных параметров
распределения признака 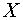 , используя
при этом данные из таблицы 3.
, используя
при этом данные из таблицы 3.
. 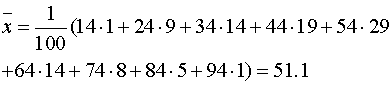
. Выборочная дисперсия:
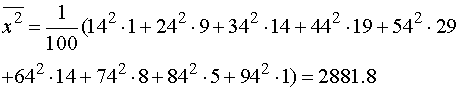
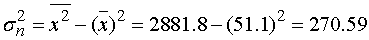
. 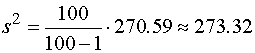
5. 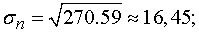
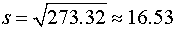 ;
;
) Для нормально распределенного
признака 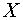 (первый
столбец исходной таблицы), представленного выборкой объема
(первый
столбец исходной таблицы), представленного выборкой объема  ,
доверительные интервалы, покрывающие с надежностью
,
доверительные интервалы, покрывающие с надежностью 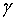 его
неизвестные математическое ожидание
его
неизвестные математическое ожидание 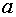 и дисперсию
и дисперсию 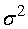 , имеют
соответственно вид
, имеют
соответственно вид
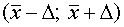 ,
, 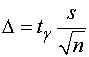 ; (1)
; (1)
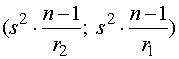 . (2)
. (2)
Величины 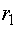 и
и 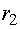 являются
критическими точками распределения
являются
критическими точками распределения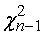 . Их находят в зависимости от числа
степеней свободы
. Их находят в зависимости от числа
степеней свободы 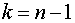 , а также
уровней значимости
, а также
уровней значимости 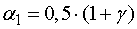 и
и 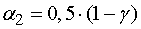 соответственно.
При заданных условиях имеем
соответственно.
При заданных условиях имеем
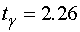 ;
;
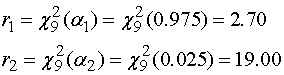
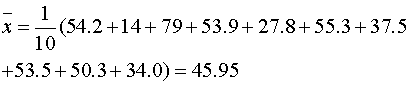
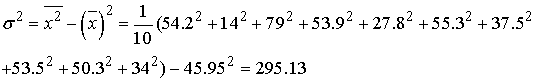
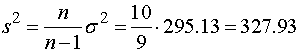
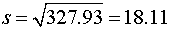
Погрешность математического ожидания
при заданной надежности
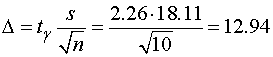
Таким образом, доверительный
интервал для математического ожидания при заданной надежности
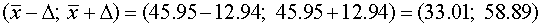
Доверительный интервал неизвестной
дисперсии 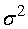 , имеют соответственно
вид
, имеют соответственно
вид
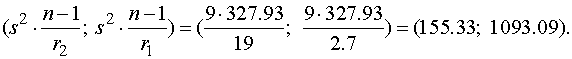
Задача 11
Даны таблицы с выборками пар
значений признаков 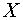 и
и 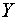 .
.
. Вычислить выборочный коэффициент
корреляции 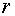 и сделать
выводы о тесноте и направлении линейной корреляционной зависимости между
признаками X и Y.
и сделать
выводы о тесноте и направлении линейной корреляционной зависимости между
признаками X и Y.
. При уровне значимости 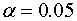 проверить
гипотезу о значимости коэффициента корреляции.
проверить
гипотезу о значимости коэффициента корреляции.
. Составить выборочное уравнение
прямой регрессии Y на X, построить полученную прямую в системе
координат вместе с исходными данными и дать оценку качества регрессии,
основываясь на визуальных соображениях.
. Вычислить коэффициент детерминации
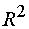 и оценить
качество регрессии.
и оценить
качество регрессии.
. При уровне значимости 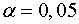 оценить
значимость регрессии с помощью критерия Фишера.
оценить
значимость регрессии с помощью критерия Фишера.
. При уровне значимости 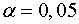 получить
доверительные интервалы для оценки генеральных параметров регрессии и сделать
выводы об их значимости, а также о значимости регрессии.
получить
доверительные интервалы для оценки генеральных параметров регрессии и сделать
выводы об их значимости, а также о значимости регрессии.
|
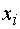 258431395 258431395
|
|
|
|
|
|
|
|
|
|
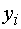 49126816166 49126816166
|
|
|
|
|
|
|
|
|
Решение.
1. Проводим вычисление выборочного коэффициента
корреляции:
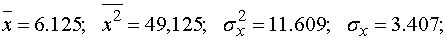
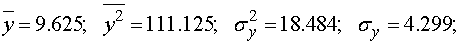
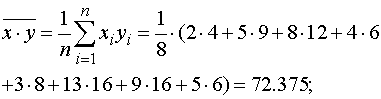
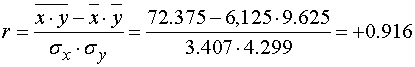
Таким образом, линейная
корреляционная зависимость сильная, прямая (положительная).
. Проверяем значимость коэффициента
корреляции.
Вычисляем ошибку репрезентативности:
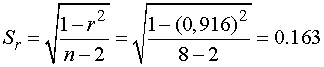 .
.
Находим 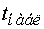 и
и 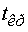 (по таблицам
приложения 6):
(по таблицам
приложения 6):
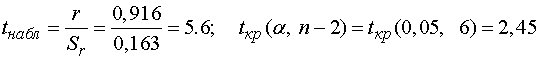 .
.
Так как 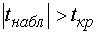 , то при
уровне значимости
, то при
уровне значимости 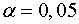 можно утверждать
достоверность коэффициента корреляции (значимость отличия от нуля), т.е.
линейная корреляционная зависимость между рассматриваемыми признаками
существует не только в выборочной, но и в генеральной совокупности.
можно утверждать
достоверность коэффициента корреляции (значимость отличия от нуля), т.е.
линейная корреляционная зависимость между рассматриваемыми признаками
существует не только в выборочной, но и в генеральной совокупности.
. Подставляем полученные результаты
в выборочное уравнение прямой регрессии
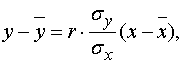
и получаем
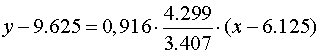
или после простых преобразований
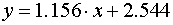 .
.
Построим и проанализировать график
прямой и исходных данных.
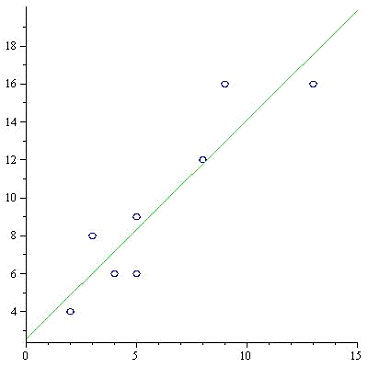
Прямая регрессии, построенная в
системе координат вместе с исходными данными в виде точек той же плоскости,
хорошо «притягивает» эти точки, что свидетельствует о достаточно сильной
корреляционной зависимости исходных данных.
. Находим модельные значения 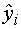 (
(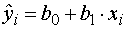 ) отклика Y,
присоединив их к таблице исходных данных:
) отклика Y,
присоединив их к таблице исходных данных:
|
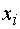 258431395 258431395
|
|
|
|
|
|
|
|
|
|
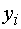 49126816166 49126816166
|
|
|
|
|
|
|
|
|
|
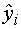 4,868,3211,797,176,0117,5712,958,32 4,868,3211,797,176,0117,5712,958,32
|
|
|
|
|
|
|
|
|
Теперь вычисляем
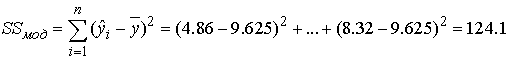
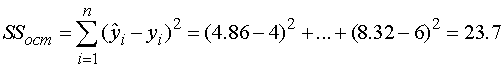 .
.
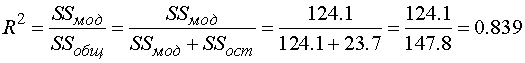 .
.
Полученное значение коэффициента
детерминации 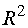 близко к 1,
поэтому полученное выборочное уравнение прямой регрессии хорошо (адекватно)
объясняет отклик Y.
близко к 1,
поэтому полученное выборочное уравнение прямой регрессии хорошо (адекватно)
объясняет отклик Y.
. Исследуем зависимость с помощью
критерия Фишера:
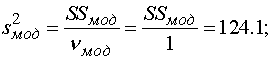
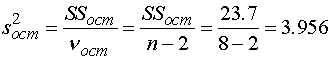 ;
;
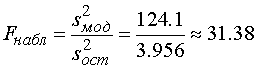 .
.
Находим по таблицам приложения 7
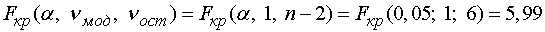 .
.
Так как 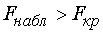 , гипотеза
, гипотеза 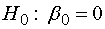 отвергается
и регрессия признается значимой с 95% уровнем надежности.
отвергается
и регрессия признается значимой с 95% уровнем надежности.
. Теперь построим доверительные
интервалы, покрывающие генеральные параметры регрессии и оценим значимость этих
параметров.
Вычисляем
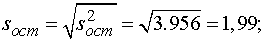
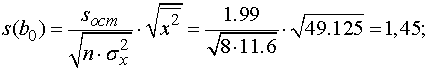
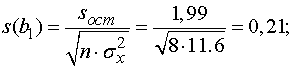
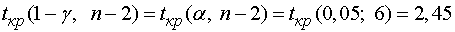 .
.
Подставляем полученные результаты в
формулы для интервалов
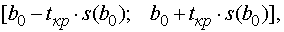
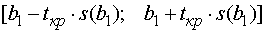 ,
,
В результате получаем доверительные
интервалы, покрывающие генеральные параметры 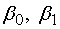 регрессии с надежностью
регрессии с надежностью 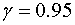
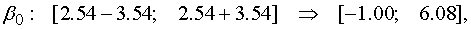
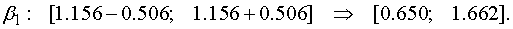
Тот факт, что доверительный интервал
для генерального коэффициента регрессии  не содержит нулевое значение, еще
раз подтверждает гипотезу о значимости регрессии.
не содержит нулевое значение, еще
раз подтверждает гипотезу о значимости регрессии.
Задача 12
На предприятии имеется сырье видов
I, II, III. Из него можно изготавливать изделия типов А и В.
Пусть запасы видов сырья на предприятии составляют 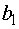 ,
, 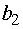 ,
, 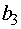 ед.
соответственно, изделие типа А дает прибыль
ед.
соответственно, изделие типа А дает прибыль 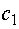 ден. ед., а
изделие типа В -
ден. ед., а
изделие типа В - 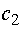 ден. ед.
Расход сырья на изготовление одного изделия задан в условных единицах таблицей.
ден. ед.
Расход сырья на изготовление одного изделия задан в условных единицах таблицей.
Составить план выпуска изделий, при
котором предприятие имеет наибольшую прибыль. Решить задачу графически и
симплексным методом.
|
Изделие
|
Сырье
|
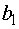 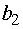 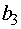 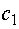 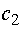
|
|
|
|
|
|
I
|
II
|
III
|
40
|
34
|
46
|
1
|
2
|
|
А
|
2
|
1
|
3
|
|
|
|
|
|
|
В
|
2
|
2
|
1
|
|
|
|
|
|
Решение.
1. Составим математическую модель
задачи. Обозначим: 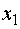 -
количество выпускаемых изделий типа
-
количество выпускаемых изделий типа 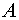 ,
, 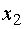 -
количество выпускаемых изделий типа
-
количество выпускаемых изделий типа 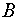 . Тогда с учетом расходов сырья на изготовление
изделия каждого типа получим следующие ограничения на
. Тогда с учетом расходов сырья на изготовление
изделия каждого типа получим следующие ограничения на 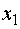 и
и 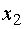 ,
учитывающие запасы сырья каждого вида:
,
учитывающие запасы сырья каждого вида:
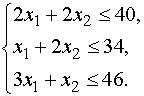 (1)
(1)
По смыслу задачи
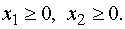 (2)
(2)
Прибыль 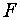 предприятия
при плане
предприятия
при плане 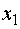 ,
, 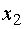 равна
равна
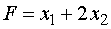 . (3)
. (3)
Итак, математическая модель задачи
получена: необходимо найти значения 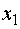 ,
, 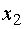 , удовлетворяющие неравенствам (1),
(2), для которых функция (3) достигает max. Полученная задача - стандартная
задача линейного программирования.
, удовлетворяющие неравенствам (1),
(2), для которых функция (3) достигает max. Полученная задача - стандартная
задача линейного программирования.
. Решим полученную задачу
графически. Для этого введем систему координат 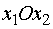 и изобразим в ней множество решений
систем неравенств (1), (2) (область допустимых решений - ОДР) в виде множества
точек плоскости.
и изобразим в ней множество решений
систем неравенств (1), (2) (область допустимых решений - ОДР) в виде множества
точек плоскости.
Условию (2) удовлетворяют точки
первой четверти. Для получения полуплоскостей, соответствующих неравенствам
системы (1), построим их границы, т.е. прямые линии:
|
Имя
прямой
|
Уравнение
Прямой
|
Таблица
для построения прямой
|
(а) 
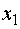
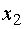
(б) 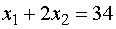
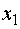
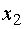
(в) 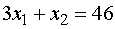
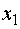
,333
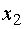
Пересечение построенных полуплоскостей с первой
четвертью - искомая ОДР (многоугольник OABCD).
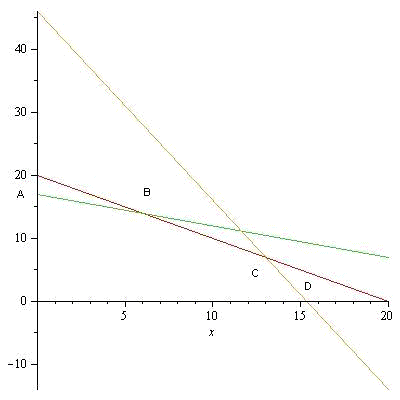
Ищем координаты вершин ОДР и значения
целевой функции F в этих вершинах:
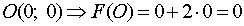 ;
;
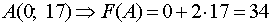 ;
;
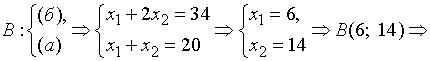
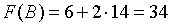 ;
;
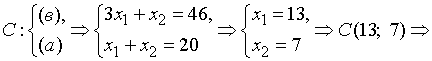
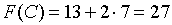 ;
;
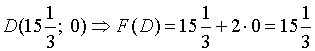 .
.
Отсюда
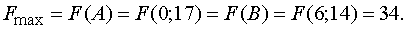
Вывод: предприятию выгодно выпустить
17 изделий типа B (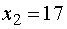 ) и не
выпускать изделия типа A (
) и не
выпускать изделия типа A (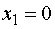 ). При этом
его прибыль будет наибольшая и составит 34 ден. ед. Такая же прибыль будет
получена при выпуске 6 изделий типа A и 14 изделий типа B. Такая же прибыль
получается при любых реализациях
). При этом
его прибыль будет наибольшая и составит 34 ден. ед. Такая же прибыль будет
получена при выпуске 6 изделий типа A и 14 изделий типа B. Такая же прибыль
получается при любых реализациях 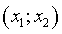 , расположенных на отрезке AB:
, расположенных на отрезке AB:
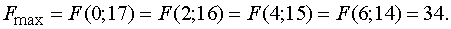
. Решим задачу симплексным методом.
Для этого приведем стандартную задачу к каноническому виду, добавив в левые
части неравенств (1) дополнительные неотрицательные переменные 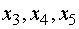 , равные
разностям правых и левых частей этих неравенств и представляющие собой остатки
сырья каждого вида после реализации намеченного плана выпуска изделий. Получим
задачу:
, равные
разностям правых и левых частей этих неравенств и представляющие собой остатки
сырья каждого вида после реализации намеченного плана выпуска изделий. Получим
задачу:
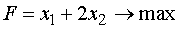 ; (4)
; (4)
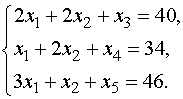 (5)
(5)
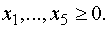 (6)
(6)
Выбираем в качестве базисных
добавленные переменные 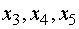 . Тогда
оставшиеся переменные
. Тогда
оставшиеся переменные 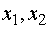 будут свободными.
Положим
будут свободными.
Положим 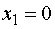 и
и 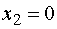 . Тогда
. Тогда 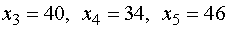 , т.е.
получаем первое базисное решение
, т.е.
получаем первое базисное решение 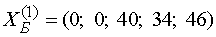 . При этом
. При этом 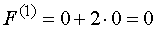 .
.
АНАЛИЗ 1. Структура
целевой функции 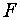 из условия
(4) позволяет утверждать, что ее значения могут быть увеличены за счет
увеличения значений как свободной переменной
из условия
(4) позволяет утверждать, что ее значения могут быть увеличены за счет
увеличения значений как свободной переменной 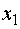 , так и свободной переменной
, так и свободной переменной 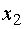 (коэффициенты
при этих переменных в
(коэффициенты
при этих переменных в 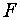 положительные).
Отсюда следует, что найденное базисное решение
положительные).
Отсюда следует, что найденное базисное решение 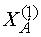 оптимальным не является.
оптимальным не является.
Назначим другой набор базисных
переменных, который обеспечит увеличение значений целевой функции. С этой целью
будем увеличивать значения свободной переменной 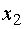 , оставляя
, оставляя 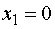 , и
определим из системы (5), какая из базисных переменных
, и
определим из системы (5), какая из базисных переменных 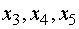 первой
станет отрицательной (чего нельзя допустить!), и назовем ее проблемной.
первой
станет отрицательной (чего нельзя допустить!), и назовем ее проблемной.
Переписав систему (5) в более
удобном для анализа виде
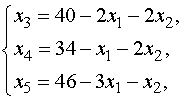
заключаем, что проблемной является
базисная переменная 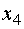 из второго
равенства системы. Выводим ее из состава базисных и обмениваем ее на свободную
переменную
из второго
равенства системы. Выводим ее из состава базисных и обмениваем ее на свободную
переменную 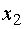 :
: 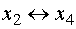 . В
результате новыми базисными переменными стали
. В
результате новыми базисными переменными стали 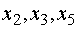 , а новыми свободными −
, а новыми свободными − 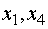 . Выражаем в
системе (5) новые базисные переменные через новые свободные, начиная с ее
проблемного второго равенства. Через эти же свободные переменные выражаем
целевую функцию
. Выражаем в
системе (5) новые базисные переменные через новые свободные, начиная с ее
проблемного второго равенства. Через эти же свободные переменные выражаем
целевую функцию 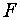 из условия
(4):
из условия
(4):
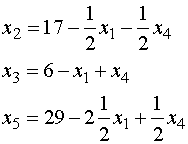
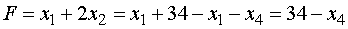
В результате математическая модель
решаемой задачи принимает следующий вид:
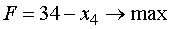 ; (4')
; (4')
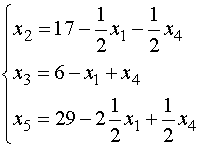 (5')
(5')
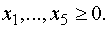 (6)
(6)
Полагаем свободные переменные 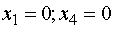 . Тогда
базисные переменные согласно системе (5') принимают значения
. Тогда
базисные переменные согласно системе (5') принимают значения 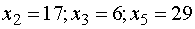 , т.е.
получаем второе базисное решение
, т.е.
получаем второе базисное решение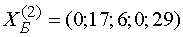 . При этом из (4')
. При этом из (4') 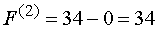 .
.
АНАЛИЗ 2. Структура
целевой функции 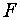 из условия
(4') позволяет утверждать, что ее значения не могут быть увеличены за счет
увеличения значений как свободной переменной
из условия
(4') позволяет утверждать, что ее значения не могут быть увеличены за счет
увеличения значений как свободной переменной 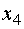 , так и свободной переменной
, так и свободной переменной 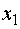 (коэффициенты
при этих переменных в
(коэффициенты
при этих переменных в 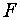 не
положительные). Отсюда следует, что найденное базисное решение
не
положительные). Отсюда следует, что найденное базисное решение 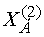 является
оптимальным:
является
оптимальным: 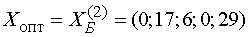 . При этом
. При этом 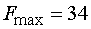 .
.
Поскольку F не зависит от свободной
переменной 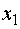 , то ее
увеличение не влияет на размер прибыли, так что найденное решение не является
единственным.
, то ее
увеличение не влияет на размер прибыли, так что найденное решение не является
единственным.
Ответ. Для
получения максимальной прибыли в количестве 34 ден. ед. предприятие должно
выпустить 17 изделий типа B и не выпускать изделия типа A, либо выпустить 2, 4
или 6 изделий типа А и 16, 15 или 14 изделий типа B соответственно. При этом
соответствующие остатки сырья приведены в следующей таблице:
|
Выпущено
изделий
|
Остатки
сырья
|
|
A
|
B
|
I
|
II
|
III
|
|
0
|
17
|
6
|
0
|
29
|
|
2
|
16
|
4
|
0
|
24
|
|
4
|
15
|
2
|
0
|
19
|
|
6
|
14
|
0
|
0
|
14
|
Задача 13
уравнение интеграл вероятность
дисперсия
Методом потенциалов решить следующую
транспортную задачу.
На трех базах 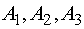 имеется
однородный груз в количествах
имеется
однородный груз в количествах 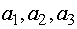 условных единиц соответственно.
Этот груз требуется перевезти в четыре пункта потребления
условных единиц соответственно.
Этот груз требуется перевезти в четыре пункта потребления 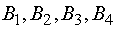 в
количествах
в
количествах 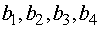 условных
единиц соответственно. Стоимости перевозок единицы груза от поставщиков
потребителям указаны в матрице стоимостей С.
условных
единиц соответственно. Стоимости перевозок единицы груза от поставщиков
потребителям указаны в матрице стоимостей С.
Спланировать перевозки так, чтобы их
общая стоимость была минимальной.
|
244.
|
а1
= 90, а2 = 40, а3 = 70; b1 = 85, b2 = 37, b3 = 40, b4 = 38.
|
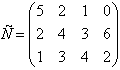
|
Решение. Эта задача
является закрытой транспортной задачей, так как 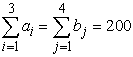 . Для ее решения воспользуемся
таблицей, в которой будем составлять последовательно планы перевозок.
. Для ее решения воспользуемся
таблицей, в которой будем составлять последовательно планы перевозок.
Составим первый план перевозок. В
этом плане отличными от нуля перевозками 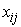 могут быть лишь
могут быть лишь 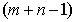 значений
(базисные переменные), где m -
число поставщиков, n -
число потребителей. Остальные значения заведомо равны нулю
(свободные переменные). Будем их в таблице помечать прочерком.
значений
(базисные переменные), где m -
число поставщиков, n -
число потребителей. Остальные значения заведомо равны нулю
(свободные переменные). Будем их в таблице помечать прочерком.
Для составления плана последовательно
заполняют клетки таблицы так, чтобы на каждом шаге исчерпывалась или
потребность какого-либо потребителя, или возможность какого-либо поставщика. В
соответствующем столбце или строке ставят в остальных пустых клетках прочерки. Если
при этом одновременно исчерпывается и потребность и возможность, то
вычеркивается что-то одно (столбец или строка). При таком построении плана
перевозок заполненными окажутся ровно 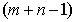 клетки, а остальные прочеркнутся.
клетки, а остальные прочеркнутся.
При построении первого плана
(таблица 2) начнем с клетки с наименьшими затратами 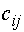 и на каждом
шаге будем выбирать такого типа клетку (метод наименьших затрат). Значения
и на каждом
шаге будем выбирать такого типа клетку (метод наименьших затрат). Значения 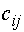 будем
записывать в левом верхнем углу клетки. В ее центре будем проставлять значения
будем
записывать в левом верхнем углу клетки. В ее центре будем проставлять значения 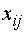 .
.
Заполняем клетку (14), так как 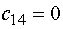 - наименьшее, значением
- наименьшее, значением 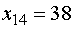 . При этом
вычеркивается четвертый столбец.
. При этом
вычеркивается четвертый столбец.
На втором шаге заполняем клетку
(31), т.к. 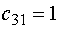 - наименьшее, значением
- наименьшее, значением 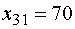 . При этом
вычеркивается третья строка.
. При этом
вычеркивается третья строка.
В оставшихся клетках наименьшее 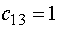 , поэтому
заполняем клетку (13) значением
, поэтому
заполняем клетку (13) значением 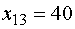 . При этом вычеркивается третий
столбец.
. При этом вычеркивается третий
столбец.
На четвертом шаге заполняем клетку
(21), т.к. 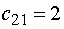 - наименьшее, значением
- наименьшее, значением 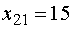 . При этом
вычеркивается первый столбец.
. При этом
вычеркивается первый столбец.
На следующем шаге заполняем клетку
(12), т.к. 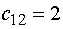 - наименьшее, значением
- наименьшее, значением 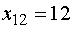 . При этом
вычеркивается первая строка.
. При этом
вычеркивается первая строка.
Оставшуюся клетку (22) с 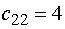 , заполняем
оставшимся значением
, заполняем
оставшимся значением 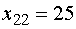 . При этом
таблица становится полностью заполненной.
. При этом
таблица становится полностью заполненной.
Число заполненных клеток при этом
составляет 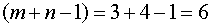 . Стоимость
перевозок F при данном
плане=2·12+1·40+0·38+2·15+4·25+1·70=24+40+30+100+70=264 (ден. ед.)
. Стоимость
перевозок F при данном
плане=2·12+1·40+0·38+2·15+4·25+1·70=24+40+30+100+70=264 (ден. ед.)
Для проверки оптимальности
полученного плана воспользуемся методом потенциалов. Введём строку потенциалов 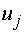 и столбец
потенциалов
и столбец
потенциалов 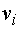 . Полагаем
. Полагаем 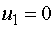 , а
остальные
, а
остальные 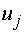 и
и 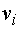 найдём так,
чтобы для заполненных клеток выполнялись равенства
найдём так,
чтобы для заполненных клеток выполнялись равенства
 .
.
Вычисляем оценки прочеркнутых клеток
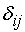 по формулам
по формулам
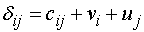 .
.
Таблица 3
|
 85374038 85374038
|
|
|
|
|
|
|
90
|
5
|
5
|
2
|
0
|
1
|
0
|
0
|
0
|
0
|
|
-
|
12
|
40
|
38
|
|
|
40
|
2
|
0
|
4
|
0
|
3
|
0
|
6
|
4
|
-
2
|
|
15
|
25
|
-
|
-
|
|
|
70
|
1
|
0
|
3
|
0
|
4
|
2
|
2
|
1
|
-
1
|
|
70
|
-
|
-
|
-
|
|
|
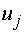 0-2-10 0-2-10
|
|
|
|
|
|
Оценки клеток будем записывать в
правых верхних углах клеток. Для оптимального плана должно выполняться условие 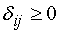 для всех
клеток.
для всех
клеток.
Таким образом, построенный нами план
перевозок является оптимальным.
По этому плану поставщик 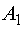 перевозит
12 ед. потребителю
перевозит
12 ед. потребителю 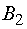 , 40 ед.
потребителю
, 40 ед.
потребителю 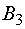 , 38 ед.
потребителю
, 38 ед.
потребителю 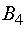 ; поставщик
; поставщик 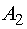 - 15 ед. потребителю
- 15 ед. потребителю 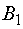 , 25 ед.
потребителю
, 25 ед.
потребителю 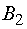 ; поставщик А3
- 70 ед.
потребителю
; поставщик А3
- 70 ед.
потребителю 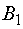 .
.
Так как среди оценок 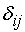 в
прочеркнутых клетках есть нули, это говорит о том, что оптимальный план не
единственный.
в
прочеркнутых клетках есть нули, это говорит о том, что оптимальный план не
единственный.
Задача 14
Двум предприятиям выделено 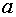 единиц
средств на 4 года. Как распределить эти средства между ними для получения
максимального дохода, если в первый год средства распределяются между
предприятиями в полном объеме, во второй год распределяется неосвоенная за
первый год часть средств (остаток) и т.д., а также известно, что
единиц
средств на 4 года. Как распределить эти средства между ними для получения
максимального дохода, если в первый год средства распределяются между
предприятиями в полном объеме, во второй год распределяется неосвоенная за
первый год часть средств (остаток) и т.д., а также известно, что
доход от 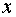 единиц
средств, вложенных на год в первое предприятие, равен
единиц
средств, вложенных на год в первое предприятие, равен 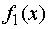 ;
;
доход от 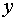 единиц
средств, вложенных на год во второе предприятие, равен
единиц
средств, вложенных на год во второе предприятие, равен 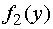 ;
;
остаток средств к концу года на
первом предприятии составляет 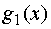 ;
;
остаток средств к концу года на
втором предприятии составляет 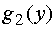 .
.
|
Номер
задачи
|
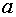 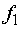 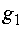 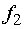 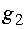
|
|
|
|
|
|
13.
|
1000
|
3x
|
0,1x
|
2y
|
0,5y
|
Решение.
Решим эту задачу методом динамического программирования.
Пусть в начале года (произвольного)
мы должны распределить 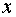 единиц
средств. Обозначим через
единиц
средств. Обозначим через 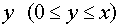 средства,
выделяемые второму предприятию. Тогда первое получит
средства,
выделяемые второму предприятию. Тогда первое получит 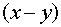 ед.
средств. Обозначим суммарный доход за этот год при таком распределении через
ед.
средств. Обозначим суммарный доход за этот год при таком распределении через 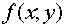 . Очевидно,
. Очевидно,
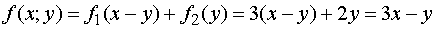 .
.
Остаток средств через год обозначим
через 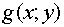 . Очевидно,
. Очевидно,
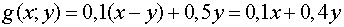 .
.
Здесь состояние системы в начале
года определяется имеющимися средствами, т.е. числом 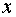 , а
управление - способом
распределения средств, т.е. числом
, а
управление - способом
распределения средств, т.е. числом 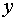 . Для состояния
. Для состояния 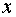 при
управлении
при
управлении 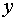 система к
концу года перейдет в состояние, определяемое остатком средств, т.е. значением
система к
концу года перейдет в состояние, определяемое остатком средств, т.е. значением 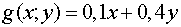 .
.
Обозначим характеристику состояния 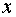 в начале
года
в начале
года 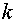 через
через 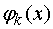 , а условное
оптимальное управление для этого состояния через
, а условное
оптимальное управление для этого состояния через 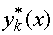 . Тогда для
. Тогда для 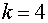
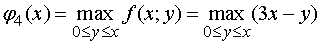 .
.
Так как функция 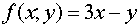 убывает по
переменной
убывает по
переменной 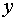 на отрезке
на отрезке 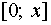 , то ее
наибольшее значение достигается при
, то ее
наибольшее значение достигается при 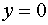 , т.е.
, т.е.
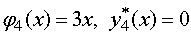 ,
,
где 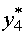 -
условное оптимальное управление на четвертом этапе.
-
условное оптимальное управление на четвертом этапе.
Для 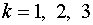 справедливо рекуррентное
соотношение
справедливо рекуррентное
соотношение
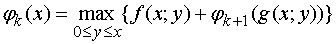 ,
,
поэтому для 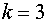 имеем
имеем
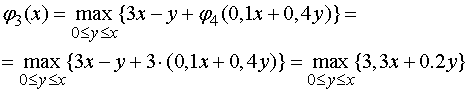 .
.
Функция 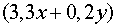 возрастает
по
возрастает
по 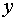 на отрезке
на отрезке 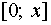 , поэтому
, поэтому
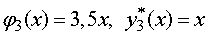 .
.
Для 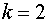
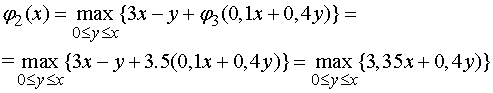
Функция 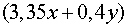 возрастает
по
возрастает
по 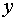 поэтому ее
максимальное значение на отрезке
поэтому ее
максимальное значение на отрезке 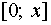 достигается при
достигается при 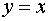 , т.е.
, т.е.
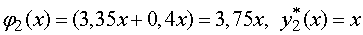 .
.
Для 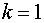
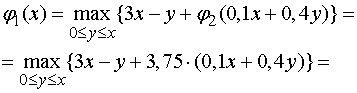
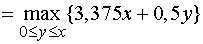 .
.
Функция 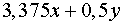 возрастает
по
возрастает
по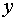 , поэтому
, поэтому
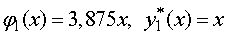 .
.
Теперь вычисляем
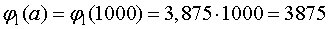 (ед.).
(ед.).
Получили наибольший суммарный доход,
который может быть получен при заданных условиях за 4 года. При этом средства
следует распределять следующим образом: в первые три года все отдавать второму
предприятию 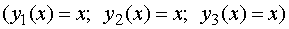 , а в
последний год - первому
предприятию
, а в
последний год - первому
предприятию 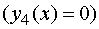 .
.