Виды нелинейных дифференциальных уравнений 1-го порядка
ПГУ им. Т.Г.
Шевченко
Курсовая
работа
Виды
нелинейных дифференциальных уравнений 1-го порядка
Выполнил:
студент
211 группы
специальности
«ИКТиСС»
Бирт
Игорь Андреевич
Тирасполь
2014 год
ВВЕДЕНИЕ
Дифференциальное уравнение - уравнение,
связывающее значение некоторой неизвестной функции в некоторой точке и значение
её производных различных порядков в той же точке. Дифференциальное уравнение
содержит в своей записи неизвестную функцию, её производные и независимые
переменные; однако не любое уравнение, содержащее производные неизвестной
функции, является дифференциальным уравнением.
Порядок дифференциального уравнения - наибольший
порядок производных, входящих в него.
Процесс решения дифференциального уравнения
называется интегрированием.
Все дифференциальные уравнения можно разделить
на линейные и не линейные.
Нелинейное дифференциальное уравнение -
дифференциальное уравнение (обыкновенное или с частными производными), в
которое по крайней мере одна из производных неизвестной функции (включая и
производную нулевого порядка - саму неизвестную функцию) входит нелинейно.
Иногда под Н.Д.У. понимается наиболее общее
уравнение определенного вида. Напр., нелинейнымобыкновенным дифференциальным
уравнением 1-го порядка наз. уравнение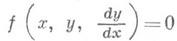 
с
произвольной функцией 
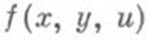при этом линейное
обыкновенное дифференциальное уравнение 1-го порядка соответствует частному
случаю
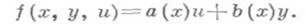
Н. д. у. с частными
производными 1-го порядка для неизвестной функции z
от независимых переменных 
имеет вид:
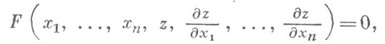
где F- произвольная функция
своих аргументов;
Виды нелинейных
дифференциальных уравнений 1-го порядка
Уравнения с разделенными переменными
П1.
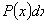
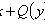
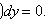
Общий интеграл
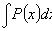
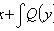
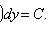
П2.
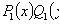
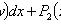
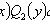
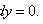
Общий интеграл
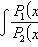
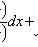
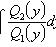
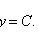
Уравнение в полных дифференциалах
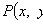
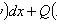
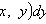
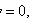
Где
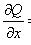
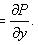
Существует такая функция u(x,
y), что
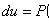
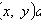
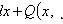
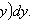
Общий интеграл уравнения в полных дифференциалах
u(x, y) = C.
Функция u может быть
представлена в виде
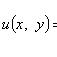
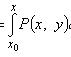
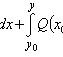
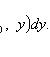
Однородное уравнение
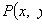
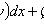
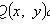
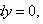
где P(x, y), Q(x, y) -
однородные функции одной и той же степени
.
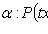
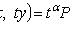
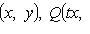
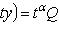
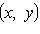Подстановка y = ux, dy = xdu +
udx переводит однородное уравнение в линейное относительно функции u:
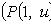
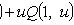
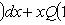
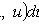
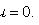
Уравнение вида
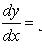
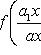
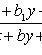
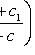
. Если прямые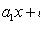 
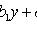
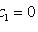и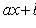 
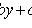
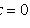пересекаются в
точке (x0; y0), то замена 
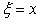
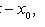
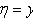
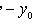приводит его к
однородному уравнению
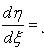
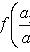
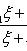
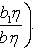
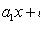
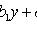
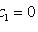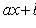
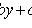
. Если прямые и 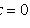параллельны, то
замена 
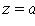
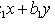приводит к
уравнению с разделяющимися переменными
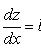
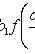
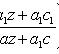
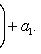
Уравнение Бернулли
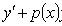
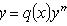
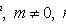
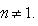
Подстановкой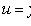 
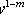сводится к
линейному
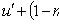
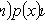
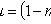
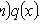
Уравнение Риккати
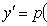
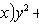
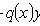
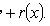
Если известно какое-либо из
решений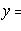 
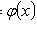, то уравнение
сводится к
линейному подстановкой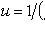 
.
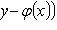Уравнение Лагранжа
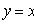
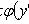
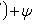
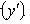
Дифференцируя по x и полагая y'
= p, приходим к линейному уравнению относительно x как функции p:
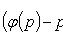
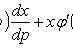
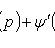
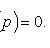
Уравнение Клеро
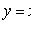
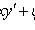
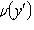- частный случай
уравнения Лагранжа.
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Уравнения Риккати
Решить дифференциальное уравнение
' = y + y2 + 1.
Решение.
Данное уравнение является простейшим уравнением
Риккати с постоянными коэффициентами. Переменные x, y здесь легко разделяются,
так что общее решение уравнения определяется в следующем виде:
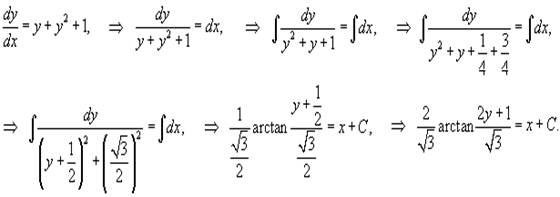
Решить уравнение Риккати
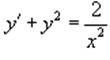
Решение
Будем искать частное решение в форме:
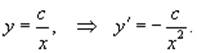
Подставляя это в уравнение, находим:
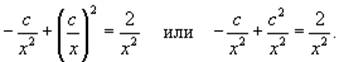
Получаем квадратное уравнение для c:
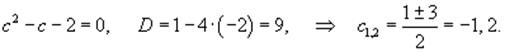
Мы можем выбрать любое значение c. Например,
пусть c = 2. Теперь, когда частное решение известно, сделаем замену:
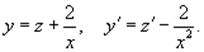
Снова подставим это в исходное уравнение
Риккати:
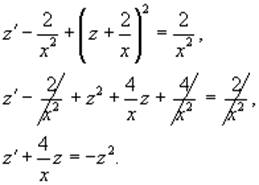
Как видно, мы получили уравнение Бернулли с
параметром m = 2. Сделаем еще одну замену:
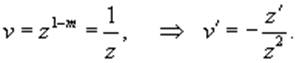
Разделим уравнение Бернулли на z2 (полагая, что
z ≠ 0) и запишем его через переменную v:
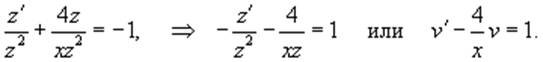
Последнее уравнение является линейным и легко
решается с помощью интегрирующего множителя:
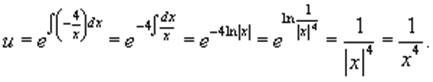
Общее решение линейного уравнения определяется
функцией
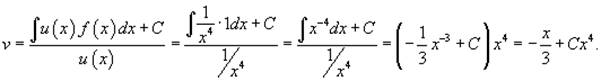
Теперь мы будем последовательно возвращаться к
предыдущим переменным. Так как z = 1/v, то общее решение для z записывается
следующим образом:
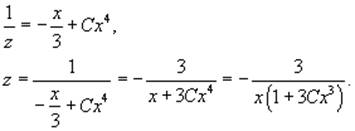
Следовательно,
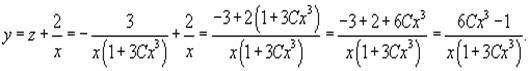
Можно переименовать константу: 3C = C1 и
записать ответ в виде
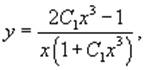
где C1 − произвольное действительное
число.
Уравнения Бернули
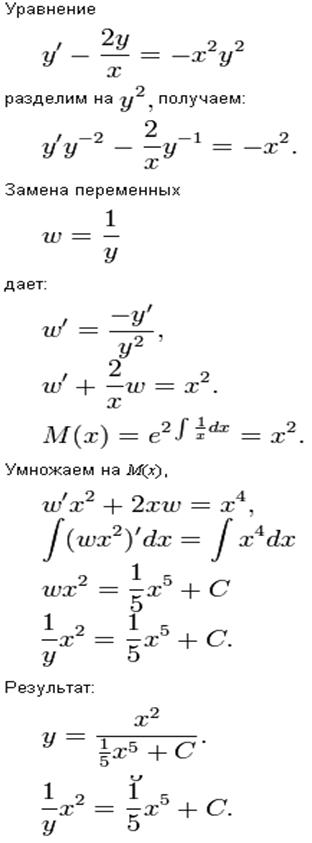
Найти все решения дифференциального уравнения
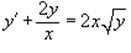
Решение.
Данное уравнение является уравнением Бернулли с
дробным параметром m = 1/2. Его
можно свести к линейному дифференциальному уравнению с помощью замены
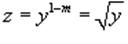
Производная новой функции z(x)
будет равна
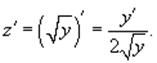
Разделим исходное уравнение Бернулли на
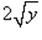
Аналогично другим примерам на этой веб-странице,
корень y = 0 также является
тривиальным решением дифференциального уравнения. Поэтому можно записать:
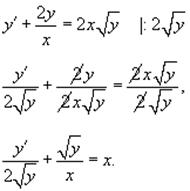
Заменяя y
на z, находим:
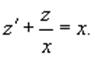
Итак, мы имеем линейное уравнение для функции z(x).
Интегрирующий множитель здесь будет равен
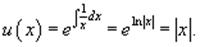
Выберем в качестве интегрирующего множителя
функцию u(x)
= x. Можно проверить,
что после умножения на u(x)
левая часть уравнения будет представлять собой производную произведения z(x)u(x):
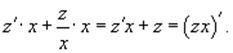
Тогда общее решение линейного дифференциального
уравнения будет определяться выражением:
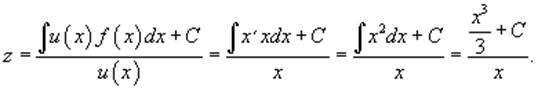
Возвращаясь к исходной функции y(x),
записываем решение в неявной форме:
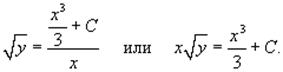
Итак, полный ответ имеет вид:
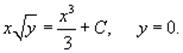
Уравнения с
разделяющимися переменными
Найти все решения дифференциального уравнения
' = −xey.
Решение.
Преобразуем уравнение следующим образом:
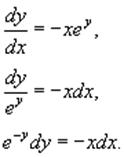
Очевидно, что деление на ey
не приводит к потере решения, поскольку ey
> 0. После интегрирования получаем
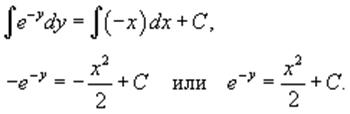
Данный ответ можно выразить в явном виде:
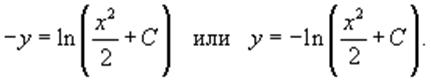
В последнем выражении предполагается, что
константа C > 0, чтобы удовлетворить области определения логарифмической
функции.
Найти частное решение уравнения, при
(0) = 0.
Решение.
Перепишем уравнение в следующем виде:
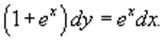
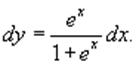
Поскольку 1 + ex
> 0, то при делении мы не потеряли никаких решений. Интегрируем полученное
уравнение:
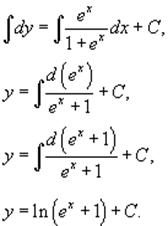
Теперь найдем константу C из начального условия
y(0) = 0.
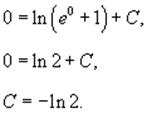
Следовательно, окончательный ответ имеет вид:
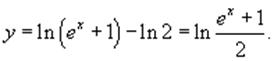
Уравнение Клеро
Найти общее и особое решения дифференциального
уравнения
= xy' + (y')2
Решение
Полагая y' = p, его можно записать в виде
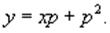
Продифференцировав по переменной x, находим:
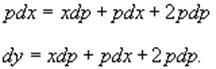
Заменим dy на pdx:
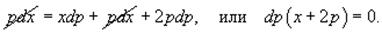
Приравнивая первый множитель к нулю, получаем:
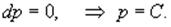
Теперь подставим это во второе уравнение:
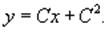
В результате получаем общее решение заданного
уравнения Клеро. Графически, это решение представляется в виде
однопараметрического семейства прямых. Приравнивая нулю второй сомножитель,
находим еще одно решение:
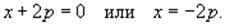
Это уравнение соответствует особому решению
дифференциального уравнения и в параметрической форме записывается как
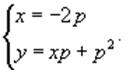
Исключая p из системы, получаем следующее
уравнение интегральной кривой:
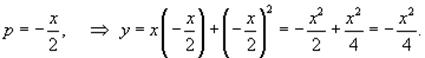
С геометрической точки зрения, парабола
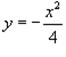
является огибающей семейства прямых,
определяемых общим решением.
Найти общее и особое решения дифференциального
уравнения
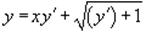
Решение.
Введем параметр y' = p:
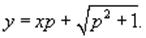
Дифференцируя обе части уравнения по переменной
x, получаем:
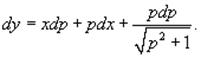
Поскольку dy = pdx, то можно записать:
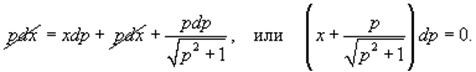
Рассмотрим случай dp = 0. Тогда p = C. Подставляя
это в уравнение, находим общее решение:
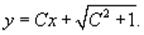
Графически это решение соответствует
однопараметрическому семейству прямых линий.
Второй случай описывается уравнением
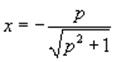
Найдем соответствующее параметрическое выражение
для y:
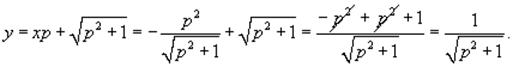
Параметр p можно исключить из формул для x и y.
Возводя последние уравнения в квадрат и складывая их, получаем:
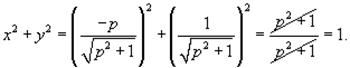
Полученное выражение является уравнением
окружности радиусом 1, расположенным в начале координат. Таким образом, особое
решение представляется единичной окружностью в плоскости xy, которая является
огибающей для семейства прямых линий.
ЛИТЕРАТУРА
1. Н.С.
Пискунов "Дифференциальное и интегральное исчисление", том второй,
издательство "Наука", Москва 1985
. В.
Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным
уравнениям. М.: Физматлит, 2001.
. К.Н.
Лунгу, В.П. Норин и др. "Сборник задач по высшей математике", второй
курс, Москва: Айрис-пресс, 2007
. Э.
Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
. Источники
информации в интернете.