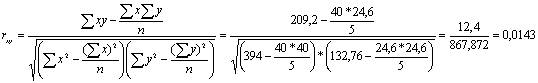Расчет статистических показателей
Министерство
образования Республики Беларусь
Учреждение
образования
БЕЛОРУССКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ
И РАДИОЭЛЕКТРОНИКИ
Контрольная
работа по курсу
"Статистика"
Вариант
№8
Проверил:
Журавлев
В.А.
Минск 2011
Задача 1
Используя имеющиеся в отделении
Национального банка следующие данные об остатках на текущих счетах на конец
месяца (млн. р.), произвести группировку организаций:
|
970
|
692
|
1396
|
1028
|
563
|
1173
|
913
|
523
|
|
473
|
782
|
695
|
878
|
793
|
935
|
1190
|
656
|
|
956
|
728
|
844
|
819
|
1296
|
1295
|
869
|
953
|
|
519
|
1093
|
756
|
1070
|
1165
|
917
|
866
|
611
|
|
417
|
1367
|
911
|
1079
|
1057
|
926
|
770
|
892
|
Необходимо образовать 5 групп с равными
интервалами.
Решение:
Для группировки организаций, необходимо
отсортировать данные по возрастанию и определить интервал группировки. Затем
определяя интервал каждой группы, определить количество организаций, входящих в
данный интервал.
i=(xmax
- xmin)/5=190 -
интервал группировки
Таблица 1
Группировка организаций по остаткам
на текущих счетах на конец месяца
|
Группы
|
1
|
2
|
3
|
4
|
5
|
|
По
остаткам на текущих счетах на конец месяца, млн. р., (∆i)
|
417-607
|
607-797
|
797-987
|
987-1177
|
1177-1367
|
|
Количество
организаций, шт. ( ni)
|
6
|
10
|
14
|
6
|
4
|
Задача 2
На предприятии в начале года
имелось 720 рабочих и 55 инженерно-технических работников (ИТР). В течение года
уволилось 180 рабочих и 20 ИТР, и было принято на работу 60 рабочих и 40 ИТР.
Определите относительные величины,
характеризующие соотношение между рабочими и ИТР на начало и конец года. К
какому виду относительных величин принадлежат эти результаты вычислений?
Проанализируйте полученные результаты.
Решение:
Относительными величинами называются показатели,
исчисляемые как отношение двух статистических величин. В нашем случае
показатель равняется отношению количества рабочих на конец года к количеству
рабочих на начало года.
Таблица 2
Относительные величины,
характеризующие соотношение между рабочими и ИТР на начало и конец года
|
Рабочие,
чел.
|
ИТР,
чел.
|
|
Начало
года
|
720
|
55
|
|
Уволено
|
180
|
20
|
|
Принято
|
60
|
40
|
|
Конец
года
|
600
|
75
|
|
Относительные
величины, %
|
83,3
|
136,36
|
Относительная величина как результат
сопоставления одноименных статистических показателей. По полученным результатам
(табл.2) видно, что количество рабочих на предприятии уменьшилось на 16,7% , а
количество инженерно-технических работников (ИТР) увеличилось на 36, 36%.
Задача 3
Определите среднюю себестоимость одного
километра пробега ведомственного автотранспорта и показатели колеблемости для
трех предприятий по следующим данным:
Таблица 3
Исходные данные
|
Предприятие
|
Себестоимость
1 км пробега, тыс. р.
|
Сумма
расходов на автотранспорт, млрд. р.
|
|
№1
|
60
|
6,6
|
|
№2
|
80
|
9
|
|
№3
|
100
|
6
|
|
ИТОГО
|
-
|
21,6
|
Решение:
Среднее арифметическое
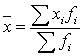
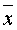 =(60·6,6 + 80·9 + 100·6)/21,6=79,44
=(60·6,6 + 80·9 + 100·6)/21,6=79,44
Дисперсия
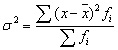
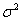 =((60 - 79,44)2·6,6+(80 -
79,44)2·9+(100 - 79,44) 2·6)/21,6=232,9
=((60 - 79,44)2·6,6+(80 -
79,44)2·9+(100 - 79,44) 2·6)/21,6=232,9
Среднее квадратичное отклонение
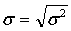
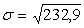 =15,26
=15,26
Коэффициент вариации
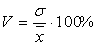
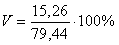 =19,08 %
=19,08 %
Задача 4
По сгруппированным данным
задачи 1 определите:
)среднее значение изучаемого
показателя, моду и медиану;
) постройте гистограмму;
) оцените характер асимметрии.
Таблица 4
Исходные данные
|
1
|
2
|
3
|
4
|
5
|
|
По
остаткам на текущих счетах на конец месяца, млн. р., (∆i)
|
417-611
|
656-844
|
866-1057
|
1070-1190
|
1295-1396
|
|
Количество
организаций, шт. ( ni)
|
6
|
10
|
14
|
6
|
4
|
Решение:
1) среднее значение изучаемого показателя:
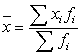
Модальный интервал: 866-1057
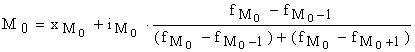
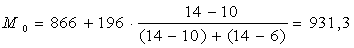
Медианный интервал: 656-844
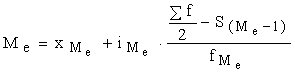
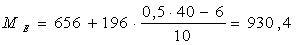
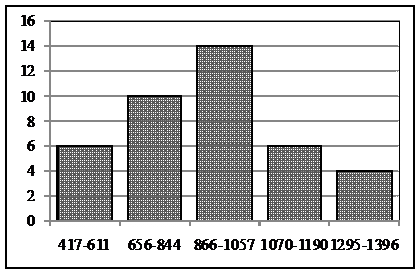
Рис. 1 Гистограмма
Имеет место левосторонняя
асимметрия, т.к. выполняется соотношение
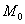 >
>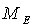 >
>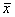 .
.
Задача 5
Используя взаимосвязь показателей
динамики, определите уровни ряда динамики и недостающие в таблице базисные
показатели динамики по следующим данным о производстве продукции «А».
Таблица 5
Исходные данные
|
Год
|
Пр-во
прод. «А», тыс. шт.
|
Базисные
показатели динамики
|
|
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
|
1-й
|
55,1
|
-
|
100
|
-
|
|
2-й
|
-
|
2,80
|
-
|
-
|
|
3-й
|
-
|
-
|
110,30
|
-
|
|
4-й
|
-
|
-
|
-
|
14,90
|
|
5-й
|
-
|
-
|
-
|
17,10
|
|
6-й
|
-
|
-
|
121,10
|
-
|
Решение
Абсолютный прирост (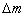 )
показывает, на сколько единиц каждый уровень больше (равен, меньше) начального
(базисного) уровня ряда, т.е.
)
показывает, на сколько единиц каждый уровень больше (равен, меньше) начального
(базисного) уровня ряда, т.е.
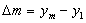
Темп роста 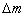 показывает,
во сколько раз каждый уровень ряда больше (меньше) базисного уровня, и
определяется по формуле
показывает,
во сколько раз каждый уровень ряда больше (меньше) базисного уровня, и
определяется по формуле

Темпы прироста (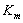 )
показывают, на сколько процентов один уровень ряда отличается от другого
(начального);
)
показывают, на сколько процентов один уровень ряда отличается от другого
(начального);
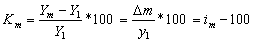
Таблица 6
Базисные показатели динамики
|
Год
|
Пр-во
прод. «А», тыс. шт.
|
Базисные
показатели динамики
|
|
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
|
1-й
|
55,1
|
-
|
100
|
-
|
|
2-й
|
57,90
|
2,80
|
105,08
|
5,08
|
|
3-й
|
60,78
|
5,68
|
110,30
|
10,30
|
|
4-й
|
63,31
|
8,21
|
114,90
|
14,90
|
|
5-й
|
64,52
|
9,42
|
117,10
|
17,10
|
|
6-й
|
66,73
|
11,63
|
121,10
|
21,10
|
По полученным показателям (табл.6) видно, что на
протяжении 6 лет объем производимой продукции увеличивается и как следствие
увеличиваются все базисные показатели динамики.
Задача 6
По следующим данным вычислить:
) базисные индексы объема
продукции в целом по предприятию;
) цепные индексы объема
продукции в целом по предприятию.
Таблица 7
Исходные данные
|
Цех
|
Объем
продукции по годам, млрд. р.
|
|
1-й
год
|
2-й
год
|
3-й
год
|
4-й
год
|
|
№1
|
975
|
1200
|
1240
|
1300
|
|
№2
|
620
|
630
|
540
|
660
|
|
№3
|
25
|
30
|
35
|
50
|
Решение
Абсолютный прирост (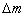 )
показывает, на сколько единиц каждый уровень больше (равен, меньше) предыдущего
или начального (базисного) уровня ряда, т.е.
)
показывает, на сколько единиц каждый уровень больше (равен, меньше) предыдущего
или начального (базисного) уровня ряда, т.е.
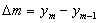 или
или 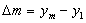
Темп роста 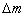 показывает,
во сколько раз каждый уровень ряда больше (меньше) предыдущего или базисного
уровня, и определяется по формуле
показывает,
во сколько раз каждый уровень ряда больше (меньше) предыдущего или базисного
уровня, и определяется по формуле
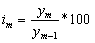 или
или 
Если вычисляются отношения каждого последующего
уровня к предыдущему, то получаются цепные темпы роста, если к начальному
уровню, то базисные темпы роста.
Темпы прироста (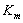 )
показывают, на сколько процентов один уровень ряда отличается от другого
(предыдущего или начального);
)
показывают, на сколько процентов один уровень ряда отличается от другого
(предыдущего или начального);
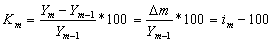
или
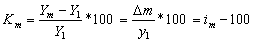
Таблица 8
Показатели динамики
для первого, второго, третьего цехов соответственно
|
Год
|
Базисные
показатели динамики
|
Цепные
показатели динамики
|
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
|
1-й
|
-
|
100,00
|
-
|
-
|
100,00
|
-
|
|
2-й
|
225,00
|
123,08
|
23,08
|
225,00
|
123,08
|
23,08
|
|
3-й
|
265,00
|
127,18
|
27,18
|
40,00
|
103,33
|
3,33
|
|
4-й
|
325,00
|
133,33
|
33,33
|
60,00
|
104,84
|
4,84
|
|
|
|
|
|
|
|
|
|
Год
|
Базисные
показатели динамики
|
Цепные
показатели динамики
|
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
|
1-й
|
100,00
|
-
|
-
|
100,00
|
-
|
|
2-й
|
10,00
|
101,61
|
1,61
|
10,00
|
101,61
|
1,61
|
|
3-й
|
-80,00
|
87,10
|
-12,90
|
-90,00
|
85,71
|
-14,29
|
|
4-й
|
40,00
|
106,45
|
6,45
|
120,00
|
122,22
|
22,22
|
|
|
|
|
|
|
|
|
Год
|
Базисные
показатели динамики
|
Цепные
показатели динамики
|
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
Абс.
прирост, тыс. шт.
|
Темпы
роста, %
|
Темпы
прироста, %
|
|
1-й
|
-
|
100,00
|
-
|
-
|
100,00
|
-
|
|
2-й
|
5,00
|
120,00
|
20,00
|
5,00
|
120,00
|
20,00
|
|
3-й
|
10,00
|
140,00
|
40,00
|
5,00
|
116,67
|
16,67
|
|
4-й
|
25,00
|
200,00
|
100,00
|
15,00
|
142,86
|
42,86
|
|
|
|
|
|
|
|
|
Задача 7
Имеются следующие данные:
Таблица 9
Исходные данные
|
Год
|
Часовая
выработка на одного рабочего, ед.
|
Продолжительность
рабочего дня, ч
|
Продолжительность
рабочего месяца, дн.
|
|
Базисный
|
35
|
7,8
|
23
|
|
Отчетный
|
30
|
7,6
|
21
|
Определите:
а) влияние динамики часовой выработки одного
рабочего, продолжительности рабочего дня и рабочего месяца на динамику
среднемесячной выработки;
б) количество продукции в расчёте на одного
рабочего, которое было получено дополнительно (или недополучено) за счет
каждого фактора.
Решение:
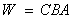 - месячная выработка.
- месячная выработка.
где А - часовая выработка на одного
рабочего; B -
продолжительность рабочего дня; C - продолжительность рабочего
месяца.
Влияние A:
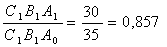
Влияние B:
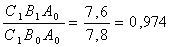
Влияние C:
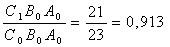
Изменение продукции за счёт A:
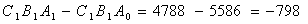
Изменение продукции за счёт B:
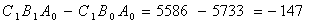
Изменение продукции за счёт C:
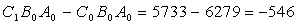
Общее изменение продукции:
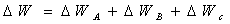 = - 798 - 147 - 546= - 1491.
= - 798 - 147 - 546= - 1491.
Задача 8
Изменение численности
городского и сельского населения области характеризуется следующими данными
(млн. чел.):
Таблица 10
Исходные данные
|
Год
|
Все
население, тыс. чел.
|
В
том числе
|
|
|
городское
|
сельское
|
|
1990
|
10,1
|
6,73
|
3,46
|
|
2000
|
10,0
|
6,99
|
3,03
|
группировка
дисперсия вариация динамика
По этим данным постройте
столбиковые и круговые диаграммы. Какие выводы можно сделать на основе
сравнения площадей соответствующих прямоугольников и секторов, относящихся к
двум сравниваемым годам?
Решение:
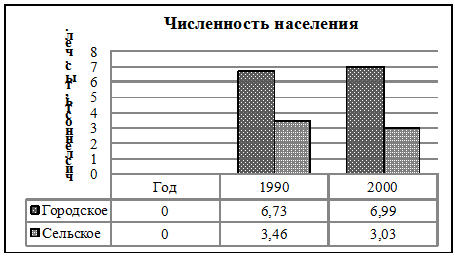
Рис. 2 Столбиковая
диаграмма характеризующая, изменение численности городского и сельского
населения области
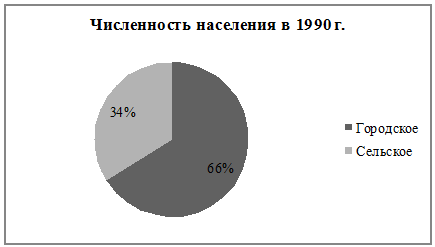
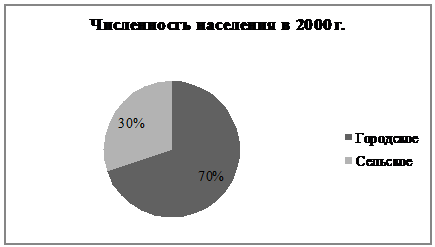
Рис. 3 Круговая
диаграмма характеризующая, изменение численности городского и сельского
населения области
На основе сравнения площадей
соответствующих прямоугольников и секторов, относящихся к двум сравниваемым
годам, можно сделать вывод, что количество городского населения увеличилось, а
сельского уменьшилось, следовательно в области наблюдается процесс урбанизации.
Задача 9
Определите: а) как изменится
ошибка повторной выборки, если среднее квадратическое отклонение признака будет
больше в 2 раза, на 10%; б) как изменится объем выборки, если вероятность,
гарантирующую репрезентативность, увеличить с 0,954 до 0,997.
Решение:
Средняя ошибка выборочной
средней при повторном отборе:
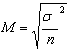
Для повторной выборки необходимый
объем выборки исчисляется по формуле:
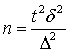
а) если 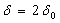 , то
, то
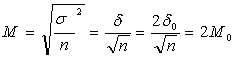 ,
,
следователь ошибка повторной выборки
увеличиться в 2 раза;
если 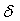 увеличиться на 10 %, то
соответственно и ошибка повторной выборки увеличиться на 10 %.
увеличиться на 10 %, то
соответственно и ошибка повторной выборки увеличиться на 10 %.
б) если увеличить вероятность с
0,954 до 0,997, то 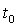 = 2, а
= 2, а 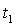 = 3,
следовательно
= 3,
следовательно
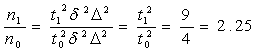 - объем выборки увеличиться в 2,25
раза.
- объем выборки увеличиться в 2,25
раза.
Задача 10
Имеются следующие данные о
стоимости основных производственных фондов и среднесуточной переработке сырья:
Таблица 11
Исходные данные
|
Стоимость
фондов, млрд. р.
|
Среднесуточная
переработка сырья, тыс. Ц.
|
|
4-6
|
6-8
|
8-10
|
8-12
|
|
2,1-3,1
|
2
|
-
|
-
|
-
|
|
3,5-4,5
|
6
|
3
|
-
|
-
|
|
4,5-5,5
|
2
|
5
|
7
|
-
|
|
5,5-6,5
|
-
|
2
|
2
|
3
|
|
6,5-7,5
|
-
|
-
|
1
|
7
|
Найдите параметры уравнения
регрессии, оцените тесноту связи.
Решение:
В качестве линии регрессии используем уравнение
прямой:
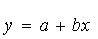
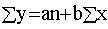
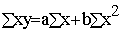
Для измерения тесноты данной связи
используем коэффициент корреляции, исчисляемый по формуле:
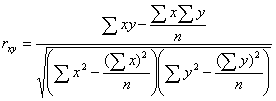
Таблица 12
Среднесуточная переработка сырья на
предприятиях
|
Среднесуточная
переработка сырья, тыс. Ц.
|
5
|
7
|
9
|
10
|
|
Число
предприятий
|
10
|
10
|
10
|
10
|
где х - число предприятий, у - среднесуточная
переработка сырья
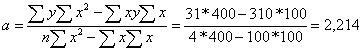
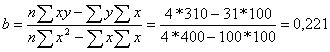
у=2,214 + 0,221*х
Коэффициент корреляции
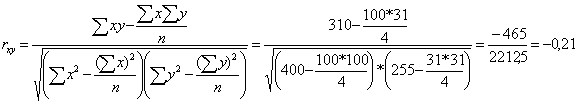
Таблица 13
Стоимость фондов
|
Стоимость
фондов, млрд р.
|
2,6
|
4
|
5
|
6
|
7
|
|
Число
предприятий
|
2
|
9
|
14
|
7
|
8
|
где х - число предприятий, у - стоимость фондов
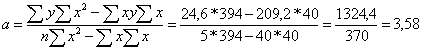
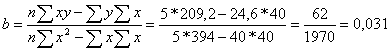
у=3,58 + 0,031*х