Анализ нелинейных систем автоматического управления

Анализ нелинейных систем автоматического управления

Новосибирский государственный технический университет

Кафедра электропривода и автоматизации промышленных установок

КУРСОВАЯРАБОТА

по дисциплине «Теория автоматического управления»

на тему:

Анализ нелинейных систем автоматического управления

Студент: Тишининов Ю.С.

Группа Эма-71

Руководитель курсовой работы

Лютц С.В.

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ:

1. Исследовать САУ с заданной структурной схемой, видом нелинейности и числовыми параметрами методом фазовой плоскости.

.1 Проверить результаты расчетов по пункту 1 с помощью структурного моделирования.

.2 Исследовать влияние входного воздействия и параметров нелинейности на динамику системы.

. Исследовать САУ с заданной структурной схемой, видом нелинейности и числовыми параметрами методом гармонической линеаризации.

.1 Проверить результаты расчетов по пункту 2 с помощью структурного моделирования.

.2 Исследовать влияние входного воздействия и параметров нелинейности на динамику системы

1. Исследуем САУ с заданной структурной схемой, видом нелинейности и числовыми параметрами методом фазовой плоскости.

Вариант №4-1-а

Исходные данные.

) Структурная схема нелинейной САУ:

Рис. 1.1

Система, в которой рабочие операции и операции управления выполняют технические устройства, называется системой автоматического управления (САУ).

Структурной схемой называется графическое изображение математического описания системы.

Звено на структурной схеме изображается в виде прямоугольника с указанием внешних воздействий и внутри него записывается передаточная функция.

Совокупность звеньев совместно с линиями связи, характеризующими их взаимодействие, образует структурную схему.

) Параметры структурной схемы:

К₁ = 10

К₂ = 1,5

Т₁ = 0,01

Т₂ = 0,03

) Вид и параметры нелинейности:

Рис. 1.2

Метод фазовой плоскости

Поведение нелинейной системы в любой момент времени определяется управляемой переменной и ее (n−1) производной, если эти величины отложить по осям координат, то полученное n−мерное пространство будет называться фазовым пространством. Состояние системы в каждый момент времени будет определяться в фазовом пространстве изображающей точкой. Во время переходного процесса изображающая точка перемещается в фазовом пространстве. Траектория ее движения называется фазовой траекторией. В установившемся режиме изображающая точка находится в состоянии покоя и называется особой точкой. Совокупность фазовых траекторий для различных начальных условий, совместно с особыми точками и траекториями называется фазовым портретом системы.

При исследовании нелинейной системы данным методом необходимо структурную схему (рис. 1.1) преобразовать к виду:

Знак минус говорит о том, что обратная связь отрицательная.

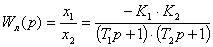
где X₁ и X₂ - выходная и входная величины линейной части системы соответственно.

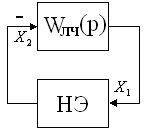
Рис. 1.3

Найдем дифференциальное уравнение системы:

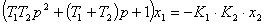
Произведем замену 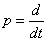, тогда

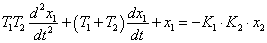
Решим это уравнение относительно старшей производной:

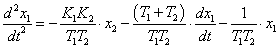
Положим, что:

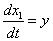,(1.1)

тогда

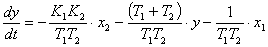(1.2)

Разделим уравнение (1.2) на уравнение (1.1) и получим нелинейное дифференциальное уравнение фазовой траектории:

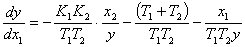(1.3)

где x₂ = f(x₁).

Если решать это ДУ методом изоклин, то можно построить фазовый портрет системы для различных начальных условий.

Изоклиной называется геометрическое место точек фазовой плоскости, которые фазовая траектория пересекает под одним и тем же углом.

В данном методе нелинейная характеристика делится на линейные участки и для каждого из них записывается линейное ДУ.

Для получения уравнения изоклины правая часть уравнения (1.3) приравнивается к постоянной величине N и решается относительно .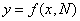

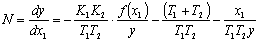(1.4)

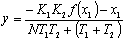
Учитывая нелинейность, получаем:

)

)

)

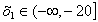
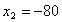
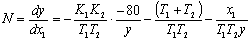
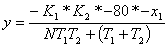
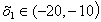
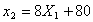
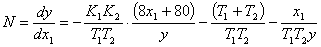
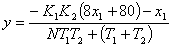
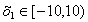
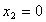
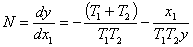
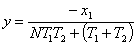
Задаваясь значениями N в диапазоне от 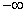 до 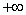, строится семейство изоклин. На каждой изоклине проводится вспомогательная прямая под углом 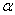 к оси абсцисс

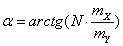,(1.5)

где m_X - масштабный коэффициент по оси х;

m_Y - масштабный коэффициент по оси у.

Выбираем m_X= 0,2 ед/см, m_Y= 40 ед/см;

Конечная формула для угла:

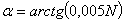
Рассчитаем семейство изоклин и угол для участка 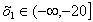, расчет сведем в таблицу 1:

Таблица 1

Рассчитаем семейство изоклин и угол для участка 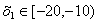, расчет сведем в таблицу 2:

Таблица 2

Рассчитаем семейство изоклин и угол для участка 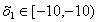, расчет сведем в таблицу 3:

Таблица 3

Построим фазовую траекторию

Для этого выбираются начальные условия на одной из изоклин (точка А), из точки А проводятся две прямые линии до пересечения со следующей изоклиной под углами α₁, α₂, где α₁, α₂ − соответственно углы первой и второй изоклины. Отрезок, отсекаемый этими линиями, делится пополам. Из полученной точки, середины отрезка, вновь проводятся две линии под углами α₂, α₃, и вновь отрезок делится пополам и т.д. Полученные точки соединяются плавной кривой.

Семейства изоклин строятся для каждого линейного участка нелинейной характеристики и разделяются между собой линиями переключения.

По фазовой траектории видно, что получена особая точка типа устойчивый фокус. Можно сделать вывод, что автоколебаний в системе нет, а переходный процесс устойчивый.

1.1 Проверим результаты расчетов с помощью структурного моделирования в программе MathLab

Структурная схема:

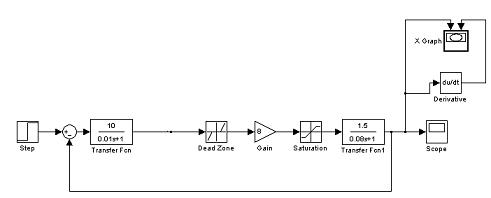
Рис. 1.4

Фазовый портрет:

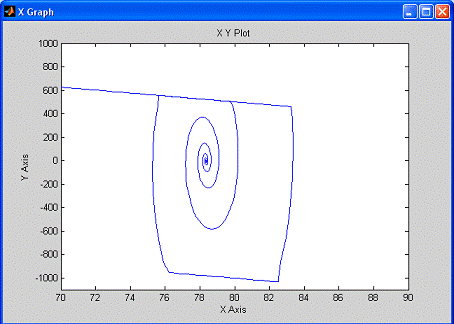
Рис. 1.5

Переходный процесс при входном воздействии равном 2:

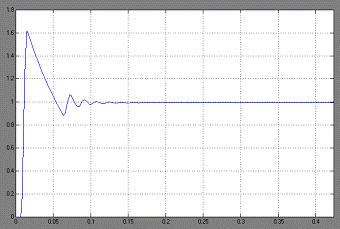
Рис. 1.6

Xвых.max = 1.6

Xвых.∞ = 1

Nкол = 6

Трег = 0,1

.2 Исследуем влияние входного воздействия и параметров нелинейности на динамику системы

Увеличим входной сигнал до 10:

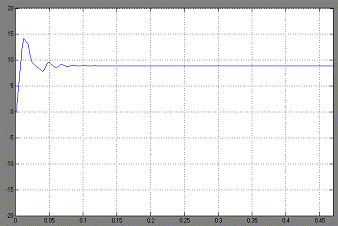
Рис. 1.7

Xвых.max = 14,3

Xвых.∞ = 8.5

Ккол = 5

Трег = 0,055

Увеличим входной сигнал до 100:

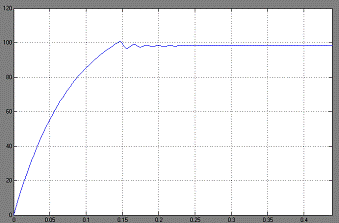
Рис. 1.8

X вых. max = 103

X вых.∞ = 98

К кол = 5

Т рег = 0,18

Увеличим зону чувствительности до 15:

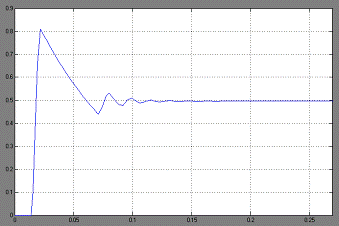
Рис. 1.9

Xвых.max = 0,81

Xвых.∞ = 0,5

Ккол = 6

Трег = 0,11

Уменьшим зону чувствительности до 1:

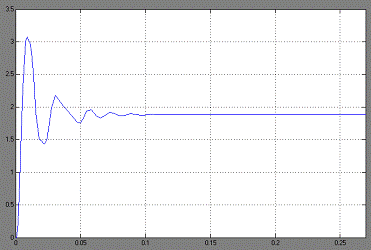
Рис. 1.10

Xвых.max = 3.2

Xвых.∞ = 1.8

Ккол = 8

Трег = 0,09

Выводы:

Результатами моделирования были подтверждены результаты расчетов: из рисунка 1.7 видно, что процесс сходящийся, автоколебаний в системе нет. Фазовый портрет смоделированной системы схож с построенным расчетным путем.

Исследовав влияние входного воздействия и параметров нелинейности на динамику системы, можно сделать выводы:

)   при увеличении входного воздействия увеличивается уровень установившегося режима, количество колебаний не меняется, время регулирования увеличивается.

) при увеличении мертвой зоны уровень установившегося режима увеличивается, количество колебаний также остается неизменным, время регулирования увеличивается.

2. Исследуем САУ с заданной структурной схемой, видом нелинейности и числовыми параметрами методом гармонической линеаризации.

Вариант №5-20-c

Исходные данные.

) Структурная схема:

Рис. 2.1

) Значения параметров:

k₁ = 15.5

k₂ = 2.2

T₁ = 0,39 с

Т₂ = 0,3 с

Т₃ = 0,14 с

) Вид и параметры нелинейности:

Рис. 2.2

Наиболее широкое распространение для исследования нелинейных САУ высокого порядка (n > 2) получил приближенный метод гармонической линеаризации с применением частотных представлений, развитых в теории линейных систем.

Основная идея метода сводится к следующему. Пусть замкнутая автономная (без внешних воздействий) нелинейная система состоит из последовательно включённых нелинейного безынерционного НЗ и устойчивой или нейтральной линейной части ЛЧ ( рис 2.3, а)

a) НЗ=0 x z Х=Х_msinwt z y

б) ЛЧ

y = Y_m1 sin (wt + )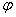

-

Рис. 2.3

Для суждения о возможности существования моногармонических незатухающих колебаний в этой системе предполагается, что на входе нелинейного звена действует гармонический синусоидальный сигнал x(t) = X_m sinwt (Рис. 2.3,б). При этом сигнал на выходе нелинейного звена z(t) = z[x(t)] содержит спектр гармонических составляющих с амплитудами Z_m1, Z_m2, Z_m3, и т.д. и частотами w, 2w, 3w и т.д. Предполагается, что этот сигнал z(t), проходя через линейную часть W_л(jw), фильтруется ею в такой степени, что в сигнале на выходе линейной части y(t) можно пренебречь всеми высшими гармониками Y_m2, Y_m3 и т.д. и считать, что

y(t)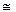Y_m1sin(wt + )

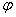Последнее предположение носит название гипотезы фильтра и выполнение этой гипотезы является необходимым условием гармонической линеаризации.

Условие эквивалентности схем, изображенных на рис. 2.3, а и б, можно сформулировать в виде равенства

x(t) + y(t) = 0(1)

При выполнении гипотезы фильтра y(t) = Y_m1sin(wt + 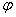) уравнение (1) распадается на два

X_m = Y_m1(2)

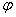=(3)

Уравнение (2) и (3) носят название уравнений гармонического баланса; первое из них выражает баланс амплитуд, а второе - баланс фаз гармонических колебаний.

Таким образом, для того, чтобы в рассматриваемой системе существовали незатухающие гармонические колебания, при соблюдении гипотезы фильтра должны выполняться условия (2) и (3)

Воспользуемся методом Гольдфарба для графоаналитического решения характеристического уравнения вида

W_ЛЧ (p) W_НЭ (A) +1 = 0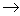jw_ЛЧ(jw) W_НЭ(A) = -1

Для приближенного определения автоколебаний строятся АФЧХ линейной части системы и обратная отрицательная характеристика нелинейного элемента.

Для построения АФЧХ линейной части преобразуем структурную схему к виду рис 2.4:

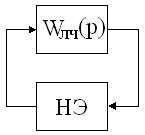
Рис 2.4

В результате преобразования получаем схему рис 2.5:

Найдем передаточную функцию линейной части системы:

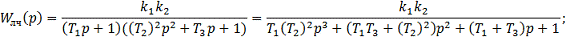
Заменим :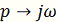

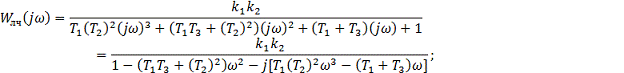
Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряженное к знаменателю, получим:

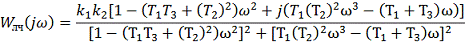
Разобьем получившееся на мнимую и действительную части:

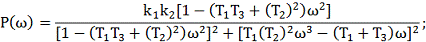
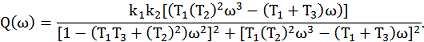
Для построения обратной отрицательной характеристики нелинейного элемента воспользуемся формулой:

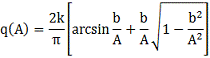
где ,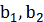

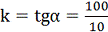 - параметры нелинейности:

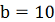,k=10

А - амплитуда, при условии что .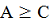

АФЧХ линейной части системы и обратная отрицательная характеристика нелинейного элемента, представлена на рис. 2.6:

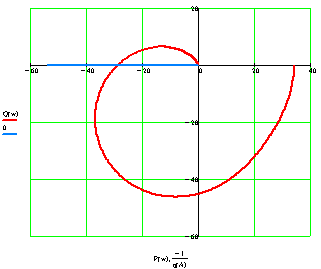
Рис. 2.6

Для определения устойчивости автоколебаний воспользуемся следующей формулировкой: если точка соответствующая увеличенной амплитуде по сравнению с точкой пересечения не охватывается частотной характеристикой линейной части системы, то автоколебания устойчивые. Как видно из рисунка 2.6 решение устойчиво, следовательно, в системе устанавливаются автоколебания.

.1 Проверим результаты расчетов с помощью структурного моделирования в программе MathLab.

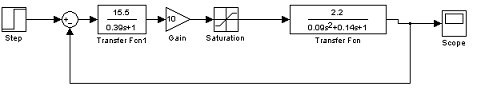
Рис 2.7: Структурная схема

Переходный процесс при входном воздействии равном 1 (рис 2.8):

автоматический управление нелинейный гармонический

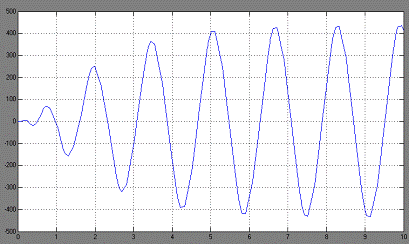
Рис. 2.8

Как видно из графика устанавливаются автоколебания. Проверим влияние нелинейности на устойчивость системы.

.2 Исследуем влияние входного воздействия и параметров нелинейности на динамику системы.

Увеличим входной сигнал до 100:

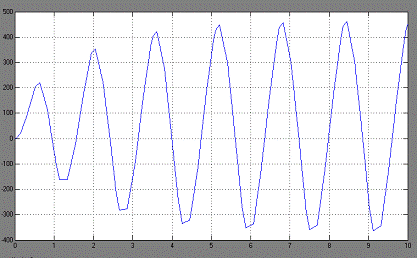
Рис. 2.9

Увеличим входной сигнал до 270

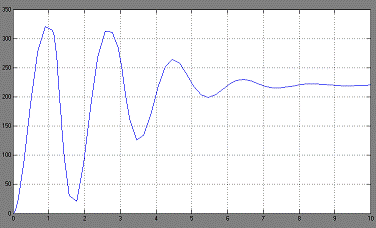
Рис. 2.10

Уменьшим входной сигнал до 50:

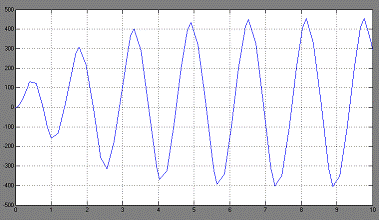
Увеличим насыщение до 200:

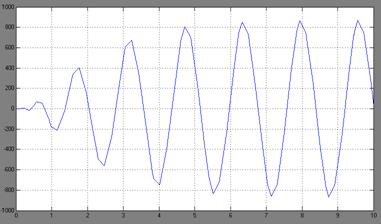
Рис. 2.11

Уменьшим насыщение до 25:

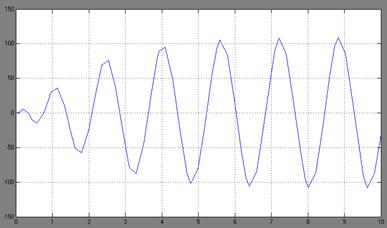
Рис. 2.12

Уменьшим насыщение до 10:

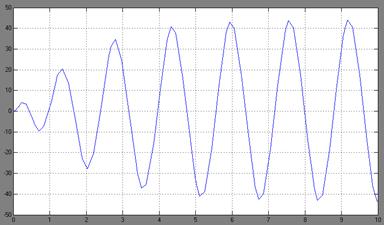
Рис. 2.13

Вывод:

Результатами моделирования не однозначно подтвердили результаты расчетов:

)   Автоколебания возникают в системе, а изменение насыщения влияет на амплитуду колебаний.

2)      При увеличении входного воздействия изменяется величина выходного сигнала и система стремиться к устойчивому состоянию.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ:

1. Сборник задач по теории автоматического регулирования и управления. Под ред. В.А. Бесекерского, издание пятое, переработанное. - М.: Наука, 1978. - 512 с.

. Теория автоматического управления. Ч. II. Теория нелинейных и специальных систем автоматического управления. Под ред. А.А.Воронова. Учеб. пособие для вузов. - М.: Высш. школа, 1977. - 288 с.

. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования: учеб. пособие. − М.: Машиностроение, 1989. − 752 с.