Идентификация и моделирование нелинейной системы электромеханического следящего привода с трехпозиционным реле

Оглавление

Введение

1.   Описание работы системы, ПФ ее элементов

2.      Составление дифференциальных уравнений замкнутой нелинейной САУ

3.   Построение фазового портрета системы, определение периодического режима, его устойчивости и параметров

4.      Исследование нелинейной САР при входном воздействии f(t)=B*sin(щt)

.        Гармоническая линеаризация нелинейности. Расчёт ЗНСАУ частотно-амплитудным методом

.        Влияние параметров ЛЧ и НЭ на процессы в ЗНСАУ. Рекомендации по стабилизации системы

.        Построение диаграммы качества

Заключение

Список использованной литературы

Введение

Теория автоматического управления - это наука занимающаяся изучением разнообразных систем автоматического управления и регулирования, математическим описанием, моделированием таких систем с целью изучения их свойств, характеристик. Теория автоматического управления включает следующие основные разделы:

а) теория линейных систем автоматического регулирования, где рассматриваются вопросы составления и линеаризации исходных уравнений движения и типовые динамические звенья, излагаются возможные подходы, которые используются при анализе систем регулирования.

б) теория особых линейных систем, к которым относятся системы с переменными параметрами, системы с постоянным временным запаздыванием и импульсные системы.

в) теория нелинейных систем.

В каждом из разделов рассматриваются вопросы устойчивости, коррекции систем.

В настоящее время существует чрезвычайно большое разнообразие автоматических систем, выполняющих те или иные функции по управлению самыми разнообразными физическими процессами во всех областях техники. В этих системах сочетаются весьма разнообразные по конструкции механические, электрические и другие устройства, составляя сложный комплекс взаимодействующих друг с другом звеньев.

Примерами автоматических систем могут служить:

1)   автомат включения освещения, в котором имеется фотоэлемент, реагирующий на силу дневного света, и специальное устройство для включения освещения, срабатывающее от определенного сигнала фотоэлемента;

2)      системы телеуправления, в которых от нажатия кнопки или от поворота ручки на пульте управления совершается определенная комбинация мощных и сложных комбинаций в управляемом блоке.

)        автоматический регулятор скорости вращения двигателя, поддерживающий постоянную угловую скорость двигателя независимо от внешней нагрузки (аналогично регуляторы температуры, давления, напряжения, частоты и пр.)

)        следящая система, на выходе которой с определенной точностью копируется произвольное во времени изменение какой-нибудь величины, поданной на вход;

)        вычислительное устройство, выполняющее определенную математическую операцию (дифференцирование, интегрирование, решение уравнений и т.п.).

Данная работа посвящена изучению нелинейных систем, в частности исследуется релейная следящая система, имеющая широкое применение в автоматизированных системах управления.

Исследование системы я провожу методом построения фазового портрета и частотно-амплитудным методом, где ищу возникает ли периодический режим. В качестве нелинейного элемента используется идеальное реле. В частотно-амплитудном методе каждое изменение параметров ЛЧ и НЭ сопровождается графиком, где наглядно видно процесс в данной системе.

Провожу исследование нелинейной САР при воздействии входного сигнала f(t)=B*sin(щt).

В конце курсового проекта строим диаграмму качества, который показывает при которых k_лч в системе могут возникать автоколебания, когда система может расходится и затухать с более меньшей скоростью.

1. Описание работы системы, ПФ ее элементов

Пример электромеханической следящей системы показан на рис.1.

Рис. 1.

Принцип её действия следующий. На входе вращением рукоятки задается произвольный закон для угла поворота во времени 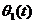. Тот же самый закон угла поворота во времени должен быть автоматически воспроизведен на выходе системы, т.е. на управляемом объекте: . Для этой цели угол поворота на выходе  передается при помощи вала обратной связи на вход системы, где он вычитается из задаваемого угла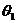. Это вычитание осуществляется при помощи механического дифференциала. Если угол на выходе  не равен углу входе 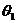, то третий валик дифференциала повернется на разность этих углов 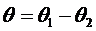 - рассогласование. Пропорциональное ей напряжение U подается через усилитель на приводной двигатель, который вращает выходной вал системы. Если же =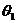, то двигатель обесточен и вращения не будет. Следовательно, система все время работает на уничтожения рассогласования 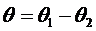_, решая, таким образом, задачу воспроизведения на выходе и₂ произвольно задаваемой на входе величины 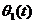. Такая система позволяет при незначительной мощности на входе управлять любыми мощными или тяжелыми объектами.

Усилитель, показанный на рис.1, функционально можно разделить на линейный усилитель и релейный усилитель с соответствующей статической характеристикой.

По принципиальной схеме рис.1 составим структурную схему электромеханического релейного следящего привода, где обозначено:

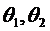- углы поворота командной и исполнительной осей соответственно;

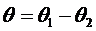 - рассогласование (ошибка);

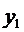- напряжение на выходе чувствительного элемента;

- напряжение на выходе линейного усилителя;

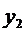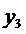- напряжение на выходе релейного усилителя;

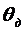 - угол поворота двигателя.

Исходные данные:

k₁=60 В/рад - крутизна статической характеристики чувствительного элемента;

k₂=2 - коэффициент усиления линейного усилителя;

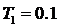с - постоянная времени линейного усилителя;

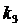- коэффициент передачи двигателя

, рад*В^-1*с^-1,

где 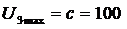В - максимальное напряжение на выходе релейного усилителя,

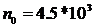 об/мин - скорость холостого хода,

тогда получим значение:

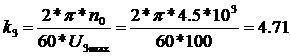 рад*В^-1*с^-1;

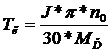 − электромеханическая постоянная времени двигателя,

где J=1,0*10^-6 кг/м² - момент инерции всех вращающихся частей, приведенный к валу двигателя,

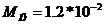 Н*м - пусковой момент двигателя,

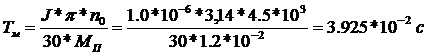
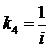 - коэффициент усиления редуктора, где

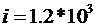- передаточное число редуктора,

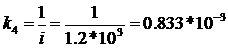
Вид нелинейности - идеальный реле (рис. 2):

Рис. 2. Идеальное реле

Система состоит из следующих элементов:

1)      Чувствительный элемент

2)      Линейный усилитель

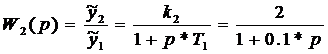
3)      Релейный усилитель

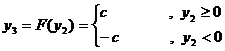
) Двигатель

5) Редуктор

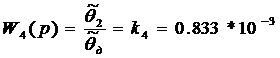
2. Составление дифференциальных уравнений замкнутой нелинейной САУ

Преобразуем схему следящей системы относительно входного сигнала нелинейного элемента.

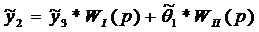
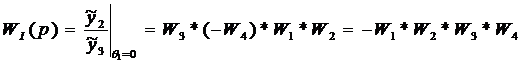
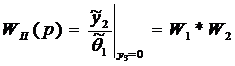
В автономной системе в режиме стабилизации угла поворота рабочего механизма входное воздействие 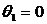, тогда

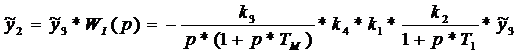
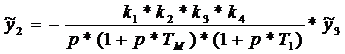
Передаточная функция линейной части имеет вид

.

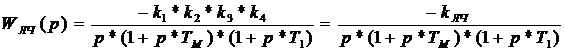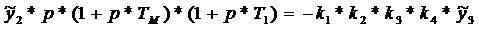
Дифференциальное уравнение линейной части:

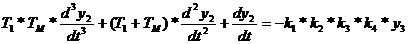
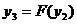 - уравнение нелинейного элемента.

Уравнение ЗНСАУ:

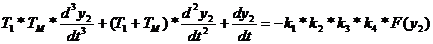
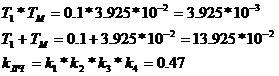
Тогда

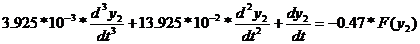
3. Построение фазового портрета системы, определение периодического режима, его устойчивости и параметров

Если пренебречь произведением T₁*T_M, то дифференциальное уравнение ЗНСАУ примет вид:

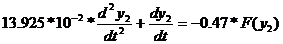
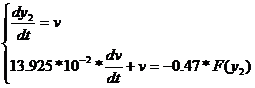
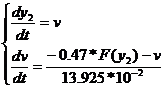
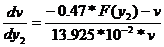 - уравнение фазовой скорости в общем виде.

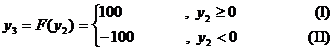
Участок (I):

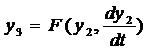= c = 100

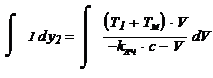
 (4.1)

(4.1) − уравнение фазовой траектории на участке (I)

где с_{1 -} постоянная интегрирования, определяемая из начальных условий.₁= -25.163 начальные условия: y₂= 0 V= 5

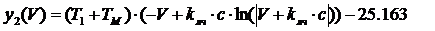
Участок (II):

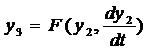= c = -100

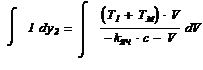
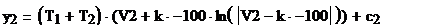 (4.2)

(4.2) - уравнение фазовой траектории на участке (II),

где с_{2 -} постоянная интегрирования, определяемая из начальных условий.₂ = 25.163 - начальные условия: y₂ =0, V= -4.65

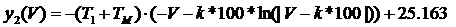
Далее мы строим фазовый портрет системы при разных начальных условиях, соответствующей для каждого участка (рис. 3).

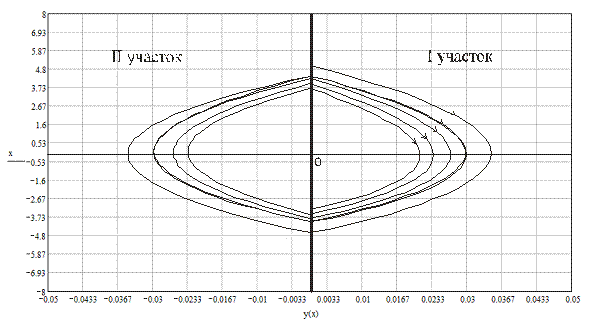
Рис. 3. Фазовый портрет системы

По фазовому портрету видно (рис. 3), что система не имеет периодического режима, так как фазовый портрет скручивается к началу координат. На графике (рис. 3) я построил 11 участков.

Таблицы значений по промежуткам:

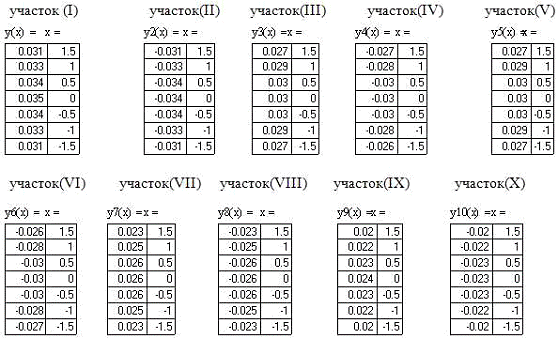
4. Исследование нелинейной САР при входном воздействии f(t)=B*sin(щt)

Рассмотрим нелинейную систему с внешним воздействием:

g(t)=B*sin(щt) (4.1)

Уравнение динамики системы имеет вид

Q(p)x+R(p)F(x,px)=S(p)f(t) (4.2)

Решение для вынужденных колебаний будем искать в форме

x= A*sin(щt+ц), (4.3) y x

где щ задано, а неизвестными являются амплитуда А и фаза ц.

Гармоническая линеаризация нелинейности:

F(x,px)={q(A)+(b(A)/щ)*p}x, (4.4)

Подставим (4.1), (4.3), (4.4) в уравнение системы (4.2):

[Q(p)x+R(p)(q(A)+(b(A)/щ)*p)]* A*sin(щt+ц)=S(p) B*sin(щt) (4.5)

Подставив сюда p=jщ, sin(щt)=e^jщt, тога получим

[Q(jщ)+R(jщ)(q(A)+jb(A))]* A*e^j(щt+ц)=S(jщ)Be^jщt, (4.6)

или Z(A)= Be^-jц, (4.7)

где Z(A)= A*[Q(jщ)+R(jщ)(q(A)+jb(A))]/S(jщ) (4.8)

Построив графики уравнений (4.7), (4.8) графически определяем наличие вынужденных колебаний и его параметров. Обратимся к нашей системе.

Выведем уравнение динамики системы вида (4.2)

,

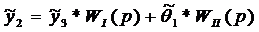где и₁=g(t)= B*sin(щt)

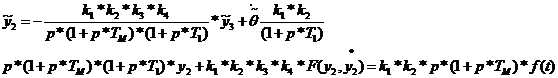
Согласно уравнению (4.2):

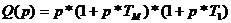
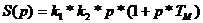
Подставим полученные значения в уравнение (4.8)

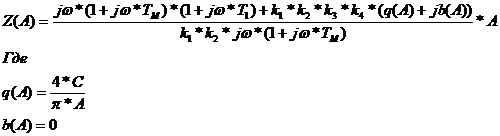
Тогда получим уравнение для построения Z(A):

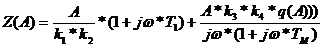
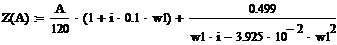
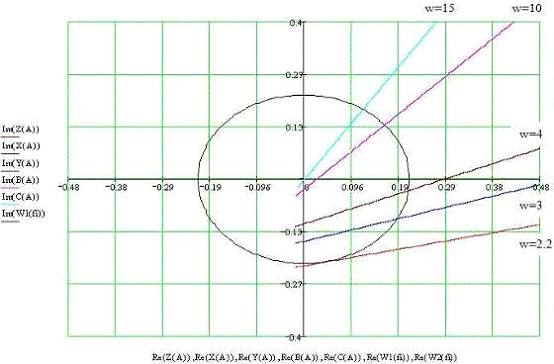
Рис. 4. Нахождение Впор при w=2.2

На комплексной плоскости (рис. 4) построено 1 график 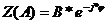при 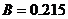 и 5 графиков Z(A) по формуле (4.8) при различных значениях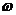: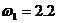, , 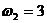, ,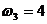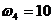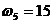. Амплитуда A изменяется в диапазоне от 0.3 до 300.

При В_пор=0.215:

- если w=3, то A=25.069

если w=4, то A= 27.859

если w=10, то A= 21.788

если w=15, то A= 16.217

Согласно графику окружность 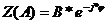пересекает кривую при данном значении частоты внешнего воздействия 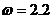 только при радиусе, большем некоторого порогового значения 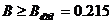. То есть, вынужденные одночастотные колебания в системе возможны только при соблюдении условия .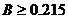

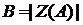
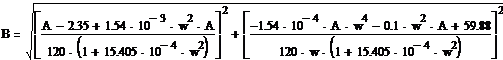
При 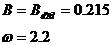 согласно формуле  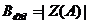при .

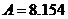Построив серию кривых 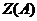 для разных значений частоты внешнего воздействия 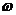, получим график зависимости порогового значения  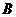от частоты 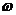(рис. 5).

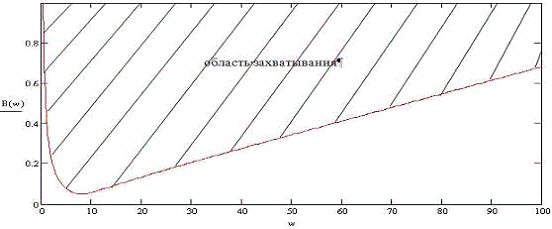
Рис. 5. Область захватывания

Получили область 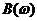 (рис. 5), в которой существуют одночастотные вынужденные колебания, так называемую область захватывания.

5. Гармоническая линеаризация нелинейности. Расчёт ЗНСАУ частотно-амплитудным методом

Рассмотрим метод гармонической линеаризации. Пусть на вход нелинейного элемента подан гармонический сигнал:

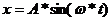 (5.1).

На выходе получим сигнал

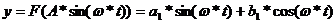 (5.2),

который можно разложить в ряд Фурье:

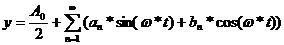
Где 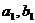 - коэффициенты ряда Фурье:

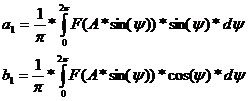
Где .

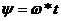Примем:

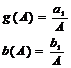
Тогда уравнение (5.2) примет следующий вид:

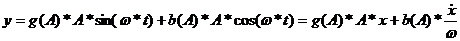
В области изображений:

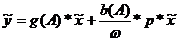
Передаточная функция гармонически линеаризованного нелинейного элемента:

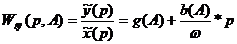
Частотная передаточная функция ГЛНЭ:

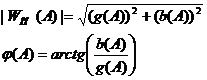
Коэффициенты для нелинейности:

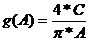
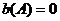 (т.к. нелинейность однозначная).

Определим наличие периодического режима частотно-амплитудным методом.

1. Гармоническая линеаризация нелинейного элемента:

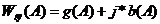
2. Условие существования периодического режима:

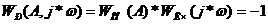 (5.3)

Где 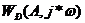- АФХ разомкнутой гармонически линеаризованной системы (РГЛС), т.е. используется критерий Найквиста: в замкнутой ГЛНС будет периодический режим, если АФХ РГЛС проходит через точку с координатами .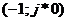

Уравнение (5.3) в иной форме:

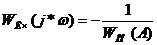
С помощью программы MathCad строим АФХ линейной части и инверсную АФХ нелинейного элемента.

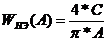
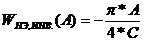
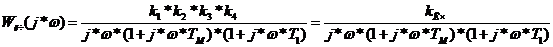
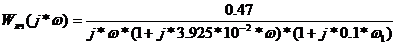
Значение амплитуды от 0 до 300.

Получаем графики W_лч(jщ) и -1/Z _НЭ(A):

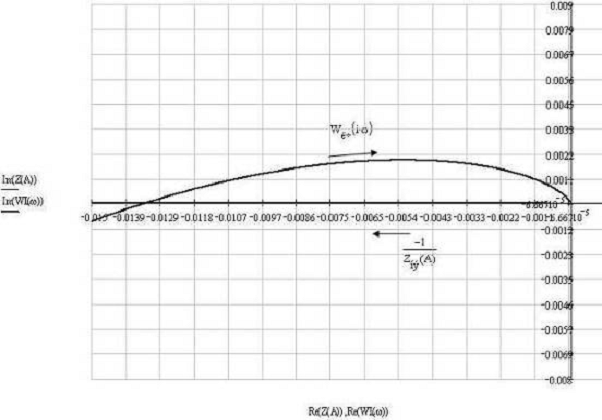
Рис. 6. Определение ПР

Из графика видно (рис. 6), что кривые пересекаются, следовательно, в данном случае периодический режим существует.

Построим кривую 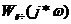, пренебрегая произведением .

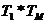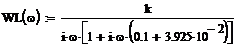
Из графика видно (рис. 7), что кривые не пересекаются, следовательно, и в данном случае периодический режим не наблюдается. Значит чем больше значение 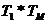, то тем круче будет проходить .

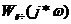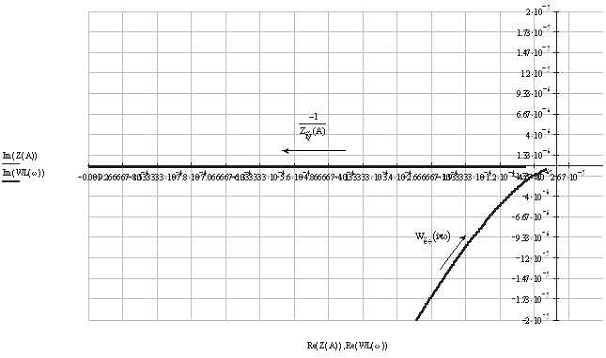
Рис. 7. Определение ПР без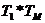

6. Влияние параметров ЛЧ и НЭ на процессы в ЗНСАУ. Рекомендации по стабилизации системы

следящий привод нелинейный автоматический

а) Оценка влияния параметров статической характеристики релейного усилителя

Значение c

При уменьшении c например при c<5.9 в системе периодический режим не происходит, что мы наблюдаем на графике (рис. 8) W_лч(jщ) и -1/Z _НЭ(A), например, с=5:

При с>17800 не будет пересечения W_лч(jщ) и -1/Z _НЭ(A), а следовательно в этом случае периодического режима возникать не будет (рис. 9). Например, при с=20000.

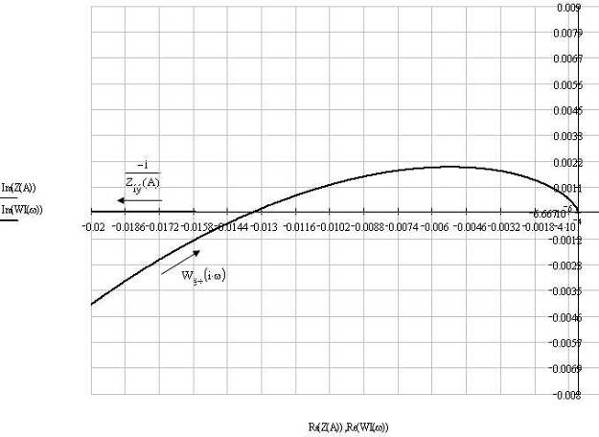
Рис. 8. При с=5

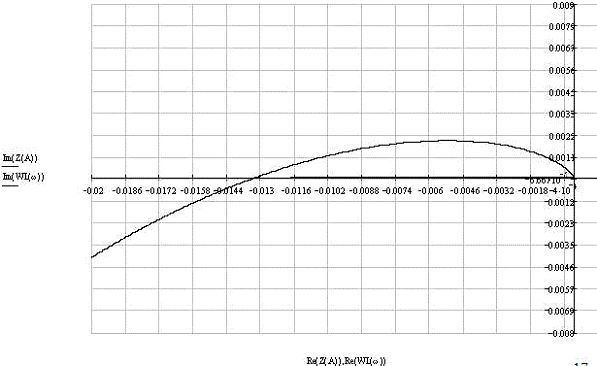
Рис. 9. При с=20000

При 5.9<с<17800 будет возникать периодический режим (рис. 10), например, при с=16000:

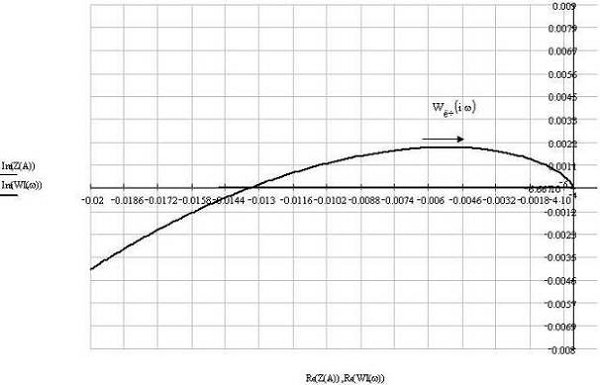
Рис. 10. При с=16000

б) Оценка влияния параметров линейной части.

) Общий коэффициент усиления линейной части k_лч.

При уменьшении k_лч в системе периодического режима не будет возникать, так как W_лч будет проходить более круче, например, при k_лч=0.0047 (рис. 11):

При увеличении k_лч процесс в системе затухает с медленней скоростью. Например при k_лч=2 (рис.12), где частота и амплитуда системы резко возрастает:

Как видно из рисунка (рис. 12) мы наблюдаем пересечение двух кривых, то в этом случае возникает периодический режим.

) Значения электромеханической постоянной времени двигателя Т_м и постоянной времени линейного усилителя Т₁.

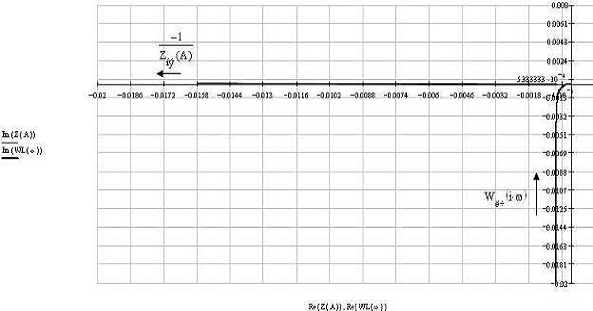
Рис.11. При k_лч=0.0047

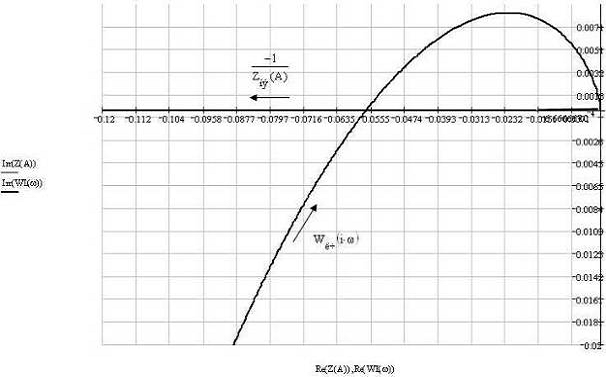
Рис. 12. При k_лч=2

При увеличении суммы T₁+T_м≥0.03926 система будет затухать с большей скоростью, а также при этом возникает периодический режим, например при T₁+T_м=2.03925 (рис.13):

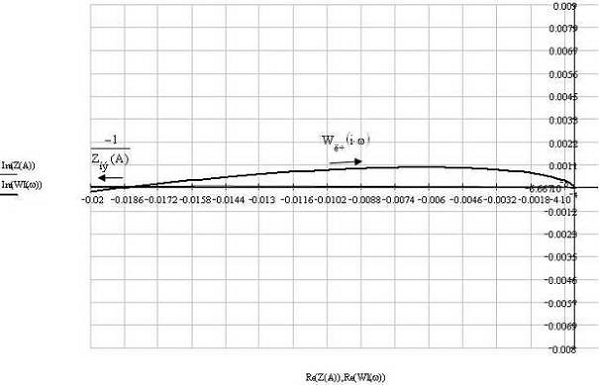
Рис.13. T₁+T_м=2.03925

При уменьшении суммы (T₁+T_м) процесс в системе затухает с большей скоростью, например при значении T₁+T_м=0.03926 (рис. 14), где частота и амплитуда резко уменьшается:

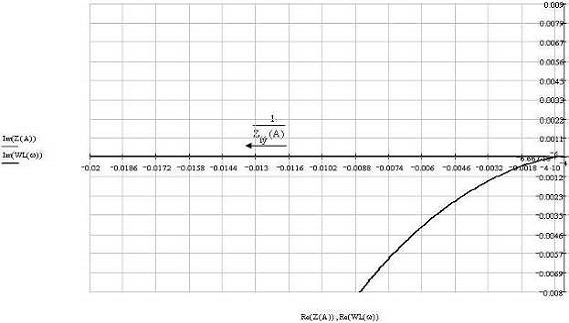
Рис.14. При T₁+T_м=0.03926

Вывод. Таким образом, система изначально находится в стабильном режиме, так как нет периодического режима. Можно использовать следующие методы для стабилизации системы, т.е. для того, чтобы в системе был затухающий процесс:

. Изменение параметров НЭ:

уменьшить значение с≤5.9 и увеличить с>17800 нелинейного элемента.

. Изменение параметров ЛЧ:

уменьшить значение коэффициента усиления при k_лч;

уменьшить значение суммы постоянных времени при T₁+T_м.

Итак, 2-мя методами (методом построения фазового портрета и частотно-амплитудным методом) система была исследована на существование периодического режима. При построении фазового портрета мы пренебрегли произведением Т₁*Т_м и нарисовали фазовый портрет с помощью уравнения 2-ого порядка, где наглядно видно, что периодического режима нет. С помощью частотно-амплитудным методом мы учитывали Т₁*Т_м и на графике наглядно видно, что есть периодический режим, т. е. в этом методе строили графики с помощью уравнения 3-его порядка.

7. Построение диаграммы качества

Уравнение нелинейной системы имеет следующий вид:

(p)x+R(p)F(x,px)=0

Будем рассматривать колебательные переходные процессы как собственные колебания и если выполнены условия метода гармонической линеаризации, то колебательный переходный процесс будем искать в виде:

x=a(t)sin(ш(t)), da/dt=a*о (a), dш/dt=щ(a).

При о<0 процесс затухает, о>0 - процесс расходится, о=0 - в системе периодический режим.

Гармоническая линеаризация нелинейности изменится:

x= a(t)sin(ш(t)), px= a(t)*щ(a)*cos(ш(t))+ a(t)* о (a)*sin(ш(t)).

Тогда получим:

(ш(t))=x/a, cos(ш(t))=(p-о)*x/(a(t)*щ(a))

Тогда получим:

(x,px)=[q(a)+b(a)*(p-о)/щ]*x

Следовательно, характеристическое уравнение гармонически линеаризованной системы:

Q(p)+R(p)[q(a)+b(a)*(p-о)/щ]=0.

Чтобы процесс был колебательным корни должны быть комплексными p= о +jщ:

Q(о+jщ)+R(о+jщ)[q(a)+jb(a)]=0.

По данному уравнению можно построить диаграмму качества системы как зависимость a=a(k) при различных постоянных значениях о.

Построим диаграмму качества переходного процесса для электромеханической следящей системы.

Характеристическое уравнение замкнутой гармонически линеаризованной нелинейной системы:

P*(1+pT₁)* (1+pT_м)+k_лч*[q(A)+jb(A)]=0. (8.1)

Для построения диаграммы качества в полиноме (8.1) произведем подстановку p= о +jщ:

(о+jщ)*(1+(о+jщ)T₁)* (1+(о+jщ)T_м)+k_лч*[q(A)+jb(A)]=0

После преобразования получим:

(T₂*о³+T₃*о²+о -щ²*(3*T₂*о +T₃))+j(3*T₂*о²+2* T₃*о +1-щ²*T₂)*щ+ k_лч*[q(a)+jb(a)]=0   (8.2)

где T₂= T₁* T_м, T₃= T₁+ T_м.

Выделив в уравнении (8.2) действительную и мнимую части, получим систему из двух уравнений:

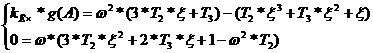
Выразим 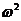из второго уравнения и подставим в первое.

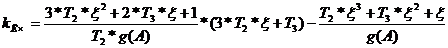
где

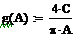
Задаваясь различными значениями амплитуды колебаний 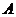 и при выбранных постоянных значениях показателя затухания 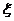 строим семейство кривых 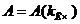(рис.15).

Диапазон изменения амплитуды: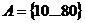

Кривая 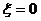соответствует автоколебаниям в системе и представляет собой зависимость амплитуды автоколебаний 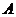 от коэффициента усиления . Область, лежащая правее прямой (о=0), является областью существования автоколебаний. Область, расположенная левее этой прямой, является областью устойчивого равновесного состояния системы.

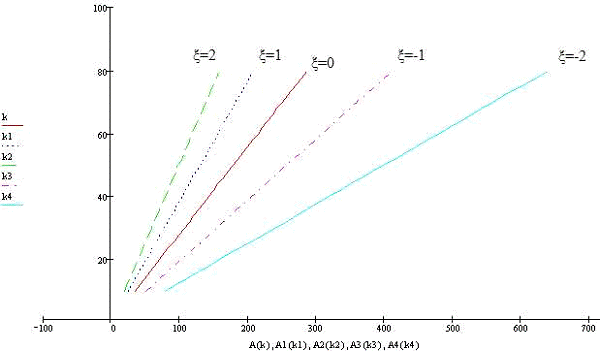
Рис.15. Диаграмма качества

Заключение

При заданных параметрах в следящей системе при отсутствии входного сигнала автоколебаний не наблюдается, что было доказано построения фазового портрета.

При синусоидальном входном воздействии в зависимости от значений амплитуды 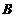и частот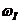ы  в системе могут наблюдаться как одночастотные вынужденные колебания, так и сложное движение, включающее в себя и собственную частоту системы.

При оценке влияния параметров ЛЧ и НЭ на процессы в ЗНСАУ получили: изменения параметров ЛЧ и НЭ влияют на амплитуду и частоту ПР и могут привести к затухающему процессу в системе.

При построении диаграммы качества были определены области параметров системы, характеризующие качество колебательных переходных процессов.

В результате работы были изучены такие программные продукты, как Mathcad13 и MATLAB7. Также были изучены основные принципы проектирования автоматических систем управления.

Список использованной литературы

1. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. − М.: Наука, 1988.

. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. − М.: Наука, 1975.

. Сборник задач по теории автоматического регулирования и управления. / Под ред. В.А. Бесекерского. − М.: Наука, 1972.