|
Параметр
|
а1
|
с
|
K1
|
K2
|
K3
|
t2,c
|
t3,c
|
t4,c
|
t5’’,c
|
t5’’’,c
|
|
Значение
|
2
|
24
|
0,4
|
75
|
22
|
1,0
|
0,25
|
1,8
|
0,6
|
2,0
|
1. Преобразование структурной схемы
системы
Для анализа нелинейных систем
необходимо так преобразовать структурную схему, что бы нелинейный элемент был
самостоятельным звеном, а вся остальная часть системы представляла бы собой
линейную часть.
При преобразовании следует соблюдать
следующие правила: нельзя перемещать звенья структурной схемы за нелинейный
элемент, так как сигнал на выходе нелинейного элемента существенно зависит от
величины входного сигнала, поэтому также не рекомендуется переносить за него
точки суммирования.
автоколебание
гармонический нелинейный логарифмический
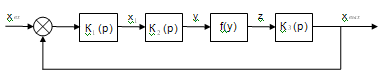
Рисунок 2. Структурная схема
исследуемой системы.
Для начала
перенесем точку сравнения входного сигнала и сигнала главной обратной связи за
элемент К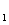
.
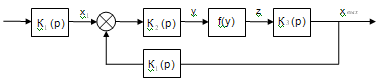
Рисунок 3.
Первый этап преобразования.
Так как
элемент, находящийся вне замкнутой системы, не оказывает влияния на её
динамические характеристики, входящим сигналом системы можно считать х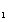
. Аналогично
поступаем с элементом К
.
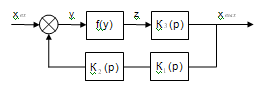
Рисунок 4. Второй этап
преобразования.
После незначительных изменений в
расположении элементов структурная схема принимает окончательный вид.
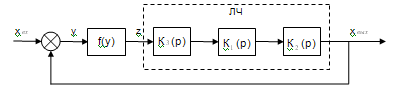
Рисунок 5. Преобразованная
структурная схема системы.
Передаточную функция линейного звена
можно определить следующим образом:
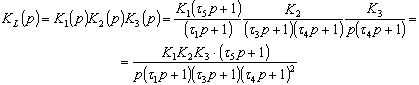
Как правило, управляющие системы
обладают свойством фильтра низких частот, т.е. они пропускают или не пропускают
с большим ослаблением вторые и более высокие гармоники.
Гармоническая линеаризация - это метод, позволяющий описать нелинейное звено
линейным уравнением, которое получается при пренебрежении высшими гармониками в
разложении нелинейной функции в ряд Фурье.
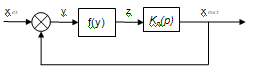
Рисунок 6.Типовая структурная
системы.
Уравнение линейной части:
,
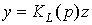При
возникновении автоколебаний процесс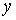 
на выходе линейной части не
является строго гармоническим, но мы будем полагать, что линейное звено
является фильтром нижних частот и подавляет все гармоники, за исключением
первой. Это предположение называется гипотезой фильтра. Если она не
подтверждается, то ошибки при применении гармонической линеаризации могут быть
значительными.
Пусть
; 
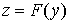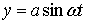
Представим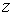 
в виде ряда
Фурье:
;
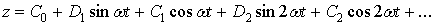Полагаем,
что
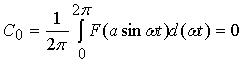
Это
справедливо, если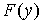 
симметрична
относительно начала координат и отсутствует внешнее воздействие. Полагая, что
высшие гармоники подавляются, будем искать только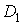 
и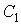 
Из уравнения (3) находим:
; 
.
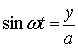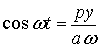Подставив
(6) в (4) и ограничив ряд слагаемыми первой гармоники, получим:
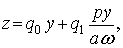
где
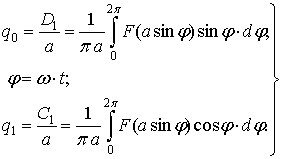
Таким
образом, нелинейное уравнение для 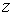заменили приближенным линейным
уравнением (7) для первой гармоник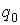и.
и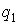 
называют гармоническими
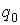коэффициентами передачи нелинейного звена. Коэффициенты и 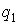в
рассматриваемом случае зависят от амплитуды, при более сложной нелинейной
зависимости зависят еще и от частоты.
Рассчитанные значения коэффициентов
гармонической линеаризации для типовых нелинейностей можно найти в учебниках и
справочной литературе.
Поскольку функция нелинейности
симметрична относительно начала координат, то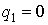 
.
Так согласно [1]
,
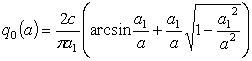где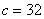 
, 
.
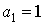Передаточная функция разомкнутой
системы может быть представлена в следующем виде:
;
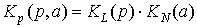где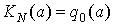 
─
эквивалентная передаточная функция нелинейно - го звена.
Частотная передаточная функция
разомкнутой системы
.
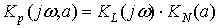Характеристическое
уравнение
.
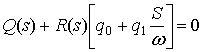Модуль
частотной передаточной функции нелинейного звена
.
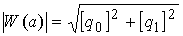Фазочастотная
характеристика
; (
)
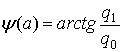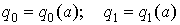Модуль
определяет отношение амплитуд, а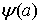 
фазовый сдвиг на выходе
относительно входного сигнала.
Если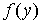 
симметрична относительно начала
координат, однозначна и не имеет гистерезиса, то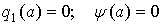 
и тогда
.
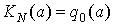Часто при
анализе используется величина обратная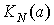 
. Она называется гармоническим
импедансом нелинейного звена:
.
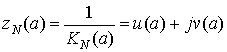В соответствии с критерием Найквиста
строится годограф частотной передаточной функции разомкнутой системы
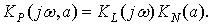
Условием возникновения в системе
колебаний является прохождение амплитудно-фазовой характеристики через точку
(-1,j0) комплексной плоскости. Для определения условий прохождения годографа
через эту точку приравняем
.
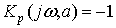Чтобы решить
это уравнение можно, задавая значение амплитуды, строить амплитудно-фазовую
характеристику(рис.3) Значение амплитуды а=А, при которой АФХ пройдет через
точку (-1,j0) будет соответствовать амплитуде собственных колебаний. Значение
частоты определяют по частоте в точке (-1,j0).
При
нелинейной зависимости вида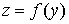 
передаточную функцию разомкнутой
системы можно представить в виде
.
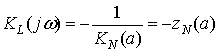Это
уравнение решается графическим методом. Строим амплитудно-фазовую
характеристику линейного звена и кривую импеданса нелинейного звена. Определяем
точку пересечения. Частоту 
определим по АФХ линейного звена в
точке пересечения. Амплитуду А определим по кривой импеданса нелинейного звена.
Итак, для анализа наличия
собственных колебаний в системе необходимо построить следующие функции
.
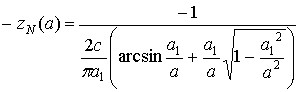
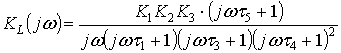Поскольку необходимо построение и
анализ двух сложных функций, двух переменных, а также при различных значениях
параметра t5, то целесообразно
воспользоваться средством компьютерного моделирования МаthCad 14.
Вначале определим исходные данные:
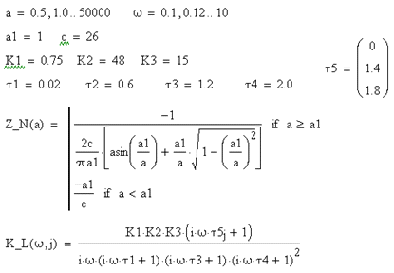
где а - значения амплитуды
колебаний, w=2pf
- значения круговой частоты, а1, с - параметры нелинейности, К1, К2, К3, t1,
t2, t3,
t4, t5,
- коэффициенты и параметры передаточной функция линейного звена.
Затем определим функции (21) и (22):
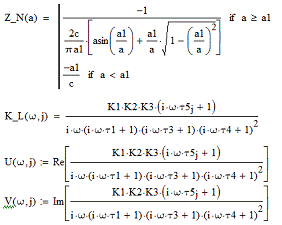
При определении передаточной функции линейного
звена К_L(w,j) использована дополнительная переменная j для
выбора значения параметра t5, при определении мнимой
единицы использован символ i.
Построим годографы звеньев и проанализируем на
предмет пересечения (рис 7).
По оси Y отложена мнимая составляющая
передаточной функции, по оси Х - действительная составляющая.
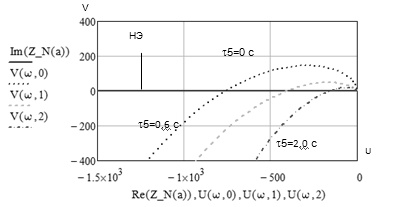
Рис.7. Годографы нелинейного и
линейного блоков..
Как видно из графиков, годографы НЭ
и линейного блока пересекаются, т.е. система неустойчива.
. Определение параметров
автоколебаний в системе, используя логарифмические характеристики системы
Благодаря методу гармонической
линеаризации становится возможным применение частотных методов для исследования
нелинейных систем. Задача исследования
устойчивости упрощается, если пользоваться логарифмическими частотными
характеристиками.
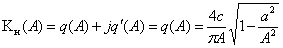
Запишем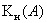 
в
показательной форме:
,
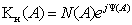где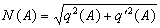 
- модуль
Введём относительную амплитуду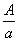 
,
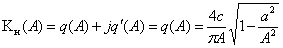где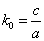 
-
нормирующий множитель
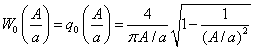- нормирующий коэффициент
Общая комплексная передаточная
функция нелинейной системы в разомкнутом состоянии:
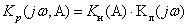
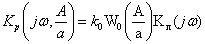
Предположим,
что замкнутая нелинейная система находится на границе устойчивости и в ней
имеют место незатухающие колебания. АФХ разомкнутой системы в этом случае,
согласно амплитудно-фазовому критерию устойчивости, должна проходить через
точку с координатами
(-1, j0),
т.е.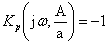 
. Отсюда
условие существования в замкнутой системе колебаний имеет вид
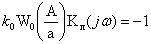
или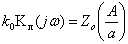 
. где
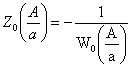
Запишем в показательной форме:
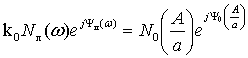
Из последней
формулы видно, что в системе возможны колебания, если одновременно выполняются
два условия:
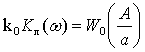и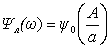 
или в
логарифмическом масштабе
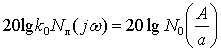
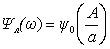
Первое условие будет выполняться при
пересечении логарифмических амплитудных характеристик ЛЧ и НЭ, а второе условие
- при пересечении их фазовых характеристик.
Колебания в системе будут возможны, если точка пересечения амплитудных
характеристик и точка пересечения фазовых характеристик соответствует одной и
той же частоте. Построим ЛАХ и ЛФХ линейной части.
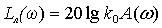
Как и ранее для расчёта и построения
характеристик воспользуемся программой и составим код расчёта:
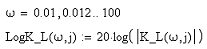
где w
- круговая частота, LogК_L() - функция (23), при
этом для построения ФЧХ используется функция arg(), рассчитывающей фазу
комплексного числа.
Рис.8 - Логарифмические
амплитудно-частотные и фазочастотные характеристики.
Видно, что точки пересечения ЛФЧХ с
линией -π лежит
значительно левее точки пересечения ЛАЧХ с осью абсцисс. Следовательно,
замкнутая система неустойчива. Частоты
собственных колебаний лежат в диапазоне от 0,3 до 0,7 рад/с. Поскольку система
неустойчива (при любом значении параметра t5),
то требуется корректирующее звено.
4. Ввод в систему коррекции и
избавление от автоколебаний
Чтобы избавиться от автоколебаний в
системе нужно, чтобы не выполнялось одно из условий существования автоколебаний
в системе.
Введём в линейную часть системы
дифференцирующие звено с передаточными функцией:
где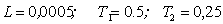 
Для расчёта корректирующего звена и
построения ЛАЧХ составим код:
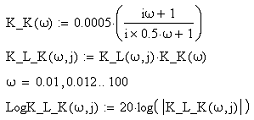
где К_К(ω)
- передаточная
функция корректирующего звена, К_L(ω) - передаточная
функция линейного каскада, К_L_K(ω) - линейный
каскад с корректирующим звеном.
На рисунке 9
представлены ЛАЧХ и логарифмические ФЧХ с учётом введения последовательного
корректирующего звена в систему.
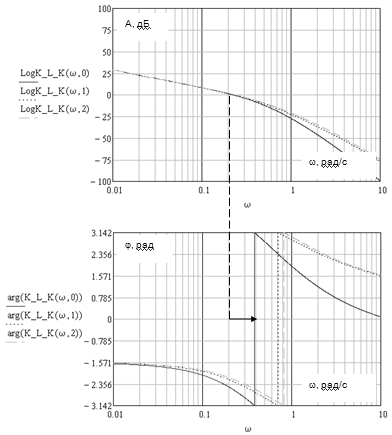
Рис. 9 -
Логарифмические амплитудно-частотные и фазочастотные характеристики системы с
корректирующем звеном.
Судя по
представленным характеристикам система должна быть устойчива, поскольку ЛАЧХ
пересекает линию нулевого усиления раньше, чем фазовая характеристика
пересекает фазовый сдвиг в -π.
Проверим
скорректированную систему на предмет наличия собственных колебаний по критерию
Найквиста. На рисунке 8 представлены годограф нелинейного и линейного блоков с
учётом введения корректирующего звена. Как видно по рисунку данные
характеристики не пересекаются, что свидетельствуют о том, что результирующая
система не имеет собственных колебаний, т.е. устойчива.
На рисунке 8
представлена структура системы с введённым последовательным корректирующим
звеном, назначение корой подавить собственные колебания системы.
Рис 10. - Структура системы с
введённым корректирующим звеном
Выводы
Анализ нелинейной системы сводится к
исследованию устойчивости и выявлению возможности возникновения автоколебаний.
Ввиду большого разнообразия нелинейных элементов не существует единого метода
анализа нелинейных систем.
Наибольшее применение получили метод
фазовой плоскости и метод гармонического баланса. Удобно производить
исследование устойчивости автоколебаний и особенно выбор корректирующих
устройств нелинейных систем методом логарифмических частотных характеристик.
Список литературы
1. Бесекерский В.А.,
Попов Е.П. Теория систем автоматического регулирования.- М.:Наука, 1975. - 768
с. 2.
. Воронов А.А. Основы
теории автоматического управления: Особые линейные и нелинейные системы. - 2-е
изд. перераб. и доп. - М.: Энергия, 1981. - 304 с.
3. Зайцев Г. Ф. Теория
автоматического управления и регулирования.- 2-е изд., перераб. и доп. Киев,
Издательство Вышая школа Головное издательство, 2004
. Ким Д. П. Теория
автоматического управления. Т. 2. Многомерные, нелинейные, оптимальные и
адаптивные системы: Учеб. пособие. - М.: ФИЗМАТЛИТ, 2004. - 64 с.
. Попов Е.П. Теория
линейных систем автоматического регулирования и управления. - М.:Наука, 1989.
. Теория автоматического
управления/Под ред. А.А. Воронова. - М.:Высшая школа, 1986. Ч.
1