Теоретические основы электротехники

Содержание

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Задача 6

Задача 1

К электрической цепи, схема которой показана на рисунке, приложено периодическое несинусоидальное напряжение u частотой f =50 Гц. Форма этого напряжения задана в табл. 2. Параметры L,R,C известны и выбираются из табл. 3 по номеру цепи и номеру приложенного напряжения. Требуется рассчитать ток i, протекающий в этой цепи. При расчетах ограничимся тремя первыми членами ряда Фурье.

Решение:

Функция обладает одновременно двумя видами симметрии. Она нечетная и вместе с тем симметричная относительно оси абсцисс. Поэтому в ее разложении присутствуют только синусоиды с нечетным порядковым номером, а значение интеграла, определяющего амплитуду (2k-1)-ой гармоники, вычисляется за четверть периода с умножением результата на 4. Тогда значение амплитуды Um2k-1 определяется выражением:

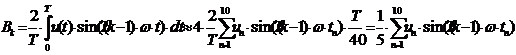. (6.1)

При использовании приближенного интегрирования период функции делится на равное число интервалов (в нашем случае их число N = 40) и производится замена dt = Т/N = Т/40. Однако, ввиду того, что значение функции определяется для конца интервала, и эти значения будут разными у двух симметричных интервалов, то с целью получения более точного результата за счёт компенсации положительной погрешности одного интервала отрицательной погрешностью симметричного интервала приближённое интегрирование должно выполняться за полпериода. Поэтому продолжим до половины периода.

Тогда последнее выражение (6.1) приводится к виду (суммирование за половину периода):

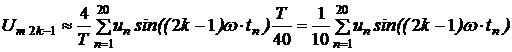,         (6.2)

где Т = 0,02 с - период функции u(t);= 1…20 - номер интервала приближенного интегрирования при Δt = T/40.

Используя данные и в соответствии с выражением (6.2) выполнив расчетные действия для амплитуд первых 10 гармонических составляющих (учитывая только нечетные), получим:

Um1 = 100 В; Um3 = -40 В; Um5 = 15 В; Um7 = 5 В; Um9 = -0,19 В.

Девятая гармоника, ввиду ее малости, может не учитываться в дальнейших действиях.

Определение мгновенного значения разложения функции u(t) в ряд Фурье (нечетные гармоники 1…9):

.

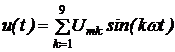Примечание: выражение для u(t), записанное в более привычной “литературной“ форме имеет вид:

u(t) = 100sin(wt) - 40sin(3wt) + 15sin(5wt) + 5sin(7wt) - 0,19sin(9wt).

Исходная электрическая схема цепи может быть упрощена и сведена к двухконтурной путем следующих преобразований:

1.      Контур с источник тока J1 преобразуем к ветви с ЭДС

.

2.      Контур с источником тока J8 и источником ЭДС E8 преобразуем к ветви с ЭДС

.

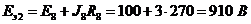3.      Последовательно соединенные сопротивления R5 и R6 с ведем к одному

.

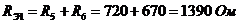4.      Последовательно соединенные сопротивления R3 и R4 с ведем к одному

.

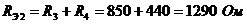5.      Треугольник сопротивлений RЭ1, RЭ2, R7 приведем к эквивалентной звезде с сопротивлениями:

Напряжение U27 может быть найдено из следующего выражения:

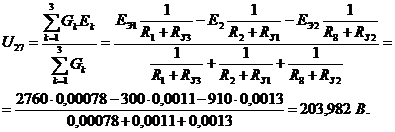
Токи I¢1, I2, I¢8, в направлениях, совпадающих с направлениями ЭДС этих ветвей, будут равны:

Остальные токи ветвей могут быть определены следующим путем :

1.      Напряжение U25 находим из II-го закона Кирхгофа для 2-й ветви:

.

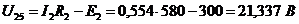2.      Напряжение U26 находим из II-го закона Кирхгофа для 8-й ветви:

.

.

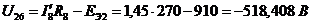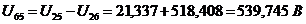4.     
Ток в направлении от 6-го узла к 4-му равен:

.

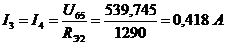5.      Ток 7-й ветви из I-го закона Киргофа для 5-го узла будет равен:

.

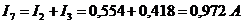6.      Ток 5-й ветви, в направлении от 6-го узла к 1-му, находим по I-му закону Кирхгофа для 6-го узла:

 .

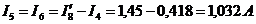7.      Токи через сопротивления R1 и R8 будут равны:

.

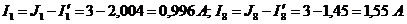Напряжение U32 равно:

.

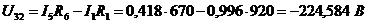Составим баланс мощностей всех источников и всех нагрузок. Мощность источников равна:

.

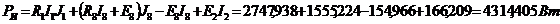Мощность всех приемников энергии равна:

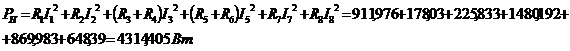
Очевидно, что расчет токов осуществлен верно, поскольку баланс мощностей наблюдается.

Задача 2

Электрические цепи, подключены к источнику постоянного напряжения U. Ключом К производится коммутация в этих цепях.

Решение:

Определим частоту сети:

.

Определим ЭДС:

;

;

.

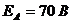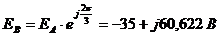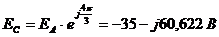Найдем сопротивления реактивных элементов:

;

.

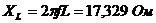Для симметричной трехфазной цепи справедливо:

;

;

.

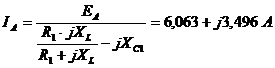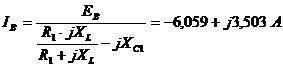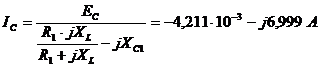Определим мощность:

.

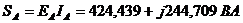Т.к. схема симметричная, то активная мощность всей цепи:

.

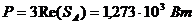Определим :

;

.

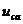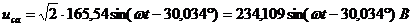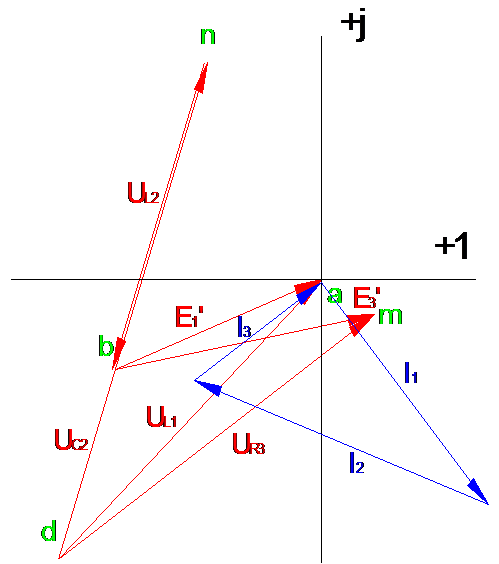
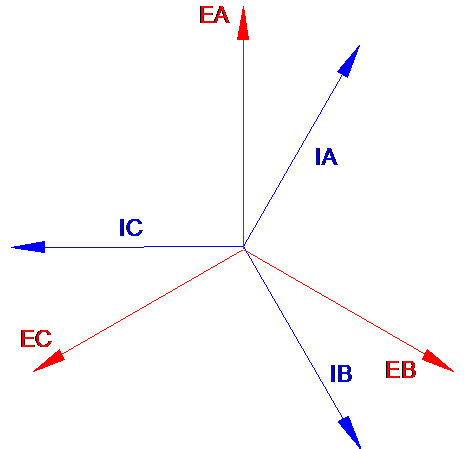
Построим векторную диаграмму:

Задача 3

Электрические цепи, подключены к источнику постоянного напряжения U. Ключом К производится коммутация в этих цепях.

Решение:

Определим частоту сети:

.

Определим ЭДС:

;

;

.

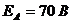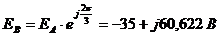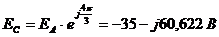Найдем сопротивления реактивных элементов:

;

.

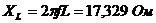Для симметричной трехфазной цепи справедливо:

;

;

.

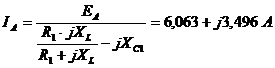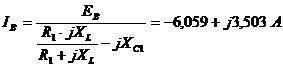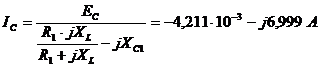Определим мощность:

.

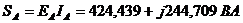Т.к. схема симметричная, то активная мощность всей цепи:

.

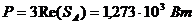Определим :

;

.

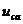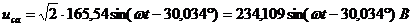Построим векторную диаграмму:

Задача 4

На рис. 4 показаны схемы электрических цепей постоянного тока с одним нелинейным элементом. Вольтамперные характеристики (ВАХ)нелинейных элементов цепей при положительных значениях тока (I ≥ 0) и напряжения (U ≥ 0) заданы аналитически двумя способами: либоI = αU + βU , либо U = aI + bI . Значения коэффициентов α и β или a и b, а также параметры линейных сопротивлений и источников энергии .

Требуется:

.Рассчитать токи во всех ветвях схемы.

.Определить напряжение на нелинейном элементе.

Решение:

Ток ветви цепи можно представить суммой токов обусловленных разностью потенциалов на концах ветви и действием источника ЭДС в ветви. Таким образом, токи будут выражены следующим образом:

Воспользовавшись последними тремя уравнениями системы (1) и выразив токи через узловые потенциалы, получим систему уравнений цепи относительно узловых потенциалов:

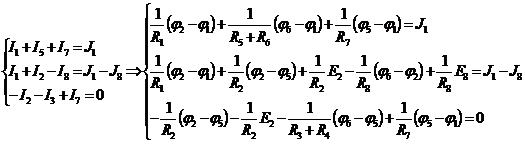(4)

Поскольку в системе (4) три уравнения и четыре неизвестных, то для ее решения один из потенциалов схемы заземляется (приравнивается 0) и система уравнений может быть упрощена. Положим , тогда получим:

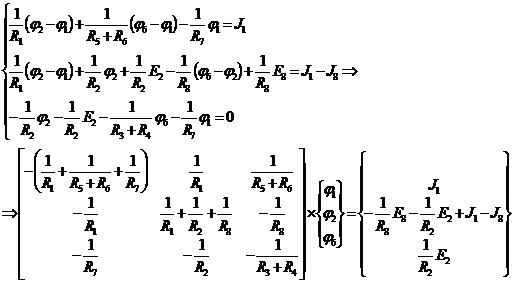(4а)

Система уравнений (4а) может быть решена с последующим определением искомых токов из уравнения (3):

цепь напряжение мощность кирхгоф

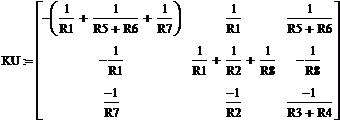
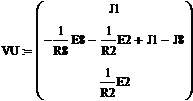
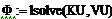
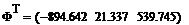
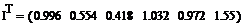
Задача 5

Сердечник и якорь П-образного магнита, имеет прямоугольные сечения различной площади. Размеры сердечника и якоря, величина зазора δ между ними, число витков обмотки w и величина силы притяжения якоря fя .

Решение:

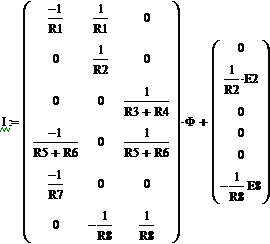
Согласно направлениям токов и обходам выбранных контуров можно записать систему уравнений цепи на основании законов Кирхгофа:

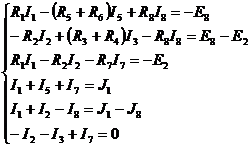(1)

В матричной форме система (1) имеет вид:

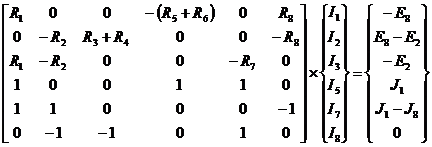(1а)

Решение системы (1а) при помощи ПО дает следующий результат:

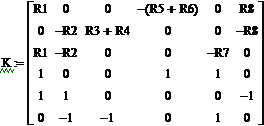
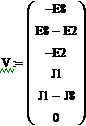
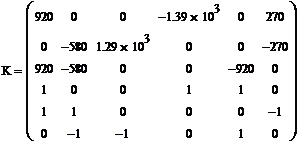
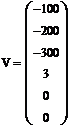
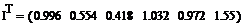
Задача 6

Электрические цепи с нелинейным инерционным сопротивлением, подключены к источнику синусоидального напряжения u = U m sin ωt , ω = 1000 рад/c. Вольтамперная характеристика

по действующим значениям нелинейного инерционного элемента задана аналитическим выражением U(I) = αI2.

Решение:

. Запишем уравнения Кирхгофа:

В дифференциальной форме:

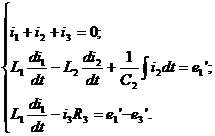
В символической форме:

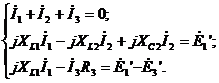
. Определим значения токов.

Используем формулы приведения для преобразования ЭДС:

.

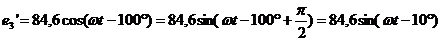Определим комплексный вид значения ЭДС:

;

.

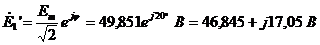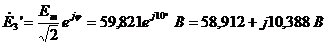Найдем сопротивления реактивных элементов:

;

;

.

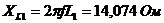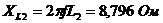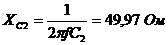Решим систему и определим токи в ветвях:

;

;

;

;

.

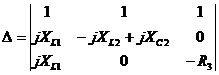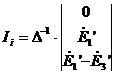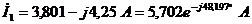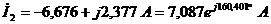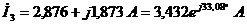. Определим показания ваттметра.

Чтобы определить показания ваттметра определим напряжение на его зажимах:

.

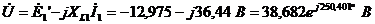Определим полную мощность этого участка цепи, развернув оси таким образом, чтобы напряжение совпало с действительной осью координат:

.

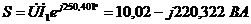Ваттметр будет показывать активную часть полной мощности:

.

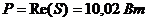Определим напряжения на всех элементах:

;

;

;

.

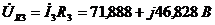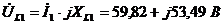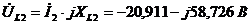Построим векторную диаграмму токов и топографическую диаграмму напряжений: