Расчет линейных электрических цепей переменного тока
Министерство образования Республики
Беларусь
Учреждение образования
«Гродненский государственный университет
имени Янки Купалы»
Технологический колледж
Специальность: 2-360331
«Монтаж и эксплуатация
электрооборудования»
Группа МиЭЭ-17з
КУРСОВАЯ
РАБОТА
по дисциплине
«Теоретические основы электротехники»
Расчет
линейных электрических цепей
переменного тока
Вариант №44
Разработал: Куликов А.Г.
Руководитель: Дубок Н.Д.
Задание на курсовую работу
Заданы три приёмника электрической энергии
со следующими параметрами: Z 1 = -j65
Ом, Z 2 = 14+j56
Ом, Z 3 =56- j23
Ом. Рассчитать режимы работы электроприёмников при следующих схемах включения:
1.Присоединить приёмники последовательно к
источнику с напряжением U = 300 В. Определить полное сопротивление цепи Z,
ток I, напряжения на участках, угол сдвига фаз, мощности
участков и всей цепи, индуктивности и ёмкости участков. Построить
топографическую векторную диаграмму цепи.
2. Присоединить приёмники параллельно к
источнику с напряжением
U = 300 В. Определить токи в ветвях и в неразветвленной части цепи, углы
сдвига фаз в ветвях и во всей цепи, мощности ветвей и всей цепи. Построить
векторную диаграмму цепи.
3. Составить из приёмников цепь с двумя
узлами, включив в каждую
ветвь соответственно электродвижущую силу E2=230 В и Е3
= j240 B. Рассчитать в комплексной форме токи в ветвях,
напряжения на участках, мощности источников и приёмников, составить уравнение
баланса мощностей. Построить векторную диаграмму в комплексной плоскости. Для
расчёта применить метод контурных токов.
4. Соединить приёмники в звезду с нулевым
проводом (ZN = -j32 Ом), и подключить их к трёхфазному источнику с
линейным напряжением UЛ =380 В. Определить фазные токи и напряжения
источника, напряжение смещения нейтрали и ток в нулевом проводе. Построить топографическую
векторную диаграмму в комплексной плоскости.
5. Соединить приёмники в треугольник и
подключить его к тому же источнику трехфазного напряжения. Определить фазные и
линейные напряжения и токи, мощности фаз и всей цепи. Построить векторную
диаграмму цепи в комплексной плоскости.
6. Присоединить приёмники последовательно
к источнику несинусоидального тока i=7Sin(wt+130)+1,2Sin(2wt-860)+0,4Sin3wt A. Определить действующие значения тока и напряжения,
активную мощность цепи. Записать уравнения мгновенных значений напряжения в
цепи. Значения сопротивлений считать для частоты первой гармоники.
Частоту напряжения считать равной f = 50
Гц.
1 Расчёт неразветвлённой цепи с помощью векторных
диаграмм
В задании на курсовую работу сопротивления
даны в комплексной форме. Так как расчёт цепи нужно выполнить с помощью
векторных диаграмм, определяем соответствующие заданным комплексам активные и
реактивные сопротивления: XС1= 65 Ом,
R2 = 14 Ом,
XL2=56 Ом, R3=56 Ом ,ХC3= 23 Ом.
Из заданных приёмников составляем
неразветвлённую цепь (рис. 1).
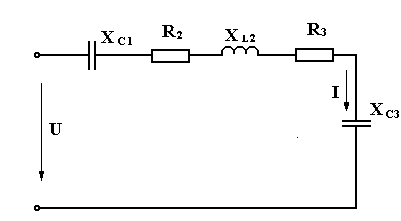
Рисунок 1
Определяем активные и реактивные
сопротивления всей цепи:
R = R2+ R3= 14 + 56 = 70 Ом;
X = -XC1+ XL2 – XC3 = - 65 +
56 - 23 = - 32 Ом.
Полное сопротивление всей цепи тогда
определяем из выражения:
Z = 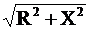 =
= 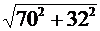 = 77 Ом.
= 77 Ом.
Ток в цепи будет общим для всех приёмников
и определится по закону Ома:
I = U / Z =
300/77 = 3.9 A.
Угол сдвига фаз между напряжением и током
определяется по синусу
Sin j = X / Z или
тангенсу Tg j = X / R,
так как эти функции являются нечётными и
определяют знак угла “плюс” или “минус”. Положительный знак угла указывает на
активно-индуктивный (или чисто индуктивный) характер нагрузки, а отрицательный
знак угла указывает на активно-ёмкостный (или чисто ёмкостный) характер. Таким
образом, угол сдвига фаз между напряжением и током определим по синусу
Sin j = X/Z = - 32/77
= - 0,4156;j = - 24.56°; Cos j = 0,9096.
Напряжения на участках цепи определяем
также из формулы закона Ома:
UC1= I * XC1 =
3.9 *65 =253.5 B.
UR2 = I * R2
= 3.9 * 14 = 54.6 B.
UL2 = I * XL2
= 3.9 * 56 = 19.5 B
UR3 = I * R3
= 3.9 * 56 = 19.5 B
UC3 = I * XC3 = 3.9 *
23 = 89.7 B.
Определяем активные и реактивные мощности
участков цепи:
QC1= I2 * XC1 =3.92 *65 = 989
вар.
P2 = I2 *
R2 =3.92 * 14 = 213 Bт.
QL2 = I2
* XL2 = 3.92*56 = 852 вар.
P3=I2*R3
= 3.92*56= 852 Вт
QС3 = I2 * XС3 = 3.92
*23 =350 вар.
Активная, реактивная и полная мощности
всей цепи соответственно будут равны:
P = P2+ P3= 213 +852 =1065 Вт.
Q = -QC1+ QL2 - QС3= -989+852- 350 = - 487 вар.
S = 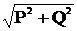 =
=
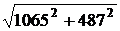 =1171 B*A.
=1171 B*A.
Полную, активную и реактивную мощности
всей цепи можно определить также по другим формулам:
S = U * I =300 *3.9
=1170 В*А.
Р = S * Cos j =1170* 0,9096 =1064 Вт,
Q = S * Sin j=1170*( -
0,4154) = - 486 вар.
Определяем ёмкость и индуктивность
участков. Угловая частота ω = 2 πf = 2 * 3,14 * 50 = 314 с-1
C1 = 1/wXc1=1/(314*65)=
0,000049 Ф = 49 мкФ
L2 = XL2/w = 56/314 = 0,178 Гн 
 С3 =
1/wXС3 = 1/(314*23) = 0,000138 Ф = 138 мкФ.
С3 =
1/wXС3 = 1/(314*23) = 0,000138 Ф = 138 мкФ.
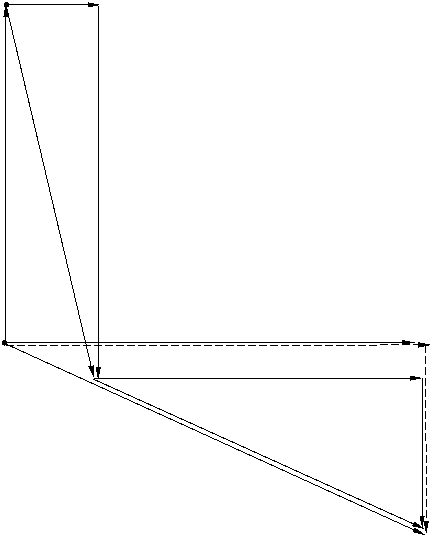
Для построения векторной диаграммы
задаёмся масштабами тока и напряжения, которые будут соответственно равны MI = 0,25 A/см и MU = 25 B/см.
Построение топографической векторной диаграммы
начинаем с вектора тока, который откладываем вдоль положительной горизонтальной
оси координат. Векторы напряжений на участках строятся в порядке обтекания их
током с учётом того, что векторы напряжений на активных элементах 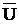 R2 и
R2 и 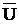 R3 совпадают по
фазе с током и проводятся параллельно вектору тока. Вектор напряжения на
индуктивности
R3 совпадают по
фазе с током и проводятся параллельно вектору тока. Вектор напряжения на
индуктивности 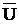 L2
опережает ток по фазе на угол 900 и поэтому откладывается на чертеже
вверх по отношению к току. Векторы напряжений на ёмкости
L2
опережает ток по фазе на угол 900 и поэтому откладывается на чертеже
вверх по отношению к току. Векторы напряжений на ёмкости 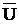 С1 и
С1 и 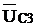 отстают от тока по фазе на угол 900
и откладываются на чертеже вниз по отношению к току. Вектор напряжения между
зажимами цепи проводится с начала вектора тока в конец вектора
отстают от тока по фазе на угол 900
и откладываются на чертеже вниз по отношению к току. Вектор напряжения между
зажимами цепи проводится с начала вектора тока в конец вектора 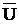 С3. На векторной диаграмме
отмечаем треугольник напряжений ОАВ, из которого активная составляющая напряжения
С3. На векторной диаграмме
отмечаем треугольник напряжений ОАВ, из которого активная составляющая напряжения
Uа = UR2 + UR3
и реактивная составляющая напряжения
Uр = -UС1 + UL2 – UС3.
Топографическая векторная диаграмма
построена на рисунке 2.
O 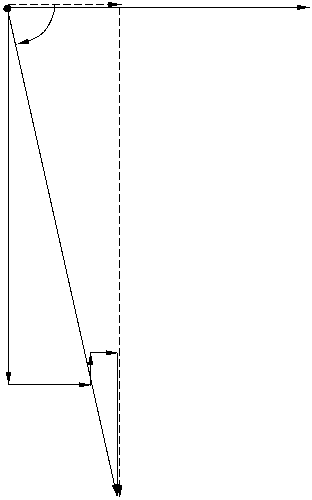
φ
MI = 0,5 А/см
МU = 25 В/см
UC1 U UP
UR3
UR2 UL2
UC3
Рисунок 2
Присоединяем заданные приёмники
параллельно к источнику напряжения. Это значит, что цепь состоит из трех
ветвей, для которых напряжение источника является общим. Схема цепи показана на
рисунке 3.
Расчёт параллельной цепи выполняем по
активным и реактивным составляющим токов.
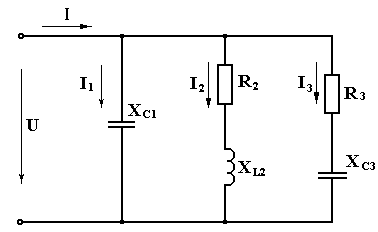
Рисунок 3
Этот метод предусматривает использование
схемы замещения с последовательным соединением элементов. В данном случае три
параллельные ветви рассматриваются как три отдельные неразветвлённые цепи,
подключенные к одному источнику с напряжением U. Поэтому в начале расчёта определяем
полные сопротивления ветвей:
Z1 = Хс1
= 65 Ом.
Z2 = 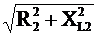 =
= 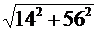 = 57.7
Ом.
= 57.7
Ом.
Z3 = 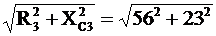 = 60.5 Ом.
= 60.5 Ом.
Углы сдвига фаз между напряжениями и
токами в ветвях определяются также по синусу (или тангенсу):
Sinφ1 = -1; j1 = - 90°;Cosφ1 = 0
Sinφ2 = XL2 / Z2 = 56 / 57.7 = O.9705; j2 = 76.05°; Cosφ2 = 0.241.
Sinφ3 = - XC3/Z3= - 23/60.5= - 0.38; φ3 = -
22.34°; Cosφ3 =
0.9249.
Затем можно определять токи в ветвях по
закону Ома:
I1 = U / Z1
=300 / 65 = 4.62 А.
I2 = U / Z2
= 300 / 57.7 = 5.2 А.
I3 = U / Z3
= 300 / 60.5 = 4.96 А.
Для определения тока в неразветвлённой
части цепи нужно знать активные и реактивные составляющие токов в ветвях и
неразветвленной части цепи:
Ip1 = I1*Sinj1= 4.62*(- 1) = - 4.62 A.
Ia2 = I2 * Cosφ2 = 5.2
* 0,241
= 1.25 A;
Ip2 = I2 * Sinφ2 = 5.2
* 0,9705 = 5.05 A;
Ia3 = I3*Cosj3 = 4.96*0.9249 = 4.59 A.
Ip3 = I3*Sinj3 = 4.96*(- 0.38) = - 1.88 A.
Активная и реактивная составляющие тока в
неразветвлённой части цепи:
Ia = Ia2 + Ia3
= 1.25+4.59 = 5.84 A.
Ip = Ip1 + Ip2 + Ip3 = - 4.62+5.05 – 1.88 = - 1.45 A.
Полный ток в неразветвлённой части цепи:
I = 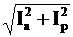 =
=
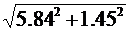 = 6.02 A.
= 6.02 A.
Угол сдвига фаз на входе цепи:
Sinφ
= IP / I = - 1.45/6.02 = - 0.2409; φ = -13.940;
Cosφ = 0.9706.
Активные, реактивные и полные мощности
ветвей:
QC1 = I12
*XC1= 4.622 *65 = 1387 вар.
S1 = U*I1
= 300*4.62 = 1387 B*A.
P2 = I22
* R2 = 5.22* 14 = 379 Вт.
QL2 = I22
* XL2 = 5.22 * 56 =1514 вар.
S2 = U * I2
= 300 * 5.2 =1560 В*А.
P3 = I32*R3
= 4.962*56 = 1378 Bт
QC3 = I32
* XC3 = 4.962 * 23 =566 вар.
S2 = U * I2 = 300 *4.96 = 1488 В*А
Активные, реактивные и полные мощности
всей цепи:
P = P2 + P3 = 379 + 1378 =1757 Вт.
Q = - QC1 + QL2 - QC3 = - 1387
+1514 -566 = - 439 вар.
S = 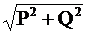 =
=
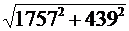 = 1811
В*А, или
= 1811
В*А, или
S = U * I = 300*6.02 = 1806 В*А.
P = S * Cosφ
= 1806 * 0,9706 = 1753
Вт.
Q = S * Sinφ
= 1806*(- 0.2404) = - 434 вар.
Для построения векторной диаграммы
задаёмся масштабами напряжений MU = 25 В/см и токов MI =
0.5 А/см. Векторную диаграмму начинаем строить с вектора напряжения, который
откладываем вдоль горизонтальной положительной оси. Векторная диаграмма токов
строится с учётом того, что активные токи Ia2 и Ia3
совпадают по фазе с напряжением, поэтому их векторы параллельны вектору
напряжения; реактивный индуктивный ток Ip2 отстает по фазе от
напряжения, и его вектор строим под углом 900 к вектору напряжения в
сторону отставания; реактивные емкостные токи Ip1 и Ip3 опережают по фазе
напряжение, и их векторы строим под углом 90° к вектору
напряжения в сторону опережения. Вектор тока в неразветвлённой части цепи
строим с начала построения в конец вектора емкостного тока Ip3. Векторная диаграмма
построена на рисунке 4.
Ia2

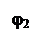 MI = 0,5 А/см
MI = 0,5 А/см
МU = 25 В/см
I2
I1=Ip1 Ip2
OIa U
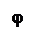
 Ia3
Ia3
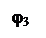
 I3 Ip3 Ip
I3 Ip3 Ip
I
3 Расчёт сложных цепей
переменного тока символическим методом
Электрическая схема цепи и комплексная
схема замещения представлены на рисунке 5а и б соответственно.
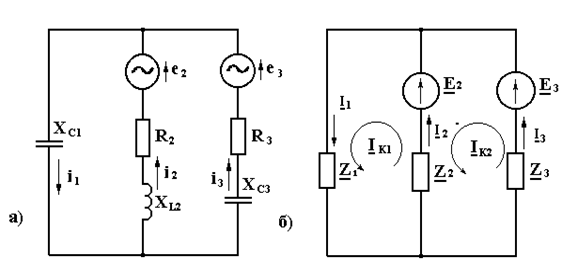
Рисунок 5
Намечаем в независимых контурах заданной
цепи, как показано на рисунке 5б, контурные токи IK1 и IK2 – некоторые расчётные
комплексные величины, которые одинаковы для всех ветвей выбранных контуров.
Направления контурных токов принимаются произвольно. Для определения контурных
токов составляем два уравнения по второму закону Кирхгофа:
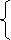 IK1*(Z1 + Z2)
– IK2*Z2 = E2
IK1*(Z1 + Z2)
– IK2*Z2 = E2
- IK1*Z2+IK2*(Z2+Z3)=
E3 - E2
Подставляем данные в систему:
IK1*(- j65+14+j56)
– IK2*(14+j56)
= 230
-IK1*(14+j56) +IK2 *(14+j56+56
– j23) = j240-230
IK1*(14-j9) –
IK2*(14+j56)
= 230
-IK1*(14+j56) + IK2*(70+j33)
= -230+ j240
Решаем систему с помощью определителей.
Определитель системы:
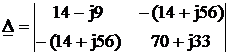 =1277-j168+2940–
j1568=4217-j1736
=1277-j168+2940–
j1568=4217-j1736
Частные определители :
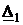 =
=  = 16100+j7590–16660-j9520=
-560–j1930.
= 16100+j7590–16660-j9520=
-560–j1930.
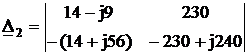 =-1060+j5430+3220+j12880
= 2160+j18310
=-1060+j5430+3220+j12880
= 2160+j18310
Определяем контурные токи:
IK1 = 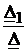 =
= 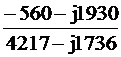 = 0.0476-j0.438 A.
= 0.0476-j0.438 A.
IK2 = 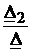 =
= 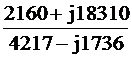 = - 1.09+ j3.89 A.
= - 1.09+ j3.89 A.
Действительные токи в ветвях цепи
определяем как результат наложения контурных токов:
I1 = IK1 = 0.0476 – j0.438 = 0.441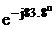 A
A
I2 = IK1-IK2 =
0.0476.- j0.438+1.09- j3.89 = 1.14 – j4.33 = 4.48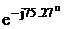 A
A
I3 = IK2 = -1.09 + j3.89 = 4.04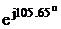 A.
A.
Составляем уравнение баланса мощностей в
заданной электрической цепи. Определяем комплексные мощности источников:
SE2 = E2*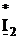 =230(1.14+j4.33) = 262+j996=1030
=230(1.14+j4.33) = 262+j996=1030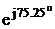 B*A
B*A
SE23= E3*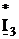 = j240*(-1.09 – j3.89) = 912 – j262
= 949
= j240*(-1.09 – j3.89) = 912 – j262
= 949 B*A
B*A
Определяем комплексные мощности приёмников
электрической энергии:
S1 = I12*Z1
=0.4412*( – j65) = – j12.6 =12.6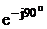 B*A
B*A
S2 = I22*Z2 =
4.482*(14+j56) = 281+j1124=1159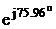 B*A
B*A
S3 = I32*Z3 = 4.042*(56 – j23)
= 914– j375 =988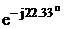 B*A.
B*A.
Уравнение баланса комплексных мощностей!
SЕ1 + SE2 = S1 + S2 + S3;
262+j996+912-j262 = –
j12.6+281+j1124+914– j375
1174+ j734 @ 1182+ j749; 1385 @ 1400
@ 1400 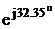
Относительная и угловая погрешности незначительны.
Для построения векторной диаграммы
задаёмся масштабами токов MI = 0.25 А/см и ЭДС ME =
50 В/см. Векторная диаграмма в комплексной плоскости построена на рисунке 6.
4 Расчёт трёхфазной цепи
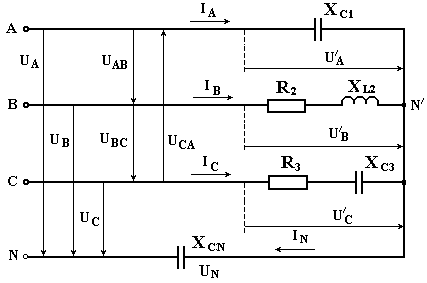
при соединении приемника в звезду
Схема заданной цепи изображена на рисунке
7.
Определяем систему фазных напряжений
генератора. Фазное напряжение:
UФ = Uл/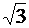 =
380/1,73=220 В.
=
380/1,73=220 В.
Комплексные фазные напряжения генератора:
UA = UФ = 220 B
UB = UAe-j120 = 220e-j120 = –110 – j191 B
UC = UAej120 = 220ej120 = –110
+ j191 B
Определяем полные проводимости фаз приёмника:
YA = 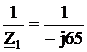 =
j0,01538 См.
=
j0,01538 См.
YB = 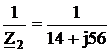 =
0.0042-j0.0168 См.
=
0.0042-j0.0168 См.
YC = 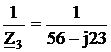 =
0.0153+j0.00628Cм.
=
0.0153+j0.00628Cм.
YN=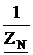 =
=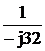 = j0.03125 См.
= j0.03125 См.
Рисунок
7
Узловым напряжением является в данном
случае напряжение смещения нейтрали, которое определяется по формуле:
UN=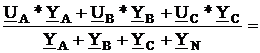

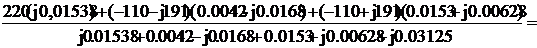
= (j3.38-3.67+j1.05-2.88+j2.23)/(0.05075+j0.00486)
= (-6.55+j6.66)/(0.0195+j0.03611)= 67+j218
= 228 B.
B.
Определяем фазные напряжения на нагрузке:
UA/ = UA – UN = 220- (67+j218) =
153-j218 = 266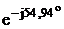 B.
B.
UB/ = UB – UN = (–110-j191) - (67+j218)
= -177-j409 =446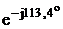 B.
B.
UC/ = UC–UN=(–110+j191) - (67+j218) =
-177 – j27 = 179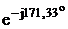 B.
B.
Определяем токи в фазах нагрузки:
IA = UA/*YA
= (153-j218)*(j0.01538) = 3.35+j2.35 = 4.1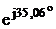 A.
A.
IB = UB/*YB
= (-177-j409)*(0.0042-j0.0168) = -7.61+j1.26 =7.72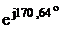 A.
A.
IC=UC/*YC=
(-177 – j27)*(0.0153+j0.00628)=- 2,53–j1,52= 2,96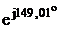 A.
A.
IN = UN*YN = (67+j218)*j0.03125
= - 6,8 + j2,09 = 7,12*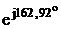
Проверяем правильность определения токов
по первому закону Кирхгофа для точки N’:
IA + IB
+ IC =IN
3.35+j2.35 -7.61+j1.26 - 2,53 –
j1,52 @ - 6,8 + j2,09;
- 6,79+j2.09 @ - 6,8 + j2,09.
Определяем комплексные мощности фаз и всей
цепи:
SB = IB2 * Z2 =
7,722*(14+j56) = 834+j3338 =3440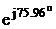 B*A
B*A
SC = IC2 * Z3 =
2,962*(56-j23) = 491 – j 202 = 530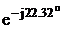 B*A.
B*A.
S= SA
+ SB + SC = -j1092+ 834+j3338+ 491 – j 202
= 1325+j2044 =
= 2436 B*A.
B*A.
Для построения векторной диаграммы
задаёмся масштабами токов MI = 1 А/см и напряжений MU =
40 B/см. Векторная диаграмма на комплексной плоскости
построена на рисунке 8.
5
Расчёт трёхфазной цепи при соединении приёмника в треугольник
Схема заданной цепи изображена на рисунке
9
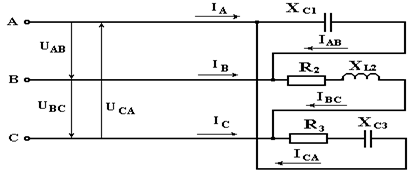
Рисунок 9.
В данном случае линейные напряжения
генератора являются фазными
напряжениями нагрузки:
UAB = UЛ = 380 В.
UBC = 380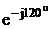 = -190-j329 B.
= -190-j329 B.
UCA = 380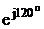 = -190+j329 B.
= -190+j329 B.
Определяем систему фазных токов нагрузки:
IAB =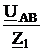 =
= 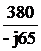 = j5,85 = 5,85
= j5,85 = 5,85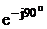 A
A
IBC = 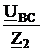 =
= 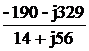 = -6,32+j1,81 = 6,58
= -6,32+j1,81 = 6,58 A
A
ICA = 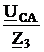 =
=
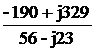 = -4,96+j3,83
= 6,27
= -4,96+j3,83
= 6,27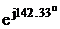 A
A
Систему линейных токов определяем из
соотношений:
IA = IAB – ICA =
j5,85+4,96-j3,83 = 4,96+j2,02 = 5,36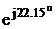 A
A
IB = IBC – IAB =
-6,32+j1,81-j5,85 = -6,32-j4,04 = 7,5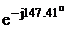 A
A
IC = ICA – IBC =
-4,96+j3,83+6,32-j1,81 = 1,36+j1,92 =2,35 A
A
Определяем
мощности фаз приемника:
SAB =IAB2*Z1 = 5,852*(-j65)
= -j2224 = 2224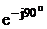 B*A.
B*A.
SBC = IBC2*Z2
= 6,582*(14+j56) = 606+j2425 = 2499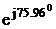 B*A.
B*A.
SCA = ICA2*Z3
= 6,272*(56 – j23) =2201– j904 = 2380*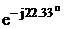 B*A.
B*A.
Определяем
мощность трехфазной нагрузки:
SAB +SBC +SCA = -j2224+606+j2425+2201– j904
=2807 – j703 =
=
2894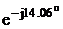 B*A.
B*A. 
Для построения векторной диаграммы
задаёмся масштабами токов MI =1 A/см и напряжений MU =
50A/см. Векторная диаграмма построена на рисунке 10.
6 Расчёт
неразветвлённой цепи с несинусоидальными напряжениями и токами
Составляем схему заданной цепи, подключая
последовательно соединённые приёмники к источнику несинусоидального напряжения,
под действием которого в цепи возникает ток с мгновенным значением
i=7Sin(wt+130)+1,2Sin(2wt-860)+0,4Sin3wt A, который на схеме замещения представляем как
последовательно соединённые три источника переменного напряжения u1,
u2 и u3 c разными частотами (рисунок 11)
Величины сопротивлений заданы для частоты
первой гармоники:
XC11 = 18
Ом, R2 = 23 Ом,
XL21 = 14
Ом, R3 = 12 Ом,
XC31 = 62
Ом. Поскольку напряжения источников имеют разные частоты, то и реактивные
сопротивления для них будут иметь разные величины. Активные сопротивления
считаем от частоты не зависящими. Поэтому расчёт ведём методом наложения, то
есть отдельно для каждой гармоники.
. 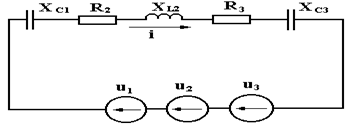
Рисунок 11.
Первая гармоника
Определяем активное и реактивное
сопротивления всей цепи:
R = R2 + R3
= 14+56 = 70 Ом. X1 = -XC11+ XL21- XC31
= - 65+56–23 =
= -32 Ом.
Полное сопротивление цепи:
Z1 = 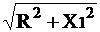 =
= 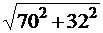 = 76,7
Ом.
= 76,7
Ом.
Амплитудные значения напряжения и тока:
Im1 = 7 A, Um1 = Im1*Z1= 7*76.7 =537 B.
Действующие значения напряжения и тока:
U1 = Um1 /  = 537 /
1,41 = 381 B.
= 537 /
1,41 = 381 B.
I1 = Im1 /  = 7 /
1,41 = 4.96 A.
= 7 /
1,41 = 4.96 A.
Угол сдвига фаз между напряжением и током
определяем по синусу:
Sinφ1 = X1/Z1 =
-32/76.7 = - 0.4172. j1= - 24.66°, Cosφ1=0.9088.
Активная и реактивная мощности первой
гармоники:
P1 = I12 * R =
4.962 * 70 =1722 Вт.
Начальная фаза тока определяется из
соотношения:
φ1 = yU1 – yI1, отсюда yU1 =yI1 + j1 = 13°- 24.66°= - 11.66°
Мгновенное значение напряжения первой гармоники
u1= Um1 * Sin (ωt + yU1) = 537 * Sin (ωt – 11.66°) B.
Вторая гармоника.
Для остальных гармоник напряжения расчёты
приводим без дополнительных разъяснений.
X2= XC11/ 2 + XL21* 2 - XC31 / 2 =
-65/ 2 + 56* 2 - 23 / 2 = 68 Ом.
Z2=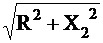 =
=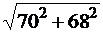 =97.6 Ом,
=97.6 Ом,
Im2=1.2 A, Um2=
Im2 *Z2=1.2*97.6 =117 B.
U2= Um2/ =117 / 1,41 = 83 B.I2= Im2/
=117 / 1,41 = 83 B.I2= Im2/ = 1.2 / 1,41 = 0.85 A.
= 1.2 / 1,41 = 0.85 A.
Sin φ2= X2/
Z2= 68/97.6= 0,6967.j2 = 44.16°, Cos φ2 = 0,7173.
P2 = I22
* R2 = 0.852 *70 = 51 Вт.
yU2 =yI2 + j2 = -86°+ 44.16°= - 41.9°
u2= Um2 *
Sin (2ωt + yU2) = 117 * Sin (2ωt
– 41.9°) B.
Третья гармоника
X3= XC11 /3 + XL11* 3 – XC31 / 3 = -
65 / 3 + 56* 3 - 23 / 3 =139 Ом.
Z3 = 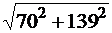 =
156 Ом. Im3 =0.4 A, Um3 = Im3
*Z3 =0.4 *156 =
=
156 Ом. Im3 =0.4 A, Um3 = Im3
*Z3 =0.4 *156 =
= 62.4 B.
Sin φ3 = X3 / Z3 =139 /156 =
0,891. j3 = 63°. Cos φ3 = 0,454.
P3 = I32
* R = 0.282 *70 = 0.5 Вт.
yU3 =yI3 + j3 = 63°.
u3= Um3 *
Sin (3ωt + yU3) =44.3 * Sin (3ωt
+63°) B.
Определяем действующие значения тока и
напряжения:
I = 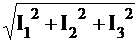 =
=
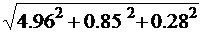 = 5.04 A.
= 5.04 A.
U = 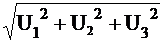 =
=
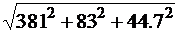 = 559 B.
= 559 B.
Активная и реактивная мощности цепи:
P = P1+P2+P3=1722+51+0.5=1774
Вт.
Средневзвешенный коэффициент мощности
цепи:
Cos Х = Р / (U * I) = 1774/ (559 *5.04) =
0,6296.
Уравнение мгновенных значений напряжения
между зажимами цепи:
u=u1+u2+u3=537
* Sin (ωt – 11.66°)+117 * Sin (2ωt
– 41.9°)+
+44.3 * Sin (3ωt +63°) B.
Литература
1.
Ф.Е. Евдокимов. Теоретические
основы электротехники. - М. “Высшая школа “,1981 г.
2.
В.С. Попов. Теоретическая
электротехника. – М. “Энергия”,
1978 г.
3.
Ю.В. Буртаев, П. И. Овсянников.
Теоретические основы электротехники.– М. “Энергоатомиздат”, 1984 г.
4.
Л.А. Частоедов. Электротехника. -
М. “Высшая школа”, 1984 г.
5.
М.Ю. Зайчик. Сборник задач и
упражнений по теоретической электротехнике. – М. “Энергоатомиздат” , 1988 г.