Простейшие системы массового обслуживания
Федеральное
агентство связи
ФГОБУ
ВПО «Сибирский государственный университет
телекоммуникаций
и информатики»
Уральский
технический институт связи и информатики (филиал)
Кафедра
информационных систем и технологий
массовый обслуживание отказ поток
КУРСОВОЙ
ПРОЕКТ
По
дисциплине: «Теория массового обслуживания»
На
тему: «Простейшие системы массового обслуживания»
Вариант
№ 26
Выполнил:
студент
группыПЕ-31б
Хашимов О.Р.
Руководитель:
ст.
преподаватель
Поведа Т.В.
г.
Екатеринбург, 2017г.
Введение
При исследовании операций часто
приходится сталкиваться с системами, предназначенными для многоразового
использования при решении однотипных задач. Возникающие при этом процессы
получили название процессов обслуживания, а системы - систем массового обслуживания
(СМО). Примерами таких систем являются телефонные системы, ремонтные
мастерские, вычислительные комплексы, билетные кассы, магазины, парикмахерские.
Под системой массового обслуживания
(СМО) понимают динамическую систему, предназначенную для эффективного
обслуживания потока заявок (требований на обслуживание) при ограничениях на
ресурсы системы. Совокупность взаимосвязанных СМО называется сетью массового
обслуживании (стохастической сетью).
Модели СМО удобны для описания
отдельных подсистем современных систем, в том числе и вычислительных, таких как
подсистема - процессор - основная память, канал ввода-вывода и т. д. Система в
целом представляет собой совокупность взаимосвязанных подсистем, взаимодействие
которых носит вероятностный характер. Заявка на решение некоторой задачи,
поступающая в систему, проходит последовательность этапов счета, обращения.
После выполнения некоторой последовательности таких этапов, заявка считается
обслуженной и покидает систему. Таким образом, систему в целом можно представлять
совокупностью СМО, каждая из которых отображает процесс функционирования
отдельного устройства или группы однотипных устройств, входящих в состав
системы. Этим обусловлена актуальность темы курсового проекта.
1.
Цели и задачи
Цель дисциплины «Системы массового
обслуживания» заключается в освоении студентами математической базы,
позволяющей исследовать и проектировать системы подвижной радиосвязи как
системы массового обслуживания (СМО). Преподавание ее предусматривает
ознакомление студентов с существующими типами СМО, овладением ими основных
методов анализа эффективности СМО, умением распространить математические методы
к решению конкретных задач с применением ПЭВМ
Курсовой проект является важной
составляющей курса и самостоятельной работой студента. Курсовой проект
завершает подготовку по дисциплине «Теория массового обслуживания».
Темой курсового проекта является
«Простейшие системы массового обслуживания». В ходе курсового проектирования
проводитсясравнительный анализ эффективности простейших систем массового
обслуживания.
К изучаемым системам относятся:
) cистемы с отказами;
) cистемы с ограничением на длину
очереди.
Задача анализа СМО заключается в
определении ряда показателей ее эффективности, которые можно разделить на
следующие группы:
показатели, характеризующие систему
в целом: число n занятых каналов обслуживания, число обслуженных (λb),
ожидающих обслуживание или получивших отказ заявок (λc)
в единицу времени и т.д.;
вероятностные характеристики:
вероятность того, что заявка будет обслужена (Pобс) или получит отказ в
обслуживании (Pотк), что все приборы свободны (p0) или определенное число их
занято(pk), вероятность наличия очереди и т.д.;
экономические показатели: стоимость
потерь, связанных с уходом не обслуженной по тем или иным причинам заявки из
системы, экономический эффект, полученный в результате обслуживания заявки, и
т.д.
Необходимость в использовании
экономических показателей связана с противоречивостью влияния выбора ряда
показателей на свойства изучаемой системы.
Часть технических показателей
(первые две группы) характеризуют систему с точки зрения потребителей, другая
часть - характеризует систему с точки зрения её эксплуатационных свойств. Выбор
показателей, улучшающих эксплуатационные свойства системы, ухудшает систему с
точки зрения потребителей и наоборот. Использование экономических показателей
позволяет разрешить указанное противоречие и оптимизировать систему с учетом
обеих точек зрения.
В ходе выполнения курсового проекта
изучаются три типа простейших систем массового обслуживания: системы с отказами
и два типа смешанных систем - с ограничениями на время пребывания в очереди и с
ограничениями на длину очереди. Это системы разомкнутого типа, бесконечный
источник заявок в систему не входит. Входной поток заявок, потоки обслуживания
и ожидания этих систем являются простейшими, то есть пуассоновскими
стационарными потоками.
2.Теоретические
сведения
.1 Основные понятия
Теория массового обслуживания
опирается на теорию вероятностей и математическую статистику. Первоначальное развитие
теории массового обслуживания связано с именем датского ученого А.К.
Эрланга(1878-1929),с его трудами в области проектирования и эксплуатации
телефонных станций.
Теория массового обслуживания -
область прикладной математики, занимающаяся анализом процессов в системах
производства, обслуживания, управления, в которых однородные события
повторяются многократно, например, на предприятиях бытового обслуживания; в
системах приема, переработки и передачи информации; автоматических линиях
производства и др. Большой вклад в развитие этой теории внесли российские
математики А.Я. Хинчин, Б.В. Гнеденко, А.Н. Колмогоров, Е.С. Вентцель и др.
Предметом теории массового
обслуживания является установление зависимостей между характером потока заявок,
числом каналов обслуживания, производительностью отдельного канала и
эффективным обслуживанием с целью нахождения наилучших путей управления этими
процессами. Задачи теории массового обслуживания носят оптимизационный характер
и в конечном итоге включают экономический аспект по определению такого,
варианта системы, при котором будет обеспечен минимум суммарных затрат от
ожидания обслуживания, потерь времени и ресурсов на обслуживание и от простоев
каналов обслуживания.
В коммерческой деятельности
применение теории массового обслуживания пока не нашло желаемого
распространения.
В основном это связано с трудностью
постановки задач, необходимостью глубокого понимания содержания коммерческой
деятельности, а также надежного и точного инструментария, позволяющего
просчитывать в коммерческой деятельности различные варианты последствий
управленческих решений.
Каждая СМО состоит из определенного
числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые
будем называть каналами обслуживания. Каналами могут быть линии связи, рабочие
точки, вычислительные машины, продавцы и др. По числу каналов СМО подразделяют
на одноканальные и многоканальные.
Заявки поступают в СМО обычно не
регулярно, а случайно, образуя так
называемый случайный поток заявок.
Обслуживание заявок продолжается какое-то случайное время. Случайный характер
потока заявок и времени обслуживания приводит к тому, что СМО оказывается
загруженной неравномерно: в какие-то периоды времени скапливается очень большое
количество заявок (они либо становятся в очередь, либо покидают СМО
необслуженными), в другие же периоды СМО работает с недогрузкой или
простаивает.
В качестве показателей эффективности
СМО используются: среднее число заявок, обслуживаемых в единицу времени;
среднее число заявок в очереди; среднее время ожидания обслуживания;
вероятность отказа в обслуживании без ожидания; вероятность того, что число
заявок в очереди превысит определенное значение и т.п.
СМО делят на два основных типа: СМО
с отказами и СМО с ожиданием (очередью).
В СМО с отказами заявка, поступившая
в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем
процессе обслуживания не участвует (например, звонок на телефонный номер в
момент, когда абонент занят разговором, получает отказ). В СМО с ожиданием
заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в
очередь на обслуживание.
СМО с ожиданием подразделяются на
разные виды в зависимости от того, как организована очередь: с ограниченной или
неограниченной длиной очереди, с ограниченным временем ожидания и т.п.
Для классификации СМО важное
значение имеет дисциплина обслуживания, определяющая порядок выбора заявок из
числа поступивших и порядок распределения их между свободными каналами. По
этому признаку обслуживание заявки может быть организовано по принципу
"первая пришла - первая обслужена", "последняя пришла - первая
обслужена" (такой порядок может применяться, например, при извлечении для
обслуживания изделий со склада, ибо последние из них оказываются часто более
доступными) или обслуживание с приоритетом (когда в первую очередь
обслуживаются наиболее важные заявки). Приоритет может быть как абсолютным,
когда более важная заявка"вытесняет" из-под обслуживания обычную
заявку (например, в случае аварийной ситуации плановые работы ремонтных бригад
прерываются до ликвидации аварии), так и относительным, когда более важная
заявка получает лишь "лучшее" место в очереди.
Математический анализ работы СМО
очень облегчается, если процесс этой работы - марковский. Для этого достаточно,
чтобы все потоки событий, переводящие систему из состояния в состояние (потоки
заявок, потоки «обслуживаний»), были простейшими. Если это свойство нарушается,
то математическое описание процесса становится гораздо сложнее и довести его до
явных, аналитических формул удается лишь в редких случаях. Однако все же
аппарат простейшей, марковской теории массового обслуживания может пригодиться
для приближенного описания работы СМО даже в тех случаях, когда потоки событий
- не простейшие. Во многих случаях для принятия разумного решения по
организации работы СМО вовсе и не требуется точного знания всех ее
характеристик - зачастую достаточно и приближенного, ориентировочного. Причем,
чем сложнее СМО, чем больше в ней каналов обслуживания, тем точнее оказываются
эти приближенные формулы.
Существуют СМО с так называемым
многофазовым обслуживанием, состоящим из нескольких последовательных этапов или
«фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар,
затем оплатить его в кассе, затем получить на контроле).
Кроме этих признаков, СМО делятся на
два класса: «открытые» и «замкнутые». Воткрытой СМО характеристики потока
заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято).
В замкнутой СМО - зависят. Например, если один рабочий обслуживает группу
станков, время от времени требующих наладки, то интенсивность потока
«требований» со стороны станков зависит от того, сколько их уже неисправно и
ждет наладки.
В зависимости от типа СМО при оценке
её эффективности могут применяться те или иные величины (показатели
эффективности). Например, для СМО с отказами одной из важнейших характеристик
её продуктивности является так называемая абсолютная пропускная способность -
среднее число заявок, которое может обслужить система за единицу времени. Наряду
с абсолютной, часто рассматривается относительная пропускная способность -
средняя доля поступивших заявок, обслуживаемая системой (отношение среднего
числа обслуживаемых в единицу времени заявок к среднему числу поступающих
заявок за это время). Помимо этого при анализе СМО с отказами могут
интересовать ещё среднее число занятых каналов, среднее относительное время
простоя системы в целом и отдельного канала и т.д.
Характеристики СМО с ожиданиями. Для
СМО с неограниченным ожиданием абсолютные и относительные пропускные
способности теряют смысл. Зато важными являются: среднее число заявок в
очереди, среднее число заявок в системе (в очереди и под обслуживанием),
среднее время ожидания заявки в очереди, среднее время пребывания заявки в
системе и другие. Для СМО с ограниченным ожиданием интерес представляют обе
группы характеристик.
Теория систем массового обслуживания
(СМО) посвящена разработке методов анализа, проектирования и рациональной
организации систем, относящихся к различным областям деятельности, таким как
связь, вычислительная техника, торговля, транспорт, военное дело. Несмотря на
все свое разнообразие, приведенные системы обладают рядом типичных свойств, что
позволяет изучать такие системы, используя обобщенные математические модели.
.2 Многоканальная система с отказами
Система состоит из одного узла
обслуживания, содержащего n каналов (приборов), каждый из которых может
обслуживать только одну заявку.
Все каналы обслуживания одинаковой
производительности и для модели системы неразличимы. Если заявка поступила в
систему и застала свободным хотя бы один канал, она мгновенно начинает
обслуживаться. Если в момент поступления заявки в систему все каналы заняты, то
заявка покидает систему не обслуженной.
.3 Смешанные системы
Система с ограничением на длину
очереди состоит из накопителя (очереди) и узла обслуживания. Заявка покидает
очередь и уходит из системы, если в накопителе к моменту ее появления уже
находятся m заявок ( m - максимально возможное число мест в очереди). Если
заявка поступила в систему и застала свободным хотя бы один канал обслуживания,
она мгновенно начинает обслуживаться. Если в момент поступления заявки в
систему все каналы заняты, то заявка не покидает систему, а занимает место в
очереди. Заявка покидает систему не обслуженной, если к моменту её поступления
заняты все места в очереди. Для каждой системы определяется дисциплина очереди.
Это система правил, определяющих порядок поступления заявок из очереди в узел
обслуживания. Если все заявки и каналы обслуживания равнозначны, то чаще всего
действует правило «кто раньше пришел, тот раньше обслуживается».
Система с ограничением на
длительность пребывания заявки вочереди состоит из накопителя (очереди) и узла
обслуживания. От предыдущей системы она отличается тем, что заявка, поступившая
в накопитель (очередь), может ожидать начала обслуживания лишь ограниченное
время Тож (чаще всего это случайная величина). Если её время Тож истекло, то
заявка покидает очередь и уходит из системы не обслуженной.
.4 Поток событий
Потоком событий называется
последовательность однородных событий, следующих одно за другим в случайные
моменты времени (поток автобусов на данной остановке, поток отказов какой-то
системы и т.п.).
Мы будем рассматривать потоки
событий, обладающие свойствами: стационарность, отсутствие последействия,
ординарность.
Поток событий называется
стационарным, если вероятность попадания n событий на интервале времени (t,t+  )
зависит от
)
зависит от  и не зависит от t.
Это означает, что интенсивность потока событий не зависит от времени. Такие
потоки событий часто встречаются на практике, об их стационарности строго можно
говорить только на ограниченном интервале времени. Распространение этого
участка до бесконечности - удобный прием.
и не зависит от t.
Это означает, что интенсивность потока событий не зависит от времени. Такие
потоки событий часто встречаются на практике, об их стационарности строго можно
говорить только на ограниченном интервале времени. Распространение этого
участка до бесконечности - удобный прием.
Поток событий называется потоком без
последействия, если для любых двух непересекающихся промежутков времени число
событий попадающих в один из них не зависит от того, сколько событий попало в
другой. Это означает, что события, образующие поток появляются независимо друг
от друга, т.е. поток есть марковский процесс.
Поток событий называется ординарным,
если вероятность осуществления на бесконечно малом отрезке времени t двух и
более событий (i=2,3,... пренебрежимо малы по сравнению с вероятностью 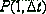 одного
события
одного
события
Поток событий называется простейшим,
если он стационарен, однороден и не имеет последействия. Для такого потока
вероятность появления на интервале  m
событий определяется формулой Пуассона
m
событий определяется формулой Пуассона 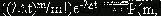
 -средняя
интенсивность потока. Для простейшего потока интервал t между соседними
событиями имеет показательное распределение:
-средняя
интенсивность потока. Для простейшего потока интервал t между соседними
событиями имеет показательное распределение:  .
Если рассматривать бесконечно малый временной интервал, то с учетом
ординарности пуассоновского разделенного событийного потока
.
Если рассматривать бесконечно малый временной интервал, то с учетом
ординарности пуассоновского разделенного событийного потока 
Поток событий называется
рекуррентным или потоком "Пальма", если он стационарен, ординарен, а интервалы
времени между событиями представляют собой независимые случайные величины с
одинаковым произвольным распределением.
.5 Уравнения Колмогорова для
вероятностей состояний. Финальные вероятности состояний
Итак, на систему, находящуюся в
состоянии 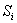 , действует
простейший поток событий. Как только появится первое событие этого потока,
происходит «перескок» системы из состояния
, действует
простейший поток событий. Как только появится первое событие этого потока,
происходит «перескок» системы из состояния 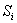 в
состояние
в
состояние 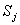 (на графе состояний
по стрелке
(на графе состояний
по стрелке 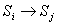 ).
).
Для нахождения всех вероятностей
состояний 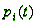 как функций времени
составляются и решаются уравнения Колмогорова - особого вида уравнения, в
которых неизвестными функциями являются вероятности состояний. Правило
составления этих уравнений приведем здесь без доказательств. Но прежде, чем его
приводить, объясним понятие финальной вероятности состояния.
как функций времени
составляются и решаются уравнения Колмогорова - особого вида уравнения, в
которых неизвестными функциями являются вероятности состояний. Правило
составления этих уравнений приведем здесь без доказательств. Но прежде, чем его
приводить, объясним понятие финальной вероятности состояния.
Финальные вероятности состояний -
это уже не переменные величины (функции времени), а простые постоянные числа.
Отсюда очевидно, что
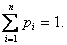
Финальная вероятность состояния 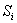 -
это по - существу среднее относительное время пребывания системы в этом
состоянии.
-
это по - существу среднее относительное время пребывания системы в этом
состоянии.
Правило составления системы
уравнений Колмогорова: в каждом уравнении системы в левой его части стоит
финальная вероятность данного состояния 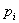 ,
умноженная на суммарную интенсивность всех потоков, ведущих из данного
состояния, а в правой его части - сумма произведений интенсивностей всех
потоков, входящих в
,
умноженная на суммарную интенсивность всех потоков, ведущих из данного
состояния, а в правой его части - сумма произведений интенсивностей всех
потоков, входящих в 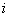 - е состояние, на
вероятности тех состояний, из которых они исходят.
- е состояние, на
вероятности тех состояний, из которых они исходят.
.Практическая часть
.1 Этап первый. СМО с отказами
.1.1Задачи этапа
На этом этапе проводится
минимизация
средней стоимости обслуживания
одной заявки в единицу времени для системы с отказами.
Требуется определить число 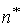 каналов
обслуживания, обеспечивающее в системе с отказами наименьшее значение параметра
C - средней стоимости обслуживания одной заявки в единицу времени.
каналов
обслуживания, обеспечивающее в системе с отказами наименьшее значение параметра
C - средней стоимости обслуживания одной заявки в единицу времени.
В соответствии с вариантом задания
определены параметры системы λ
и 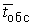 .
Задаваясь значениями n (число каналов обслуживания) от единицы до шести,
вычисляются финальные вероятности и в соответствии с ними - показатели
эффективности системы. Результаты вычислений представляются в виде таблиц,
формы которых приведены в приложении 2, и в виде графиков функций С = С(n),
.
Задаваясь значениями n (число каналов обслуживания) от единицы до шести,
вычисляются финальные вероятности и в соответствии с ними - показатели
эффективности системы. Результаты вычислений представляются в виде таблиц,
формы которых приведены в приложении 2, и в виде графиков функций С = С(n), 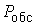 =
=
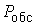 (n),
(n),
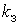 =
=
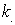 (n),
(n),
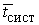 =
=
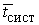 (n),
построенных в масштабе в зависимости от n. В качестве оптимального числа
каналов
(n),
построенных в масштабе в зависимости от n. В качестве оптимального числа
каналов 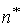 следует
принять такое значение n, при котором принимает наименьшее значениесредняя
стоимость С обслуживания одной заявки в единицу времени (с учетом ограничения
следует
принять такое значение n, при котором принимает наименьшее значениесредняя
стоимость С обслуживания одной заявки в единицу времени (с учетом ограничения 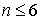 ).
Следовательно,
).
Следовательно, 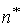 либо точка
минимума на графике функции С = С(n), либо
либо точка
минимума на графике функции С = С(n), либо 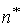 =
6, если С = С(n) - монотонно убывающая функция.
=
6, если С = С(n) - монотонно убывающая функция.
Запоминаются значения основных
показателей эффективности оптимальной СМО с отказами:
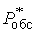 =
= 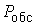 (
(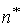 )(3.1)
)(3.1)
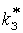 =
= 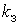 (
(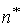 )
(3.2)
)
(3.2)
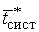 =
= 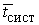 (
(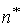 )
(3.3)
)
(3.3)
Вычисляется допустимое для смешенных
СМО значение времени пребывания заявки в системе 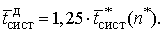
Исходные значения:
λ
= 4,0 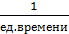 ;
;
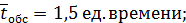
ск=  ;
;
спк=  ;
;
соч = 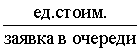 ;
;
сотк = ед.стоим. * ед.врем.
Условия:

.1.2Расчетная часть
)Расчет показателей эффективности
для СМО с отказами при n=1;
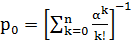 = 0.143;
= 0.143;
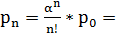 0.857;
0.857;
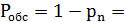 0.143;
0.143;
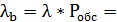 0.571;
0.571;
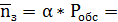 0.857;
0.857;
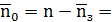 0.143;
0.143;
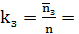 0.857;
0.857;
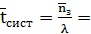 0.214;
0.214;
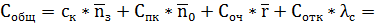 1.143;
1.143;
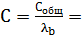 2.000;
2.000;
Таблица 3.1- Результаты вычислений
эффективности СМО с отказами
|
Система с отказами λ=4,0
1/ед врем. , tобс=1,5 ед.врем. , α=6,0
|
|
|
Результирующие показатели
|
|
n
|
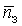
|
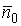
|
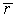
|
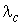 1/ед.вр. 1/ед.вр.
|
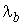 1/ед.вр. 1/ед.вр.
|
Cобщ
|
С
|
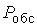
|
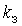
|
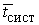 ед.вр ед.вр
|
|
|
|
|
|
|
ед.ст
|
ед.ст
|
|
|
|
|
1
|
0.857
|
0.143
|
0
|
3.429
|
0.571
|
1.143
|
2.000
|
0.143
|
0.857
|
0.214
|
|
2
|
1.680
|
0.320
|
0
|
2.880
|
1.120
|
1.480
|
1.321
|
0.280
|
0.840
|
0.420
|
|
3
|
2.459
|
0.541
|
0
|
2.361
|
1.639
|
1.810
|
1.104
|
0.410
|
0.820
|
0.615
|
|
4
|
3.183
|
0.817
|
0
|
1.878
|
2.122
|
2.130
|
1.004
|
0.530
|
0.796
|
0.796
|
|
5
|
3.838
|
1.162
|
0
|
1.442
|
2.558
|
2.440
|
0.954
|
0.640
|
0.768
|
0.959
|
|
6
|
4.410
|
1.590
|
0
|
1.060
|
2.940
|
2.735
|
0.930
|
0.735
|
0.735
|
1.103
|
Таблицы 3.2- Результаты вычислений
общей стоимости обслуживания заявок в единицу времени для СМО с отказами
|
К вычислению общей стоимости обслуживания
заявок в единицу времени
|
|
n
|
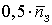 ед. стоим. ед. стоим.
|
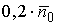 ед.стоим. ед.стоим.
|
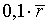 ед.стоим. ед.стоим.
|
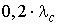 ед.стоим. ед.стоим.
|
Cобщ
|
|
|
|
|
|
ед.стоим.
|
|
1
|
0.429
|
0.029
|
0
|
0.686
|
1.143
|
|
2
|
0.840
|
0.064
|
0
|
0.576
|
1.480
|
|
3
|
1.230
|
0.108
|
0
|
0.472
|
1.810
|
|
4
|
1.591
|
0.163
|
0
|
0.376
|
2.130
|
|
5
|
1.919
|
0.232
|
0
|
0.288
|
2.440
|
|
6
|
2.205
|
0.318
|
0
|
0.212
|
2.735
|
Зависимость средней стоимости
обслуживания одной заявки в единицу времени (C) от количества каналов
обслуживания (n) показана на Графике 3.1
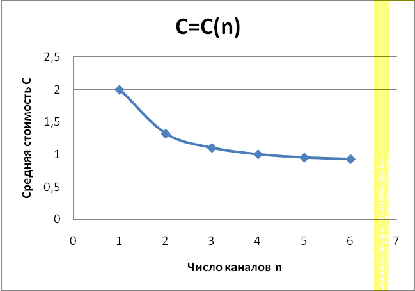
График 3.1- График зависимости
средней стоимости обслуживания одной заявки в единицу времени (C) от количества
каналов обслуживания (n)
Зависимость вероятности обслуживания
заявки (Робс) от количества каналов обслуживания (n) показана на Графике 3.2
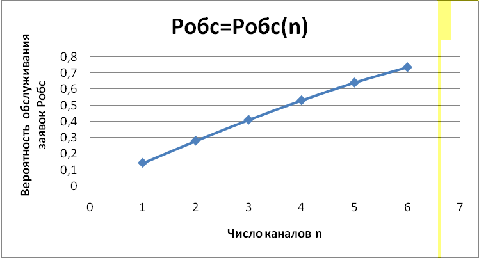
График 3.2- График зависимости
вероятности обслуживания заявки (Робс) от количества каналов обслуживания (n)
Зависимость коэффициента загрузки
системы (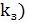 от
количества каналов обслуживания (n) показана на Графике3.3
от
количества каналов обслуживания (n) показана на Графике3.3
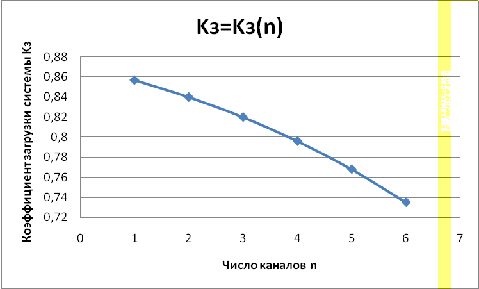
График 3.3-График
зависимостикоэффициента загрузки системы (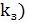 от
количества каналов обслуживания (n)
от
количества каналов обслуживания (n)
Зависимость времени пребывания
заявки в системе (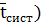 от количества
каналов обслуживания (n) показана на Графике 3.4
от количества
каналов обслуживания (n) показана на Графике 3.4
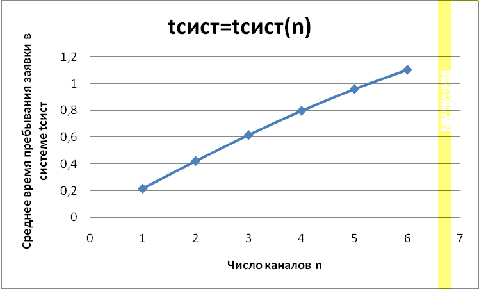
График 3.4-График зависимости
времени пребывания заявки в системе (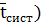 от
количества каналов обслуживания (n)
от
количества каналов обслуживания (n)
.1.3Вывод
Вычислимдопустимое для смешанных СМО
значение времени пребывания заявки в системе
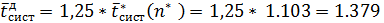
Вычислив показатели эффективности
для СМО с отказами, учитывая число каналов обслуживания равное от единицы до
шести, мы выяснили, что СМО с отказами при использовании шести каналов
обслуживания является наилучшей т.к. минимальная стоимость обслуживания одной
заявки в единицу времени (С) в этом случае является наименьшей. Из этого
следует, что система с шестью каналами обслуживания(n=6) является оптимальной.
.2Смешенная система массового
обслуживания с ограничением на длину очереди
.2.1Задачи этапа
Изучается одна из смешанных систем,
соответствующая заданию на курсовое проектирование.Определяется наименьшее
значение С - средней стоимостиобслуживания одной заявки в единицу времени.
На этом этапе решается вопрос о
возможности с введением очереди обеспечить уменьшение значения оптимального для
рассматриваемой системы значения экономического показателя С и улучшить другие
показатели эффективности изучаемой системы.
СМО с ограничением на длину очереди.
В рассматриваемом случае
анализируется влияние на эффективность системы ограничения на длину очереди.
Длина очереди не должна превышать заданной величины m.
Исходные данные изучаемой системы:
λ
- интенсивность входного потока,
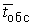 - среднее время
обслуживания одной заявки для рассматриваемого варианта системы.=
- среднее время
обслуживания одной заявки для рассматриваемого варианта системы.= 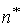 -
число каналов обслуживания рассматриваемой смешенной системы должно совпадать с
найденным ранее числом каналов оптимальной системы с отказами.-допустимая длина
очереди.
-
число каналов обслуживания рассматриваемой смешенной системы должно совпадать с
найденным ранее числом каналов оптимальной системы с отказами.-допустимая длина
очереди.
Задаваясь рядом значений параметра,
m вычисляются зависимости 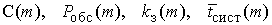 . Оптимальной
считается система, имеющая наименьший показатель эффективности С. В том случае,
когда зависимость
. Оптимальной
считается система, имеющая наименьший показатель эффективности С. В том случае,
когда зависимость 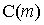 имеет монотонный
характер, наилучшим значением показателя
имеет монотонный
характер, наилучшим значением показателя 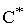 является
наименьшее значение C, при котором ещё выполняется условие
является
наименьшее значение C, при котором ещё выполняется условие 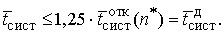
.2.2Расчетная часть
)Расчет показателей эффективности
для СМО с ограничением на длину очереди при m=1:
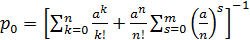 =0.237;
=0.237;
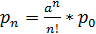 =0.231;
=0.231;
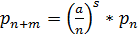 =0.128;
=0.128;
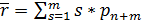 =0,128
=0,128
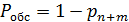 =0,872;
=0,872;
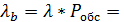 3,487;
3,487;
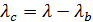 =0,513;
=0,513;
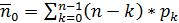 =1,386;
=1,386;
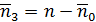 =5,615;
=5,615;
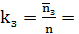 0,936;
0,936;
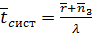 =1,436;
=1,436;
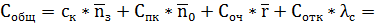 3,000;
3,000;
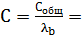 0,860.
0,860.
Таблица 2.3- Результаты вычислений
эффективности СМО с ограничением на длину очереди
|
Система с ограничениями на длину очереди
|
Результирующие
|
|
показатели
|
|
m
|
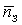
|
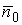
|
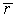
|
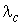 1/ед.вр. 1/ед.вр.
|
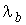 1/ед.вр. 1/ед.вр.
|
Cобщ ед.ст
|
C
|
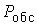
|
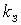
|
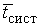 ед.вр ед.вр
|
|
|
|
|
|
|
|
ед.ст
|
|
|
|
|
|
Данные системы с отказами
|
|
m = 0
|
4,410
|
1,590
|
0
|
1,060
|
2,940
|
2,735
|
0,930
|
0,735
|
0,735
|
1,103
|
|
Данные системы cограничениемна длину очереди
|
|
1
|
5,615
|
1,386
|
0,128
|
0,513
|
3,487
|
3,000
|
0,860
|
0,872
|
0,936
|
1,436
|
|
2
|
5,143
|
3,086
|
0,857
|
1,143
|
2,857
|
3,057
|
1,070
|
0,714
|
0,857
|
1,500
|
|
3
|
5,333
|
2,400
|
1,333
|
0,889
|
3,111
|
3,111
|
1,000
|
0,778
|
0,889
|
1,667
|
|
4
|
5,455
|
1,964
|
1,818
|
0,727
|
3,273
|
3,164
|
0,967
|
0,818
|
0,909
|
|
5
|
5,538
|
1,662
|
2,308
|
0,615
|
3,385
|
3,215
|
0,950
|
0,846
|
0,923
|
1,962
|
|
6
|
5,600
|
1,440
|
2,800
|
0,533
|
3,467
|
3,267
|
0,942
|
0,867
|
0,933
|
2,100
|
Таблица 2.4- Результаты вычислений
общей стоимости обслуживания заявок в единицу времени для СМО с огриничением на
длину очереди
|
К вычислению общей стоимости обслуживания
заявок в единицу времени
|
|
m
|
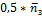 ед.стоим. ед.стоим.
|
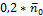 ед.стоим. ед.стоим.
|
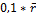 ед.стоим. ед.стоим.
|
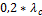 ед.стоим. ед.стоим.
|
Cобщ
|
|
|
|
|
|
ед.стоим.
|
|
Данные системы с отказами
|
|
m = 0
|
2.205
|
0.318
|
0
|
0.212
|
2.735
|
|
Данные системы ограничениями на длину очереди
|
|
1
|
2,808
|
0,077
|
0,013
|
0,103
|
3,000
|
|
2
|
2,571
|
0,171
|
0,086
|
0,229
|
3,057
|
|
3
|
2,667
|
0,133
|
0,133
|
0,178
|
3,111
|
|
4
|
2,727
|
0,109
|
0,182
|
0,145
|
3,164
|
|
5
|
2,769
|
0,092
|
0,231
|
0,123
|
3,215
|
|
6
|
2,800
|
0,080
|
0,280
|
0,107
|
3,267
|
Зависимость средней стоимости
обслуживания одной заявки в единицу времени (C) от ограничения на длины
очереди(m) показана на Графике 3.5.
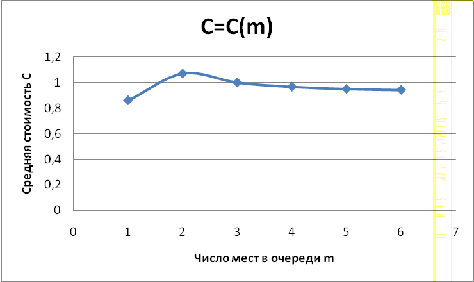
График 3.5 - График
зависимостисредней стоимости обслуживания одной заявки в единицу времени (C) от
ограничения на длину очереди(m)
Зависимость вероятности обслуживания
заявки (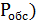 от ограничения на длину очереди (m) показана на Графике 3.6.
от ограничения на длину очереди (m) показана на Графике 3.6.
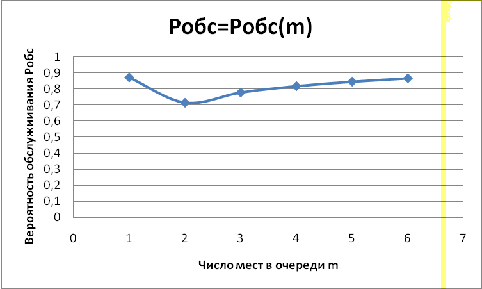
График 3.6- График зависимостивероятности
обслуживания заявки (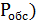 от ограничения на
длину очереди (m)
от ограничения на
длину очереди (m)
Зависимость коэффициента загрузки
системы (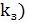 от
ограничения на длину очереди (m) показана на Графике 3.7.
от
ограничения на длину очереди (m) показана на Графике 3.7.
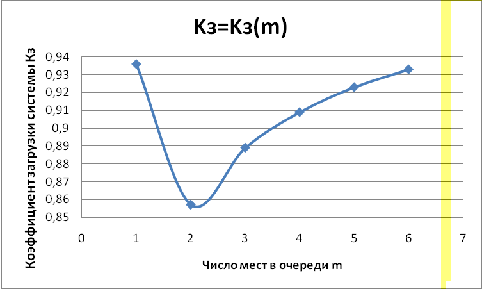
График3.7-График
зависимостикоэффициента загрузки системы (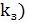 от
ограничения на длину очереди (m)
от
ограничения на длину очереди (m)
Зависимость времени пребывания
заявки в системе (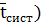 от ограничения на
длину очереди показана(m) на Графике 3.8.
от ограничения на
длину очереди показана(m) на Графике 3.8.
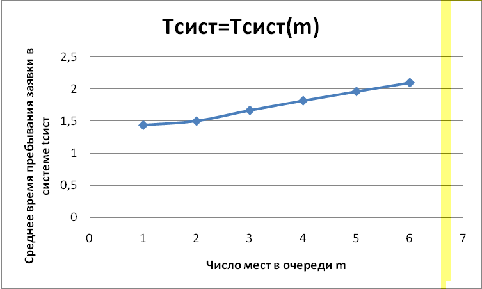
График3.8-График зависимостивремени
пребывания заявки в системе (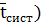 от ограничения на
длину очереди(m)
от ограничения на
длину очереди(m)
3.2.3Вывод
Сравнив показатели (С) для СМО с
отказами равное 0,930 и смешанной СМО равное 0,860и из-за условия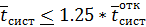 для
дальнейших расчетов мы выбираем чистую СМО с отказами. Не смотря на то что
смешанная СМО имеет более низкую среднюю стоимость обслуживания заявки (меньше
на 8%) чем чистая СМО с отказами, мы все равно выбираем чистую СМО с отказами,
т. к. даже при вводе очереди с одним элементом мы превысили допустимое
системное время.
для
дальнейших расчетов мы выбираем чистую СМО с отказами. Не смотря на то что
смешанная СМО имеет более низкую среднюю стоимость обслуживания заявки (меньше
на 8%) чем чистая СМО с отказами, мы все равно выбираем чистую СМО с отказами,
т. к. даже при вводе очереди с одним элементом мы превысили допустимое
системное время.
3.3Влияние производительности
каналов
.3.1Задачи этапа
На этом этапе изучается влияние
производительности каналов обслуживания на эффективность системы, определяемой
показателями С, 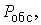
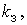
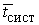 .
.
Исходные данные изучаемой системы:
λ
- интенсивность входного потока,
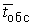 - среднее время
обслуживания одной заявки для рассматриваемого варианта системы.=
- среднее время
обслуживания одной заявки для рассматриваемого варианта системы.= 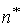 -
число каналов обслуживания рассматриваемой смешенной системы совпадает с
найденным ранее числом каналов оптимальной системы с отказами.
-
число каналов обслуживания рассматриваемой смешенной системы совпадает с
найденным ранее числом каналов оптимальной системы с отказами.
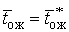 - признанное
оптимальным среднее время пребывания заявки в очереди.
- признанное
оптимальным среднее время пребывания заявки в очереди.
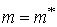 - признанная
оптимальной допустимая длина очереди.
- признанная
оптимальной допустимая длина очереди.
Производительность канала обслуживания
определяется величиной параметра 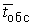 -
средним временем обслуживания одной заявки. Рассматривается смешанная система,
признанная оптимальной. Показатели эффективности этой первоначальной системы
сравниваются с аналогичными показателями двух вариантов этой системы:
-
средним временем обслуживания одной заявки. Рассматривается смешанная система,
признанная оптимальной. Показатели эффективности этой первоначальной системы
сравниваются с аналогичными показателями двух вариантов этой системы:
Вариант a) системы с уменьшенной
производительностью каналов обслуживания за счет увеличения в два раза среднего
времени обслуживания и с уменьшенными затратами, связанными с эксплуатацией и
простоем оборудования
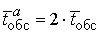 ,
, 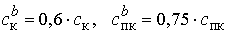 .
.
Вариант b) системы с увеличенной
производительностью каналов обслуживания за счет уменьшения в два раза среднего
времени обслуживания и увеличенными затратами, связанными с эксплуатацией и
простоем оборудования
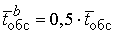 ,
, 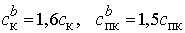 .
.
3.3.2Расчетная часть
Таблица 3.5- Результаты расчетов
влияния производительности каналов обслуживания на эффективность системы
|
Заданная смешанная система
|
Результирующие показатели
|
|
Первонач вариант
|
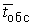 ед.вр ед.вр
|
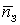
|
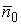
|
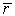
|
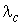 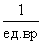
|
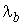 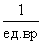
|
Cобщ ед.ст
|
С ед.ст
|
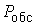
|
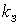
|
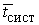 ед.вр ед.вр
|
|
1,5
|
4,410
|
1,590
|
0
|
1,060
|
2,940
|
2,735
|
0,930
|
0,735
|
0,735
|
1,103
|
|
Вариант а
|
3
|
5,327
|
0,673
|
0
|
2,224
|
1,776
|
2,144
|
1,207
|
0,444
|
0,888
|
1,332
|
|
Вариант б
|
0.75
|
2,844
|
3,156
|
0
|
0,209
|
3,791
|
3,263
|
0,861
|
0,948
|
0,474
|
0,711
|
Таблица 3.6- Результаты расчетов
вычисления общей стоимости обслуживания заявок в единицу времени
|
К вычислению общей стоимости обслуживания
заявок в единицу времени
|
|
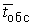 ед.вр ед.вр
|
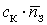 ед.стоим. ед.стоим.
|
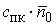 ед.стоим. ед.стоим.
|
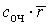 ед.стоим ед.стоим
|
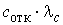 ед.стоим. ед.стоим.
|
Cобщ ед.стоим.
|
|
Первонач вариант
|
1,5
|
2.205
|
0.318
|
0
|
0.212
|
2.735
|
|
Вариант а
|
3
|
1,598
|
0,101
|
0
|
0,445
|
2,144
|
|
Вариант б
|
0,75
|
2,275
|
0,947
|
0
|
0,042
|
3,263
|
.3.4 Вывод
На данном шаге выполнения курсового
проекта мы сравнили показатели эффективности оптимальной системы с некоторыми
изменениями: системы с уменьшенной производительностью каналов обслуживания за
счет увеличения в два раза среднего времени обслуживания и с уменьшенными
затратами, связанными с эксплуатацией и простоем оборудования Результаты
расчетов приведены в Таблице 3.5 и Таблице 3.6.
Сравнив показатели данной системы и
систем, параметры которых были изменены по варианту “а” и варианту “б”, можно
сделать вывод, чтоСМО, измененная по варианту “б” имеет среднюю стоимость
обслуживания заявки равной 0,861 что на 8% меньше чем в изначальной СМО. Так
же, вероятность обслуживания заявки повысилась на 22% и стала равной 0,948.
Оптимальной является СМО в варианте “б”.
Заключение
Выполнение курсовой работы закрепило
мои теоретические знания в ТМО. Я приобрел базовый опыт работы с СМО для дальнейшего
использования этого опыта на практике.
Во втором этапе, сравнив показатели
(С) для СМО с отказами равное 0,930 и смешанной СМО равное 0,860 и из-за
условия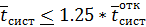 для
дальнейших расчетов мы выбраличистую СМО с отказами.Не смотря на то, что
смешанная СМО имеет более низкую среднюю стоимость обслуживания заявки (меньше
на 8%) чем чистая СМО с отказами, мы все равно выбрали чистую СМО с отказами,
т. к. даже при вводе очереди с одним элементом мы превысили максимальное допустимое
системное время.
для
дальнейших расчетов мы выбраличистую СМО с отказами.Не смотря на то, что
смешанная СМО имеет более низкую среднюю стоимость обслуживания заявки (меньше
на 8%) чем чистая СМО с отказами, мы все равно выбрали чистую СМО с отказами,
т. к. даже при вводе очереди с одним элементом мы превысили максимальное допустимое
системное время.
Проанализировав полученные данные,
можно сделать вывод, что чистая СМО с уменьшенным средним временем обслуживания
одной заявки, по сравнению с оптимальной СМО полученной во втором этапе, более
оптимальна как с точки зрения клиента так и с точки зрения эксплуататора.Легко
заметить, что вероятность обслуживания заявки повысилась на 22%, а так же на
36% понизилось среднее время пребывания заявки в системе, что
гораздеоптимальнее с точки зрения клиента. Конечно, коэффициент загрузки системы
упало на 35%, но т. к. средняя стоимость обслуживания заявки понизилась на 8%,
то система варианта “б” оптимальна так же и с точки зрения эксплуатации.
Список используемых источников
Вентцель
Е.С. Теория вероятностей: учеб.для вузов/ Е.С. Вентцель.7 - е изд. стер. М.:
Высш. шк., 2001
Овчаров
Л.А. Прикладные задачи теории массового обслуживания/ Л.А.Овчаров. М.:
Машиностроение, 1969
Лифшиц
А.Л. Статистическое моделирование систем массового обслуживания/ А.Л. Лифшиц,
Э.А. Мальц. М.: Сов.радио, 1978
Ермаков
С.М. Статистическое моделирование/ С.М. Ермаков, Г.А. Михайлов. 2-е изд., доп.
М.: Наука, 1982
Новиков
О.А. Прикладные вопросы теории массового обслуживания. О.А.Новиков,
С.Н.Петухов. М.: Сов.радио, 1969
Самусевич
Г.А. Основы теории массового обслуживания: учебное пособие / Г.А. Самусевич.
Екатеринбург: УГТУ-УПИ, 2007