Системы массового обслуживания
СОДЕРЖАНИЕ
Введение
.
Математическое описание метода
.1 Общие
сведения о системах массового обслуживания
.2
Многоканальные СМО с отказами
. Обоснование
и выбор инструментальной среды для проведения расчетов
.
Алгоритмическое обеспечение
.1 Постановка
задачи
.2
Математическая модель
.3 Построение
моделей СМО с отказами в Simulink
.3.1 Для 3-х
канальной СМО
.3.2 Для
5-канальной СМО
.4 Расчет
показателей эффективности
.4.1 для 3-х
канальной СМО
.4.2 Для
5-канальной СМО
.5 Анализ
результатов моделирования
Заключение
Список
использованной литературы
ВВЕДЕНИЕ
На сегодняшний день метод имитационного моделирования является одним из
наиболее эффективных методов исследования процессов и систем самой различной
природы и степени сложности. Сущность метода состоит в составлении модели,
имитирующей процесс функционирования системы, и расчета характеристик этой
модели с целью получения статистических данных моделируемой системы. Используя
результаты имитационного моделирования, можно описать поведение системы,
оценить влияние различных параметров системы на ее характеристики, выявить
преимущества и недостатки предлагаемых изменений, прогнозировать поведение
системы.
Лучшей иллюстрацией области применения имитационного моделирования
являются системы массового обслуживания. В терминах СМО описываются многие
реальные системы: вычислительные системы, узлы сетей связи, магазины,
производственные участки - любые системы, где возможны очереди и отказы в
обслуживании. Цель данной курсовой работы - создание блок-схемы в среде MatLab
Simulink, наглядно иллюстрирующей алгоритм расчета параметров модели
многоканальной СМО с отказами и формирование рекомендаций по выбору
оптимального количества каналов обслуживания.
Для достижения поставленной цели выделим основные задачи:
- подробное описание многоканальной СМО с отказами;
выбор контрольного примера и постановка задачи;
определение алгоритма решения;
создание имитационной модели в среде MATLAB (Simulink);
анализ результатов и обоснование выбора оптимального количества
каналов для исследуемой СМО
1.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДА
.1
Общие сведения о системах массового обслуживания
В жизни часто встречаются системы, предназначенные для многоразового
использования при решении однотипных задач: очередь в магазине, обслуживание
автомобилей на автозаправках, билетные кассы и т.п. Возникающие при этом
процессы получили название процессов обслуживания, а системы - систем массового
обслуживания (СМО).
Процессы поступления и обслуживания заявок в СМО являются случайными, что
обусловлено случайным характером потока заявок и длительности их обслуживания.
Будем рассматривать СМО с марковским случайным процессом, когда
вероятность состояния СМО в будущем зависит только от ее настоящего состояния и
не зависит от прошлого (процесс без последействия или без памяти). Условие
марковского случайного процесса необходимо, чтобы все потоки событий, при
которых система переходит из одного состояния в другое (потоки заявок, потоки
обслуживания и т.д.), были пуассоновскими. Пуассоновский поток событий обладает
рядом свойств, в том числе свойствами отсутствия последействия, ординарности,
стационарности.
В простейшем пуассоновском потоке событий случайная величина распределена
по показательному закону:
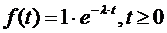 , (1.1)
, (1.1)
где λ - интенсивность потока.
Целью теории систем массового обслуживания является выработка
рекомендаций по рациональному их построению, организации работы и регулированию
потока заявок. Отсюда вытекают задачи, связанные с теорией массового
обслуживания: установление зависимостей работы СМО от ее организации, характера
потока заявок, числа каналов и их производительности, правил работы СМО.
Основой СМО является определенное число обслуживающих устройств - каналов
обслуживания.
Назначение СМО состоит в обслуживании потока заявок (требовании),
представляющих последовательность событий, поступающих нерегулярно и в заранее
неизвестные и случайные моменты времени. Само обслуживание заявок также
имеет непостоянный и случайный характер. Случайный характер потока заявок и
времени их обслуживания обусловливает неравномерность загрузки СМО: на входе
могут накапливаться необслуженные заявки (перегрузка СМО) либо заявок нет или
их меньше, чем свободных каналов (недогрузка СМО).
Таким образом, в СМО поступают заявки, часть из которых принимается на
обслуживание каналами системы, часть становится в очередь на обслуживание, а
часть покидает систему необслуженными.
Основными элементами СМО являются:
1. входной поток заявок;
2. очередь;
. каналы обслуживания;
. выходной поток заявок (обслуженные заявки).
Эффективность функционирования СМО определяется ее пропускной
способностью - относительным числом обслуженных заявок.
По числу каналов n все
СМО разделяются на одноканальные (n = 1) и многоканальные (n >
1). Многоканальные СМО могут быть как однородными (по каналам), так и
разнородными (по продолжительности обслуживания заявок).
По дисциплине обслуживания различаются три класса СМО:
1. СМО с отказами (нулевое ожидание или явные потери).
"Отказная" заявка вновь поступает в систему, чтобы ее обслужили
(например, вызов абонента через АТС).
2. СМО с ожиданием (неограниченное ожидание или очередь). При
занятости системы заявка поступает в очередь и, в конце концов, будет выполнена
(торговля, сфера бытового и медицинского обслуживания).
. СМО смешанного типа (ограниченное ожидание). Имеется
ограничение на длину очереди (сервис по обслуживанию автомобилей). Ограничение
на время пребывания заявки в СМО (ПВО, особые условия обслуживания в банке)
также может рассматриваться.
Различают открытые (поток заявок не ограничен), упорядоченные
(заявки обслуживаются в порядке их поступления) и однофазные (однородные
каналы выполняют одну и ту же операцию) СМО.
Эффективность работы систем массового обслуживания характеризуют
показатели, которые можно разбить на три групп:
1. Группа показателей эффективности использования СМО:
- абсолютная пропускная способность (А) - среднее число
заявок, обслуживаемых в единицу времени, или интенсивность выходящего потока
обслуженных заявок (это часть интенсивности входящего потока заявок);
относительная пропускная способность (Q) - отношение абсолютной пропускной
способности к среднему числу заявок, поступивших в систему за единицу времени;
средняя продолжительность периода занятости СМО (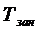 );
);
интенсивность нагрузки (ρ) показывает степень согласованности
входного и выходного потоков заявок канала обслуживания и определяет
устойчивость СМО;
коэффициент использования СМО - средняя доля времени, в течение
которого система занята обслуживанием заявок.
2. Показатели качества обслуживания заявок:
среднее время ожидания заявки в очереди (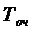 );
);
среднее время пребывания (обслуживания) заявки в СМО (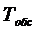 );
);
вероятность отказа заявки в обслуживании без ожидания (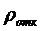 );
);
вероятность немедленного приема заявки (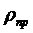 );
);
закон распределения времени ожидания заявки в очереди в СМО;
среднее число заявок в очереди (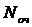 );
);
среднее число заявок, находящихся в СМО (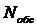 ).
).
. Показатели эффективности функционирования пары "СМО -
потребитель" (вся совокупность заявок или их источник, например средний
доход в единицу времени от СМО). Эта группа полезна, когда доход от СМО и
затраты на ее обслуживание измеряются в одних и тех же единицах, и отражает
специфику работы СМО.
1.2
Многоканальные СМО с отказами
Система M/M/n/0 представляет собой n- линейную СМО с r местами ожидания
(r=0), в которую поступает пуассоновский поток интенсивности 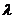 , а времена обслуживания заявок
независимы и при этом время обслуживания каждой заявки на любом приборе
распределено по экспоненциальному закону с параметром
, а времена обслуживания заявок
независимы и при этом время обслуживания каждой заявки на любом приборе
распределено по экспоненциальному закону с параметром 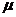 . В случае, когда
. В случае, когда 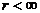 , заявка, поступившая в переполненную
систему (т.е. когда заняты все приборы и все места ожидания), теряется и вновь
в нее не возвращаются. Система M/M/n/r также относится к экспоненциальным СМО.
, заявка, поступившая в переполненную
систему (т.е. когда заняты все приборы и все места ожидания), теряется и вновь
в нее не возвращаются. Система M/M/n/r также относится к экспоненциальным СМО.
Уравнения, описывающие распределение заявок в системе
Рассматривая 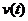 -число заявок в системе в момент t, нетрудно показать, что
процесс
-число заявок в системе в момент t, нетрудно показать, что
процесс 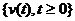 является однородным Марковским
процессом с множеством состояний
является однородным Марковским
процессом с множеством состояний  . Ниже мы покажем, что процесс
. Ниже мы покажем, что процесс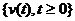 представляет собой ПРГ.
представляет собой ПРГ.
Выпишем систему дифференциальных уравнений Колмогорова. Для этого
рассмотрим моменты t и 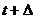 . Предполагая, что в момент t процесс v(t) пребывает в
состоянии i, определим, куда он может попасть в момент
. Предполагая, что в момент t процесс v(t) пребывает в
состоянии i, определим, куда он может попасть в момент 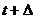 , и найдем вероятности
, и найдем вероятности 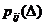 его переходов за время
его переходов за время 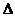 . Здесь возможны три случая.
. Здесь возможны три случая.
А. i<n. В этом случае все находящиеся в системе заявки обслуживаются
на приборах (если i=0- заявок в системе вообще нет). Вероятность того, что за
время 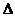 процесс
процесс 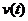 не выйдет из состояния i равна
произведению вероятности
не выйдет из состояния i равна
произведению вероятности 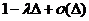 не поступления заявки за время
не поступления заявки за время 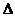 на вероятность
на вероятность 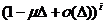 того, что за это время не обслужится
ни одна из i заявок, т.е. равна
того, что за это время не обслужится
ни одна из i заявок, т.е. равна 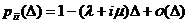 . Вероятность перехода за время
. Вероятность перехода за время 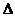 в состояние i+1 равна
в состояние i+1 равна 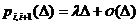 - вероятности поступления заявки в
систему. Наконец поскольку каждый прибор закончит за время
- вероятности поступления заявки в
систему. Наконец поскольку каждый прибор закончит за время 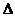 обслуживание находящейся в нем
заявки с вероятностью
обслуживание находящейся в нем
заявки с вероятностью 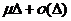 , а таких приборов i, то вероятность перехода в состояние i-1
равна
, а таких приборов i, то вероятность перехода в состояние i-1
равна 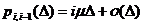 . Остальные переходы имеют
вероятность
. Остальные переходы имеют
вероятность 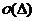 .
.
Таким образом, мы фактически доказали, что процесс 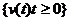 является процессом рождения и гибели
с интенсивностями
является процессом рождения и гибели
с интенсивностями 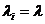 при
при 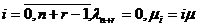 при
при 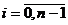 и
и 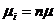 при
при 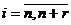 . Обозначая через
. Обозначая через 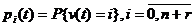 , распределение числа заявок в
системе в момент t, получаем следующие выражения для
, распределение числа заявок в
системе в момент t, получаем следующие выражения для 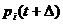 в случае, когда
в случае, когда 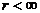 :
:
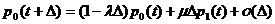 ,
,
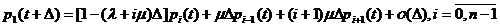 ,
,
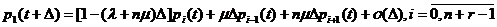 ,
,
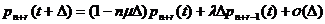
Если же 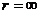 , то, что очевидно последнего выражения не будет, а в
предпоследнем индекс i может принимать значения i=n,n+1,… .
, то, что очевидно последнего выражения не будет, а в
предпоследнем индекс i может принимать значения i=n,n+1,… .
Вычитая теперь 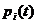 из обеих частей равенства, деля на
из обеих частей равенства, деля на 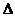 и переходя к пределу
и переходя к пределу
при 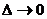 , получаем систему дифференциальных уравнений:
, получаем систему дифференциальных уравнений:
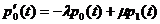 ,
,
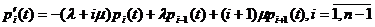 ,
,
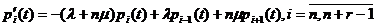 , (1.2)
, (1.2)
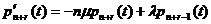 .
.
Стационарное распределение очереди
В случае конечного r, например r=0, процесс 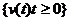 является эргодическим. Также он
будет эргодическим в случае
является эргодическим. Также он
будет эргодическим в случае 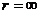 при выполнении условия, о котором будет сказано ниже. Тогда
из (1) при
при выполнении условия, о котором будет сказано ниже. Тогда
из (1) при 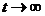 получаем, что стационарные вероятности состояний pi
удовлетворяют систему уравнений:
получаем, что стационарные вероятности состояний pi
удовлетворяют систему уравнений:
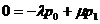 ,
,
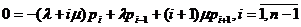 , (1.3)
, (1.3)
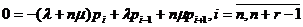 ,
,
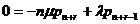 .
.
Поясним теперь вывод системы уравнений (1.3), исходя из принципа
глобального баланса. Так, например, согласно диаграмме переходов для
фиксированного состояния i, 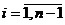 , имеем, что суммарные потоки вероятностей входящий в
состояние i и выходящий из него равны, соответственно,
, имеем, что суммарные потоки вероятностей входящий в
состояние i и выходящий из него равны, соответственно, 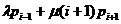 и
и 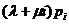 .
.
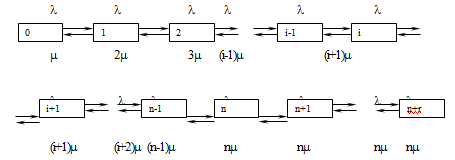
Рисунок 1 Диаграмма переходов
Исходя теперь из принципа локального баланса, что баланс потоков
вероятностей между состояниями i и i+1 отражается равенствами :
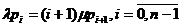 ,
,
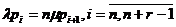 , (1.4)
, (1.4)
являющимися уравнениями локального баланса для данной СМО. Проверка справедливости
равенств (1.4) производится непосредственным суммированием системы уравнений
(1.3) по i при i=0,1,…,n+r-1.
Из соотношения (1.4), выражая рекуррентно вероятности 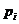 через
через 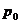 ,
,
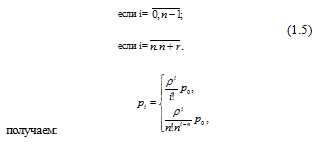
где 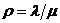 , а
, а 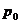 определяется из условия нормировки
определяется из условия нормировки 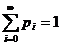 , т.е.
, т.е.
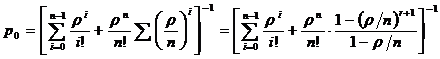 . (1.6)
. (1.6)
Ясно, что формулы можно получить из общих соотношений для стационарных
вероятностей состояний процесса рождения и гибели при указанных выше значениях 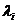 и
и 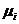 .
.
Если 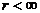 , то стационарный режим существует при любом
, то стационарный режим существует при любом 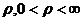 .
.
Выпишем теперь выражения для некоторых характеристик очереди.
Стационарная вероятность 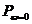 немедленного обслуживания заявки (обслуживания без ожидания)
совпадает со стационарной вероятностью того, что в системе находится 0,1,…,n-1
заявок, т.е.
немедленного обслуживания заявки (обслуживания без ожидания)
совпадает со стационарной вероятностью того, что в системе находится 0,1,…,n-1
заявок, т.е.
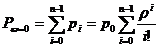
Рассмотрим интересующий нас частный случай, когда r=0. тогда в системе
отсутствуют места для ожидания (система с потерями M/M/n/0) и такая система
носит название системы Эрланга. Система Эрланга описывает процессы,
происходящие в простейших телефонных сетях, и названа так в честь А. К.
Эрланга, впервые её исследовавшего. Для системы M/M/n/0 стационарные
вероятности определяются формулой Эрланга

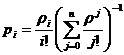 ,
, 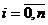 .
.
Следовательно, стационарная вероятность потери заявки определяется
формулой:
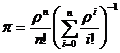 ,
,
которую также называют формулой Эрланга.
Наконец, когда 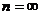 , то мы имеем систему
, то мы имеем систему 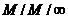 , для которой при любом
, для которой при любом 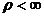 стационарные вероятности существуют
и, как следует из формул Эрланга при
стационарные вероятности существуют
и, как следует из формул Эрланга при 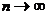 , имеют вид
, имеют вид
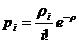 ,
, 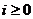 .
.
Вернемся теперь к соотношениям (1.4). Суммируя эти равенства по
i=0,1,…,n+r-1 , получаем
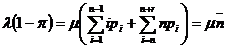 ,
,
где 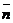 - среднее число занятых приборов. Выписанное соотношение
выражает равенство интенсивностей принятого в систему и обслуживаемого ею
потоков в стационарном режиме. Отсюда мы можем получить выражение для
пропускной способности системы
- среднее число занятых приборов. Выписанное соотношение
выражает равенство интенсивностей принятого в систему и обслуживаемого ею
потоков в стационарном режиме. Отсюда мы можем получить выражение для
пропускной способности системы 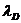 , определяемой как среднее число заявок, обслуженных системой
в единицу времени, и называемой иногда интенсивностью выхода:
, определяемой как среднее число заявок, обслуженных системой
в единицу времени, и называемой иногда интенсивностью выхода:
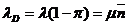 .
.
Выражение для стационарного числа N заявок в системе нетрудно получить
либо непосредственно из распределения вероятностей (4), либо воспользовавшись
очевидным соотношением 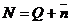 .
.
Стационарное распределение времени пребывания заявки в системе
Стационарное распределение W(x) времени ожидания начала обслуживания
принятой в систему M/M/n/r заявки вычисляется практически так же, как и для
системы 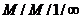 . Заметим, что заявка, заставшая при
поступлении i других заявок в системе, немедленно начинает обслуживаться, если
i<n. При полностью загруженной системе заявки выходят из нее через
экспоненциально распределенные с параметром
. Заметим, что заявка, заставшая при
поступлении i других заявок в системе, немедленно начинает обслуживаться, если
i<n. При полностью загруженной системе заявки выходят из нее через
экспоненциально распределенные с параметром 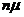 времена.
времена.
Путем несложных преобразований находим, учитывая независимость времени
обслуживания от времени ожидания начала обслуживания, находим, что стационарное
распределение V(x) времени пребывания в системе принятой к обслуживанию заявки
имеет ПЛС
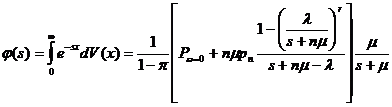 .
.
Стационарные средние времена ожидания начала обслуживания 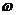 и пребывания заявки в системе
и пребывания заявки в системе 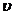 задаются формулами:
задаются формулами:
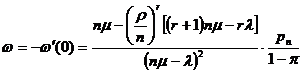 ,
,
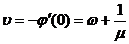 .
.
Последнее выражение можно также получить из формул Литтла.
Нестационарные характеристики
Нестационарное распределение числа заявок в системе 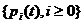 получается интегрированием системы
(1) с учетом начального распределения
получается интегрированием системы
(1) с учетом начального распределения 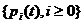 .
.
Если 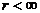 , то система (1) представляет собой линейную однородную
систему обыкновенных дифференциальных уравнений первого порядка с постоянными
коэффициентами.
, то система (1) представляет собой линейную однородную
систему обыкновенных дифференциальных уравнений первого порядка с постоянными
коэффициентами.
Выходящий поток
В системе 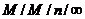 , в установившемся режиме поток заявок, покидающих систему,
является пуассоновским. То же самое можно сказать и о выходящем потоке из
системы M/M/n/r, если понимать под ним суммарный поток как обслуженных, так и
потерянных заявок. Доказательство этого с помощью метода обращения времени
полностью совпадает с доказательством аналогичного факта для системы
, в установившемся режиме поток заявок, покидающих систему,
является пуассоновским. То же самое можно сказать и о выходящем потоке из
системы M/M/n/r, если понимать под ним суммарный поток как обслуженных, так и
потерянных заявок. Доказательство этого с помощью метода обращения времени
полностью совпадает с доказательством аналогичного факта для системы 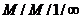 .
.
2.
Обоснование и выбор инструментальной среды для проведения расчетов
Моделирование систем является важным инструментом, когда необходимо понять,
объяснить непонятную проблему или решить поставленную задачу с помощью
компьютера. Серией компьютерных экспериментов исследуют модель и получают
подтверждение или опровержение передэкспериментальных гипотез о поведении
модели.
Результаты поведения модели менеджер использует для реального объекта, то
есть принимает плановое или прогнозируемое решение, полученное с помощью
исследования модели.- это компьютерная программная система для моделирования
систем управления. Simulink является составным элементом Matlab и использует
для моделирования все возможности. С помощью Matlab Simulink моделируются
линейные, нелинейные, дискретные, стохастические и гибридные системы.
При этом, в отличие от классических способов моделирования, пользователю
не нужно досконально изучать язык программирования и многочисленные методы
математики, а достаточно общих знаний, которые нужны для работы с компьютером,
и знаний о той предметной области, в которой он работает.
При работе в Matlab Simulink можно моделировать динамические системы,
выбирать методы решения дифференциальных уравнений, а также способов изменения
модельного времени (с фиксированным или переменным шагом). В ходе моделирования
имеется возможность следить за процессами, которые происходят в системе. Для
этого используются специальные устройства наблюдения, входящие в состав
библиотеки Simulink. Результаты моделирования могут быть представлены в виде
графиков и таблиц.
Преимущество Simulink заключается в том, что он позволяет пополнять
библиотеки блоков с помощью программ, написанных как на языке Matlab, так и на
языках С++, Fortran и Ada.
Исследуемую модель системы составляют в виде блок-схемы. Каждый типичный
блок является объектом с графическими чертежами, графическими и математическими
символами исполняемой программой и числовыми или формульными параметрами. Блоки
соединяются линиями, которые отражают движение материальных, финансовых и
информационных потоков между объектами.
Одной из самых распространенных областей, в которой используется
инструментарий Matlab Simulink, является экономика. Simulink, в частности
используется при исследовании таких экономических процессов как рыночное
равновесие, проектирование оптимальных ставок налогообложения бизнеса, анализ
динамики циклов и кризисов, оптимальное планирование на фирмах, в банках,
страховых компаниях и пенсионных фондах. массовый обслуживание многоканальный имитационный
Итак, Matlab Simulink - это система имитационного моделирования, которая
позволяет удобно и легко строить и исследовать модели экономических процессов.
3. Алгоритмическое обеспечение
.1
Постановка задачи
В качестве многоканальной СМО с отказами рассмотрим работу
вычислительного центра.
Требуется определить основные характеристики эффективности данной СМО,
если интенсивность, с которой каждая ЭВМ обслуживает заказ, равна 1/3 заявки в
час, а интенсивность, с которой заявки поступают в вычислительный центр, равна
0,25 единиц в час. Рассмотреть случай увеличения количества ЭВМ на 2 единицы в
центре и проследить, как изменятся основные характеристики этой системы. По
результатам анализа полученных результатов, дать рекомендации относительно
оптимального числа каналов обслуживания.
Рекомендации к решению задачи: здесь n = 3; λ
= 0.25 ед. в час.; 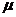 = 1/3 в час.
= 1/3 в час.
3.2
Математическая модель
Пусть СМО содержит n каналов, интенсивность входящего потока заявок равна
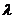 , а интенсивность обслуживания заявки
каждым каналом равна
, а интенсивность обслуживания заявки
каждым каналом равна 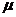 . Размеченный граф состояний системы изображён на рисунке 2.
. Размеченный граф состояний системы изображён на рисунке 2.

Рисунок 2 - График состояний многоканальной СМО с отказами
Состояние S0 означает, что все каналы свободны, состояние Sk
(k = 1, n) означает, что обслуживанием заявок заняты k каналов. Переход из
одного состояния в другое соседнее правое происходит скачкообразно под
воздействием входящего потока заявок интенсивностью 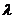 независимо от числа работающих
каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее
левое неважно, какой именно канал освободится. Величина
независимо от числа работающих
каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее
левое неважно, какой именно канал освободится. Величина 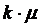 характеризует интенсивность
обслуживания заявок при работе в СМО k каналов (нижние стрелки).
характеризует интенсивность
обслуживания заявок при работе в СМО k каналов (нижние стрелки).
Легко увидеть, что многоканальная СМО с отказами является частным случаем
системы рождения и гибели, если в последней принять 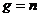 и
и
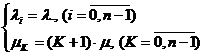 (3.1)
(3.1)
При этом для нахождения финальных вероятностей можно воспользоваться
формулами (4) и (5). С учётом (16) получим из них:
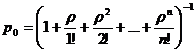 (3.2)
(3.2)
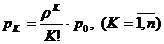 (3.3)
(3.3)
Формулы (3.2) и (3.3) называются формулами Эрланга - основателя теории
массового обслуживания.
Вероятность отказа в обслуживании заявки р_отк равна вероятности того,
что все каналы заняты, т.е. система находится в состоянии Sn. Таким
образом,
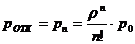 (3.4)
(3.4)
Относительную пропускную способность СМО найдём из (3.4):
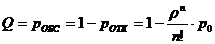 (3.5)
(3.5)
Абсолютную пропускную способность найдём из (3,5):
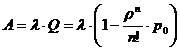
Среднее число занятых обслуживанием каналов можно найти таким образом:
так как каждый занятый канал в единицу времени обслуживает в среднем 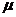 заявок, то
заявок, то  можно найти по формуле:
можно найти по формуле:
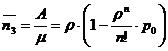
3.3
Построение моделей СМО с отказами в Simulink
.3.1 для
3-х канальной СМО
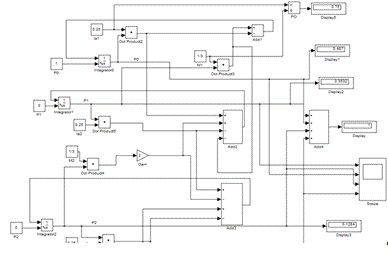
Рисунок 3 Модель СМО с 3-мя каналами обслуживания
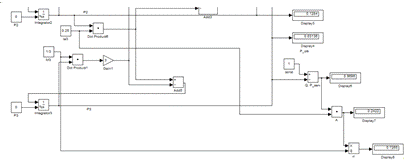
Рисунок 3 (продолжение) Модель СМО с 3-мя каналами обслуживания
В моделях, реализованных в Simulink, есть возможность вывести значения
показателей эффективности СМО. При изменении входных параметров, значения будут
пересчитываться автоматически.
Система массового обслуживания с тремя каналами может находиться в
четырех состояних: S0 - все каналы свободны, S1 - 1 канал занят, S2 - 2 канала
занято, S3 - все 3 канала заняты. Вероятности этих состояний представлены на
рисунке 4.
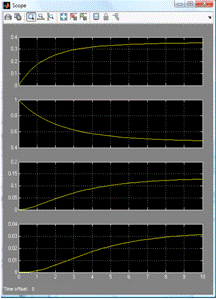
Рисунок 4 Вероятности состояний для СМО с 3-мя каналами
3.3.2 Для
5-канальной СМО
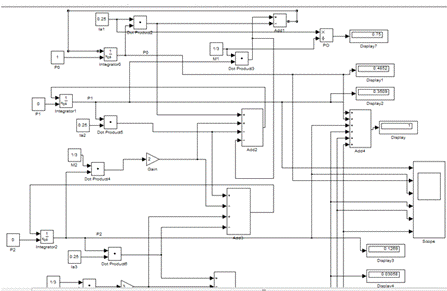
Рисунок 5 Модель СМО с 5-ю каналами
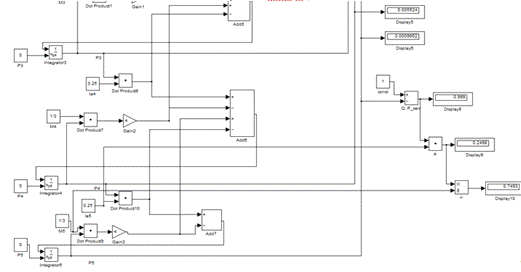
Рисунок 5 (продолжение) Модель СМО с 5-ю каналами
Как и в случае n=3 для СМО с n=5 реализован вывод значений показателей
эффективности в самой модели.
Система массового обслуживания с пятью каналами может находиться в шести
состояних: S0 - все каналы свободны, S1 - 1 канал занят, S2 - 2 канала занято,
S3 -3 канала заняты, S4 -4 канала заняты, S5 -все 5 каналов заняты. Вероятности
этих состояний представлены на рисунке 7
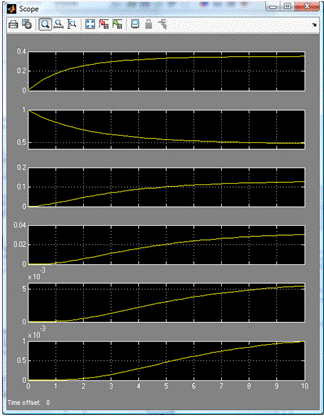
Рисунок 6 Вероятности состояний для СМО с 5-ю каналами
3.4
Расчет показателей эффективности
Расчет показателей эффективности систем массового обслуживания с тремя и
пятью каналами был произведен с помощью пакета MS Excel по формулам, описанным
в параграфе 3.2
.4.1 для
3-х канальной СМО
Таблица 1 Расчет показателей эффективности трехканальной СМО
|
n (число каналов
обслуживания)
|
3
|
|
ʎ (интенсивность
входящего потока заявок)
|
0,25
|
|
µ (интенсивность потока
обслуженных заявок, выходящих из одного канала)
|
0,33333
|
|
ρ
(приведенная интенсивность потока
заявок)
|
0,75
|
|
вероятности состояний
|
|
|
P_0
|
0,47584
|
|
P_1
|
0,35688
|
|
P_2
|
0,13383
|
|
P_3
|
0,03346
|
|
сумма вероятностей
|
1
|
|
Q (относительная пропускная
способность СМО)
|
0,96654
|
|
A (абсолютная пропускная способность
СМО)
|
0,24164
|
|
P_serv (вероятность того,
что заявка будет обслужена)
|
0,96654
|
|
P_otk (вероятность того,
что заявка получит отказ)
|
0,03346
|
|
n' (среднее число занятых
каналов)
|
0,72491
|
3.4.2 Для
5-канальной СМО
Таблица 2 Расчет показателей эффективности пятиканальной СМО
|
n (число каналов
обслуживания)5
|
0,25
|
|
µ (интенсивность потока
обслуженных заявок, выходящих из одного канала)
|
0,33333
|
|
ρ
(приведенная интенсивность потока
заявок)
|
0,75
|
|
вероятности состояний
|
|
|
P_0
|
0,47243
|
|
P_1
|
0,35432
|
|
P_2
|
0,13287
|
|
P_3
|
0,03322
|
|
P_4
|
0,00623
|
|
P_5
|
0,00093
|
|
сумма вероятностей
|
1
|
|
Q (относительная пропускная
способность СМО)
|
0,99907
|
|
A (абсолютная пропускная
способность СМО)
|
0,24977
|
|
P_serv (вероятность того,
что заявка будет обслужена)
|
0,99907
|
|
P_otk (вероятность того,
что заявка получит отказ)
|
0,00093
|
|
n' (среднее число занятых
каналов)
|
0,7493
|
3.5
Анализ результатов моделирования
Таблица 3 Сравнение результатов моделирования с теоретическими расчетами
для трехканальной СМО
|
Параметр
|
Теоретическое значение
|
Эмпирическое значение
|
Отклонение (в долях)
|
|
P_0
|
0,47584
|
0,487
|
0,023
|
|
P_otk
|
0,03346
|
0,03136
|
0,07
|
|
Q
|
0,96654
|
0,9686
|
0,002
|
|
A
|
0,24164
|
0,2422
|
0,002
|
|
n'
|
0,72491
|
0,7265
|
0,002
|
Таблица 4 Сравнение результатов моделирования с теоретическими расчетами
для пятиканальной СМО
|
ПараметрТеоретическое
значениеЭмпирическое значениеОтклонение
(в долях)
|
|
|
|
|
P_0
|
0,47242823
|
0,4852
|
0,026
|
|
P_otk
|
0,000934245
|
0,0009952
|
0,061
|
|
Q
|
0,96678239
|
0,999
|
0,032
|
0,241695598
|
0,2498
|
0,032
|
|
n'
|
0,725086793
|
0,7493
|
0,032
|
Из таблиц видно, что отклонения эмпирических значений от теоретических не
превышает ε=7%. Это означает, что построенные нами модели адекватно
описывают поведение системы и они применимы для поиска оптимальных соотношений
количества каналов обслуживания.
Таблица 5 Сравнение эмпирических показателей СМО где n=3 и СМО где n=5
|
Параметр
|
Показатели СМО где n=3
|
Показатели СМО где n=5
|
|
P_0
|
0,487
|
0,4852
|
|
P_otk
|
0,03136
|
0,0009952
|
|
Q
|
0,9686
|
0,999
|
|
A
|
0,2422
|
0,2498
|
|
n'
|
0,7265
|
0,7493
|
Очевидно, что чем выше число каналов обслуживания, тем меньше вероятность
отказа системы и выше вероятность того, что заявка будет обслужена. Абсолютная
пропускная способность системы в случае функционирования 5 каналов хоть и
незначительно выше, чем если бы функционировало всего 3 канала, однако это
свидетельствует о том, что необходимо сделать выбор в пользу увеличения числа
каналов обслуживания.
Таким образом, проведенный эксперимент показал, насколько можно доверять
результатам моделирования и выводам, сделанным на основе интерпретации этих
результатов.
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы были решены все поставленные задачи и
достигнута поставленная цель, а именно - были созданы модели, описывающие
экономический процесс, рассчитаны показатели этих моделей и сформированы
рекомендации для практического применения.
Моделирование было выполнено в системе Matlab Simulink в виде блок-схем,
которые в простой и удобной форме показывают сущности экономических процессов.
Так же была произведена проверка адекватности построенных моделей путем расчета
теоретических показателей эффективности выбранных типов СМО, по результатам
которой модели были признаны с большой вероятностью приближенными к реальности.
Из этого следует, что при рассмотрении аналогичных процессов и для экономии времени,
мы можем воспользоваться моделями, разработанными в ходе этой работы.
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Рыжиков
Ю.И. Имитационное моделирование. Теория и технологии. - СПб.: КОРОНА принт: М.:
Альтекс-А, 2004.
2. Варфоломеев
В.И. Алгоритмическое моделирование элементов экономических систем: Практикум.
Учеб. пособие . - М.: Финансы и статистика, 2000.
. Гмурман
В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов.
- М.: Высшая школа, 1998
. Самаров
К.Л. Учебно-методическое пособие по разделу ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО
ОБСЛУЖИВАНИЯ Учеб. пособие для вузов. - М.: Резольвента, 2009
. Советов
Б.А., Яковлев С.А. Моделирование систем. М: Высшая школа, 1985.
. Вентцель
Е.С. Исследование операций. М: Наука, 1980.