Теория массового обслуживания
Содержание
Введение
1.
Основные понятия теории массового обслуживания
1.1
Цепь Маркова и Марковские процессы
1.2
Теория массового обслуживания
1.3
Сеть массового обслуживания
2.
Мультипликативность стационарного распределения в открытых сетях с многорежимными
стратегиями обслуживания
2.1.
Основная модель
.1.1
Обслуживание заявок
.2
Уравнения равновесия
.3
Уравнения трафика
Заключение
Список
используемой литературы
Введение
Одним из важных разделов
экономико-математического моделирования является теория массового обслуживания,
представляющая собой теоретические основы эффективного конструирования и
эксплуатации систем массового обслуживания. Системы массового обслуживания
(СМО) встречаются во многих областях экономики (производство, техника-военная область,
быт и др.) и предназначены для многократного использования при выполнении
однотипных задач.
Основоположником теории массового обслуживания
считается датский ученый А. К. Эрланг. Являясь сотрудником Копенгагенской
телефонной компании, он опубликовал в 1909 году работу «Теория вероятностей и
телефонные переговоры», в которой решил ряд задач по теории систем массового
обслуживания с отказами. Значительный вклад в создание и разработку общей
теории массового обслуживания внес выдающийся советский математик Александр
Яковлевич Хинчин (1984 - 1959), который предложил сам термин теория массового
обслуживания. В зарубежной литературе чаще используется название теория
очередей.
В 1957г. Дж.Р.Джексон впервые ввел в
рассмотрение понятие открытой сети массового обслуживания, а в 1967г. Гордон и
Ньюэлл ввели аналогичное понятие замкнутой сети. В отличие от системы массового
обслуживания сеть представляет собой более сложное образование, состоящее из
систем массового обслуживания, называемых узлами сети, которые взаимодействуют
между собой с помощью некоторого вероятностного механизма. В открытых сетях
заявки могут поступать извне, а также уходить из сети. В замкнутых сетях
сохраняется постоянное число заявок, которые с помощью случайной маршрутизации
могут перемещаться между узлами сети; при этом поступление заявок в сеть и уход
заявок из сети невозможны.
Состояние сети массового обслуживания обычно
характеризуется вектором, координаты которого описывают состояния отдельных
узлов сети. В силу многомерности случайного процесса состояний и статистической
зависимости между координатами исследование сетей массового обслуживания на
порядок сложнее, чем исследование систем массового обслуживания.
Предметом исследования теории массового
обслуживания являются вероятностные модели физических систем обслуживания, в
которых случайные и не случайные моменты времени возникают заявки на
обслуживание и имеются устройства на обработку данных заявок.
. Основные понятия теории массового обслуживания
Цепь Маркoва - последовательность случайных
событий с конечным или счётным числом исходов, характеризующаяся тем свойством,
что при фиксированном настоящем будущее независимо от прошлого.
Цепь Маркова с дискретным временем - это
последовательность дискретных случайных величин 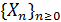 ,
в которой выполняется условие:
,
в которой выполняется условие:
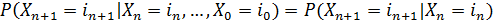
Таким образом, в простейшем случае условное
распределение последующего состояния цепи Маркова зависит только от текущего
состояния и не зависит от всех предыдущих состояний.
Матрица 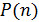 ,
где
,
где
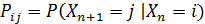
называется матрицей переходных вероятностей на 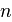 -м
шаге, а вектор
-м
шаге, а вектор 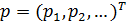 , где
, где 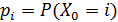 -
начальным распределением цепи Маркова.
-
начальным распределением цепи Маркова.
Цепь Маркова называется одноро́дной,
если матрица переходных вероятностей не зависит от номера шага, то есть
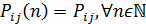
В противном случае цепь Маркова называется
неоднородной.
Цепь Маркова с непрерывным временем или
Марковский процесс - это семейство дискретных случайных величин 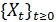 ,
в котором выполняться:
,
в котором выполняться:
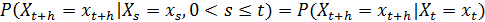
Цепь Маркова с непрерывным временем называется
однородной, если
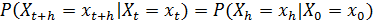
Конечномерные распределения однородной цепи
Маркова с непрерывным временем полностью определены начальным распределением
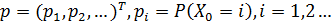
и ма́трицей
перехо́дных
фу́нкций
(переходных вероятностей)
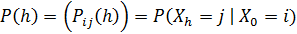
Матрица переходных вероятностей удовлетворяет
уравнению Колмогорова - Чепмена:
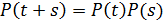
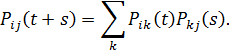
.2 Теория массового обслуживания
Теория массового обслуживания (теория очередей)
- раздел теории вероятностей, целью исследований которого является рациональный
выбор структуры системы обслуживания и процесса обслуживания на основе изучения
потоков требований на обслуживание, поступающих в систему и выходящие из неё,
длительности ожидания и длины очередей.
Однородный стационарный поток без
последействий является простейшим, потоком Пуассона
<#"698162.files/image016.gif"> событий
такого потока, выпадающих на интервал длины 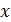 , распределено по Закону Пуассона
<#"698162.files/image018.gif">
, распределено по Закону Пуассона
<#"698162.files/image018.gif">
Пуассоновский поток заявок удобен
при решении задач ТМО. Строго говоря, простейшие потоки редки на практике,
однако многие моделируемые потоки допустимо рассматривать как простейшие.
Поток заявок стационарен, если
вероятность появления n событий на интервале времени 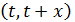 не зависит
от времени
не зависит
от времени 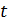 , а зависит
только от длины
, а зависит
только от длины 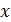 этого
участка.
этого
участка.
.3 Сеть массового обслуживания
Сеть массового обслуживания (СеМО) -
сеть, которая производит обслуживание поступающих в неё требований.
Обслуживание требований в СМО производится обслуживающими приборами.
Классическая СМО содержит от одного до бесконечного числа приборов. В
зависимости от наличия возможности ожидания поступающими требованиями начала
обслуживания СМО подразделяются на:истемы с потерями, в которых требования, не
нашедшие в момент поступления ни одного свободного прибора, теряются;истемы с
ожиданием, в которых имеется накопитель бесконечной ёмкости для буферизации
поступивших требований, при этом ожидающие требования образуют очередь;истемы с
накопителем конечной ёмкости (ожиданием и ограничениями), в которых длина
очереди не может превышать ёмкости накопителя; при этом требование, поступающее
в переполненную СМО (отсутствуют свободные места для ожидания), теряется.
Каждая СМО предназначена для
обслуживания (выполнения) некоторого потока заявок (или требований),
поступающих на вход системы большей частью не регулярно, а в случайные моменты
времени. Обслуживание заявок, в общем случае, также длится не постоянное,
заранее известное, а случайное время. После обслуживания заявки канал
освобождается и готов к приему следующей заявки. Случайный характер потока и
времени их обслуживания приводит к неравномерной загруженности СМО: в некоторые
промежутки времени на входе СМО могут скапливаться необслуженные заявки (они
либо становятся в очередь, либо покидают СМО необслуженными), в другие же
периоды при свободных каналах на входе СМО заявок не будет, что приводит к
недогрузке СМО, т.е. к простаиванию каналов.
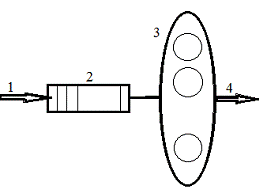
Таким образом, во всякой СМО можно
выделить следующие основные элементы:
) входящий поток заявок;
) очередь;
) каналы обслуживания;
) выходящий поток обслуженных
заявок.
Каждая СМО в зависимости от своих
параметров: характера потока заявок, числа каналов обслуживания и их
производительности, а также от правил организации работы, обладает определенной
эффективностью функционирования (пропускной способностью), позволяющей ей более
или менее успешно справляться с потоком заявок.
Предметом изучения теории массового
обслуживания являются СМО.
Цель теории массового обслуживания -
выработка рекомендаций по рациональному построению СМО, рациональной
организации их работы и регулированию потока заявок для обеспечения высокой
эффективности функционирования СМО.
Для достижения этой цели ставятся
задачи теории массового обслуживания, состоящие в установлении зависимостей
эффективности функционирования СМО от ее организации (параметров): характера
потока заявок, числа каналов и их производительности и правил работы СМО.
Случайный характер потока заявок и
длительности их обслуживания порождает в СМО случайный процесс.
Простейший поток событий и его
свойства
Под потоком событий понимается
последовательность однородных событий, следующих одно за другим в какие-то
случайные моменты времени (например, поток вызовов на телефонной станции, поток
покупателей, поток заказных писем, поступающих в почтовое отделение и т.п.).
Поток характеризуется интенсивностью 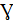 - частотой появления событий или
средним числом событий, поступающих в СМО в единицу времени. Поток событий
называется регулярным, если события следуют одно за другим через определенные
равные промежутки времени. Например, поток изделий на конвейере сборочного цеха
(с постоянной скоростью движения) является регулярным. Такой поток сравнительно
редко встречается в реальных системах, но представляет интерес как предельный
случай. Типичным для системы массового обслуживания является случайный поток
заявок.
- частотой появления событий или
средним числом событий, поступающих в СМО в единицу времени. Поток событий
называется регулярным, если события следуют одно за другим через определенные
равные промежутки времени. Например, поток изделий на конвейере сборочного цеха
(с постоянной скоростью движения) является регулярным. Такой поток сравнительно
редко встречается в реальных системах, но представляет интерес как предельный
случай. Типичным для системы массового обслуживания является случайный поток
заявок.
Поток событий называется
стационарным, если его вероятностные характеристики не зависят от времени. В
частности, интенсивность стационарного потока есть величина постоянная: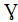 (t) =
(t) = 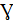 . Это
отнюдь не значит, что фактическое число событий, появляющееся в единицу
времени, постоянно, - нет, поток неизбежно (если только он не регулярный) имеет
какие-то случайные сгущения и разрежения. Важно, что для стационарного потока
эти сгущения и разрежения не носят закономерного характера: на один участок
длины может попасть больше, на другой - меньше событий, но среднее число
событий, приходящееся на единицу времени, постоянно и от времени не зависит.
. Это
отнюдь не значит, что фактическое число событий, появляющееся в единицу
времени, постоянно, - нет, поток неизбежно (если только он не регулярный) имеет
какие-то случайные сгущения и разрежения. Важно, что для стационарного потока
эти сгущения и разрежения не носят закономерного характера: на один участок
длины может попасть больше, на другой - меньше событий, но среднее число
событий, приходящееся на единицу времени, постоянно и от времени не зависит.
. Стационарное распределение
двухузловой СеМО с симметричным трафиком
массовое обслуживание
сеть заявка
2.1 Основная модель
.1.1 Обслуживание заявок
Обслуживание - экспоненциальное с
параметрами 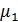 и
и 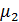 соответственно.
соответственно.
После обслуживания в первом узле
заявка с вероятностью  переходит
во второй узел, а с вероятностью
переходит
во второй узел, а с вероятностью  покидает сеть. А после обслуживания
заявки во втором узле, она с вероятностью
покидает сеть. А после обслуживания
заявки во втором узле, она с вероятностью  переходит в первый узел, и с
вероятностью
переходит в первый узел, и с
вероятностью  покидает
сеть.
покидает
сеть.
Состояние сети 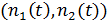 , где
, где 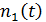 - число
заявок в первом узле в момент времени
- число
заявок в первом узле в момент времени 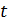 ,
, 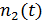 - число заявок во втором узле в
момент времени
- число заявок во втором узле в
момент времени 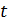 .
.
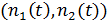 - марковский процесс.
- марковский процесс.
.2 Уравнения равновесия
Составим уравнение равновесия для
сети:
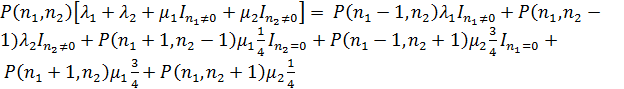
.3 Уравнения трафика
Уравнения трафика в данной сети
будут выглядеть:
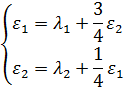
Решая систему уравнений трафика
можно выразить 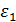 и
и 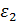 через
через 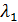 и
и 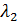 :
:
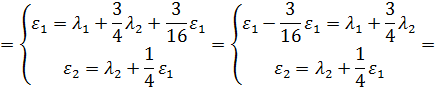
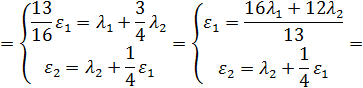
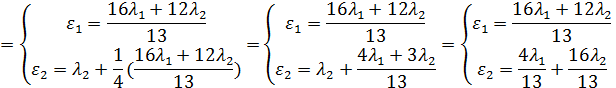
Заключение
В данном курсовом проекте представлена тема
"Теория массового обслуживания". Системы массового обслуживания имеют
огромное практическое применение в наше время. СМО разделяются на большое
количество типов. Первые задачи теории массового обслуживания были рассмотрены
сотрудником Копенгагенской телефонной компании, ученым Агнером Эрлангом, в
период между 1908 и 1922 годами. Стояла задача упорядочить работу телефонной
станции и заранее рассчитать качество обслуживания потребителей в зависимости
от числа используемых устройств.
Установлены необходимые и достаточные условия,
которые надо наложить на изолированные узлы открытой сети массового обслуживания
с двурежимными стратегиями обслуживания, чтобы стационарное распределение
состояний сети имело мультипликативную форму с множителями, зависящими от
состояний отдельных узлов. Эти условия выписаны в аналитической форме и
выражают квазиобратимость нетерминальных узлов сети. Искусственная случайная
среда характеризуется пуассоновским входным потоком.
В аналитической форме найдены множители в
мультипликативном представлении стационарного распределения. Построен алгоритм
для расчета стационарных вероятностей состояний сети. Доказано, что выходящие
из сети потоки заявок являются независимыми пуассоновскими потоками.
Список используемой литературы
.
Д.Кениг, Д.Штойян. Методы теории массового обслуживания: Пер. с нем.
/Под. ред. Г.П.Климова. М., 1981.
.
Т.Л.Саати. Элементы теории массового обслуживания и ее приложения: Пер.
с англ. /Под. ред. И.Н. Коваленко, изд-ие 2. М., 1971.
Малинковский
Ю.В., Нуеман А.Ю. Мультипликативность стационарного распределения в открытых
сетях с многорежимными стратегиями обслуживания / / Весщ НАИБ. Серы я
ф1з.-мат.навук. - 2001. - № 3. - С.129-134.