Построение регрессионной модели экономического объекта
Курсовая
работа
по курсу
«Эконометрика»
на тему
«Построение регрессионной модели экономического объекта»
Введение
Данная курсовая работа по теме «Построение
регрессионной модели экономического объекта» предполагает выполнение
практического задания, которое включает в себя:
·
оценку
распределения заданной переменной;
·
исследование
зависимости между переменными;
·
построение
первоначальной регрессионной модели экономического объекта;
·
проверку
качества построенной модели, определение резервов повышения качества;
·
изменение
спецификации модели и расчет параметров новой модели;
·
проверку
качества новой регрессионной модели;
·
расчет
прогнозного значения моделируемой переменной.
Целью курсовой работы является:
• углубление, закрепление и конкретизация
теоретических знаний, полученных на занятиях по данной дисциплине;
• выработка умения делать обоснованный
выбор типа регрессионной модели, методов оценивания параметров, выводы по
результатам.
При решении данной курсовой работы используются
следующие методы:
) графический метод;
) метод средних величин;
) группировка;
) представление данных в виде аналитических
таблиц.
Задание: Изучается зависимость выпуска продукции
(Y, тыс. ед.) от ее
материалоемкости (Х, кг на единицу продукции в некоторой отрасли).
Имеется следующая выборка:
|
Х
|
9
|
6
|
5
|
4
|
3,7
|
3,6
|
3,5
|
6
|
7
|
3,4
|
|
Y
|
100
|
220
|
230
|
400
|
520
|
590
|
700
|
150
|
120
|
750
|
|
Х
|
4,2
|
4,8
|
5,1
|
5,4
|
7
|
6,6
|
5,6
|
8,1
|
6
|
|
Y
|
410
|
470
|
310
|
250
|
130
|
160
|
240
|
110
|
200
|
Задание:
1. Оцените распределение переменной Х:
·
найдите
закон распределения переменной и постройте гистограмму;
·
определите,
можно ли признать имеющийся набор данных нормально распределенным; укажите, как
можно устранить существующие проблемы в данных;
·
определите
наиболее типичное значение переменной и средний разброс ее значений;
·
сделайте
вывод о наиболее типичном значении данного показателя в генеральной
совокупности с 90%-ной уверенностью.
2. Исследуйте взаимосвязь между переменными
У и Х:
·
рассчитайте
коэффициент корреляции между переменными и оцените силу и направление связи
между ними;
·
проверьте
сделанные выводы с помощью поля корреляции;
·
определите
форму зависимости между переменными.
3. Произведите моделирование взаимосвязи
между переменными У и Х с помощью линейной функции:
·
оцените
с помощью метода наименьших квадратов линейное уравнение регрессии Ŷ = b0
+ b1 · X;
·
проверьте
качество построенной модели при уровне значимости 0,05;
·
проверьте
наличие автокорреляции остатков графическим методом и с помощью критерия
Дарбина-Уотсона при уровне значимости 0,01;
·
проверьте
наличие гетероскедастичности графическим методом и с помощью теста
Голдфелда-Квандта при уровне значимости 0,05;
·
сделайте
вывод, можно ли использовать линейную модель для прогнозирования. Совпадают ли
ваши выводы с предположениями, сделанными в п. 2?
4. Составьте спецификацию гиперболической
регрессионной модели и рассчитайте параметры нового уравнения.
5. Проверьте качество новой модели при том
же уровне значимости, а также наличие автокорреляции остатков. Как вы объясните
изменения показателей?
. Если необходима дальнейшая
корректировка модели, внесите предложения по изменению спецификации.
. Нанесите на поле корреляции графики
двух функций регрессии. Сравните качество построенных моделей. Какая из
моделей, на ваш взгляд, предпочтительнее для выражения исследуемой зависимости
и почему?
Рассчитайте 90%-ые доверительные интервалы для
теоретических коэффициентов наилучшей регрессии.
8. По наилучшей регрессионной модели
рассчитайте точечные прогнозы среднего значения выпуска при потреблении 3 кг и
6 кг материала на единицу продукции и 99%-ные доверительные интервалы для
индивидуальных значений объема продаж бензина. Какой прогноз является более
точным?
Таблица 1 - Исходные данные
|
Х
|
Y
|
|
9
|
100
|
|
6
|
220
|
|
5
|
230
|
|
4
|
400
|
|
3,7
|
520
|
|
3,6
|
590
|
|
3,5
|
700
|
|
6
|
150
|
|
7
|
120
|
|
3,4
|
750
|
|
4,2
|
410
|
|
4,8
|
470
|
|
5,1
|
310
|
|
5,4
|
250
|
|
7
|
130
|
|
6,6
|
160
|
|
5,6
|
240
|
|
8,1
|
110
|
|
6
|
200
|
1. Оценивание распределения переменной Х
.1 Нахождение закона распределения переменной и
построение гистограммы
Для построения закона распределения случайной
величины (Х) необходимо выполнить следующее:
1. Необходимо упорядочить набор данных, т.е.
расположить данные в порядке возрастания (см. таблицу 1).
. Разбить набор данных на несколько интервалов
равной ширины = 1.
Частота - это количество попаданий значений
случайной величины в определенный интервал.
Частота определяется с помощью статистической
функции Microsoft
Excel.
Функция ЧСТРОК (1)
Синтаксис:
ЧСТРОК (диапазон _ ячеек)
Результат:
Подсчитывает количество строк в
выделенном диапазоне ячеек.
Аргументы:
·диапазон _ ячеек: диапазон ячеек,
для которого нужно подсчитать количество строк.
Функцию ЧСТРОК удобно использовать для подсчета
частоты попадания значений в определенный интервал.
Закон распределения случайной величины -
представляет собой соотношение между средним значением случайной величины (Хi)
в интервале и вероятности попадания в этот интервал (Рi).
Таблица 2 - Нахождение закона распределения
|
Группировка
случайной величины по интервалам
|
Закон
распределение случайной величины
|
|
интервалы
|
частота
|
Хi
|
Рi
|
|
3
|
4
|
4
|
3,5
|
0,21
|
|
4
|
5
|
3
|
4,5
|
0,16
|
|
5
|
6
|
4
|
5,5
|
0,21
|
|
6
|
7
|
4
|
6,5
|
0,21
|
|
7
|
8
|
2
|
7,5
|
0,11
|
|
8
|
9
|
2
|
8,5
|
0,11
|
Нахождение значений случайной величины (Хi)
определяется по следующей формуле:
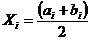(2)
где: ai
- нижняя граница i -
интервала;
bi - верхняя
граница i - интервала.
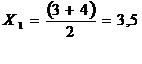
Или с использованием встроенной
функции СРЗНАЧ
Вероятность попадания (Рi)
значений случайной величины (Хi)
определяется по следующей формуле:
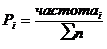(3)
где: частотаi
- количество попаданий значений в соответствующий i
- интервал;
n - объём выборки (n
= 19).
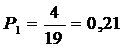
На основе закона распределения строим диаграмму.
Для того чтобы построить диаграмму, следует выбрать команду «Диаграмма» меню
«Вставка» или нажать соответствующую пиктограмму.
В диалоговом окне «Мастер диаграмм» необходимо
выбрать тип диаграммы (в данном случае - гистограмма), указать диапазон данных
для построения диаграммы (Хi
и Pi), а также, при
необходимости, подписи по
оси Х (закладка «Ряд»).
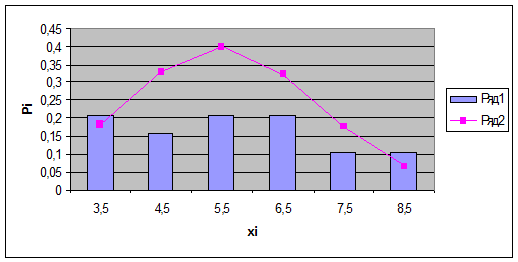
Рис. 1 Гистограмма закона распределения
случайной величины
При анализе построенной гистограммы видно, что
присутствует ассиметричное распределение.
1.2 Определение, можно ли признать имеющийся набор
данных нормально распределенным и укажем, как можно устранить существующие
проблемы в данных
Нормальное распределение - это непрерывное
распределение, имеющее графическое представление в виде симметричной
колоколообразной кривой.
гиперболический регрессионный переменная гистограмма
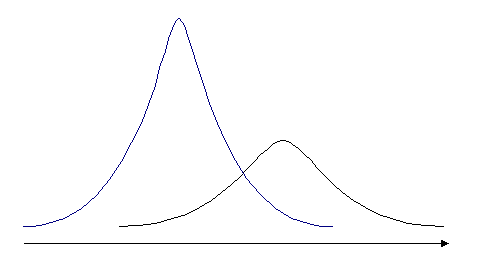
Рис. 2 Кривые нормального
распределения
Набор данных можно считать нормально
распределённым, если форма гистограммы их напоминает колокол, в котором
большинство значений сконцентрировано в средней части, а остальные распределены
равномерно с затуханием по обе стороны от центра. Данный набор данных не имеет
значений, которые требуют специальной обработки, но характер затухания для
малых и больших значений данных не одинаков, поэтому его нельзя признать
нормально распределённым, т. к. присутствует ассиметричное распределение.
Асимметричность данных можно убрать,
прологарифмировав данные или увеличив количество данных.
1.3 Определение наиболее типичного значения
переменной и средний разброс ее значений
Так как чаще всего отсутствует информация обо
всех объектах генеральной совокупности, есть данные лишь о нескольких объектах
из генеральной совокупности - о выборке.
Каждый параметр генеральной совокупности имеет
оценку - выборочный параметр, который приблизительно его определяет:
- оценкой математического ожидания является
выборочное среднее (далее ВС);
- оценкой среднего квадратичного отклонения -
выборочное среднее квадратичное отклонение (далее ВСКО).
Наиболее типичное значение
переменной: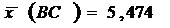 
Определяется с помощью
статистической функции Microsoft Excel:
Функция СРЗНАЧ (4)
Синтаксис:
СРЗНАЧ (диапазон _ ячеек)
Результат:
Рассчитывает математическое
ожидание (среднее значение) набора данных.
Аргументы:
·диапазон _ ячеек: диапазон ячеек, в
котором содержится набор данных.
Средний разброс её значений
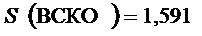
Определяется с помощью
статистической функции Microsoft Excel:
Функция СТАНДОТКЛОН (5)
Синтаксис:
СТАНДОТКЛОН (диапазон _ ячеек)
Результат:
Рассчитывает среднее
квадратичное отклонение набора данных.
Аргументы:
·диапазон _ ячеек: диапазон ячеек, в
котором содержится набор данных.
1.4 Вывод о наиболее типичном значении данного
показателя в генеральной совокупности с 90%-ой уверенностью
Имея информацию о выборке, можно приблизительно
оценить, чему может быть равна ошибка оценивания - разность между выборочным
средним (ВС) и математическим ожиданием генеральной совокупности (МОГС). Такой
оценкой является стандартная ошибка, которая рассчитывается по формуле:
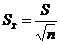(6)
где: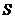 
- выборочное среднее квадратичное
отклонение;
n - объём выборки.
Таким образом, чем больше объём выборки, тем
точнее выборочное среднее оценивает математическое ожидание генеральной совокупности.
Для более точного вывода о типичном значении
параметра генеральной совокупности оценивание завершается определением
интервальной оценки - доверительного интервала.
Доверительным интервалом называется интервал,
который с определенной вероятностью содержит значение неизвестного параметра
генеральной совокупности.
Поскольку на практике извлекается только одна
выборка, т.е. определяется только одно значение выборочного среднего. Можно
заменить среднее квадратичное отклонение (СКО) его оценкой - стандартной
ошибкой (далее СТО).
Причем чем меньше объем выборки, тем сильнее
уменьшится точность, так как величина стандартной ошибки зависит от объема
выборки.
Рассчитаем доверительный интервал с 90%-ой
вероятностью.
Объём выборки: n
= 19
Число степеней свободы: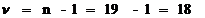 
Доверительная вероятность
(надежность):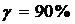 
Уровень значимости: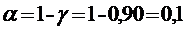 
Критическая точка: tкр = 1,734 (по
таблице Стьюдента tкр = 1,734)
Критическая точка распределения
Стьюдента определяется с помощью статистической функции Microsoft Excel (см.
формулу 7) или с помощью таблицы распределения Стьюдента (см. приложение А).
Функция
СТЬЮДРАСПОБР (7)
Синтаксис:
СТЬЮДРАСПОБР (диапазон _ ячеек)
Результат:
Рассчитывает критические точки для распределения
Стьюдента
Аргументы:
вероятность: уровень значимости α,
соответствующий двустороннему распределению Стьюдента;
степени _ свободы: число степеней свободы.
Границы доверительного интервала рассчитываются
по следующей формуле:
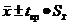(8)
где: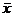 
- выборочное среднее;
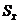- стандартная ошибка.
Нижняя граница доверительного
интервала равна:
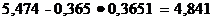
Верхняя граница доверительного
интервала равна:
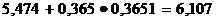
4,841
5,474 6,107
Рис. 3 Границы доверительного интервала
Вывод: можно быть на 90% уверенным, что значение
параметра генеральной совокупности лежит в пределах от 4,841 до 6,107 т.е.
значение материалоемкости лежит в пределах от 4,841 до 6,107.
2. Исследование взаимосвязи между переменными Y
и Х
.1 Расчет коэффициента корреляции между
переменными и оценивание силы и направление связи между ними
Одним из показателей силы взаимосвязи между
двумя переменными является коэффициент корреляции, который можно рассчитать с
помощью статистической функции Microsoft Excel.
Функция КОРРЕЛ (10)
Синтаксис:
КОРРЕЛ (массив _ 1; массив _ 2)
Результат:
Рассчитывает коэффициент корреляции между двумя
переменными.
Аргументы:
массив _ 1: диапазон значений первой переменной;
массив _ 2: диапазон значений второй переменной.
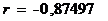
Так как коэффициент корреляции равен
-0,87497, то это означает, что существует обратная связь средней силы. Точки на
поле корреляции сгруппированы вокруг прямой линии, направленной вниз и вправо,
но имеют некоторый разброс.
.2 Проверка выводов с помощью поля
корреляции
Структуру двумерных данных проще
всего увидеть с помощью поля корреляции. Каждая точка на этом графике
соответствует одному наблюдению - по горизонтали откладывается значение одной
из переменных (Х), полученное в результате наблюдения, по вертикали - значение
второй переменной (Y), полученное в результате того же наблюдения.
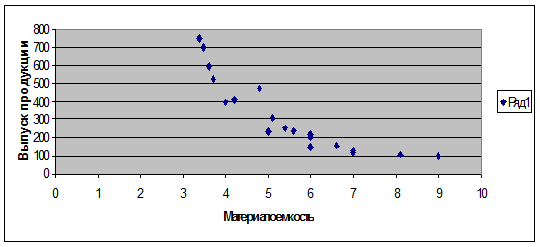
Рис. 4 Поле корреляции
Вывод: при анализе поля корреляции
видно, что между точками на поле корреляции присутствует обратная связь средней
силы, т.к. точки на поле корреляции сгруппированы вокруг прямой линии,
направленной вниз и вправо, но имеют некоторый разброс.
.3 Определение формы зависимости
между переменными
Из построенного поля корреляции
видно, что точки расположены хаотично, но вокруг некой прямой, т.о.
присутствует линейная форма зависимости между переменными.
3. Моделирование взаимосвязи между
переменными Y и X с помощью линейной функции
.1 Оценка с помощью метода
наименьших квадратов линейное уравнение регрессии Ŷ = b0 + b1 · X
Линейный регрессионный анализ
позволяет предсказывать одну переменную на основании другой с использованием
прямой линии, характеризующей взаимосвязь между этими переменными:
Ŷ = b0 + b1 ·
X (11)
где: b0
- свободный член - коэффициент регрессии;
b1 - угловой
коэффициент - коэффициент регрессии.
Результирующим показателем в данном случае
является выпуск продукции, тыс. ед. Фактором - материалоемкость, кг на единицу
продукции.
Построим уравнение линейной регрессии методом
наименьших квадратов
С помощью этого метода строится уравнение
регрессии, которое характеризуется наименьшей суммой квадратов отклонений
реальных точек наблюдений от линии регрессии.
Метод наименьших квадратов использует следующие
формулы для расчета коэффициентов регрессии:
для расчёта углового коэффициента регрессии
используется следующая формула:
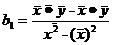(12)
для расчёта свободного члена регрессии
используется следующая формула:
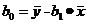(13)
Для каждого наблюдаемого значения хi можно
вычислить прогнозируемое значение ŷi на основании уравнения регрессии,
которое рассчитывается по следующей формуле:
ŷi = b0 + b1 ·
хi (14)
Таблица 4 - Расчёт значений для определения
коэффициентов регрессии (b1
и b0) и случайного
отклонения
|
Х
|
Y
|
х·y
|
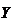х2
|
 еiеi2
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
3,4
|
750
|
2550
|
11,56
|
551,1054
|
198,895
|
39559,077
|
|
3,5
|
700
|
2450
|
12,25
|
539,9099
|
160,09
|
25628,832
|
|
3,6
|
590
|
2124
|
12,96
|
528,7145
|
61,2855
|
3755,9137
|
|
3,7
|
520
|
1924
|
13,69
|
517,5191
|
2,48095
|
6,1550931
|
|
4
|
400
|
1600
|
16
|
483,9327
|
-83,933
|
7044,7057
|
|
4,2
|
1722
|
17,64
|
461,5419
|
-51,542
|
2656,5646
|
|
4,8
|
470
|
2256
|
23,04
|
394,3693
|
75,6307
|
5720,0096
|
|
5
|
230
|
1150
|
25
|
371,9784
|
-141,98
|
20157,861
|
|
5,1
|
310
|
1581
|
26,01
|
360,7829
|
-50,783
|
2578,9076
|
|
5,4
|
250
|
1350
|
29,16
|
327,1966
|
-77,197
|
5959,3208
|
|
5,6
|
240
|
1344
|
31,36
|
304,8058
|
-64,806
|
4199,7871
|
|
6
|
150
|
900
|
36
|
260,024
|
-110,02
|
12105,285
|
|
6
|
200
|
1200
|
36
|
260,024
|
-60,024
|
3602,8829
|
|
6
|
220
|
1320
|
36
|
260,024
|
-40,024
|
1601,9221
|
|
6,6
|
160
|
1056
|
43,56
|
192,8514
|
-32,851
|
1079,2146
|
|
7
|
120
|
840
|
49
|
148,0697
|
-28,07
|
787,90563
|
|
7
|
130
|
910
|
49
|
148,0697
|
-18,07
|
326,5125
|
|
8,1
|
110
|
891
|
65,61
|
24,91986
|
85,0801
|
7238,6306
|
|
9
|
100
|
900
|
81
|
-75,83907
|
175,839
|
30919,378
174928,87
|
|
|
|
|
|
|
174928,87
|
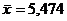(см. п. 1.3)
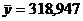(см. п. 1.3)
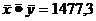(см. формулу 4)
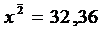(см. формулу 4)
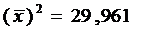
Следовательно, угловой коэффициент
регрессии равен:
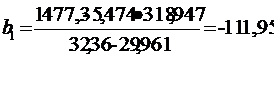
Следовательно, свободный член
регрессии равен:
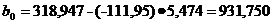
Линейное уравнение регрессии: Ŷ
= 931,750 - 111,95 · X
Проверим полученные значения с
помощью функции ЛИНЕЙН, которая определяется с помощью статистической функции
Microsoft Excel.
Функция ЛИНЕЙН (14)
Синтаксис:
ЛИНЕЙН (известные _ значения _ у; известные _
значения _ х; константа; статистика)
Результат:
Рассчитывает массив данных, описывающих
уравнение линейной регрессии на основе метода наименьших квадратов.
Аргументы:
известные _ значения _ у: диапазон значений результирующего
показателя Y;
известные _ значения _ х: диапазон значений
фактора Х;
константа: логическое значение:
если оно равно 0, свободный член b0 равен 0;
если оно равно 1, то b0 вычисляется обычным
образом.
статистика: логическое значение:
если оно равно 0, то функция рассчитывает только
коэффициенты b0 и b1;
если оно равно 1, то функция рассчитывает
дополнительную регрессионную статистику, и возвращаемый массив будет иметь вид,
указанный в таблице 5.
Таблица 5 - Рассчитанные значения функцией ЛИНЕЙН
|
b1
|
-111,95
|
931,75
|
b0
|
|
Sb1
|
15,026
|
85,4749
|
Sb0
|
|
R2
|
0,7656
|
101,439
|
Se
|
|
F
|
55,515
|
17
|
ν
|
|
SSоб
|
571250
|
174929
|
SSост
|
где: b1-
угловой коэффициент регрессии;
b0- свободный член
регрессии;
Sb1 и Sb0
- стандартные ошибки коэффициентов регрессии;
R2 -величина коэффициента
детерминации;
Se - величина
стандартной ошибки регрессии;
F - значение
критерия Фишера для проверки гипотезы о значимости R2.
Чтобы функция регрессии возвратила массив из
десяти ячеек, необходимо ввести ее как функцию массива. Это можно осуществить
двумя способами:
. Выделяются десять ячеек, в которые нужно
поместить результат функции. Затем вводится функция ЛИНЕЙН (сразу во все
выделенные ячейки), причем закончить ввод нужно комбинацией клавиш Ctrl
+ Shift + Enter.
. Функция ЛИНЕЙН вводится в одну ячейку - эта
ячейка будет верхней левой ячейкой массива результатов. Затем выделяются десять
ячеек, в которые нужно поместить результат, начиная с ячейки, где введена
функция. Выделив ячейки, нужно нажать клавишу F2,
а затем - комбинацию клавиш Ctrl
+ Shift + Enter.
На поле корреляции линия регрессии отражает
основную структуру данных, однако каждая отдельная точка отклоняется от этой
линии на некоторую случайную величину еi, которая называется случайным
отклонением:
еi = yi - ŷi (15)
Построим линию регрессии, добавив на поле
корреляции рассчитанные значения ŷi.
Для этого необходимо добавить новый ряд данных,
выделив область диаграммы и выполнить команду "Добавить данные" меню
"Диаграмма". В появившемся диалоговом окне следует выбрать диапазон
добавляемых значений данных.
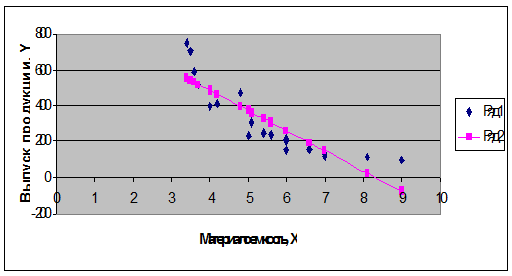
Рис. 5 Линия регрессии на поле корреляции
3.2 Проверка качества построенной модели при
уровне значимости 0, 05
.2.1 Проверка адекватности уравнения
эмпирическим данным
Для двумерных данных существуют отклонения
относительно линии регрессии, которые, в общем, характеризуются стандартной
ошибкой регрессии:
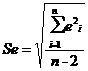(16)
где: ei
- величина случайного отклонения (см. таблицу 4);
n - объём выборки.
Следовательно, стандартная ошибка регрессии
равна:
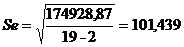или по таблице 5.
Стандартная ошибка регрессии
показывает величину, на которую в среднем отклоняются реальные наблюдаемые
значения результирующего показателя от уравнения регрессии. Чем меньше эта
величина, тем точнее предсказания, осуществляемые на основании этого уравнения.
Более удобной характеристикой
точности предсказания, или качества уравнения регрессии, является коэффициент
детерминации.
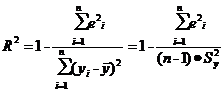(17)
где: ei
- величина случайного отклонения (см. таблицу 4);
n - объём выборки;
Sy2 -
дисперсия переменной Y, для её нахождения необходимо Sy возвести в
квадрат, т.е.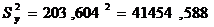 
Следовательно, коэффициент
детерминации равен:
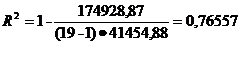или по таблице 5.
Значение коэффициента детерминации
R2 = 0,76557 показывает, что 76,56% вариации результирующего показателя Y
объясняется с помощью уравнения регрессии (действием фактора Х), а 23,44% -
случайностью.
.2.2 Проверка адекватности уравнения
данным генеральной совокупности
Соответствие прогнозируемых
значений, рассчитанных на основе уравнения регрессии, данным генеральной
совокупности, называют адекватностью уравнения данным генеральной совокупности.
Если существует значимая линейная
взаимосвязь между фактором и результирующим показателем, построенное уравнение
регрессии будет адекватно данным генеральной совокупности. Таким образом,
проверка адекватности уравнения сводится к проверке значимости линейной
взаимосвязи между переменными.
Проверить значимость линейной
взаимосвязи можно несколькими способами:
) проверить значимость коэффициента
детерминации;
) проверить значимость углового
коэффициента регрессии;
Оба способа основаны на методе
проверки статистических гипотез.
. Проверим значимость коэффициента
детерминации на уровне 0,05
Проверим гипотезу о значимости
коэффициента детерминации R2
Нулевая и альтернативная гипотезы
формулируются следующим образом:
Н0: R2 = 0 - значение коэффициента
детерминации незначимо, связь между фактором и результирующим показателем
отсутствует.
Н1: R2 > 0 - значение
коэффициента детерминации значимо, существует значимая связь между фактором и
результирующим показателем.
Для проверки используется критерий
Фишера:
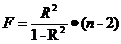(20)
где: R2 - коэффициент детерминации (см. п.
3.2.1)
Критерий F имеет распределение Фишера с числами
степеней свободы 1 = 1 и 2 = n-2.
ν1 = 1 и 2 = 19-2 =
17
Объём выборки: n
= 19
Уровень значимости: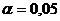 
Критическая точка: fкр = 4,451,
рассчитывается по следующей формуле:
Функция FРАСПОБР (21)
Синтаксис:РАСПОБР (вероятность; степени _
свободы 1; степени _ свободы2)
Результат:
Рассчитывает критические точки для распределения
Фишера.
Аргументы:
вероятность: уровень значимости α,
соответствующий одностороннему распределению Фишера;
степени_свободы1: первое число степеней свободы;
степени_свободы2: второе число степеней свободы.
Определим критерий Фишера:
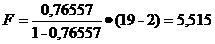(или по таблице 5)
Так как значение критерия F попадает
в критическую область (F ≥ fкр), то нулевая гипотеза отклоняется и
принимается альтернативная гипотеза.
) коэффициент детерминации
признаётся значимым;
) существует значимая линейная связь
между фактором и результирующим показателем;
) построенное уравнение адекватно
данным генеральной совокупности.
Влияние материалоемкости объясняет
значительную долю разброса показателя выпуска продукции (Y)
. Проверим значимость углового
коэффициента регрессии при уровне значимости 0,05:
а) дадим словесную интерпретацию:
Угловой коэффициент b1 показывает
изменение результирующего показателя при изменении фактора на 1 ед.
Угловой коэффициент b1 показывает
изменение объёма выпуска продукции (показателя Y, тыс. ед.) при изменении
материалоемкости (фактора Х, кг на единицу продукции) на одну единицу.
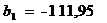
Гипотеза: При изменении (увеличении)
материалоемкости на 1 ед, выпуск продукции уменьшится на 111,954 тыс. ед.
Проверим гипотезу о значимости
углового коэффициента регрессии b1
Нулевая и альтернативная гипотезы
формулируются следующим образом:
Н0: 1 = 0 - значение углового
коэффициента генеральной совокупности незначимо, связь между фактором и
результирующим показателем отсутствует.
Н1: 1 ≠ 0 - значение углового
коэффициента генеральной совокупности значимо, существует значимая связь между
фактором и результирующим показателем.
Для проверки используется критерий
Стьюдента, который рассчитывается по следующей формуле:
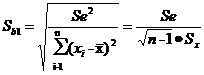(18)
где: Se2 - остаточная дисперсия;- стандартная
ошибка регрессии;- среднее квадратичное отклонение переменной Х (СКО);
Рассчитаем стандартную ошибку углового
коэффициента регрессии:
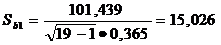(или по таблице 5)
Рассчитаем критерий Стьюдента:
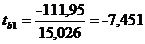
Критерий tb1 имеет распределение
Стьюдента с числом степеней свободы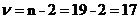
Объём выборки: n = 19
Уровень значимости: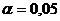
Критическая точка: tкр = 2,1098 (по
таблице Стьюдента tкр = 2,093)
Так как значение t-критерия (tb1)
попадает в одну из критических областей (│tb1│≥│tкр│),
то нулевая гипотеза отклоняется и принимается альтернативная гипотеза.
) угловой коэффициент признаётся
значимым;
) существует значимая линейная связь
между фактором и результирующим показателем;
) построенное уравнение адекватно
данным генеральной совокупности.
Материалоемкость влияет на выпуск
продукции.
. Проверим значимость свободного
члена регрессии при уровне значимости 0,05:
Нулевая и альтернативная гипотезы
формулируются следующим образом:
Н0: b0 = 0 - значение
свободного члена генеральной совокупности незначимо.
Н1: b0 ≠ 0 - значение
свободного члена генеральной совокупности значимо.
Для проверки используется
критерий Стьюдента:
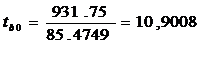
Критерий tb0 имеет распределение
Стьюдента с числом степеней свободы n-2
Число степеней свободы 17
Уровень значимости 0,05
tкр=2,1098156
Вывод: Так как значение t-критерия (tb0)
попадает в одну из критических областей (│tb0│≥│tкр│),
то нулевая гипотеза отклоняется и принимается альтернативная.
В этом случае значение свободного члена
генеральной совокупности значимо, следовательно, линия регрессии не должна
проходить через начало координат.
.2.3 Проверка статистической значимости
коэффициентов уравнения
Проверим ранее полученные значения с помощью
режима "Регрессия".
Для проведения статистической обработки
информации табличный процессор Microsoft
Excel включает в себя
программную надстройку «Пакет анализа» и библиотеку из 78 статистических
функций. Надстройка «Пакет анализа» вызывается командой меню Сервис > Анализ
данных. В появившемся диалоговом окне можно выбрать один из режимов
статистической обработки данных.
Режим работы «Регрессия» служит
для расчета параметров уравнения линейной регрессии и проверки его качества. В
диалоговом окне данного режима задаются следующие параметры:
1.Входной
интервал Y- вводится ссылка
на ячейки, содержащие значения результирующего показателя. Диапазон должен
состоять из одного столбца.
2.Входной
интервал X- вводится ссылка
на ячейки, содержащие значения факторов. Для парной регрессии диапазон должен
состоять из одного столбца.
3.Метки -
флажок устанавливается в активное состояние, если первая строка содержит
названия переменных. Если заголовки отсутствуют, флажок следует отключить.
4.Выходной
интервал/Новый рабочий лист/Новая рабочая книга.
В положении Выходной интервал
активизируется поле, в которое необходимо ввести ссылку на левую верхнюю ячейку
выходного диапазона. Размер выходного диапазона будет определен автоматически,
и на экране появится сообщение в случае возможного наложения выходного
диапазона на исходные данные.
В положении Новый рабочий лист
открывается новый лист, в который, начиная с ячейки А1 вставляются результаты
анализа. Если необходимо задать имя открываемого нового рабочего листа, следует
ввести его имя в поле, расположенное напротив соответствующего положения
переключателя.
В положении Новая рабочая книга
открывается новая книга (новый файл Microsoft
Excel), на первом листе
которой начиная с ячейки А1 вставляются результаты анализа.
5.Остатки -
данный флажок устанавливается в активное состояние, если требуется включить в
выходной диапазон столбец случайных отклонений.
6.График
остатков - данный флажок устанавливается в активное состояние, если требуется
вывести на рабочий лист точечные графики зависимости случайных отклонений ei
от значений факторов xi.
7.График
подбора - данный флажок устанавливается в активное состояние, если требуется
вывести на рабочий лист точечные графики зависимости прогнозируемых значений ŷi
от значений факторов xi.
Режим «Регрессия» формирует группы показателей
такие как:
В таблице «Регрессионная статистика»
генерируются результаты, соответствующие следующим статистическим показателям:
1. Множественный R
- коэффициенту корреляции r.
2. R-квадрат
- коэффициенту детерминации R2.
. Стандартная ошибка -
стандартной ошибке регрессии Sе.
. Наблюдения - числу
наблюдений n.
В таблице «Дисперсионный анализ» генерируются
результаты дисперсионного анализа, из которых наибольший интерес представляет
значение коэффициента Фишера (F),
используемое для проверки значимости коэффициента детерминации R2.
В следующей таблице
генерируются значения коэффициентов регрессии и их статистические оценки.
Значения в строке
«Y-пересечение» соответствуют свободному члену регрессии (b0),
значения во второй строке - угловому коэффициенту (b1).
Столбцы данной таблицы имеют
следующую интерпретацию:
. Коэффициенты - значения
коэффициентов bi.
2. Стандартная ошибка - стандартные
ошибки коэффициентов Sbi.
3. t-статистика
- значения t-критерия Стьюдента
. Нижние 95 % и Верхние 95 % -
соответственно нижние и верхние границы доверительных интервалов для
коэффициентов регрессии bi.
В таблице «Вывод остатка»
генерируются прогнозируемые значения результирующего показателя ŷi
и значения случайных отклонений ei.
ВЫВОД ИТОГОВ
Регрессионная статистика
|
Множественный
R
|
0,8749669
|
|
R-квадрат
|
0,7655671
|
|
Нормированный
R-квадрат
|
0,751777
|
|
Стандартная
ошибка
|
101,43931
|
|
Наблюдения
|
19
|
Дисперсионный анализ
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
Регрессия
|
1
|
571250,082
|
571250,08
|
55,515
|
9,5E-07
|
|
Остаток
|
17
|
174928,865
|
10289,933
|
|
|
|
Итого
|
18
|
746178,947
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
931,7502
|
85,4748642
|
10,90086781
|
4,31055E-09
|
|
Переменная
X 1
|
-111,9544
|
15,025681
|
-7,450867825
|
9,47837E-07
|
|
Нижние
95%
|
Верхние
95%
|
Нижние
99,0%
|
Верхние
99,0%
|
|
751,414
|
1112,0864
|
751,4139979
|
1112,086395
|
|
-143,66
|
-80,25295
|
-143,6557782
|
-80,25294733
|
ВЫВОД ОСТАТКА
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
|
1
|
551,10536
|
198,894637
|
|
2
|
539,90993
|
160,090073
|
|
3
|
528,71449
|
61,2855097
|
|
4
|
517,51905
|
|
5
|
483,93275
|
-83,932745
|
|
6
|
461,54187
|
-51,541873
|
|
7
|
394,36925
|
75,6307451
|
|
8
|
371,97838
|
-141,97838
|
|
9
|
360,78295
|
-50,782946
|
|
10
|
327,19664
|
-77,196637
|
|
11
|
304,80576
|
-64,805765
|
|
12
|
260,02402
|
-110,02402
|
|
13
|
260,02402
|
-60,02402
|
|
14
|
260,02402
|
-40,02402
|
|
15
|
192,8514
|
-32,851402
|
|
16
|
148,06966
|
-28,069657
|
|
17
|
148,06966
|
-18,069657
|
|
18
|
24,919858
|
85,0801423
|
|
19
|
-75,83907
|
175,839069
|
.2.4 Проверка выполнения предпосылок МНК
Статистические выводы о качестве уравнения
регрессии будут обоснованными только в том случае, если выполняются
определенные условия относительно свойств случайного отклонения, называемые
предпосылками метода наименьших квадратов (МНК).
Если предпосылки МНК не выполняются, могут быть
существенные проблемы с интерпретацией полученных выводов. Поэтому, построив
уравнение регрессии, необходимо проверить выполнение этих условий.
Наиболее наглядный способ проверки состоит в
построении диагностической диаграммы: поля корреляции между случайными
отклонениями (ошибками прогнозирования) еi и прогнозируемыми значениями
результирующего показателя ŷi.
Значения случайного отклонения откладываются по
вертикальной оси, прогнозируемые значения результирующего показателя - по
горизонтальной оси.
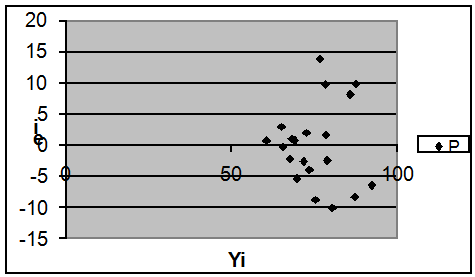
Рис. 6 Диагностическая диаграмма
(проверка автокорреляции)
При анализе диагностической
диаграммы можно сделать следующий вывод: между точками на поле взаимосвязи не
наблюдается, диаграмма представляет собой облако из точек, расположенных
хаотично и неупорядоченно, следовательно, автокорреляция остатков отсутствует,
значит, предпосылки МНК выполняются.
.3 Проверка наличия автокорреляции
остатков графическим методом и с помощью критерия Дарбина - Уотсона при уровне
значимости 0,01
Одной из предпосылок МНК является
независимость между собой значений случайных отклонений. Если присутствует
корреляция между ними, то говорят о наличии автокорреляции остатков.
Автокорреляцией остатков называется
зависимость между значениями случайных отклонений, упорядоченными по значениям
фактора Х.
Таблица 6 - Расчет значений критерия
Дарбина - Уотсона
|
Х
|
ei
|
ei-1
|
(ei
- ei-1)2
|
ei2
|
|
198,89464
|
-
|
-
|
39559,07669
|
198,89464
|
|
160,09007
|
198,894637
|
1505,794166
|
25628,83162
|
160,09007
|
|
61,28551
|
160,090073
|
9762,341812
|
3755,913702
|
61,28551
|
|
2,480946
|
61,2855097
|
3457,976714
|
6,155093065
|
2,480946
|
|
-83,93275
|
2,480946
|
7467,326021
|
7044,70571
|
-83,93275
|
|
-51,54187
|
-83,932745
|
1049,168625
|
2656,564632
|
-51,54187
|
|
75,630745
|
-51,541873
|
16172,87469
|
5720,0096
|
75,630745
|
|
-141,9784
|
75,6307451
|
47353,73235
|
20157,86106
|
-141,9784
|
|
-50,78295
|
-141,97838
|
8316,607598
|
2578,907614
|
-50,78295
|
|
-77,19664
|
-50,782946
|
697,6830809
|
5959,320804
|
-77,19664
|
|
-64,80576
|
-77,196637
|
153,5337227
|
4199,787138
|
-64,80576
|
|
-110,024
|
-64,805765
|
2044,690575
|
12105,28489
|
-110,024
|
|
-60,02402
|
-110,02402
|
2500
|
3602,882927
|
-60,02402
|
|
-40,02402
|
-60,02402
|
400
|
1601,922144
|
-40,02402
|
|
-32,8514
|
-40,02402
|
51,44644428
|
1079,214608
|
-32,8514
|
|
-28,06966
|
-32,851402
|
22,86508635
|
787,9056327
|
-28,06966
|
|
-18,06966
|
-28,069657
|
100
|
326,5124968
|
-18,06966
|
|
85,080142
|
-18,069657
|
10639,88105
|
7238,630609
|
85,080142
|
|
175,83907
|
85,0801423
|
8237,182741
|
30919,37811
|
175,83907
|
|
198,89464
|
-
|
-
|
39559,07669
|
198,89464
|
|
|
|
119933,1047
|
174928,8651
|
Критерий Дарбина - Уотсона рассчитывается по
формуле:
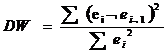
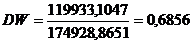
Критические точки d1 и du при уровне
значимости α = 0,01
n = 19
m = 1 (m - число
объясняющих переменных в уравнении регрессии)
|
dl
|
0,928
|
|
du
|
1,132
|
|
4-du
|
2,868
|
|
4-dl
|
3,072
|
Поскольку DW<dl , то это означает, что
присутствует положительная автокорреляция.
.4 Проверка наличия гетероскедастичности
графическим методом и с помощью теста ранговой корреляции при уровне значимости
0,05
Проверим наличие гетероскедастичности
графическим методом.
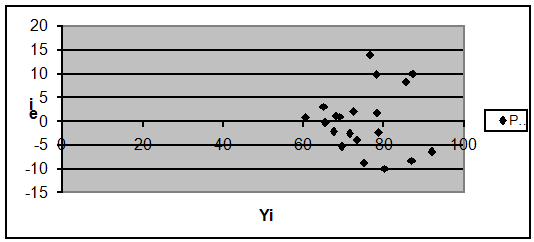
Рис. 7 Диагностическая диаграмма
(проверка гетероскедантичности)
При анализе диагностической
диаграммы можно сделать следующий вывод: что присутствует гетероскедантичность,
т.к. при движении вдоль оси Х ширина полосы разброса меняется и дисперсия
непостоянна.
Проверим наличие
гетероскедантичности с помощью теста Голдфелда-Квандта
Предпосылками данного теста
являются:
) Пропорциональность дисперсии
случайного отклонения (ei) и фактора х.
) Случайное отклонение ei имеет нормальное
распределение и неподвержено автокорреляции.
Алгоритм проведения теста:
) Вся совокупность наблюдений n
упорядочивается по возрастанию фактора х.
) Вся упорядоченная совокупность
делится на три части, размерностью k, (n-2k),k.
) Оцениваются уравнения регрессии
для первой и третьей частей выборки: рассчитываются остаточные дисперсии каждой
из рассматриваемых частей.
) Находится расчетное значение F-критерия:
) По таблице F-распределения
определяется fкр в соответствии
с имеющимся уровнем значимости и степенями свободы.
) Предпосылка Гаусса-Маркова
Признается адекватной, если справедливо неравенство F<fкр. В
противном случае F > fкр, делается
вывод о присутствии гетероскедастичности случайных отклонений.
Таблица 7 - Расчет значений теста
Голдфелда-Квандта
|
n
|
X
|
y
|
|
1
|
3,4
|
750
|
|
2
|
3,5
|
700
|
|
3
|
3,6
|
590
|
|
4
|
3,7
|
520
|
|
5
|
4
|
400
|
|
6
|
4,2
|
410
|
|
7
|
4,8
|
470
|
|
8
|
5
|
230
|
|
9
|
5,1
|
310
|
|
10
|
5,4
|
250
|
|
11
|
5,6
|
240
|
|
12
|
6
|
150
|
|
13
|
6
|
200
|
|
14
|
6
|
220
|
|
15
|
6,6
|
160
|
|
16
|
7
|
120
|
|
17
|
7
|
130
|
|
18
|
8,1
|
110
|
|
19
|
9
|
100
|
) Определим размерность по частям:
K=11*19/30=6.967
Определим, что размерности частей упорядоченной
совокупности:
|
1
части
|
k
|
7
|
|
2
части
|
n-2*k
|
5
|
|
3
части
|
k
|
7
|
) Оценим уравнение регрессии для первой части
выборки:
|
n
|
X
|
Y
|
|
1
|
3,4
|
750
|
|
2
|
3,5
|
700
|
|
3
|
3,6
|
590
|
|
4
|
3,7
|
520
|
|
5
|
4
|
400
|
|
6
|
4,2
|
410
|
|
7
|
4,8
|
470
|
Воспользуемся встроенной функцией Microsoft
Excel ЛИНЕЙН
|
b1
|
-203,7475
|
1340,27613
|
b0
|
|
Sb1
|
85,825564
|
335,77122
|
Sb0
|
|
R2
|
0,5298872
|
103,296742
|
Se
|
|
F
|
5,6357457
|
5
|
v
|
|
SSоб
|
60134,629
|
53351,0848
|
SSост
|
(Se1)^2=10670,217
) Оценим уравнение регрессии для третьей части
выборки:
|
n
|
X
|
Y
|
|
13
|
6
|
200
|
|
14
|
6
|
220
|
|
15
|
6,6
|
160
|
|
16
|
7
|
120
|
|
17
|
7
|
130
|
|
18
|
8,1
|
110
|
|
19
|
9
|
100
|
Воспользуемся встроенной функцией Microsoft
Excel ЛИНЕЙН
|
b1
|
-36,57534
|
408,25636
|
b0
|
|
Sb1
|
9,2456548
|
66,3196801
|
Sb0
|
0,7578638
|
24,9803837
|
Se
|
|
F
|
15,649536
|
5
|
v
|
|
SSоб
|
9765,6164
|
3120,09785
|
SSост
|
(Se3)^2=624,0196
) Критерий Голдфелда-Квандта
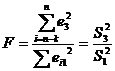
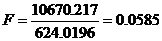
) По таблице F-распределенияя с
соответствующими параметрами, для уровня значимости 0,05 определим Fкр = 5,05.
) Так как Fкр> F - это говорит о
присутствии гетероскедастичности случайных отклонений.
Вывод, можно ли использовать
линейную модель для прогнозирования
Точки на поле корреляции связаны
линейной связью. Коэффициенты регрессии: угловой и свободный член значимы,
присутствует положительная автокорреляция остатков и гетероскедастичность. Это
означает, что линейную модель не желательно использовать для прогнозирования.
4. Составление спецификации
гиперболической регрессионной модели и расчет параметров нового уравнения
Первым этапом регрессионного анализа
является спецификация регрессионной модели, под которой подразумевается
математическая функция, с помощью которой можно описать взаимосвязь между
заданными переменными.
Гиперболическая функция представляет
собой зависимость:
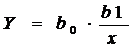
Для определения коэффициентов гиперболической
функции необходимо построить уравнение линейной регрессии, в котором
результирующим показателем является переменная Y’
=, а фактором - переменная X:
Ŷ’ = b0
+ b1 X’
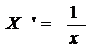
Угловой коэффициент этого уравнения b1
равен коэффициенту b1 в степени
экспоненты функции.
Коэффициент b0
гиперболической функции можно определить следующим образом:
0 = e
b0’
где b0’
- свободный член линейного уравнения.
Для определения коэффициентов гиперболической
функции необходимо воспользоваться функцией ЛИНЕЙН
Таблица 9 - Рассчитанные значения
|
b1
|
3430,1242
|
-359,12336
|
b0'
|
|
Sb1
|
259,91431
|
53,3419011
|
Sb0
|
|
R2
|
0,9110713
|
62,4766931
|
Se
|
|
F
|
174,16436
|
17
|
v
|
|
SSоб
|
679822,22
|
66356,7321
|
SSост
|
Вывод: значение коэффициента детерминации 0,9112
показывает, что 91,1% результирующего показателя (выпуска продукции)
объясняется уравнением регрессии.
Гиперболическое уравнение регрессии имеет вид:
= (3430,12 /X)-359,123
5. Проверка качества новой модели при том же
уровне значимости, а также наличие автокорреляции остатков
.1 Проверка качества гиперболической функции при
уровне
значимости 0,05
.1.1 Проверим адекватность уравнения данным
генеральной совокупности
Проверить значимость линейной взаимосвязи можно
несколькими способами:
) проверить значимость коэффициента
детерминации;
) проверить значимость углового коэффициента
регрессии;
Оба способа основаны на методе проверки
статистических гипотез.
. Проверим значимость коэффициента детерминации
на уровне 0,05
Проверим гипотезу о значимости коэффициента
детерминации R2
Нулевая и альтернативная гипотезы формулируются
следующим образом:
Н0: R2 = 0 - значение коэффициента детерминации
незначимо, связь между фактором и результирующим показателем отсутствует.
Н1: R2 > 0 - значение коэффициента детерминации
значимо, существует значимая связь между фактором и результирующим показателем.
Для проверки используется критерий Фишера,
который рассчитывается по формуле 20 (см. п. 3.2.1)
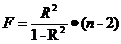
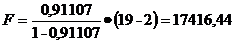
Критерий F имеет распределение
Фишера с числами степеней свободы
1 = 1 и = n-2.
ν1 = 1 и 2 = 19-2 = 17
Объём выборки: n = 19
Уровень значимости: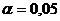
Критическая точка: fкр = 4,45132
Значение критерия F попадает в
критическую область (F ≥ fкр), то нулевая гипотеза отклоняется и
принимается альтернативная гипотеза.
) коэффициент детерминации
признаётся значимым;
) существует значимая линейная связь
между фактором и результирующим показателем;
) построенное уравнение адекватно
данным генеральной совокупности.
Влияние материалоемкости объясняет
значительную долю разброса показателя выпуска продукции (Y).
. Проверим значимость углового
коэффициента регрессии при уровне значимости 0,05:
Нулевая и альтернативная гипотезы
формулируются следующим образом:
Н0: 1 = 0 - значение углового
коэффициента генеральной совокупности незначимо, связь между фактором и
результирующим показателем отсутствует.
Н1: 1 ≠ 0 - значение углового
коэффициента генеральной совокупности значимо, существует значимая связь между
фактором и результирующим показателем.
Для проверки используется критерий
Стьюдента, который рассчитывается по формуле 18 (см. п. 3.2.2).
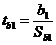
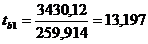
Критерий tb1 имеет распределение
Стьюдента с числом степеней свободы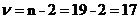
Объём выборки: n = 19
Уровень значимости: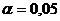
Критическая точка: tкр = 2,1098
Так как значение t-критерия (tb1)
попадает в одну из критических областей (│tb1│≥│tкр│),
то нулевая гипотеза отклоняется и принимается альтернативная гипотеза.
) угловой коэффициент признаётся
значимым;
) существует значимая линейная связь
между фактором и результирующим показателем;
) построенное уравнение адекватно
данным генеральной совокупности.
Материалоемкость влияет на выпуск
продукции.
. Проверим значимость свободного
члена регрессии при уровне значимости 0,05:
Нулевая и альтернативная гипотезы
формулируются следующим образом:
Н0: b0 = 0 - значение
свободного члена генеральной совокупности незначимо.
Н1: b0 ≠ 0 - значение
свободного члена генеральной совокупности значимо.
Для проверки используется
критерий Стьюдента:
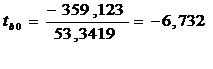
Критерий tb0 имеет распределение
Стьюдента с числом степеней свободы n-2
Число степеней свободы 17
Уровень значимости 0,05
tкр=2,1098156
Вывод: Так как значение t-критерия (tb0) попадает
в одну из критических областей (│tb0│≥│tкр│), то
нулевая гипотеза отклоняется и принимается альтернативная.
В этом случае значение свободного члена
генеральной совокупности значимо, следовательно, линия регрессии не должна
проходить через начало координат.
.1.2
Проверим статистическую значимость коэффициентов уравнения
Проверим ранее полученные значения с помощью
режима "Регрессия" (см. 3.2.3).
ВЫВОД ИТОГОВ
Регрессионная статистика
|
Множественный
R
|
0,9545005
|
|
R-квадрат
|
0,9110713
|
|
Нормированный
R-квадрат
|
0,9058402
|
|
Стандартная
ошибка
|
62,476693
|
|
Наблюдения
|
19
|
Дисперсионный
анализ
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
679822,2153
|
679822,22
|
174,16
|
2,3E-10
|
|
|
Остаток
|
17
|
66356,73205
|
3903,3372
|
|
|
|
|
Итого
|
18
|
746178,9474
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-359,1234
|
53,34190112
|
-6,7324814
|
4E-06
|
|
Переменная
X 1
|
3430,1242
|
259,9143144
|
13,197134
|
2E-10
|
|
|
|
|
|
|
|
|
|
|
|
|
Нижние
95%
|
Верхние
95%
|
Нижние
99,0%
|
Верхние
99,0%
|
|
-471,66
|
-246,5818
|
-471,6649279
|
-246,5817821
|
|
2881,75
|
3978,4954
|
2881,752895
|
3978,495424
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
Стандартные
остатки
|
|
1
|
649,73669
|
100,2633081
|
1,6513373
|
|
2
|
620,91212
|
79,08788091
|
1,3025779
|
|
3
|
593,68891
|
-3,688911479
|
-0,0607564
|
|
4
|
567,93723
|
-47,9372286
|
-0,7895264
|
|
5
|
498,40768
|
-98,40768483
|
-1,6207752
|
|
6
|
457,57287
|
-47,57287341
|
-0,7835255
|
|
7
|
355,48584
|
114,5141551
|
1,8860488
|
|
8
|
326,90148
|
-96,90147686
|
-1,5959679
|
|
9
|
313,45001
|
-3,450009572
|
-0,0568217
|
|
10
|
276,08482
|
-26,08482265
|
-0,4296172
|
|
11
|
253,39882
|
-13,39881631
|
-0,2206786
|
|
12
|
212,564
|
-62,56400489
|
-1,0304295
|
|
13
|
212,564
|
-12,56400489
|
-0,2069292
|
|
14
|
212,564
|
7,435995115
|
0,1224709
|
|
15
|
160,59243
|
-0,592426713
|
-0,0097573
|
|
16
|
130,89438
|
-10,89438204
|
-0,1794305
|
|
17
|
130,89438
|
-0,894382044
|
-0,0147305
|
|
18
|
64,348763
|
45,65123657
|
0,7518761
|
|
19
|
22,001552
|
77,99844841
|
1,2846349
|
5.1.3 Проверим наличие автокорреляции остатков
графическим методом
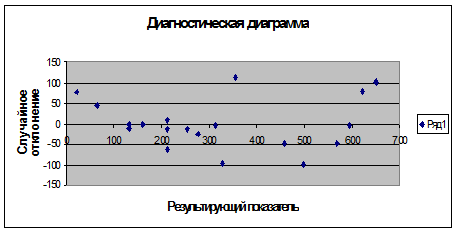
Рис. 8 Диагностическая диаграмма (проверка
автокорреляции)
Вывод: между точками на поле взаимосвязи не
наблюдается, диаграмма представляет собой облако из точек, расположенных
хаотично и неупорядоченно, следовательно, автокорреляция остатков отсутствует.
Проверим наличия автокорреляции остатков
графическим методом и с помощью критерия Дарбина - Уотсона при уровне значимости
0,05
Таблица 6 - Расчет значений критерия Дарбина -
Уотсона
|
ei
|
ei-1
|
(ei
- ei-1)2
|
ei2
|
|
100,26331
|
-
|
-
|
10053
|
|
79,087881
|
100,263
|
448,399
|
6254,9
|
|
-3,688911
|
79,088
|
6851,997
|
13,608
|
|
-47,93723
|
-3,689
|
1957,914
|
2298
|
|
-98,40768
|
-47,937
|
2547,267
|
9684,1
|
|
-47,57287
|
-98,408
|
2584,178
|
2263,2
|
|
114,51416
|
-47,573
|
26272,205
|
13113
|
|
-96,90148
|
114,514
|
44696,569
|
9389,9
|
|
-3,45001
|
-96,901
|
8733,177
|
11,903
|
|
-26,08482
|
-3,450
|
512,335
|
680,42
|
|
-13,39882
|
-26,085
|
160,935
|
179,53
|
|
-62,564
|
-13,399
|
2417,216
|
3914,3
|
|
-12,564
|
-62,564
|
2500,000
|
157,85
|
|
7,4359951
|
-12,564
|
400,000
|
55,294
|
|
-0,592427
|
7,436
|
64,456
|
0,351
|
|
-10,89438
|
-0,592
|
106,130
|
118,69
|
|
-0,894382
|
-10,894
|
100,000
|
0,7999
|
|
45,651237
|
-0,894
|
2166,495
|
2084
|
|
77,998448
|
45,651
|
1046,342
|
6083,8
|
|
|
103565,614
|
66357
|
Критерий Дарбина - Уотсона рассчитывается по
формуле:
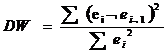
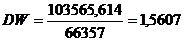
Критические точки d1 и du при уровне
значимости α = 0,05
n = 19
m = 1 (m - число
объясняющих переменных в уравнении регрессии)
|
dl
|
0,928
|
|
du
|
1,132
|
|
4-du
|
2,868
|
|
4-dl
|
Вывод: значение DW=2,1074 попадает в интервал в
интервал от du=1,132 до (4- du)= 2,868. Это означает, что автокорреляция
остатков отсутствует.
6. Нанесение на поле корреляции графиков двух
функций регрессии. Сравнение качества построенных моделей. Выбор модели для
выражения исследуемой зависимости
Построение линий тренда можно
использовать для определения коэффициентов уравнения регрессии и величины
коэффициента детерминации, что удобно для сравнения качества нескольких
регрессионных моделей.
Линии тренда наносятся на уже
готовое поле корреляции.
Чтобы построить линию тренда
необходимо:
выделить область диаграммы;
выбрать команду меню Диаграмма
> Добавить линию тренда;
на закладке «Тип» выбрать тип
линии тренда;
на закладке «Параметры»
установить флажки: «показывать уравнение на диаграмме» и «поместить на
диаграмму величину достоверности аппроксимации».
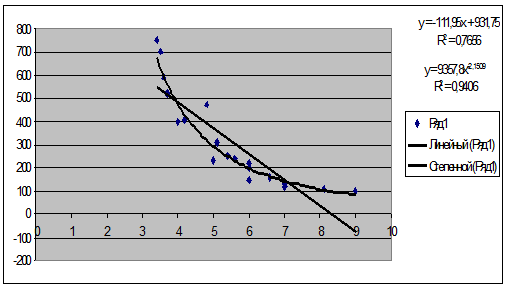
Рис. 9 Линейная и гиперболическая регрессионные
модели
Сравним имеющиеся модели по основным параметрам:
) Адекватность.
Т.к. коэффициент детерминации у гиперболической
(0,9406) функции больше, чем у линейной функции (0,7656), то исходя из этого
лучшей считается гиперболическая функция.
) Простота.
Линейная модель проще чем гиперболическая, т.к.
при выборе между линейной и нелинейной моделью предпочтение отдается линейной
модели
) Выполняемость предпосылок МНК.
Все предпосылки МНК выполняются только для
гиперболической модели. Для линейной модели установлены гетероскедастичность
(не выполняется 2-я предпосылка МНК) и автокорреляция остатков.
) Адекватность эмпирическим данным
В линейной модели стандартная ошибка
равна101,44, а в гиперболической 62,477, следовательно данные гиперболической
модели более адекватны эмпирическим данным. А значит прогнозы, выполненные на
основании гиперболического уравнения будут более точны.
Вывод: наиболее качественной признается
гиперболическая модель (т.к. имеет большую точность прогнозирования, и
значительно большие значения коэффициента детерминации .(для данной модели
выполняются предпосылки МНК и она является адекватной эмпирическим данным).
Построение 90%-ого доверительного интервала для
теоретических коэффициентов наилучшей регрессии, т.е. для гиперболической
регрессионной модели
а) построим 90% доверительный интервал для
теоретического значения углового коэффициента
Критерий tb1 имеет распределение
Стьюдента с числом степеней свободы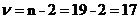
Объём выборки: n = 19
Доверительная вероятность
(надежность):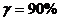 
Уровень значимости: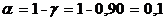 
Критическая точка: tкр = 1,7396
|
Sb1
|
259,91431
|
|
b1
|
3430,1242
|
Нижняя граница интервала равна:
,1242-259,91431*1,7396=2977,975
Верхняя граница интервала равна:
,1242+259,91431*1,7396=3882,273
Вывод: можно быть на 90% уверенным, что значение
углового коэффициента лежит в интервале от 2977,94 до 3882,27
б) построим 90% доверительный интервал для
теоретического значения свободного члена регрессии
Критерий tb0 имеет распределение
Стьюдента с числом степеней свободы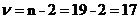
Объём выборки: n = 19
Доверительная вероятность
(надежность):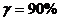
Уровень значимости: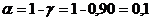 
Критическая точка: tкр = 1,7396
|
tкр
|
1,7396067
|
|
Sb0
|
53,341901
|
|
b0
|
-359,1234
|
Нижняя граница интервала равна:
,1234-53,3419*1,7396=-451,91
Верхняя граница интервала равна:
,1234+53,3419*1,7396=-266,329
Вывод: можно быть на 90% уверенным, что значение
свободного члена лежит в интервале от -451,91 до 266,32
7. По наилучшей регрессионной модели рассчитаем
точечные прогнозы среднего значения выпуска при потреблении 3 кг и 6 кг
материала на единицу продукции
Построим 99%-ые доверительных интервалов для
индивидуальных значений выпуска. Определим наиболее точный прогноз.
а) определение точечной оценки
Точечная оценка - определяется путём подстановки
заданного значения фактора х0 в уравнение регрессии
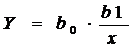
= (3430,12 /X)-359,123
При заданном значении
материалоемкости, равном 3 кг на единицу продукции:
Х01=3
1=(3430,12 /3)-359,123=784.25
Выпуск продукции составит 784,25
тысяч единиц.
При заданном значении
материалоемкости, равном 6 кг на единицу продукции:
Х01=6
1=(3430,12 /6)-359,123=212.56
Выпуск продукции составит 212,56
тысяч единиц.
б) определение 99% доверительного
интервала для отдельных значений результирующего показателя
Для отдельного наблюдения
результирующего показателя Y при заданном значении х0, доверительный интервал
строится следующим образом:
(Ŷ0 - tкр ·
SY|X0; Ŷ0 + tкр · SY|X0)
где SY|X0
- стандартная ошибка нового наблюдения, которая рассчитывается по формуле:
Число степеней свободы
Объём выборки: n = 19
Доверительная вероятность
(надежность):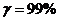 
Уровень значимости: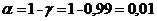 
Критическая точка: tкр = 2,898
|
X
|
(xi-¯x¯)^2
|
|
0,111
|
0,00752
|
|
0,123
|
0,00559
|
|
0,143
|
0,00300
|
|
0,143
|
0,00300
|
|
0,152
|
0,00209
|
|
0,167
|
0,00094
|
|
0,167
|
0,00094
|
|
0,167
|
0,00094
|
|
0,179
|
0,00035
|
|
0,185
|
0,00016
|
|
0,196
|
0,00000
|
|
0,2
|
0,00001
|
|
0,208
|
0,00011
|
|
0,238
|
0,00162
|
|
0,25
|
0,00273
|
|
0,27
|
0,00522
|
|
0,278
|
0,00644
|
|
0,286
|
0,00779
|
|
0,294
|
0,00927
|
|
0,05773
|
|
Se
|
62,476693
|
|
Se²
|
3903,3372
|
|
n
|
19
|
|
Sb1
|
259,91431
|
|
S²b1
|
67555,451
|
|
МО
|
0,1977368
|
|X0 (3) =38,061|X0 (6) =16,453
для х0 (3)= 3
Нижняя граница интервала равна:
784,25-2,898*38,061 = 673,94
Верхняя граница интервала равна:
784,25+2,898*38,061 = 894,561
Можно быть на 99% уверенным, что среднее
значение выпуска продукции при заданном значении материалоемкости х0=3, лежит в
пределах от 673,94 до 894,561 тысяч единиц для х0(6) = 6
Нижняя граница интервала равна:
,56-2,898*16,453=164,878
Верхняя граница интервала равна:
,56+2,898*16,453=260,249
Можно быть на 99% уверенным, что среднее
значение выпуска продукции при заданном значении материалоемкости х0=6, лежит в
пределах от 164,878до 260,249 тысяч единиц. Интервальная оценка среднего
значения доверительный интервал для среднего значения переменной Y при заданном
значении х0 в генеральной совокупности. Доверительный интервал при заданном
значении х0 =3 шире, чем при заданном х0=6, что подтверждается большим
значением величины стандартной ошибки. Поэтому прогноз для значения х0=6 будет
более точным.
Заключение
После выполнения данной курсовой работы мы на
практике можем применять навыки, полученные в ходе выполнения работы. Знаем
основные методы построения моделей линейной и множественной регрессии, основные
признаки неудовлетворительного качества экономических моделей, основные приемы
повышения качества экономических моделей, методы прогнозирования значений
моделируемой величины. Развили умение применять на практике математический
аппарат регрессионного анализа для оценки параметров финансово-экономических
моделей, проверять качество эконометрических моделей и анализировать их с
помощью аппарата статистической проверки гипотез; определять ошибки
спецификации моделей и возможности для повышения качества моделей, устранять
причины, приводящие к низкому качеству моделей, использовать построенные
эконометрические модели финансово-экономических объектов для прогнозирования
экономической ситуации и выработки рекомендаций.
Список используемой литературы
1. И.И. Елисеева. Социальная статистика. - М:
"Статистика и финансы", 2007.
2. М.Г. Назаров и др. - Курс
социально-экономической статистики. - М: "Финстатинформ", 2014.
. И.И. Елисеева, М.М. Юзбашев. - Общая
теория статистики. - М.: "Финансы и статистика", 2010.
. Р.А.. Шмойлова- Теория статистики. - М:
"Финансы и статистика", 2009.
. "Социальная статистика" под
редакцией И.И.Елисеевой. - М: "Статистика и финансы", 2011.
. И.И. Елисеевой и Б.Г. Плошко
"История статистики" (М.: Финансы и статистика, 2007).
Приложение
Таблица распределения Стьюдента
|
Уровень
значимости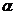 
|
|
Двусторонний
|
0,20
|
0,10
|
0,05
|
0,02
|
0,01
|
0,002
|
0,001
|
|
Односторонний
|
0,10
|
0,05
|
0,025
|
0,01
|
0,005
|
0,001
|
0,0005
|
|
Число
степеней свободы 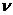 Критические
точки tкр
|
|
|
1
|
3,078
|
6,314
|
12,706
|
31,821
|
63,657
|
318,309
|
636,619
|
|
2
|
1,886
|
2,920
|
4,303
|
6,965
|
9,925
|
22,327
|
31,599
|
|
3
|
1,638
|
2,353
|
3,182
|
4,541
|
5,841
|
10,215
|
12,924
|
|
4
|
1,533
|
2,132
|
2,776
|
3,747
|
4,604
|
7,173
|
8,610
|
|
5
|
1,476
|
2,015
|
2,571
|
3,365
|
4,032
|
5,893
|
6,869
|
|
6
|
1,440
|
1,943
|
2,447
|
3,143
|
3,707
|
5,208
|
5,959
|
|
7
|
1,415
|
1,895
|
2,365
|
2,998
|
3,499
|
4,785
|
5,408
|
|
8
|
1,397
|
1,860
|
2,306
|
2,896
|
3,355
|
4,501
|
5,041
|
|
9
|
1,383
|
1,833
|
2,262
|
2,821
|
3,250
|
4,297
|
4,781
|
|
10
|
1,372
|
1,812
|
2,228
|
2,764
|
3,169
|
4,144
|
4,587
|
|
11
|
1,363
|
1,796
|
2,201
|
2,718
|
3,106
|
4,025
|
4,437
|
|
12
|
1,356
|
1,782
|
2,179
|
2,681
|
3,055
|
3,930
|
4,318
|
|
13
|
1,350
|
1,771
|
2,160
|
2,650
|
3,012
|
3,852
|
4,221
|
|
14
|
1,345
|
1,761
|
2,145
|
2,624
|
2,977
|
3,787
|
4,140
|
|
15
|
1,341
|
1,753
|
2,131
|
2,602
|
2,947
|
3,733
|
4,073
|
|
16
|
1,337
|
1,746
|
2,120
|
2,583
|
2,921
|
3,686
|
4,015
|
|
17
|
1,333
|
1,740
|
2,110
|
2,567
|
2,898
|
3,646
|
3,965
|
|
18
|
1,330
|
1,734
|
2,101
|
2,552
|
2,878
|
3,610
|
3,922
|
|
19
|
1,328
|
1,729
|
2,093
|
2,539
|
2,861
|
3,579
|
3,883
|
|
20
|
1,325
|
1,725
|
2,086
|
2,528
|
2,845
|
3,552
|
3,850
|
|
21
|
1,323
|
1,721
|
2,080
|
2,518
|
2,831
|
3,527
|
3,819
|
|
22
|
1,321
|
1,717
|
2,074
|
2,508
|
2,819
|
3,505
|
3,792
|
|
23
|
1,319
|
2,069
|
2,500
|
2,807
|
3,485
|
3,768
|
|
24
|
1,318
|
1,711
|
2,064
|
2,492
|
2,797
|
3,467
|
3,745
|
|
25
|
1,316
|
1,708
|
2,060
|
2,485
|
2,787
|
3,450
|
3,725
|
|
26
|
1,315
|
1,706
|
2,056
|
2,479
|
2,779
|
3,435
|
3,707
|
|
27
|
1,314
|
1,703
|
2,052
|
2,473
|
2,771
|
3,421
|
3,690
|
|
28
|
1,313
|
1,701
|
2,048
|
2,467
|
2,763
|
3,408
|
3,674
|
|
29
|
1,311
|
1,699
|
2,045
|
2,462
|
2,756
|
3,396
|
3,659
|
|
30
|
1,310
|
1,697
|
2,042
|
2,457
|
2,750
|
3,385
|
3,646
|
|
31
|
1,309
|
1,696
|
2,040
|
2,453
|
2,744
|
3,375
|
3,633
|
|
32
|
1,309
|
1,694
|
2,037
|
2,449
|
2,738
|
3,365
|
3,622
|
|
33
|
1,308
|
1,692
|
2,035
|
2,445
|
2,733
|
3,356
|
3,611
|
|
34
|
1,307
|
1,691
|
2,032
|
2,441
|
2,728
|
3,348
|
3,601
|
|
35
|
1,306
|
1,690
|
2,030
|
2,438
|
2,724
|
3,340
|
3,591
|
|
36
|
1,306
|
1,688
|
2,028
|
2,434
|
2,719
|
3,333
|
3,582
|
|
37
|
1,305
|
1,687
|
2,026
|
2,431
|
2,715
|
3,326
|
3,574
|
|
38
|
1,304
|
1,686
|
2,024
|
2,429
|
2,712
|
3,319
|
3,566
|
|
39
|
1,304
|
1,685
|
2,023
|
2,426
|
2,708
|
3,313
|
3,558
|
|
Бесконечность
|
1,282
|
1,645
|
1,960
|
2,326
|
2,576
|
3,090
|
3,291
|
|
|
|
|
|
|
|
|
|
|
|
|