Теория машин и механизмов
Министерство
образования и науки Российской Федерации
федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
"Московский
государственный индустриальный университет"
(ФГБОУ
ВПО "МГИУ")
Расчетно
- графическая работа
по
разделу "Теория машин и механизмов"
Москва
- 2015
ДАНО
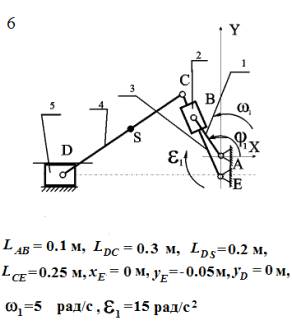
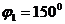
ТРЕБУЕТСЯ:
Построить планы скоростей и ускорений;
определить линейные скорости и ускорения точек, отмеченных на рисунке; угловые
скорости и ускорения звеньев 2,3,4,5.
РЕШЕНИЕ
. Построим схему механизма в масштабе: 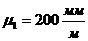 :
:
скорость
ускорение плоскопараллельный движение
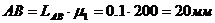 ;
; 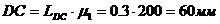
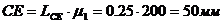 ;
; 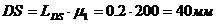
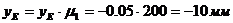
Схему механизма вычерчиваем следующим образом:
От оси Ax откладываем заданный угол 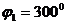 и
строим отрезок AB длиной 20 мм. От точки А откладываем по оси Аy
отрезок AE=10 мм.
Соединяем точки Е и В. После чего стоим через точки Е и В прямую длиной 50мм и
находим точку С. Далее проводим дугу окружности радиусом R= DC
с центром в точке C и находим
точку пересечения этой окружности с осью Ax- точку D.
От точки D откладываем по
линии DC отрезок DS=40мм.
и
строим отрезок AB длиной 20 мм. От точки А откладываем по оси Аy
отрезок AE=10 мм.
Соединяем точки Е и В. После чего стоим через точки Е и В прямую длиной 50мм и
находим точку С. Далее проводим дугу окружности радиусом R= DC
с центром в точке C и находим
точку пересечения этой окружности с осью Ax- точку D.
От точки D откладываем по
линии DC отрезок DS=40мм.
Рис.1. Схема механизма
Звено 1 - АВ
Звено 2 - ЕВ
Звено 3 - ЕС
Звено 4 - DC
Определение плана скоростей
Определение скоростей точек выполняем методом
построения плана скоростей. Звено 1 совершает вращательное движение, поэтому
скорость точки В определяют по формуле 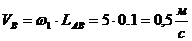 .
Вектор этой скорости перпендикулярен линии АВ и направлен в сторону угловой
скорости
.
Вектор этой скорости перпендикулярен линии АВ и направлен в сторону угловой
скорости 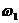 .
Выбираем масштаб плана скоростей
.
Выбираем масштаб плана скоростей 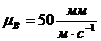 .
Тогда длина отрезка, изображающего вектор скорости
.
Тогда длина отрезка, изображающего вектор скорости 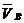 ,
равна
,
равна 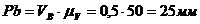 .
На плоскости чертежа в произвольном месте отмечаем полюс плана скоростей точку
Р. На плане изображаем скорость
.
На плоскости чертежа в произвольном месте отмечаем полюс плана скоростей точку
Р. На плане изображаем скорость 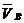 . Для этого от
точки Р вдоль линии, перпендикулярной звену АВ откладываем отрезок Pb1 в
сторону угловой скорости
. Для этого от
точки Р вдоль линии, перпендикулярной звену АВ откладываем отрезок Pb1 в
сторону угловой скорости 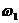 .
.
Скорость точки В2 определяют по теореме о
сложении скоростей при сложном движении точки. Неподвижную систему координат
жестко связывают со стойкой Е, подвижную систему координат - со звеном 1. При
таком выборе систем координат переносная скорость точки В2 будет равна скорости
точки B1. Тогда абсолютная
скорость рассматриваемой точки B2
определяют из векторного уравнения:
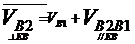
Переносная скорость известна по величине и
направлению. Относительная скорость 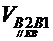 известна
только по направлению. В абсолютном движении точка B2 движется вместе со звеном
2, которое совершает вращательное движение. Угловая скорость рассматриваемого
2-го звена неизвестна. Поэтому абсолютная скорость
известна
только по направлению. В абсолютном движении точка B2 движется вместе со звеном
2, которое совершает вращательное движение. Угловая скорость рассматриваемого
2-го звена неизвестна. Поэтому абсолютная скорость 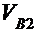 также
известна только по направлению.
также
известна только по направлению.
Для построения плана скоростей из точки b1
проводят прямую, параллельную звену ЕВ, а из точки P - прямую перпендикулярную
линии ЕВ. На пересечении этих прямых лежит точка b2. Образовавшийся отрезок Pb2
изображает скорость 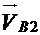 .
.
Скорость точки С определяем из теоремы подобия.
Теорема подобия.
Точки одного звена на плане
механизма и концы векторов скоростей (ускорений) этих точек на плане скоростей
(ускорений) образуют подобные и сходственно расположенные фигуры.
Точки Е, В, С принадлежат одному звену и
располагаются на отрезке EС.
По теореме подобия концы векторов скоростей этих точек (т. e,
b2, c)
расположены на одной прямой. На плане скоростей замеряем длину отрезка eb2
(eb2= 22,88мм).
Коэффициент подобия указанных отрезков eb2
и ЕВ равен: 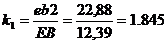 . Длину отрезка ec
определяем через коэффициент подобия:
. Длину отрезка ec
определяем через коэффициент подобия: 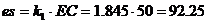 мм.
мм.
Где ВЕ=12,39 мм- определена графически при
построении схемы рис. 1.
Далее откладываем полученный отрезок на плане
скоростей и изображаем вектор скорости рассматриваемой точки с направленным
отрезком 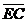 .
Так как точка Е4, принадлежащая звену 4, перемещается вместе с точкой Е2,
принадлежащей звену 2, то
.
Так как точка Е4, принадлежащая звену 4, перемещается вместе с точкой Е2,
принадлежащей звену 2, то 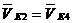 .
.
Звено CD
совершает плоскопараллельное движение, поэтому для определения скорости т.D
используем теорему о сложении скоростей:
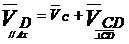
В этом векторном уравнении скорость 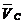 известна
по величине и направлению. Скорость
известна
по величине и направлению. Скорость 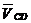 представляет
собой скорость точки C
при относительном вращении звена 2 вокруг точки E.
При этом подвижная система координат движется поступательно вместе с точкой C.
Вектор скорости
представляет
собой скорость точки C
при относительном вращении звена 2 вокруг точки E.
При этом подвижная система координат движется поступательно вместе с точкой C.
Вектор скорости 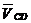 известен только по
направлению (
известен только по
направлению (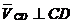 ). Точка D
совершает прямолинейное движение вдоль оси Ах. Скорость
). Точка D
совершает прямолинейное движение вдоль оси Ах. Скорость 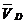 также
известна только по направлению (
также
известна только по направлению (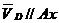 ).
).
Далее на плане скоростей измеряем длины отрезков
и определяем величины скоростей различных точек механизма:
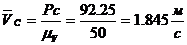 ;
;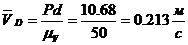 ;
;
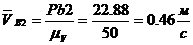
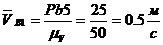 ;;
;; 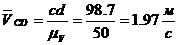 ;
;
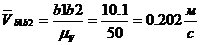
Угловые скорости 2- ого и 3- ого звеньев
определяем по формуле:
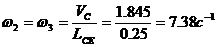 ;
; 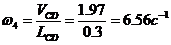
Звено 5 совершает поступательное движение,
поэтому 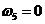
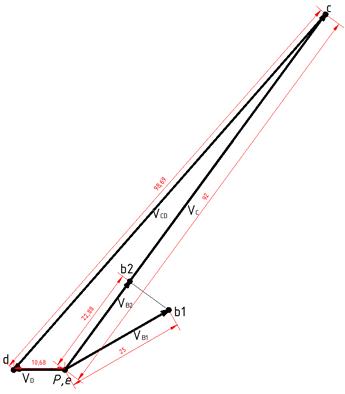
Рис.2. План скоростей
Ускорение точек. Метод построения плана
ускорений
Звено 1 совершает вращательное движение, поэтому
ускорение точки В1 равно геометрической сумме нормального и касательного
ускорений:
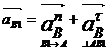
Нормальное ускорение определяем по формуле:
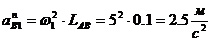
касательное - по формуле:
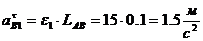
Выбираем масштаб плана ускорений: 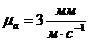 .
Тогда длины отрезков, изображающих вектора ускорений
.
Тогда длины отрезков, изображающих вектора ускорений 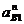 и
и
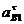 равны:
равны:
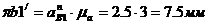 и
и
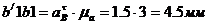 .
Нормальное ускорение
.
Нормальное ускорение 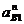 направлено к
центру вращения, т.е. от В к А. Касательное ускорение
направлено к
центру вращения, т.е. от В к А. Касательное ускорение 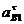 направлено
перпендикулярно линии АВ в сторону углового ускорения
направлено
перпендикулярно линии АВ в сторону углового ускорения 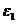 .
.
Для построения плана ускорений на плоскости
чертежа в произвольном месте отмечаем полюс плана ускорений точку 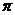 .
На плане изображают ускорения
.
На плане изображают ускорения 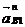 и
и 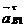 .
Для этого от точки π откладываем
отрезок
.
Для этого от точки π откладываем
отрезок 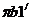 параллельный
звену AB в направлении от В к А, а от точки
параллельный
звену AB в направлении от В к А, а от точки  откладываем
отрезок
откладываем
отрезок 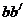 перпендикулярный
звену AB в направлении
перпендикулярный
звену AB в направлении 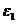 . Соединяя точки π
и
b , получаем вектор полного ускорения точку B.
. Соединяя точки π
и
b , получаем вектор полного ускорения точку B.
Ускорение точки В2 определяем по теореме о
сложении ускорений при сложном движении точки. Неподвижная система координат
жестко связана со стойкой, подвижная система координат- со звеном 1. абсолютное
ускорение точки В2 определяем из векторного уравнения:
Переносное ускорение 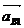 известно
по величине и направлению. Относительное ускорение
известно
по величине и направлению. Относительное ускорение 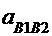 известное
только по направлению
известное
только по направлению 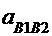 //ЕВ. В абсолютном
движении точка В2 движется со звеном 2, совершая круговое движение. Нормальное
ускорение точки В2:
//ЕВ. В абсолютном
движении точка В2 движется со звеном 2, совершая круговое движение. Нормальное
ускорение точки В2: 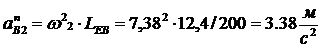 и направлено к
центру вращения, т.е. от точки В2 к точке Е. Угловое ускорение рассматриваемого
2го звена неизвестно, поэтому ускорение
и направлено к
центру вращения, т.е. от точки В2 к точке Е. Угловое ускорение рассматриваемого
2го звена неизвестно, поэтому ускорение 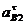 известно
только по направлению
известно
только по направлению 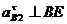 .
.
Величина ускорения Кориолиса:
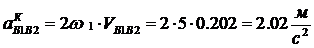
Данное относительное ускорение // EB
по направлению
Для построения плана ускорения откладываем
отрезок:
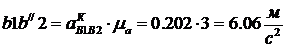
в направлении ускорения Кориолиса. Далее от
точки п откладываем отрезок:
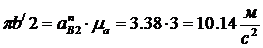
в направлении от точки В к точке Е. Из
полученной точки 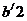 проводим прямую
перпендикулярную звену ВЕ, а из точки
проводим прямую
перпендикулярную звену ВЕ, а из точки 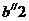 прямую,
// звену ВЕ по направлению относительного ускорения
прямую,
// звену ВЕ по направлению относительного ускорения 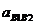 .
В точке пересечения данных прямых находится точка b2.
.
В точке пересечения данных прямых находится точка b2.
Ускорение точки С находим по теореме подобия:
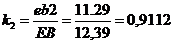 ;
; 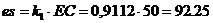
На плане ускорений отрезок es
совпадает по направлению с отрезком eb.
Для определения ускорения точки D
используют теорему о сложении ускорений при плоскопараллельном движении 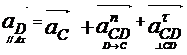
В этом векторном уравнении ускорение 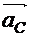 известно
по величине и направлению. Ускорение
известно
по величине и направлению. Ускорение 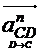 и
и
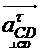 -
нормальное и касательное ускорения точки C при относительном вращении вокруг
точки C
-
нормальное и касательное ускорения точки C при относительном вращении вокруг
точки C
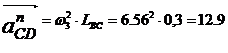
Вектор этого ускорения к центру относительного
вращения от точки D к точке C. Вектор касательного ускорения известен только по
направлению. Точка D совершает прямолинейное движение вдоль оси Ах. Ускорение 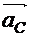 известно
только по направлению.
известно
только по направлению.
Для построения плана ускорений от точки с
откладываем отрезок 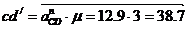 в направлении от
точки D к точке С.
в направлении от
точки D к точке С.
Далее, из точки 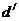 откладываем
перпендикуляр к звену CD
до пересечения горизонтальной прямой из точки п. Отрезок
откладываем
перпендикуляр к звену CD
до пересечения горизонтальной прямой из точки п. Отрезок 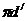 является
ускорением точки D.
является
ускорением точки D.
Ускорение точки S
находим из теоремы подобия на прямой cd.
Отрезок 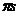 является
ускорением точки S.
является
ускорением точки S.
Определяем величины ускорений каждой точки:
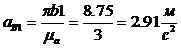 ;
;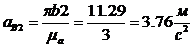
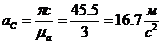
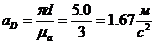
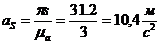 ;;
;;
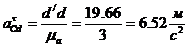 ;
; 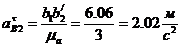
Угловые ускорения 2-ого и 5-ого звеньев
определяют по формулам:
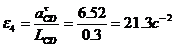 ;
; 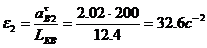
-е звено совершает поступательное движение,
потому:
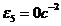
Литература
1.Теория механизмов и машин / Под.
ред. К.В.Фролова. - М.: Высш. шк., 1998. - 496 с., ил.
. Теория механизмов и машин: Учеб.
Пособие / Г.А.Тимофеев, С.А. Попов, В.А. Никоноров и др.; Под. ред. Г.А.Тимофеева.
- М.: Изд-во МГТУ им. Н.Э.Баумана, 2002. - 96с., ил.