Оптимальное решение двойственной задачи
Задание 1
Данные исходной задачи запишем в виде таблицы
(таблица 1).
Таблица 1
|
Сырье
|
Вид
продукции
|
Запасы
сырья
|
|
А1
|
А2
|
|
|
S1
|
1
|
1
|
10
|
|
S2
|
1
|
4
|
28
|
|
S3
|
3
|
1
|
24
|
|
Доход
от реализации
|
4
|
8
|
|
Предположим, что будет использовано х1
сырья S1
для изготовления продукции А1, х2 сырья для продукции
вида А2. Тогда общий доход от реализации составит 4х1 +
8х2.
Так как общее количество сырья S1
не может превышать 10, то должно выполняться следующее неравенство: х1+х2
≤ 10
Аналогичные рассуждения относительно возможного
использования остального количества сырья приведут к следующим неравенствам:
х1 + 4х2 ≤ 28;
х1+х2 ≤ 24.
При этом, так как количество продукции не может
быть отрицательным, то: х1 ≥ 0, х2 ≥ 0
Пусть F
- прибыль предприятия, так как по условию необходимо составить план
производства двух видов продукции, обеспечивающий максимальную прибыль,
следовательно, функция F,
при условии, что изготовлено х1 единиц продукции вида А1
и х2 единиц продукции вида А2 будет максимизироваться:
издержка теневой цена прибыль
F = 4х1 +
8х2 → max.
Таким образом, мы приходим к следующей
математической задаче:
Дана система:
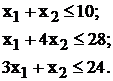 (1)
(1)
трех линейных неравенств с двумя
неизвестными хi (i=1,2). И
линейная функция относительно этих же переменных:
F = 4х1
+ 8х2 (2)
требуется среди всех неотрицательных
решений системы неравенств (2), найти такое, при котором функция (3) примет
максимальное значение.
Найдем решение сформулированной
задачи, используя ее геометрическую интерпретацию. Сначала определим
многоугольник решений. Для этого в неравенствах системы ограничений и условиях
не отрицательности переменных знаки неравенств заменим на знаки точных равенств
и найдем соответствующие прямые.
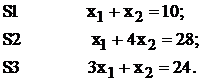
Прямые S1 - S3,
изображены на рисунке 1.
Каждая из построенных прямых делит
плоскость на две полуплоскости. Координаты точек одной полуплоскости
удовлетворяют исходному неравенству, а другой - нет. Определим искомую
полуплоскость через точку О (0;0).
Пресечение полученных плоскостей
определяет многоугольник решений данной задачи.
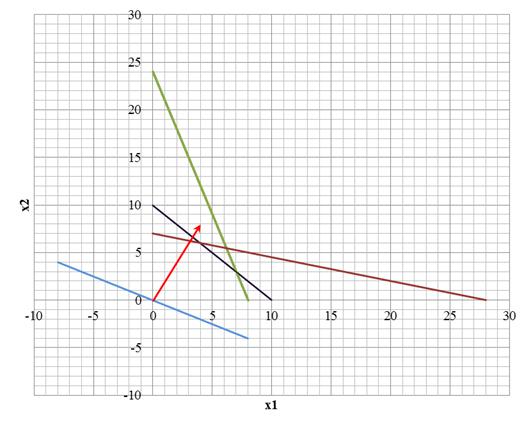
Рисунок 1 - Многоугольник решений
Как видно из рисунка 1, многоугольником решений
является пятиугольник ОАВСD.
Таким образом, среди точек пятиугольника ОАВСD
нам нужно найти такие, в которых функция F
= 4х1 + 8х2 принимает максимальное значение. Для
нахождения этих точек построим нулевую линию уровня (F0)
4х1 + 8х2 = 0 и вектор N
= (4;8).
Передвигая данную прямую параллельно самой себе
в направлении вектора N,
видим, что ее последней точкой с многоугольником решений задачи является точка
В. Следовательно, в этой точке функция F
принимает максимальное значение. Так как В - точка пересечения прямых S1
и S2, то ее координаты
удовлетворяют уравнениям этих прямых:
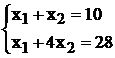
Решив эту систему уравнений мы
получили: х1 = 4 и х2 = 6.
Таким образом, максимальное значение
функции Fmax = 4*4+8*6 =
16 + 48 = 64.
Решение симплекс-методом
Математическая модель задачи:
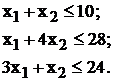
х1, х2 ≥
0
F = 4х1
+ 8х2
Запишем эту задачу в форме основной
задачи ЛП:
Для этого перейдем от ограничений
неравенств - к ограничениям равенствам.
Введем 3 дополнительные переменные,
в результате чего ограничения запишутся в виде систем ограничений:
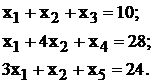
Преобразованную систему ограничений
запишем в векторной форме:
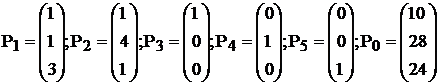
Поскольку среди векторов Р1-Р5
имеются 3 единичных вектора, для данной задачи можно непосредственно записать
опорный план.
Таковым является план Х =
(0;0;0;10;28;24), определяемый системой трехмерных единичных векторов Р3,
Р4, Р5, которые образуют базис трехмерного векторного
пространства.
Составим симплексную таблицу для I итерации
(таблица 2), подсчитав значения F0, zi - ci и проверяем
исходный план на оптимальность.
F0 = (c, P0);
z1 = (c, P1) = 0; z2 = (c, P2) = 0;
z3 = (c, P3) = 0;4 = (c, P4) = 0; z5
= (c, P5) = 0;1 - c1 = 0 - 4 = -4; z2
- c2 = 0 - 8 = -8.
Для векторов базиса zi
- ci = 0.
Таблица 2
|
i
|
Базис
|
Р0
|
4
|
8
|
0
|
0
|
0
|
|
|
|
|
Р1
|
Р2
|
Р3
|
Р4
|
Р5
|
|
1
|
Р3
|
0
|
10
|
1
|
1
|
1
|
0
|
0
|
|
2
|
Р4
|
0
|
28
|
1
|
4
|
0
|
1
|
0
|
|
3
|
Р5
|
0
|
24
|
3
|
1
|
0
|
0
|
1
|
|
4
|
|
|
0
|
-4
|
-8
|
0
|
0
|
0
|
Таким образом, по 4 строке таблицы 2 видно, что
план не оптимален, т.к. значения zi
- ci - отрицательны.
Далее определяем вектор, подлежащий исключению
из базиса. Для этого находим Q0min
(bi/ai1)
для ai1>0
и Q0min
(bi/ai2)
для ai2>0.
Таким образом, Q0min
(bi/ai1)
= min (10/1;28/1;24/4) =
24/4, а Q0min
(bi/ai2)=
min (10/1;28/4;24/1) =
28/4.
Min (24/4;28/4)
= 28/4.
Таким образом, мы нашли разрешающий элемент,
находящийся на пересечении 2-ой строки и столбца вектора Р2.
Следовательно, вектор Р4 подлежит
исключению из базиса.
Столбец вектора Р2 и вторая строка
являются направляющими.
Далее, составляем таблицу для итерации II
(таблица 3).
Сначала заполняем строку вектора вновь
введенного в базис. Элементы этой строки таблицы 3 получаются из
соответствующих элементов таблицы 2 делением на разрешающий элемент.
Затем, заполняем элементы столбцов для векторов,
входящих в новый базис. В этих столбцах на пересечении строк и столбцов
одноименных векторов проставляем единицы, а все остальные элементы полагаем
равными нулю. Для определения остальных элементов таблицы 3 применяем правило
прямоугольника.
Данный цикл продолжается до тех пор, пока все
значения zi
- ci
-
не станут положительными.
Таким образом, в таблице 3 мы запишем все
итерации вычислительного процесса.
Таблица 3
|
i
|
Базис
|
Сб
|
Р0
|
4
|
8
|
0
|
0
|
0
|
|
|
|
|
Р1
|
Р2
|
Р3
|
Р5
|
|
1
|
Р3
|
0
|
3
|
0,75
|
0
|
1
|
-0,25
|
0
|
|
2
|
Р2
|
8
|
7
|
0,25
|
1
|
0
|
0,25
|
0
|
|
3
|
Р5
|
0
|
17
|
2,75
|
0
|
0
|
-0,25
|
1
|
|
4
|
|
|
56
|
-2
|
0
|
0
|
2
|
0
|
|
|
|
|
|
|
|
|
|
|
1
|
Р1
|
4
|
4
|
1
|
0
|
1,33
|
0,33
|
0
|
|
2
|
Р2
|
8
|
6
|
0
|
1
|
-0,33
|
0,33
|
0
|
|
3
|
Р5
|
0
|
6
|
0
|
0
|
-3,67
|
0,67
|
1
|
|
5
|
|
|
64
|
0
|
0
|
2,67
|
1,33
|
0
|
Итак, среди значений zi
- ci нет отрицательных,
следовательно, опорный план оптимален и Fmax
= 64.
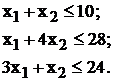 х1, х2 ≥
0
х1, х2 ≥
0
F = 4х1
+ 8х2
Хопт. = (4; 6).
Max F = 64.
Составим двойственную модель и с
помощью теорем двойственности найдем оптимальное решение двойственной модели:
Двойственная модель:
Z = 10y1
+ 28y2
+ 24y3→
min
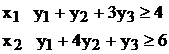
Так как мы уже нашли решение
исходной задачи (таблица 3), следовательно, мы нашли и решение двойственной
задачи:
y1 = 2,67; y2 = 1,33; y3 = 0.
(итерация III в
симплекс-таблице 3).
Таким образом оптимальное решение
двойственной задачи = yопт(2,67;1,33;0).
Подставим компоненты оптимального
решения двойственной задачи в функцию двойственной модели:
Z =
10*2,67+28*1,33+24*0 = 26,7+37,3+0 = 64
Итак, Z = F = 64.
Задание 2
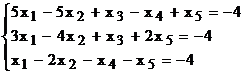
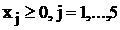
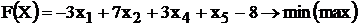
Запишем и преобразуем матрицу
коэффициентов системы.
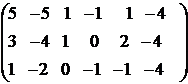 →
→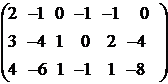 →
→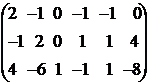
Таким образом, мы получили систему
ограничений с единичным базисом (х3, х4, х5):
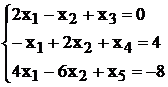
Отбрасывая базисные переменные,
получим стандартную задачу ЛП:
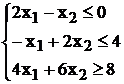
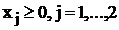
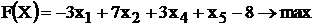
Выразим функцию цели через свободные
неизвестные х1 и х2. Имеем:
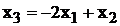
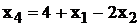
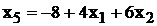
Тогда:
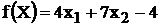
Таким образом, φmin
вспомогательной задачи не равно 0, следовательно, исходная задача не обладает
опорным решением (несовместна).
Задание 3
Таблица 4 Исходные данные задачи
|
Поставщик
|
Потребитель
|
Запасы
груза
|
|
В1
|
В2
|
В3
|
В4
|
В5
|
|
|
А1
|
13
|
9
|
15
|
3
|
18
|
53
|
|
А2
|
7
|
8
|
6
|
10
|
9
|
17
|
|
А3
|
16
|
4
|
10
|
11
|
29
|
30
|
|
Потребность
|
20
|
20
|
20
|
13
|
27
Предложение = 53+17+30 = 100
Таким образом, данная ТЗ - закрытая.
Составим первоначальный план по методу
наименьшей стоимости (таблица 5).
Таблица 5
|
Поставщик
|
Потребитель
|
Запасы
груза
|
|
В1
|
В2
|
В3
|
В4
|
В5
|
|
|
А1
|
20
13
|
9
|
15
|
13
3
|
20
18
|
53
|
|
А2
|
7
|
8
|
17
6
|
10
|
9
|
17
|
|
А3
|
16
|
20
4
|
3
10
|
11
|
7
29
|
30
|
|
Потребность
|
20
|
20
|
20
|
13
|
27
|
|
n+m
-1 =3+5-1 = 7 - не соответствует числу заполненных клеток
Общие транспортные издержки равны:
Z1
= 20*13+20*4+17*6+3*10+13*3+20*18+7*29 = 260+80+102+30+39+360+203 = 1074
Проверим составленный план на оптимальность
методом потенциалов.
Рассчитаем потенциалы, исходя из того, что
потенциал строки А1 = 0 (таблица 6).
Таблица 6
|
Поставщик
|
Потребитель
|
Запасы
груза
|
|
|
В1
|
В2
|
В3
|
В4
|
В5
|
|
|
|
А1
|
20
13
|
9
|
15
|
13
3
|
20
18
|
53
|
U1=0
|
|
А2
|
7
|
8
|
17
6
|
10
|
9
|
17
|
U2=7
|
|
А3
|
20
4
|
3
10
|
11
|
7
29
|
30
|
U3=11
|
|
Потребность
|
20
|
20
|
20
|
13
|
27
|
|
|
|
V1=13
|
V2=-7
|
V3=-1
|
V4=3
|
V5=18
|
|
|
Далее, рассчитаем теневые цены (таблица 7 -
теневые цены серым цветом).
Таблица 7
|
Поставщик
|
Потребитель
|
Запасы
груза
|
|
|
В1
|
В2
|
В3
|
В4
|
В5
|
|
|
|
А1
|
20
13
|
16
9
|
16
15
|
13
3
|
20
18
|
53
|
U1=0
|
|
А2
|
-13
7
|
8
8
|
17
6 -
|
0
10
|
-16
9 +
|
17
|
U2=7
|
|
А3
|
-8
16
|
20
4
|
3
10 +
|
-3
11
|
7
29 -
|
30
|
U3=11
|
|
Потребность
|
20
|
20
|
20
|
13
|
27
|
|
|
|
V1=13
|
V2=-7
|
V3=-1
|
V4=3
|
V5=18
|
|
|
Наличие теневых цен означает не оптимальность
имеющегося плана, следовательно, для улучшения плана намечаем маршрут с
наименьшей отрицательной теневой ценой и для этого маршрута определяем цикл
перераспределения. Объем перевозимого груза численно равен минимальному
значению из тех объемов груза, которые указаны в клетках со знаком минус. Таким
образом, ∆ (А2, В5) = min
(17;7) = 7.
Итак, составляем новый план (таблица 8).
Данный цикл длится до тех пор, пока все теневые
цены не станут положительными.
Таблица 8
|
Поставщик
|
Потребитель
|
Запасы
груза
|
|
|
В1
|
В3
|
В4
|
В5
|
|
|
|
А1
|
20
13
|
0
9
|
0
15
|
13
3
|
20
18
|
53
|
U1=0
|
|
А2
|
3
7
|
8
8
|
10
6
|
16
10
|
7
9
|
17
|
U2=-9
|
|
А3
|
8
16
|
20
4
|
10
10
|
13
11
|
16
29
|
30
|
U3=-5
|
|
Потребность
|
20
|
20
|
20
|
13
|
27
|
|
|
|
V1=13
|
V2=9
|
V3=15
|
V4=3
|
V5=18
|
|
|
Общие транспортные издержки равны:
Z2
= 20*13+20*4+10*6+10*10+13*3+20*18+7*9 = 260+80+60+100+39+360+63 = 962
В таблице 8 все теневые цены положительны,
следовательно, план оптимален.
Похожие работы на - Оптимальное решение двойственной задачи
|