|
j / i
|
1
|
2
|
3
|
4
|
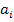
|
|
1
|
1
|
2
|
2
|
1
|
50
|
|
2
|
2
|
2
|
1
|
2
|
70
|
|
3
|
1
|
2
|
1
|
3
|
30
|
|
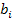
|
40
|
25
|
60
|
25
|
|
1. Построить
математическую модель транспортной задачи.
. Найти опорный план перевозок транспортной задачи методом
северо-западного угла.
. Найти опорный
план перевозок транспортной задачи методом минимального элемента.
. Решить методом
потенциалов транспортную задачу дважды, используя найденные в пунктах 2 и 3
опорные планы перевозок.
Решение:
Задача
№1:
.
Графический метод
Преобразуем задачу
на минимум к задаче на максимум:
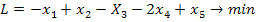
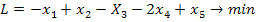 =
= 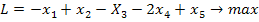
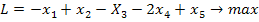
Основные ограничения
задачи содержат 3 уравнения с 5-ю неотрицательными переменными. Так как число
переменных n = 5 и число ограничений т = 3 отличаются на 2, то можно
предположить, что эту задачу можно решить графическим методом. Соотношение n-m = 2 сохранится, если основные ограничения задачи линейно
независимые.
Преобразуем исходную
задачу, разделив переменные на базисные и свободные, предварительно записав
целевую функцию как уравнение
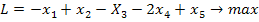
Все вычисление проведём
в таблице, используя метод полного исключения (Метод Жардана - Гаусса). ∑
- контрольная сумма.
|
X1
|
X2
|
X3
|
X4
|
X5
|
B
|
|
1
|
4
|
1
|
0
|
1
|
15
|
|
4
|
-3
|
-1
|
1
|
1
|
6
|
|
2
|
-4
|
-1
|
1
|
0
|
-3
|
|
-1
|
1
|
-1
|
-2
|
1
|
0
|
|
1
|
4
|
1
|
0
|
1
|
15
|
|
0
|
-19
|
-5
|
1
|
-3
|
-54
|
|
0
|
-12
|
-3
|
1
|
-2
|
-33
|
|
0
|
5
|
0
|
-2
|
2
|
15
|
|
1
|
4
|
1
|
0
|
1
|
15
|
|
0
|
-19
|
-5
|
1
|
-3
|
-54
|
|
0
|
7
|
2
|
0
|
1
|
21
|
|
0
|
-33
|
-10
|
0
|
-4
|
-93
|
|
1
|
-3
|
-1
|
0
|
0
|
-6
|
|
0
|
2
|
1
|
1
|
0
|
9
|
|
0
|
7
|
2
|
0
|
1
|
21
|
|
0
|
-5
|
-2
|
0
|
0
|
-9
|
|
-1/3
|
1
|
1/3
|
0
|
0
|
2
|
|
2/3
|
0
|
1/3
|
1
|
0
|
5
|
|
7/3
|
0
|
-1/3
|
0
|
1
|
7
|
|
-5/3
|
0
|
-1/3
|
0
|
0
|
1
|
Выполнив 4 шага
вычислений метода полного исключения, мы получили следующую систему уравнений:
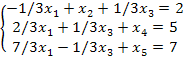
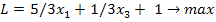
Разрешив эту систему
относительно базисных переменных 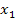
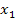 ,
, 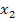
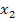 ,
, 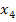
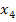 и
и 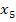
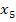 учитывая, что
учитывая, что 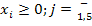
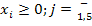 мы получим следующую
задачу:
мы получим следующую
задачу:
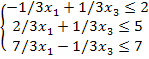
Эта задача содержит 2
переменных и её можно решить графическим методом. Запишем уравнения границ
области, точки для их построения и укажем полуплоскости, определяемые
неравенствами основных ограничений задачи
(1) 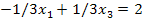
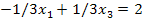 (0; 6) (-6; 0)
(0; 6) (-6; 0)
(2) 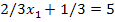
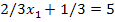 (0; 15) (7,5; 0)
(0; 15) (7,5; 0)
(3) 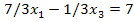
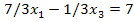 (0; - 21) (3; 0)
(0; - 21) (3; 0)
Строим область
допустимых решений системы неравенств в прямоугольной системе 
 .
.
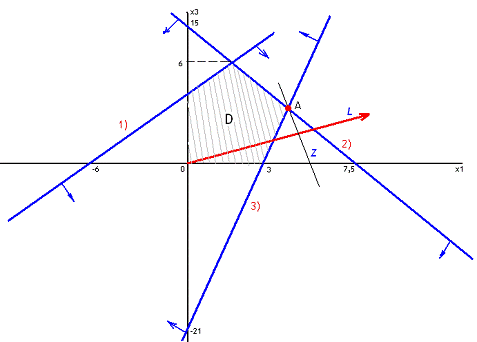
Область D - это точки 1-ой четверти. Вектор L в данном случае имеет вид L
= (1,6; 0,3).
Строим прямую Z перпендикулярно вектору L. Таким образом, получаем пересечение перпендикуляра с прямыми 2) и
3), в результате чего получаем точку А. В соответствии в этим составляем
систему уравнений. Решая систему уравнении: 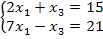
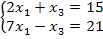 находим координаты этой
точки.
находим координаты этой
точки.
А = (4; 7), подставим в
целевую функцию 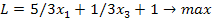
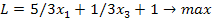 получим следующие
значения:
получим следующие
значения:
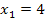
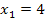 ,
, 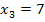
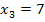 , получим:
, получим: 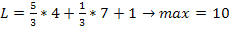
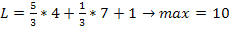 .
.
2. Симплекс метод
Разделим переменные на
базисные и свободные методом полного исключения (см. Графический метод),
получим:
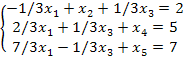
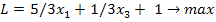
Составим таблицу
итераций:
|
БАЗИС
|
С
|
A0
|
ВЕКТОРЫ
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
A5
|
|
A2
|
0
|
2
|
-1/3
|
1
|
1/3
|
0
|
0
|
|
A4
|
0
|
-5
|
2/3
|
0
|
1/3
|
1
|
0
|
|
A5
|
0
|
7
|
7/3
|
0
|
-1/3
|
0
|
1
|
|
∆
|
|
1
|
-5/3
|
0
|
-1/3
|
0
|
1
|
|
2-я итерация
|
|
А2
|
0
|
3
|
0
|
1
|
1/21
|
0
|
1/7
|
|
А4
|
0
|
3
|
0
|
0
|
3/7
|
1
|
-2/7
|
|
А1
|
5/3
|
3
|
1
|
0
|
-1/7
|
0
|
5/7
|
|
∆
|
|
6
|
0
|
0
|
-12/21
|
0
|
5/7
|
|
3-я итерация
|
|
А2
|
0
|
8/3
|
0
|
1
|
0
|
-1/9
|
11/63
|
|
А3
|
1/3
|
7
|
0
|
0
|
1
|
7/3
|
-2/3
|
|
А4
|
5/3
|
4
|
1
|
0
|
0
|
1/3
|
1/3
|
|
∆
|
|
10
|
0
|
0
|
0
|
4/3
|
1/3
|
На первой итерации
видим, что среди ∆ есть отрицательные - это значит что решение не
оптимально. Вектор А1 выводим в базис, так как 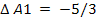
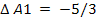 . Для того чтобы выбрать
какой элемент мы будем выводить из базиса делаем следующее: элемент столбца
. Для того чтобы выбрать
какой элемент мы будем выводить из базиса делаем следующее: элемент столбца 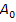
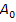 делим на элемент
столбца
делим на элемент
столбца 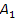
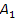 по принципу первый на
первый, второй на второй. Из полученных результатов деления выбираем наименьшее
положительное.
по принципу первый на
первый, второй на второй. Из полученных результатов деления выбираем наименьшее
положительное.
Из этого следует что
выводим элемент 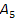
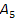 . Далее пересчитываем
таблицу по методу Жардано-Гаусса и получаем таблицу второй итерации.
. Далее пересчитываем
таблицу по методу Жардано-Гаусса и получаем таблицу второй итерации.
Видим, что среди ∆
есть отрицательные - это значит что решение не оптимально. Вектор 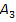
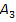 выводим в базис потому,
что
выводим в базис потому,
что 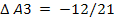
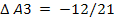 . По вышеизложенному
принципу выбираем элемент для вывода из базиса. Выводим из базиса
. По вышеизложенному
принципу выбираем элемент для вывода из базиса. Выводим из базиса 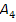
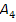 . Далее пересчитываем
таблицу по методу Жардана-Гаусса и получаем таблицу третей итерации.
. Далее пересчитываем
таблицу по методу Жардана-Гаусса и получаем таблицу третей итерации.
Видим, что среди ∆
нет отрицательных - это значит что решение оптимально.
3. Двойственная задачи
Любая задача
математического программирования имеет обратную ей задачу, так называемую
двойственную ей задачу, причем соблюдается условие: 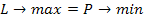
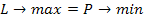 и на оборот.
и на оборот.
Строим двойственную
задачу по такому принципу: A
[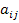
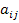 ] - матрица задачи,
тогда матрица обратной задачи будет
] - матрица задачи,
тогда матрица обратной задачи будет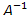
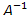 , причем
, причем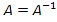
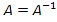 .
.
Разделим переменные на
базисные и свободные методом полного исключения (см. Графический метод),
получим:
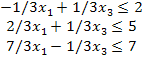
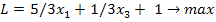
Тогда двойственная этой
задачи будет иметь вид:
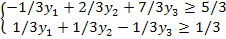
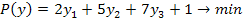
4. Решение двойственной
задачи с помощью первой основной теоремы теории двойственности
Первая теорема
двойственности позволяет решить двойственную задачу по решению прямой задачи,
используя полученные симплекс таблицы.
Теорема: Если одна из
двойственных задач имеет оптимальное решение, то и двойственная ей задача имеет
оптимальное решение, причем 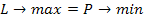
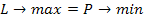 - эти задачи совпадают.
- эти задачи совпадают.
Из доказательства
теоремы следует, что 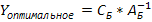
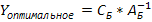 . Матрица решений
. Матрица решений 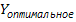
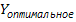 получается
перемножением матриц
получается
перемножением матриц 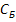
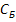 (вектор-строка
коэффициентов в целевой функции при базисных переменных);
(вектор-строка
коэффициентов в целевой функции при базисных переменных); 
 (матрица обратная
матрицы
(матрица обратная
матрицы 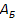
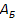 , составленная из
векторов оптимального базиса, тоесть матрица на исходных векторах, но взятых из
последней симплекс таблицы).
, составленная из
векторов оптимального базиса, тоесть матрица на исходных векторах, но взятых из
последней симплекс таблицы).
Решаем двойственную
задачу с помощью симплексных таблиц (см. Симплекс метод).
|
БАЗИС
|
С
|
A0
|
ВЕКТОРЫ
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
A5
|
|
A2
|
0
|
2
|
-1/3
|
1
|
1/3
|
0
|
0
|
|
A4
|
0
|
-5
|
2/3
|
0
|
1/3
|
1
|
0
|
|
A5
|
0
|
7
|
7/3
|
-1/3
|
0
|
1
|
|
∆
|
|
1
|
-5/3
|
0
|
-1/3
|
0
|
1
|
|
2-я итерация
|
|
А2
|
0
|
3
|
0
|
1
|
1/21
|
0
|
1/7
|
|
А4
|
0
|
3
|
0
|
0
|
3/7
|
1
|
-2/7
|
|
А1
|
5/3
|
3
|
1
|
0
|
-1/7
|
0
|
5/7
|
|
∆
|
|
6
|
0
|
0
|
-12/21
|
0
|
5/7
|
|
3-я итерация
|
|
А2
|
0
|
8/3
|
0
|
1
|
0
|
-1/9
|
11/63
|
|
А3
|
1/3
|
7
|
0
|
0
|
1
|
7/3
|
-2/3
|
|
А4
|
5/3
|
4
|
1
|
0
|
0
|
1/3
|
1/3
|
|
∆
|
|
10
|
0
|
0
|
0
|
4/3
|
1/3
|
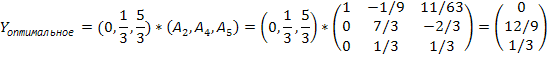
Отсюда следует, что:
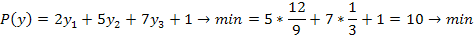
5.
Решение двойственной задачи с помощью второй основной теоремы теории
двойственности
Вторая теорема
двойственности также позволяет решить двойственную задачу, используя решение
первой задачи и используя ограничения.
Разделим переменные
на базисные и свободные методом полного исключения (см. Графический метод) и
возьмем точку А (см. Графический метод) получим:
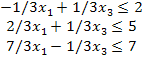
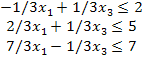 А=(4; 7)
А=(4; 7)
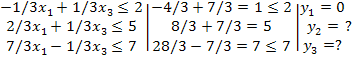
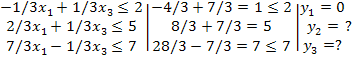
Отсюда следует, что
необходимо искать 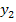
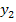 и
и 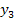
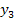 .
.
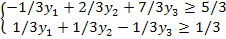
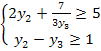
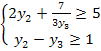
Решив, систему уравнений
получим: 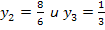
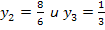 .
.
Отсюда 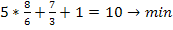
Ответ:
Максимальная прибыль будет равна 10.
Задача
№2
1. Построение
математической модели транспортной задачи
Транспортные задачи
- это задачи в которых нужно решить проблему: доставку продукции от множества
поставщиков к множеству потребителей с минимальными затратами на
транспортировку.
Для решения этих задач
нужно знать матрицу поставщиков 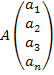
 , матрицу потребителей
, матрицу потребителей 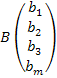
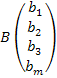 и матрицу перевозок
и матрицу перевозок 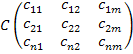
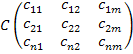 . Матрица перевозок
показывает стоимость перевозки от i
поставщика к j потребителю.
. Матрица перевозок
показывает стоимость перевозки от i
поставщика к j потребителю.
Обычно условие такой
задачи задается или сводится к таблице перевозок. Верхняя строчка таблицы
показывает ресурсы поставщиков, самый левый столбец указывает потребности
потребителя. Остальная матрица таблицы показывает затраты на доставку продукции
от поставщиков к потребителям.
Решение задачи будет
определение количество товара, которое необходимо поставить от каждого
поставщика к каждому потребителю.
Исходя из условий задачи
получаем:
Матрица поставщиков
имеет вид: 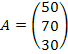
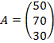
Матрица потребителей
имеет вид: 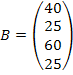
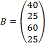
Матрица перевозок имеет
вид: 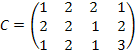
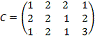
Система ограничений по поставки
имеет вид: 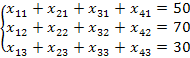
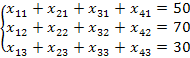
Система ограничений по
потреблению имеет вид: 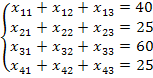
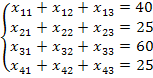
Функция цели имеет вид:
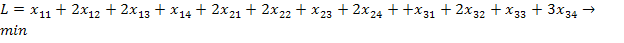
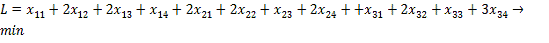
2. Поиск опорного
плана транспортной задачи методом северо-западного угла
Выбираем первую пустую
северо-западную клетку, и заполняем ее максимальным допустимым значением. После
выбираем следующую северо-западную клетку и заполняем. Процедура повторяется до
тех пор, пока не будут удовлетворены все поставщики и потребители. В итоге
получаем опорный план методом северо-западного угла:
|
i / j
|
40
|
25
|
60
|
25
|
|
50
|
1 40
|
2 10
|
2
|
1
|
|
70
|
2
|
2 15
|
1 55
|
2
|
|
30
|
1
|
2
|
1 5
|
3 25
|
Стоимость перевозок: L=40+20+30+55+5+75=225
3. Поиск опорного плана
транспортной задачи методом минимального элемента
Выбираем клетку с наименьшей
стоимостью перевозки и заполняем ее максимально допустимым значением. После
выбираем следующую клетку и заполняем ее. Процедура повторяется до тех пор,
пока не будут удовлетворены все поставщики и потребители. В итоге получаем
опорный план методом минимального элемента.
|
i / j
|
40
|
25
|
60
|
25
|
|
50
|
1 40
|
2
|
2
|
1 10
|
|
70
|
2
|
2
|
1 60
|
2 10
|
|
30
|
1
|
2 25
|
1
|
3 5
|
Стоимость перевозок: L=40+50+60+10+20+15=195
4. Решение транспортной
задачи методом потенциалов
Введем для обозначения
потенциалов буквы: для обозначения потенциала строки букву «U», обозначения потенциалов столбца букву «V».
Возьмем опорный план, найденный в третьем пункте задачи, и заполним таблицу с
учетом потенциалов. Причем для потенциалов будет выполняться условие: 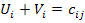
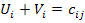 .
.
|
i / j
|
40
|
25
|
60
|
25
|
U
|
|
50
|
1 40
|
2
|
2
|
1 10
|
U1
|
|
70
|
2
|
2
|
1 60
|
2 10
|
U2
|
|
30
|
1
|
2 25
|
1
|
3 5
|
U3
|
|
V
|
V1
|
V2
|
V3
|
V4
|
|
Составить систему уравнений по
заполненным клеткам.
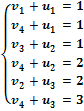
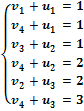
Поскольку уравнений
шесть, а неизвестных переменных семь, зададим потенциал 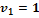
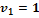 . Отсюда
. Отсюда 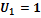
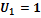 ,
,
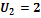
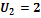 ,
, 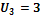
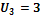 и
и
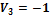
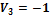 ,
, 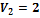
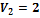 ,
, 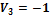
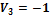 ,
, 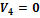
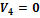 .
.
Составляем косвенные
стоимости (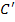
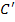 ) для пустых клеток по
найденным потенциалам.
) для пустых клеток по
найденным потенциалам.
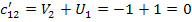
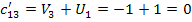
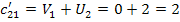
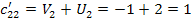
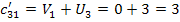
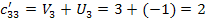
Определяем оценки (г)
для пустых клеток по формуле: прямая минус косвенная стоимость.
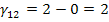
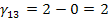
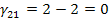
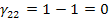
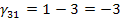
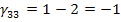
Поскольку отрицательных
оценок есть, то данный план не оптимален. Составляем новый план с другим позиционированием
коэффициентов.
|
i / j
|
40
|
25
|
60
|
25
|
U
|
|
50
|
1 25
|
2
|
2
|
1 25
|
U1
|
|
70
|
2
|
2 10
|
1 60
|
2
|
U2
|
|
30
|
1 15
|
2 15
|
1
|
3
|
U3
|
|
V
|
V1
|
V2
|
V3
|
V4
|
|
Составить систему уравнений по
заполненным клеткам.
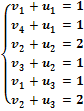
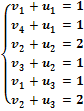
Поскольку уравнений
шесть, а неизвестных переменных семь, зададим потенциал 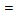
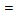 . Отсюда
. Отсюда 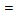
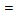 ,
,
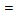
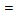 ,
, 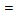
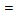 и
и
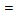
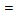 ,
, 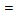
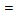 ,
, 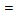
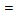 ,
, 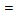
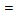 .
.
Составляем косвенные
стоимости (
 ) для пустых клеток по
найденным потенциалам.
) для пустых клеток по
найденным потенциалам.
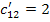
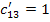
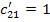
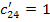
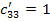
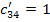
Определяем оценки (г)
для пустых клеток по формуле: прямая минус косвенная стоимость.
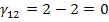
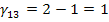
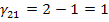
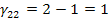
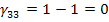
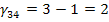
Так как отрицательных
оценок нет, то план перевозок оптимален. L=175
Ответ:
Себестоимость перевозок равна L=175.