Математическое программирование
Лекция 1, 2
Математическое программирование.
Понятие об оптимизационных задачах. Задача линейного программирования (ЗЛП).
Графический метод решения ЗЛП
Вопросы:
1. Предмет - математическое программирование,
краткая классификация методов.
. Основные понятия теории оптимизации.
. Постановка ЗЛП, различные формы записи.
Примеры экономических задач.
. Графический метод решения ЗЛП. Основные
свойства ЗЛП.
1. Предмет
- математическое программирование
Среди многочисленных проблем, возникновение
которых связано с бурно развивающейся научно-технической революцией, пожалуй,
наиболее важной является проблема совершенствования управления во всех звеньях
хозяйства.
Современные промышленные предприятия,
предприятия бытового обслуживания, транспортные агентства, научно-технические
организации представляют собой сложные системы «человек-машина». Эффективность
работы таких систем зависит от качества организационного управления. Чтобы
добиться качества современному руководителю не всегда бывает достаточно личного
опыта, интуиции и организаторских способностей в их традиционном понимании. При
формировании стратегических и тактических решений руководитель должен учитывать
множество подчас противоречивых соображений, опираться на сложные критерии
эффективности путей достижения конечных целей. В связи с этим возникла
необходимость применять для анализа и синтеза экономических ситуаций и систем
математические методы и современную вычислительную технику. Такие методы
объединяются под общим названием - математическое программирование.
Математическое программирование -
область математики, разрабатывающая теорию и численные методы решения
многомерных экстремальных задач с ограничениями, т.е. задач на экстремум
функций многих переменных с ограничениями на область изменения этих переменных.
Для того, чтобы успешно руководить крупным
предприятием в условиях конкуренции руководителю, возможно, и не надо быть
самому классным специалистом в области математического программирования, но
чтобы понимать суть и смысл решаемой задачи, получаемых результатов и не
«упустить руль», он должен понимать способ решения, быстро реагировать на
возникающие изменения, чтобы эффективно использовать возможности
математического программирования. Математическое программирование в настоящее
время используется практически во всех областях жизни и производства:
·
в
экономике - для решения больших макроэкономических моделей (типа модели
Леонтьева и др.), микроэкономических моделей или моделей предпринимательства,
для оптимизации технико-экономических систем (планирование, эконометрика),
транспортные задачи, в теории принятия решений, теории игр и т.п.;
·
в
технике - управление размерами и оптимизация структур, оптимальное планирование
сложных технических систем, как информационные системы, сети компьютеров,
транспортные и телекоммуникационные сети и др.;
·
в
автоматике - распознавание систем и объектов, оптимальное управление системами,
фильтрация, роботы, автоматизированные линии и т.п.;
·
в
медицине, политике, социологии и т.п., и т.д.
Дадим ряд определений.
·
Функцию,
экстремальное значение которой нужно найти в условиях экономических
возможностей, называют целевой, показателем эффективности или критерием
оптимальности.
·
Экономические
возможности формализуются в виде системы ограничений.
Все это составляет математическую модель. Математическая
модель - это отражение оригинала в виде функций, уравнений, неравенств, цифр и
т.д. Модель задачи математического программирования включает:
·
совокупность
неизвестных величин х = (х1, х2, …, хn),
действуя на которые систему можно совершенствовать. Их называют планом задачи
(вектором управления, решением, стратегией, поведением и т.п.);
·
целевую
функцию, которая позволяет выбрать наилучший вариант из множества возможных.
Целевая функция обозначается F(x).
Это может быть прибыль, объем выпуска или реализации, затраты производства,
издержки обращения, уровень обслуживания или дефицитности и т.д.;
·
условия
(система ограничений), налагаемые на неизвестные величины. Эти условия следуют
из ограниченности ресурсов, которыми располагает общество, из необходимости
удовлетворения насущных потребностей, из условий производственных и
технологических процессов. Математически ограничения выражаются в виде
уравнений и неравенств. Их совокупность образует область допустимых решений.
Т.о., модель задачи математического
программирования примет вид:
Найти план х = (х1, х2,
…, хn), доставляющий экстремальное
значение целевой функции F(x) → max(min), при
ограничениях gi(x) ≤
(=, ≥) bi, i=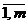 .
.
Из экономических или физических
соображений на план задачи или некоторые его компоненты, как правило,
налагаются условия неотрицательности, хj ≥ 0,
иногда - целочисленности.
≥ 0,
иногда - целочисленности.
План х, удовлетворяющий системе
ограничений задачи, называют допустимым. Допустимый план, доставляющий целевой
функции экстремальное значение, называют оптимальным. Оптимальный
план обозначают х*, экстремальное значение функции F(x*) = F*.
В зависимости от особенностей
целевой функции F(x) и функций
ограничений gi(x), задачи
математического программирования делятся на ряд типов.
1. Задача
линейного программирования (ЗЛП) - задача оптимизации линейной функции при
линейных ограничениях.
2. Задача
нелинейного программирования (ЗНП) - задача оптимизации нелинейной функции при
ограничениях или без них (когда или F(x)
и/или gi(x)
нелинейны).
3. Задача
дискретного (в частности целочисленного) программирования - Задача оптимизации,
в которой на переменные наложено дополнительное требование принимать лишь
дискретные (в частности целочисленные) значения.
4. Задача
динамического программирования - задача оптимизации динамических систем (т.е.
развивающихся с течением времени).
5. Задача
вероятностного или стохастического программирования - задача оптимизации,
содержащая случайные величины.
1. Основные
понятия теории оптимизации
Говорят, что функция F(x)
имеет в т. х*(х1,х2, … , хn)
локальный максимум (минимум), если существует такая окрестность т. х*, в
которой для любого х выполняется неравенство F(x)
≤ F(x*)
(F(x)
≥ F(x*)).
Необходимое условие экстремума: чтобы F(x) имела в т.
х* экстремум необходимо, чтобы ∂F(x*)/∂xj = 0, 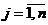 .
.
Достаточное условие экстремума: если F(x) в т. х*
имеет ∂F(x*)/∂xj = 0, 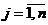 , то чтобы в
этой точке F(x) имела
экстремум достаточно, чтобы квадратичная форма
, то чтобы в
этой точке F(x) имела
экстремум достаточно, чтобы квадратичная форма
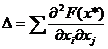 была положительно (минимум)
или отрицательно (максимум) определена.
была положительно (минимум)
или отрицательно (максимум) определена.
Очевидно, что точки локального
экстремума могут не давать наибольшего или наименьшего значений функции в
некоторой области, кроме того, их может быть несколько. Большое значение в этой
связи приобретает понятие выпуклости множества допустимых значений и выпуклости
(вогнутости) функции.
Множество S называется
выпуклым, если для любых двух точек этого множества оно содержит и отрезок,
соединяющий эти точки: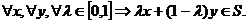
Функция F(x),
определенная на выпуклом множестве S, выпукла,
если ее график целиком лежит ниже (не выше) отрезка, соединяющего любые две
точки графика: 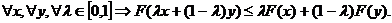
Функция F(x),
определенная на выпуклом множестве S, вогнута,
если ее график целиком лежит выше (не ниже) отрезка, соединяющего любые две
точки графика: 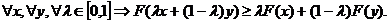
Теорема 1: пересечение
выпуклых множеств является выпуклым множеством.
Теорема 2: сумма
выпуклых функций является выпуклой функцией, сумма вогнутых функций - вогнутой
функцией.
Теорема 3 (основное свойство
выпуклых задач):
Всякий локальный оптимум является
глобальным.
Теорема Вейерштрасса:
Непрерывная функция, определенная на
непустом замкнутом ограниченном множестве, достигает максимума (минимума) по
крайней мере в одной точке этого множества.
Из сказанного можно определить общий
принцип решения задач оптимизации: максимум (минимум) F(x) при х,
принадлежащих замкнутому допустимому множеству, если оно существует, является
либо точкой экстремума, либо граничной точкой допустимого множества, либо и тем
и другим одновременно.
При численных расчетах часто
необходимо использовать еще два важных понятия.
Вектор, указывающий направление
наискорейшего возрастания функции, называется градиентом функции grad F(x) = (∂F/∂x1, … ,∂F/∂xn).
Противоположный ему вектор называют антиградиентом, он указывает направление
наискорейшего убывания функции.
Линией уровня (или линией равного
значения) функции F(x) называют
геометрическое место точек, координаты которых удовлетворяют уравнению F(x) = Const. Линия уровня
и вектор градиент в каждой точке взаимно перпендикулярны.
1. Постановка
ЗЛП, различные формы записи. Примеры экономических задач
Линейное программирование - раздел
математического программирования, рассматривающий задачи оптимизации линейных
функций многих переменных при линейных ограничениях на область изменения
переменных.
Особенностью ЗЛП является то, что линейная
целевая функция не имеет экстремума и достигает наибольшего или наименьшего
значения на границе допустимой области.
Рассмотрим постановку ЗЛП на примере задачи и
наилучшем использовании ресурсов. Имеется m
видов ресурсов в ограниченном количестве b
= (b1,
b2,
… , bm).
Ресурсы используются предприятием для выпуска n
видов продукции. Известна экономическая выгода производства каждого вида
продукции, исчисляемая, например, ценой реализации С = (С1, С2,
… , Сn).
Известны технологические коэффициенты аij,
соответствующие количеству i-го
вида ресурса, необходимого для производства единицы j
-го вида продукции - А = ( аij
). Необходимо составить план производства х = (х1,х2, … ,
хn),
приносящий предприятию максимальную прибыль.
В общем виде математическую модель задачи (ЗЛП)
можно записать следующим образом:
F(x) = C1x1 +
C2x2 + … + Cnxn → max
a11x1
+ a12x2 + … + a1nxn ≤ b1,
xj ≥ 0, j= 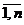 21x1
+ a22x2 + … + a2nxn ≤ b2,
21x1
+ a22x2 + … + a2nxn ≤ b2,
… … … … m1x1
+ am2x2 + … + amnxn ≤ bm.
Рассмотрим задачу о диете.
Необходимо составить диету (рацион), содержащую определенные питательные
вещества. Имеем n видов продуктов, каждый из которых
сожержит необходимые m видов питательных веществ. Единица j-го продукта
содержит аij единиц i-го
питательного вещества. Для нормальной жизнедеятельности необходимо не менее bi единиц i-го
вещества. Известна стоимость единицы каждого вида продукта С = (С1,
С2, … , Сn).
Необходимо составить диету минимальной стоимости.
Математическая модель задачи примет
вид:
F(x) = C1x1
+ C2x2 + … + Cnxn → min 11x1
+ a12x2 + … + a1nxn ≥ b1,
xj ≥ 0, j= 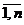 21x1
+ a22x2 + … + a2nxn ≥ b2,
21x1
+ a22x2 + … + a2nxn ≥ b2,
… … … … m1x1
+ am2x2 + … + amnxn ≥ bm.
Здесь хj -
количество j - го
продукта в рационе.
В матричной форме общая ЗЛП выглядит
так:
F(x) = CTx → max
(min) ≤ (=,≥)
B ; x
≥
0.
Кроме того, для записи ЗЛП можно использовать
знак суммы:
F(x) = 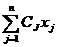 → max (min)
→ max (min)

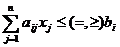 ,
, 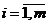 .
.
Рассмотрим задачу о размещении
заказа. Имеется m однородных групп оборудования, на
котором нужно выполнить заказ на выпуск n видов
продукции в объемах х*j, 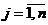 . Мощность
оборудования ограничена, например, временем Тi.
Производительность оборудования задана коэффициентами аij. Известны
коэффициенты затрат Сij - затраты i - го
оборудования на производство j - го продукта. Построить план хij размещения
заказа (загрузки оборудования). Составим математическую модель задачи.
. Мощность
оборудования ограничена, например, временем Тi.
Производительность оборудования задана коэффициентами аij. Известны
коэффициенты затрат Сij - затраты i - го
оборудования на производство j - го продукта. Построить план хij размещения
заказа (загрузки оборудования). Составим математическую модель задачи.
F(x) = 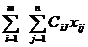 → min , xij ≥ 0, j=
→ min , xij ≥ 0, j= 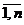 ,
, 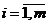 ,
,
по мощности - 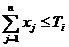 ,
, 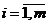 ,
,
по видам продукции, план по которой
может быть перевыполнен
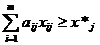 , j=
, j= 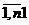 ,
,
по видам продукции, план по которой
должен соответствовать заказу
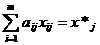 , j=
, j= 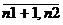 ,
,
по видам продукции, заказ на которую
принимается для более полной загрузки
оборудования
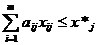 , j=
, j= 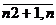 .
.
4. Графический метод решения ЗЛП.
Основные свойства ЗЛП
Графический метод решения ЗЛП
используется, если число неизвестных задачи не больше 2 или если разность между
числом неизвестных и ограничений задачи, записанных в виде уравнений не более
двух.
Схема решения.
1) Строим
область допустимых решений.
2) Строим
линию уровня.
3) Определяем
направление градиента.
4) Определяем
точку максимума (минимума):
Точка максимума - точка допустимой области,
наиболее удаленная от линии уровня в направлении градиента, точка минимума -
точка допустимой области, наиболее удаленная от линии уровня в направлении
антиградиента.
При решении ЗЛП возможны следующие случаи:
Основные свойства ЗЛП (см. рис.).
1. ЗЛП
является выпуклой задачей, поэтому решение всегда единственно.
2. Оптимальное
решение достигается по крайней мере в одной из вершин допустимой области: а)
только в одной вершине; б) в двух вершинах и имеет бесконечное множество
планов.
3. Если
допустимая область не ограничена, то ЗЛП может быть разрешима или не разрешима,
что зависит от целевой функции: в) задача на max
не разрешима, а на min
- разрешима; г) ЗЛП не разрешима.
4. Если
допустимая область состоит из единственной точки, то в ней достигается и
максимум и минимум - д).
5. Если
допустимая область пуста, то ЗЛП не разрешима - е).
6. Если
допустимая область ограничена и не пуста, то ЗЛП всегда имеет решение.
Лекция 3
Симплекс-метод решения ЗЛП
Вопросы:
1. Стандартная форма ЗЛП, правила построения.
. Канонический вид ЗЛП, начальное допустимое
базисное решение (НДБР), метод искусственного базиса.
. Симплекс-метод.
1. Стандартная форма ЗЛП, правила
построения
Графический метод решения ЗЛП можно
использовать, если число неизвестных равно 2 или разность между числом
неизвестных и числом ограничений, записанных в виде уравнений, равна 2. В общем
случае эти требования не всегда выполняются. Чтобы использовать для решения
некий универсальный метод решения, ЗЛП необходимо записать в определенной,
стандартной форме.
Стандартная форма ЗЛП представляет
собой такой вид задачи, в котором:
) все переменные неотрицательны;
) все ограничения заданы в виде
уравнений;
) целевая функция сформулирована на
минимум.
Требования эти оправданы. Во-первых, поиск
максимума линейной функции сводится к поиску минимума функции с
противоположными по знаку коэффициентами: оптимальные точки совпадают, а
значения целевых функций равны по абсолютному значению. Во-вторых, линейная
функция не имеет экстремумов и достигает своего наибольшего или наименьшего
значения на границе допустимой области, поэтому и решать необходимо не
неравенства, а уравнения. Запишем правила приведения любой ЗЛП к стандартному
виду.
Правила построения стандартной формы
ЗЛП:
1) Если F(x) = C1x1 + C2x2 + … + Cnxn 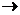 max, то можно
искать
max, то можно
искать
F(x) = - C1x1 - C2x2 - … - Cnxn 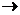 min.
min.
) Ограничения в виде неравенств (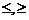 ) могут
быть сведены к уравнениям введением дополнительных, уравновешивающих
неотрицательных уравнений.
) могут
быть сведены к уравнениям введением дополнительных, уравновешивающих
неотрицательных уравнений.
Например: 2х1 + 3х2
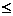 4
4 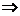 2х1
+ 3х2 + х3 = 4, х3
2х1
+ 3х2 + х3 = 4, х3 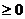 -
уравновешивающая переменная.
-
уравновешивающая переменная.
x1 + 2x2  5
5 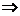 4x1 + 2x2 - x4 = 5, x4
4x1 + 2x2 - x4 = 5, x4 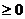
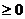 - уравновешивающая переменная.
- уравновешивающая переменная.
) Если некоторая переменная х может
быть не ограничена знаком, то в стандартном виде такую переменную можно
представить в виде разности двух неотрицательных переменных: x = x' - x'', x' 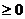 , x''
, x'' 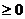 .
.
При этом дополнительные переменные
не входят в целевую функцию. Стандартная форма ЗЛП в матричном виде выглядит
так: Ax = b, x 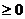 , F(x) = CTx
, F(x) = CTx 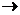 min.
min.
2. Канонический вид ЗЛП, начальное
допустимое базисное решение (НДБР), метод искусственного базиса
Чтобы ЗЛП имела решение необходимо,
чтобы система ограничений была совместна. Это возможно, если ранг m системы
(число линейно независимых уравнений) был не больше числа неизвестных n. Случай
m > n
невозможен. При m = n система имеет единственное
решение, которое определяется методами обычной алгебры. Если m < n, то
система имеет m линейно
независимых векторов - базис, через которые любой вектор системы может быть выражен
как линейная комбинация. Таких базисов может быть несколько, но не больше, чем
Сnm. Переменные
ЗЛП, соответствующие m векторам базиса, являются
базисными, остальные переменные - свободные.
Базисом называют любой набор m
переменных такой, что определитель, составленный из коэффициентов при этих
переменных, отличен от нуля. Соответствующее решение называю базисным решением.
Переменные, входящие в базис,
называют базисными (б.п.), остальные n - m переменных
называют свободными.
Чтобы получить простейшее частное
решение системы необходимо свободные переменные приравнять нулю, учитывая при
этом неотрицательность всех переменных.
Допустимым базисным решением (ДБР)
является такое, при котором все переменные неотрицательны. В противном случае
базисное решение недопустимо.
Частное допустимое базисное решение,
с которого начинают решение, называют начальным допустимым базисным решением
(НДБР).
Чтобы найти НДБР, удобно ЗЛП
записать в каноническом виде.
Канонический вид ЗЛП - это такой
стандартный вид, в котором в каждом i-ом уравнении найдется такая переменная х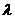 I, что
коэффициент перед ней в данном уравнении равен +1, а в других уравнениях и в
выражении целевой функции эти коэффициенты равны нулю. Если при
этом все b
I, что
коэффициент перед ней в данном уравнении равен +1, а в других уравнениях и в
выражении целевой функции эти коэффициенты равны нулю. Если при
этом все b 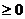 , то говорят
о допустимом каноническом виде, в противном случае - о недопустимом.
, то говорят
о допустимом каноническом виде, в противном случае - о недопустимом.
Например.
Случай. Исходная задача ЗЛП содержит
все ограничения со знаком 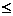 .
.
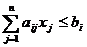 ,
, 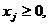
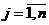 ,
, 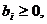
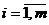 ,(x) =
,(x) = 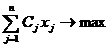 .
.
Стандартная форма ЗЛП является
одновременно и каноническим допустимым видом.
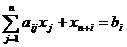 ,
, 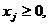
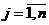 ,
, 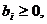
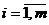 ,
,
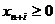 ,
, 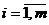 - дополнительные, уравновешивающие
переменные
- дополнительные, уравновешивающие
переменные
(x) = - 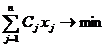 .
.
При этом хj = 0, 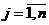 - свободные
переменные, хn+I = bi,
- свободные
переменные, хn+I = bi, 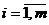 -
-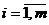 - базисные
переменные - НДБР.
- базисные
переменные - НДБР.
Случай. Ограничения исходной ЗЛП
содержат неравенства разных знаков и уравнения.
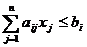 ,
, 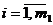 ,
, 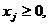
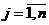 ,
,
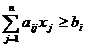 ,
, 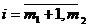
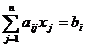 ,
, 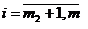 ,
, 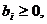
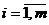 , (x) =
, (x) = 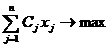 .
.
Стандартная форма ЗЛП не совпадает с
каноническим видом.
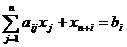 ,
, 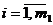 ,
,
 ,
, 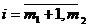 ,
,
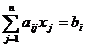 ,
, 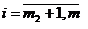 ,
,
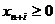 ,
, 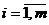 - дополнительные, уравновешивающие
переменные.(x) = -
- дополнительные, уравновешивающие
переменные.(x) = - 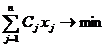 .
.
Чтобы построить канонический вид и
получить НДБР используют метод искусственного базиса. В каждое
уравнение, не содержащее переменную, создающую канонический вид, вводят
искусственную неотрицательную переменную.
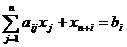 ,
, 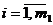 ,
,
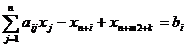 ,
, 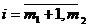 ,
, 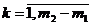 ,
,
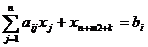 ,
, 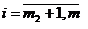 ,
, 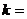
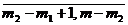 , (x) = -
, (x) = - 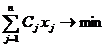 .
.
Новые искусственные переменные
создают канонический вид. Однако, вводя в ограничения-равенства искусственную переменную,
изменяют исходные условия.
Чтобы преобразованная задача
соответствовала исходной, необходимо, чтобы в окончательном решении
искусственные переменные равнялись нулю. Этого можно достичь, если
вспомогательная целевая функция, равная сумме искусственных переменных, будет
равна нулю, то естьb
G(x) = 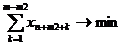 или G(x) =
или G(x) = 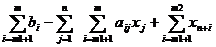
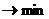 .
.
Оптимальное решение вспомогательной
задачи соответствует НДБР исходной задачи.
3. Симплекс-метод
При решении ЗЛП симплекс-методом удобно
представить задачу в табличном виде.
|
№
|
б.п.
|
х1
|
...
|
хj*
|
...
|
xn
|
b
|
|
0
|
xa1
|
a11
|
...
|
a1j*
|
...
|
a1n
|
b1
|
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
|
xai*
|
ai*1
|
...
|
ai*j*
|
...
|
ai*n
|
bi*
|
|
...
|
...
|
...
|
...
|
...
|
...
|
...
|
|
xam
|
am1
|
...
|
amj*
|
...
|
amn
|
bm
|
|
F(x)
|
C1
|
...
|
Cj*
|
...
|
Cn
|
F0
|
ПРИЗНАК ОПТИМАЛЬНОСТИ. План х* = (х1,
х2, ..., хn) считается
оптимальным, если все коэффициенты целевой функции неотрицательны, Сj ³ 0,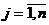 . Тогда
значение Fmax равно
значению, стоящему в правом нижнем углу таблицы.
. Тогда
значение Fmax равно
значению, стоящему в правом нижнем углу таблицы.
Если имеется хотя бы один
отрицательный коэффициент целевой функции, следует перейти к новому базисному
решению, значение целевой функции при котором будет меньше. Для этого
используют следующие правила:
1) Среди
отрицательных коэффициентов целевой функции выбирают максимальный по модулю.
Столбец, в котором стоит этот коэффициент, называют разрешающим и помечают *.
Находят отношения 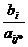 , т.е.
отношения свободных членов ограничений к элементам матрицы коэффициентов
ограничений, стоящим в разрешающем столбце и имеющим положительные значения.
Среди этих отношений выбирают минимальное. Строка, в которой стоит это
минимальное отношение, называется разрешающий и помечается *. Если среди
элементов разрешающего столбца не будет ни одного положительного, то задача
оптимизации не имеет решения.
, т.е.
отношения свободных членов ограничений к элементам матрицы коэффициентов
ограничений, стоящим в разрешающем столбце и имеющим положительные значения.
Среди этих отношений выбирают минимальное. Строка, в которой стоит это
минимальное отношение, называется разрешающий и помечается *. Если среди
элементов разрешающего столбца не будет ни одного положительного, то задача
оптимизации не имеет решения.
1) Элемент,
стоящий на пересечении разрешающих строки и столбца, называется разрешающим и
отмечается .
2) Производится
замена базисного допустимого решения на другое, при этом таблица будет иметь
следующее содержание:
а) свободная переменная хj*,
стоящая в разрешающем столбце, становится базисной, а
базисная переменная хai* , стоящая в
разрешающей строке, - свободной;
б) все элементы разрешающей строки в новой
таблице имеют значения
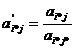
(штрихом отмечены новые значения);
в) все остальные элементы таблицы
определяются по формулам:
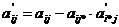 (i¹i*),
(i¹i*), 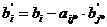 (i¹i*),
(i¹i*),
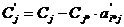 (i¹i*),
(i¹i*), 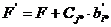 .
.
Каждая новая таблица проверяется на
оптимальность. Операции 1)-4) осуществляются до тех пор, пока не будет получено
оптимальное значение целевой функции.
Лекция 4, 5
Устойчивость решений ЗЛП при
небольших изменениях условий. Двойственный симплекс-метод
Вопросы:
. Обращенный базис, симплекс -
множители.
. Изменение значений правых частей
ограничений.
. Изменение значений коэффициентов
целевой функции.
. Включение дополнительных
переменных.
. Включение дополнительных
ограничений.
. Двойственный симплекс-метод.
. Проблемы вырождения, зацикливания.
1. Обращенный базис, симплекс -
множители
Рассмотрим решение ЗЛП
симплекс-методом с точки зрения алгебры. В матричном виде стандартная форма ЗЛП
имеет вид:  , Ах = b,
где Аmxn. Представим
матрицу А в виде «склеенных» двух матриц А = Вmxm Rmx(n-m). Здесь Вmxm - матрица,
состоящая из столбцов матрицы А, соответствующих переменным, которые в
оптимальной таблице являются базисными. Матрица Rmx(n-m) состоит из
всех оставшихся столбцов. Предположим известна матрица В-1. Умножим
слева ограничения ЗЛП на В-1:
, Ах = b,
где Аmxn. Представим
матрицу А в виде «склеенных» двух матриц А = Вmxm Rmx(n-m). Здесь Вmxm - матрица,
состоящая из столбцов матрицы А, соответствующих переменным, которые в
оптимальной таблице являются базисными. Матрица Rmx(n-m) состоит из
всех оставшихся столбцов. Предположим известна матрица В-1. Умножим
слева ограничения ЗЛП на В-1:
В-1(ВR)x = B-1b, здесь х =
(хб.п., хсв.п.) 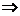 (ЕmB-1R)x = B-1b
(ЕmB-1R)x = B-1b 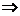 xб.п. = B-1b, хсв.п.
= 0.
xб.п. = B-1b, хсв.п.
= 0.
В НДБР базисным переменным
соответствует единичная матрица, то есть А = Сn-mEm. Так как А
умножается на В-1, то В-1А = В-1(Сn-mEm) = В-1
С В-1, что соответствует матрице коэффициентов оптимальной таблицы.
Следовательно, в оптимальной таблице в столбцах тех переменных, которые были
базисными в НДБР, находится матрица В-1.
Матрица В-1 называется
обращенный базис. В оптимальной таблице В-1 находится среди
коэффициентов ограничений, стоящих в столбцах тех переменных, которые были
базисными в исходной таблице.
Запишем теперь канонический вид
задачи.
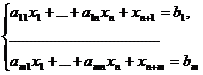 xn+I, I =
xn+I, I = 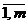 -
уравновешивающие переменные.
-
уравновешивающие переменные.
С1х1 +…+ Сnxn = F(x) 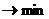
Умножим каждое ограничение на
некоторое число 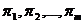 ,
соответственно и сложим с выражением целевой функции, получим
,
соответственно и сложим с выражением целевой функции, получим
х1(С1 + 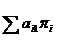 ) + … + хn(Cn +
) + … + хn(Cn + 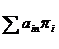 ) +
) + 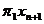 + … +
+ … +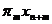 = F(x) +
= F(x) +
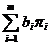 . (1)
. (1)
Значения 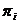 можно
подобрать таким образом, чтобы коэффициенты перед базисными переменными
равнялись нулю. Без ограничения общности, например, первые m переменных
являются базисными, тогда
можно
подобрать таким образом, чтобы коэффициенты перед базисными переменными
равнялись нулю. Без ограничения общности, например, первые m переменных
являются базисными, тогда 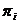 можно
определить из системы
можно
определить из системы
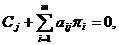
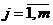 .
.
Если предположить, что 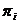 подобрали
таким образом, что перед базисными переменными коэффициенты равны нулю, а перед
свободными - неотрицательны, то вид (1) будет соответствовать оптимальному виду
таблицы. Следовательно, в оптимальной таблице коэффициенты в выражении целевой
функции перед переменными, которые были базисными в исходной таблице, есть
подобрали
таким образом, что перед базисными переменными коэффициенты равны нулю, а перед
свободными - неотрицательны, то вид (1) будет соответствовать оптимальному виду
таблицы. Следовательно, в оптимальной таблице коэффициенты в выражении целевой
функции перед переменными, которые были базисными в исходной таблице, есть 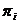 . Это и есть
симплекс - множители. При этом,
. Это и есть
симплекс - множители. При этом,
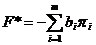 .
.
Симплекс - множители - это такие
числа 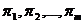 , при
умножении на которые каждого ограничения, соответственно, и сложении с
выражением целевой функции будет получен такой вид целевой функции, что перед
базисными переменными коэффициенты равны нулю, а перед свободными
неотрицательны.
, при
умножении на которые каждого ограничения, соответственно, и сложении с
выражением целевой функции будет получен такой вид целевой функции, что перед
базисными переменными коэффициенты равны нулю, а перед свободными
неотрицательны.
Замечание: если не все коэффициенты
свободных переменных в выражении целевой функции неотрицательны, то это
симплекс - множители промежуточного решения.
Обращенный базис и симплекс -
множители позволяют использовать найденное решение ЗЛП, если происходят
изменения условий задачи.
Пример.
2. Изменение значений правых частей
ограничений
Правые части ограничений выражают
ограниченные объемы ресурсов или минимальные нормы потребления и т.п.
Предположим правые части ограничений изменились на 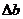 . Другими
словами, встает задача найти новый оптимальный план, при b’ = b +
. Другими
словами, встает задача найти новый оптимальный план, при b’ = b + 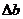 . Можно ли
использовать результаты уже решенной задачи? Если задача была решена для
прежнего значения b, то известными являются обращенный базис В-1 и
симплекс - множители
. Можно ли
использовать результаты уже решенной задачи? Если задача была решена для
прежнего значения b, то известными являются обращенный базис В-1 и
симплекс - множители 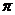 . При этом
при определении В-1 и
. При этом
при определении В-1 и 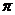 значения b никак не
учитывались, эти значения влияют лишь на оптимальное значение целевой функции.
Следовательно, новые значения целевой функции и переменных можно получить по
формулам
значения b никак не
учитывались, эти значения влияют лишь на оптимальное значение целевой функции.
Следовательно, новые значения целевой функции и переменных можно получить по
формулам
F’(x) = - 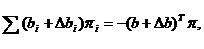
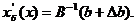
Замечание. Указанный прием можно использовать
лишь при небольших изменениях в b, то есть базисное решение должно остаться
допустимым (неотрицательным). Таким образом, если для базисных переменных
получено хотя бы одно отрицательное значение, то решение задачи можно
продолжить двойственным симплекс-методом.
Пример.
. Изменение значений коэффициентов
целевой функции
Коэффициенты целевой функции
выражают цены реализации, стоимость затрат и т.п. Если изменения произошли в
коэффициентах целевой функции, можно ли воспользоваться решением задачи с
прежними коэффициентами? То есть, если j’ = Cj +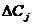 , а
изменений в b не
произошло, то и оптимальный план не изменится, а изменятся лишь оптимальные
значения целевой функции и ее коэффициентов. В исходной таблице целевая функция
имеет вид
, а
изменений в b не
произошло, то и оптимальный план не изменится, а изменятся лишь оптимальные
значения целевой функции и ее коэффициентов. В исходной таблице целевая функция
имеет вид
F(x) = -C1x1
- C2x2 - … - Cnxn 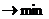
Пусть в оптимальной таблице
базисными оказались первые m переменных, следовательно,
коэффициенты перед ними в оптимальной таблице должны быть равны нулю, исключим
эти переменные из выражения целевой функции. Чтобы получить выражение целевой
функции оптимальной таблицы в общем виде, используют оптимальную таблицу.
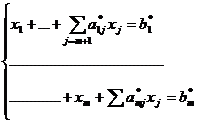
Умножим все уравнения системы
соответственно на С1, С2, … , Сn и сложим с
выражением целевой функции исходной таблицы в общем виде. Получим
х1 + … +0хm + 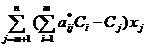 = F’(x) +
= F’(x) + 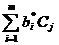
Полученное выражение представляет
оптимальное выражение целевой функции. При этом оптимальность таблицы также
определятся коэффициентами целевой функции. Заметим, что Сj не влияют
на ограничения задачи. Если изменить Сj, то
изменятся условия оптимальности:
если для Сj’ коэффициента
целевой функции окажутся неотрицательными, то найденное решение сохранится, то
есть если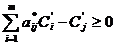 ,
, 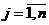 , то решение
не изменится
, то решение
не изменится
хб’ = хб,
F’(x) = - 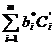 .
.
если хотя бы один коэффициент
окажется меньше нуля, то следует перейти к другому базисному решению, то есть
продолжить решение обычным симплекс-методом.
Пример.
4. Включение дополнительных переменных
Каждая переменная ЗЛП, если она не
является уравновешивающей или искусственной, определяет план производства
некоторой продукции, объем потребления и т.п. Предположим, поступило
предложение выпускать новый вид продукции или использовать новую технологию.
Стоит ли менять уже налаженное производство? Будет ли увеличение прибыли
(сокращение расходов) весомым?
Пусть объем нового вида продукции хn+1,
технологические коэффициенты известны
Р = (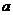 1(n+1),
1(n+1), 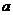 2(n+1), … ,
2(n+1), … , 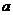 m(n+1))T,
предполагаемая прибыль от реализации единицы продукции Сn+1. Все
остальные условия остаются прежними. Чтобы учесть эти изменения, не решая
задачу с самого начала, необходимо дополнительные данные записать в оптимальную
таблицу. Новая «исходная» матрица коэффициентов A’ = A P, чтобы
привести ее к виду оптимальной таблицы, необходимо умножить ее на В-1.
Таким образом, в оптимальной таблице добавляется еще один столбец Р* = В-1Р.
При этом свободные члены не изменяются. Осталось записать коэффициент целевой
функции, это можно сделать с помощью симплекс - множителей. Умножим
коэффициенты Р на соответствующие симплекс - множители и прибавим к
коэффициенту целевой функции в стандартном виде:
m(n+1))T,
предполагаемая прибыль от реализации единицы продукции Сn+1. Все
остальные условия остаются прежними. Чтобы учесть эти изменения, не решая
задачу с самого начала, необходимо дополнительные данные записать в оптимальную
таблицу. Новая «исходная» матрица коэффициентов A’ = A P, чтобы
привести ее к виду оптимальной таблицы, необходимо умножить ее на В-1.
Таким образом, в оптимальной таблице добавляется еще один столбец Р* = В-1Р.
При этом свободные члены не изменяются. Осталось записать коэффициент целевой
функции, это можно сделать с помощью симплекс - множителей. Умножим
коэффициенты Р на соответствующие симплекс - множители и прибавим к
коэффициенту целевой функции в стандартном виде:
Cn+1 +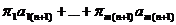 = Cn+1*.
= Cn+1*.
Если Cn+1*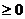 , то хn+1 останется
свободной ( то есть равной нулю), так как сохранится признак оптимальности.
Следовательно, план менять не стоит.
, то хn+1 останется
свободной ( то есть равной нулю), так как сохранится признак оптимальности.
Следовательно, план менять не стоит.
Если Cn+1* < 0, то
следует улучшить решение, а именно хn+1 ввести в
базисные переменные. Следовательно, план изменится. При этом решение
продолжается обычным симплекс-методом.
Пример.
5. Включение дополнительных
ограничений
Экономическая ситуация, в которой
приходится решать производственные и плановые задачи, изменяется. Может
оказаться так, что некоторый ресурс, считавшийся ранее неограниченным, окажется
лимитирован. Например, введение веерного распределения электроэнергии т.п. Другими
словами, необходимо проверить. Удовлетворяет ли рассчитанный план новым
ограничениям, и как его изменить, если ограничения нарушаются.
Итак, пусть 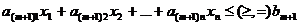 - новое
дополнительное ограничение к уже решенной задаче. То есть х* уже найдено.
- новое
дополнительное ограничение к уже решенной задаче. То есть х* уже найдено.
Если найденное х* = (х1,
х2, … , хn)
удовлетворяет поставленному дополнительному ограничению, то план никак не
изменится (ограничение не ограничивает данное производство).
Если х* = (х1, х2,
… , хn) не удовлетворяет
новому ограничению, то необходимо изменить план, то есть продолжить решение.
Чтобы продолжить решение. Необходимо
учесть новое ограничение, записав его в каноническом виде, соответствующем
оптимальной таблице: дополнительное ограничение должно содержать одну
переменную с коэффициентом 1, и чтобы в других уравнениях и выражении целевой
функции она отсутствовала, кроме того, это уравнение не должно содержать
базисных переменных оптимальной таблицы. Чтобы исключить базисные переменные
оптимальной таблицы, используют оптимальный канонический вид. При этом решение
продолжается двойственным симплекс-методом.
Пример.
6. Двойственный симплекс-метод
Для решения задачи двойственным
симплекс-методом она должна иметь недопустимый канонический вид. И признак оптимальности
должен выполняться.
Общая идея: начиная с
недопустимого базисного решения при выполнении признака оптимальности,
последовательно перейти к допустимому базисному решению, сохранив признак
оптимальности.
Правила.
. Недопустимый канонический
вид ограничений и оптимальный вид (Сj 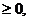
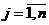 ) целевой
функции записывают в исходную таблицу.
) целевой
функции записывают в исходную таблицу.
. Среди отрицательных
свободных членов выбирают 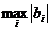 ,
соответствующую строку помечают * и называют разрешающей.
,
соответствующую строку помечают * и называют разрешающей.
. Среди всех отношений
коэффициентов целевой функции к отрицательным элементам разрешающей строки
выбирают 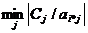 ,
соответствующий столбец помечают, выполняют обычные симплекс-преобразования и
называют разрешающим.
,
соответствующий столбец помечают, выполняют обычные симплекс-преобразования и
называют разрешающим.
Замечание: 1. Обычный симплекс-метод при
сохранении допустимости решения переходит последовательно к оптимальному
решению. А двойственный симплекс-метод при сохранении оптимальности переходит
последовательно от недопустимого решения к допустимому.
. Правила двойственного симплекс-метода
отличаются от правил обычного выбором разрешающих столбца и строки.
. Если в разрешающей строке (для двойственного
метода) нет ни одного отрицательного элемента, то задача не разрешима.
7. Проблемы вырождения, зацикливания
Как правило, все базисные переменные
отличны от нуля (то есть в симплекс-таблице все свободные члены 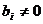 ). Однако,
нет никаких ограничений к тому, чтобы одна или несколько базисных переменных
обратились в ноль.
). Однако,
нет никаких ограничений к тому, чтобы одна или несколько базисных переменных
обратились в ноль.
Базисное решение (базис) является
невырожденным, если оно содержит ровно m отличных от
нуля компонент. В противном случае - вырожденным.
Если начальный план задачи
невырожден, то никаких сложностей при решении не возникает, при правильном
выборе разрешающего элемента. Если хотя бы одна базисная переменная в НДБР
приняла нулевое значение, то по правилам симплекс-метода именно она должна
будет войти в базис на следующем шаге, так как min bi/aij* = 0. При
этом значение целевой функции не изменится.
Лекция 6.
Двойственность в линейном
программировании
Вопросы:
1. Понятия двойственности, теневой цены,
двойственной оценки.
2. Правила построения двойственной задачи.
. Основные теоремы двойственности и их экономическое
содержание.
1. Понятия двойственности, теневой
цены, двойственной задачи
Двойственность является одним из фундаментальных
понятий в линейном программировании, приводящим к важному результату
теоретического и практического характера. Рассмотрим понятие двойственности на
примере задачи оптимального использования ресурсов.
На производство n видов продукции
предприятие затрачивает m видов ресурсов, имеющихся в ограниченных количествах
b = (b1, b2, …, bm). На
производство единицы j-го вида продукции требуется aij единиц i-го
вида ресурса. Прибыль от реализации единицы продукции Сj, j = 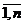 . Необходимо
определить такой план производства х = (х1, х2,…, хn), при
котором прибыль предприятия была бы максимальной. Математическая модель задачи
выглядит следующим образом.
. Необходимо
определить такой план производства х = (х1, х2,…, хn), при
котором прибыль предприятия была бы максимальной. Математическая модель задачи
выглядит следующим образом.
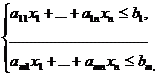 С1х1 + … + Сnxn =F(x)
С1х1 + … + Сnxn =F(x) 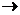 m ax , xj
m ax , xj 0, j =
0, j = 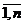 .
.
В общем случае задача решается
симплекс-методом. Что ограничивает производство? Зададимся вопросом, какова с
точки зрения предприятия ценность имеющихся в его распоряжении ресурсов? При
решении этого вопроса будем иметь в виду, что ресурсы, которые предприятие не
может полностью использовать, имеют для него очень низкую ценность, в том
смысле, что предприятие не согласно нести даже небольшие расходы на увеличение
запасов этих ресурсов. Дорогое оборудование, не участвующее в технологическом
процессе, составляет для предприятия нулевую ценность.
Наибольшую ценность, очевидно, будут
иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции,
а, следовательно, и прибыль предприятия и на увеличение запасов которых
предприятие согласно затратить значительные средства.
Можно считать, что каждый вид
ресурса обладает некоторой «теневой» ценой, определяющей ценность данного
ресурса для предприятия с точки зрения прибыли от реализации выпускаемой
продукции и зависящей от наличного количества этого ресурса и потребности в
нем.
Кроме того, если сейчас используется
один технологический процесс, требующий больших затрат некоторого ресурса,
запасы которого ограничены, значит «теневая» цена велика, то завтра этот
процесс может быть изменен таким образом, что позволит более экономно
использовать все запасы ресурсов, следовательно изменятся «теневые» цены. Но
как бы ни усовершенствовался технологический процесс совсем без ресурсов не
обойтись. Таким образом, можно предположить, что существуют оптимальные
теневые цены, соответствующие оптимальному распределению ресурсов.
В экономической литературе «теневые»
цены часто называют объективно-обусловленными или оптимальными оценками,
двойственными или учетными, неявными оценками.
Чтобы определить оптимальные
«теневые» цены ресурсов необходимо составить и решить задачу оптимизации. Имеем
те же исходные данные, что и для задачи оптимального использования ресурсов.
Только теперь необходимо найти такие «теневые» цены ресурсов y = (y1, y2,… ,ym), при
которых стоимость всех ресурсов была бы минимальна, yi - «теневая»
цена единицы i-го ресурса,
yi  0.
0.
«Теневые» цены y = (y1, y2,… ,ym) должны
быть такими, чтобы «теневая» цена всех ресурсов, затраченных на производство
единицы продукции каждого вида, была бы не меньше получаемого от ее реализации
дохода. Другими
словами, стоимость затраченных ресурсов не может быть меньше стоимости
окончательного продукта (так как существуют неизбежные издержки):
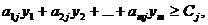
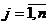 .
.
Оптимальными «теневыми» ценами
естественно считать такие, которые минимизируют общую стоимость ресурсов.
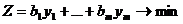 .
.
Запишем обе задачи в матричном виде:
Прямая задача Двойственная задача
Ах 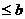 АТy
АТy  C
C
F = CTx 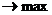 Z =
Z = 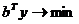
x  0 y
0 y  0
0
Эти задачи называют парой
двойственных задач. Пара двойственных задач может быть экономически
интерпретирована следующим образом.
Прямая задача: Сколько и какой
продукции xj необходимо
производить, чтобы при заданных стоимостях Cj и размерах
ресурсов bi максимизировать выпуск продукции в
стоимостном выражении?
Двойственная задача: Какова должна
быть цена каждого ресурса yi, чтобы при
заданных количествах bi и
стоимостях Cj минимизировать затраты?
2. Правила построения двойственной
задачи
Исходя из общего вида прямой и двойственной
задач можно установить связь между этими задачами, позволяющую для любой ЗЛП
строить двойственную ей задачу.
Свойства двойственных задач
(правила).
1. Число неизвестных двойственной задачи равно
числу ограничений прямой задачи. Число ограничений двойственной задачи равно
числу неизвестных прямой задачи.
2. Матрица коэффициентов двойственной
задачи является транспонированной матрицей коэффициентов прямой задачи.
. Коэффициенты целевой функции
двойственной задачи являются свободными членами ограничений прямой задачи.
. Свободные члены ограничений
двойственной задачи являются коэффициентами целевой функции прямой задачи.
5. Если ограничения прямой
задачи записаны со знаком меньше или равно (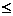 ), то ограничения двойственной
задачи записываются со знаком больше или равно (
), то ограничения двойственной
задачи записываются со знаком больше или равно ( ).
).
. Если ограничение прямой
задачи задано в виде уравнения, то соответствующее неизвестное двойственной
задачи не ограничено знаком.
. Если какое-либо
неизвестное прямой задачи не ограничено знаком, то соответствующее ограничение
двойственной задачи будет задано в виде равенства.
. Если целевая функция
прямой задачи сформулирована на максимум, то целевая функция двойственной
задачи будет сформулирована на минимум.
Существует много различных комбинаций
ограничений и целевой функции для записи исходной задачи. Для упрощения задачи
построения двойственной задачи запишем прямую задачу в некотором стандартном
виде прямой задачи. Этот вид предполагает, что:
1) все ограничения имеют знак 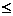 ;
;
2) целевая функция
сформулирована на максимум;
) все неизвестные
неотрицательны.
Чтобы записать прямую задачу в стандартном виде,
необходимо:
1) неравенство со знаком  умножить на
(-1);
умножить на
(-1);
) равенство заменить на два
неравенства противоположных знаков, одно из которых следует умножить на (-1);
) формулировку целевой
функции меняют заменой знаков коэффициентов на противоположные;
) если переменное xj не
ограничено знаком, его можно представить в виде разности двух неотрицательных
переменных.
Пример.
Составить двойственную задачу к исходной.
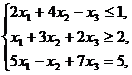
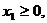

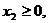
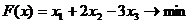 .
.
Решение. 1)
Стандартный вид прямой задачи.
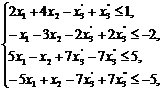
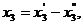
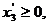
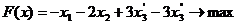
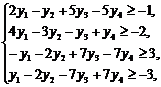
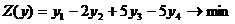
Задачу можно записать в виде,
соответствующем исходной прямой задаче, если заменить: а) 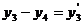 - не
ограничена знаком,
- не
ограничена знаком,
б) два последних ограничения
соответствуют равенству.
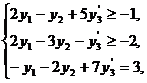
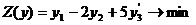 .
.
3. Основные теоремы двойственности и
их экономическое содержание
Теорема 1. Двойственная задача к
двойственной есть прямая задача.
Доказательство:
Пусть имеем пару двойственных задач в матричном виде.
Ах 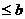 АТy
АТy  C
C
F = CTx 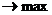 Z =
Z = 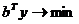
x  0 y
0 y  0
0
Построим к двойственной задаче
двойственную:
) запишем в стандартном виде -АТy 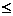 -C
-C
Z = -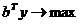
2) -Ах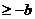 Ах
Ах 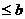
F = - CTx 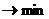 F = CTx
F = CTx 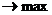
Что и требовалось доказать.
Теорема 2. Значение функции F,
соответствующее любому допустимому решению прямой задачи, не больше значения
функции Z, соответствующего любому допустимому решению двойственной задачи.
Доказательство:
Пусть X и Y соответственно произвольные допустимые решения прямой и
двойственной задач. Следовательно,
1) Ах 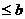 и Y
и Y 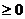
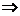 YТ
YТ 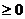 , YTAX
, YTAX 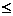 YTb = bTY = Z.
YTb = bTY = Z.
) ATY  C и X
C и X  0
0 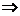 XТ
XТ 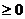 , XTATY
, XTATY  XTC = CTX = F.
XTC = CTX = F.
) выражение XTATY - скалярная
величина (число) 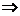 она равна
своей
она равна
своей
транспозиции, т.е. XTATY = YTAX. Итак,
имеем,
F 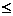 XTATY = YTAX
XTATY = YTAX 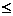 Z
Z 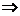 F
F 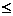 Z. Что и
требовалось доказать.
Z. Что и
требовалось доказать.
Следствия: 1) если в
прямой задаче допустимая область не пуста, а целевая функция не ограничена
сверху, то у двойственной задачи допустимая область пуста;
) если в двойственной задаче
допустимая область не пуста, а целевая функция не ограничена снизу, то у прямой
задачи допустимая область пуста.
Теорема 3. Если прямая задача имеет
конечное оптимальное решение F = Fmax, то
двойственная задача имеет конечное оптимальное решение Z = Zmin. При этом Fmax = Zmin, а
симплекс-множители оптимального решения прямой задачи являются значениями
переменных в оптимальном решении двойственной задачи.
Доказательство: Запишем прямую
задачу
Ах 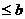 , x
, x  0 , b
0 , b 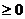 , F = CTx
, F = CTx 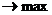 .
.
Запишем задачу в стандартном виде Ах
+ хР = b, где хР = (х1,…,хn+m)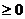 -
дополнительные, уравновешивающие переменные,
-
дополнительные, уравновешивающие переменные, 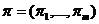 Т-
симплекс-множители оптимального решения. Известно, что прямая задача разрешима,
следовательно, можно определить значения симплекс-множителей оптимального
решения. Получим оптимальное выражение целевой функции, то есть
Т-
симплекс-множители оптимального решения. Известно, что прямая задача разрешима,
следовательно, можно определить значения симплекс-множителей оптимального
решения. Получим оптимальное выражение целевой функции, то есть
+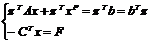
(-СT+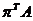 )x+
)x+ = F + bT
= F + bT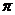 . (*)
. (*)
Так как это оптимальный вид целевой
функции, то все коэффициенты
неотрицательны.
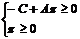 или
или 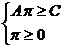 .
.
Т.о., если y = 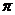 , то
ограничения двойственной задачи выполняются.
, то
ограничения двойственной задачи выполняются.
Так как (*) - оптимальный вид
целевой функции, то коэффициенты перед базисными переменными равны нулю, а
свободные переменные сами равны нулю 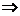 Fmin = -bT
Fmin = -bT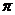 или Fmax = bT
или Fmax = bT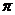 . Если y =
. Если y = 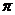 , то это и
есть целевая функция двойственной задачи, то есть Z = Fmax = Zmin. Что и
требовалось доказать.
, то это и
есть целевая функция двойственной задачи, то есть Z = Fmax = Zmin. Что и
требовалось доказать.
Теорема 4. Если двойственная задача
имеет конечное оптимальное решение Z = Zmin,
то прямая задача имеет конечное оптимальное решение F
= Fmax.
При этом Zmin
= Fmax
, а значения симплекс-множителей оптимального решения двойственной задачи
являются значениями переменных в оптимальном решении прямой задачи с
противоположными знаками (если обе задачи решаются прямым симплекс-методом).
Доказательство:
В матричной форме двойственная задача имеет вид.
АТy  C , y
C , y  0, С
0, С  0, Z =
0, Z = 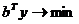
1) Запишем в стандартном виде ATy - yS = C, где yS= (ym+1,…,ym+n)T  0 -
дополнительные, уравновешивающие переменные,
0 -
дополнительные, уравновешивающие переменные, 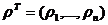 - симплекс-множители оптимального
решения двойственной задачи. Для двойственной задачи
- симплекс-множители оптимального
решения двойственной задачи. Для двойственной задачи 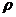
 имеют то же значение, то есть
имеют то же значение, то есть
+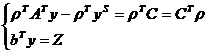
(bT + 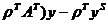 = Z +
= Z + 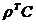 . (**)
. (**)
Так как это оптимальный вид целевой
функции Z, то все коэффициенты неотрицательны.
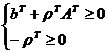 или
или 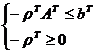
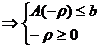 .
.
Таким образом, если 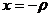 , то
ограничения прямой задачи удовлетворяются, значит это решение.
, то
ограничения прямой задачи удовлетворяются, значит это решение.
) Так как (**) - оптимальное решение
для целевой функции, то коэффициенты перед базисными переменными равны нулю, а
свободные переменные сами равны нулю. Следовательно, min = -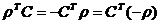 , а это есть
целевая функция прямой задачи, если
, а это есть
целевая функция прямой задачи, если 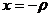 . Что и требовалось доказать.
. Что и требовалось доказать.
Экономическое содержание теорем
состоит в следующем: если задача оптимизации плана, максимизирующего выпуск
продукции, разрешима, то разрешима и задача определения оценок ресурсов. План
производства и оценки ресурсов являются оптимальными тогда и только тогда,
когда цена произведенной продукции и суммарная оценка ресурсов совпадают.
Оценки выступают как инструмент балансирования затрат и результатов. Так как F 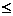 Z,
Z, 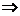 Z - F =
Z - F = 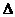
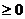 - издержки производства, которые
равны нулю
- издержки производства, которые
равны нулю 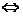 когда F*
= Z*.
когда F*
= Z*.
Двойственные оценки обладают тем
свойством, что они гарантируют рентабельность оптимального плана, то есть
равенство общей оценки продукции и ресурсов, и обуславливают убыточность
всякого другого плана, отличного от оптимального.
Кроме того, если yi > 0, то
при оптимальной производственной программе этот ресурс используется полностью;
если yi = 0, то
ресурс используется не полностью.
Лекция 7, 8
Элементы теории игр и принятия
решений
Вопросы:
1. Основные понятия.
. Теоремы теории игр.
. Способы решения задач теории игр.
. Методы принятия решений: в условиях
определенности; в условиях риска; в условиях неопределенности.
1. Основные понятия теории игр
Теория игр принадлежит к наиболее молодым
математическим дисциплинам, её возникновение относится к концу II-й Мировой
войны.
Теория игр представляет собой математическую
дисциплину, предметом исследования которой являются методы принятия решений в
конфликтных ситуациях.
Ситуация называется конфликтной,
если в ней сталкиваются интересы нескольких лиц, преследующих противоположные
цели.
Каждая из конфликтующих сторон может проводить
ряд мероприятий для достижения своих целей, причём успех одной из сторон
означает неудачу другой. При наличии свободной конкуренции в роли борющихся
сторон торговые фирмы, промышленные предприятия и т. п. Однако, конфликтные
ситуации встречаются и во многих других областях. К конфликтным ситуациям
относятся почти все ситуации, возникающие при планиро-вании военных операций,
выборе системы оружия, охране объектов от нападения, преследовании и перехвате
цели. Чтобы сделать возможным математический анализ конфликтной ситуации, ее
необходимо упростить, учтя только основные факторы.
Упрощенная, формализованная модель
конфликтной ситуации, называется игрой, а конфликтующие 7стороны - игроками.
Игра представляет собой совокупность правил,
описывающих поведение игроков.
Допустимые действия любого из
игроков в игре называются правилами игры.
Каждый случай разыгрывания игры некоторым
конкретным образом от начала и до конца представляет собой партию игры.
Элементами игры являются ходы. Правила игры предусматривают, какова
должна быть последовательность ходов, и указывают характер каждого хода. Ходы
бывают личными и случайными.
Личный ход представляет собой выбор
игроком одного из данного множества вариантов.
Например, в шахматах каждый ход - личный, причем
1-й - выбор из 20 вариантов. Решение, принятое игроком при личном ходе,
называется выбором.
Случайный ход представляет собой
выбор одного из вариантов, но не игроком, а некоторым механизмом случайного
выбора.
Например, сдача карт, бросание монеты и т.п.
Выбор при случайном ходе называется исходом хода.
Исходом игры является выигрыш или
проигрыш. Величина этого выигрыша или проигрыша называется ценой игры.
Для личного хода правила игры перечисляют все
возможные варианты выбора и определяют какой игрок его делает. Для случайного
хода - указывают варианты и вероятности их выбора.
Однозначное описание выбора игрока в
каждой из возможных ситуаций, при которой он должен сделать личный ход,
называется стратегией игрока.
Стратегии могут быть чистыми и смешанными.
Стратегия, выбираемая в результате личного хода, является чистой. Стратегия,
основанная на случайном выборе, называется смешанной.
Стратегия игрока называется
оптимальной, если при многократном повторении игры она обеспечивает игроку
максимально возможный средний выигрыш ( или минимально возможный средний
проигрыш).
В зависимости от числа возможных стратегий игры
делятся на конечные и бесконечные. В игре могут сталки-ваться интересы двух или
более противников. В 1-м случае игра называется парной, во 2-м - множественной.
Ограничимся рассмотрением только парных игр.
Парная игра называется игрой с
нулевой суммой, если проигрыш одного игрока равен выигрышу другого.
Рассмотрим парную игру с нулевой
суммой. 1-й игрок имеет m возможных стратегий, а 2-й - n возможных стратегий.
Не зная выбора друг друга, 1-й игрок выбирает i-ю стратегию, а 2-й игрок -j-ю
стратегию. В результате игры 1-й игрок выигрывает величину 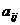 , а 2-й -
проигрывает эту же величину. Из чисел составляют матрицу, которая называется
платежной или матрицей игры,
, а 2-й -
проигрывает эту же величину. Из чисел составляют матрицу, которая называется
платежной или матрицей игры,
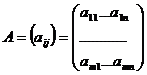 .
.
Строки матрицы соответствуют
стратегиям 1-го игрока, а столбцы - стратегиям 2-го. Это чистые стратегии.
Игра, определяемая матрицей А,
имеющей m строк и n столбцов, называется конечной игрой размерности mхn.
Чтобы описание игры было
законченным, необходимо указать цели, которыми руководствуются игроки при
выборе своих стратегий. Эти цели просты: 1-й игрок стремится обеспечить себе
наибольший выигрыш, а 2-й - наименьший проигрыш. Специфической трудностью
является то, что ни один из игроков не контролирует полностью значение 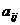 , т.к. 1-й
игрок распоряжается только выбором i, а 2-й - j. Преодоление этой трудности,
т.е. определение наиболее рационального способа ведения игры каждым игроком, и
представляет собой существо теории игр.
, т.к. 1-й
игрок распоряжается только выбором i, а 2-й - j. Преодоление этой трудности,
т.е. определение наиболее рационального способа ведения игры каждым игроком, и
представляет собой существо теории игр.
Для того, чтобы понять принципы,
которые лежат в основе выбора каждым игроком своей стратегии, рассмотрим игру
со следующей матрицей А
1 y2
y3 А(х)
х1 7 2 5 2
А = х2 2 2 3 2
х3 3 5 4 3
В(y) 7 5 5
При выборе 1-м игроком, например, 1-й стратегии,
х1, его выигрыш может быть равен 7, 2 или 5. Может ли 1-й игрок
рассчитывать на максимальный выигрыш ? Да, если 2-й игрок выберет 1-ю свою
стратегию, y1. Однако он может выбрать и 2-ю стратегию, y2,
и выигрыш будет равен 2. Но уже меньше 2 выигрыш не может быть ни при какой
стратегии 2-го игрока. Поэтому число 2, являющееся минимальным элементом
стратегии х1, есть гарантированный выигрыш 1-го игрока при
стратегии х1. Аналогично можно определить гарантированные выигрыши
для любой стратегии 1-го игрока - А(х). Предполагается, что игроки избегают
необоснованного риска и выбирают ту стратегию, которая дает максимальный из
всех гарантированных выигрышей.
Число 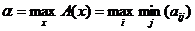 называется
нижней ценой игры или максимином.
называется
нижней ценой игры или максимином.
А соответствующая стратегия - максиминной.
Также можно рассуждать и в отношении 2-го
игрока. Только в А указаны его проигрыши, которые он стремится минимизировать.
Например, стратегия y1 может принести 2-му игроку проигрыш 7, 2 или
3. Но уже больше 7 он не проиграет. Следовательно, число 7, являющееся
максимальным элементом стратегии y1, есть гарантированный
проигрыш2-го игрока при y1. Определим все гарантированные
проигрыши - В(y). Каким же проигрышем может ограничиться 2-й игрок ?
Число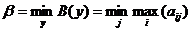 называется
верхней ценой игры или минимаксом.
называется
верхней ценой игры или минимаксом.
А соответствующая стратегия -
минимаксной.
. Теоремы теории игр
Теорема 1. (основная
теорема теории игр).
Всякая конечная игра имеет цену и у
каждого игрока существует по меньшей мере одна оптимальная стратегия.
Терема 2. Нижняя цена
игры всегда не превосходит верхней цены игры,  .
.
Рассмотрим два случая.
. Пусть 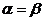 .
.
Игра, для которой, 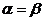 ,
называется игрой с седловой точкой. Если
,
называется игрой с седловой точкой. Если 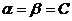 , то С является ценой игры, а
стратегии игроков, обеспечивающие им выигрыш или проигрыш, равный С, являются
оптимальными. Если игра с седловой точкой имеет С=0, то она является
справедливой, если С
, то С является ценой игры, а
стратегии игроков, обеспечивающие им выигрыш или проигрыш, равный С, являются
оптимальными. Если игра с седловой точкой имеет С=0, то она является
справедливой, если С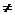 0, -
несправедливой.
0, -
несправедливой.
. Пусть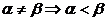 . В этом
случае трудно определить цену игры и оптимальные стратегии игроков. Вернемся к
рассмотренному примеру.
. В этом
случае трудно определить цену игры и оптимальные стратегии игроков. Вернемся к
рассмотренному примеру. 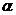 = 3, а
= 3, а 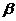 = 5. Значит,
первый игрок может гарантировать себе выигрыш, равный 3, а второй - ограничить
свой проигрыш 5. Область между
= 5. Значит,
первый игрок может гарантировать себе выигрыш, равный 3, а второй - ограничить
свой проигрыш 5. Область между 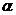 и
и 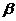 является как бы ничейной, и каждый
игрок может попытаться улучшить свой результат за счет этой области. Каковы в
этом случае оптимальные стратегии игроков? Если каждый игрок будет применять
стратегию, соответствующую его максимальному гарантированному выигрышу или
проигрышу, противник может догадаться о его намерениях и улучшить свой
результат. Например, первый игрок использует х3, а второй - y2.
Второй игрок заметил, что первый все время применяет x3, и решил
применить y1, сведя свой проигрыш к меньшему числу. Таким образом,
чтобы иметь успех, каждый игрок должен хранить свой выбор в секрете. Это трудно
сделать, если игра повторяется многократно.
является как бы ничейной, и каждый
игрок может попытаться улучшить свой результат за счет этой области. Каковы в
этом случае оптимальные стратегии игроков? Если каждый игрок будет применять
стратегию, соответствующую его максимальному гарантированному выигрышу или
проигрышу, противник может догадаться о его намерениях и улучшить свой
результат. Например, первый игрок использует х3, а второй - y2.
Второй игрок заметил, что первый все время применяет x3, и решил
применить y1, сведя свой проигрыш к меньшему числу. Таким образом,
чтобы иметь успех, каждый игрок должен хранить свой выбор в секрете. Это трудно
сделать, если игра повторяется многократно.
Секретность можно сохранить, если
каждый раз выбирать стратегию случайным образом (бросая монету, кость и т.п.).
При этом выигрыш и проигрыш будут случайными величинами. Результат можно
оценить средней величиной проигрыша или выигрыша. Так, в нашем случае, если
второй игрок использует свои стратегии y1, y2, y3
случайным образом, например, с вероятностями 1/3; 1/3; 1/3, соответственно, то
среднее значение его проигрыша может быть:
если первый использует х1:
Сср = 1/3 а11
+ 1/3 а12 + 1/3 а13 = 7/3 + 2/3 + 5/3 = 14/3;
если первый использует х2:
Сср = 1/3 а21 +
1/3 а22 + 1/3 а23 = 2/3 + 2/3 + 3/3 = 7/3;
если первый использует х3:
Сср = 1/3 а31 +
1/3 а32 + 1/3 а33 = 3/3 + 5/3 + 4/3 = 4. Таким образом,
второй игрок может ограничить свой проигрыш уже не 5, а 14/3, независимо от
стратегии первого игрока. Следовательно, в ряде случаев оказывается
целесообразным не намечать заранее стратегии, а выбирать ту или иную случайным
образом. Стратегия, основанная на случайном выборе, называется смешанной
стратегией.
Вектор, каждая компонента которого
показывает относительную частоту (вероятность) использования игроком
соответствующих чистых стратегий, называется смешанной стратегией.
Пусть u=(u1,...,um)
и z=(z1,...,zn), соответственно, вероятности отдельных
исходов механизма случайного выбора 1-го и 2-го игроков.
Из теории вероятностей должно быть
известно, что
1) ui  0, i=
0, i=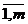 ; zj . 0, j=
; zj . 0, j=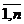 ; (т.к. 0
; (т.к. 0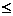 р
р 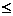 1);
1);
) 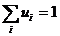 и
и  (т.к. р(U)
= 1, U- достоверное событие). Если u* - оптимальная стратегия
1-го игрока, z* - оптимальная стратегия 2-го игрока, то число
(т.к. р(U)
= 1, U- достоверное событие). Если u* - оптимальная стратегия
1-го игрока, z* - оптимальная стратегия 2-го игрока, то число 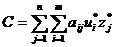 является
ценой игры.
является
ценой игры.
Определение оптимальных стратегий и
цены игры составляет процесс решения игры.
Теорема 3 (о цене
игры).
Всякая матричная игра с нулевой
суммой имеет решение в смешанных стратегиях. Для того, чтобы число С было ценой
игры, а u* и z* - оптимальными стратегиями игроков,
необходимо и достаточно выполнения неравенств:
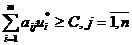 и
и 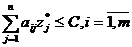 .
.
Теорема дает ответ на вопрос о
существовании решения игры и определяет путь решения.
В частном случае, когда по крайней
мере у одного из игроков имеется только 2 стратегии, справедлива теорема.
Теорема 4. Если один
из игроков применяет оптимальную смешанную стратегию, то его выигрыш или
проигрыш равен цене игры вне зависимости от того, с какими частотами
(вероятностями) будет применять другой игрок свои стратегии, вошедшие в
оптимальную.
3. Способы решения задач теории игр.
4. Методы принятия решений: в
условиях определенности; в условиях риска; в условиях неопределенности.
До сих пор рассматривались игры, в
которых участвовали два, как бы равноправные, противника, преследовавшие
противоположные цели. Каждый стремился так выбрать свою стратегию, чтобы
получить для себя наибольшую выгоду и свести до минимума выгоду противника.
Однако, во многих практических
ситуациях приходится сталкиваться со случаями, когда один из противников
оказывается нейтральным, т.е. таким, который не стремится извлечь для себя
максимальную выгоду, а, следовательно, не стремится обратить в свою пользу
ошибки, совершаемые противником. К таким играм относят игры, в которых в
качестве одного из игроков выступает "природа".
Здесь в понятие "природа"
входит вся совокупность внешних обстоятельств, в которых приходится принимать
решение. Любая хозяйственная деятельность человека может быть представлена как
игра с "природой".
Человек в играх с
"природой" старается действовать осмотрительно, используя, например,
минимаксную стратегию, позволяющую получить наименьший проигрыш.
"Природа" действует совершенно случайно, возможные стратегии
определяются как ее состояния (например, условия погоды, спрос на определенную
продукцию, объем перевозок, некоторое сочетание производственных факторов и
т.п.).
Неизбежной платой за попытку
получить решение в условиях неполной информации о законе "природы",
является возможность принятия ошибочных решений. Качество решений зависит от
информированности, его квалификации. При этом, на практике бывают ситуации, в
которых отказаться от решения вообще невозможно. К тому же отказ от решения
есть тоже решение, которое может иметь столь же нежелательные последствия. Выход
- выработка человеком такой стратегии в отношении принятия решения, которая
хотя и не исключает возможность принятия неправильных решений, но сводит их к
минимуму. Для того, чтобы решить свою задачу - принять наилучшее решение в
каждой конкретной ситуации, человек имеет возможность изучать
"природу" - проводить эксперимент. Этому мешают два обстоятельства:
время и затраты.
Игры, в которых один противник
"природа", а другой - человек или, в которых один из игроков
действует несознательно, а в соответствии с определенными законами, называются
играми с "природой" или статистическими играми.
Теория таких игр - теория
статистических решений. Человек, который участвует в игре против природы,
называется статистиком (экономистом).
В теории принятия решений используют « разумные»
процедуры выбора наилучшей из нескольких возможных альтернатив. Насколько
правильным будет выбор, зависит от качества данных, используемых при описании
ситуации, в которой принимается решение. С этой точки зрения процесс принятия
решений может принадлежать к одному из трез возможных условий:
. Принятие решений в условиях определенности,
когда данные известны точно.
. Принятие решений в условиях риска, когда
данные можно описать с помощью вероятностных распределений.
. Принятие решений в условиях неопределенности,
когда данным нельзя приписать относительные веса, которые представляли бы
степень их значительности в процессе принятия решений.
Рассмотрим все эти условия.
Принятие решений в условиях
определенности. Метод анализа иерархий.
Модели ЛП являются примером принятия решений в
условиях определенности. Эти модели применимы лишь в тех случаях, когда
альтернативные решения можно связать между собой точными линейными функциями.
Рассмотрим другой подход к принятию решений, когда идеи, чувства, эмоции
определяются некоторыми количественными показателями, обеспечивающими шкалу
предпочтений. Этот подход называют методом анализа иерархий.
Рассмотрим пример. Выпускник-отличник средней
школы на основании свидетельства о ЕГЭ поступил сразу в три университета: А, В,
С. Чтобы выбрать университет он сформулировал 2 критерия: местоположение
университета и его академическая репутация. Будучи отличным учеником, он
оценивает академическую репутацию в 5 раз выше, чем его местоположение.
Используя метод анализа иерархий, можно дать выпускнику рекомендации.
Сложность метода анализа иерархий
заключается в определении относительных весовых коэффициентов для оценки
альтернативных решений. Создается матрица парных сравнений Аnxn , где n - число
критериев на заданном уровне иерархии. Матрица А отражает суждение лица,
принимающего решение, относительно важности разных критериев. Парное сравнение
выполняется таким образом, что критерий в строке i (i=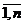 ) оценивается
относительно каждого из критериев, представленных n столбцами:
А = (
) оценивается
относительно каждого из критериев, представленных n столбцами:
А = (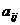 ). Для
описания оценок используют числа от 1 до 9. При этом
). Для
описания оценок используют числа от 1 до 9. При этом 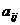 = 1, когда i - й и j - й
критерии одинаково важны,
= 1, когда i - й и j - й
критерии одинаково важны, 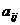 = 5, когда i - й
критерий значительно важнее, чем j - й.
= 5, когда i - й
критерий значительно важнее, чем j - й.
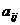 = 9, когда i - й
критерий чрезвычайно важнее, чем j - й. Другие значения критерия
интерпретируются аналогично.
= 9, когда i - й
критерий чрезвычайно важнее, чем j - й. Другие значения критерия
интерпретируются аналогично.
Согласованность таких обозначений
обеспечивается условием: если 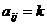 , то
, то 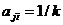 . Кроме того,
. Кроме того, 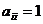 . В нашем
примере можно построить 3 матрицы сравнений. На главном иерархическом уровне
существуют 2 критерия, следовательно:
. В нашем
примере можно построить 3 матрицы сравнений. На главном иерархическом уровне
существуют 2 критерия, следовательно:
м р
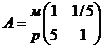 , так как академическая репутация
значительно важнее, то
, так как академическая репутация
значительно важнее, то 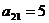 , а
, а 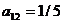 .
.
В пределах каждого критерия строятся
матрицы сравнений для альтернативных решений, например
А В С
А В С
Ам = 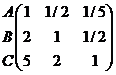 и Ар
=
и Ар
= 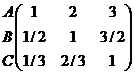 .
.
Относительные веса критериев можно
определить делением элементов каждого столбца на сумму элементов этого столбца.
В результате получают нормализованные матрицы сравнений.
Средние значения элементов строк
м р
N = 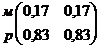
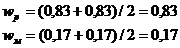
А В С
Nм = 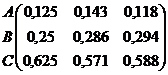
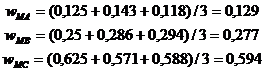
А В С
Nр = 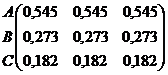
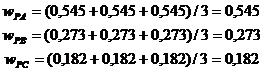
Одинаковые столбцы нормализованных
матриц N и Np означают,
что результирующие относительные веса сохраняют одно и то же значение независимо
от того, как выполняется сравнение. В этом случае говорят, что исходные матрицы
сравнения являются согласованными. Как видно из примера, не все матрицы
сравнений являются согласованными. Принимая во внимание, что такие матрицы
строятся на основе человеческих суждений, можно ожидать некоторую степень
несогласованности, и к ней следует относиться терпимо при условии, что она не
выходит за определенные «допустимые» рамки. Чтобы выяснить, является ли уровень
несогласованности допустимым, необходимо определить соответствующую
количественную меру - коэффициент согласованности CR:
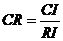 , где
, где 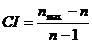 -
коэффициент согласованности матрицы;
-
коэффициент согласованности матрицы;
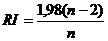 - стохастический коэффициент
согласованности
- стохастический коэффициент
согласованности
матрицы (определяется эмпирическим
путем).
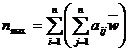 или
или 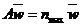 , где
, где 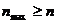 .
.
Для матрицы Nм будем иметь
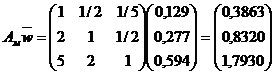 ,
, 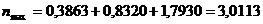 ,
,
 ,
, 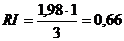 ,
, 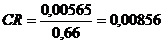 .
.
Если 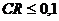 , то уровень несогласованности
матрицы сравнений является приемлемым. Если
, то уровень несогласованности
матрицы сравнений является приемлемым. Если 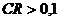 , то уровень несогласованности
матрицы сравнений высокий и, лицу, принимающему решение, рекомендуется проверить
элементы парного сравнения. В примере уровень несогласованности матрицы
является приемлемым.
, то уровень несогласованности
матрицы сравнений высокий и, лицу, принимающему решение, рекомендуется проверить
элементы парного сравнения. В примере уровень несогласованности матрицы
является приемлемым.
Задача имеет единственный
иерархический уровень с двумя критериями (местоположение и репутация) и три
альтернативных решения (А, В, С). Структура задачи принятия решения имеет вид.
На основе этих вычислений
университет А получает наивысший комбинированный вес и, следовательно, является
наиболее оптимальным выбором выпускника.
Принятие решений в условиях риска.
Если решение принимается в условиях
риска, то стоимости альтернативных решений обычно описываются вероятностными
распределениями. По этой причине принимаемое решение основывается на
использовании критерия ожидаемого значения, в соответствии с которым
альтернативные решения сравниваются с точки зрения максимизации ожидаемой
прибыли или минимизации ожидаемых затрат. Такой подход имеет свои недостатки,
которые не позволяют использовать его в некоторых ситуациях. Для них
разработаны модификации упомянутого критерия.
Критерий ожидаемого значения сводится
либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых
затрат. В данном случае предполагается, что прибыль (затраты), связанные с
каждым альтернативным решением, является случайной величиной. В приведенном
ниже примере рассматривается простая ситуация, связанная с принятием решения
при наличии конечного числа альтернатив и точных значений матрицы доходов.
Предположим, что вы хотите вложить
на фондовой бирже 10000 долл. В акции одной из двух компаний: А или В. Акции
компании А являются рискованными, но могут принести 50 % прибыли от суммы
инвестиции на протяжении следующего года. Если условия фондовой биржи будут
неблагоприятны, сумма инвестиции может обесцениться на 20 %. Компания В
обеспечивает безопасность инвестиций с 15 % прибыли в условиях повышения
котировок на бирже и только 5 % - в условиях понижения котировок. Все
аналитические публикации, с которыми можно познакомиться (а они всегда есть в
изобилии в конце года), с вероятностью 60 % прогнозируют повышение котировок и
с вероятностью 40 % - понижение котировок. В какую компанию следует вложить
деньги?
Условия игры задаются в виде матрицы
А = (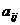 ), в которой
строки соответствуют стратегиям человека, а столбцы - возможным состояниям
"природы". В некоторых задачах для состояний "природы"
может быть задано распределение вероятностей, в других - оно неизвестно.
Элемент
), в которой
строки соответствуют стратегиям человека, а столбцы - возможным состояниям
"природы". В некоторых задачах для состояний "природы"
может быть задано распределение вероятностей, в других - оно неизвестно.
Элемент 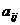 равен
выигрышу человека, если он использует i-ю стратегию при j-том состоянии
"природы". При решении игры часто рассматривают матрицу рисков R = (
равен
выигрышу человека, если он использует i-ю стратегию при j-том состоянии
"природы". При решении игры часто рассматривают матрицу рисков R = (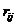 ). Элемент
). Элемент 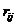 равен
разности между выигрышем, который получил бы человек, если бы знал состояние
природы, и выигрышем, который он получит в тех же условиях, применяя i-ю
стратегию, то есть
равен
разности между выигрышем, который получил бы человек, если бы знал состояние
природы, и выигрышем, который он получит в тех же условиях, применяя i-ю
стратегию, то есть
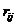 =
= 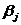 -
-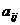 ,
, 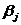 =
= 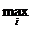
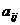 .
.
Оптимальную стратегию можно
получить, используя критерий ожидаемого значения.
Пусть распределение вероятностей
различных состояний "природы" известно p = (p1, ..pn),
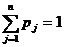 . Следовательно, выбирая i-ю
стратегию, человек может рассчитывать на средний выигрыш
. Следовательно, выбирая i-ю
стратегию, человек может рассчитывать на средний выигрыш
Мi =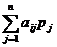 (Математическое ожидание).
(Математическое ожидание).
Критерием принятия решения служит
критерий Байеса: наилучшей является стратегия, имеющая максимум математического
ожидания выигрыша (минимум математического ожидания риска).
Для сформулированной выше задачи
будем иметь:
А =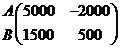
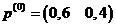
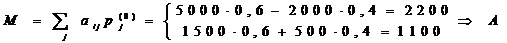
Существуют и другие модификации критерия
ожидаемого значения. Например, определение апостериорных вероятностей на основе
эксперимента над исследуемой системой или определение полезности реальной
стоимости.
Принятие решения в условиях
неопределенности.
Отличие между принятием решения в условиях риска
и неопределенности состоит в том. Что в условиях неопределенности вероятностное
распределение, соответствующее состояниям природы, неизвестно, либо не может
быть определено. Этот недостаток информации обусловил развитие следующих
критериев для анализа ситуации: критерий Лапласа, максиминный (минимаксный)
критерий Вальда, критерий минимального риска Сэвиджа, критерий Гурвица и
другие.
Если распределение вероятностей различных
состояний "природы" неизвестно, то его можно оценить, например, по
принципу "недостаточного основания Лапласа", согласно которому, все
состояния "природы" равновероятны, р1 = р2
= ...= рn = 1/n.
Если не оценивать распределение вероятностей
состояний "природы", то можно использовать следующие критерии:
1. Максиминный критерий Вальда:
наилучшей является стратегия, имеющая нижнюю цену игры для двух лиц с нулевой
суммой, при этом гарантируется выигрыш не меньше, чем 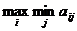 .
.
. Критерий минимального риска
Сэвиджа: наилучшей является стратегия, имеющая наименьшее значение риска в
самой неблагоприятной ситуации, при этом обеспечивается 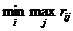 .
.
. Критерий Гурвица: наилучшей
является стратегия, при которой 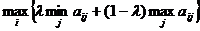 , где
, где 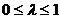 .
.
Критерии 1 и 2 основаны на самой
пессимистической оценке обстановки. Критерий 3 при 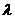 = 0
является критерием крайнего оптимизма, при
= 0
является критерием крайнего оптимизма, при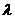 = 1 - критерием крайнего пессимизма.
Значение
= 1 - критерием крайнего пессимизма.
Значение 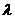 выбирается
субъективно: чем больше желание подстраховаться, тем ближе к 1 должно быть
выбирается
субъективно: чем больше желание подстраховаться, тем ближе к 1 должно быть 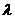 .
.
Лекция 9
Транспортная задача
Вопросы:
1. Постановка транспортной задачи. Закрытая
модель. Теорема о существовании решения.
2. Метод потенциалов: а) построение
опорного плана; б) схема решения.
. Метод дифференциальных рент.
. Дополнительные ограничения
транспортной задачи.
1. Постановка транспортной задачи.
Закрытая модель. Теорема о существовании решения
Транспортная задача является одним из наиболее
важных частных случаев общей задачи линейного программирования, в силу
специфики ее построения и области применения. Транспортная модель изначально
предназначена для выбора наиболее экономного планирования грузопотоков и работы
различных видов транспорта. Однако сфера применения транспортной модели этим не
ограничивается. Примерами использования транспортной модели могут служить
задачи календарного планирования производства, рационального использования
природных и людских ресурсов и др.
Пусть в пунктах А1,А2,...,Аm
производится некоторый продукт, причем объем производства в п. Аi составляет
ai единиц, 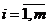 .
Произведенный про-дукт должен быть доставлен в пункты потребления В1,В2,...,Вn, причем
объем потребления в п. Вj составляет
bj единиц,
.
Произведенный про-дукт должен быть доставлен в пункты потребления В1,В2,...,Вn, причем
объем потребления в п. Вj составляет
bj единиц, 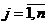 .
Предполагается, что тран-спортировка готовой продукции возможна из любого
пункта производства в лю-бой пункт потребления, транспортные издержки на
перевозку единицы продукции из п. Аi в п. Вj составляют
cij денежных
единиц. Задача состоит в организа-ции такого плана перевозок, при котором
суммарные транспортные издержки были бы минимальными.
.
Предполагается, что тран-спортировка готовой продукции возможна из любого
пункта производства в лю-бой пункт потребления, транспортные издержки на
перевозку единицы продукции из п. Аi в п. Вj составляют
cij денежных
единиц. Задача состоит в организа-ции такого плана перевозок, при котором
суммарные транспортные издержки были бы минимальными.
Математически транспортная задача
может быть записана следующим образом. Пусть xij - количество
продукта, перевозимого из п. Аi в п. Вj . Требуется
определить совокупность (m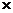 n)величин xij ,
удовлетворяющих условиям:
n)величин xij ,
удовлетворяющих условиям:
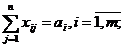 (1)
(1)
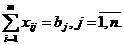
и обращающих в минимум линейную
форму
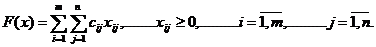 (2)
(2)
Специфическими для транспортной
задачи являются следующие два обстоятельства: а) каждое из переменных xij входит в
два уравнения системы (1); б) все коэффициенты при переменных xij принимают
лишь два значения 0 или 1.
ОПРЕДЕЛЕНИЕ 1. Если общая
потребность в продукте в пунктах потребления равна общему запасу продукта в
пунктах производства, т.е.
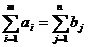 , (3)
, (3)
то модель транспортной задачи
называется закрытой. Если это условие не выполняется, то модель называется открытой.
ТЕОРЕМА: Для
разрешимости транспортной задачи необходимо и достаточно, чтобы запасы продукта
в пунктах производства были равны потребностям в пунктах потребления, т.е.
чтобы выполнялось равенство (3).
Замечания: 1.Если запас превышает
потребность, т.е. 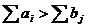 , вводится
фиктивный (n+1)-й пункт потребления с потребностью
, вводится
фиктивный (n+1)-й пункт потребления с потребностью
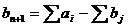 , а соответствующие транспортные
издержки равны нулю, сi(n+1) = 0, i =
, а соответствующие транспортные
издержки равны нулю, сi(n+1) = 0, i = 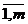 .
.
2.Если потребности превышают запасы,
т.е. 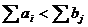 вводится
фиктивный (m+1)-й пункт производства с запасом
вводится
фиктивный (m+1)-й пункт производства с запасом
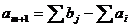 ,
,
а соответствующие тарифы равны нулю,
c(m+1)j = 0,j = 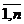 .
.
ОПРЕДЕЛЕНИЕ 2. Всякое
неотрицательное решение системы линейных уравнений (1) называется планом
транспортной задачи.
ОПРЕДЕЛЕНИЕ 3. План X*
=  ,
, 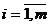 ;
; 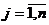 , при
котором функция (2) принимает минимальное значение, называется оптимальным
планом транспортной задачи.
, при
котором функция (2) принимает минимальное значение, называется оптимальным
планом транспортной задачи.
Часто план транспортной задачи, с
которого начинают решение, называют опорным.
Число переменных xij в
транспортной задаче с m пунктами производства и n пунктами потребления равно m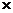 n, а число
уравнений в системе (1) равно m+n. Т.к. предполагается, что выполняется условие
(3), то число линейно независимых уравнений равно n+m-1. Следовательно, опорный
план может иметь не более n+m-1 отличных от нуля неизвестных.
n, а число
уравнений в системе (1) равно m+n. Т.к. предполагается, что выполняется условие
(3), то число линейно независимых уравнений равно n+m-1. Следовательно, опорный
план может иметь не более n+m-1 отличных от нуля неизвестных.
Если в опорном плане число отличных
от нуля компонент равно в точности n+m-1 , то план является невырожденным, а
если - меньше - то вырожденным.
Для определения оптимального плана
транспортной задачи разработаны алгоритмы, существенно более простые, чем
симплекс-метод, который является одним из основных методов решения задач
линейного программирования. Наиболее известными из этих алгоритмов являются
метод потенциалов и метод дифференциальных рент (или венгерский).
2. Метод потенциалов
Общий принцип определения оптимального плана
транспортной задачи методом потенциалов аналогичен принципу решения задачи
линейного программирования симплекс-методом: сначала находят опорный план
(начальное допустимое базисное решение), а затем его последовательно улучшают
до получения оптимального. Рассмотрим три метода построения опорного плана. При
заполнении клеток таблицы необходимо помнить, что суммы величин по столбцам и
строкам должны соответствовать потребностям и запасам.
Методы построения опорного плана
а) Метод северо-западного угла.
Метод позволяет за n+m-1 шаг заполнить клетки
таблицы таким образом, чтобы удовлетворить все потребности, исчерпав при этом
все запасы. Заполнение клеток таблицы начинается с левой верхней клетки
("северо-западной"), в которую ставят максимально возможное число,
т.е. минимальное из чисел запасов и потребностей для этой клетки. При этом
исчерпываются либо запасы, либо потребности (вычеркивается строка или столбец),
выбирается следующая «северо-западная» клетка и т.д.
б) Метод минимального элемента.
Заполнение клеток осуществляется по принципу:
"Самая дешевая перевозка осуществляется первой". Выбирается клетка с
минимальным тарифом и заполняется максимально возможным числом, при этом
исчерпываются либо запасы, либо потребности (вычеркивается строка или столбец),
выбирается следующая клетка с минимальным тарифом и т.д.
в) Метод аппроксимации Фогеля.
Для заполнения каждой клетки необходимо найти
разности между двумя минимальными тарифами по всем столбцам и строкам, записать
их, соответственно, внизу и справа таблицы. Среди найденных разностей выбирают
максимальную. В строке (или столбце), которой соответствует данная разность,
заполняют клетку с минимальным тарифом. Если максимальных разностей несколько
одинаковых, выбирают ту, которой соответствует минимальный тариф. Если
минимальный тариф одинаков для нескольких клеток в строке (столбце), то
заполняют ту, которая стоит в столбце (строке), имеющем наибольшую разность
между двумя минимальными тарифами.
Как правило, при построении опорного
плана этими тремя методами выполняется следующее соотношение: Fв(x)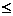 Fб(x)
Fб(x)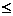 Fа(x).
Fа(x).
Схема решения.
1. Строят опорный план одним из
методов.
. Построенный опорный план следует
проверить на оптимальность, для чего используют следующую теорему.
ТЕОРЕМА. Если для
некоторого опорного плана транспортной задачи существуют такие числа 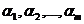 и
и 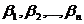 , что
, что
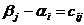 при xij > 0 (4)
при xij > 0 (4)
и 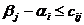 при xij = 0 (5)
при xij = 0 (5)
для всех 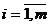 и
и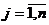 , то этот
план является оптимальным.
, то этот
план является оптимальным.
ОПРЕДЕЛЕНИЕ 4. Числа 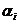 и
и 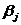 (
(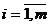 ,
,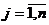 ) называются
потенциалами, соответственно, поставщиков и потребителей.
) называются
потенциалами, соответственно, поставщиков и потребителей.
Т.о., найдя потенциалы поставщиков и
потребителей, удовлетворяющие условиям теоремы, мы докажем оптимальность
построенного плана. Как их найти? Т.к. число заполненных клеток, xij > 0, равно
n+m-1 (невырожденный план), то система (4) с n+m неизвестными содержит n+m-1
уравнение. Положим одно из неизвестных равным нулю и последовательно найдем
значения остальных неизвестных. Затем для всех свободных клеток, xij = 0,
определим числа 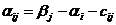 .
.
Если среди чисел 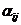 нет
положительных, то условия теоремы выполнены, и план является оптимальным. Если
существует
нет
положительных, то условия теоремы выполнены, и план является оптимальным. Если
существует 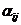 > 0, то
построенный план не оптимален, и его следует улучшить.
> 0, то
построенный план не оптимален, и его следует улучшить.
. Алгоритм улучшения плана:
1) среди всех 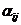 > 0
выбирают максимальное;
> 0
выбирают максимальное;
2) для соответствующей клетки строят
цикл пересчета;
3) помечают вершины цикла пересчета
последовательно знаками "+" и "-" , начиная с "+"
в исходной клетке;
4) среди чисел, стоящих в клетках,
помеченных "-" , определяют минимальное;
5) к значениям, стоящим в
"+"-клетках, прибавляют это минимальное число, а из значений, стоящих
в "-"-клетках, это число вычитают.
ОПРЕДЕЛЕНИЕ 5. Циклом
пересчета называется ломаная линия, вершины которой расположены в занятых
клетках, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла может
быть только два звена.
. Измененный таким образом план
опять проверяют на оптимальность, т.е. переход к п. 2.
3. Метод дифференциальных рент
В отличие от метода потенциалов, для
которого сначала строился опорный план, а затем он последовательно улучшался,
при решении задачи методом дифференциальных рент сразу наилучшим образом
распределяют часть продукции между потребителями и на последующих итерациях
постепенно уменьшают общую величину нераспределенных поставок.
Для определения решения транспортной
задачи методом дифференциальных рент используют следующий алгоритм:
. В каждом столбце определяют
минимальный тариф и выделяют сответствую-щую клетку.
2. Выделенные клетки заполняют
максимально возможными числами.
3. Т.к. в общем случае это распределение
не удовлетворяет всех потребите-лей, чтобы на последующих шагах сокращать
величину неудовлетворенных потребностей, необходимо оценить поставщиков.
ОПРЕДЕЛЕНИЕ 6. Строки,
соответствующие поставщикам, запасы которых исчерпаны, а потребности выделенных
потребителей не удовлетворены, являются отрицательными.
ОПРЕДЕЛЕНИЕ 7. Строки,
соответствующие поставщикам, запасы которых не исчерпаны полностью, являются
положительными.
ОПРЕДЕЛЕНИЕ 8. Строки,
соответствующие поставщикам, запасы которых исчерпаны, а потребности выделенных
потребителей удовлетворены, имеют нулевую оценку. При этом, если вторая
заполненная клетка, стоящая в столбце, связанном с данной строкой еще одной
заполненной клеткой, расположена в положительной строке, данная строка с
нулевой оценкой считается положительной. В противном случае - отрицательной.
4. Для каждого столбца, имеющего
выделенный тариф в отрицательной строке, находят разности между выделенным
тарифом и ближайшим к нему по величине тарифом, стоящим в положительной строке.
5. Среди полученных разностей
определяют минимальную. Это число называют промежуточной рентой.
6. Строят новую таблицу, при этом
тарифы, стоящие в положительных строках, переписываются без изменения, а
тарифы, стоящие в отрицательных строках, увеличиваются на величину
промежуточной ренты.
7. Переходят к п.1.
ЗАМЕЧАНИЕ: а) если в
строке или столбце оказывается более одной выделенной клетки, то заполняют, в
первую очередь, те выделенные клетки, которые являются единственными в столбце
или строке;
б) если удается распределить все
запасы, то получают оптимальный план транспортной задачи.
4. Дополнительные ограничения
транспортной задачи
1. Запрещенные маршруты.
Если по каким-либо причинам
невозможно поставлять продукцию из п. Аi в п. Вj ,
предполагают тариф этого пути сколь угодно большой величиной М, сij = М, и
решают задачу обычным способом.
2. Обязательные поставки.
а) Если необходимо из п. Аi перевезти в
п. Вj
определенное количество продукции dij,
соответствующую клетку заполняют сразу числом dij, а в
дальнейшем решают задачу, считая заполненную клетку свободной, но с тарифом, сij = М, равным
очень большому числу, а запасы 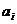 и потребности
и потребности 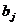 уменьшают
на величину dij.
уменьшают
на величину dij.
б) Если необходимо из п. Аi в п. Вj перевезти
не меньше определенного количества продукции dij, то считают
запасы 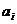 и
потребности
и
потребности 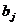 меньше на
величину dij, это количество dij считают
перевезенным по маршруту Аi
меньше на
величину dij, это количество dij считают
перевезенным по маршруту Аi  Вj, и решают
задачу далее обычным способом.
Вj, и решают
задачу далее обычным способом.
в) Если необходимо перевезти из п. Аi в п. Вj не более
определенного количества продукции dij, вводят
дополнительный пункт назначения с потребностью, равной (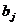 - dij), потребность
в п. Вj делают
равной dij. Тарифы на
перевозки в дополнительный пункт назначения равны тарифам п. Вj , кроме
i-той строки, тариф в которой будет равен сколь угодно большому числу М. Решают
задачу обычным образом, а при записи ответа объединяют основного и
дополнительного потребителя (складывают содержимое столбцов).
- dij), потребность
в п. Вj делают
равной dij. Тарифы на
перевозки в дополнительный пункт назначения равны тарифам п. Вj , кроме
i-той строки, тариф в которой будет равен сколь угодно большому числу М. Решают
задачу обычным образом, а при записи ответа объединяют основного и
дополнительного потребителя (складывают содержимое столбцов).
Лекция 14, 15
Метод динамического программирования
Вопросы:
1. Основные понятия. Общая постановка задачи ДП.
. Принцип оптимальности. Функциональные
уравнения Беллмана.
. Задача оптимального распределения ресурсов.
. Задача о замене.
. Задача управления производством и запасами.
1. Основные
понятия. Общая постановка задачи динамического программирования
Динамическое программирование -
метод оптимизации, приспособленный к операциям, в которых процесс принятия
решений может быть разбит на отдельные этапы, шаги.
Такие операции называются многошаговыми. Многие
экономические процессы расчленяются на шаги естественным образом. Это процессы
планирования и управления, развиваемые во времени. Естественным шагом может
быть год, квартал, месяц и т.д. Т.о., если управление сводится к
однократному принятию решения, то соответствующая задача называется одноэтапной
или одношаговой. Ранее решаемые задачи линейного и нелинейного
программирования - примеры подобных задач. Если управление требует некоторой
последовательности принятых решений, то такая задача называется многоэтапной
или многошаговой.
Рассмотрим некоторую управляемую систему,
характеризующуюся определенным набором параметров, задающих ее состояния.
Система под влиянием управления переходит из начального состояния в конечное.
Введем обозначения.
1. xi
- многомерный вектор, компоненты которого определяют состояние системы на i-том
шаге. Дальнейшее изменение состояния зависит только от
данного состояния и не зависит от того, каким путем система перешла в него
(процесс без последствия).
2. На каждом
шаге выбирается одно решение, управление ui
,
под действием которого система переходит из предыдущего состояния xi-1
в новое xi.
Это
новое состояние является функцией состояния на начало шага xi-1
и принятого в начале решения ui
, т.е.
xi
= xi ( xi-1
, ui ).
. Действие на
каждом шаге связано с определенным выигрышем (доходом, прибылью) или потерей
(издержками), которые зависят от состояния на начало шага и принятого решения.
Fi
- приращение целевой функции задачи в результате i-того
шага, аналогично, Fi
= Fi
( xi-1
, ui
).
Тогда значение целевой функции при переходе системы из начального состояния в
конечное за n шагов
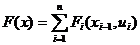 .
.
. На векторы состояния хi и
управления ui могут быть
наложены ограничения, объединение которых составляет область допустимых решений
u 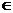 U.
U.
5. Требуется найти такое
допустимое управление u* = (u1* ,…, un* ) (для
каждого шага), чтобы получить экстремальное значение функции цели F* за все n шагов.
Любая последовательность действий
для каждого шага, переводящая систему из начального состояния в конечное,
называется стратегией управления.
Допустимая стратегия управления,
доставляющая функции цели экстремальное значение, называется оптимальной.
2. Принцип оптимальности.
Функциональные уравнения Беллмана
Метод динамического программирования
состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На
каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом
шаге управление выбирается с учетом последствий, т.к. управление,
оптимизирующее целевую функцию только для данного шага, может привести к
неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть
оптимальным с точки зрения процесса в целом. В основе метода динамического
программирования лежит принцип оптимальности, сформулированный Беллманом.
Принцип оптимальности: если
некоторая последовательность решений оптимальна, то на любом шаге последующие
решения образуют оптимальную стратегию по отношению к результату предыдущих
решений.
Другими словами, каково бы не было
состояние системы перед очередным шагом, надо выбрать управление на этом шаге
так, чтобы выигрыш на данном шаге (проигрыш) плюс оптимальный выигрыш
(проигрыш) на всех последующих шагах был бы максимальным (минимальным). На
основе принципа оптимальности Беллмана строится схема решения монгошаговой
задачи, состоящая из 2-х частей:
1) Обратный ход: от
последнего шага к первому получают множество возможных оптимальных
(«условно-оптимальных») управлений.
2) Прямой ход: от
известного начального состояния к последнему из полученного множества
«условно-оптимальных» управлений составляется искомое оптимальное управление
для всего процесса в целом.
Оптимальную стратегию управления
можно получить, если сначала найти оптимальную стратегию управления на n-м шаге,
затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до
первого шага.
Чтобы можно было использовать
принцип оптимальности практически, необходимо записать его математически.
Обозначим через z1(xn-1), z2(xn-2),…, zn(x0)
условно-оптимальные значения приращений целевой функции на последнем шаге, двух
последних,…, на всей последовательности шагов, соответственно.
Тогда для последнего шага:
z1(xn-1) = 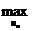 (min) {Fn(xn-1, un)},
(min) {Fn(xn-1, un)},
где un - множество
допустимых (возможных) управлений на n-ом шаге, xn-1 - возможные
состояния системы перед n-ым шагом.
Для двух последних шагов:
z2(xn-2) = 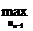 (min) {Fn-1(xn-2, un-1) + z1(xn-1)}.
(min) {Fn-1(xn-2, un-1) + z1(xn-1)}.
Для k последних
шагов:
zk(xn-k) = 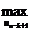 (min) {Fn-k+1(xn-k, un-k+1) + zk-1(xn-k+1)}.
(min) {Fn-k+1(xn-k, un-k+1) + zk-1(xn-k+1)}.
Для всех n шагов:
zn(x0)
= 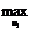 (min) {F1(x0,
u1) + zn-1(x1)}.
(min) {F1(x0,
u1) + zn-1(x1)}.
Полученные рекуррентные соотношения
называют функциональными уравнениями Беллмана.
При этом согласно определению zn(x0) = F*.
3. Задача оптимального распределения
ресурсов
а) Постановка задачи.
Задачи на оптимальное распределение
ресурса, который можно использовать различным образом, возникают при разработке
оперативных и перспективных планов особенно часто. К ним относятся задачи о
распределении средств на приобретение оборудования, закупку сырья и найм
специалистов; задачи о распределении товара по торговым предприятиям и складам;
задачи по определению последовательности пропорций между продукцией с/х
производства, предназначенной для реализации и воспроизводства и т.д.
Рассмотрим задачу оптимального
распределения заданного объема капиталовложений в несколько предприятий.
Пусть на реконструкцию и
модернизацию 4-х своих филиалов фирма имеет возможность выделить 200 млн. руб.
Ожидаемый прирост прибыли зависит как от финансируемого филиала, так и от
объема этого финансирования. Однако, прирост прибыли в отдельно взятом филиале
не зависит от вложенных средств в другие филиалы, а общая прибыль фирмы равна
сумме всех приростов по филиалам. Следует определить оптимальное распределение
капиталовложений между филиалами, максимизирующее общий прирост прибыли фирмы.
В данном случае речь идет об
однократном распределении средств, и поэтому задача сама по себе не является
динамической. Однако, ее можно наиболее просто решить как «многошаговую»,
если объекты капиталовложений (филиалы) включать в рассмотрение
последовательно, т.е. на каждом шаге к рассмотренным добавлять следующий.
При таком подходе можно использовать
функциональные уравнения Беллмана. Для их решения в табулированном виде общий
объем капиталовложений разбивается на N интервалов
с шагом  (для нашей
задачи положим N = 4, тогда
(для нашей
задачи положим N = 4, тогда 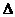 = 200/4=50
млн. руб.). Т.е. значения функций, входящих в уравнения Беллмана, будут
определяться только в точках, кратных
= 200/4=50
млн. руб.). Т.е. значения функций, входящих в уравнения Беллмана, будут
определяться только в точках, кратных 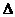 (в нашем примере в точках 0, 50,
100, 150, 200).
(в нашем примере в точках 0, 50,
100, 150, 200).
Пусть ожидаемый прирост прибыли
филиалов при соответствующих капиталовложениях задан таблицей.
|
Кап.
Вложения
|
Прирост
прибыли по филиалам
|
|
1
|
2
|
3
|
4
|
|
50
|
25
|
30
|
36
|
28
|
|
100
|
60
|
70
|
64
|
56
|
|
150
|
100
|
90
|
95
|
110
|
|
200
|
140
|
122
|
130
|
142
|
С =200 - общий объем распределяемых средств;
х - объем средств, выделяемых филиалам (на
каждом шаге), 0≤ х ≤C.
Fi(xi)
- ожидаемый прирост i-той фирмы
при выделении ей хi
средств. Тогда целевая функция
F = F1(x1) + F2(x2)
+ F3(x3) + F4(x4) → max
при ограничении x1 + x2 + x3 + x4 = C, xi ≥ 0, i =  .
.
б) Схема решения.
1. Введем последовательность
функций:
z2(x) - max прибыль
фирмы, если x средств
распределить между 1-м и 2-м филиалами;
z3(x) - max прибыль
фирмы, если х средств распределить между 3-м и двумя первыми филиалами;
z4(x) - max прибыль
фирмы, при распределении x средств между всеми 4-мя филиалами.
Очевидно, что z4(C) = max F = F*, a zi(0) = 0.
. «Обратный ход».
Рассмотрим финансирование только
1-го филиала, тогда по определению
z1(x) = F1(x). (1)
Пусть теперь средства в объеме x
распределяются между 1-м и 2-м филиалами: 2-му в объеме x2, тогда х -
х2 = х1 выделяется 1-му. Общая прибыль двух филиалов
z2(x) = 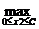 (F2(x2) + z1(x - x2)). (2)
(F2(x2) + z1(x - x2)). (2)
Теперь включим в рассмотрение
дополнительно 3-й филиал: из общей суммы х выделим 3-му филиалу х3,
тогда остальная часть х - х3 оптимальным образом распределяется
между двумя первыми
z3(x) = 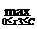 (F3(x3) + z2(x - x3)). (3)
(F3(x3) + z2(x - x3)). (3)
Наконец, по аналогии находим
z4(x) = 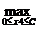 (F4(x4) + z3(x - x4)). (4)
(F4(x4) + z3(x - x4)). (4)
. «Прямой ход».
Функциональные уравнения Беллмана
(1) - (4) позволяют рассчитать значения zi и Fi для всех
возможных х. Среди них находим z4(C) = F* и
оптимальное x4* такое, что
F4(x4*) = F4*, после
чего результаты вычислений просматриваются в обратном порядке. Зная x4*, находим
С-х4* - объем финансирования остальных трех филиалов, а
следовательно, и F3* и х3*,
и т.д. до нахождения х1* и F1* = F1(x1*).
в) Расчет.
….
4. Задача о замене
а) Постановка задачи.
Оборудование со временем
изнашивается и стареет морально, падает его производительность, растут издержки
на ремонт. Поэтому на каком-то этапе его эксплуатация становится менее
выгодной, чем замена на новое. Возникает задача определения оптимальной
стратегии замены оборудования в рассматриваемый временной промежуток - плановый
период (п/п) с тем, чтобы суммарная прибыль за этот период была оптимальной.
Введем обозначения.
r(t) -
стоимость продукции, производимой за год на оборудовании возраста t;
s(t) -
остаточная стоимость оборудования возраста t;
u(t) - эксплуатационные
издержки за год оборудования возраста t;
p - цена
нового оборудования, которым можно заменить устаревшее:
n - число лет
в рассматриваемом п/п.
Для дискретности решения задачи
возраст оборудования t будем отсчитывать с интервалом 1
год. Управление составляют два возможных решения на каждом этапе (в начале
каждого года): «сохранение» - продолжение эксплуатации имеющегося оборудования;
«замена» - реализация старого оборудования по остаточной стоимости и
приобретение нового по цене p. Целевая функция - суммарная
прибыль за п/п F→max.
Ограничения определяются критерием замены оборудования: прибыль при дальнейшей
эксплуатации старого меньше прибыли после его замены с учетом всех издержек.
Если прибыль от нового оборудования равна прибыли при старом, то старое
сохраняется еще на год, т.к. оно уже досконально изучено.
б) Схема решения.
Задача решается методом ДП на основе
принципа оптимальности Беллмана. В процессе «обратного хода» рассматриваются
этапы - временные шаги от конца п/п к его началу.
Введем последовательность функций: zi(t), i = 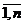 -
максимальная прибыль за последние i лет п/п.
Очевидно, что zn(t0) = max F = F*, где t0 - возраст
оборудования в начале п/п. Итак, сначала рассматриваем только последний n-ый год п/п,
i = 1. Пусть
в начале этого года, когда оборудование имеет возраст t лет,
выбирается одно из управлений: 1) сохранение оборудования на n-ый год,
тогда прибыль за оставшийся год п/п составит r(t) - u(t); 2) замена
новым, продажа старого по остаточной стоимости, тогда прибыль составит s(t) - p + r(0) - u(0), где r(0) -
стоимость продукции, на новом оборудовании за 1-й год его эксплуатации, u(0) -
эксплуатационные издержки нового оборудования за 1-й год. Определяем оптимальное
управление, исходя из критерия замены:
-
максимальная прибыль за последние i лет п/п.
Очевидно, что zn(t0) = max F = F*, где t0 - возраст
оборудования в начале п/п. Итак, сначала рассматриваем только последний n-ый год п/п,
i = 1. Пусть
в начале этого года, когда оборудование имеет возраст t лет,
выбирается одно из управлений: 1) сохранение оборудования на n-ый год,
тогда прибыль за оставшийся год п/п составит r(t) - u(t); 2) замена
новым, продажа старого по остаточной стоимости, тогда прибыль составит s(t) - p + r(0) - u(0), где r(0) -
стоимость продукции, на новом оборудовании за 1-й год его эксплуатации, u(0) -
эксплуатационные издержки нового оборудования за 1-й год. Определяем оптимальное
управление, исходя из критерия замены:
если s(t) - p + r(0) - u(0) ≤ r(t) - u (t), то
«сохранить»,
если s(t) - p + r(0) - u(0) > r(t) - u(t), то
«заменить».
1(t) = max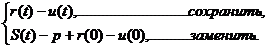
Теперь включаем в рассмотрение
предпоследний шаг, (n - 1)-й год, i = 2 и
установим прибыль за два последних года z2 (t).
Пусть в начале (n - 1)-го
года возраст оборудования t, и было принято решение о его
сохранении. Тогда прибыль к концу года зависит r (t) - u (t). При этом
на начало n-го года
оборудование уже будет иметь возраст t+1,
следовательно, в последнем году оно даст прибыль z1(t+1), а общая
прибыль за два последних года составит r (t) - u (t) + z1(t+1).
Если же в начале (n-1)-го года
выбрано управление ”замена”, то прибыль за два последних года составит s (t) - p + r (0) - u (0) + z1(1),
следовательно,
z2(t) = max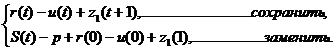
Аналогично для i последних
лет:
zi(t) = max 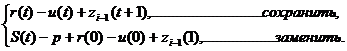
Дойдя до последнего шага (i = n), попадаем
в начало п/п, где t известно: t = t0, и,
следовательно, можно начать ”прямой ход”.
Задавая t0 и
длительность п/п, находим F* = zn(t0) и строим
последовательность оптимальных управлений, начиная с первого года и заканчивая
последним.
в) Расчет.
Для заполнения расчетной таблицы
можно использовать следующий алгоритм.
. Определить φ (t) = r(t) - u(t), m1 = S(t) - p + φ(0):
если m1 = const, то справа
к таблице прибавляется дополнительный столбец mi;
если m1 = m1(t), то над
каждой строкой zi(t) вводится
дополнительная строка mi = mi(t) (или mi(t)
вписывается в клетки значений zi(t) как тарифы
транспортной задачи).
. Заполнить строку z1(t), переписав
из таблицы данных соответствующие значения φ(t) ≥ m1, все
значения φ(t) < m1 заменить на
m1.
. Начиная с индекса i = 2, расчет
по строкам производится в следующей последовательности:
а) вычислить mi = m1 + zi-1(1), где zi-1(1) берется
из уже заполненной строки;
б) вычислить zi(t) = z1(t) + zi-1(t+1), где
сумма и слагаемые образуют треугольник, у которого одна из вершин всегда в
первой строке над искомым значением, а 2-ая - в последней заполненной строке
следующего столбца. Получаемые значения zi(t) ≥ mi вносить в
соответствующие клетки строки; начиная с первого zi(t) < mi, оставшиеся
клетки заполнить значением mi;
в) клетки с первым значением zi(t) < mi в процессе
заполнения таблицы отделить от расположенных в строке левее разделительной
границей смены управления;
г) если таблица не заполнена до
последней строки, перейти к п. а) и выполнить расчет для следующего значения
индекса i.
Замечания:
. Для задачи об оптимальном
распределении капиталовложений по полученной расчетной таблице можно получить
стратегию вложения средств, например, только в первые 3 филиала, исключив из
рассмотрения 4-й, или, например, для суммы в 150 млн. руб. (а не 200 ) между
4-мя филиалами, или только 3-мя первыми и т.д.
Для задачи о замене по расчетной
таблице можно получить решение на любой п/п длительностью, не превосходящей
исходный.
Это так называемый «принцип
погружения» метода динамического программирования.
2. Решенную задачу о замене
оборудования можно усложнить, например, допуская замену не новым оборудованием,
а уже проработавшим некоторое время. При этом имеется три возможных управления:
сохранить старое, купить новое, купить не новое.
5. Задача управления производством и
запасами
Предприятие производит партиями
некоторые изделия. Оно получило заказы на n месяцев.
Необходимо составить план производства на указанные n месяцев с
учетом затрат на производство и хранение. Обозначим:
) xj - число
изделий, производимых в j-м месяце;
) yj - величина
запаса к началу j-го месяца (Это число не содержит
изделий, производимых в j-й месяц, величина запаса к началу
1-го месяца (y1) и к концу
последнего (yn+1) заданы);
) dj - число
изделий, которые должны быть отгружены в j-й месяц;
) 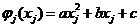 - функция затрат на производство xj изделий в j-м месяце
(может иметь и другой вид);
- функция затрат на производство xj изделий в j-м месяце
(может иметь и другой вид);
) hj - затраты
на хранение единицы запаса, переходящей из месяца j в месяц (j+1);
) 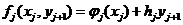 - функция затрат на производство и
хранение в j-м месяце.
- функция затрат на производство и
хранение в j-м месяце.
Задача состоит в определении плана
производства (х1,х2,…,хn),
компоненты которого удовлетворяют условиям материального баланса
xj +yj -dj = yj+1 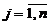
и минимизируют суммарные затраты за
весь период
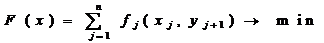 .
.
По смыслу 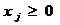 ,
, 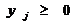 ,
,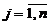 . Заметим,
что:
. Заметим,
что:
1) для любого месяца j
величина запаса к концу месяца должна удовлетворять ограничениям
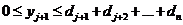 ,
,
то есть объем производимой продукции
xj в j-м месяце
может быть настолько велик, что запас yj+1
удовлетворяет спрос на всех последующих месяцах, но не имеет смысла иметь yj+1 больше
суммарного спроса всех последующих месяцев;
) из балансового уравнения получим 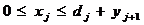 .
.
Если учесть, что xj и yj должны быть
целыми и неотрицательными, то имеем задачу целочисленного нелинейного
программирования.
Составим функциональные уравнения.
Пусть Fk(yk+1) -
минимальные затраты за первые k месяцев.
Для k = 1:

при 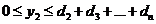 и
и  . На начальном этапе при
фиксированном значении y1 исходного
запаса каждому значению y2 отвечает
только одно значение x1.
. На начальном этапе при
фиксированном значении y1 исходного
запаса каждому значению y2 отвечает
только одно значение x1.
Для k 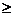 2 :
2 : 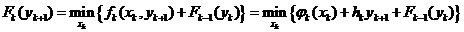
при 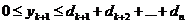 ,
, 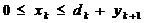 и
и 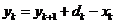 .
.
Применив процедуру динамического
программирования, на последнем шаге k = n
определяется значение xn*
оптимального решения, а остальные компоненты определяются в результате прямого
хода по формуле
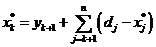
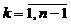 .
.
Пример.
Лекция 16, 17
Программирование на сетях
Вопросы:
1. Основные понятия теории графов.
. Матричное задание графов.
Упорядочение вершин.
. Сети и потоки на сетях. Постановка
задачи о максимальном потоке.
. Понятие разреза. Теорема
Форда-Фалкерсона. Алгоритм решения задачи о максимальном потоке.
. Элементы сетевого планирования.
1. Основные понятия теории графов
Теория графов - область дискретной
математики, особенностью которой является геометрический подход к изучению
объектов.
Основным объектом является граф и
его обощения. Синонимами графа являются карта, диаграмма, сеть, лабиринт.
Результаты и методы теории графов
используются в физике, химии, электротехнике, биологии, экономике, социологии и
т.п. В экономике методы теории графов применяются при решении транспортных
задач о перевозках, задач о назначениях, в календарном и сетевом планировании,
при моделировании сложных технологических процессов, в решении задач массового
обслуживания и задач управления динамическими процессами и т.п.
Формально граф определяется заданием
двух (конечных) дискретных множеств: множеством вершин Х = {х1, …, хn} и
множеством линий связи между ними
U = {u1,…,um}.
Линии связи ui называют
ребрами, если не указана их ориентация, и - дугами, если задано направление
связи.
Граф с дугами называют
ориентированным графом (орграфом), - с ребрами - неориентированным.
Пример. а) орграф б)
неориентированный граф
Вершины хi и хj, связанные
дугой/ребром uk, называют
концевыми вершинами этой дуги/ребра. Если концевые вершины совпадают, то
дуга/ребро называется петлей. Дуги/ребра с одинаковыми концевыми вершинами
называются параллельными. Граф без петель и параллельных линий связи называют
простым.
Концевые вершины хi и хj одной
дуги/ребра или дуги up и uq с общей
вершиной называют смежными.
Если вершина хi является
концевой для дуги/ребра uk, то эти xi и uk инцидентны:
вершина хi инцидентна
дуге/ребру uk, а
дуга/ребро uk - вершине хi.
Т.о., смежность - отношение
связанности между однородными элементами (вершинами или дугами/ребрами), а
инцидентность - между разнородными (вершинами и дугами/ребрами).
Вершина, не имеющая отношений
смежности, называется излированной.
Графы с одинаковым отношением
инцидентности называются изоморфными.
Пример.
Изоморфные графы отличаются только
геометрической конфигурацией.
Число дуг/ребер, инцидентных вершине
хi, называют
степенью этой вершины P(xi). В орграфе
различают полустепень захода P+(xi) и
полустепень исхода P-(xi) вершины хi, равные
соответственно числу заходящих в хi и исходящих
из хi дуг. P+(xi) + P-(xi) = P(xi).
В ряде случаев дугам ставятся в
соответствие числовые характеристики (длина пути, время смены состояний,
пропускная способность связи и т.д.), называемые весом дуг/ребер, а графы с
такими числами называют взвешенными.
Граф называют простым, если он не
содержит петель и параллельных дуг/ребер. Простой граф, в котором каждая пара
вершин смежна, называют полным.
Путь в орграфе - последовательность
неповторяющихся дуг, в которой конец каждой предыдущей дуги совпадает с началом
следующей. Путь, проходящий через все вершины только по одному разу, называется
гамильтоновым. Путь, содержащий все дуги только по одному разу, называют
эйлеровым. Конечный путь, у которого начальная вершина совпадает с конечной,
называют контуром. В неориентированном графе путь называют цепью, а контур -
циклом.
Орграф (неориентированный граф)
называют связным, если любые две его вершины можно соединить путем (цепью). В
противном случае - несвязным. Связный орграф называют сильно связным, если для
любых двух вершин хi и хj существуют
пути из хi в хj и из хj в хi.
Пример.
2. Матричное задание графа.
Упорядочение вершин
При большом числе вершин и дуг/ребер
изображение графа теряет наглядность. В этих случаях для задания графов и
работы с ними используют матрицы.
. Граф без петель, имеющий n вершин и m дуг/ребер
можно задать матрицей инциденций, строки которой соответствуют вершинам,
а столбцы - дугам. Элементы матрицы, размерности n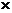 m,
определяются по формуле
m,
определяются по формуле
+1, если дуга uj входит в
вершину xi,
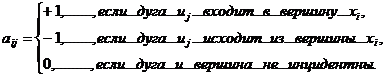
Для неориентированного графа вместо
”-1” ставится 1.
Пример.
. Граф можно матрицей смежности
вершин, строки и столбцы которой соответствуют вершинам графа. Элементы
матрицы Sij равны числу
дуг/ребер, идущих из хi в хj. Матрица
смежности для неориентированного графа будет симметричной.
Пример.
Аналогично может быть задана матрица
смежности дуг/ребер.
Расчеты в задачах, связанных с
графами, заметно упрощаются, если их элементы упорядочены.
Если существует путь из хi в хj, то вершина
хi называется
предшествующей вершине хj, а хj -
последующей хi.
Упорядочение вершин связного графа
без контуров означает разбиение его вершин на группы так, чтобы:
) вершины 1-й группы не имели
предшествующих, а вершины последней - последующих;
) вершины любой другой группы не
имели предшествующих в следующей группе;
) вершины одной и той же группы не
соединялись с дугами.
Графический способ упорядочения
вершин (алгоритм Фалкерсона).
1. Находятся вершины графа, в которые
не входит ни одна дуга. Такие вершины образуют 1-ю группу.
. Вершины и выходящие из них дуги
установленной группы исключаются из дальней- шего рассмотрения.
. Устанавливается следующая группа
вершин, в которые не входит ни одна дуга.
. Если процесс упорядочения не
окончен, то переход п. 2.
. В полученном графе, изоморфном
исходному, перенумеровываются вершины.
3. Сети и потоки на сетях.
Постановка задачи о максимальном потоке
Сеть - конечный взвешенный связный
орграф без контуров и петель, ориентированный в одном общем направлении от
вершины I (исток,
вход) к вершине S (сток, выход).
Для наглядности представим, что по
ребрам от истока к стоку направляется некоторое вещество (груз, ресурс,
информация и т.п.).
Максимальное количество rij вещества,
которое может пропустить за единицу времени ребро (i, j),
называется его пропускной способностью. В общем случае rij ≠ rji. Если
вершины не соединены, rij = 0. Т.к.
нет петель, то rii = 0. Пропускную способность
можно задать квадратной матрицей.
Количество хij вещества,
проходящего по ребру (i, j) в единицу
времени, называется потоком по ребру (i, j).
Предполагается, что если из хi в хj
направляется поток хij , то из xj в xi
направляется поток (-хij)
xij = - xji . (1)
Поток по каждому ребру не превышает
его пропускную способность
xij 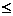 rij (i =
rij (i = 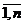 ; j =
; j = 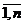 ) . (2)
) . (2)
Количество вещества, притекающее в
вершину, равно количеству вещества, вытекающего из неё
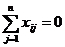 (i
(i 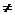 I, S ). (3)
I, S ). (3)
Совокупность Х = 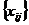 потоков по
всем рёбрам сети называют потоком по сети. Общее количество вещества
вытекающего из истока I, совпадает с общим количеством
вещества, поступающего в сток S, т.е.
потоков по
всем рёбрам сети называют потоком по сети. Общее количество вещества
вытекающего из истока I, совпадает с общим количеством
вещества, поступающего в сток S, т.е.
F = 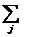 xIj =
xIj = 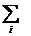 xiS. (4)
xiS. (4)
Функцию F называют
мощностью потока.
Если на сети задан поток Х = 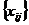 , то ребро (i,j) называется
насыщенным, если поток xij по нему
совпадает с его пропускной способностью rij (xij = rij) , и
ненасыщенным, если xij < rij .
, то ребро (i,j) называется
насыщенным, если поток xij по нему
совпадает с его пропускной способностью rij (xij = rij) , и
ненасыщенным, если xij < rij .
Задачу о максимальном потоке можно
сформулировать следующим образом: найти совокупность Х* = {x*ij} потоков x*ij по всем
рёбрам сети, которая удовлетворяет условиям (1) - (3) и максимизирует линейную
функцию (4) . Это типичная ЗЛП.
Замечание. Не всякие n2 чисел могут
задавать поток по сети. Только такие n2 чисел xij задают
поток, которые удовлетворяют условиям (1) - (3) .
Пример.
4. Понятие разреза. Теорема Форда-Фалкерсона.
Алгоритм решения задачи о максимальном потоке
Пусть дана некоторая сеть. Разобьём
множество вершин сети на два непересекающихся множества А и В так, чтобы исток I попал в А,
а сток S - в В. В
этом случае на сети задан разрез. Совокупность ребер (i,j), начальные
вершины которых принадлежат А, а конечные - В, называется разрезом сети (А/B).
Пропускной способностью разреза
называют сумму пропускных способностей всех рёбер разреза R (A/B) = 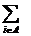
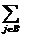 rij.
rij.
Сумма всех потоков xij по всем
рёбрам разреза называется потоком через разрез
X(A/B) =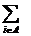
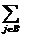 xij.
xij.
Теорема Форда-Фалкерсона: на любой
сети максимальная величина потока равна минимальной пропускной способности
разреза.
Теорема позволяет определить
максимальный поток для относительно простых сетей. В общем случае используют
следующий алгоритм.
Алгоритм решения задачи о
максимальном потоке.
1. Построить начальный поток Х =
= 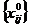 (чем больше
величина выбранного потока, тем быстрее решается задача).
(чем больше
величина выбранного потока, тем быстрее решается задача).
. На основе заданной сети
строится новая сеть:
а) каждая дуга, для которой 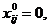 остаётся в
новой сети с первоначальной rij;
остаётся в
новой сети с первоначальной rij;
б) каждая дуга для которой 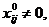 заменяется
на две:
заменяется
на две:
одна дуга того же направления с
пропускной способностью rij-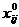 ;
;
вторая дуга противоположенного
направления с пропускной способностью 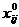 .
.
. Если в новой сети можно найти
ненулевой поток из I в S, то этот
поток прибавляет-ся к начальному. В результате получается новый поток 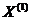 и переходят
к п. 2.
и переходят
к п. 2.
Если же в новой сети отсутствуют
ненулевые потоки из I в S, то
максимальный поток сети построен.
Пример.
5. Элементы сетевого планирования
Сетевой график - сеть, вершины
которой - «события», результаты определённых работ или состояния этапов
промежуточных работ), а дуги - «работы» (протяжённый во времени процесс,
приводящий к соответствующему «событию»). Веса дуг, как правило, - время
выполнения работ.
Пример.
Составление сетевого графика требует
выполнения определённых организационных и формальных правил.
Организационные правила:
) составляется подробный перечень
всех работ от отправного момента до целевого результата;
) определяется продолжительность
всех работ;
) устанавливаются технологические
связи между всеми промежуточными событиями и упорядочивается их
последовательность, т.е. для каждого события определяются все предшествующие и
все последующие работы.
Формальные правила:
1) сетевой график должен иметь
только одно исходное событие - исток и только одно завершающее - сток;
) любые два события должны быть
связанны не более чем одной работой и, наоборот, каждая работа должна
заключаться между двумя событиями;
) сеть не должна иметь контуров,
петель, изолированных участков, не связанных работами с её остальной частью;
) сетевой график должен быть
упорядочен по вершинам.
Замечание: для выполнения формальных
правил и учёта ряда технологических процессов вводят фиктивные события и
работы. В частности.
1. Если комплекс работ начинается с нескольких
работ, не имеющих предшествующих (нарушается п. 1 формальных правил), вводится
фиктивный «исток» с дугами к указанным работам.
2. Если два события связанны параллельными
дугами (нарушается п.2 формальных правил), вводится фиктивное событие, на
которое замыкается одна из работ.
. Если следует учесть зависимость
событий, не связанных реальными работами (различные работы a
и b выполняются на
одном оборудовании), то вводится фиктивная работа c:
В случаях 1) - 3) фиктивные работы не имеют
протяжённости во времени.
. Если технологический процесс требует
естественного дозревания, брожения, затвердевания, высушивания и т. д., т.е.
когда реальная работа не производится, но следующее событие без учёта этих
процессов начаться не может, то вводится фиктивная работа, имеющая протяжённость
во времени.
К основным параметрам сетевого графика
относятся:
1) продолжительность
t* критического пути,
т.е. наиболее протяжённого во времени пути от истока к истоку;
2) резервы времени событий R(i),определяющие
предельно допустимые задержки событий i,
не приводящие к изменению t*;
3) полный резерв времени
промежуточной работы Rij,
определяющий максимальный запас времени, на который можно задержать начало
работы или увеличить её продолжительность, не изменяя t*;
4) свободный резерв времени
промежуточной работы rij,
определяющий максимальный запас времени, на которое можно задержать начало
работы или увеличить её продолжительность, не нарушая самые ранние сроки начала
всех последующих работ.
Критический путь -
последовательность работ и событий, не имеющих резервов времени. Общий срок
завершения комплекса работ определяется продолжительностью критического пути.
Если события i
дают начало работам, продолжающимся tij
ед. времени и завершающимся событием j,
то ожидаемый (ранний) срок ti
наступления j-ого события равен
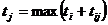 ,
, 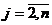 (1)
(1)
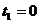 (1-е событие - «исток»),
(1-е событие - «исток»),
где ti - ожидаемый
(ранний) срок i - го
события (i<j).
Наиболее поздний срок наступления i - го
события
Ti
= min(Tj - tij), i = 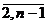 n = tn = t* (n-e coбытие -
«сток») (2)
n = tn = t* (n-e coбытие -
«сток») (2)
Т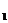 =
= 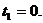
Резерв времени наступления i-го события
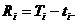 (3)
(3)
Свободный резерв времени работы (i,j)
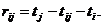 (4)
(4)
Полный резерв времени работы (i,j)
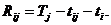 (5)
(5)
Расчёты параметров сетевого графика
проводят в 5 этапов, изображая события кружками с четырьмя секторами, которые
заполняются по ходу выполнения этапов:
1) находят все ti
по формулам (1), при этом перемещаются по сетевому графику согласно номерам
событий слева направо;
2) находят Ti
по формулам (2), при этом перемещаются по сетевому графику от стока влево по
мере убывания номеров событий;
) определяю Ri
по
формуле (3)
) выделяют критический путь;
) вычисляют все остальные параметры.
Пример.
Замечания:
1. Резерв времени наступления
события Ri позволяет
варьировать сроки готовности события i в пределах ti 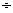 Ti.
Ti.
. Свободные резервы времени
работ с учётом их значений можно использовать (отсрочить начало или затянуть
окончание) по всем некритическим работам сети одновременно, не изменив t*.
. Полные резервы времени
использовать одновременно удаётся не всегда.
Правила построения двойственной
задачи.
Исходя из общего вида прямой и двойственной
задач можно установить связь между этими задачами, позволяющую для любой ЗЛП
строить двойственную ей задачу.
Свойства двойственных задач
(правила).
9. Число неизвестных двойственной задачи равно
числу ограничений прямой задачи. Число ограничений двойственной задачи равно
числу неизвестных прямой задачи.
10. Матрица коэффициентов двойственной
задачи является транспонированной матрицей коэффициентов прямой задачи.
. Коэффициенты целевой функции
двойственной задачи являются свободными членами ограничений прямой задачи.
. Свободные члены ограничений
двойственной задачи являются коэффициентами целевой функции прямой задачи.
13. Если ограничения прямой
задачи записаны со знаком меньше или равно (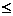 ), то ограничения двойственной
задачи записываются со знаком больше или равно (
), то ограничения двойственной
задачи записываются со знаком больше или равно ( ).
).
. Если ограничение прямой
задачи задано в виде уравнения, то соответствующее неизвестное двойственной
задачи не ограничено знаком.
. Если какое-либо
неизвестное прямой задачи не ограничено знаком, то соответствующее ограничение
двойственной задачи будет задано в виде равенства.
. Если целевая функция
прямой задачи сформулирована на максимум, то целевая функция двойственной
задачи будет сформулирована на минимум.
Существует много различных комбинаций
ограничений и целевой функции для записи исходной задачи. Для упрощения задачи
построения двойственной задачи запишем прямую задачу в некотором стандартном
виде прямой задачи. Этот вид предполагает, что:
4) все ограничения имеют знак 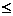 ;
;
5) целевая функция
сформулирована на максимум;
) все неизвестные
неотрицательны.
Чтобы записать прямую задачу в стандартном виде,
необходимо:
5) неравенство со знаком  умножить на
(-1);
умножить на
(-1);
) равенство заменить на два
неравенства противоположных знаков, одно из которых следует умножить на (-1);
) формулировку целевой
функции меняют заменой знаков коэффициентов на противоположные;
) если переменное xj не
ограничено знаком, его можно представить в виде разности двух неотрицательных
переменных.
Пример.
Составить двойственную задачу к исходной.
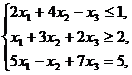
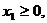

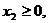
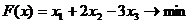 .
.
программирование
симплекс матричный граф
Решение. 1)
Стандартный вид прямой задачи.
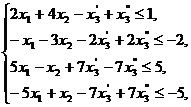
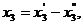
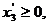
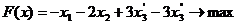
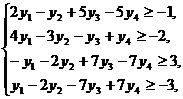
) Двойственная задача: 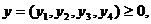
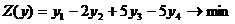
Задачу можно записать в виде,
соответствующем исходной прямой задаче, если заменить: а) 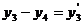 - не
ограничена знаком,
- не
ограничена знаком,
б) два последних ограничения
соответствуют равенству.
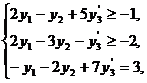
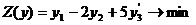 .
.