Обоснование принятия оптимальных решений для хлебозавода

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

"Тульский государственный университет"

Кафедра финансов и менеджмента

Методы оптимальных решений

 

 

 

 

 

 

КУРСОВАЯ РАБОТА

"Обоснование принятия оптимальных решений для хлебозавода"

Содержание

Введение

Обоснование оптимального плана перевозок

Обоснование ценовой стратегии

Обоснование распределения финансовых ресурсов между проектами

Заключение

Список использованной литературы

Введение

Темой данной работы является обоснование принятия оптимальных решений для хлебозавода.

Целью выполнения типового расчета по дисциплине "Методы оптимальных решений" является овладение математическими методами решения экономических задач.

Задачи выполнения типового расчета:

научиться строить экономико-математические модели;

освоить симплекс-метод табличного решения задачи линейного программирования;

освоить двойственный симплекс-метод решения задачи линейного программирования;

освоить метод потенциалов решения транспортной задачи;

освоить методику решения антагонистических игр;

освоить методику решения задачи динамического программирования.

обоснование оптимального плана производства

В состав хлебозавода входят 2 производства: хлебобулочное и кондитерское. ОАО " Пышка" - хлебозавод. Он находится в Туле и распространяет свою продукцию по территории, данной области.

Основная задача хлебозавода:

обеспечение населения хлебобулочной и кондитерской продукцией.

Принципы и цели:

постоянное обновление и совершенствование ассортимента продукции;

использование только натурального и высококачественного сырья.

Главная задача предприятия - предлагать покупателю вкусный и полезный хлеб, сохраняющий здоровье, помогающий в работе и создающий хорошее настроение.

Хлебозавод выпускает следующие изделия:

П1 - Хлеб

Это пищевой продукт, получаемый путём выпечки, паровой обработки или жарки теста <#"825463.files/image001.gif">

при ограничениях:

. Построение двойственной задачи к задаче распределения ресурсов.

оптимальное решение хлебозавод экономический

.

Тогда транспонированная матрица, отражающая коэффициенты при переменных в системе ограничений ДЗЛП, имеет вид:

.

Таким образом, экономико-математическая модель ДЗЛП имеет вид:

при ограничениях

. Решение прямой и двойственной задач линейного программирования

Соответствие переменных прямой и двойственной задачи

Во взаимодвойственных задачах линейного программирования первоначальным переменным ПЗЛП соответствуют дополнительные переменные ДЗЛП и аналогично первоначальным переменным ДЗЛП соответствуют дополнительные переменные ПЗЛП.

х1 y4

х2 y5

х3 y6

х4 y1

х5 y2

х6 у3

Одновременное решение ПЗЛП и ДЗЛП с помощью симплекс-таблиц

Решаем ПЗЛП.

Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплекс-таблицу. Все строки таблицы 1-го шага, за исключением строки Δ_j (индексная строка), заполняем по данным системы ограничений и целевой функции канонической формы записи ПЗЛП.

сi	сj	32	67	43	0	0	0
	Базисные переменные (БП)	х1	х2	х3	х4	х5	х6	bi
0	x4	1	4	12	1	0	0	65
0	x5	4	6	8	0	1	0	56
0	х6	1	11	9	0	0	1	15
Δj		-32	-67	-43	0	0	0	0

Первое опорное решение имеет вид:  = (0, 0, 0, 65, 56, 15),  = 0. Базисные переменные имеют значения х₄ = 65, х₅ = 56, х₆ = 15.

В рассматриваемом случае первое опорное решение не оптимальное, поскольку имеются три отрицательные оценки Δ₁ = - 32, Δ₂ = - 67 Δ₃ = - 43.

Следовательно, нужно сделать следующий шаг симплекс-метода: ввести в базис переменную, которую нужно улучшить.

Такой переменной является переменная из столбца с наибольшей по абсолютной величине оценкой |Δ₂| = 67, т.е. переменная х₃.

сi	сj	32		67	43	0	0	0		min
	Базисные переменные (БП)	х1		х2	х3	х4	х5	х6	bi	bi/ hij
0	x4	1		4	12	1	0	0	65
0	x5	4		6	8	0	1	0	56
0	х6	1		11	9	0	0	1	15
Δj		-32		-67	-43	0	0	0	0
0	x4		1	4	12	1	0	0	65	65/4
0	x5		4	6	8	0	1	0	56	56/6
0	х6		1	11	9	0	0	1	15	15/11
Δj			-32	-67	-43	0	0	0	0	-

На пересечении ключевой строки и ключевого столбца находится ключевой элемент "11".

Переход ко второму шагу симплекс-метода.

Заполним симплекс-таблицу второго шага. Вместо переменной х₅ вводим в базис переменную х₂, в целевой функции ей соответствует коэффициент 67, который вносится в соответствующую клетку столбца с_i.

сi	сj	32	67	43	0	0	0		min
	Базисные переменные (БП)	х1	х2	Х3	х4	х5	х6	bi	bi/ hij
0	x4	7/11	0	96/11	1	0	-4/11	655/11
0	X5	38/11	0	34/11	0	1	-6/11	526/11
67	Х2	1/11	1	9/11	0	0	1/11	15/11
Δj		-285/1	0	130/11	0	0	67/11	1005/11	-

Поскольку не все оценки положительные Δ_j, то полученное опорное решение не является оптимальным. Вместо переменной х₅ вводим в базис переменную х₁, в целевой функции ей соответствует коэффициент 32, который вносится в соответствующую клетку столбца с_i.

сi	сj	32	67	43	0	0	0		min
	Базисные переменные (БП)	х1	х2	Х3	х4	х5	х6	bi	bi/ hij
0	x4	0	0	155/19	1	-7/38	-5/19	964/19
32	X1	1	0	17/19	0	11/38	-3/19	263/19
67	Х2	0	1	14/19	0	-1/38	2/19	2/19
Δj		0	0	35	0	15/2	2	450	-

Поскольку все оценки положительные Δ_j, то полученное опорное решение является оптимальным:  = (263/19; 2/19; 0; 964/19; 0; 0), а максимальное значение целевой функции равно  =450.

Учитывая соответствие переменных взаимодвойственных задач, можно выписать оптимальное решение двойственной задачи.

сi	сj	4	6	8	0	0	0
	Базисные переменные (БП)	х1	х2	х3	х4	х5	х6	bi
0	x4	0	0	1	-7/38	-5/19	964/19
32	X1	1	0	17/19	0	11/38	-3/19	263/19
67	Х2	0	1	14/19	0	-1/38	2/19	2/19
Δj		0	0	35	0	15/2	2	450
yi		y4	y5	y6	y1	y2	y3

Таким образом, 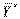 = (0, 15/2, 2, 0, 0, 35), поскольку y₁ ↔ x₄, y₂ ↔ x₅, y₃ ↔ x₆, y₄ ↔ x₁, y₅ ↔ x₂, y₆ ↔ x₃. Значение целевой функции 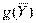= 450.

Анализ решения ПЗЛП

Подставим оптимальные значения переменных x^* в исходную систему ограничений ПЗЛП:

) 1⋅х₁ + 4⋅х₂ + 12⋅х₃ ≤ 65

⋅263/19 + 4⋅2/19 + 12⋅0 = 271/19

/19≤ 65, следовательно, х₄ = 50,73, ресурс Р₁ используется не полностью;

) 4⋅х₁ + 6⋅х₂ + 8⋅х₃ ≤ 56

⋅263/19 + 6⋅2/19 +8⋅0 = 56

= 56 следовательно, х₅ = 0, ресурс Р₂ используется полностью;

) 1⋅х₁ + 11⋅х₂ + 9⋅х₃ ≤ 15

⋅263/19 + 11⋅2/19 + 9⋅0 = 15

=15, следовательно, х₆ = 0, ресурс Р₃ используется полностью.

Анализ решения ДЗЛП

Подставим оптимальные значения переменных у^* в исходную систему ограничений ПЗЛП:

1) 1⋅у₁ + 4⋅у₂ + 1⋅у₃ ≥ 32, 1⋅0 + 4⋅15/2 + 1⋅2 = 32

= 32, следовательно, у₄ = 0, убытки от производства первого вида продукции П₁, которая вошла в оптимальный план производства отсутствуют;

) 4⋅у₁ + 6⋅у₂ + 11⋅у₃ ≥ 67

⋅0 + 6⋅15/2 + 11⋅2= 67

=67, следовательно, у₅ = 0, убытки от производства второго вида продукции П₂, которая вошла в оптимальный план производства отсутствуют;

) 12⋅у₁ + 8⋅у₂ + 9⋅у₃ ≥ 43

⋅0 + 8⋅15/2 + 9⋅2 = 78

≥43, следовательно, у₆ = 35, убытки от производства третьего вида продукции П₃, которая не вошла в оптимальный план производства, в случае ее производства будут составлять 35 ден. ед. с каждого изделия третьего вида

. Расчет границ изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана

Система неравенств для базисных переменных ПЗЛП, используя элементы из столбца свободных членов b_i и столбца, соответствующего переменной у₁. Определяем допустимый интервал изменения границ первого вида ресурса Р₁

 ⇒ .

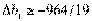Учитывая, что b₁ =65, допустимый интервал изменения границ первого вида ресурса составит 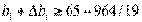или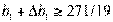

Аналогично, определяем допустимый интервал изменения границ второго вида ресурса Р₂:

 ⇒  ⇒ .

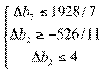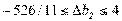Учитывая, что b₂ = 56, допустимый интервал изменения границ второго вида ресурса составит .

Аналогично, определяем допустимый интервал изменения границ третьего вида ресурса Р₃:

 ⇒ ⇒

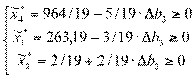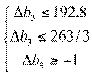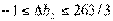
Учитывая, что b₃ = 15, допустимый интервал изменения границ третьего вида ресурса составит

Проверим границы с помощью вычислительного эксперимента:

Зададим b₃ = 10

ПЗЛП

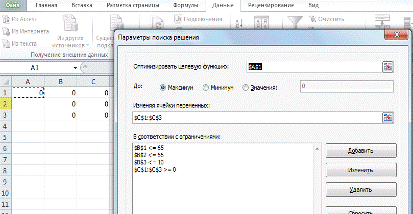
Рисунок 1

Получили новую структуру оптимального плана прямой задачи: (х₁=0, х₂=0, х₃=0).

Зададим b₃ = 20

ПЗЛП

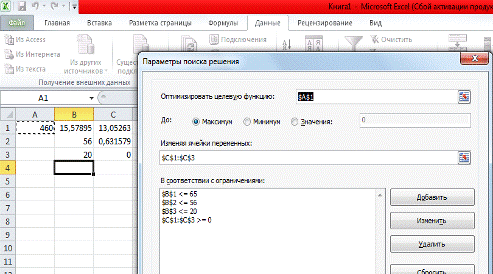
Рисунок 2

Получили структуру оптимального плана, соответствующую исходной ().

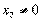Также проверим ДЗЛП:

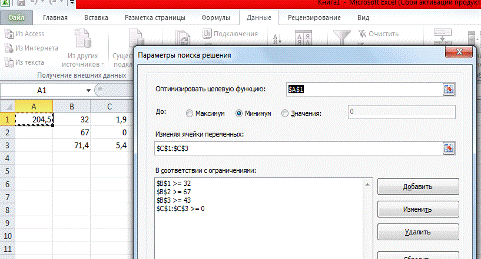
Рисунок 3

Внутри границы решение ДЗЛП не меняет структуру. ()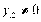

Эти эксперименты подтверждают правильность границы .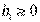

. Уточнение значения недефицитных ресурсов, при которых оптимальный план не изменится

Значение остатка недефицитного ресурса определяется значением соответствующей дополнительной переменной.

В рассматриваемом случае недефицитный ресурс является первый, а второй и третий ресурс - дефицитные.

. Расчет границ изменения цены изделия, попавших в оптимальный план производства, в пределах которых оптимальный план не изменится

В план производства вошел третий вид продукции П₃.

 ⇒  ⇒ .

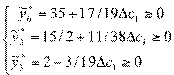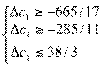Учитывая цену третьего вида продукции с₁ = 32, интервал устойчивости изменения цен составит .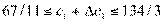

Для видов продукции, не попавших в оптимальный план производства, исследование допустимых границ изменения цен не проводится.

⇒  ⇒ .

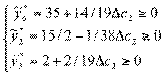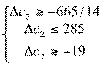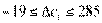Учитывая цену третьего вида продукции с₂ = 67, интервал устойчивости изменения цен составит .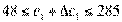

Для видов продукции, не попавших в оптимальный план производства, исследование допустимых границ изменения цен не проводится.

Зададим с₃ = 5

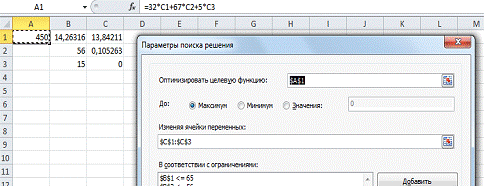
Рисунок 4

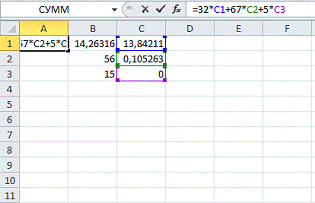
Рисунок 5

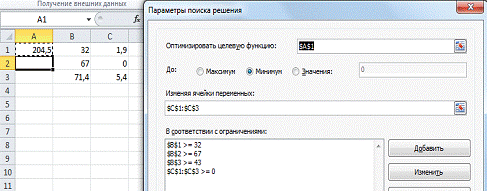
Рисунок 6

. Определение величины ∆b_s ресурса Р_s, введением которого в производство можно компенсировать убыток и сохранить максимальный доход на прежнем уровне (ресурсы предполагаются взаимно заменяемыми), получаемый при исключении из производства ∆b_r единиц ресурса Р_r

В рассматриваемом случае: r = 3; ∆b_r = 0,1; s = 1.

Для взаимозаменяемых ресурсов (коэффициент взаимозаменяемости 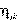>0, но отличен от бесконечности) количество ресурса ∆b_i вида i, необходимое для замены выбывающего количества ∆b_k ресурса k, определяется по формуле:

.

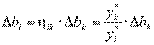Таким образом, 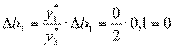. Следовательно, замена первого ресурса невозможна.

. Оценка целесообразности приобретения ∆b_k единиц ресурса Р_k по цене с_k за единицу

Приобретение дополнительного количества ресурса целесообразно, если выполняется условие непревышения новой цены над теневой ценой

 

с_k ≤ .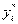

В противном случае приобретение дополнительного количества ресурса нецелесообразно.

В рассматриваемом случае:

∆b_k = 0,5; k = 2, c_k =24.

Поскольку 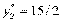 < 24, то приобретение дополнительного количества ресурса не целесообразно.

. Оценка целесообразности выпуска нового изделия П₄, на единицу которого ресурсы Р₁, Р₂, Р₃ расходуются в количествах a₁₄, a₂₄, a₃₄ единиц, а цена единицы изделия составляет с₄ денежных единиц

Включение дополнительного вида продукции n+1 в план производства целесообразно, если соотношение дополнительных затрат и цены реализации дополнительного вида продукции удовлетворяет следующему условию

.

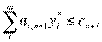Расчет затрат осуществим по формуле

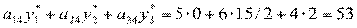 ден. ед.

Учитывая, что затраты на ресурсы для производства продукции третьего вида меньше цены реализации с₄ = 15 ден. ед., то включение ее в план производства целесообразно.

. Решение прямой и двойственной задач линейного программирования в среде Microsoft Exсel

Решение задач линейного программирования с помощью программы Microsoft Excel осуществляется через меню Сервис и вкладку Поиск решения. Если данная вкладка не установлена, то ее установка осуществляется следующими действиями:

. Войти в меню Сервис.

. Выбрать команду Надстройки.

. В появившемся диалоговом окне Надстройки установить флажок напротив строки Поиск решения и нажать кнопку ОК.

После произведенных действий в меню Сервис появится команда Поиск решения.

Прежде чем начать выполнение команды Поиск решения следует провести подготовительные действия по введению данных задания в таблицу.

Выбираем ячейку для введения целевой функции (например, ячейку А1). При записи целевой функции в ячейку А1 вместо значений переменной х_i подставляют названия пустых ячеек, в которых хотим получить искомые значения х₁, х₂, х₃, например, С1, С2, С3. Тогда запись целевой функции в ячейке А1 будет иметь вид = 32*С1+67*С2+43*С3. После введения целевой функции в ячейку А1 нажимаем клавишу "Enter", в ячейке А1 отобразится 0.

Условия ограничений вписываем в ячейки столбца В. В выбранные ячейки записываются только левые части неравенств в следующем виде:

Ячейка В1: =1*С1+4*С2+12*С3 "Enter"

Ячейка В2: =4*С1+6*С2+8*С3 "Enter"

Ячейка В3: =1*С1+11*С2+9*С3 "Enter"

Ячейка В4: =С1 "Enter"

Ячейка В5: =С2 "Enter"

Ячейка В6: =С3 "Enter"

Через меню Сервис / Поиск решения открыть окно поиска решения:

В поле ввода Установить целевую ячейку вводим ссылку на ячейку А1.

В поле ввода Изменяя ячейки укажем ссылки на ячейки С1: С3.

Данная операция осуществляется следующими действиями:

. Щелкнуть левой кнопкой мыши в поле ввода Изменяя ячейки.

. Выделить при помощи левой кнопки мыши ячейки, начиная с С1 и до ячейки С3 (поле ввода изменения ячейки должно автоматически заполниться).

В поле ввода Ограничения введем ограничения, соответствующие ячейкам В1, В2, В3. Ввод значений осуществляется в следующем порядке:

. Нажать кнопку Добавить. Появится диалоговое окно Добавление ограничения.

. Для каждого логического выражения, находящихся в ячейках В1, В2, В3 вводим свое условие и свое ограничение, последовательно нажимая кнопку Добавить. По окончании нажать кнопку ОК.

. Должен появиться следующий результат:

. Для поиска максимального значения устанавливаем флажок.

Для осуществления вычислений нажмем кнопку Выполнить. Откроется окно диалога Результаты поиска решения. В окне Тип отчета выберем строку Результаты и нажмем кнопку ОК.

Получим следующие результаты:

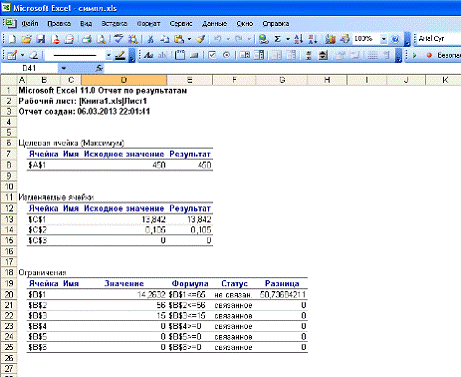
В ячейке А1 отражено максимально возможное значение функции при заданных условиях 450.

В столбце В отражены значения логических выражений, удовлетворяющих исходным ограничениям. (кроме В1)

х₁ + 4х₂ +12х₃ = 14

х₁ + 6х₂ + 8х₃ = 56

х₁ + 11х₂ + 9х₃ =15

В столбце С отражены значения переменных, при которых значение функции принимает максимальную величину:

х₁ = 13,842 х₂ = 0,105, х₃ = 0.

На листе "Отчет по результатам" появится следующая информация, отражающая результаты расчета:

Б. Двойственный симплекс-метод

. Выражение базисных переменных ПЗЛП и ДЗЛП через свободные.

Выразим базисные переменные ПЗЛП и ДЗЛП через свободные:

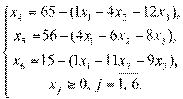
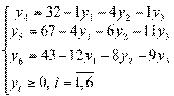
. Определение исходного решения прямой и двойственной задач и проверка его на оптимальность.

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	1	4	12	65
y2	x5	4	6	8	56
y3	x6	1	11	9	15
cj		-32	-67	-43	0

Решение ПЗЛП выписывается по строкам, значения базисных переменных берутся из столбца b_i, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: 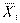= (0, 0, 0, 65, 56, 15),  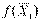= 0.

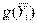Решение ДЗЛП выписывается по столбцам, значения базисных переменных берутся из строки c_j, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 0, −32, −67, −43),  = 0.

Данное решение не является оптимальным, поскольку решение не допустимое (не выполнено условие неотрицательности переменных), ему соответствуют отрицательные элементы в строке 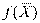. Поэтому следует провести замену переменных в базисе.

В рассматриваемом примере в строке 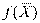 три отрицательных элемента

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	1	4	12	65
y2	x5	4	6	8	56
y3	x6	1	11	9	15
cj		-32	-67	-43	0

Можно выбрать любой из них, поэтому выбираем "−67", а над ним выбираем элемент из первой строки "11". Следовательно, третья строка - разрешающая (выделена жирным шрифтом).

Заполнение нижних частей клеток для разрешающей строки и разрешающего столбца варианта 0:

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	1	4 4	12	65
y2	x5	4	6 6	8	56
y3	x6	1 1	"11" 1	9 9	15 15
cj		-32	-67 67	-43	0

. Заполнение нижних частей для остальных клеток.

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	1 7	4 4	12 96	65 655
y2	x5	4 38	6 6	8 34	56 526
y3	x6	1 1	"11" 1	9 9	15 15
cj		-32 285	-67 67	-43 130	0 1005

. Построение новой симплекс-таблицы.

Переходим к следующей симплекс-таблице. При этом в первую строку включается пара переменных х₂, у₅, соответствующих разрешающему столбцу, а во второй столбец вводится пара переменных х₆, у₃, соответствующая разрешающей строке. Верхние части клеток заполняются элементами, полученными в результате деления соответствующих (стоящих на аналогичном месте) элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент "11":

	yбаз	y4	у3	y6
yсв	xсв xбаз	- x1	- x6	- x3	bi
y1	x4	7/11	-4/11	96/11	655/11
y2	x5	38/11	-6/11	34/11	526/11
y5	x2	1/11	1/11	9/11	15/11
cj		-285/11	67/11	130/11	1005/11

Решение ПЗЛП на втором шаге двойственного симплекс-метода также выписывается по строкам: 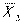= (0, 15/11, 0, 655/11, 526/11, 0),  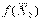= 1005/11, решение ДЗЛП выписывается по столбцам: 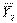= (67/11, 0, 0, - 285/11, 0, 130/11),  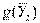= 1005/11. Данное решение также не оптимальное, поскольку в строке 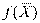 еще остались отрицательные элементы. Необходимо продолжить поиск оптимального решения.

В строке 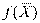 выбираем отрицательный элемент "−285/11". Над ним выбираем положительный, предпочтительнее "38/11", поскольку третья строка была выбрана на предыдущем шаге метода, следовательно, вторая строка - разрешающая (выделена жирным шрифтом):

	yбаз	y4	у3	y6
yсв	xсв xбаз	- x1	- x3	bi
y1	x4	7/11	-4/11	96/11	655/11
y2	x5	"38/11"	-6/11	34/11	526/11
y5	x2	1/11	1/11	9/11	15/11
cj		-285/11	67/11	130/11	1005/11

Разрешающий элемент "38/11" находится на пересечении разрешающей строки и разрешающего столбца.

Заполнение нижних частей клеток осуществляется аналогично рассмотренному выше.

Получаем следующую таблицу:

	yбаз	y4	у3	y6
yсв	xсв xбаз	- x1	- x6	- x3	bi
y1	x4	7/11 7/11	-4/11 110/121	96/11 3410/121	655/11 21208/121
y2	x5	"38/11" 1	-6/11 6/11	34/11 34/11	526/11 526/11
y5	x2	1/11 1/11	1/11 44/121	9/11 308/121	15/11 44/121
cj		-285/11 285/11	67/11 836/121	130/11 14630/121	1005/11 188100/121

Переходим к следующей симплекс-таблице. При этом во вторую строку включается пара переменных х₁, у₄, соответствующих разрешающему столбцу, а в первый столбец вводится пара переменных х₅, у₂, соответствующая разрешающей строке. Клетки следующей таблицы заполняются элементами, полученными в результате деления соответствующих элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент "38/11". Поскольку в нижних частях клеток таблицы все элементы положительные и разрешающий элемент также положительный, то в следующей таблице будет получено оптимальное решение и нет необходимости делить на две части клетки в последней таблице.

Сократим и получим следующую таблицу:

	yбаз	y2	у3	y6
yсв	xсв xбаз	- x5	- x6	- x3	bi
y1	x4	-7/38	-110/418	3410/418	964/19
y4	x1	11/38	-6/38	34/38	263/19
y5	x2	-1/38	9,5	308/418	2/19
Сj		15/2	2	35	450

Оптимальное решение ПЗЛП: 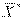= (263/19, 2/19, 0, 964/19, 0, 0), 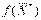= 450, оптимальное решение ДЗЛП: 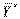= (0, 15/2, 2, 0, 0, 35), 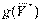 = 450.

Данное решение аналогично решению, полученному в соответствии с методом одновременного решения пары взаимодвойственных задач для ПЗЛП и совпадает с решением ДЗЛП в отношении значения целевой функции. Однако поскольку ДЗЛП имеет альтернативные решения, то полученное в результате расчета решение является альтернативным по отношению к полученному первым методом.

Обоснование оптимального плана перевозок

На трех базах (пунктах отправления) A₁, A₂, A₃ находится однородный груз в количествах, соответственно равных а₁, а₂ и а₃ единицам. Этот груз требуется перевести в три пункта назначения B₁, B₂, B₃ соответственно в количествах b₁, b₂ и b₃. единиц. Стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения составляет c_ij денежных единиц. Определить оптимальный план перевозок, при котором общая стоимость перевозок будет минимальной.

Исходные данные:

Стоимость перевозки	В1	В2	В3	В4	Запасы
А1	с11 = 21	с12 = 19	с13 = 11	с14 = 12	а1 = 24
А2	с21 =26	с22 = 29	с23 = 14	с24 = 26	а2 = 12
А3	с31 = 21	с32 = 22	с33 = 18	с34 = 25	а3 = 18
А4	с41 = 23	с42 = 40	с43 = 26	с44 = 28	а4 = 16
Потребности	b1 = 11	b2 = 13	b3 = 26	b4 =20	-

. Проверка разрешимости транспортной задачи

Проверим условие разрешимости транспортной задачи:

.

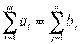+13+26+20=24+12+18+16; 70=70

Условие разрешимости транспортной задачи выполнено.

. Экономико-математическая модель транспортной задачи.

Обозначим x_ij - количество груза, перевозимого из пункта А_i в пункт B_j:

Объем перевозок	В1	В2	В3	В4	Запасы
А1	21 х11	19 х12	11 х13	12 х14	а1 = 24
А2	26 х21	29 х22	14 х23	26 х24	а2 = 12
А3	21 х31	22 х32	18 х33	25 х34	а3 = 18
А4	23 х41	40 х42	26 х43	28 х44	а4 = 16
Потребности	b1 = 11	b2 = 16	b3 = 26	b4 = 20	-

Математическая модель транспортной задачи имеет вид

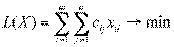
при ограничениях:

.

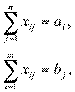
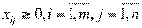Таким образом, целевая функция транспортной задачи имеет вид

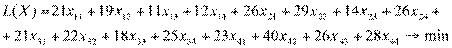
Ограничения транспортной задачи:

 .

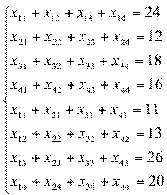
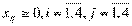. Начальное решение транспортной задачи

Найдем исходное опорное решение по методу минимальной стоимости. Для этого заполним распределительную таблицу:

		1	2	3	4
		11/0	13/6/0	26/2/0	20/10/0
1	24/0	21	19	11 24	12
2	12/2	26	29	14 2	26 10
3	18/7	21 11	22 7	18	25
4	16/6/0	23	40 6	26	28 10

Таким образом, все поставки распределены, получено начальное решение транспортной задачи:

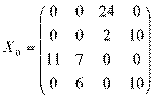
Значение целевой функции:

.

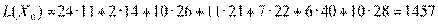. Решение транспортной задачи методом потенциалов

Проверка решения Х₀ на невырожденность. Количество ненулевых элементов в решении транспортной задачи Х₀ равно 7, ранг матрицы rang X = m + n - 1 = 4 + 4 - 1= 7. Поскольку 7= 7, то условие невырождености выполнено.

Проверка решения Х₀ на оптимальность.

Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец u_i и строку v_j: Полагаем u₁ = 0, запишем это значение в последнем столбце первой строки таблицы. Находим оставшиеся потенциалы.

Таким образом, найдены все значения потенциалов:

		1	2	3	4	Ui
		11	13	26	20
1	24	21	19	11 24	12	0
2	12	26	29	14 2	26 10	3
3	18	21 11	22 7	18	25	-13
4	16	23	40 6	26	28 10	5
Vj		34	35	11	23

Вычисляем оценки свободных клеток:

,

,

,

,

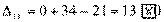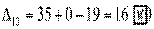
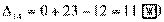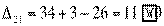
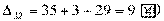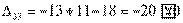
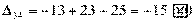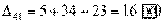
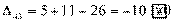
Получили шесть положительных оценок свободных клеток: Δ₁₁₌ 13, Δ₁₂ = 16, Δ₁₄ = 11, Δ₂₁ =11Δ₂₂ = 9, Δ₄₁ = 16. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.

24                                       14                   10

2                 10                    12                    0

		1	2	3	4	Ui
		11	13	26	20
1	24	21	19	11 14	12 10	0
2	12	26	29	14 12	26	3
3	18	21 11	22 7	18	25	-2
4	16	23	40 6	26	28 10	16
Vj		23	24	11	12

,

,

,

,

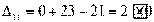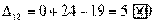
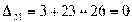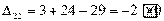
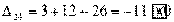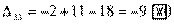
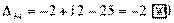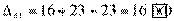
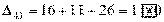
Получили три положительных оценки свободных клеток: Δ₁₁₌ 2, Δ₁₂ = 5, Δ₄₁ = 16. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.

  11               7            5                 13

    

                    6              6                 0

		1	2	3	4	Ui
		11	13	26	20
1	24	19	11 14	12 10	0
2	12	26	29	14 12	26	3
3	18	21 5	22 13	18	25	14
4	16	23 6	40	26	28 10	16
Vj		7	8	11	12

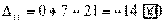
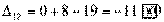
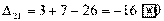
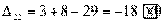
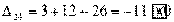
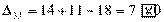
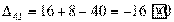
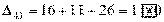
Получили три положительных оценки свободных клеток: Δ₃₃₌ 7, Δ₃₄ = 1, Δ₄₃ = 1. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.

5                                                      5

   

6                 10              11          5

		1	2	3	4	Ui
		11	13	26	20
1	24	21	19	11 14	12 10	0
2	12	26	29	14 12	26	3
3	18	21	22 13	18	25 5	13
4	16	23 11	40	26	28 5	16
Vj		7	9	11	12

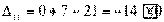
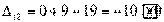
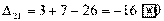
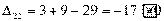
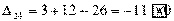
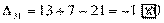
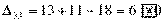
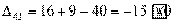
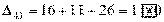
Получили две положительные оценки свободных клеток: Δ₃₃₌ 6, Δ₄₃ = 1. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.

14                 10           9            15

   

5.           5         

		1	2	3	4	Ui
		11	13	26	20
1	24	21	19	11 9	12 15	0
2	12	26	29	14 12	26	3
3	18	21	22 13	18 5	25	7
4	16	23 11	40	26	28 5	16
Vj		7	15	11	12

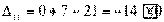
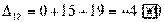
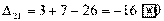
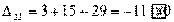
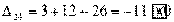
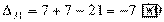
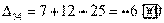
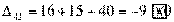
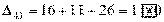
Получили одну положительную оценку свободной клетки: Δ₄₃ = 1.

Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.

9                   15            4                 20

   

                     5              5      

		1	2	3	4	Ui
		11	13	26	20
1	24	21	19	11 4	12 20	0
2	12	26	29	14 12	26	3
3	18	21	22 13	18 5	25	7
4	16	23 11	40	26 5	28	15
Vj		8	15	11	12

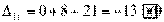
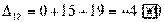
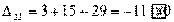
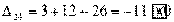
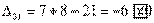
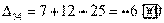
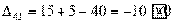
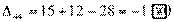
Все оценки свободных клеток положительные, следовательно, решение оптимально. Значение целевой функции:

L (x) min=4*11+20*12+12*14+13*22+5*18+11*23+5*26=1211

Таким образом, решение транспортной задачи:

 

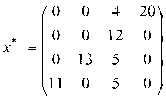
Решение транспортной задачи в среде Microsoft Exсel

Ввод исходных данных (в области C3: F6 - тарифы на перевозку продукции; в столбце H3: H6 - запасы; в ячейках С7, D7, E7, F7 - потребности).

В области решения в ячейке H10 введите формулу стоимости перевозок: =СУММПРОИЗВ (C13: F16; C3: F6). Для этого необходимо нажать на значок f (x) на панели инструментов, выбрать математическую функцию СУММПРОИЗВ и ввести два массива C13: F16 и C3: F6. Далее в области C12: F15 проставьте любое первоначальное решение (например, единицы) / В ячейке С16 записывается формула: =СУММ (C13: C15), т.е. сумма значений по столбцу (можно выделить значения столбца и нажать на знак автосуммы Σ на панели инструментов). Аналогично в C18, D18, E18, F18. Автоматически суммируются значения по столбцам.

В ячейке H13 записывается формула: =СУММ (C13: F15), т.е. сумма значений по строке (можно выделить значения строки и нажать на знак автосуммы Σ на панели инструментов). Аналогично в H13, H14, H15, H16. Автоматически суммируются значения по строкам:

Далее выполняют команду Поиск решения (вкладка Сервис или Данные).

Установить целевую ячейку H9, равной минимальному значению.

В поле ввода Изменяя ячейки установить C13: F16

В поле ввода Ограничения установить C13: F16>= 0

C7: F7 = C18: E18: H6 = H13: H16

Далее нажимают на кнопку Параметры и устанавливают флажок на метод поиска сопряженных градиентов:

Вычисления производятся при нажатии кнопки Выполнить два раза. Получим решение задачи:

Обоснование ценовой стратегии

Предприятие может выпускать m видов продукции, получая при этом прибыль (убытки), зависящие от спроса. Спрос может принимать n состояний. Известна матрица Н прибыли (убытка), которую получит предприятие при выпуске i-й продукции при j-м состоянии спроса.

Обоснование ценовой стратегии:

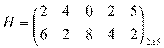
Определим нижнюю цену игры - α. Нижняя цена игры α - это максимальный выигрыш, который мы можем гарантировать себе, в игре против разумного противника, если на протяжении всей игры будем использовать одну и только одну стратегию (такая стратегия называется "чистой").

Найдем в каждой строке платежной матрицы минимальный элемент и запишем его в дополнительный столбец

Затем найдем максимальный элемент дополнительного столбца (отмечен звездочкой), это и будет нижняя цена игры.

Стратегии "A"	Стратегии "B"					Минимумы строк
	B1	В2	В3	B4	B5
A1	2	4	0	2	5	0
A2	6	2	8	4	2	2*

В нашем случае нижняя цена игры равна: α = 2, и для того чтобы гарантировать себе выигрыш не хуже чем 2 мы должны придерживаться стратегии A2.

Определим верхнюю цену игры - β

Верхняя цена игры β - это минимальный проигрыш, который может гарантировать себе игрок "В", в игре против разумного противника, если на протяжении всей игры он будет использовать одну и только одну стратегию.

Найдем в каждом столбце платежной матрицы максимальный элемент и запишем его в дополнительную строку снизу

Затем найдем минимальный элемент дополнительной строки (отмечен плюсом), это и будет верхняя цена игры.

Стратегии "A"	Стратегии "B"					Минимумы строк
	B1	В2	В3	B4	B5
A1	2	4	0	2	5	0
A2	6	2	8	4	2	2
Максимумы столбцов	6	4*	8	4*	5

В нашем случае верхняя цена игры равна: β = 4, и для того чтобы гарантировать себе проигрыш не хуже чем 4 противник (игрок "B") должен придерживаться стратегии B4 или В2

Сравним нижнюю и верхнюю цены игры, в данной задаче они не совпадают, т.е. α ≠β ⇒ 2υ4. Это значит, что игра не имеет Седловой точки.

Способ - аналитический:

Выполним доминирование. Для этого вычеркнем 1,3,5 столбцы.

⇒

 

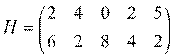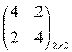
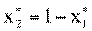
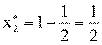
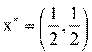
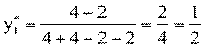
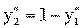
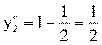
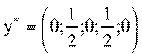
Цена игры:

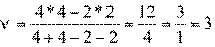
Способ - графический:

Выполним доминирование. Для этого вычеркнем 1столбец.

⇒

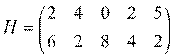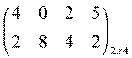
Чистые стратегии 2 игрока	Ожидаемые выигрыши 1 игрока
1	(4-2) *х1+2= 2*х1+2
2	(0-8) * х1+8= - 8*х1+8
3	(2-4) * х1+4= - 2* х1+4
4	(5-2) * х1+2= 3*х1+2

*х1+2= - 2* х1+4

*х1=2

х1=,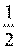

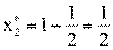
v=2* х1+ 2=2*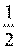+2=1+2=3

v = 3

Оптимальная стратегия 1 игрока:

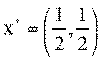
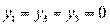
Чистые стратегии 1 игрока	Ожидаемые проигрыши 2 игрока
1
2

,

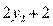
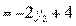
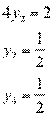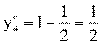
V=2* 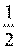 +2=3

Оптимальная стратегия 2 игрока:

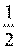Y*= (0; 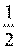; 0; ; 0)

Проверка:

Х* ∙ Н ∙ Y*^T= V (H)

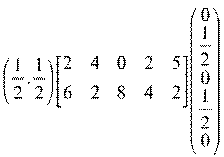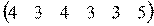
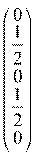==3

=3

Решим данную игру на компьютере.

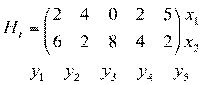
ПЗЛП:

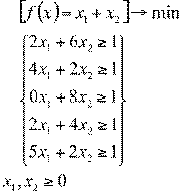
X*= (0,5; 0,5)

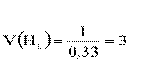
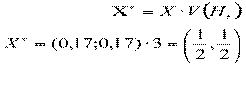
ДЗЛП:

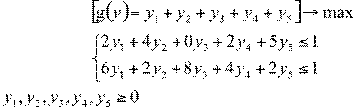
Обоснование распределения финансовых ресурсов между проектами

На развитие трех предприятий выделено В млн. руб. Известна эффективность капитальных вложений x_i в каждое j-е предприятие, заданная таблично значением нелинейной функции f_j (x_i), где 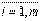, , n - количество предприятий, m - количество возможных сумм капитальных вложений.

Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.

Исходные данные варианта:

Объем капиталовложений Xi (тыс. руб.)	Прирост выпуска продукции ѓі (Xi) в зависимости от объема капиталовложений (тыс. руб.)
	предприятие 1	предприятие 2	предприятие 3
0 100 200 300 400 500 600 700	0 50 80 90 150 190 210 220	0 50 60 120 130 190 230 250

Математическая модель задачи.

,

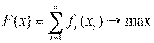
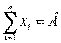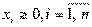
Математическая модель задачи варианта 0:

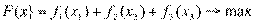
при ограничениях:

,

.

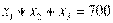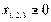Условная оптимизация.

Максимально возможный доход, который может быть получен с предприятий (с k-го по n-е), определяется с помощью функции Беллмана:

,

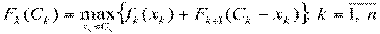где С_k - количество средств, инвестируемых в k-е предприятие, 0≤ С_k ≤ В.

На первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может остаться количество средств С_n, 0 ≤ С_n ≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т.е. F_n (С_n) = f_n (С_n) и х_n = С_n.

Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах x_i = {0, 100, 200, 300, 400, 500, 600, 700} тыс. руб.

Решение.этап. Условная оптимизация.

-й шаг: k = 3.

x3 C3	0	100	200	300	400	500	600	700	F3 (C3)
0	0								0	0
100		50							50	100
200			60						60	200
300				120					120	300
400					130				130	400
500						190			190	500
600							230		230	600
700								250	250	700

В шапке таблицы отражены варианты значений капиталовложений х₃, которые могут быть предоставлены третьему предприятию. В столбце C₃ отражены варианты значений капиталовложений, которые могут быть выделены всем трем предприятиям в совокупности.

Предположим, что все средства в количестве x₃ = 700 тыс. руб. отданы третьему предприятию. В этом случае максимальный доход составит f₃ (x₃) = 700 тыс. руб., следовательно: F₃ (C₃) = f₃ (x₃) и x₃ = C₃.

-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:

.

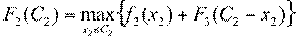Представим в таблице расчет функции Беллмана.

Таблица 2

x2 C2	0	100	200	300	400	500	600	700	F2 (C2)
0	0+0								0	0
100	0+50	50+0							50	0/100
200	0+60	50+50	80+0						100	100
300	0+120	50+60	80+50	90+0					130	200
400	0+130	50+120	80+60	90+50	150+0				170	100
500	0+190	50+130	80+120	90+60	150+50	190+0			200	200/400
600	0+230	50+190	80+130	90+120	150+60	190+50	210+0		240	100/500
700	0+250	50+230	80+190	90+130	150+120	190+60	210+50	220+0	280	100

В шапке таблицы отражены варианты значений капиталовложений х₂, которые могут быть предоставлены второму предприятию при условии, что часть средств выделяется третьему предприятию. В клетках таблицы первое слагаемое - это возможный прирост выпуска продукции второго предприятия f₂ (х₂) в результате освоения капиталовложений х₂; второе слагаемое - значение функции Беллмана, полученной на предыдущем шаге F₃ (C₂ - х₂), т.е. возможный прирост выпуска продукции третьего предприятия, если ему будет выделена оставшаяся часть капиталовложений, определяемая как C₂ - х₂. 3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:

,

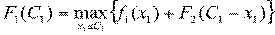на ее основе составлена табл.3.

В шапке таблицы отражены варианты значений капиталовложений х₁, которые могут быть предоставлены первому предприятию при условии, что часть средств выделяется второму и третьему предприятию. В клетках таблицы первое слагаемое - это возможный прирост выпуска продукции первого предприятия f₁ (х₁) в результате освоения капиталовложений х₁; второе слагаемое - значение функции Беллмана, полученной на предыдущем шаге F₂ (C₁-х₁), т.е. возможный прирост выпуска продукции второго и третьего предприятий, если им будет выделена оставшаяся часть капиталовложений, определяемая как C₁ - х₁.

Таблица 3

x1 C1	0	100	200	300	400	500	600	700	F1 (C1)
0	0+0								0	0
100	0+50	40+0							50	0
200	0+100	40+50	60+0						10	0
300	0+130	40+100	60+50	100+0					140	100
400	0+170	40+130	60+100	100+50	120+0				170	0/100
500	0+200	40+170	60+130	100+100	120+50	180+0			210	100
600	0+240	40+200	60+170	100+130	120+100	180+50	190+0		240	0/100
700	0+280	40+240	60+200	100+170	120+130	180+100	190+50	220+0	280	0/100/500

Значение функции Беллмана F₁ (С₁) представляет собой максимально возможный доход со всех предприятий, а значение 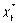, на котором достигается максимум дохода, является оптимальным количеством средств, вложенных в первое предприятие.

Значение целевой функции равно максимальному значению функции Беллмана F₁ (С₁) из табл.3.

Следовательно, значение целевой функции равно F_max (x^*) = 280 тыс. руб.этап. Безусловная оптимизация.

Далее на этапе безусловной оптимизации для всех последующих шагов вычисляется величина С_k = (С_k-1 - х_k-1) оптимальным управлением на k-м шаге является то значение х_k, которое обеспечивает максимум дохода при соответствующем состоянии системы S_k.

Определяем компоненты оптимальной стратегии. Для этого значения функций Беллмана и соответствующие им оптимальные значения х вносим в итоговую табл.4.

Таблица 4.

C1	F3 (C3)		F2 (C2)		F1 (C1)
0	0	0	0	0	0	0
100	50	100	50	0/100	50	0
200	60	200	100	100	10	0
300	120	300	130	200	140	100
400	130	400	170	100	170	0/100
500	190	500	200	200/400	210	100
600	230	600	240	100/500	240	0/100
700	250	700	280	100	280	0/100/500

-й шаг. По данным из табл.4 максимальный доход при распределении 700 тыс. руб. между тремя предприятиями составляет: C₁ = 700, F₁ (700) = 280 тыс. руб.

При этом возможны следующие варианты.

Первому предприятию нужно выделить:

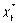) = 0 тыс. руб.;

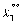) = 100 тыс. руб.;

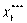) = 500 тыс. руб.

-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:

) С₂ = C₁ - 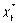= 700 - 0 = 700 тыс. руб.;

) С₂ = C₁ - 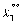= 700 - 100 = 600 тыс. руб.;

) С₂ = C₁ - 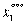= 700 - 500 = 200 тыс. руб.

По данным табл.4 находим, что оптимальный вариант распределения между вторым и третьим предприятиями денежных средств размером:

) 700 тыс. руб. составляет: F₂ (700) = 280 тыс. руб. при выделении второму предприятию 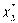= 100 тыс. руб.;

) 600 тыс. руб. составляет: F₂ (600) = 240 тыс. руб. при выделении второму предприятию 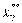= 100/500 тыс. руб.;

) 200 тыс. руб. составляет: F₂ (200) = 100 тыс. руб. при выделении второму предприятию 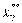= 100 тыс. руб.

-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия:

) С₃ = C₂ - 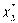 = 700 - 100 = 600 тыс. руб.;

) С₃ = C₂ - 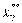 = 600 - 100 =500;

С₃ = C₂ - 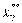 = 600 - 500 =100;

) С₃ = C₂ - 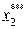= 200 - 100 = 100 тыс. руб.

По данным табл.4 находим:

) F₃ (600) = 230 и 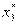= 600 тыс. руб.;

) F₃ (500) = 190 и 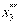=500 тыс. руб.;

F₃ (100) = 50 и 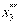=100 тыс. руб.;

) F₃ (100) = 50 и 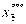= 100 тыс. руб.

Таким образом, возможны два альтернативных варианта оптимального плана инвестирования предприятий:

) х^* = (0, 100, 600),

F (700) = f₁ (0) + f₂ (100) + f₃ (600) = 0 + 50 + 230 = 280 тыс. руб.;

) х^** = (100, 100/500, 500/100),

F (700) = f₁ (100) + f₂ (100/500) + f₃ (500/100) = 50 + 50 + 200+190+50 = 540 тыс. руб.

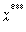) = (500, 100, 100),

F (700) = f₁ (500) + f₂ (100) + f₃ (100) = 210 + 50 + 50 =310 тыс. руб.

Заключение

В данной курсовой работе были рассмотрены различные методы, обосновывающие принятие оптимальных решений для хлебозавода, специализирующегося на продаже выпечки и кондитерских изделий.

Мною были рассмотрены простой и двойственный симплекс-метод решения задач линейного программирования, метод потенциалов решения транспортной задачи, а также методы решения антагонистических игр и задач линейного программирования.

Использование данных методов может значительно облегчить процесс принятия решений на предприятии и повысить его эффективность.

Список использованной литературы

1.      Васин А.А. Исследование операций: учеб. пособие для вузов / А.А. Васин, П.С. Краснощеков, В.В. Морозов. - М.: Академия, 2008. - 464 с.

2.      Горбунова Р.И. Экономико-математические методы и модели: учеб. пособие / Р.И. Горбунова [и др.]; под ред.С.И. Макарова. - М.: КНОРУС, 2007. - 232с.

.        Методические указания по выполнению курсовой работы: Н.Е. Гучек, 2012

.        Исследование операций в экономике: учеб. пособие для вузов / Н.Ш. Кремер [и др.]; под ред.Н.Ш. Кремера. - 2-е изд., перераб. и доп. - М.: Юрайт, 2010. - 431 с.

.        Солодовников А.С. Математика в экономике: учебник для вузов. Ч.1/А.С. Солодовников [и др.]. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2007. - 384с.