Исследование проблемы автокорреляции (первого порядка) случайных отклонений с помощью теста Сведа-Эйзенхарта и статистики Дарбина-Уотсона

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Экономический факультет

Кафедра аналитической экономики и эконометрики

КУРСОВОЙ ПРОЕКТ

на тему: Исследование проблемы автокорреляции (первого порядка) случайных отклонений с помощью теста Сведа-Эйзенхарта и статистики Дарбина-Уотсона

Студентки 3 курса Т.С. Ефременко

Научный руководитель Е.Г. Господарик

Минск, 2013

Содержание

Введение

1. Построение и анализ модели

2. Методы выявления автокорреляции

2.1 Графический метод

2.2 Метод Дарбина-Уотсона

2.3 Метод Сведа-Эйзенхарта

Заключение

Список использованных источников

Приложение 1

Приложение 2

Введение

Автокорреляция - это корреляция между наблюдаемыми показателями, упорядоченными во времени или в пространстве. Причиной возникновения автокорреляции отклонения модели, как правило служит то, что в модели не учтены такие свойства экономических показателей инерционность и "эффект паутины" В некоторых случаях причиной автокорреляции могут являться внутренние стохастические свойства, используемые для модели временных рядов.

Данная работа посвящена построению эконометрической модели и исследованию проблемы автокорреляции случайных отклонений с помощью теста Сведа-Эйзенхарта, статистики Дарбина-Уотсона и графического метода.

Для анализа будет использоваться модель зависимости ставки рефинансирования, рентабельности, валютного курса и платежй по экспорту товаров и услуг, доходам и трансфертам от консолидированного б, где 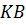 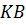(Консолидированный бюджет) - это свод бюджетов всех уровней, STR (Ставка рефинансирования) - размер процентов подлежащий уплате центральному банку страны за кредиты, предоставленные кредитным организациям., ROA (рентабельность) - относительный показатель экономической юджета Республики Беларусь.

В качестве данных используется динамика платежей, рентабельности, официального курса белорусского рубля по отношению к стоимости корзины валют, ставки рефинансирования и доходов в гос. Бюджет за период с июня 2010 по сентябрь 2013.

Соответствующие статистические данные представлены в приложении.

Для анализа модели будет использоваться эконометрический пакет Eviews. При помощи теста Сведа-Эйзенхарта, статистики Дарбина-Уотсона и графического метода будут проверены остатки построенной модели на наличие автокорреляции. Целью данной работы является выявление методов автокорреляции отклонения модели временного ряда.

1. Построение и анализ модели

С помощью программы EViews 5.1, построим модели вида:

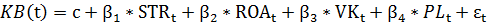
эффективности, VK (валютный курс) - Официальный курс белорусского рубля по отношению к стоимости корзины валют, PL (Платежи по экспорту товаров и услуг, доходам и трансфертам) - это поступления денежных средств от экспорта товаров и услуг нефинансового характера, другие поступления нефинансовых организаций и домашних хозяйств Республики Беларусь от нерезидентов в виде доходов от оплаты труда, инвестиций за границей, текущих и капитальных трансфертов из-за рубежа. Исходные данные представлены в Приложении А.

автокорреляция модель отклонение статистика

По этим данным строим регрессионную модель и анализируем её впоследствии:

KB = - 93728.8823 + 23.92811788*PL + 4871.123628*ROA - 3486.350193*STR + 51.81899603*VK

Задача состоит в оценке параметров множественной линейной регрессии, а также проверке как индивидуальной статистической значимости коэффициентов, так и общего качества модели.

.        Статистическая значимость коэффициента детерминации.

Для характеристики общего качества модели регрессии вводится величина, называемая коэффициент детерминации, равный в нашем случае R² = 0.591073. Эта величина показывает, какую долю общей вариации эндогенной переменной VK объясняет построенная модель. Другими словами, модель объясняет до 59% правильности модели, а 41% составляют ошибки.

Анализ происходит на основе F-статистики, для этого выдвигаются две гипотезы:

Н₀: R²= 0 [статистически незначим]

Н₁: R² ≠ 0 [статистически значим]

Сначала определяем наблюдаемую точку:

F_н =         R²/m        = 13,6363

       1 - R²/ n-m-1

Затем сравниваем её с критической: F_{0.05; 4; 40} = 2.6060. Мы видим, что F_н> F_кр. Эти результаты говорят о том, что мы принимаем гипотезу Н₁ о значимости коэффициента.

Однако R² увеличивается при введении в модель экзогенной переменной, даже если последняя не коррелирует с переменной KB. Следовательно, необходимо проверить на значимость коэффициенты при объясняющих переменных.

.        Гипотеза о статистической значимости коэффициентов.

Анализ происходит на основе Т-статистики, для этого выдвигаем две гипотезы:

Н₀: b_i = 0

Н₁: b_i ≠ 0

Наши наблюдаемые параметры:

Наша критическая точка высчитывается по таблице распределения Стьюдента:

t _{0.025; 40}= 2.042.

Она больше, чем наблюдаемые t-статистики, следовательно мы принимаем гипотезу Н₁ о том, что коэффициенты являются статистически.

.        Проверка модели на мультиколлинеарность.

Чем ближе коэффициент к 1, тем теснее линейная связь. При величине коэффициента корреляции менее 0,3 связь оценивается как слабая, от 0,31 до 0,5 - умеренная, от 0,51 до 0,7 - значительная, от 0,71 до 0,9 - тесная, 0,91 и выше - очень тесная. Как мы видим, связь между переменными тесная.

Один из методов выявления - это метод инфляционных факторов VIF.

Проверим построенную модель на мультиколлинеарность:

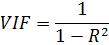
Вспомогательная модель для переменной VK:

VIF (VK) =3,764976

Вспомогательная модель для переменной STR

VIF (STR) =3,8871785

Вспомогательная модель для переменной ROA

VIF (ROA) =1,177654

Вспомогательная модель для переменной PL

VIF (PL) =1,3166193

Значение 1<VIF<10, что свидетельствует об отсутствии мультиколлинеарнности.

2. Методы выявления автокорреляции

2.1 Графический метод

По формальному признаку можно заподозрить автокорреляцию в модели, если t-статистика неправдоподобно высока. Анализ графической зависимости отклонений от наблюдаемой автокорреляции установлен при сравнительном графическом отклонении с известными функциями.

Построим корреляцию с помощью RESID модели VK и лагом этой же модели RESID (-2):

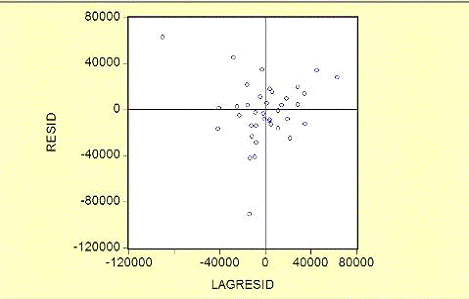
Рисунок 1. Корреляционное поле

В итоге мы видим распределение точек:

четверть - 12

четверть - 8

четверть - 10

четверть - 8.

По этим данным с полной уверенностью нельзя сказать есть ли корреляция, т.к. данные распределены достаточно равномерно, но всё же есть вероятность, из-за преобладания точек в 1 и 3 четвертях.

2.2 Метод Дарбина-Уотсона

Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий Дарбина-Уотсона.

Статистика Дарбина-Уотсона является важнейшей характеристикой качества регрессионной модели.

Суть его состоит в вычислении статистики Дарбина-Уотсона и на основе ее величины - осуществлении выводов об автокорреляции:

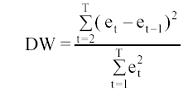
Статистика Дарбина-Уотсона тесно связана с выборочным коэффициентом корреляции :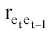

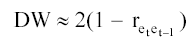
Таким образом, 0 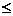 DW 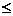 4 и его значения могут указать на наличие либо отсутствие автокорреляции.

Если выборочный коэффициент корреляции равен 0 (автокорреляция отсутствует), то DW = 2.

Если выборочный коэффициент корреляции равен 1 (положительная автокорреляция), то DW = 0.

Если выборочный коэффициент корреляции равен - 1 (отрицательная автокорреляция), то DW = 4.

Разработаны специальные таблицы критических точек статистики Дарбина-Уотсона, позволяющие при данном числе наблюдений n, количестве объясняющих переменных m и заданном уровне значимости 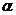 определять границы приемлемости (критические точки) наблюдаемой статистики DW.

Для заданных n, m, 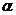 в таблице указывается два числа: d 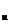- верхняя граница и d 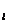- нижняя граница.

Выводы осуществляются по следующей схеме.

Если DW < d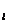, то это свидетельствует о положительной автокорреляции остатков.

Если DW > 4 - d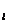, то это свидетельствует об отрицательной автокорреляции остатков,

При d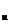< DW < 4 - d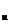, гипотеза об отсутствии автокорреляции остатков принимается.

Если d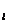 < DW < d 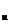или 4 - d 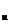< DW < 4 - d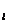, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.

Не обращаясь к таблице критических точек Дарбина-Уотсона, можно пользоваться "грубым" правилом и считать, что автокорреляция остатков отсутствует, если 1,5 < DW < 2,5. Для более надежного вывода следует обращаться к таблицам.

При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным.

Нужно отметить, что при использовании критерия Дарбина-Уотсона необходимо учитывать следующие ограничения:

1)      Критерий DW применяется лишь для тех моделей, которые содержат свободный член.

2)      Предполагается, что случайные отклонения определяются по следующей итерационной схеме: 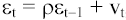, называемой авторегрессионной схемой первого порядка АR (1). Здесь V - случайный член.

)        Статистические данные должны иметь одинаковую периодичность, т.е. не должно быть пропусков в наблюдениях.

)        Критерий Дарбина-Уотсона не применим для регрессионных моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период, т.е. для так называемых авторегрессионных моделей вида:

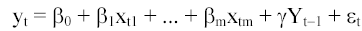
Для авторегрессионных моделей разработаны специальные тесты обнаружения автокорреляции, в частности h-статистика Дарбина, которая определяется по формуле:

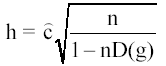
где 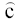 - оценка автокорреляции первого порядка,

D (g) - выборочная дисперсия коэффициента при лаговой переменной у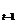,- число наблюдений.

При большом объеме выборки n и справедливости нулевой гипотезы Н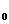: 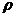=0 статистика h имеет стандартизированное нормальное распределение (h ~ N (0, 1)). Поэтому по заданному уровню значимости определяется критическая точка 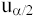 из условия 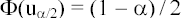и сравнивается h с 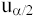. Если 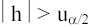, то нулевая гипотеза об отсутствии автокорреляции должна быть отклонена. В противном случае она не отклоняется,

Обычно значение 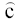 рассчитывается по формуле 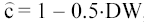, а D (g) равна квадрату стандартной ошибки оценки g коэффициента 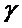. Поэтому h легко вычисляется на основе данных оцененной регрессии.

Основная проблема с использованием этого теста заключается в невозможности вычисления h при nD (g) > 1.

Согласно данным, полученным в Eviews, наблюдаемая точка DW = 1.375019

Затем, опираясь на данные, что количество объясняющих переменных в уравнении регрессии m=4, a объем выборки n=40, находим критические точки по таблице распределения Дарбина-Уотсона:

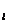= 1.285, d=1.721

Согласно полученным данным, нарисуем следующую схему:

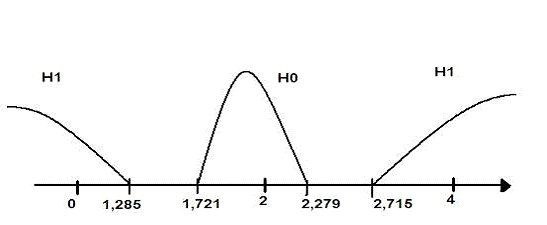
Следовательно, гипотеза об отсутствии автокорреляции первого порядка не может быть ни принята, ни отклонена.

2.3 Метод Сведа-Эйзенхарта

В методе необходимо подсчитать количество положительных и отрицательных отклонений, а также выделить в ряду отклонений подрядов последовательных отношений имеющих один знак. Количество таких подрядов обозначить "к".

При использовании метода рядов последовательно определяются знаки отклонений е. Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.

Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция.

Для более детального анализа предлагается следующая процедура. Пусть:

·        n - объем выборки;

·        n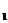 - общее количество знаков "+" при n наблюдениях (количество положительных отклонений е);

·        n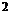 - общее количество знаков " - " при n наблюдениях (количество отрицательных отклонений е);

·        к - количество рядов.

При достаточно большом количестве наблюдений (n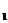|> 10, n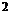> 10) и отсутствии автокорреляции мы имеем асимптотически нормальное распределение с

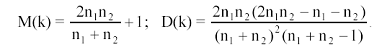
Тогда, если:

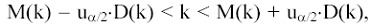
то гипотеза об отсутствии автокорреляции не отклоняется.

При небольшом числе наблюдений (n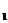|> 20, n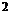> 20) Свед и Эйзенхарт разработали таблицы критических значений количества рядов при n наблюдениях.

Суть таблиц заключается в следующем.

На пересечении строки n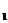 и столбца n 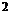определяются нижнее к 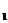и верхнее к 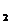значения при уровне значимости 5%.

Если к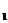 < к < к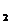, то говорят об отсутствии автокорреляции.

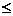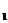Если к  к , то говорят о положительной автокорреляции остатков.

Если к 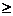 к, то говорят об отрицательной автокорреляции остатков,

Этот метод основан на определении знаков отклонений RESID (см. Приложение Б).

На примере нашей модели:

"+", 6"-", 7"+", 7"-", 2"+", 5"-", 2"+",2"-", 6"+" при 40 наблюдениях.

Рядом называется непрерывная последовательность одинаковых знаков, то есть количество рядов в данной модели k=11.

По таблице критических значений количества рядов при n наблюдениях определяем нижнее k₁ = 2 и верхнее k₂ = 9. Наша переменная k = 9 находится в промежутке k₁ < k < k_2, что говорит об отсутствии автокорреляции или о её слабом проявлении.

Заключение

В данной работе был произведен анализ построения эконометрической модели и исследования проблемы автокорреляции случайных отклонений с помощью теста Сведа-Эйзенхарта, статистики Дарбина-Уотсона и графического метода. Все эти подходы дополняют друг друга. Первоначальный анализ коррелограммы остатков позволяет определить наиболее вероятный порядок серийной корреляции, если она существует. Для критического уровня значимости α = 5% коэффициенты при экзогенных переменных являются статистически значимыми. В целом модель оказалась качественной, адекватной, в ней отсутствует мультиколлинеарность, ошибки распределены по нормальному закону. Ее недостатком является завышенная F-статистика.

Список использованных источников

1.      Вводный курс эконометрики: Учебное пособие / Бородич С.А. - Мн.: БГУ, 2000.

2.      НАЦИОНАЛЬНЫЙ БАНК РЕСПУБЛИКИ БЕЛАРУСЬ [Электронный ресурс]. - 2013. - Режим доступа: http://www.nbrb. by/statistics/bulletin/ - Дата доступа: 15.12.2013.

Приложение 1