Численные методы
Задание № 1
Найти решение системы 4 линейных уравнений с
4-мя неизвестными х1,х2, х3, х4 с
точностью до 10-4 следующими методами:
а) методом Гаусса;
б) методом простой итерации;
в) методом Зейделя.
Проверкой полученного решения является
совпадение найденных разными методами решений с заданной точностью.
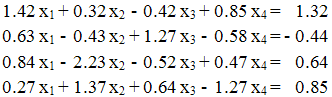
а) метод Гаусса.
Найти решение системы уравнений:
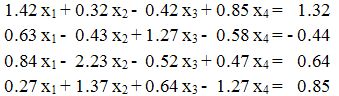
1. Сформируем расширенную матрицу:
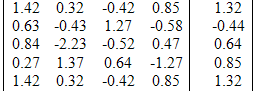
Применяя к расширенной матрице,
последовательность элементарных операций стремимся, чтобы каждая строка, кроме,
быть может, первой, начиналась с нулей, и число нулей до первого ненулевого
элемента в каждой следующей строке было больше, чем в предыдущей.
2. Разделим строку 1 на a11 = 1.42
Получим матрицу:
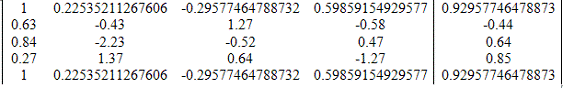
3. Вычтем из строки
2 строку 1 умноженную на a21= 0.63
Вычитаемая строка:
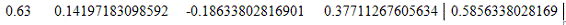
Модифицированная матрица:
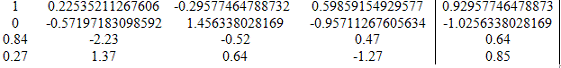
4. Вычтем из строки
3 строку 1 умноженную на a31= 0.84
Вычитаемая строка:
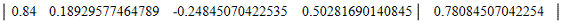
Модифицированная матрица:
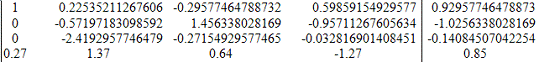
5. Вычтем из строки
4 строку 1 умноженную на a41= 0.27
Вычитаемая строка:

Модифицированная матрица:
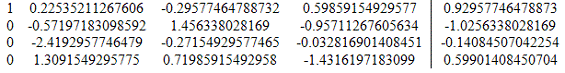
6. Разделим строку 2 на a22 = -0.57197183098592
Получим матрицу:
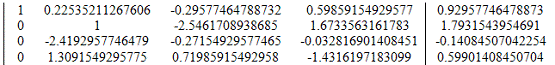
7. Вычтем из строки 3 строку 2 умноженную на a32= -2.4192957746479
Вычитаемая строка:
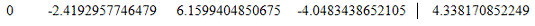
Модифицированная матрица:
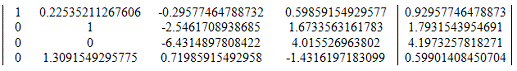
8. Вычтем из строки 4 строку 2 умноженную на a42= 1.3091549295775
Вычитаемая строка:
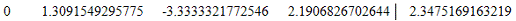
Модифицированная матрица:
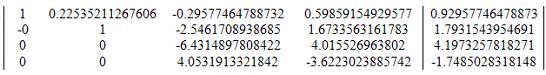
9. Разделим строку 3 на a33 = -6.4314897808422
Получим матрицу:
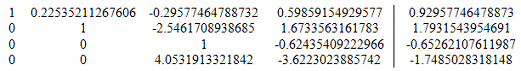
10. Вычтем из строки 4 строку 3 умноженную на a43=
4.0531913321842
Вычитаемая строка:
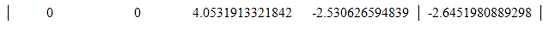
Модифицированная матрица:
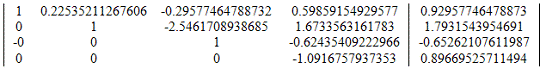
11. Разделим строку 4 на a44 = -1.0916757937353
Получим матрицу:
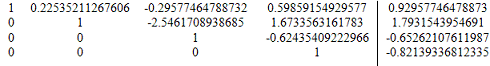
12. Вычтем из строки 3 строку 4 умноженную на a34=
0.62435409222966
Вычитаемая строка:
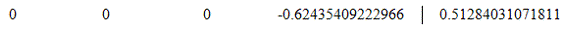
Модифицированная матрица:
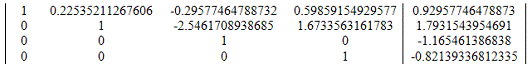
13. Вычтем из строки 2 строку 4 умноженную на a24=1.6733563161783
Вычитаемая строка:
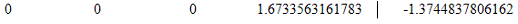
Модифицированная матрица:
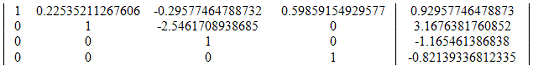
14. Вычтем из
строки 1 строку 4 умноженную на a14=0.59859154929577
Вычитаемая строка:
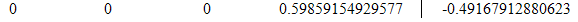
Модифицированная матрица:
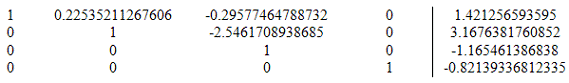
Вычитаемая строка:
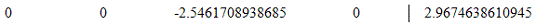
Модифицированная матрица:
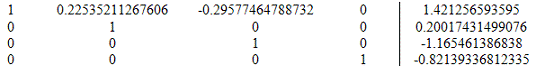
16. Вычтем из строки 1 строку 3 умноженную на a13=0.29577464788732
Вычитаемая строка:
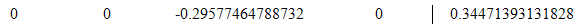
Модифицированная матрица:
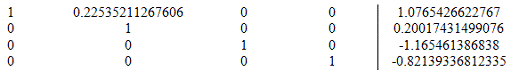
17. Вычтем из строки 1 строку 2 умноженную на a12=0.22535211267606
Вычитаемая строка:
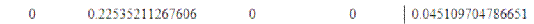
Модифицированная матрица:
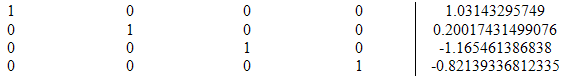
Выпишем систему уравнений по последней
расширенной матрице:
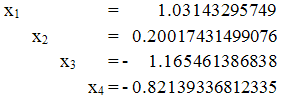
Заданная система уравнений имеет единственное
решение:
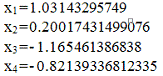
б) метод простой итерации.
Найти решение системы уравнений:
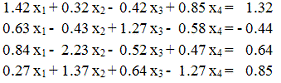
Заметим, что метод простой итерации расходится,
т. к. не выполняется условие преобладания диагональных элементов:
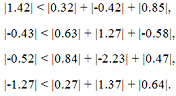
Пусть требуемая точность e
= 10-4.
Приведем систему к виду:
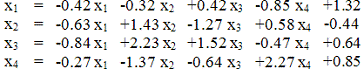
Последовательно вычисляем:
Шаг 1.
В качестве начального приближения возьмем
элементы столбца свободных членов: (1.32, -0.44, 0.64, 0.85).

Шаг 2.
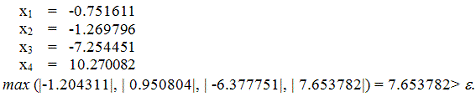
Шаг 3.
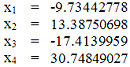
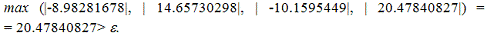
Ответ: итерационный процесс расходится.
в) метод Зейделя.
Найти решение системы уравнений:
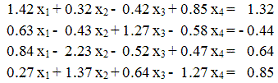
Заметим, что метод Зейделя расходится, т. к. не
выполняется условие преобладания диагональных элементов:
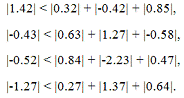
Пусть требуемая точность e
= 10-4.
Приведем систему к виду:
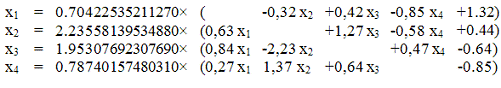
Последовательно вычисляем:
Шаг 1.
В качестве начального приближения возьмем: (0,
0, 0, 0).
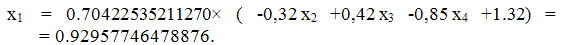
= 0.92957746478876.
При вычислении x2 используем уже
полученное значение x1:
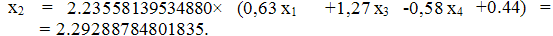
При вычислении x3 используем уже
полученное значение x1 и x2:
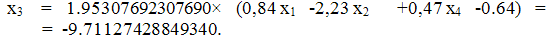
При вычислении x4 используем уже
полученное значение x1, x2
и x3:
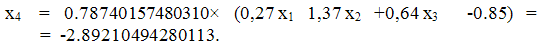
Шаг 2.
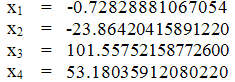
Шаг 3.
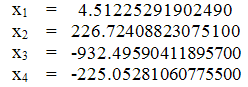
Ответ: итерационный процесс расходится.
Задание № 2
Отделить один корень уравнения x4+2x-1=0
и
вычислить его на полученном отрезке [а,b] с точностью до 0.0001 тремя методами:
а) методом дихотомии;
б) методом хорд;
в) методом простой итерации.
Убедиться, что корни, полученные при помощи этих
методов, удовлетворяют уравнению F(х) = 0 и мало отличаются друг от друга.
[а,b]=[-1;2]
а) метод дихотомии

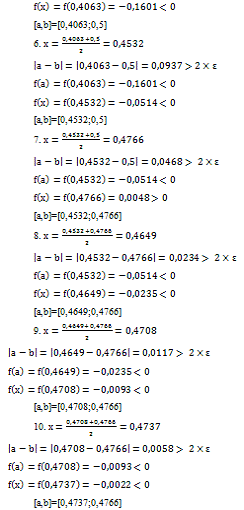





Ответ: 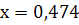
в) метод простой итерации
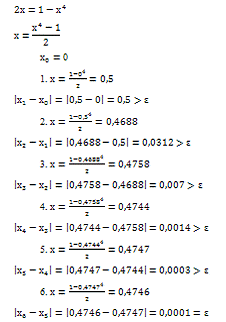
Ответ: 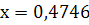
Задание № 3
уравнение итерация
интеграл симпсон
Найти приближённо значение интеграла с точностью
до 0,001 методом Симпсона.
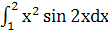
Начальное количество разбиений 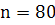 .
.
Имеем 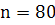 .
Отсюда
.
Отсюда 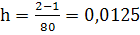 .
Результаты вычислений приведены в таблице.
.
Результаты вычислений приведены в таблице.
|
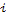
|
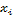
|
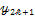
|
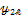
|
|
0
|
1
|
|
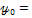 0,909297 0,909297
|
|
1
|
1,0125
|
0,921216
|
|
|
2
|
1,025
|
|
0,932285
|
|
3
|
1,0375
|
0,942458
|
|
|
4
|
1,05
|
|
0,951688
|
|
5
|
1,0625
|
0,959931
|
|
|
6
|
1,075
|
|
0,967141
|
|
7
|
1,0875
|
0,973273
|
|
|
8
|
1,1
|
|
0,978281
|
|
9
|
1,1125
|
0,982121
|
|
|
10
|
1,125
|
|
0,984749
|
|
11
|
1,1375
|
0,986121
|
|
|
12
|
1,15
|
|
0,986195
|
|
13
|
1,1625
|
0,984928
|
|
|
14
|
1,175
|
|
0,982278
|
|
15
|
1,1875
|
0,978204
|
|
|
16
|
1,2
|
|
0,972667
|
1,2125
|
0,965627
|
|
|
18
|
1,225
|
|
0,957046
|
|
19
|
1,2375
|
0,946886
|
|
|
20
|
1,25
|
|
0,935113
|
|
21
|
1,2625
|
0,92169
|
|
|
22
|
1,275
|
|
0,906585
|
|
23
|
1,2875
|
0,889764
|
|
|
24
|
1,3
|
|
0,871197
|
|
25
|
1,3125
|
0,850855
|
|
|
26
|
1,325
|
|
0,828709
|
|
27
|
1,3375
|
0,804732
|
|
|
28
|
1,35
|
|
0,7789
|
|
29
|
1,3625
|
0,751189
|
|
|
30
|
1,375
|
|
0,721578
|
|
31
|
1,3875
|
0,690046
|
|
|
32
|
1,4
|
|
0,656577
|
|
33
|
1,4125
|
0,621153
|
|
|
34
|
1,425
|
|
0,58376
|
|
35
|
1,4375
|
0,544386
|
|
|
36
|
1,45
|
|
0,503022
|
|
37
|
1,4625
|
0,459658
|
|
|
38
|
1,475
|
|
0,414288
|
|
39
|
1,4875
|
0,36691
|
|
|
40
|
1,5
|
|
41
|
1,5125
|
0,26612
|
|
|
42
|
1,525
|
|
0,212712
|
|
43
|
1,5375
|
0,157302
|
|
|
44
|
1,55
|
|
0,099898
|
|
45
|
1,5625
|
0,040508
|
|
|
46
|
1,575
|
|
-0,02086
|
|
47
|
1,5875
|
-0,08418
|
|
|
48
|
1,6
|
|
-0,14944
|
|
49
|
1,6125
|
-0,21662
|
|
|
50
|
1,625
|
|
-0,2857
|
|
51
|
1,6375
|
-0,35666
|
|
|
52
|
1,65
|
|
-0,42946
|
|
53
|
1,6625
|
-0,50408
|
|
|
54
|
1,675
|
|
-0,58049
|
|
55
|
1,6875
|
-0,65865
|
|
|
56
|
1,7
|
|
-0,73851
|
|
57
|
1,7125
|
-0,82005
|
|
|
58
|
1,725
|
|
-0,90323
|
|
59
|
1,7375
|
-0,98798
|
|
|
60
|
1,75
|
|
-1,07427
|
|
61
|
1,7625
|
-1,16205
|
|
|
62
|
1,775
|
|
-1,25126
|
|
63
|
1,7875
|
-1,34186
|
|
|
64
|
|
-1,43377
|
|
65
|
1,8125
|
-1,52694
|
|
|
66
|
1,825
|
|
-1,6213
|
|
67
|
1,8375
|
-1,7168
|
|
|
68
|
1,85
|
|
-1,81336
|
|
69
|
1,8625
|
-1,91092
|
|
|
70
|
1,875
|
|
-2,0094
|
|
71
|
1,8875
|
-2,10872
|
|
|
72
|
1,9
|
|
-2,20881
|
|
73
|
1,9125
|
-2,30959
|
|
|
74
|
1,925
|
|
-2,41097
|
|
75
|
1,9375
|
-2,51288
|
|
|
76
|
1,95
|
|
-2,61523
|
|
77
|
1,9625
|
-2,71793
|
|
|
78
|
1,975
|
|
-2,82089
|
|
79
|
1,9875
|
-2,92401
|
|
|
80
|
2
|
|
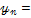 -3,02721 -3,02721
|
|
|
|
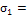 -6,854834099 -6,854834099
|
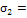 -7,942676655 -7,942676655
|
По формуле Симпсона получим:
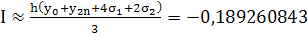 .
.
Подсчитаем погрешность полученного результата.
Полная погрешность 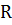 складывается из
погрешностей действий
складывается из
погрешностей действий 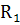 и остаточного
члена
и остаточного
члена 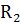 .
.
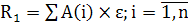 ,
,
где 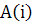 -
коэффициенты формулы Симпсона и
-
коэффициенты формулы Симпсона и 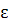 - максимальная
ошибка округления значений подынтегральной функции.
- максимальная
ошибка округления значений подынтегральной функции.
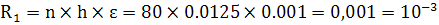
Оценим остаточный член.
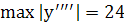 при
при 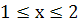 и,
следовательно,
и,
следовательно,
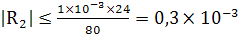 .
.
Таким образом, предельная полная погрешность
равна:
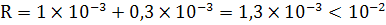
и, значит,  .
.
Ответ:  .
.
Задание № 4
Найти четыре первых, отличных от нуля члена
разложения в ряд частного решения дифференциального уравнения, удовлетворяющего
заданным начальным условиям и проверить это решение при помощи метода Пикара.
Оценить точность при применении метода Пикара.
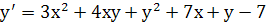
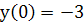
Последовательно дифференцируя уравнение
необходимое число раз, найдем четыре первых ненулевых производных функции 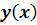 в
точке
в
точке 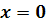 .
.
Таким образом, решение 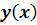 ,
с точностью до первых четырех ненулевых разложения в ряд, равно
,
с точностью до первых четырех ненулевых разложения в ряд, равно
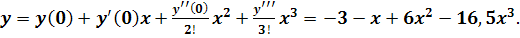
Решим методом Пикара уравнение 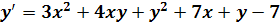 с
начальным условием
с
начальным условием 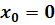 ,
, 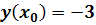 .
.
Переходим к интегральному уравнению:
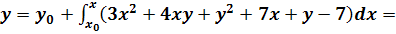
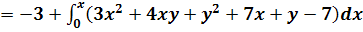
Получаем последовательность
приближений:
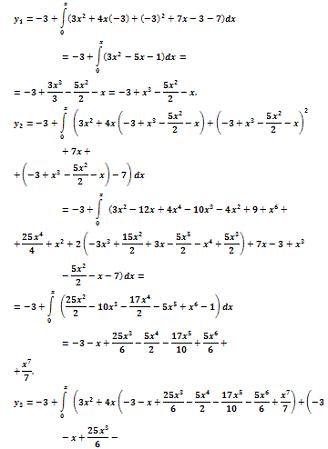
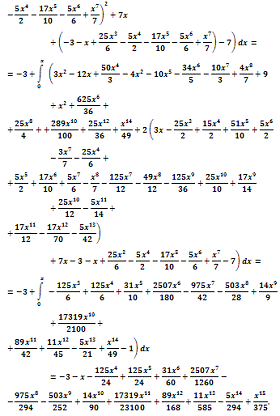
Видно, что при 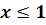 ряд
быстро сходится. Оценим погрешность третьего приближения. Так как функция
ряд
быстро сходится. Оценим погрешность третьего приближения. Так как функция 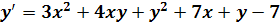 определена
и непрерывна во всей плоскости, то в качестве a и b можно взять любые числа.
Для определенности возьмем прямоугольник:
определена
и непрерывна во всей плоскости, то в качестве a и b можно взять любые числа.
Для определенности возьмем прямоугольник:
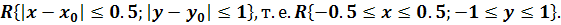
Тогда
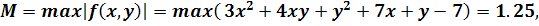
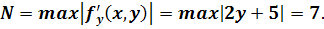
Поскольку a
= 0.25 , b/M
= 1/1.25 = 0.8, имеем h
= min (a,
b/M)
= 0.5.
Решение y
будет задано для 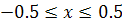 . При n=4
имеем:
. При n=4
имеем:
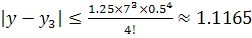
Список использованной литературы
1. Волков Е.А. Численные методы.-
М.: Наука, 1982.- 254 с.
. Заварыкин В.М., Житомирский В.Г.,
Ланчик М.П. Численные методы. -
М.: Просвещение, 1991. - 175 с.
. Калиткин Н.Н. Численные методы.-
М.: Наука, 1978.-512 с.
. Турчак Л.И. Основы численных
методов.- М.: Наука, 1987.- 319 с.