Численные методы решения уравнений
Содержание
Численные методы
§1. Приближённое решение уравнений
§2. Метод хорд
§3. Правило Ньютона (метод касательных)
§4. Комбинированный метод
§5. Метод итераций
§6. Интерполирование. Интерполяционная формула Лагранжа
§7. Дополнительный член формулы Лагранжа
§8. Интерполяционная формула Ньютона
§9. Интерполирование с кратными узлами. Формула Эрмита
§10. Эмпирические формулы
§11. Точечное квадратичное аппроксимирование функций
§12. Нормальная система определения коэффициентов для
метода наименьших квадратов
§13. Численное дифференцирование. Вычисление производной
по её определению
§14. Конечно-разностные аппроксимации производных
§15. Использование интерполяционных многочленов Лагранжа
для формул численного дифференцирования
§16. Численное интегрирование.Формула прямоугольников
§17. Формула трапеций
§18. Формула Симпсона (парабол)
§19. Приемы приближенного вычисления несобственных
интегралов
§20. Численное решение обыкновенных дифференциальных
уравнений. Понятие о численном решении задачи Коши
§21. Метод Эйлера
§ 22. Методы Рунге - Кутта
§23. Приближенное решение систем уравнений. Приближенное
решение систем линейных уравнений
§24. Приближенные методы решения систем нелинейных
уравнений
Численные методы
§1.
Приближённое решение уравнений
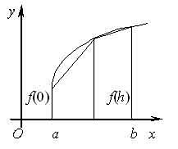
Рассмотрим задачу нахождения нулей функции f
(x), т.е. корней уравнения f (x) =0. предположим, что
интересующий нас корень x изолирован, т.е., что
найден содержащий его промежуток [a, b], в котором других корней
нет.
Если на концах отрезка [a, b]
функция f (x) имеет значения f (а) и f (b)
разных знаков, то по 1 теореме Больцано - Коши, деля на части [аk, bk], содержащее корень, и определяя знак функции f в точках
деления, можно произвольно сужать этот промежуток и таким образом осуществлять
приближённое вычисление корня. Такой метод называется методом половинного
деления. Однако этот приём, не смотря на его принципиальную простоту,
на практике часто оказывается непригодным, так как требует слишком большого
количества вычислений.
Рассмотрим основные приёмы приближённого вычисления
изолированного корня уравнения f (x) =0. При этом будем
использовать основные понятия и методы дифференцированного исчисления.
Теорема. Пусть выполнены следующие
условия:
(1) функция f в промежутке [a, b]
непрерывна вместе со своими производными f ¢ (x) и f ¢¢ (х);
(2) значения f (а) и f (b)
функции на концах промежутка имеют разные знаки f (а) f (b)
<0;
(3) обе производные f' (x) и f¢¢ (х) сохраняют каждая определённый
знак на всём промежутке [a, b].
Тогда уравнение f (x) =0 на этом
промежутке имеет единственный корень.
Следствия: Из непрерывности функции f
и условия (2) следует, что между а и b содержится корень x уравнения f (x) =0. Так как производная
f ¢ (x) сохраняет
знак, то f в промежутке [a, b] возрастает или убывает и,
следовательно, обращается в 0 лишь однажды, корень x изолирован.
Условие (3) геометрически означает, что кривая y=f
(x) не только идёт в одном направлении, но к тому же строго выпукла или
вогнута, смотря по знаку f ¢¢ (х).
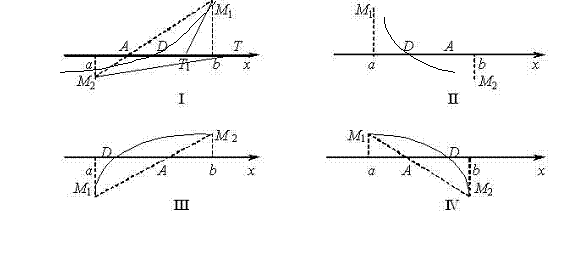
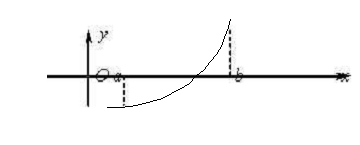
На чертеже изобразим 4 возможных случая, соответствующих различным
комбинациям знаков f ¢ (x) и f¢¢ (х).
§2.
Метод хорд
Если промежуток [a, b] достаточно
мал, то с приближением можно считать, что при изменении х в его пределах
- приращение функции f (x) пропорционально приращению аргумента.
Обозначая через x корень функции, имеем, в
частности,
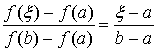 ,
,
откуда, с учётом того, что
численный метод дифференциальное уравнение
f (x) =0,x=a-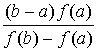 .
.
Таким образом, за приближённое значение
корня принимается число
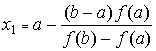 (1).
(1).
Это выражение можно представить и в такой
форме:
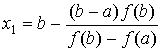 (2).
(2).
Изложенное правило получения приближённого
значения корня называется правилом пропорциональных частей. Оно
допускает простое геометрическое истолкование. Заменим дугу М1М2
хордой М1М2. Уравнение хорды может
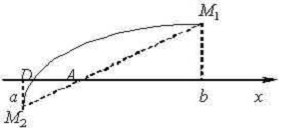
быть записано в виде:
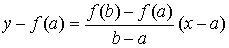 .
.
Правило по существу сводится к тому, что
вместо точки пересечения с осью Ox дуги М1М2
мы находим точку пересечения с осью Oх её хорды.
Действительно, полагая в уравнении хорды y=0
для абсциссы х1 точки D, мы получаем именно выражение
(1). В связи с этим правило пропорциональных частей называют методом хорд.
Рассмотрим вопрос о положении точки х1
по отношению к корню x. Ясно, что точка х1 лежит между а
и b, но с какой стороны от x?
В случаях I и IV А левее D,
а в случаях II и III - А правее D. Ограничимся случаями I и IV,
применим снова выведенное правило, на этот раз к промежутку [x1,
b], заменяя в (1) а на х1, получим новое
приближённое значение корня x:
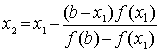 ,
,
содержащееся, по доказанному между х1
и x.
Этот процесс можно продолжать неограниченно и построить последовательность
возрастающих приближённых значений:
a<x1<x2<…<xn<…<x.
При этом любые два последовательных
значения хn и хn+1 связаны
формулой:
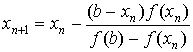 (3).
(3).
Очевидно, что 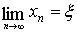 , т.к. (хn) -
возрастающая и ограниченная сверху числом
, т.к. (хn) -
возрастающая и ограниченная сверху числом 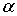 последовательность.
Если перейти к пределу в равенстве (3), используя при этом непрерывность
функции f, то получим, что
последовательность.
Если перейти к пределу в равенстве (3), используя при этом непрерывность
функции f, то получим, что
 ,
,
откуда f (a) =0. Т.к. других корней
уравнения f (x) =0, кроме x, в промежутке [a, b]
нет, то a =
x.
Таким образом, применив достаточное число раз указанное выше правило, можно
вычислить корень x с любой степенью точности. При этом остаётся открытым вопрос, как
оценить точность уже вычисленного приближённого значения хn.
Для решения его применим к разности f (xn) - f
(x)
формулу конечных приращений
f (xn) - f (x) = (xn-x) f' (c), x<c<xn (x>c>xn).
Отсюда 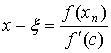 , если обозначить через m наименьшее значение ½f ' (x) ½в рассматриваемом промежутке
(которое можно вычислить), то получим оценку
, если обозначить через m наименьшее значение ½f ' (x) ½в рассматриваемом промежутке
(которое можно вычислить), то получим оценку
½xn-x½£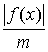 .
.
Так по самой величине f (xn)
оказывается возможным судить о близости xn к корню.
Пример. Уравнение х3-2х2-4х-7=0
имеет корень между 3 и 4, так как, если f (x) =x3-2x2-4x-7,
то f (3) =-10<0, f (4) =9>0. Вычислим этот корень с
точностью 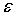 =0,01. В промежутке [3,4] обе производные f'
(x) =3x2-4x-4 и f" (x) =6x-4
сохраняют знак "плюс". Наименьшее значение первой из них равно m=11.
=0,01. В промежутке [3,4] обе производные f'
(x) =3x2-4x-4 и f" (x) =6x-4
сохраняют знак "плюс". Наименьшее значение первой из них равно m=11.
Имеем:
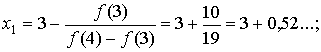
округляя, положим х1=3,52.
Т.к. f (3,52) = - 2,246592, то по неравенству для оценки точности,
требуемая точность ещё не достигнута.
Продолжаем:
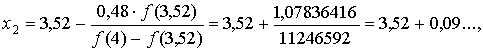
или, округляя, х2=3,61.
Вычислим f (3,61) =-0,458319 и, пользуясь формулой оценки, снова видим,
что цель ещё не достигнута. Наконец,
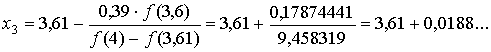
или, округляя, положим х3=3,63.
Т.к. мы округлили в сторону корня, то могли и перескочить через него; что этого
не произошло видно по знаку числа f (3,63) = - 0,041653.
На этот раз 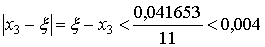 . Таким образом, 3,630<x<3,634, то есть x=3,63+0,004.
. Таким образом, 3,630<x<3,634, то есть x=3,63+0,004.
Метод хорд все же мало эффективен, поэтому
рассмотрим еще несколько методов решения уравнений.
§3. Правило Ньютона (метод касательных)
Пусть f удовлетворяет тем же условиям:
(1) f (x) непрерывна в [a,
b] вместе со своими производными f', f”;
(2) f (a) и f (b)
имеют разные знаки;
(3) обе производные f' и f" сохраняют
каждая определённый знак во всём [a, b].
Кроме того, искомый корень f (x) =0
изолирован в [a, b]: a<x<b. Отправляясь
от какого-нибудь из концов этого промежутка, например, от b, запишем
формулу Тейлора с дополнительным членом в форме Лагранжа:
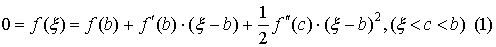 .
.
Отбрасывая дополнительный член,
приближённо положим: f (b) +f' (b) (x-b) =0, откуда 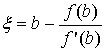 . Таким образом, мы приходим к
приближённому значению корня x:
. Таким образом, мы приходим к
приближённому значению корня x: 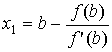 (2).
(2).
Получение этого значения можно наглядно
использовать геометрически.
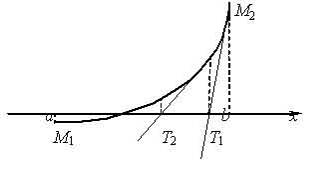
Рассмотрим касательную к кривой y=f
(x) в точке М2 с абсциссой b. Её уравнение имеет вид: y-f
(b) =f' (b) (x-b). Полагая здесь у=0,
найдём абсциссу точки Т1 пересечения касательной с осью Оx,
она в точности совпадает с точкой х1, найденной выше. Значит,
суть дела в приближённой замене дуги кривой М1М2 - касательной к
ней в одном из её концов.
Это правило, называемое именем Ньютона,
называется также методом касательных.
Покажем, что если значение f (b)
одного знака с f" (x), то х1 лежит между x и b.
Действительно, т.к. f (b) и f
' (b) одного знака, то из 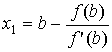 ясно, что x1<b. С другой стороны, из
(1) и (2) следует:
ясно, что x1<b. С другой стороны, из
(1) и (2) следует:
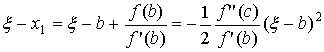 .
.
Но f" (x) в
рассматриваемом случае имеет одинаковый знак с f ' (x),
следовательно, x-х1<0
или x<x1<b.
Аналогично, если исходить из точки а,
и касательную к кривой провести в точку М1 (с абсциссой а),
то взамен (2), получим приближённое значение 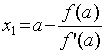 . Относительно вычисленного по этой
формуле значения можно установить, как и выше: если значение f" (x)
имеет одинаковый знак с f ' (x), то x1 лежит
между а и x. Таким образом, для каждого из четырёх возможных случаев понятно,
с какого конца гарантирована успешность приближения к корню по правилу Ньютона.
Повторное применение его в случаях I и IV дает последовательность убывающих
значений:
. Относительно вычисленного по этой
формуле значения можно установить, как и выше: если значение f" (x)
имеет одинаковый знак с f ' (x), то x1 лежит
между а и x. Таким образом, для каждого из четырёх возможных случаев понятно,
с какого конца гарантирована успешность приближения к корню по правилу Ньютона.
Повторное применение его в случаях I и IV дает последовательность убывающих
значений:
b>x1>x2>…>xn>xn+1>…>x,
а в случаях II и III - последовательность
возрастающих значений:
a<x1<x2<…<xn<xn+1<…<x.
Причём вычисление последующего значения по
предыдущему всегда производится по формуле:
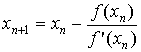 (3).
(3).
Покажем, что 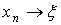 . Монотонная и ограниченная
последовательность имеет конечный предел b. Переходя к пределу в (1), с
учётом непрерывности обеих функций f и f' найдём
. Монотонная и ограниченная
последовательность имеет конечный предел b. Переходя к пределу в (1), с
учётом непрерывности обеих функций f и f' найдём 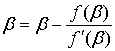 , откуда f (b) =0 и b=x. Таким образом, правило
Ньютона, повторно применённое, позволяет вычислить корень x с любой степенью точности. При
этом точность уже вычисленного приближённого значения оценивается по формуле:
, откуда f (b) =0 и b=x. Таким образом, правило
Ньютона, повторно применённое, позволяет вычислить корень x с любой степенью точности. При
этом точность уже вычисленного приближённого значения оценивается по формуле:
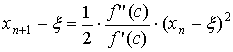 .
.
Обозначим через М наибольшее
значение 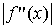 в заданном промежутке [a, b]
и через m - наименьшее значение
в заданном промежутке [a, b]
и через m - наименьшее значение 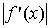 на [a, b]. Отсюда тогда получим:
на [a, b]. Отсюда тогда получим:
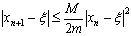 .
.
Поскольку справа стоит квадрат, этим
обеспечено весьма быстрое приближение xn к x (по крайней мере, начиная с
некоторого места), что и делает метод касательных одним из самых эффективных
методов приближённого вычисления корня.
Замечание: Последнее неравенство выполняет ещё одну
функцию. Если точность приближённого значения xn уже найдена
то последнее неравенство позволяет оценить точность ещё не вычисленного
значения xn+1. Это может оказаться полезным при
решении вопроса о том, на каком знаке целесообразно его округлять.
Пример. Вычислить внутри отрезка [3,4] с точностью
до ε=0,01 корень уравнения х3-2х2-4х-7=0,Решение:
f (x) =x3-2x2-4x-7,
f (3) =-10<0, f (4) =9>0, f' (x) =3x2-4x-4>0,
f" (x) =6x-4>0 при 3£ х £4.
Методом хорд мы нашли x=3,63+0,004. Наименьшее
значение 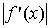 есть m=11. Отправляемся от b=4,
так как в этом конце отрезка [3,4] знак f (x) совпадает со знаком
f" (x). Тогда, используя формулу (2) получим:
есть m=11. Отправляемся от b=4,
так как в этом конце отрезка [3,4] знак f (x) совпадает со знаком
f" (x). Тогда, используя формулу (2) получим: 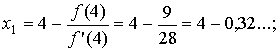 округляя, положим х1=4-0,3=3,7.
Т.к. f (x1) =f (3,7) =1,473, то по неравенству
округляя, положим х1=4-0,3=3,7.
Т.к. f (x1) =f (3,7) =1,473, то по неравенству 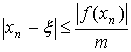 имеем:
имеем:
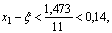
т.е. достигнутая точность недостаточна.
Далее,
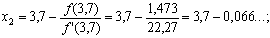
положим x2=3,7-0,066=3,634.
На этот раз f (x2) =f (3,634) =0,042…, так что
в силу того же неравенства: 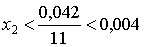 . Поэтому 3,630<x<3,634 и x=3,63 с требуемой точностью.
Получение этого результата методом хорд потребовало трёх шагов.
. Поэтому 3,630<x<3,634 и x=3,63 с требуемой точностью.
Получение этого результата методом хорд потребовало трёх шагов.
§4.
Комбинированный метод
Этот метод состоит в одновременном использовании
как метода касательных, так и метода хорд. Для определённости предположим, что
мы имеем дело со случаем I.
Приближенные значения x1 и
x1'
вычислим по формулам:
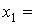
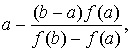
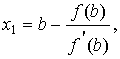
тогда по доказанному: 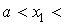
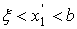 . При следующем же шаге мы заменяем в этих формулах a и b
на x1 и x1':
. При следующем же шаге мы заменяем в этих формулах a и b
на x1 и x1':
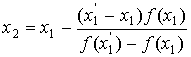 ;
;
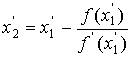 .
.
Этот процесс можно продолжать; имея два
приближённых значения xn и xn',
между которыми содержится корень 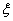 , мы переходим к следующей паре приближенных значений по формулам:
, мы переходим к следующей паре приближенных значений по формулам:
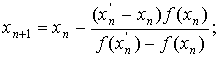
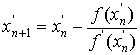 .
.
Таким образом, при комбинированном методе
мы получаем одновременно с недостатком и с избытком приближённые значения
корня, которые стремятся к точному с разных сторон.
Пример. Найти корни уравнения 2x3-x2-7x+5=0
с точностью до ε =0,001.
Решение: Подставляя целочисленные значения в
выражение функции f (x) =2x3-x2-7x+5,
находим, что искомые корни содержатся в промежутках:
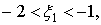
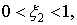
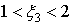 .
.
Решим для первого неравенства, то есть в
промежутке (-2,-1):
f ' (x) =6x2-2x-7>0,
f '' (x) =12x-2<0.
Значит, это случай (II). Так как, f
(-2) =-1<0, f (-1) =9>0, то правило Ньютона применяем к левым
концам промежутков. Имеем f' (-2) =21 и следующие значения x1'
и x1:
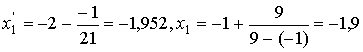
Округляя x1' в
сторону уменьшения, получим число - 1,96 > x1.
Если же округлить его в сторону
увеличения, т.е. в сторону корня, то получим число - 1,95; но f (-1,95)
=0,01775>0, то есть в этом случае мы перескочим через корень. Это
обстоятельство выгодно для нас, ибо даёт возможность сузить промежуток,
содержащий корень, и отбросив прежнее значение x1, положить x1'=
- 1,96, x1= - 1,95.
Далее имеем f (-1,96) = - 0,180672,
f ' (-1,96) =19,9696,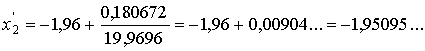 ,
,
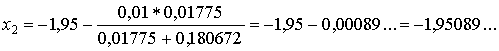 .
.
Поскольку x1 должно быть заключено между
этими границами, то ясно, что 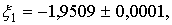 так что требуемая точность превзойдена.
так что требуемая точность превзойдена.
Оставшиеся два случая рассмотреть
самостоятельно.
§5.
Метод итераций
Рассмотрим вначале сущность итерационного метода.
В отличие от прямых или точных методов, итерационные дают возможность получить
решение лишь приближенно, путем повторения некоторой совокупности операций,
позволяющей по исходному приближенному значению решения определить его
уточненное значение. Выполнение этой совокупности операций составляет одну
итерацию. Многократное повторение итераций позволяет получать все более точное
решение при условии, что итерационный процесс сходится к искомому решению.
Если данное уравнение f (x)
=0 приведено к виду x=j (x), где |j' (х) |£r<1 всюду на отрезке [a,
b], на котором оно имеет единственный корень, то исходя из некоторого
начального значения х0, принадлежащего отрезку [a,
b], можно построить такую последовательность: х1=j (х0), х2=j (х1),…, хn=j (xn-1),….
Пределом этой последовательности является единственный корень уравнения f
(x) =0 на отрезке [a, b]. Погрешность приближенного
значения xm корня  определяется неравенством:
определяется неравенством: 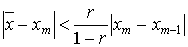 .
.
Пример: Методом итераций решить с точностью до
0,01 уравнение x3-12x-5=0.
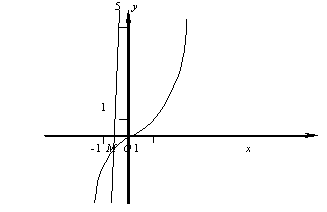
Решение:
Найдем интервал изоляции действи - тельного
корня уравнения. представим данное уравнение в виде x3=12x+5
и построим графики двух функций y = x3 (1) и y=12x+5
(2). Абцисса точки М пересечения этих графиков на ходится в
промежутке [-1,0], поэтому за начальное значение 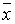 можно взять
можно взять 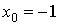 . Запишем исходное уравнение в виде:
. Запишем исходное уравнение в виде: 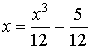 . Здесь
. Здесь 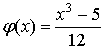 ,
, 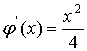 , то есть
, то есть 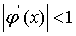 в промежутке [-1,0] и поэтому метод
итераций применим. Найдем теперь первое приближенное значение:
в промежутке [-1,0] и поэтому метод
итераций применим. Найдем теперь первое приближенное значение:
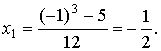
Найдём второе и последующие приближения:
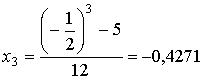 ;
; 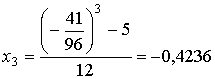 ;
; 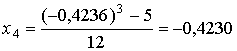 .
.
Следовательно, искомый корень x»0,42.
Замечание 1. Уравнение y=f (x)
можно записать иначе. Одним из самых распространенных представлений является
представление в виде: x=x+cf (x), где с -
произвольная постоянная.
Замечание 2. Для нахождения приближенного значения
корня с погрешностью, не превышающей e, достаточно определить m
так, чтобы выполнялось неравенство 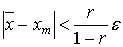 .
.
§6.
Интерполирование. Интерполяционная формула Лагранжа
Пусть для некоторой функции f (x),
определённой на [a, b] вычислены (m+1) её значений в
точках x0, x1, …, xm: f
(x0), f (x1), f (xm)
и требуется по этим значениям вычислить значение f (x) при
некотором новом значении x. В этом состоит простейшая задача
интерполирования. Обычно задачу понимают так: ищется многочлен L (x)
наинизшей степени, который в заданных точках xi (k=0,1,…,
m), называемых узлами интерполирования, принимает те же
значения f (xi), что и функция f (x), и
приближённо полагают для любого x из [a, b] f (x)
@L (x).
Подобное приближённое равенство называется
интерполяционной формулой. Итак, нужно прежде всего найти интерполяционную
формулу, а затем при определённых предположениях относительно функции f
(x) - оценить погрешность приближённой формулы.
Для отыскания многочлена L (x),
удовлетворяющего условиям L (xi) = f (xi)
(i=0,1,…,m), удобно ввести базисный многочлен m-й степени lk
(x), k=0,1,…,m, который, соответственно индексу, принимает
значение 1 при x = xk и обращается в 0
при x=xi, если i ¹ k.
Замечание 1. Индекс этого многочлена,
в отличие от общепринятых обозначений многочленов, указывает не степень, а
номер многочлена k.
Конкретизируем многочлен lk (x).
Так как при при x=xi, если i ¹ k имеет место lk (x) =0, то
его можно записать в виде:
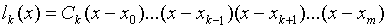
так как при x = xk
имеет место lk (x) =1, то подставляя в выражение lk
(x) значения x = xk и приравнивая результат
единице, получим:
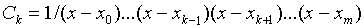
В результате получим:
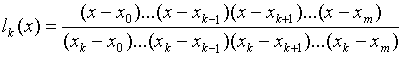 , (1)
, (1)
а многочлен L (x) = 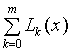 вычисляется по формуле:
вычисляется по формуле:
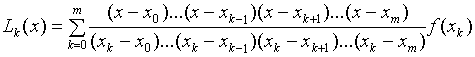 (2)
(2)
Тогда многочлен 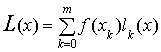 удовлетворяет всем из условий L (xi)
= f (xi). Степень этого многочлена не выше m и
значит условиями L (xi) =f (xi)
он определяется однозначно; его называют интерполяционным многочленом Лагранжа,
а приближённое равенство f (x) @L (x) - интерполяционной
формулой Лагранжа.
удовлетворяет всем из условий L (xi)
= f (xi). Степень этого многочлена не выше m и
значит условиями L (xi) =f (xi)
он определяется однозначно; его называют интерполяционным многочленом Лагранжа,
а приближённое равенство f (x) @L (x) - интерполяционной
формулой Лагранжа.
Замечание. многочлен lk (x)
можно записать более сжато, если ввести выражение w (x) =
(x-x0) (x-x1) … (x-xm),
обращающееся в 0 в узлах интерполирования x0, x1,…,
xm.
Покажем это: 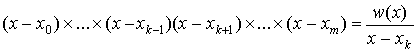 (x¹xk) а
(x¹xk) а
(xk-x0) …
(xk-xk-1) (xk-xk+1)
… (xk-xm) = 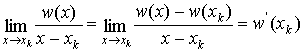
Таким образом, 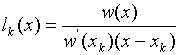 и
и 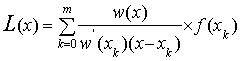 . (3)
. (3)
§7.
Дополнительный член формулы Лагранжа
Оценим разность f (x) - L (x), где
x-любое фиксированное значение из отрезка [a, b], отличное от узлов интерполирования. Предположим, что функция f
(z) на этом отрезке имеет производные всех порядков до (m+1) - го
включительно. Какова бы ни была постоянная К, функция j (z) =f (z) - l (z) - Kw
(z) тоже имеет (m+1) производных и к тому же обращается в 0
в узлах xi (i=0,1,…,m). выберем
постоянную K так, чтобы и при z = x было j (x) =0, т.е. положим
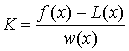 (1), (так как x¹xi, то w (x) ¹0).
(1), (так как x¹xi, то w (x) ¹0).
По теореме Ролля в (m+1)
промежутках между m+2 корнями x, x0,
x1, …, xm функции j (z) найдётся m+1
различных корней её производной j' (z). Применяя снова теорему Ролля
к функции j' (z) и к m промежуткам между её (m+1)
корнями, установим существование m различных корней второй производной и
так далее. Продолжая это рассуждение, на (m+1) - ом его шаге придём к
существованию корня x (m+1) - й производной j (m+1) (z), так что:
j (m+1) (x) =0 (a<x<b) (2).
Но L (m+1) (z)
º0 ибо степень многочлена L
(z) не выше m, a w (m+1) (z) º (m+1)! Учитывая
определение вспомогательной функции j (z), имеем:
j (m+1) (z) =f (m+1) (z)
- K (m+1)!
Так что из (1) получается, что 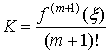 . Окончательно получим:
. Окончательно получим:
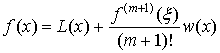 (a<x<b) (3).
(a<x<b) (3).
Это интерполяционная формула
Лагранжа с дополнительным членом. В отличие от f (x)
@L (x) она является точной.
Замечание: Если на отрезке [a, b] 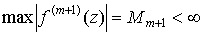 то, так как на этом отрезке
то, так как на этом отрезке 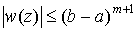 , получаем такую оценку для погрешности
формулы f (x) @L (x):
, получаем такую оценку для погрешности
формулы f (x) @L (x): 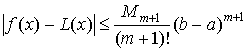 .
.
§8.
Интерполяционная формула Ньютона
Пусть f (x0), f (x1),
f (xm) - (m+1) значений некоторой функции y=f
(x), определённой на [a, b], которые вычислены в узловых
точках x0, x1, …, xm. При
этом функция y=f (x) задана на сетке равностоящих узлов
интерполирования xk=kh (k=0,1,…, m) и
для нее построена таблица конечных разностей.
Замечание 1. Конечные разности
представляют собой выражения вида:
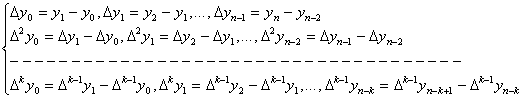
вплоть до k-го порядка включительно
(при этом 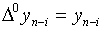 , где i=0,1,2,.,n).
, где i=0,1,2,.,n).
Таблица конечных разностей.
|
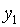 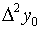
|
|
|
|
|
|
|
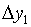
|
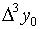
|
|
|
|
|
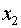
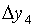
|
…
|
|
|
|
|
|
|
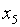 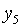 … …
|
|
|
|
|
|
|
|
|
…
|
|
|
|
|
|
…
|
…
|
|
|
|
|
|
|
|
|
|
|
|
|
Будем строить интерполяционный многочлен Pn
(x) в виде:
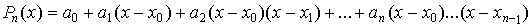 (1)
(1)
Его n+1 коэффициент 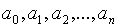 находится из n+1 интерполяционных
равенств
находится из n+1 интерполяционных
равенств 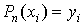 (i=0,1,…, n) следующим
образом: пусть i=0, x=x0, тогда
(i=0,1,…, n) следующим
образом: пусть i=0, x=x0, тогда 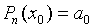 , а по условию интерполяции
, а по условию интерполяции 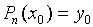 , следовательно, а0=у0.
, следовательно, а0=у0.
Аналогичными рассуждениями, при i=1
выводится равенство
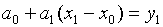
в которое подставим уже найденное значение
а0=у0. Разрешая полученное равенство
относительно а1 получим
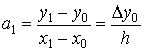 .
.
При i=2 имеем:
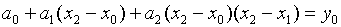
отсюда
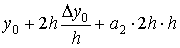
и в результате получим:
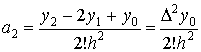 .
.
В итоге, аk коэффициент
вычисляется по формуле: 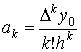 (это можно доказать, применив метод
математической индукции). Подставляя найденные коэффициенты
(это можно доказать, применив метод
математической индукции). Подставляя найденные коэффициенты 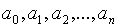 в формулу (1) получим многочлен
в формулу (1) получим многочлен
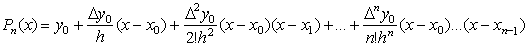 . (2)
. (2)
Полученный многочлен называется первым
интерполяционным многочленом Ньютона.
Так как каждое слагаемое многочлена,
начиная со второго, содержит множитель 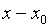 , то многочлен (2) наиболее приспособлен для интерполирования в
окрестности узла
, то многочлен (2) наиболее приспособлен для интерполирования в
окрестности узла 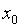 . В таких случаях узел
. В таких случаях узел 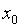 называется базовым. Введем
новую переменную q, которая определяется равенством:
называется базовым. Введем
новую переменную q, которая определяется равенством: 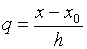 , то есть
, то есть 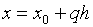 . Тогда
. Тогда 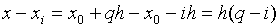 и многочлен Ньютона примет вид:
и многочлен Ньютона примет вид:
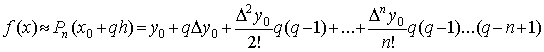 (3)
(3)
Полученная формула называется первой
интерполяционной формулой Ньютона
Замечание 2. Первая интерполяционная формула Ньютона
обычно применяется при значениях 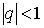 , для интерполирования вперед (при
, для интерполирования вперед (при 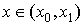 , то есть при
, то есть при 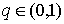 ).
).
Так как реально степени интерполяционных
многочленов бывают не так велики, в то время как таблицы значений функций
достаточно обширны, и так как в реальной числовой таблице нет никаких индексов
- номеров узлов, то за базовый для формулы (3) узел 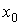 можно принимать узел, ближайший к заданной
фиксированной точке x, если за ним имеется достаточное число узлов для
построения необходимых для (3) разностей. Поскольку в первой формуле Ньютона
используются исходящие диагонали таблицы конечных разностей (см. таб.), то
такое смещение узла, принимаемого за базовый, в конце таблицы будет
неприемлемо.
можно принимать узел, ближайший к заданной
фиксированной точке x, если за ним имеется достаточное число узлов для
построения необходимых для (3) разностей. Поскольку в первой формуле Ньютона
используются исходящие диагонали таблицы конечных разностей (см. таб.), то
такое смещение узла, принимаемого за базовый, в конце таблицы будет
неприемлемо.
Учёт этого обстоятельства приводит к
потребности в симметричной, в определённом смысле слова, формулы для (3),
которая была бы пригодной для интерполирования в конце таблицы. Для этого, в
отличие от (1), форма интерполяционного многочлена 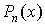 берётся такой, которая предусматривает
поочерёдное подключение узлов в обратном порядке: сначала последний, потом
предпоследний и так далее, то есть
берётся такой, которая предусматривает
поочерёдное подключение узлов в обратном порядке: сначала последний, потом
предпоследний и так далее, то есть
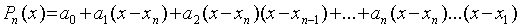 (4)
(4)
Его коэффициенты 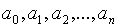 находится из n+1 интерполяционных
равенств
находится из n+1 интерполяционных
равенств 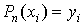 (i=0,1,…, n) аналогичным
выше изложенному способом, но подстановка узловых точек вместо х и
рассмотрение интерполяционных равенств производится в обратном порядке. Полагая
x=xn, x=xn-1, …, x=x1
получим:
(i=0,1,…, n) аналогичным
выше изложенному способом, но подстановка узловых точек вместо х и
рассмотрение интерполяционных равенств производится в обратном порядке. Полагая
x=xn, x=xn-1, …, x=x1
получим:
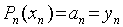 ,
,
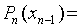
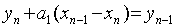 , отсюда
, отсюда 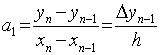 ,
,
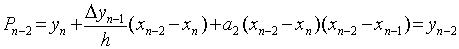 ,
,
Следовательно
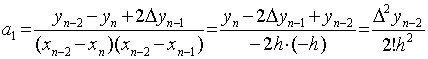
и так далее.
в результате: 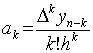 (это можно доказать, применив метод
математической индукции). Подставляя найденные коэффициенты
(это можно доказать, применив метод
математической индукции). Подставляя найденные коэффициенты 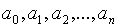 в формулу (*) получим многочлен
в формулу (*) получим многочлен
 (5)
(5)
Полученный многочлен называется вторым
интерполяционным многочленом Ньютона в котором базовым является узел
xn и коэффициенты которого определяются конечными разностями,
расположенными на восходящей от yn диагонали.
Пусть 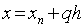 , то есть введем новую переменную q, которая определяется
равенством:
, то есть введем новую переменную q, которая определяется
равенством: 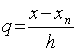 и преобразуем к ней входящие в (5)
разности. Тогда
и преобразуем к ней входящие в (5)
разности. Тогда 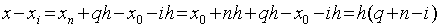 и многочлен Ньютона примет вид:
и многочлен Ньютона примет вид:
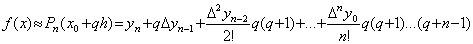 (6)
(6)
Полученная формула называется второй
интерполяционной формулой Ньютона.
Замечание 3. Вторая интерполяционная формула Ньютона
обычно применяется при значениях 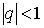 , для интерполирования назад при
, для интерполирования назад при 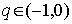 , то есть в окрестности узла xn.
, то есть в окрестности узла xn.
Дополнительный член формулы Ньютона.
Замечание 4. Конечноразностный многочлен Ньютона
является одной из форм представления интерполяционного многочлена Лагранжа,
поэтому справедливо представление остаточного члена в форме Лагранжа.
То есть, многочлен w (x) -
вспомогательный многочлен формулы Лагранжа, с учетом того, что m=n,
преобразуется к 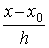 (новой переменной) следующим образом: w
(x) = (x-x0) (x-x1) …
(x-xm) =
(новой переменной) следующим образом: w
(x) = (x-x0) (x-x1) …
(x-xm) =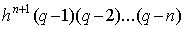 , тогда
, тогда
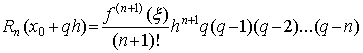
для первой интерполяционной формулы Ньютона,
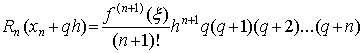
для второй интерполяционной формулы
Ньютона.
В итоге точное равенство имеет вид: f
(x) =Pn (x+qh) +Rn (x+qh).
§9.
Интерполирование с кратными узлами. Формула Эрмита
Можно поставить более общую задачу
интерполирования, задав в узлах x0, x1,…, xm,
кроме значений самой функции f, также и значения последовательных её
производных:
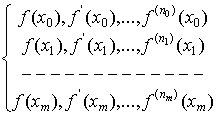 (1)
(1)
где n0, n1,…,
nm - неотрицательные целые числа. Общее число этих условий
равно (n0+1) + (n1+1) +…+ (nm+1)
=N.
Задача вычисления функции f (x)
при любом отличном от узлов значении x на [a, b] с
использованием всех данных (1) понимается так: имеется многочлен H (x)
наинизшей степени, который в каждом узле xi, вместе со своими
производными до порядка ni включительно, принимает те же
значения, что и сама функция f и её соответствующие производные, а затем
приближенно предполагается, что f (x) @H (x) (2). Узлы xi
называются узлами интерполирования соответственно кратности
ni+1.
Можно доказать существование и
единственность многочлена H (x) степени не выше N-1,
удовлетворяющего всем поставленным условиям. Его называют интерполяционным
многочленом Эрмита, а формулу (2) - интерполяционной формулой
Эрмита.
Замечание 1. Если все ni положить
равными 0, то получится формула Лагранжа f (x) @L (x).
Замечание 2. Если взять один лишь узел x0,
но кратности (n+1), т.е. от многочлена не выше n-й степени T
(x) потребовать, чтобы в точке x0 его значение и
значения n его производных совпадали, соответственно, со значениями
самой функции f (x) и её производных, то получится многочлен
Тейлора.
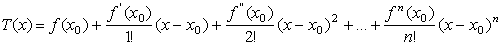
Таким образом, формула Лагранжа f (x)
@L (x) и приближенная формула f
(x) @T (x) (многочлен Тейлора)
являются частными случаями интерполяционной формулы Эрмита.
Дополнительный член формулы (2),
восстанавливающий её точность, выводится с помощью рассуждений, аналогичных
приведённым выше. Рассмотрим многочлен N-ой степени:
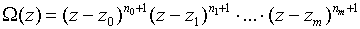
и положим для a£ z£ b
Ф (z) =f (z) - H
(z) - KW (z),
где K=const.
Если предположить, что функция f (z)
на отрезке [a, b] имеет N последовательных производных, то
это будет справедливо и для Ф (z). Фиксируя значения z=x,
отличное от узлов, мы выберем постоянную К так:
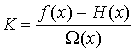 (W (х) ¹0) (3)
(W (х) ¹0) (3)
при таком выборе функция Ф (х)
обращается в 0 и при z=x. Всего она будет иметь N+1
корней, если каждый корень считать столько раз, какова его кратность.
Определение. Число a называется корнем р-ой
кратности функции Ф (z), если a обращает в 0 вместе с Ф (z)
и р-1 её производных.
Применяя последовательно теорему Ролля как
и выше (с тем лишь усложнением, что каждый кратный корень функции Ф (z)
ещё в течение нескольких шагов будет фигурировать и как корень её
последовательных производных), окончательно придём к утверждению, что в
некоторой точке x обратится в 0 производная Ф (N) (z).
Отсюда 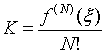 и в виду (3)
и в виду (3)
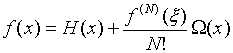 (4).
(4).
§10.
Эмпирические формулы
Пусть, изучая функциональную зависимость y=f
(x) мы провели ряд измерений величин x и y и в результате
получили таблицу значений;
|
x
|
x1
|
x2
|
…
|
xn
|
|
y
|
y1
|
y2
|
…
|
yn
|
Если аналитическое выражение функции f
(x) неизвестно или весьма сложно, то возникает практически важная
задача: найти эмпирическую формулу 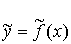 , значения которой при x=xi возможно мало
отличалось бы от опытных данных yi
, значения которой при x=xi возможно мало
отличалось бы от опытных данных yi 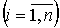 . В такой постановке наша задача весьма
неопределённа, поэтому обычно, по ряду соображений, указывают достаточно узкий
класс функций К (например, множество функций линейных, показательных и
так далее), которому должна принадлежать искомая функция
. В такой постановке наша задача весьма
неопределённа, поэтому обычно, по ряду соображений, указывают достаточно узкий
класс функций К (например, множество функций линейных, показательных и
так далее), которому должна принадлежать искомая функция 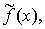 и дело, таким образом, сводится к
нахождению лишь наилучших значений параметров. Во многих случаях класс К
определяется требованием простоты эмпирической формулы; иногда этот класс
подсказывается самой природой явления.
и дело, таким образом, сводится к
нахождению лишь наилучших значений параметров. Во многих случаях класс К
определяется требованием простоты эмпирической формулы; иногда этот класс
подсказывается самой природой явления.
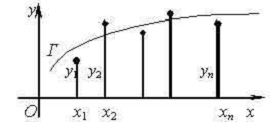
Геометрически задача построения
эмпирической формулы состоит в проведении кривой Г вида 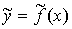 из некоторого класса К
"возможно ближе примыкающей" к системе точек Mi (xi,yi),
i=1,2,…,n. Разумеется, при этом должен быть выяснен точный
математический смысл понятия близости кривой Г и конфигурации точек М.
из некоторого класса К
"возможно ближе примыкающей" к системе точек Mi (xi,yi),
i=1,2,…,n. Разумеется, при этом должен быть выяснен точный
математический смысл понятия близости кривой Г и конфигурации точек М.
Заметим, что задача построения
эмпирической формулы отлична от задачи интерполирования. Как правило, исходный
материал весьма обширен и ищется сравнительно простая аналитическая зависимость
между данными переменными x, y.
Эта зависимость обычно не сводится к интерполяционным формулам (которые дают
значения, совпадающие в заданных точках с заданными значениями), так как график
эмпирической функции 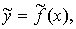 вообще говоря, не проходит точно через
соответствующую систему точек Mi (xi,yi)
вообще говоря, не проходит точно через
соответствующую систему точек Mi (xi,yi)
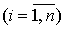 . Кроме того, сами исходные эмпирические
данные xi и yi, как правило, являются
приближёнными и содержат ошибки. Поэтому интерполяционная формула, повторяющая
эти ошибки, не говоря даже об её сложности, не является идеальным решением
поставленной задачи. Возможно простая эмпирическая формула, сглаживающая местные
неправильности, лучше отобразит действительность.
. Кроме того, сами исходные эмпирические
данные xi и yi, как правило, являются
приближёнными и содержат ошибки. Поэтому интерполяционная формула, повторяющая
эти ошибки, не говоря даже об её сложности, не является идеальным решением
поставленной задачи. Возможно простая эмпирическая формула, сглаживающая местные
неправильности, лучше отобразит действительность.
Построение эмпирической формулы слагается
из двух этапов:
1)
выяснение общего вида этой формулы,
2) определение лучших её параметров.
Если неизвестен характер зависимости между
данными величинами x и y, то вид эмпирической формулы является
произвольным. Предпочтение отдаётся простым формулам, обладающим хорошей
точностью. Если отсутствуют сведения о промежуточных данных, то обычно
предполагается, что эмпирическая функция аналитическая, без точек разрыва, и
график её - плавная кривая.
При известном навыке по положению точек,
определяющих некоторую гладкую кривую, можно примерно угадать общий вид
зависимости путём установления сходства между построенным графиком и образцами
известных кривых (отдельные неправильности при этом игнорируются).
Во многих случаях можно ограничиться
многочленом 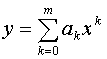 . Нередко употребляются другие
элементарные функции (дробно-линейная, степенная, показательная, логарифмическая
т.п.). Имеются приёмы, облегчающие выбор вида эмпирической формулы. Что
касается определения наилучших значений параметров, входящих в эмпирическую
формулу, то эта задача более лёгкая, и решается определёнными методами.
. Нередко употребляются другие
элементарные функции (дробно-линейная, степенная, показательная, логарифмическая
т.п.). Имеются приёмы, облегчающие выбор вида эмпирической формулы. Что
касается определения наилучших значений параметров, входящих в эмпирическую
формулу, то эта задача более лёгкая, и решается определёнными методами.
Замечание: При построении эмпирической формулы
можно предполагать, что исходные данные (xi, yi)
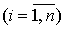 положительны.
положительны.
Действительно, если бы, например, все xi<0
(или все yi<0), то достаточно рассмотреть таблицу значений
(-xi, yi) или соответственно (xi,
- yi). Аналогично при xi<0, yi<0
достаточно построить эмпирическую формулу для таблицы (-xi, yi).
Пусть теперь имеем общий случай, когда
знаки xi и yi переменные. Так
как таблица значений (xi, yi) конечна, то
всегда можно подобрать положительные числа m и n такие, что xi=m+xi>0 и hi=n+yi>0. Отсюда получаем, что
решение поставленной задачи сводится к нахождению эмпирической формулы для
системы положительных значений (xi, hi). Поэтому в дальнейшем будем
рассматривать таблицы с положительными элементами.
§11.
Точечное квадратичное аппроксимирование функций
Метод наименьших квадратов.
При точечном квадратичном аппроксимировании за
меру отклонений многочлена
 (1)
(1)
от данной функции 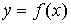 на множестве точек
на множестве точек 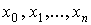 принимают величину
принимают величину
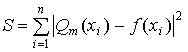 (2)
(2)
называемую квадратичным отклонением
(способ наименьших квадратов).
Для построения аппроксимирующего
многочлена требуется подобрать коэффициенты 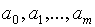 так, чтобы величина S была наименьшей. Предположим, что m£n. В случае m=n коэффициенты aj
так, чтобы величина S была наименьшей. Предположим, что m£n. В случае m=n коэффициенты aj
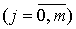 можно определить из системы уравнений
можно определить из системы уравнений
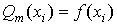 ,
, 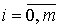 (3)
(3)
причём S=0 и приходим к проблеме
интерполирования функций. При m<n система (3), вообще говоря,
несовместна. Кроме того, следует иметь в виду, что во многих случаях значения
функции f (x) определяются эксперементально и содержат ошибки,
поэтому сама постановка о точном решении системы (3) теряет смысл.
Для решения задачи аппроксимирования
воспользуемся общим приёмом дифференциального исчисления, а именно, найдём
частные производные от величины
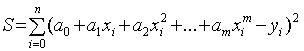 ,
,
где 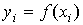 , по всем переменным
, по всем переменным 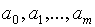 . Приравнивая эти частные производные нулю, получим для определения неизвестных
. Приравнивая эти частные производные нулю, получим для определения неизвестных 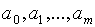 систему m+1 уравнений с m+1
неизвестными.
систему m+1 уравнений с m+1
неизвестными.
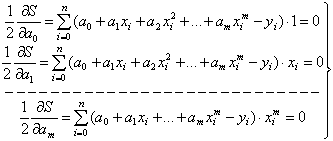 (4)
(4)
Введём обозначения
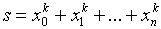 (k=0,1,2,…)
(k=0,1,2,…)
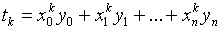 (k=0,1,2,…)
(k=0,1,2,…)
Преобразуя систему (4) и используя
введённые обозначения, будем иметь
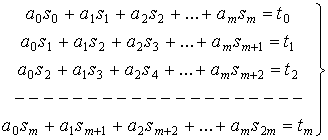 (5) где s0=n+1.
(5) где s0=n+1.
Теорема. если среди точек 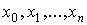 нет совпадающих и m£n; то определитель системы (5) отличен от
нуля и, следовательно, эта система имеет единственное решение
нет совпадающих и m£n; то определитель системы (5) отличен от
нуля и, следовательно, эта система имеет единственное решение 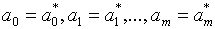 .
.
Многочлен (1) с такими коэффициентами
будет обладать минимальным квадратичным отклонением Smin.
Если m=n, то аппроксимирующий многочлен Qm (x)
совпадает с многочленом Лагранжа для системы точек 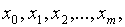 причём Smin=0.
причём Smin=0.
Замечание. На практике обычно бывает, что степень
многочлена Qm (x) значительно меньше числа точек xi
(i=0,1,…,n) и поэтому построение точного интерполяционного
многочлена, вообще говоря, невозможно. Таким образом, аппроксимирование функций
представляет собой более общий процесс, чем интерполирование.
Пример. Подобрать аппроксимирующий многочлен
второй степени 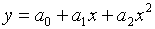 для данных
для данных
|
x
|
0,78
|
1,56
|
2,34
|
3,12
|
3,81
|
|
y
|
2,50
|
1, 20
|
1,12
|
2,25
|
4,28
|
Решение. Вычисления, которые нам
нужно произвести, расположим по схеме (для m=2, n=4) в таблице 1:
|
x0
|
x
|
x2
|
x3
|
x4
|
y
|
xy
|
x2y
|
|
1
|
x0
|
x02
|
x03
|
x04
|
y0
|
x0y0
|
x02y0
|
|
1
|
x1
|
x12
|
x13
|
x14
|
y1
|
x1y1
|
x12y1
|
x2
|
x22
|
x23
|
x24
|
y2
|
x2y2
|
x22y2
|
|
1
|
x3
|
x32
|
x33
|
x34
|
y3
|
x3y3
|
x32y3
|
|
1
|
x4
|
x42
|
x43
|
x44
|
y4
|
x4y4
|
x42y4
|
|
s0
|
s1
|
s2
|
s3
|
s4
|
t0
|
t1
|
t2
|
Для данного примера получим таблицу 2 (вычисления
проводим с тремя десятичными знаками).
Таблица 2. Вычисления по способу
наименьших квадратов.
|
x0
|
x
|
x2
|
x3
|
x4
|
y
|
xy
|
x2y
|
|
1
|
0,78
|
0,608
|
0,475
|
0,370
|
2,50
|
1,950
|
1,521
|
|
1
|
1,56
|
2,434
|
3,796
|
5,922
|
1, 20
|
1,872
|
2,920
|
|
1
|
2,34
|
5,476
|
12,813
|
29,982
|
1,12
|
2,621
|
6,133
|
|
1
|
3,12
|
9,734
|
30,371
|
94,759
|
2,25
|
7,020
|
21,902
|
|
1
|
3,81
|
14,516
|
55,306
|
210,717
|
4,28
|
16,307
|
62,128
|
|
5
|
11,61
|
32,768
|
102,761
|
341,750
|
11,35
|
29,770
|
94,604
|
Отсюда система для определения коэффициентов a0,
a1, a2 имеет вид:
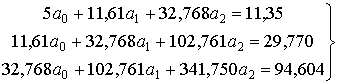
Решив систему, будем иметь: a0=5,045;
a1=-4,043; a2=1,009.
Следовательно, искомый многочлен имеет
вид: y=5,045-4,043x+1,009x2.
Сравним исходные значения для y с
соответствующими значениями  . Соответствующие результаты приведём в таблице 3.
. Соответствующие результаты приведём в таблице 3.
Таблица 3. Погрешность вычисления по способу
наименьших квадратов.
|
x
|
y
|
 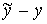
|
|
|
0,78
|
2,50
|
2,505
|
+0,005
|
|
1,56
|
1, 20
|
1, 194
|
-0,006
|
|
2,34
|
1,12
|
1,110
|
-0,010
|
|
3,12
|
2,25
|
2,252
|
+0,002
|
|
3,81
|
4,28
|
4,288
|
+0,008
|
§12. Нормальная система определения коэффициентов для метода
наименьших квадратов
Пусть известен вид эмпирической формулы
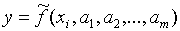 (1)
(1)
Согласно методу наименьших квадратов
наилучшими коэффициентами a1, a2,…,am
считаются те, для которых сумма квадратов отклонений
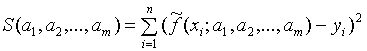 (2),
(2),
будет минимальной. Отсюда, используя
необходимые условия экстремума функции нескольких переменных, получаем так
называемую нормальную систему для определения коэффициентов ai
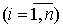
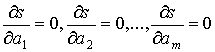 (3).
(3).
Если система (3) имеет единственное
решение, то оно будет искомым.
Утверждение. Система (3) упрощается, если эмпирическая
функция 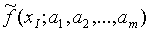 является линейной относительно параметров
является линейной относительно параметров
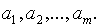
Доказательство:
пусть 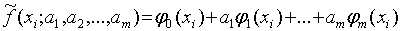 ,
,
тогда будем иметь:
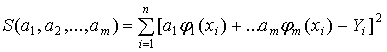 ,
,
где 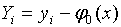 .
.
Отсюда, 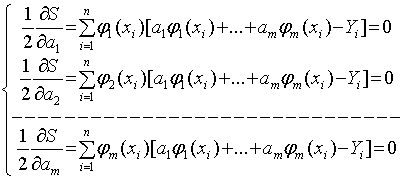 (4)
(4)
Введя сокращённые обозначения
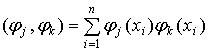 и
и 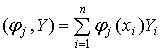
систему (4) можно записать в виде
нормальной системы
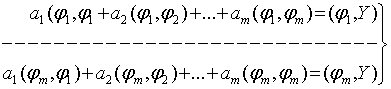 (5)
(5)
В частном случае, если эмпирическая
формула представляет многочлен (для удобства обозначений изменим нумерацию
коэффициентов ai)
Y=a0+a1x+…+amxm, то 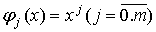 .
.
Отсюда: 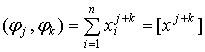 ,
, 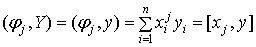 .
.
Следовательно, нормальная система (5)
будет иметь вид:
 (6)
(6)
Замечание 1. Метод наименьших квадратов обладает тем
преимуществом, что если сумма S квадратов отклонений ei мала, то сами эти отклонения
также малы по абсолютной величине.
Замечание 2. Недостатком метода наименьших квадратов
является громоздкость вычислений. Поэтому к нему прибегают обычно при обработке
наблюдений высокой точности, когда нужно получить также весьма точные значения
параметров. в этом случае промежуточные вычисления нужно проводить с надлежащим
количеством десятичных знаков, так как в противном случае при неблагоприятных
условиях искомые коэффициенты будут иметь мало верных знаков. Но грубые
значения этих коэффициентов могут быть получены значительно проще, т.е. применение
метода не будет оправдано.
Пример. Используя метод наименьших квадратов,
вывести эмпирическую формулу для табличной функции Q=f (x), Q-количество
вещества в процентах, оставшегося в системе через t минут от начала
химической реакции.
|
t
|
7
|
12
|
17
|
22
|
27
|
32
|
37
|
|
Q
|
83,7
|
72,9
|
63,2
|
54,7
|
47,5
|
41,4
|
36,3
|
Пусть y=ax2+bx+c. Для
вычисления коэффициентов нормальной системы введем таблицу.
|
t0t1t2t3t4QtQt2Q
|
|
|
|
|
|
|
|
|
1
|
7
|
49
|
343
|
2401
|
83,7
|
585,9
|
4101,3
|
|
1
|
12
|
144
|
1728
|
20736
|
72,9
|
874,8
|
10497,6
|
|
1
|
17
|
289
|
4913
|
83521
|
63,2
|
1074,4
|
18264,8
|
|
1
|
22
|
484
|
10648
|
234256
|
54,7
|
1203,4
|
26474,8
|
|
1
|
27
|
729
|
19683
|
531441
|
45,5
|
1282,5
|
34627,5
|
|
1
|
32
|
1024
|
32768
|
10485576
|
41,4
|
1324,8
|
42393,6
|
|
1
|
37
|
1364
|
50653
|
1874161
|
36,3
|
1343,1
|
49694,7
|
|
7
|
154
|
4088
|
120736
|
3795092
|
399,7
|
7688,9
|
186054,3
|
Тогда имеем следующую систему нормальных
уравнений:
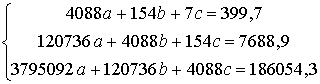
Решив эту систему, получим: 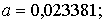 b=-2,6066, c=100,791.
b=-2,6066, c=100,791.
Следовательно, искомая эмпирическая
формула запишется так:
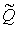 =0,02338 t2-2,6066t+100,791
=0,02338 t2-2,6066t+100,791
Следующая таблица показывает
согласованность полученной эмпирической формулы с опытными данными:
i Q 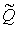 , вычисленное по формуле
, вычисленное по формуле 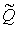 =0,02338 t2-2,6066t+100,791 Отклонение
=0,02338 t2-2,6066t+100,791 Отклонение
|
|
|
|
|
1
|
83,7
|
83,69
|
+0,01
|
|
2
|
72,9
|
72,88
|
+0,02
|
|
3
|
63,2
|
63,24
|
-0,04
|
|
4
|
54,7
|
54,76
|
-0,06
|
|
5
|
47,5
|
47,46
|
+0,04
|
|
6
|
41,4
|
41,32
|
+0,08
|
|
7
|
36,3
|
36,36
|
-0,06
|
|
Имеем 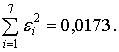
|
§13. Численное дифференцирование. Вычисление производной по её
определению
Пусть функция y=f (x)
определена в некоторой окрестности точки x0 и имеет
производную в этой точке, т.е. существует предел отношения приращения функции 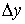 к приращению аргумента
к приращению аргумента 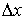 при стремлении
при стремлении 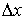 к нулю
к нулю
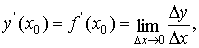
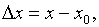
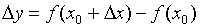 (1).
(1).
Значение производной в точке x0
можно получить, переходя к пределу в (1) по последовательности целых чисел n
и полагая, например 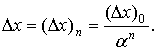 Здесь (Dx) 0 - некоторое начальное
приращение аргумента, a - некоторое число, большее 1, n=0, 1,
2,…. Тогда значение производной функции f (x) в точке x0
запишется так:
Здесь (Dx) 0 - некоторое начальное
приращение аргумента, a - некоторое число, большее 1, n=0, 1,
2,…. Тогда значение производной функции f (x) в точке x0
запишется так: 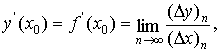
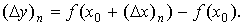
Отсюда получим приближённое равенство
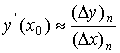 (2).
(2).
Для функции y=f (x), имеющей
непрерывную производную до второго порядка включительно в окрестности точки x0,
точность приближения производной соотношением (2) можно установить, воспользовавшись
формулой Тейлора
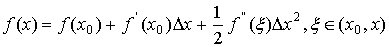 .
.
Тогда 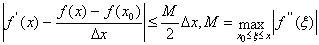
и окончательно имеем

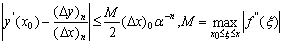 .
.
Замечание. Для достижения заданной точности e приближения производной при
определённом числе вычислений можно использовать неравенство
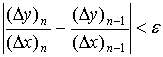 (3).
(3).
Пример. Вычислить производную функции y=sin
x в точке 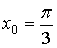 с точностью e=10-3 (p/3»1,047198).
с точностью e=10-3 (p/3»1,047198).
Решение:
Пусть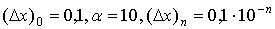 ,
,
тогда 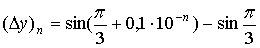 .
.
Определим приближённое значение
производной:
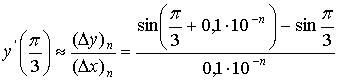 (n=0,1,2,…).
(n=0,1,2,…).
Найдём отношения, аппроксимирующие
производную
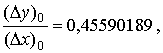
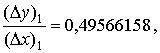
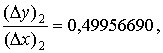
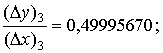
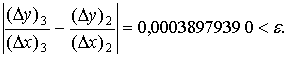
Итак, начиная с третьего приближения в
соответствии с оценкой (3) получаем искомое приближение производной данной
функции 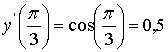 с точностью, не меньшей, чем заданное e=0,001.
с точностью, не меньшей, чем заданное e=0,001.
§14. Конечно-разностные аппроксимации производных
Пусть отрезок [a, b] разбит на n, n³2 равных частей точками xi,
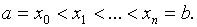 Разность между соседними значениями
аргумента постоянна, то есть шаг
Разность между соседними значениями
аргумента постоянна, то есть шаг 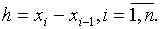 Пусть на отрезке [a, b] определена функция y=f
(x), значения которой в точках xi равны yi=f
(xi), i=0,1,…,n.
Пусть на отрезке [a, b] определена функция y=f
(x), значения которой в точках xi равны yi=f
(xi), i=0,1,…,n.
Запишем выражения для первой производной
функции в точке xi с помощью отношения конечных разностей:
a) аппроксимация с помощью разностей вперёд
(правых разностей)
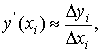
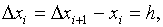
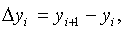
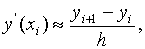 i=0,1,…n-1.
i=0,1,…n-1.
b) аппроксимация с помощью разностей назад
(левых разностей)
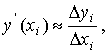
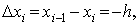
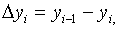
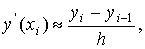
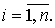
c) аппроксимация с помощью центральных
разностей (точка xi является центром системы точек
xi-1, xi,, xi+1).
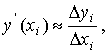
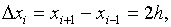
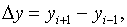
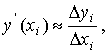 i=1,…, n-1.
i=1,…, n-1.
Замечание 1. Аппроксимация производной с помощью
центральных разностей представляет собой среднее арифметическое производных с
помощью левых и правых разностей в точках xi,, 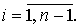
Замечание 2. Соотношения (a) и (c) не
позволяют вычислить производную в точке xn=b, а (b) и
(c) - в точке x0=a.
Теорема. для функции y=f (x), имеющей
непрерывную производную до второго порядка включительно, погрешность
аппроксимации производных разностями вперёд и назад имеет один и тот же порядок
0 (h), а погрешность аппроксимации центральными разностями для функции y=f
(x), имеющей непрерывную производную до третьего порядка включительно,
имеет порядок 0 (h2).
Доказательство:
Приближённое значение производной второго
порядка в точке xi выразим через значение функции yi-1,
yi,yi+1. Для этого представим вторую
производную с помощью правой разности: 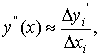
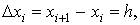
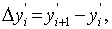
а производные первого порядка y'i+1
и 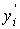 - c помощью левых разностей:
- c помощью левых разностей:
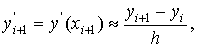
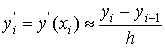
и окончательно получим
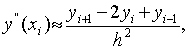
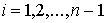 (1).
(1).
Погрешность последней аппроксимации имеет
порядок 0 (h2) для функции y=f (x), имеющей
непрерывную производную до четвёртого порядка включительно на отрезке [a,
b]. Естественно, представление (1) с помощью конечных разностей
позволяет вычислить значения второй производной только во внутренних точках
отрезка.
§15.
Использование интерполяционных многочленов Лагранжа для формул численного
дифференцирования
Пусть функция y=f (x) определена на
отрезке [a, b] и в точках xi (i=0,1,2,…,n)
принимает значения yi=f (xi).
Разность между соседними значениями
аргумента xi постоянна и является шагом h=xi-xi-1
(i=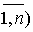 разбиения отрезка на n частей,
причём a=x0 и b=xn.
разбиения отрезка на n частей,
причём a=x0 и b=xn.
Найдём аппроксимации производных первого и
второго порядков с помощью значений функции yi в узловых
точках xi с погрешностью одного и того же порядка в
зависимости от шага h, причём этот порядок не ниже, чем
достигаемый при конечно-разностной аппроксимации производных для того же шага.
Для того, чтобы выразить значения
производных через значения функции yi в узлах интерполяции xi,
построим интерполяционный многочлен Лагранжа Lm (x)
степени m, удовлетворяющий условиям: Lm (xk)
=f (xk) =yk, k=i, i+1,…,
i+m; i+m£ n. Многочлен Lm
(x) интерполирует функцию f (x) на отрезке [xi,
xi+1]. Дифференцируя многочлен Lm (x),
получаем значения производных в точках xk, k=i, i+1,…,
i+m.
Если m=1, то L1 (x)
- линейная функция, график которой проходит через точки (xi,yi)
и (xi+1,yi+1). Тогда
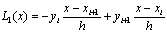 ,
, 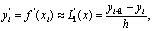
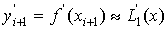 .
.
Если m=2, график интерполяционного
многочлена Лагранжа L2 (x) - парабола, проходящая
через три точки (xi, yi), (xi+1,yi+1),
(xi+2, yi+2) Вычислим
первую и вторую производные многочлена L2 (x) на
отрезке (xi,xi+2):
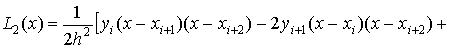
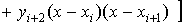
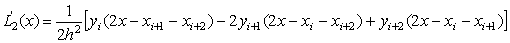
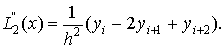
Первая и вторая производные многочлена
Лагранжа L2 (x) в точках xi, xi+1,
xi+2 являются приближениями производных
соответствующих функции f (x) в этих точках:
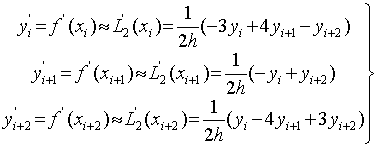 (1).
(1).
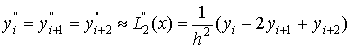 (2).
(2).
Если функция f (x) на
отрезке [xi, xi+2] имеет непрерывную
производную до третьего порядка включительно, то справедливо представление
функции в виде суммы f (x) =L2 (x) +R2
(x) (3), где R2 (x) - остаточный член
интерполяционной формулы, причём
 xÎ(xi, xi+2)
xÎ(xi, xi+2)
В этом случае можно дать оценку
погрешности приближений производных соотношениями (1) и (2). Дифференцируя (3),
получим
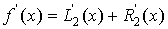 (4)
(4)
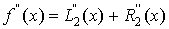 (5)
(5)
Здесь
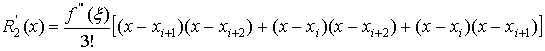 ,
,
xÎ (xi, xi+2)
(6)
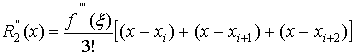
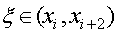 , (7)
, (7)
Погрешности при вычислении производных в
точках xi, xi+1, xi+2
определяются следующими значениями остатков:
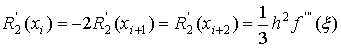 (8)
(8)
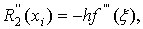
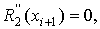
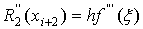 (9)
(9)
Следствие 1. Таким образом, равенство (8) показывает,
что погрешности аппроксимации первой производной f ' (x)
c помощью формул (1) имеют один и тот же порядок 0 (h2) и
естественна следующая рекомендация по их применению на отрезке [a, b]
в точках xi, i=0,1,2,…, n при n³2
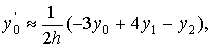
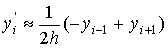
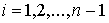 (10)
(10)
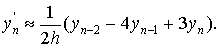
Следствие 2. Из равенства (9) следует, что приближение
второй производной с помощью формулы (2) имеет различный порядок в зависимости
от h в разных точках: в точках xi и xi+2
имеет погрешность порядка h, а в точке xi+1
порядок погрешности выше 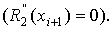
Пример. Значения функции y=sin x
определены таблицей
|
x
|
0
|
p/6
|
p/3
|
|
sin x
|
0
|
0,5
|
0,866
|
С помощью формул (1) и (2) приближения найти y'
(0) и y'' (0) и оценить погрешность результатов вычислений.
Решение:
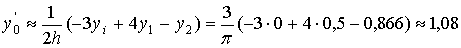
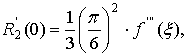
Так как 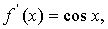
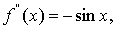
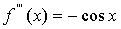 ,
, 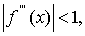
то 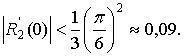
Итак 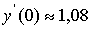 ±0,09 (точное значение y' (0) =cos 0=1. Теперь
воспользуемся формулой (2):
±0,09 (точное значение y' (0) =cos 0=1. Теперь
воспользуемся формулой (2):
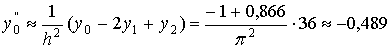

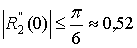 .
.
Как видим, для лучшей оценки производной
второго порядка необходимо увеличить число узловых точек и выбрать меньший шаг.
§16.
Численное интегрирование.Формула прямоугольников
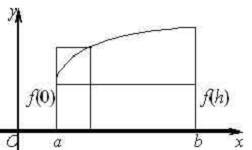
Для приближённого вычисления определённого
интеграла 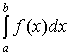 разобьём отрезок интегрирования [a,
b] на n равных частей точками x0=a, x1=x0+h,…,
xi+1=xi+h,…,xn=b
разобьём отрезок интегрирования [a,
b] на n равных частей точками x0=a, x1=x0+h,…,
xi+1=xi+h,…,xn=b
(h - шаг разбиения, 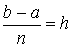 ). Значения функции f (x) в
точках разбиения xi обозначим yi.
Непрерывная подинтегральная функция y=f (x) заменяется сплайном
(кусочно-полиномиальной функцией) S (x), аппроксимирующей данную
функцию. Интегрируя функцию на отрезке [a, b], придём к некоторой
формуле численного интегрирования (квадратурной формуле).
). Значения функции f (x) в
точках разбиения xi обозначим yi.
Непрерывная подинтегральная функция y=f (x) заменяется сплайном
(кусочно-полиномиальной функцией) S (x), аппроксимирующей данную
функцию. Интегрируя функцию на отрезке [a, b], придём к некоторой
формуле численного интегрирования (квадратурной формуле).
В зависимости от функции S (x),
аппроксимирующей подинтегральную функцию, будем получать различные квадратурные
формулы.
Если на каждой части  [xi-1, xi],
i=
[xi-1, xi],
i=
 деления отрезка [a, b] функцию f (x)
заменить функцией, принимающей постоянное значение, равное, например, значению
функции f (x) в серединной точке i-й части, то есть
деления отрезка [a, b] функцию f (x)
заменить функцией, принимающей постоянное значение, равное, например, значению
функции f (x) в серединной точке i-й части, то есть 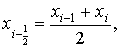 то функция S (x) будет
иметь ступенчатый вид:
то функция S (x) будет
иметь ступенчатый вид:
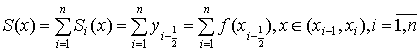 .
.
В этом случае 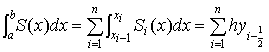 и получаем квадратурную формулу
прямоугольников
и получаем квадратурную формулу
прямоугольников
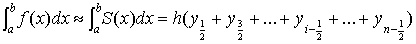 (1).
(1).
Пример. Найти приближённое значение интеграла 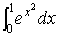 по формуле прямоугольников.
по формуле прямоугольников.
Решение. Пусть n=10.
Тогда x0=0, 
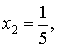 …, x10=1.
…, x10=1.
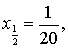
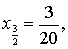
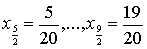 ,
, 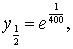
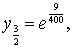
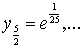
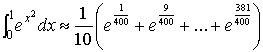 =
=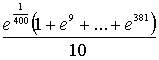
Погрешность квадратурной формулы
оценивается величиной остаточного члена R (h), зависящего от шага
разбиения h (или от числа разбиений n).
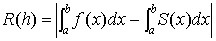
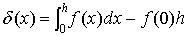
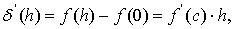 где 0£с£h.
где 0£с£h.
Если 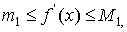 то
то 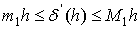 Заменим h на x и
проинтегрируем неравенство на отрезке [0, h]:
Заменим h на x и
проинтегрируем неравенство на отрезке [0, h]:
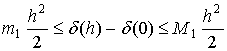
Но легко заметить, что 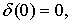 тогда
тогда 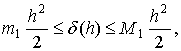 откуда:
откуда:  , где
, где 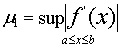 . Получаем общую погрешность на [a, b]
. Получаем общую погрешность на [a, b]
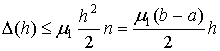 (так как hn= b - a).
(так как hn= b - a).
§17.
Формула трапеций
Если функцию f (x) на каждом
отрезке [xi-1, xi] заменить её линейной
интерполяцией по точкам (xi-1,yi-1),
(xi, yi) то получим непрерывную кусочно-линейную
функцию
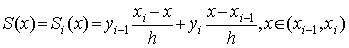
 .
.
Здесь yi=f (xi).
Графиком этой функции является ломаная линия. В этом случае
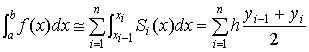
и получаем квадратурную формулу трапеций:
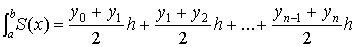 таким образом:
таким образом:
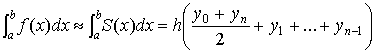 (1).
(1).
Оценка погрешности этой формулы:
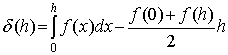
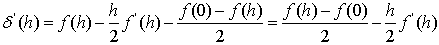
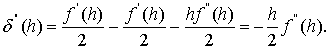
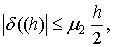 где
где 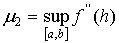 , а
, а 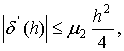
тогда 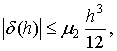
а
общая погрешность на [a, b] тогда равна
 .
.
§18.
Формула Симпсона (парабол)
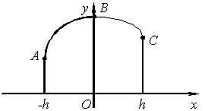
Рассмотрим точки A (-h, y-1),
B (0, y0), C (h, y1).
Уравнение параболы, проходящей через эти точки: y=a+bx+cx2
(1) 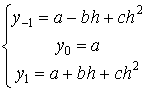
Площадь параболы, проходящей через точки A,
B, и С вычисляется по формуле:
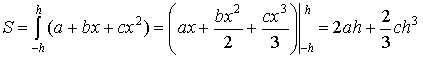 (2).
(2).
Из (1), сложив первое и третье равенства,
найдём:
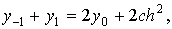
откуда
2ch2=y-1-2y0+y1
и тогда 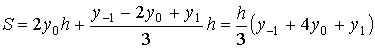 .
.
Рассмотрим теперь функцию y=f (x),
заданную на [a, b]. Требуется вычислить 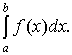 Разобьём отрезок [a, b] на
2n отрезков a=x0<x1<…<x2n=b.
Заменим дугу кривой y=f (x) (
Разобьём отрезок [a, b] на
2n отрезков a=x0<x1<…<x2n=b.
Заменим дугу кривой y=f (x) ( ) параболой, проходящей через эти точки и тогда площадь
криволинейной трапеции, ограниченной сверху параболой, будет вычисляться по
формуле:
) параболой, проходящей через эти точки и тогда площадь
криволинейной трапеции, ограниченной сверху параболой, будет вычисляться по
формуле:
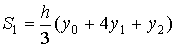 .
.
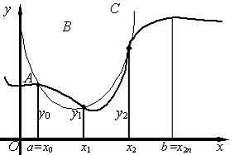
Вычислим площадь следующей криволинейной трапеции
на [x2, x4]:
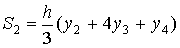
и так далее. Искомая площадь будет
приближённо равна:
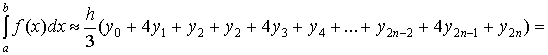
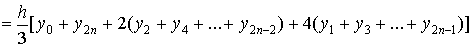
Оценка погрешности для формулы Симпсона
(без вывода):
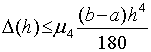
Пример 1. Найти приближённое значение интеграла 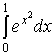 с помощью квадратурных формул
прямоугольников, трапеций и Симпсона, если отрезок [0, 1] разбит на 10 равных
частей.
с помощью квадратурных формул
прямоугольников, трапеций и Симпсона, если отрезок [0, 1] разбит на 10 равных
частей.
Решение: 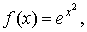
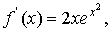
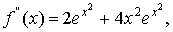
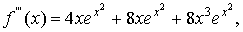

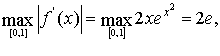

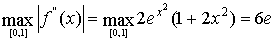 .
.
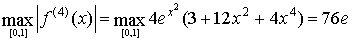
При n=10 получим следующие оценки
величин погрешности результатов:

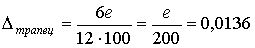
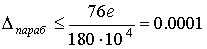
Пример 2. Вычислить интеграл 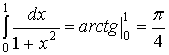 . по формуле Симпсона.
. по формуле Симпсона.
Решение: Возьмём 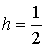 .
.
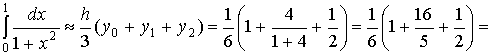
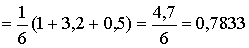 . Тогда
. Тогда 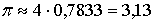 .
.
§19.
Приемы приближенного вычисления несобственных интегралов
Рассмотрим интегралы вида:
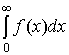 (1),
(1), 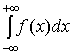 (2),
(2), 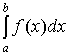 (3).
(3).
Для случая (3) функция f (x)
имеет бесконечный разрыв либо в точке x=a, либо x=b, либо x=cÎ [a, b].
Вычисляемые несобственные интегралы при этом предполагаются сходящимися.
Одним из источников получения численных
значений несобственных интегралов (1) и (2) являются квадратурные формулы вида:
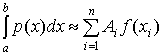 (Гаусса-Кристоффеля). Для их применения
нужно выделить под интегралом подходящую весовую функцию и воспользоваться
соответствующей квадратурой.
(Гаусса-Кристоффеля). Для их применения
нужно выделить под интегралом подходящую весовую функцию и воспользоваться
соответствующей квадратурой.
Тогда для интеграла (1):
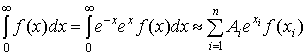 - формула Лагерра,
- формула Лагерра,
где 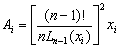 , Ln-1 - n-1-ый многочлен
Лагерра.
, Ln-1 - n-1-ый многочлен
Лагерра.
Аналогично, для интеграла (2) имеем:
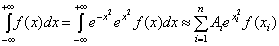 - формула Эрмита,
- формула Эрмита,
где 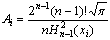 , Hn-1 - n-1-вый многочлен
Эрмита.
, Hn-1 - n-1-вый многочлен
Эрмита.
К вычислению интегралов с бесконечной
верхней границей можно применять различные формулы численного интегрирования,
пользуясь равенством, определяющим несобственный интеграл:
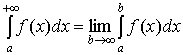 .
.
Оно позволяет считать, что для достаточно
больших значений b выполняется 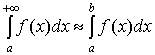 и вычислять интеграл
и вычислять интеграл 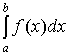 с помощью известных квадратурных правил. предполагая исходный
интеграл абсолютно сходящимся, величину абсолютной погрешности, то есть
с помощью известных квадратурных правил. предполагая исходный
интеграл абсолютно сходящимся, величину абсолютной погрешности, то есть 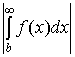 , за счет увеличения b можно
сделать как угодно малой.
, за счет увеличения b можно
сделать как угодно малой.
В случае (2) без ограничения общности
можно считать, что подынтегральная функция имеет особенность на границе
промежутка интегрирования, то есть если точкой c, где f (x)
обращается в бесконечность, окажется внутренняя точка интервала (a, b),
то данный интеграл можно представить символически как 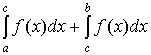 . Также без потери общности, достаточно
рассматривать
. Также без потери общности, достаточно
рассматривать 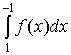 . Но к таким интегралам, в которых
подынтегральная функция имеет особыми точками значения - 1 и (или) 1, можно
применить квадратурную формулу Эрмита (Мелера) в виде
. Но к таким интегралам, в которых
подынтегральная функция имеет особыми точками значения - 1 и (или) 1, можно
применить квадратурную формулу Эрмита (Мелера) в виде
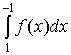 =
=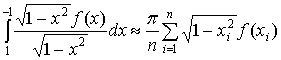
или более общую формулу, где параметры a > - 1, b > - 1 желательно подобрать
так, чтобы функция 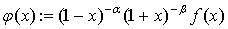 была как можно более гладкой. Такой прием
при вычислении несобственных интегралов называют мультипликативным
выделением особенностей. Существует несколько специальных квадратурных
формул, позволяющих "загнать" в весовые функции различные типы
особенностей: степенную, логарифмическую и другие.
была как можно более гладкой. Такой прием
при вычислении несобственных интегралов называют мультипликативным
выделением особенностей. Существует несколько специальных квадратурных
формул, позволяющих "загнать" в весовые функции различные типы
особенностей: степенную, логарифмическую и другие.
Применяются и другие приемы вычисления
несобственных интегралов. Надо отметить, что иногда достаточно сделать удачную
замену переменной, чтобы преобразовать несобственный интеграл к более
подходящему для вычисления виду.
§20.
Численное решение обыкновенных дифференциальных уравнений. Понятие о численном
решении задачи Коши
Дифференциальное уравнение первого порядка,
разрешённое относительно производной имеет вид
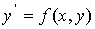 (1).
(1).
Решением дифференциального уравнения
называется функция j (x), подстановка которой в уравнение обращает его в
тождество:
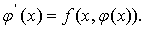
График решения 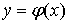 называется интегральной кривой. Например,
решением уравнения
называется интегральной кривой. Например,
решением уравнения 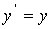 является функция
является функция 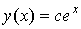 при любом значении произвольной
постоянной С.
при любом значении произвольной
постоянной С.
Задача Коши для дифференциального
уравнения (2) состоит в том, чтобы найти решение этого уравнения,
удовлетворяющее начальному условию
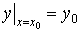 (2).
(2).
Пару чисел 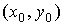 называют начальными данными. Решение задачи
Коши называют частным решением уравнения (1) при условии (2).
называют начальными данными. Решение задачи
Коши называют частным решением уравнения (1) при условии (2).
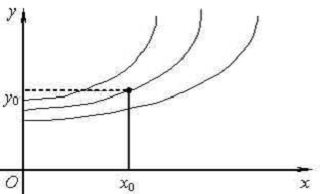
Пример:
частным решением задачи Коши 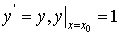 является функция
является функция 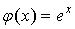 .
.
Частному решению соответствует одна из
интегральных кривых, проходящая через точку 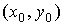 .
.
Условия существования и единственности
решения задачи Коши содержатся в следующей теореме.
Теорема. Пусть функция f (x, y)
- правая часть дифференциального уравнения (2) - непрерывная
вместе со своей частной производной 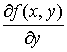 в некоторой области D на плоскости. Тогда при любых
начальных данных
в некоторой области D на плоскости. Тогда при любых
начальных данных 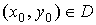 задача Коши (1) - (2) имеет единственное
решение
задача Коши (1) - (2) имеет единственное
решение 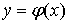 .
.
При выполнении условий теоремы через точку
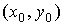 на плоскости проходит единственная
интегральная кривая. Будем считать, что условия теоремы существования и
единственности выполняются. Численное решение задачи Коши (1) - (2) состоит в
том, чтобы искомое решение
на плоскости проходит единственная
интегральная кривая. Будем считать, что условия теоремы существования и
единственности выполняются. Численное решение задачи Коши (1) - (2) состоит в
том, чтобы искомое решение 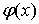 получить в виде таблицы его приближённых значений для заданных
значений аргумента x на некотором отрезке (a, b): а=x0,
x1, x2,…,xm=b (3).
получить в виде таблицы его приближённых значений для заданных
значений аргумента x на некотором отрезке (a, b): а=x0,
x1, x2,…,xm=b (3).
Точки (3) называют узловыми точками,
а множество этих точек называют сеткой на отрезке [a,
b]. Будем использовать равномерную сетку с шагом h. 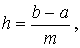
 или
или 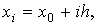
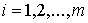 . Приближённые значения численного решения задачи Коши в узловых
точках xi обозначим yi; таким образом,
. Приближённые значения численного решения задачи Коши в узловых
точках xi обозначим yi; таким образом, 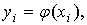
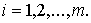
Для любого численного метода решения
задачи Коши начальное условие (2) выполняется точно, то есть 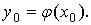
Величина погрешности численного метода
решения задачи Коши на сетке отрезка [a, b] оценивается величиной
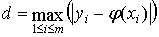 , то есть расстоянием между векторами
приближённого решения (y0, y1, …, ym)
и точного решения
, то есть расстоянием между векторами
приближённого решения (y0, y1, …, ym)
и точного решения 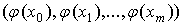 на сетке по m-норме.
на сетке по m-норме.
Определение. численный метод имеет p-й
порядок точности по шагу h на сетке, если расстояние d
можно представить в виде степенной функции от h: d=chp,
p>0, где c-некоторая положительная постоянная, зависящая от
правой части уравнения (1) и от рассматриваемого метода.
В данном случае очевидно, что когда h
cтремится к нулю, погрешность d также стремится к нулю.
§21.
Метод Эйлера
Простейшим численным методом решения задачи Коши
(1) - (2) (§20) является метод Эйлера, называемый иногда методом
ломаных Эйлера.
Угловой коэффициент касательной к
интегральной кривой в точке P0 (x0,y0)
есть 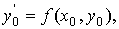 . Hайдём ординату y1
касательной, соответствующей абциссе x1=x0+h.
Так как уравнение касательной к кривой в точке P0 имеет
вид
. Hайдём ординату y1
касательной, соответствующей абциссе x1=x0+h.
Так как уравнение касательной к кривой в точке P0 имеет
вид 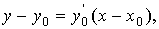 то
то 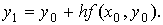 Угловой коэффициент в точке P1 (x1,y1)
также находится из данного дифференциального уравнения
Угловой коэффициент в точке P1 (x1,y1)
также находится из данного дифференциального уравнения 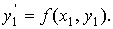 На следующем шаге получаем новую точку P2
(x2, y2), причём
На следующем шаге получаем новую точку P2
(x2, y2), причём 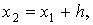
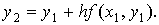
Продолжая вычисления в соответствии с
намеченной схемой, получим формулы Эйлера для m приближённых значений
решения задачи Коши с начальными данными (x0, y0)
на сетке отрезка [a, b] с шагом h: 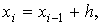
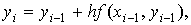
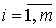 (1).
(1).
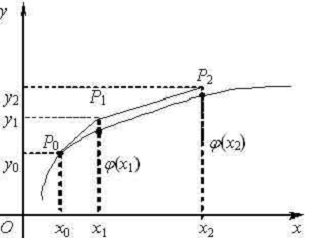
Графической иллюстрацией приближённого
решения является ломаная, соединяющая последовательно точки P0,
P1, P2, …,Pm, которую
называют ломаной Эйлера.
Оценим погрешность метода Эйлера на одном
шаге. Для этого запишем разложение точного решения задачи Коши в точке x1
по формуле Тейлора с дополнительным членом в форме Лагранжа:
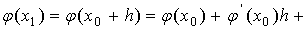
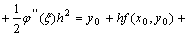
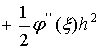 ,
, 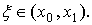
Погрешность метода на одном шаге имеет h2,
т.к.
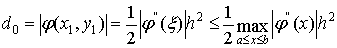
После m шагов погрешность
вычисления значения ym в концевой точке отрезка возрастёт не
более чем в m раз. Погрешность метода Эйлера можно оценить неравенством
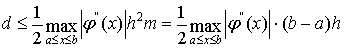
или представить в виде
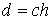 , где
, где 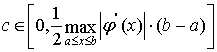
Это означает, что метод Эйлера имеет
первый порядок точности. В частности, при уменьшении шага h в 10 раз
погрешность примерно уменьшится в 10 раз.
Практическую оценку погрешности решения,
найденного на сетке с шагом 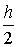 , в точке
, в точке 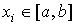 производят с помощью приближённого
равенства-правила Рунге:
производят с помощью приближённого
равенства-правила Рунге:
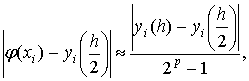 (2)
(2)
где p-порядок точности численного
метода. Таким образом, оценка полученного результата по формуле (2) вынуждает
проводить вычисления дважды: один раз с шагом h, другой - с шагом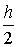 .
.
Пример. Решить задачу Коши 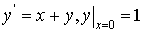 методом Эйлера на отрезке [0; 0,4]. Найти
решение на равномерной сетке с шагом h1=0,1, h2=0,05
в четырёх узловых точках. Аналитическое решение задачи имеет вид
методом Эйлера на отрезке [0; 0,4]. Найти
решение на равномерной сетке с шагом h1=0,1, h2=0,05
в четырёх узловых точках. Аналитическое решение задачи имеет вид  .
.
Решение: Здесь 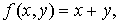 m=4, a=0, b=0,4
m=4, a=0, b=0,4
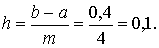 Используя рекуррентные формулы x0=0,
y0=1, xi=xi-1+0,1; yi=yi-1+0,1
(xi-1+yi-1); i=1,2,3,4
последовательно находим
Используя рекуррентные формулы x0=0,
y0=1, xi=xi-1+0,1; yi=yi-1+0,1
(xi-1+yi-1); i=1,2,3,4
последовательно находим
при i=1: x1=0,1; y1=1+0,1
(0+1) =1,1
при i=2: x2=0,2; y2=1,1+0,1
(0,1+1,1) =1,22
при i=3: x3=0,3; y3=1,22+0,1
(0,2+1,22) =1,362
при i=4: x4=0,4; y4=1,362+0,1
(0,3+1,362) =1,5282
Обозначим 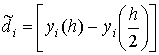 ,
, 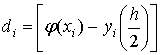
 и представим результаты вычислений в таблице:
и представим результаты вычислений в таблице:
|
i
|
xi
|
yi
(h)
|
yi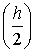 j (xi) j (xi)   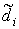 di di
|
|
|
|
|
1
|
0,1
|
1,1
|
1,105
|
1,110342
|
0,005
|
0,005332
|
|
2
|
0,2
|
1,22
|
1,231012
|
1,242805
|
0,011012
|
0,011793
|
|
3
|
0,3
|
1,362
|
1,380191
|
1,399718
|
0,018191
|
0,019527
|
|
4
|
0,4
|
1,5282
|
1,554911
|
1,583649
|
0,026711
|
0,028738
|
Отметим, что оценка погрешностей 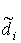 решения
решения 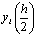 , вычисляемых по формулам (2), близки к отклонениям di
и обе величины достигают значения
, вычисляемых по формулам (2), близки к отклонениям di
и обе величины достигают значения 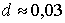 -ошибки метода Эйлера при вычислении с шагом 0,05. Для сравнения
заметим, что погрешность при вычислениях с шагом 0,1 составляет
-ошибки метода Эйлера при вычислении с шагом 0,05. Для сравнения
заметим, что погрешность при вычислениях с шагом 0,1 составляет 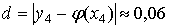 .
.
§
22. Методы Рунге - Кутта
Определение. Численные методы решения задачи Коши 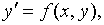
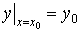 на равномерной сетке (x0=a, x1,
x2,…, xm=b) отрезка [a, b]
с шагом
на равномерной сетке (x0=a, x1,
x2,…, xm=b) отрезка [a, b]
с шагом 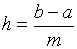 называются методами Рунге - Кутта,
если, начиная с данных (x0, y0), решение
ведётся по следующим рекуррентным формулам:
называются методами Рунге - Кутта,
если, начиная с данных (x0, y0), решение
ведётся по следующим рекуррентным формулам:
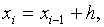
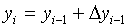
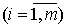 (1)
(1)
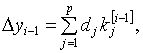
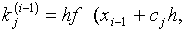
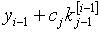 )
)
Метод называется методом Рунге - Кутта порядка
p, если он имеет p-й порядок точности по шагу h на сетке.
Порядок точности p достигается с помощью формул (1) при определённых
значениях коэффициентов cj и dj (j=1,2,.,p);
причем c1 всегда полагают равным нулю. Эти коэффициенты
вычисляются по следующей схеме:
) точное решение  и его приближение
и его приближение 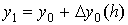 представляют в виде разложения по формуле
Тейлора с центром x0 вплоть до слагаемого порядка hp+1;
представляют в виде разложения по формуле
Тейлора с центром x0 вплоть до слагаемого порядка hp+1;
) из равенств подобных членов при
одинаковых степенях h в двух разложениях получают уравнения, решая которые
находят коэффициенты cj и dj.
Замечание 1. что метод Эйлера можно
назвать методом Рунге - Кутта первого порядка.
Покажем это. Пусть p=1, c1=0,
d1=1, формулы (1) преобразуются в соотношения: xi=xi-1+h,
yi=yi-1+Dyi-1, i=1,2, …, m
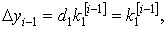
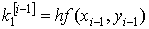 или
или
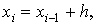
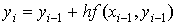 .
.
Замечание 2. Метод Рунге-Кутта второго
порядка
можно назвать методом Эйлера - Коши. Покажем это. Пусть p=2,
c1=0, c2=1, d1=d2=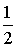 . Алгоритм метода Эйлера - Коши получается
из формул (1):
. Алгоритм метода Эйлера - Коши получается
из формул (1):
xi=xi-1+h, yi=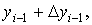
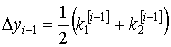
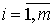 (2)
(2)
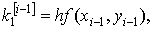
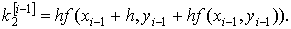
Для практической оценки решения можно
применять правило Рунге, полагая в приближённом равенстве (правиле Рунге) p=2.
Пример. Решить задачу Коши y'=x+y,
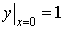 методом Эйлера - Коши на отрезке [0;
0,4]. Найти решение на равномерной сетке с шагом 0,1 в четырёх узловых точках.
методом Эйлера - Коши на отрезке [0;
0,4]. Найти решение на равномерной сетке с шагом 0,1 в четырёх узловых точках.
Решение. Формулы (2) в данном случае примут вид:
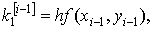
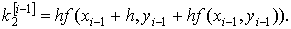
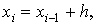
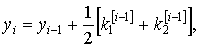
Полагая x0=0, y0=1
при i=1 последовательно находим
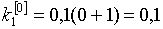 ;
; 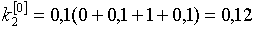
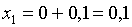 ;
; 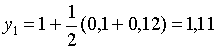
при i=2
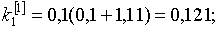
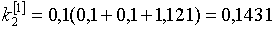
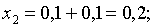
 .
.
Далее получаем: при i=3, x3=0,3
- y3=1,398405, при i=4, x4=0,4 - y4=1,581804.
Погрешность полученного решения не
превышает величины
Замечание 3. Метод Рунге - Кутта
четвёртого порядка называют классическим методом Рунге - Кутта.
Пусть p=4, c1=0, c2=c3=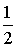 c4=1, d1=d4=
c4=1, d1=d4=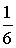 , d2=d3=
, d2=d3=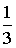 . Из рекуррентных формул (1) получим
алгоритм решения задачи Коши классическим методом Рунге - Кутта:
. Из рекуррентных формул (1) получим
алгоритм решения задачи Коши классическим методом Рунге - Кутта:
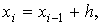
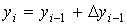
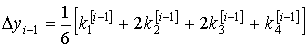
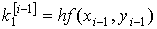
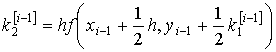 (3)
(3)
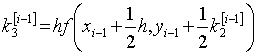
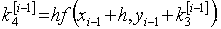
Графиком приближённого решения является
ломаная, последовательно соединяющая точки Pi (xi,yi)
(i=0,1,…,m). С увеличением порядка численного метода, звенья
ломаной приближаются к ломаной, образованной хордами интегральной кривой y=j (x), последовательно
соединяющими точки (xi,j (xi)) на
интегральной кривой.
Правило Рунге практической оценки
погрешности решения для численного метода четвёртого порядка имеет вид:
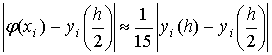
Пример. Решить задачу Коши y'=x+y,
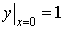 классическим методом Рунге - Кутта на
отрезке [0; 0,4]. Найти решение на равномерной сетке с шагом 0,1 в четырёх
узловых точках.
классическим методом Рунге - Кутта на
отрезке [0; 0,4]. Найти решение на равномерной сетке с шагом 0,1 в четырёх
узловых точках.
Решение: Так как f (x,y) =x+y, то
согласно формулам (3) получаем
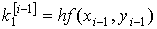 ;
; 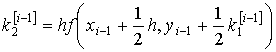
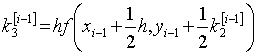 ;
; 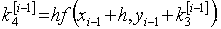
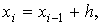

Полагая x0=0, y0=1,
последовательно находим при i=1:
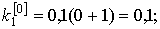
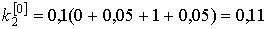
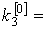 0,1 (0+0,05+1+0,055) =0,1105
0,1 (0+0,05+1+0,055) =0,1105
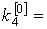 0,1 (0+0,1+1+0,1105) =0,121050
0,1 (0+0,1+1+0,1105) =0,121050
x1=0+0,1=0,1; y1=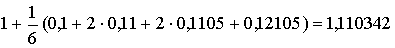
при i=2:
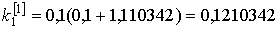
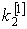 =0,1 (0,1+0,05+1,110342+0,0605171) =0,1320859
=0,1 (0,1+0,05+1,110342+0,0605171) =0,1320859
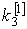 =0,1 (0,1+0,05+1,110342+0,06604295) =0,1326385
=0,1 (0,1+0,05+1,110342+0,06604295) =0,1326385
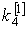 =0,1 (0,1+0,1+1,110342+0,1326385) =0,1442980
=0,1 (0,1+0,1+1,110342+0,1326385) =0,1442980
x2=0,1+0,1=0,2; y2=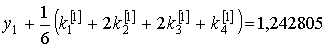 .
.
Далее получаем при i=3, x3=0,3,
y3=1,399717; при i=4, x4=0,4; y4=1,583648.
Погрешность полученного решения не
превышает величины 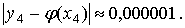
§23.
Приближенное решение систем уравнений. Приближенное решение систем линейных
уравнений
Рассмотрим сущность итерационного метода
при решении систем линейных уравнений на примере. Пусть дана система Ax=B,
где А= (аij) - матрица коэффициентов при переменных хij
размерности n´n,
x= (x1, x2, …, xn)
- матрица переменных,  - матрица свободных членов. Она может
быть преобразована к эквивалентной ей системе вида x=Bx+c, где В и
с - некоторые новые матрица и свободный член соответственно. Данную
систему можно трактовать как задачу о неподвижной точке линейного отображения В
в пространстве Rn и определить
последовательность приближений х (k) к неподвижной
точке х* рекуррентным равенством x (k+1) =Bx
(k) +c, k=0, 1, 2, …. Итерационный процесс,
начинающийся с некоторого значения
- матрица свободных членов. Она может
быть преобразована к эквивалентной ей системе вида x=Bx+c, где В и
с - некоторые новые матрица и свободный член соответственно. Данную
систему можно трактовать как задачу о неподвижной точке линейного отображения В
в пространстве Rn и определить
последовательность приближений х (k) к неподвижной
точке х* рекуррентным равенством x (k+1) =Bx
(k) +c, k=0, 1, 2, …. Итерационный процесс,
начинающийся с некоторого значения 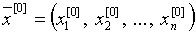 называется методом простых итераций.
называется методом простых итераций.
Пусть исходная линейная система уравнений
имеет вид:
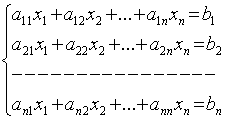
 (1)
(1)
При решении этой системы необходимо:.
Задать начальное приближенное решение 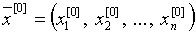 (индекс в скобках указывает номер итерации), которое будет
уточняться в процессе итераций. При этом надо учитывать, что, если метод
сходится, то он сходится при любом начальном приближении. Обычно в качестве
начального приближения, в зависимости от задачи, берутся либо вектор правых
частей
(индекс в скобках указывает номер итерации), которое будет
уточняться в процессе итераций. При этом надо учитывать, что, если метод
сходится, то он сходится при любом начальном приближении. Обычно в качестве
начального приближения, в зависимости от задачи, берутся либо вектор правых
частей  и тогда
и тогда 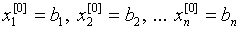 , либо нулевой вектор и тогда
, либо нулевой вектор и тогда 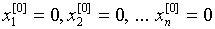 .. Привести исходную систему (1) к виду,
удобному для проведения итераций, то есть к виду
.. Привести исходную систему (1) к виду,
удобному для проведения итераций, то есть к виду
 (2)
(2)
где  - произвольные линейные функции переменных
- произвольные линейные функции переменных  , причем некоторые переменные могут
отсутствовать в правых частях системы (2), но каждая переменная должна
присутствовать в левой части соответствующего уравнения.. Указать совокупность
действий, которые составляют одну итерацию (переход от
, причем некоторые переменные могут
отсутствовать в правых частях системы (2), но каждая переменная должна
присутствовать в левой части соответствующего уравнения.. Указать совокупность
действий, которые составляют одну итерацию (переход от 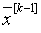 к
к 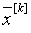 ). Достаточно рассмотреть два алгоритма вычисления корней
уравнений системы.
). Достаточно рассмотреть два алгоритма вычисления корней
уравнений системы.
1.
Метод простой итерации записывается в виде:
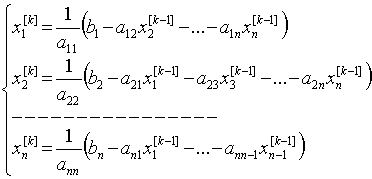 (3)
(3)
1.
Метод Зейделя (обобщение метода простой итерации) заключается в
следующем: уже полученные значения переменных используются при вычислении остальных
искомых переменных на этой итерации. То есть имеет место:
2.
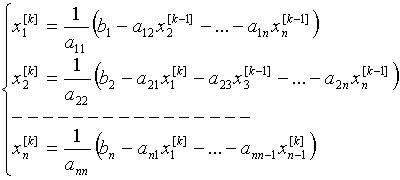 (4)
(4)
Применяя каждый из методов, необходимо
учитывать, что метод Зейделя сходится на порядок быстрее метода простой итерации..
Выяснить условия сходимости итерационного процесса. При решении практических
задач используется следующая теорема: Если матрица А исходной системы
имеет диагональное преобладание, то методы простой итерации и Зейделя
сходятся.. Указать условия окончания итерационного процесса. В этой роли обычно
выступает оценка 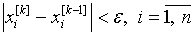 , где ε - наперед заданная точность
вычислений.
, где ε - наперед заданная точность
вычислений.
§24. Приближенные методы решения систем нелинейных уравнений
Многие практические задачи при их математическом
моделировании сводятся к решению системы нелинейных уравнений. Система n
нелинейных уравнений с n неизвестными в общем случае имеет вид
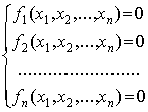 (1)
(1)
Решением системы уравнений (1) называется n
чисел 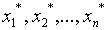 которые при подстановке в (1) обращают все
уравнения в нули.
которые при подстановке в (1) обращают все
уравнения в нули.
Задача (1) тесно связана с другой очень
часто встречающейся задачей - минимизации функции многих переменных
 (2)
(2)
Эта связь проявляется в том, что каждую из
этих задач можно свести к решению другой. Пусть, например, вектор 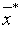
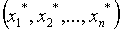 является решением системы (1). Построим функцию
является решением системы (1). Построим функцию
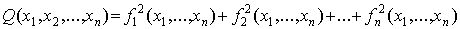 (3)
(3)
Так как 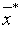 обращает в нуль все уравнения системы (1), то
обращает в нуль все уравнения системы (1), то 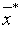 обращает функцию
обращает функцию 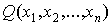 в нуль. Поскольку
в нуль. Поскольку 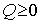 , то
, то 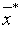 обращает функцию Q в минимум, и этот минимум равен нулю.
Справедливо и обратное утверждение. Пусть совокупность чисел
обращает функцию Q в минимум, и этот минимум равен нулю.
Справедливо и обратное утверждение. Пусть совокупность чисел 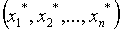 обращает функцию
обращает функцию 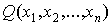 в минимум, равный нулю. Тогда каждый член
суммы, входящий в (3), обращается в нуль и, следовательно, совокупность
в минимум, равный нулю. Тогда каждый член
суммы, входящий в (3), обращается в нуль и, следовательно, совокупность 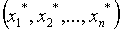 является решением системы (1). Таким
образом, задача (1) сводится к нахождению минимума (3).
является решением системы (1). Таким
образом, задача (1) сводится к нахождению минимума (3).
В свою очередь, для задачи минимизации (2)
точка минимума является решением системы нелинейных уравнений.
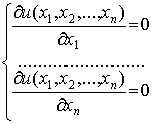
Возможность сведения одной задачи к другой
не означает, что можно ограничиться рассмотрением только одной из них. Каждая
из них является весьма сложной и имеет многочисленные подводные камни, которые
проявляются при практической реализации существующих методов их решения.
По-видимому, не существует никаких универсальных методов решения этих задач.
Установление связи между задачами (1) и (2) удобно тем, что в каждом конкретном
случае мы можем использовать ту из них, которая быстрее приводит к цели при
располагаемых ресурсах вычислительной техники и математического обеспечения.
Трудности при решении систем нелинейных уравнений проявляются в следующем:
1)
Определение количества корней системы и их отделение проводить
достаточно сложно в силу невозможности при больших n использовать
простые геометрические соображения.
2)
Многие надёжные методы нахождения корня одного нелинейного
уравнения, имеющие гарантированную сходимость, такие как метод половинного
деления или метод хорд и т.д., не допускают обобщения на случай n
неизвестных.
3)
Решение системы (1) ищут, как правило, методом итераций или
эффективным по скорости методом Ньютона, сходимость которых возможна только при
наличии хорошего начального приближения.
4)
нахождение хорошего начального приближения для сложной системы (1)
является весьма непростым делом и требует, помимо математического анализа
системы, привлечение других соображений (физических, инженерных, экономических
и др.), связанных с постановкой решаемых задач.
Замечание 1. никаких универсальных
методов преодоления отмеченных трудностей и решения этих задач не существует.
Каждый раз приходится, наряду с теоретическими исследованиями системы (1),
использовать эвристические соображения и проводить экспериментальные численные
исследования. Рассмотрим названные в пункте 3 методы.
Метод простой итерации.
Запишем систему (1) в виде, удобном для итераций:
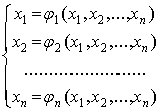 (4)
(4)
Зададим начальное приближенное решение 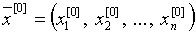 (индекс в скобках указывает номер
итерации), которое будет уточняться в процессе итераций. При этом надо
учитывать, что, если метод сходится, то он сходится при любом начальном
приближении. Первое приближение вычисляется по формулам:
(индекс в скобках указывает номер
итерации), которое будет уточняться в процессе итераций. При этом надо
учитывать, что, если метод сходится, то он сходится при любом начальном
приближении. Первое приближение вычисляется по формулам:
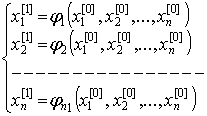 ,
,
где 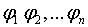 - нелинейные функции переменных
- нелинейные функции переменных 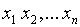 . Затем полученное первое приближение подставляем в правую часть
системы (4) и вычисляем второе приближение, и так далее. В общем случае формулы
метода простой итерации можно записать в виде:
. Затем полученное первое приближение подставляем в правую часть
системы (4) и вычисляем второе приближение, и так далее. В общем случае формулы
метода простой итерации можно записать в виде:
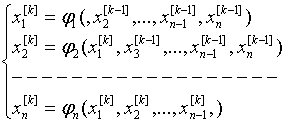 (5)
(5)
В роли условия окончания итерационного
процесса. обычно выступает оценка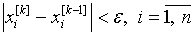 (6), где ε - наперед заданная точность
вычислений.
(6), где ε - наперед заданная точность
вычислений.
Уравнение (4) удобно записать в векторном
виде: 
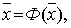 (7)
(7)
где 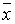 - вектор-столбец искомого решения, а Ф - вектор-функция
- вектор-столбец искомого решения, а Ф - вектор-функция
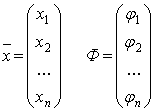
Итерационный процесс (5) можно также
записать в векторном виде
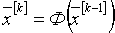 . (8)
. (8)
Условия сходимости итерационного метода
(5) (или в векторном виде (8) определяется принципом сжатых соображений: если
отображение (7), задаваемое вектор-функцией Ф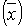 будет сжатым, то итерационный процесс (8)
сходится при условии, что начальное приближение
будет сжатым, то итерационный процесс (8)
сходится при условии, что начальное приближение 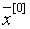 достаточно близко к корню.
достаточно близко к корню.
Достаточное условие сходимости метода простой итерации.
Рассмотрим матрицу Якоби для
преобразования (4)
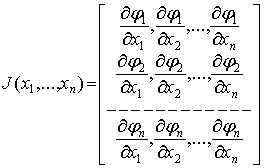 (9)
(9)
Матрица Якоби (или якобиан) зависит от
переменных 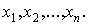
Теорема. если матрица Якоби в точке  , которая даёт решение системы (4), и в
некоторой её окрестности имеет все собственные значения, по модулю меньше
единицы
, которая даёт решение системы (4), и в
некоторой её окрестности имеет все собственные значения, по модулю меньше
единицы 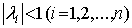 , то метод простой итерации сходится.
, то метод простой итерации сходится.
Замечание 2. Для выполнения этого условия достаточно,
например, выполнения следующих неравенств для элементов матрицы Якоби
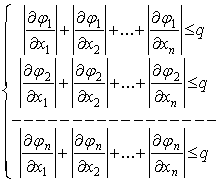 (10)
(10)
где q - некоторое положительное
число, меньшее единицы, т.е. 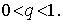 Неравенства (10) должны выполнятся в точке
Неравенства (10) должны выполнятся в точке  и в некоторой её окрестности.
и в некоторой её окрестности.
Возможно естественное обобщение метода
простой итерации (5), аналогичное методу Зейделя для систем линейных уравнений.
Оно заключается в том, что переменные  , уже полученные на данном итерационном шаге, используются для
получение других величин на этом шаге. Соответствующие формулы имеют вид
, уже полученные на данном итерационном шаге, используются для
получение других величин на этом шаге. Соответствующие формулы имеют вид
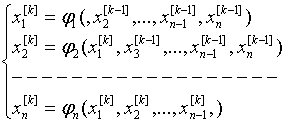 (11)
(11)
Если бы оба метода (5) и (11) сходятся, то
метод (11) сходится, вообще говоря, быстрее, так как получаемые на каждом шаге
итерации новые значения переменных сразу используются в дальнейших вычислениях
на этом шаге.
Метод Ньютона и его модификации.
Метод Ньютона - метод, который сводит
решение системы нелинейных уравнений к последовательному решению систем
линейных уравнений для нахождения поправок к предыдущим приближениям.
Рассмотрим общий вид нелинейной системы
(1). Зададим начальное приближение 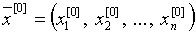 . Будем искать решение системы (1) в виде
. Будем искать решение системы (1) в виде
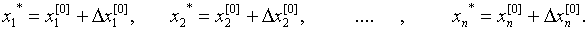 (12)
(12)
Разложим левые части системы (1) в ряд
Тейлора в точке 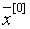 , считая величины
, считая величины 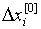 малыми и в силу этого ограничиваясь
только линейными членами в ряде Тейлора. Для функции
малыми и в силу этого ограничиваясь
только линейными членами в ряде Тейлора. Для функции 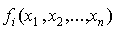 получим
получим
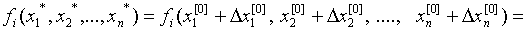
=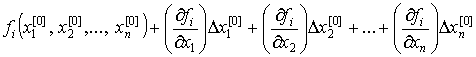 , (i=1,2,…,n) (13)
, (i=1,2,…,n) (13)
Обозначение 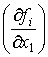 указывает, что соответствующая частная производная вычисляется в
базовой точке
указывает, что соответствующая частная производная вычисляется в
базовой точке 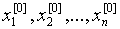 , для которой записывается разложение в
ряд Тейлора. Поскольку
, для которой записывается разложение в
ряд Тейлора. Поскольку 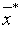 является точным решением системы (1),
левые части в уравнениях (13) равны нулю. В результате для неизвестных
приращений
является точным решением системы (1),
левые части в уравнениях (13) равны нулю. В результате для неизвестных
приращений 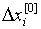 получим систему линейных уравнений
получим систему линейных уравнений
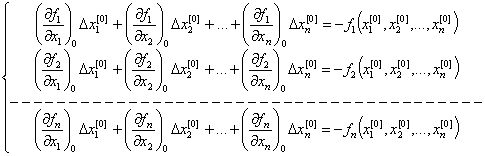 (14)
(14)
Матрицей этой системы является якобиан.
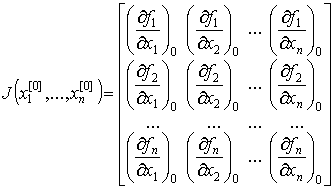 (15)
(15)
Если определитель этой матрицы не равен
нулю, то из системы уравнений (14) можно найти неизвестные приращения 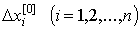 . Поскольку в разложении Тейлора мы
отбросили все члены, кроме линейных, соотношения (12) определяют не точное
решение
. Поскольку в разложении Тейлора мы
отбросили все члены, кроме линейных, соотношения (12) определяют не точное
решение 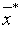 , а уточнение к нулевому приближению
, а уточнение к нулевому приближению
 ,
,
или в координатном виде:
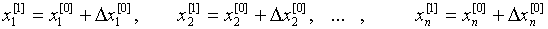 (16).
(16).
Один шаг метода Ньютона заключается в
решении системы линейных уравнений (14), все коэффициенты которой и правые
части зависят от начального приближения 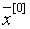 , и в получении уточнённого решения
, и в получении уточнённого решения 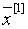 по формулам (16). Приняв теперь полученное первое приближение за
начальное и проделав те же операции, которые были сделаны на первом шаге, можно
получить следующее приближение к решению
по формулам (16). Приняв теперь полученное первое приближение за
начальное и проделав те же операции, которые были сделаны на первом шаге, можно
получить следующее приближение к решению 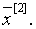 Этот итерационный процесс продолжается до тех пор, пока все
получаемые приращения становятся малыми по абсолютной величине
Этот итерационный процесс продолжается до тех пор, пока все
получаемые приращения становятся малыми по абсолютной величине
 (17)
(17)
Систему линейных уравнений, которую
необходимо решать на каждом шаге метода Ньютона, в общем виде можно записать
следующим образом:
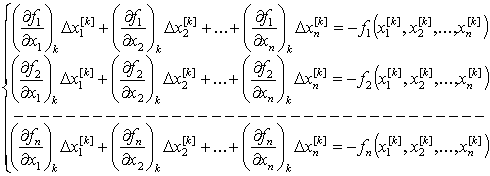 (18)
(18)
Индекс k у частных производных
указывает, что соответствующая частная производная вычисляется при 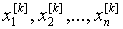 (для значений искомых переменных на k-ой
итерации).
(для значений искомых переменных на k-ой
итерации).
Решив эту линейную систему и определив из
неё величины поправок 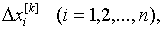 находим следующее приближение
находим следующее приближение
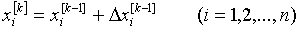 (19)
(19)
выражения (18) и (19) полностью определяют
один шаг метода Ньютона. Таким образом, метод Ньютона сводит решение систем
нелинейных уравнений к многократному решению систем линейных уравнений (18).
Замечание 3. если метод Ньютона сходится, то сходимость
имеет второй порядок, как и в случае уравнения с одной неизвестной.
Для сходимости метода требуется, чтобы
начальное приближение было близко к точному решению, а функции 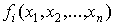 и их первые и вторые производные
удовлетворяли некоторым ограничениям. Несмотря на быструю сходимость, метод
Ньютона имеет существенный недостаток: на каждом его шаге требуется вычислять n2
частных производных
и их первые и вторые производные
удовлетворяли некоторым ограничениям. Несмотря на быструю сходимость, метод
Ньютона имеет существенный недостаток: на каждом его шаге требуется вычислять n2
частных производных 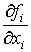 , определяющих коэффициенты при
неизвестных в линейной системе (18), то есть якобиан. В то же время в методе
простой итерации (5) требуется вычислять всего n функций
, определяющих коэффициенты при
неизвестных в линейной системе (18), то есть якобиан. В то же время в методе
простой итерации (5) требуется вычислять всего n функций 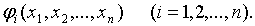 Чтобы компенсировать этот недостаток
метода Ньютона, были предложены различные его упрощения. Идея большинства из
этих упрощений заключается в том, чтобы матрицу коэффициентов линейной системы
(18) вычислять не на каждом итерационном шаге, а лишь на некоторых из них,
считая на остальных шагах все элементы якобиана постоянными, равными их
последним вычисленным значениям на том шаге, на котором производится пересчёт
всех членов. В простейшем случае якобиан вычисляется один раз, в начальной
точке
Чтобы компенсировать этот недостаток
метода Ньютона, были предложены различные его упрощения. Идея большинства из
этих упрощений заключается в том, чтобы матрицу коэффициентов линейной системы
(18) вычислять не на каждом итерационном шаге, а лишь на некоторых из них,
считая на остальных шагах все элементы якобиана постоянными, равными их
последним вычисленным значениям на том шаге, на котором производится пересчёт
всех членов. В простейшем случае якобиан вычисляется один раз, в начальной
точке 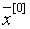 , а затем якобиан остаётся постоянным в
течение всего итерационного процесса. Такой метод обычно называется упрощённым
методом Ньютона. Матрица коэффициентов линейной системы (18) в этом случае
остаётся постоянной, и в процессе итераций изменяются только правые части
системы, которые пересчитываются на каждом шаге итераций и решения системы
, а затем якобиан остаётся постоянным в
течение всего итерационного процесса. Такой метод обычно называется упрощённым
методом Ньютона. Матрица коэффициентов линейной системы (18) в этом случае
остаётся постоянной, и в процессе итераций изменяются только правые части
системы, которые пересчитываются на каждом шаге итераций и решения системы 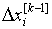 , после нахождения которых происходит
пересчёт
, после нахождения которых происходит
пересчёт 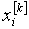 по формулам (19). Конечно, этот метод
сходится медленнее, чем метод Ньютона, но на каждом итерационном шаге требуется
гораздо меньше арифметических операций.
по формулам (19). Конечно, этот метод
сходится медленнее, чем метод Ньютона, но на каждом итерационном шаге требуется
гораздо меньше арифметических операций.