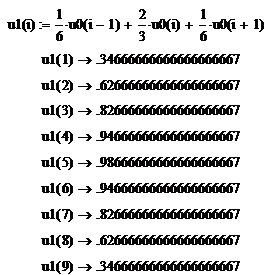Численные методы решения дифференциальных уравнений параболического типа
Введение
Появление современных вычислительных машин
привело к своему роду революции в численных методах. Сейчас численные методы
применяются во многих разделах математики. Среди задач с которыми приходится
иметь дело в вычислительной практике значительную часть составляют различные
задачи дифференциальных уравнений в частных производных. Такие задачи возникают
непосредственно при математическом моделировании многих реальных физических
явлений в таких областях, как динамика жидкости, электричество и магнетизм,
оптика, теплопередача.
Аналитические методы позволяют найти точное
решение задачи лишь для ограниченного класса уравнений, поэтому в начале XIX
века широко развиваются численные методы решений дифференциальных уравнений,
такой как метод сеток. Конечно-разностные методы решения уравнений в частных
производных были предложены еще в 1928 году в знаменитой статье Куранта,
Фридрихса и Леви, но на практике эти методы стали применяться лишь 15 лет
спустя. Отметим, что члены Лос-Аламосского персонала в Абердине численно решили
на машине ЭНИАК сложные задачи, относящиеся к системам уравнений в частных
производных. Вслед за тем в различных местах США были решены многие задачи,
связанные с движением жидкостей и газов, диффузией и переносом нейронов,
переносом лучистой энергии, термоядерными реакциями.
На сегодняшний день решение уравнений
параболического типа численными методами актуально, так как нахождение
аналитического решения задачи в явном виде, т. е. получение формулы,
характеризующей зависимость функции состояния системы от координат и параметров
процесса, удается найти лишь в исключительных случаях. Как правило, находится
лишь приближенное решение задачи. Среди множества способов практического
анализа выбран метод численного решения метод сеток в виду его достаточно
высокой эффективности и чрезвычайно широкой популярности. При этом
рассматриваемая область разбивается на участки, на каждом из которых
соответствующие производные аппроксимируются некоторыми разностными схемами. В
дипломной работе рассматриваются дифференциальные уравнения в частных
производных параболического типа, решаемые разностными методами.
Целью исследования является рассмотрение
основных методов решения дифференциальных уравнений в частных производных
конечно-разностными методами: однородные и консервативные конечно-разностные
схемы для задач теплопроводности с граничными условиями, содержащими
производные; неявно-явная конечно-разностная схема с весами; схема
Кранка-Николсона; метод дробных шагов Н.Н. Яненко; метод переменных направлений
с экстраполяцией В.Ф. Формалева.
Предметом исследования считаются численные
методы решения дифференциальных уравнений в частных производных параболического
типа.
Основными задачами написания дипломной работы
являются
Рассмотрение сути методов: неявно-явной
конечно-разностной схемы с весами; схемы Кранка-Николсона; метода дробных шагов
Н.Н. Яненко; метода переменных направлений с экстраполяцией В.Ф. Формалева;
однородные и консервативные конечно-разностные схемы для задач теплопроводности
с граничными условиями, содержащими производные;
Рассмотрение достоинств и недостатков
исследуемых методов дифференциальных уравнений в частных производных
параболического типа.
Написание программ для типовых задач.
Для решения задач использовались математическая
система MathCAD 7.0 Professional Edition (PRO) и язык программирования Turbo
Pascal 6.0.
Системы MathCAD традиционно занимают особое
место среди множества таких систем (Eureka, Mercury, MatLAB, Mathematica 2 и 3,
Maple V R3 и R4 и др.) и по праву могут называться самыми современными,
универсальными и массовыми математическими системами. Они позволяют выполнять
как численные, так и аналитические (символьные) вычисления, имеют чрезвычайно
удобный математико-ориентированный возможности и прекрасные средства графики. Системы
класса MathCAD предоставляют уже привычные, мощные, удобные и наглядные
средства описания алгоритмов решения математических задач. Система имеет
достаточные возможности для выполнения наиболее массовых символьных
(аналитических) вычислений и преобразований. Pascal 6.0, так как этот язык
позволяет работать с математическими формулами, приводить различного рода
математические операции и действия. Turbo Pascal фирмы Borland является
расширением стандарта языка и содержит интегрированную среду, данного ускоряющую
и облегчающую процесс разработки программ. В языке программирования Turbo
Pascal 6.0 используется типизированный адресный оператор, открытые массивы и
строки, что предоставляет пользователю дополнительные возможности при решении
математических задач.
На защиту выносится методика вычисления решений
дифференциальных уравнений в частных производных параболического типа
численными методами - метод сеток, вопросы устойчивости и аппроксимации решения
дифференциальных уравнений в частных производных параболического типа, а также
анализ численного решения типовых примеров.
Практической значимостью считается решение
дифференциальных уравнений в частных производных параболического типа
численными методами.
При написании данной дипломной работы была
изучена литература следующих авторов: Киреев В.И., Пантелеев А.В. «Численные
методы в примерах и задачах»; Формалев В.Ф., Ревизников Д.Л. «Численные
методы»; Рихтмайер Р.Д. «Разностные методы решения краевых задач»; Вержбицкий
В.М. «Основы численных методов»; Демидович Б.П., Марон И.А. «Основы
вычислительной математики»; Данко П.Е., Попов А.Г., Кожевникова Т.Я. «Высшая
математика в примерах и задачах»; Кабдыкайыр К. «Курс математики»; Плис А.И.,
Сливина Н.А. «Лабораторный практикум по высшей математике»; Такабаев М.К. «Курс
высшей математики».
1. Дифференциальные уравнения в
частных производных
.1 Определение дифференциальных
уравнений в частных производных параболического типа
Физические явления в таких областях, как
динамика жидкости, электричество и магнетизм, механика, оптика, теплопередача,
описываются с помощью дифференциальных уравнений в частных производных.
Производные появляются в уравнениях потому, что они описывают важнейшие
физические величины (такие, как скорость, ускорение, сила, поток, трение, электрический
ток и т.д.). В отличие от обыкновенных дифференциальных уравнений, в которых
неизвестная функция зависит только от одной независимой переменной, в
уравнениях с частными производными неизвестная функция зависит от нескольких
переменных.
Наиболее часто встречаются дифференциальные
уравнения второго порядка.
Определение 1. Уравнением с частными
производными второго порядка с двумя неизвестными переменными x и y называется
соотношение между неизвестной функцией 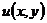 и
её частными производными до второго порядка включительно:
и
её частными производными до второго порядка включительно:
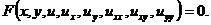 (1.1)
(1.1)
В общем случае уравнение в частных производных
может быть записано в виде
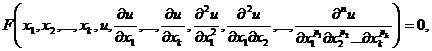 (1.1¢)
(1.1¢)
где 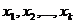 -
независимые переменные,
-
независимые переменные, 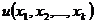 - неизвестная
(искомая) функция,
- неизвестная
(искомая) функция, 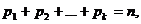
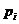 -
целые неотрицательные числа.
-
целые неотрицательные числа.
Определение 2. Уравнение называется линейным
относительно старших производных, если оно имеет вид
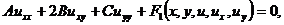 (1.2)
(1.2)
где 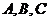 являются
функциями x и y.
являются
функциями x и y.
Определение 3. Если коэффициенты 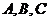 зависят
не только от x и y, а являются, подобно F1, функциями то уравнение называется
квазилинейным.
зависят
не только от x и y, а являются, подобно F1, функциями то уравнение называется
квазилинейным.
Определение 4. Уравнение называется линейным,
если оно линейно как относительно старших производных 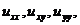 так
и относительно функции u и ее первых производных
так
и относительно функции u и ее первых производных 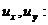
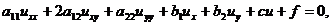 (1.3)
(1.3)
где 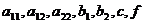 -
функции только x и y.
-
функции только x и y.
Определение 5. Если коэффициенты уравнения (1.3)
не зависят от x и y, то оно представляет собой линейное уравнение с постоянными
коэффициентами.
Определение 6. Уравнение (1.3) называется
однородным, если 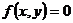 , в противном
случае неоднородным.
, в противном
случае неоднородным.
Задачи математической физики состоят в отыскании
решений уравнений в частных производных, удовлетворяющих некоторым
дополнительным условиям. Такими дополнительными условиями чаще всего являются
условия, заданные на границе рассматриваемой среды, т. е. граничные условия и
начальные условия, относящиеся к одному какому-нибудь моменту времени, с
которого начинается изучение данного физического явления.
Определение 7. Задача математической физики
считается поставленной корректно, если решение задачи, удовлетворяющее всем ее
условиям, существует, единственно и устойчиво.
Устойчиво, т. е. в данных любой конкретной
задачи, особенно если они получены из опыта, всегда содержится погрешность и
нужно, чтобы малая погрешность а данных приводила к малой неточности в решении.
Требование существования и единственности означает, что среди данных задачи нет
несовместных и их достаточно для выделения единственного решения.
1.2 Приведение уравнения второго
порядка параболического типа к каноническому виду
Рассмотрим уравнение 2-го порядка с двумя
независимыми переменными, линейное относительно производных второго порядка:
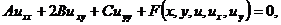 (1.4)
(1.4)
где A,B и C - функции, зависящие от x и y,
имеющие непрерывные производные до 2-го порядка включительно.
С помощью преобразования переменных
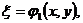
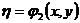 (1.5)
(1.5)
допускающего обратное преобразование получим
новое уравнение. Пусть (1.5) дважды непрерывно дифференцируемые функции, причем
якобиан
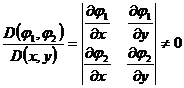 (1.6)
(1.6)
в рассматриваемой области.
Преобразуя производные к новым переменным,
получаем:
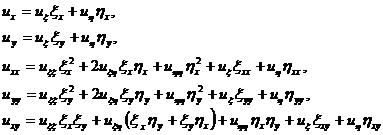 (1.7)
(1.7)
Подставляя значения производных из (1.7) в
уравнение (1.4), будем иметь
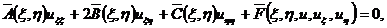 (1.8)
(1.8)
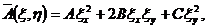
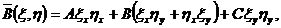
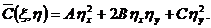
Непосредственной подстановкой нетрудно
проверить, что
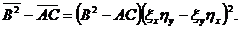 (1.9)
(1.9)
Рассмотрим дифференциальное уравнение 1-го
порядка
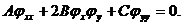 (1.10)
(1.10)
Исследуем случай, когда во всей рассматриваемой
области 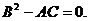 Тогда
уравнение (1.4) принадлежит параболическому типу. Пусть в рассматриваемой
области коэффициенты уравнения (1.4) не обращаются одновременно в нуль. В силу
условия
Тогда
уравнение (1.4) принадлежит параболическому типу. Пусть в рассматриваемой
области коэффициенты уравнения (1.4) не обращаются одновременно в нуль. В силу
условия 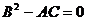 из
этого предположения следует, что в каждой точке этой области один из
коэффициентов A и C отличен от нуля. Не нарушая общности, можно считать, что в
рассматриваемой области всюду
из
этого предположения следует, что в каждой точке этой области один из
коэффициентов A и C отличен от нуля. Не нарушая общности, можно считать, что в
рассматриваемой области всюду 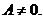 Тогда уравнение
(1.10) можно записать в виде
Тогда уравнение
(1.10) можно записать в виде
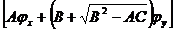
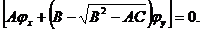
Это уравнение распадается на два:
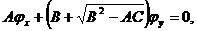 (1.10а)
(1.10а)
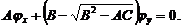 (1.10б)
(1.10б)
Решения каждого из уравнений (1.10а) и (1.10б)
будут решениями уравнения (1.10). Оба уравнения (1.10а) и (1.10б) совпадают и
обращаются в уравнение
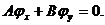 (1.11)
(1.11)
Всякое решение уравнения (1.11), в силу 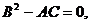 удовлетворят
также уравнению
удовлетворят
также уравнению
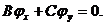 (1.12)
(1.12)
Для интегрирования уравнений (1.10а) и (1.10б)
составим соответствующие им системы обыкновенных дифференциальных уравнений
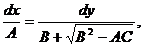
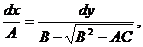
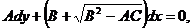 (1.13)
(1.13)
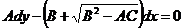 .
.
Уравнение (1.13) можно записать в виде одного
уравнения
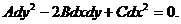 (1.13а)
(1.13а)
Пусть
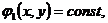
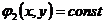 (1.14)
(1.14)
интегралы уравнений (1.13). Тогда их левые части
будут решениями уравнений (1.10а) и (1.10б), а значит и уравнения (1.10).
Кривые (1.14) называются характеристическими кривыми или просто
характеристиками уравнения (1.4), а уравнение (1.10) - уравнением
характеристик.
Для уравнения параболического типа интегралы
(1.14) совпадают, и получаем семейство вещественных характеристик 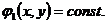
Возьмем
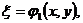
где 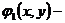 решение
уравнения решение уравнения (1.11), а за
решение
уравнения решение уравнения (1.11), а за 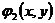 -
любую функцию так, чтобы якобиан
-
любую функцию так, чтобы якобиан 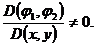 Так
как
Так
как 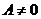 и,
следовательно,
и,
следовательно, 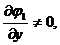 то можно принять
то можно принять 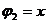 .
Тогда в уравнение (1.8)
.
Тогда в уравнение (1.8) 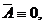 что следует из
(1.9), а коэффициент при
что следует из
(1.9), а коэффициент при 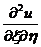 принимает
следующий вид:
принимает
следующий вид:
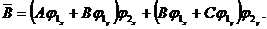
Согласно (1.11) и (1.12) 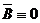 в
рассматриваемой области. Коэффициент
в
рассматриваемой области. Коэффициент 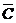 в
уравнении (1.8) преобразуется к виду
в
уравнении (1.8) преобразуется к виду
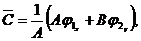
откуда 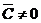 ,
так как в противном случае в силу (1.11) якобиан
,
так как в противном случае в силу (1.11) якобиан 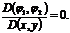 Разделив
на
Разделив
на 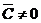 уравнение
(1.8) приведем его к виду
уравнение
(1.8) приведем его к виду
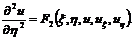 (1.15)
(1.15)
Это канонический вид уравнения параболического
типа.
Если уравнение (1.4) линейно, то и уравнение
(1.15) также будет линейным:
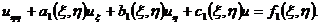 (1.16)
(1.16)
1.3 Постановки задач для уравнений
параболического типа
Классическим примером уравнения параболического
типа является уравнение теплопроводности (диффузии). В однородной среде (без
источников энергии) уравнение теплопроводности или диффузии имеет вид
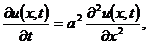
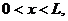
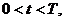 (1.17)
(1.17)
где u - температура, 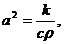 k
- коэффициент теплопроводности, c - удельная теплоемкость,
k
- коэффициент теплопроводности, c - удельная теплоемкость, 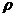 -
плотность (в задаче диффузии u - концентрация диффундирующего вещества,
-
плотность (в задаче диффузии u - концентрация диффундирующего вещества, 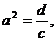 d
- коэффициент диффузии, c - коэффициент пористости среды, который определяется
отношением объема пор к рассматриваемому объему), x=0 и x=L левый и правый
концы отрезка изменения пространственной переменной, t=0 и t=T - моменты начала
и окончания процесса. На множестве
d
- коэффициент диффузии, c - коэффициент пористости среды, который определяется
отношением объема пор к рассматриваемому объему), x=0 и x=L левый и правый
концы отрезка изменения пространственной переменной, t=0 и t=T - моменты начала
и окончания процесса. На множестве 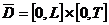 рассматриваются
различные начально-краевые задачи для уравнения (4) (рис. 1.1)
рассматриваются
различные начально-краевые задачи для уравнения (4) (рис. 1.1)
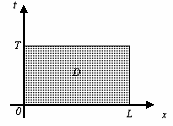
Рис. 1.1 - Область D ограниченная
прямоугольником
Первая начально-краевая задача:
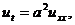
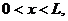
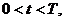 (1.18)
(1.18)
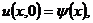
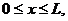 (начальное
условие)
(начальное
условие)
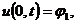
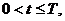 (краевое
условие на левой границе)
(краевое
условие на левой границе)
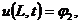
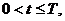 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит функциональное начальное условие (при
t=0) и функциональные краевые условия на левой (x=0) и правой (x=L) границах
области. Где 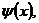
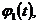
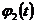 - заданные функции.
- заданные функции.
Вторая начально-краевая задача:
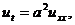
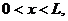
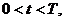 (1.19)
(1.19)
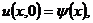
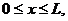 (начальное
условие)
(начальное
условие)
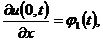
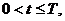 (краевое
условие на левой границе)
(краевое
условие на левой границе)
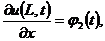
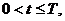 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит функциональное начальное условие (при
t=0) и дифференциальные краевые условия на левой (x=0) и правой (x=L) границах
области.
Третья начально-краевая задача:
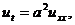
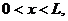
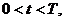 (1.20)
(1.20)
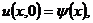
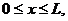 (начальное
условие)
(начальное
условие)
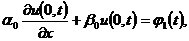
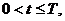 (краевое
условие на левой границе)
(краевое
условие на левой границе)
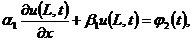
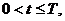 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит функциональное начальное условие (при
t=0) и функционально-дифференциальные краевые условия на левой (x=0) и правой
(x=L) границах области. Где 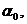
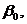
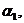
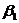 - заданные числа
- заданные числа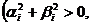
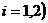 .
.
Задача Коши:
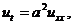
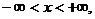
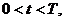
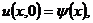
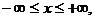 (начальное
условие)
(начальное
условие)
содержит только функциональное начальное условие
(при t=0) и рассматривается в бесконечной области изменения пространственной переменной.
Примером физической задачи, приводящей к первой
начально-краевой задаче служит процесс теплопередачи по длинному тонкому
стержню, лежащему вдоль оси Ox от x=0 до x=L (ось стержня совпадает с осью Ox).
Предполагается, что в точке x=0 температура изменяется со временем по закону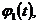 а
в точке x=L по закону
а
в точке x=L по закону 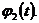 В начальный момент
времени при t=0 функцией
В начальный момент
времени при t=0 функцией 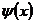 задано начальное
распределение температуры вдоль стержня. Тогда распределение температуры вдоль
него во все последующие моменты времени определяется решением начально-краевой
задачи с уравнением (1.7), где
задано начальное
распределение температуры вдоль стержня. Тогда распределение температуры вдоль
него во все последующие моменты времени определяется решением начально-краевой
задачи с уравнением (1.7), где 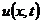 - температура
стержня в некоторой точке x в момент времени t.
- температура
стержня в некоторой точке x в момент времени t.
Во всех перечисленных задачах требуется найти
функцию 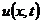 ,
которая удовлетворяет дифференциальному уравнению (1.7) в области D и
соответствующим условиям на ее границе.
,
которая удовлетворяет дифференциальному уравнению (1.7) в области D и
соответствующим условиям на ее границе.
2. Численное решение
дифференциальных уравнений
.1 Основные определения и
конечно-разностные схемы для дифференциальных уравнений параболического типа
.1.1 Основные определения. Принцип
построения разностных схем
Точное решение задач математической физики (в
виде явных формул, рядов и т.п.) можно найти только в редких случаях. Среди
приближенных методов, наиболее применимы разностные методы (методы сеток).
Сущность разностных методов состоит в том, что исходная область изменения
независимых переменных заменяется дискретным множеством точек - сеток, а производные,
входящие в уравнение, аппроксимируются на этой сетке разностными соотношениями.
В результате исходная линейная задача заменяется системой конечного числа
линейных алгебраических уравнений, называемой разностной схемой (задачей), а
исходная нелинейная задача заменяется нелинейной разностной схемой. За
приближенное решение исходной задачи принимается решение разностной схемы.
Точность приближения зависит от способа аппроксимации и от густоты сетки.
Пусть дана исходная (дифференциальная) задача в
виде
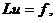 (2.1)
(2.1)
где u - искомая функция, определенная на
множестве 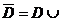 Г; D - область
пространства независимых переменных с границей Г; f - заданная функция, L -
линейный дифференциальный оператор. Все производные, входящие в
дифференциальной уравнение, перенесены в левую часть, а остальные функции
образуют правую часть; дополнительные условия (начальные и краевые) также
включены, а оператор и правую часть f.
Г; D - область
пространства независимых переменных с границей Г; f - заданная функция, L -
линейный дифференциальный оператор. Все производные, входящие в
дифференциальной уравнение, перенесены в левую часть, а остальные функции
образуют правую часть; дополнительные условия (начальные и краевые) также
включены, а оператор и правую часть f.
Для численного решения задачи вводится сетка 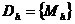 -
конечное множество точек Mh (узлов сетки), принадлежащих
-
конечное множество точек Mh (узлов сетки), принадлежащих 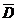 ,
плотность размещения которых характеризуется параметром h - шагом сетки. В
общем случае h - вектор, компонентами которого являются шаги по всем
независимым переменным решаемой задачи, с длиной
,
плотность размещения которых характеризуется параметром h - шагом сетки. В
общем случае h - вектор, компонентами которого являются шаги по всем
независимым переменным решаемой задачи, с длиной 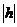 .
Обычно сетка задается так, что при
.
Обычно сетка задается так, что при 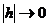 множество
Dh стремится заполнить множество
множество
Dh стремится заполнить множество 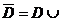 Г.
Г.
Рассмотрим некоторую дифференциальную задачу с
двумя независимыми переменными x и t. Для простоты изложения множество D
представляет собой прямоугольник длины l и высоты T, ограниченный отрезками
прямых, параллельных осям Ox и Ot (рис. 2.1), т. е. задана двумерная
прямоугольная сетка
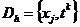 ,
,
где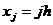 ,
,
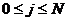 ;
;
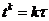 ,
N, K - целые положительные числа; h,
,
N, K - целые положительные числа; h, 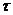 -
величины шагов по пространству и времени (для простоты принимаются
постоянными);
-
величины шагов по пространству и времени (для простоты принимаются
постоянными); 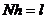 ,
, 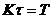 .
Такая сетка называется равномерной (регулярной). В данном случае
.
Такая сетка называется равномерной (регулярной). В данном случае 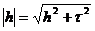 или
или
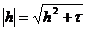 .
Узлы, принадлежащие промежуткам
.
Узлы, принадлежащие промежуткам 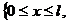
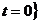 ,
,
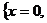
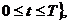
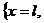
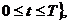
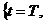
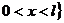 ,
называются граничными, а остальные - внутренними. Слоем
,
называются граничными, а остальные - внутренними. Слоем 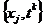 ,
,
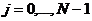 ;
;
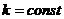 называется
множество всех узлов сетки, имеющих одну и ту же временную координату
называется
множество всех узлов сетки, имеющих одну и ту же временную координату 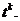
Рис. 2.1 - Конечно-разностная сетка
Функции, определенные в точках сетки 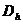 ,
называются сеточными. Введем сеточную функцию
,
называются сеточными. Введем сеточную функцию
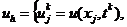
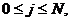
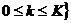 , (2.2)
, (2.2)
с пространственным шагом 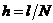 и
шагом по времени
и
шагом по времени 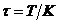 (рис. 2.1). Данная
функция является сеточным представлением решения исходной (дифференциальной)
задачи или точным решением дифференциальной задачи в узлах сетки. Вычислить
(рис. 2.1). Данная
функция является сеточным представлением решения исходной (дифференциальной)
задачи или точным решением дифференциальной задачи в узлах сетки. Вычислить 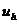 не
удается, поэтому находят другую сеточную функцию
не
удается, поэтому находят другую сеточную функцию 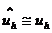 ,
приближенно совпадающую с точным решением в узлах сетки. Она вычисляется как
решение разностной схемы
,
приближенно совпадающую с точным решением в узлах сетки. Она вычисляется как
решение разностной схемы
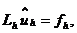 (2.3)
(2.3)
в некотором смысле соответствующей задаче (2.1).
Здесь Lh - разностный оператор, аппроксимирующий линейный дифференциальный
оператор B (он формируется в результате аппроксимации частных производных,
входящих в B, соответствующими конечно-разностными соотношениями); 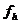 -
сеточная функция, возникающая в результате замены правой части уравнения (2.1)
значениями в узлах сетки. Под разностной схемой понимается совокупность
разностных уравнений, аппроксимирующих основное дифференциальное уравнение во
всех внутренних узлах сетки и дополнительные условия (начальные и краевые) - в
граничных узлах. Разностную схему будем называть разностной задачей по аналогии
с дифференциальной задачей.
-
сеточная функция, возникающая в результате замены правой части уравнения (2.1)
значениями в узлах сетки. Под разностной схемой понимается совокупность
разностных уравнений, аппроксимирующих основное дифференциальное уравнение во
всех внутренних узлах сетки и дополнительные условия (начальные и краевые) - в
граничных узлах. Разностную схему будем называть разностной задачей по аналогии
с дифференциальной задачей.
Введем на конечно-разностной сетке (2.2) два
временных слоя: нижний 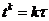 , на котором
распределение искомой функции
, на котором
распределение искомой функции 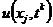 ,
, 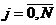 ,
и верхний временной слой
,
и верхний временной слой 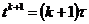 , на котором
распределение искомой функции
, на котором
распределение искомой функции 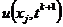 ,
, 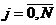 подлежит
определению.
подлежит
определению.
На введенной сетке (2.2) введем сеточные функции
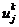 ,
,
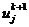 ,
первая из которых известна, вторая - подлежит определению. Для ее определения в
задаче (1.18) заменим (аппроксимируем) дифференциальные операторы отношением
конечных разностей, получим
,
первая из которых известна, вторая - подлежит определению. Для ее определения в
задаче (1.18) заменим (аппроксимируем) дифференциальные операторы отношением
конечных разностей, получим
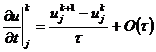 , (2.4)
, (2.4)
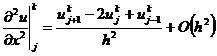 (2.5)
(2.5)
Подставляя (2.4), (2.5) в задачу (1.18), получим
явную конечно-разностную схему для этой задачи в форме
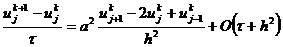 ,
,  ,
,
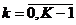 ;
;
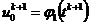 ,
, 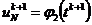 ,
,
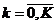 (2.6)
(2.6)
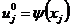 ,
, 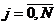 .
.
В каждом уравнении этой задачи все значения
сеточной функции известны, за исключением одного, 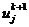 ,
которое может быть определено явно из соотношений (2.6). В соотношения (2.6)
краевые условия входят при значениях j=1 и j=N-1, а начальное условие - при
k=0.
,
которое может быть определено явно из соотношений (2.6). В соотношения (2.6)
краевые условия входят при значениях j=1 и j=N-1, а начальное условие - при
k=0.
Определение 1. Схема называется явной, если
оператор L аппроксимируется с использованием известных значений функции 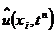 на
n-м слое, а аппроксимирующее уравнение содержит только одно неизвестное
значение функции на следующем
на
n-м слое, а аппроксимирующее уравнение содержит только одно неизвестное
значение функции на следующем 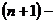 м слое, которое
нетрудно выразить явно.
м слое, которое
нетрудно выразить явно.
Если в (2.5) дифференциальный оператор по
пространственной переменной аппроксимировать отношением конечных разностей на
верхнем временном слое:
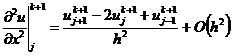
 (2.7)
(2.7)
то после подстановки (2.4), (2.7) в задачу
(1.18), получим неявную конечно-разностную схему для этой задачи:
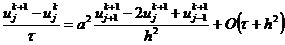 ,
,  ,
,
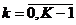 ;
;
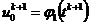 ,
, 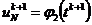 ,
,
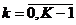 (2.8)
(2.8)
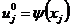 ,
, 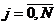 .
.
Теперь сеточную функцию 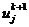 на
верхнем временном слое можно получить из решения СЛАУ (2.8) с трехдиагональной
матрицей.
на
верхнем временном слое можно получить из решения СЛАУ (2.8) с трехдиагональной
матрицей.
Определение 2. Схема называется неявной, если
оператор аппроксимируется с использованием нескольких неизвестных значений
искомой функции на 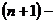 м слое.
м слое.
Узлы сетки 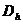 ,
значения в которых используется при аппроксимации оператора B, образуют шаблон.
,
значения в которых используется при аппроксимации оператора B, образуют шаблон.
Шаблоном конечно-разностной схемы называют ее
геометрическую интерпритацию на конечно-разностной сетке.
При изображении шаблона светлыми кружочками
обозначаются узлы на k-м слое с известными значениями функции, а зачеркнутыми -
узлы на 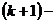 м
слое с неизвестными значениями функции, подлежащие определению. Шаблон,
содержащий p узлов, называется p-точечным.
м
слое с неизвестными значениями функции, подлежащие определению. Шаблон,
содержащий p узлов, называется p-точечным.
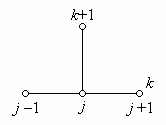
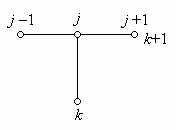
На рис. 2.2 приведены шаблоны для явной (2.6) и
неявной (2.8) конечно-разностных схем при аппроксимации задачи (1.18).
а б
Рис. 2.2 - Шаблоны явной (а) и неявной (б)
конечно-разностных схем для уравнения теплопроводности
2.1.2 Аппроксимация и сходимость
разностных схем
Рассмотрим дифференциальную задачу в операторной
форме (2.1) и операторную форму конечно-разностной схемы (2.3).
Введем норму сеточной функции с помощью
выражения
 ,
, 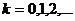 (2.9)
(2.9)
Определение 3. Конечно-разностная схема (2.3)
аппроксимирует дифференциальную задачу на точном решении, если какая-либо норма
разности (не обязательно в виде (2.9)) 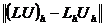 стремится
к нули при
стремится
к нули при 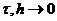 :
:
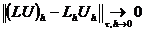 . (2.10)
. (2.10)
Определение 4. Конечно-разностная схема (2.3)
аппроксимирует дифференциальную задачу на точном решении с порядком p по
времени и порядком q по пространственной переменной, если какая-либо норма
разности 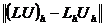 удовлетворяет
равенству
удовлетворяет
равенству
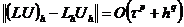 . (2.11)
. (2.11)
Таким образом, если конечно-разностная схема
аппроксимирует дифференциальную задачу, то речь идет о близости
дифференциального и конечно-разностного операторов в узлах сетки.
Из определения порядка аппроксимации ясно, что
чем выше порядок аппроксимации, тем лучше конечно-разностная схема приближается
к дифференциальной задаче. Это не означает, что решение по разностной схеме
может быть так же близко к решению дифференциальной задачи, так как разностная
схема может быть условно устойчивой или абсолютно неустойчивой вовсе.
Для нахождения порядка аппроксимации
используется аппарат разложения в ряды Тейлора точных (неизвестных, но
дифференцируемых) решений дифференциальной задачи в узлах сетки (подчеркнем:
значения сеточной функции 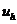 дискретны,
следовательно, не дифференцируемы и поэтому не разлагаются в ряды Тейлора).
дискретны,
следовательно, не дифференцируемы и поэтому не разлагаются в ряды Тейлора).
В соответствии с определением порядка
аппроксимации проанализируем порядок аппроксимации конечно-разностной схемы
(2.6), для чего эту схему запишем на точном решении 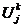 :
:
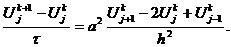 (2.12)
(2.12)
Разложим в ряды Тейлора по переменной х значения
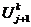 ,
,
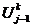 в
окрестности узла
в
окрестности узла 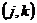 до четвертой
производной включительно, а значение
до четвертой
производной включительно, а значение 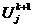 -
в Тейлора по переменной t в окрестности узла
-
в Тейлора по переменной t в окрестности узла 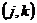 до
второй производной включительно, получим
до
второй производной включительно, получим
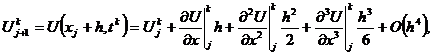 (2.13)
(2.13)
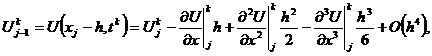 (2.14)
(2.14)
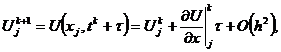 (2.15)
(2.15)
Подставляя (2.13)-(2.15) в (2.12), находим
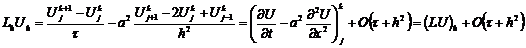 .
.
Таким образом,
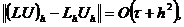
т. е. явная схема (2.6) для уравнения
теплопроводности имеет первый порядок аппроксимации по времени и второй - по
пространственной переменной. Аналогично, тот же порядок аппроксимации можно
получить и для неявной схемы (2.8).
Определение 5. Решение 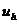 ,
полученное с помощью конечно-разностной схемы (2.3), сходится к точному решению
U, если какая-либо норма разности
,
полученное с помощью конечно-разностной схемы (2.3), сходится к точному решению
U, если какая-либо норма разности 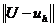 стремится
к нулю при стремлении к нулю сеточных характеристик
стремится
к нулю при стремлении к нулю сеточных характеристик 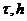 :
:
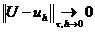 (2.16)
(2.16)
Определение 6. Конечно-разностная схема (2.3)
имеет p-й порядок сходимости (порядок точности) по времени и q-й порядок
сходимости по пространственной переменной, если какая-либо норма разности 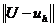 удовлетворяет
равенству
удовлетворяет
равенству
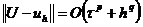 .
.
Таким образом, порядок сходимости (порядок
точности) характеризует близость конечно-разностного и точного (неизвестного)
решения.
2.1.3 Исследование устойчивости
конечно-разностных схем
Пусть в конечно-разностной схеме (2.3) входные
данные 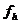 получили
возмущения и приняли значения
получили
возмущения и приняли значения 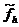 . Тогда сеточная
функция
. Тогда сеточная
функция 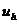 также
получит возмущение и примет значение
также
получит возмущение и примет значение 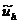
Определение 7. Конечно-разностная схема (2.3)
устойчива по входным данным, если найдется такая ограниченная константа 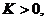 не
зависящая от сеточных характеристик
не
зависящая от сеточных характеристик 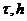 и
входные данные
и
входные данные 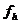 , что выполняется
неравенство
, что выполняется
неравенство
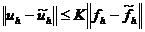 . (2.17)
. (2.17)
Таким образом, понятие устойчивости
интерпритируется следующим образом: конечно-разностная схема устойчива, если
для малых возмущений входных данных (начально-краевых условий и правых частей)
конечно-разностная схема (2.3) обеспечивает малые возмущения сеточной функции 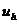 ,
т.е. решение с помощью конечно-разностной схемы находится под контролем входных
данных.
,
т.е. решение с помощью конечно-разностной схемы находится под контролем входных
данных.
Если во входных данных 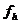 входят
только начальные условия или только краевые условия, или только правые части,
то говорят об устойчивости соответственно по начальным условиям, по краевым
условиям или по правым частям.
входят
только начальные условия или только краевые условия, или только правые части,
то говорят об устойчивости соответственно по начальным условиям, по краевым
условиям или по правым частям.
Определение 8. Конечно-разностная схема (2.3)
называется абсолютно устойчивой, если неравенство (2.17) выполняется при любом
соотношении шагов 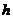 и
и 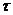 .
.
Определение 9. Конечно-разностная схема (2.3),
неустойчивые при любом соотношении шагов 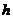 и
и
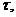 называются
абсолютно неустойчивыми.
называются
абсолютно неустойчивыми.
Определение 10. Конечно-разностная схема (2.3)
называется условно устойчивой, если неравенство (2.17) выполняется для сеточных
характеристик 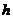 и
и 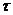 ,
на которые накладываются определенные ограничения.
,
на которые накладываются определенные ограничения.
Поскольку устойчивость является одной из
основных характеристик конечно-разностных схем, то в данном параграфе
рассматриваются различные методы исследования устойчивости конечно-разностных
схем по начальным условиям. Наиболее распространенными методами исследования
устойчивости являются следующие:
метод гармонического анализа (Фурье);
принцип максимума;
спектральный метод;
энергетический метод.
Каждый из этих методов имеет достоинства и
недостатки.
Метод гармонического анализа. Из математической
физики известно, что решение начально-краевых задач представляется в виде
следующего ряда:
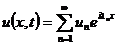 ,
,
где 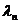 -
собственные значения, а
-
собственные значения, а 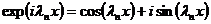 - собственные
функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т. е.
решение может быть представлено в виде суперпозиции отдельных гармоник
- собственные
функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т. е.
решение может быть представлено в виде суперпозиции отдельных гармоник 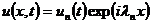 ,
каждая из которых есть произведение функции времени t и функции
пространственной переменной х, причем последняя по модулю ограничена сверху
единицей при любых значениях переменной х.
,
каждая из которых есть произведение функции времени t и функции
пространственной переменной х, причем последняя по модулю ограничена сверху
единицей при любых значениях переменной х.
В то же время функция времени 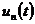 ,
называемая амплитудной частью гармоники, никак не ограничена, и, по всей
вероятности, именно амплитудная часть гармоник является источником
неконтролируемого входными данными роста функции и, следовательно, источником
неустойчивости.
,
называемая амплитудной частью гармоники, никак не ограничена, и, по всей
вероятности, именно амплитудная часть гармоник является источником
неконтролируемого входными данными роста функции и, следовательно, источником
неустойчивости.
Таким образом, если конечно-разностная схема
устойчива, то отношение амплитудной части гармоники на верхнем временном слое к
амплитудной части на нижнем временном слое по модулю должно быть меньше
единицы.
Если разложить значение сеточной функции 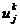 в
ряд Фурье по собственным функциям:
в
ряд Фурье по собственным функциям:
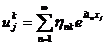 (2.18)
(2.18)
где амплитудная часть 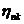 может
быть представлена в виде произведения
может
быть представлена в виде произведения
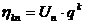 , (2.19)
, (2.19)
- размерный и постоянный сомножитель амплитудной
части, а k - показатель степени (соответствующий номеру временного слоя)
сомножителя, зависящего от времени, то, подставив (2.18) в конечно-разностную
схему, можно по модулю оценить отношение амплитудных частей на соседних
временных слоях.
Однако поскольку операция суммирования линейна и
собственные функции ортогональны для различных индексов суммирования, то в
конечно-разностную схему вместо сеточных значений достаточно подставить одну
гармонику разложения (2.18) (при этом у амплитудной части убрать индекс n), т.
е.
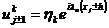 ,
, 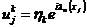 ,
,
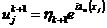 .
(2.20)
.
(2.20)
Таким образом, если конечно-разностная схема
устойчива по начальным данным, то
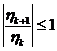 , (2.21)
, (2.21)
т. е. условие (2.21) является необходимым
условием устойчивости.
Исследование устойчивости методом гармонического
анализа явной и неявной схем для уравнения теплопроводности. Подставим
выражения (2.20) в явную конечно-разносную схему (2.6) для уравнения
теплопроводности, получим
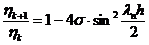 ,
, 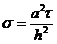 (2.22)
(2.22)
Здесь использована формула, вытекающая из
формулы Эйлера:
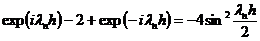 ,
,
и формула 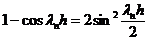 ,
причем
,
причем 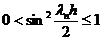 ,
поскольку
,
поскольку 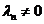 и
и 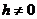 .
.
В соответствии с (2.22) получаем выражение
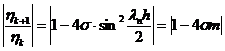 ,
, 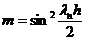 ,
,
или, с учетом (2.21), неравенство

Отсюда получаем следующие два неравенства:
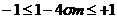 ,
,
из которых правое выполнено всегда, а из левого
следует знаменитое условие устойчивости Куранта: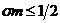 ,
или более жесткое для
,
или более жесткое для 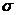 условие
условие
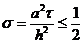 (2.23)
(2.23)
Из (2.23) следует, что явная схема для уравнения
теплопроводности условно устойчива с условием (2.23), накладываемым на сеточные
характеристики 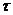 и h.
и h.
Подставим теперь гармоники (2.20) в неявную
конечно-разностную схему (2.8) для уравнения теплопроводности, получим
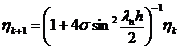 ,
,
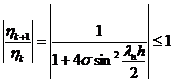
всегда, так как а и квадрат синуса больше нуля.
Следовательно, неявная схема для уравнения
теплопроводности абсолютно устойчива, так как для выполнения неравенства 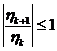 на
сеточные характеристики
на
сеточные характеристики 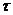 и h не
накладывалось никаких ограничений.
и h не
накладывалось никаких ограничений.
Комплекс 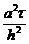 называют
числом Куранта для уравнения теплопроводности.
называют
числом Куранта для уравнения теплопроводности.
Принцип максимума. В математической физике
известен принцип, в соответствии с которым решение начально-краевой задачи
внутри расчетной области не может превышать значений искомой функции на
пространственно-временной границе. Этот принцип положен в основу метода
исследования устойчивости конечно-разностных схем, называемого принципом
максимума.
Для его использования рассмотрим явную
конечно-разностную схему (2.6) для уравнения теплопроводности в форме
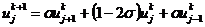 (2.24)
(2.24)
и введем норму сеточной функции 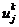 в
виде
в
виде 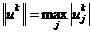 .
.
Тогда из (2.24) получим
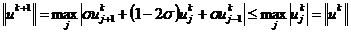 (2.25)
(2.25)
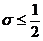 , (2.26)
, (2.26)
то из (2.25) имеем неравенство
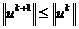 ,
,
откуда, продолжая цепочку неравенств вплоть до
начального условия, получим
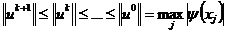 , (2.27)
, (2.27)
где 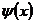 -
начальное условие из (1.18).
-
начальное условие из (1.18).
Неравенства (2.27) в вычислительной математике
называют принципом максимума. Он является достаточным условием устойчивости
явной схемы (2.24) для уравнения теплопроводности.
Таким образом, если выполнено условие Куранта
(2.26), то из цепочки (2.27) видно, что значение сеточной функции на любом
временном слое по норме не превысит начального условия, т. е. рассматриваемая
схема устойчива по начальному условию, причем условие (2.26) является теперь не
только необходимым в соответствии с методом гармонического анализа, но и
достаточным.
Спектральный метод исследования устойчивости.
Рассмотрим сеточные функции 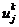 и
и 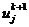 ,
,
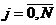 ,
на двух временных слоях
,
на двух временных слоях 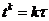 и
и 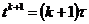 и
представим конечно-разностную схему в следующей операторной форме:
и
представим конечно-разностную схему в следующей операторной форме:
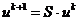 , (2.28)
, (2.28)
где S - оператор перехода от слоя tk к слою
tk+1. Такой оператор можно построить не для всякой конечно-разностной схемы
(например, метод прогонки нельзя представить в
форме (6.64)). Для явных конечно-разностных схем (2.6) оператор S
представляется следующей матрицей перехода:
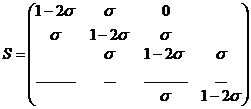 .
.
Составим от левой и правой частей равенства
(2.28) операцию нормы и используем свойство нормы: норма произведения
операторов не превышает произведения норм, получим
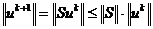 . (2.29)
. (2.29)
Если выполнено неравенство вида
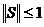 , (2.30)
, (2.30)
то из условий (2.29) и (2.30) следует принцип
максимума
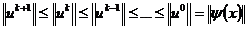 .
.
Таким образом, если схема устойчива, то норма
оператора перехода S не превышает единицы и, следовательно, условие (2.30)
является необходимым условием устойчивости конечно-разностных схем.
Энергетический метод исследования устойчивости
конечно-разностных схем. Как видно из предыдущих разделов, метод гармонического
анализа и спектральный метод являются необходимыми условиями устойчивости
конечно-разностных схем, а принцип максимума - достаточным условием
устойчивости. В данном пункте рассматривается один из самых мощных и
распространенных методов - энергетический метод, развитый в работах А.А.
Самарского и базирующийся на понятиях энергетического пространства с
энергетической нормой, энергетического тождества (неравенства) и принципа
максимума. Ниже будет показано, что условия, используемые в энергетическом
методе, являются достаточными условиями устойчивости конечно-разностных схем.
Для понимания энергетического метода рассмотрим
применение его с целью исследования устойчивости конечно-разностных схем при
численном решении следующей первой начально-краевой задачи для уравнения
теплопроводности с однородными краевыми условиями:
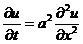 ,
, 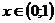 ,
t > 0; (2.31)
,
t > 0; (2.31)
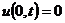 , x = 0, t > 0;
(2.32)
, x = 0, t > 0;
(2.32)
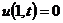 , x = 1, t > 0;
(2.33)
, x = 1, t > 0;
(2.33)
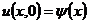 ,
, 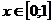 ,
t = 0; (2.34)
,
t = 0; (2.34)
На сетке (2.2) будем аппроксимировать эту задачу
с помощью явной (2.6) и неявной (2.8) конечно-разностных схем, записанных в
векторно-операторной форме следующим образом:
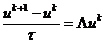 , (2.35)
, (2.35)
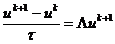 , (2.36)
, (2.36)
где конечно-разностный оператор 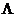 аппроксимирует
дифференциальный оператор по пространственной переменной x, т.е.
аппроксимирует
дифференциальный оператор по пространственной переменной x, т.е.
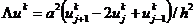 .
.
Энергетическое пространство. Введем
энергетическое пространство HA сеточных функций 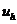 ,
являющееся гильбертовым пространством, в котором определено скалярное
произведение для двух элементов
,
являющееся гильбертовым пространством, в котором определено скалярное
произведение для двух элементов 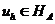 и
и 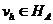 :
:
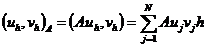 , (2.37)
, (2.37)
и, следовательно, с нормой
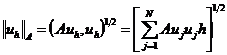 . (2.38)
. (2.38)
Как известно, гильбертово пространство - это
полное нормированное пространство, в котором определено скалярное произведение.
Здесь полнота определяется в том смысле, что если последовательность сеточных
функций 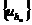 сходится
к своему пределу при
сходится
к своему пределу при 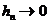 (в данном случае -
к решению дифференциальной задачи), то она является фундаментальной, т.е.
выполняется условие Коши
(в данном случае -
к решению дифференциальной задачи), то она является фундаментальной, т.е.
выполняется условие Коши
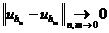 . (2.39)
. (2.39)
Действительно, если конечно-разностная схема
аппроксимирует дифференциальную задачу и устойчива, то по теореме
эквивалентности решение с помощью конечно-разностной схемы сходится к решению
дифференциальной задачи при измельчении сетки.
Для двух сеточных функций 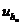 и
и
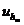 (двух
элементов гильбертова пространства HA) на различных сетках с шагами hn и hm
понятие полноты означает, что при измельчении сетки, т. е. при
(двух
элементов гильбертова пространства HA) на различных сетках с шагами hn и hm
понятие полноты означает, что при измельчении сетки, т. е. при 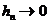 (или
(или
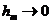 )
последовательности
)
последовательности 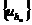 и
и 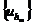 сходятся
к одному и тому же пределу, т. е. выполняется (2.39).
сходятся
к одному и тому же пределу, т. е. выполняется (2.39).
В дальнейшем потребуются следующие понятия,
характеризующие конечно-разностные операторы: сопряженность, самосопряженность,
положительная определенность.
Определение 11. Конечно-разностный оператор А*
называется сопряженным оператору А, если выполняется равенство
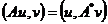 . (2.40)
. (2.40)
Например, если оператор А - симметрическая
матрица с действительными элементами (А = АТ), то А - сопряженный оператор (это
можно проверить непосредственно).
Определение. Конечно-разностный оператор А
называется самосопряженным, если выполняется равенство
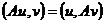 . (2.41)
. (2.41)
Определение 12. Конечно-разностный оператор А
называется положительно определенным 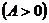 или
положительно полуопределенным
или
положительно полуопределенным 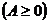 на гильбертовом
пространстве сеточных функций
на гильбертовом
пространстве сеточных функций 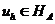 , если
, если
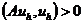 или
или 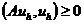 .
(2.42)
.
(2.42)
Можно показать, что разностный оператор 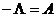 является
самосопряженным, т. е.
является
самосопряженным, т. е.
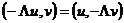 .
.
С целью определения собственных функций и
собственных значений конечно-разностного оператора А, рассмотрим вначале задачу
на собственные значения и собственные функции оператора 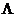 :
:
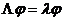 (2.43)
(2.43)
Собственные функции 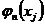 должны
удовлетворять следующим условиям:
должны
удовлетворять следующим условиям:
быть ортогональными на отрезке 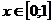 при
при
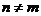 ,
т. е.
,
т. е. 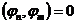 на
на
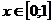 при
при
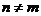 ;
;
удовлетворять однородным краевым уравнениям
(2.32), (2.33);
их число должно совпадать с числом собственных
значений 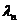 .
.
Таким условиям удовлетворяют функции:
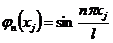 ,
, 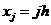 ,
,
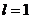 ,
,
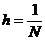 ,
,
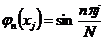 ,
, 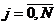 ;
;
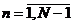 .
(2.44)
.
(2.44)
Для нахождения собственных значений 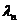 подставим
(2.44) в (2.43), получим
подставим
(2.44) в (2.43), получим
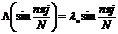 ,
,
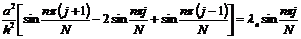 ,
,
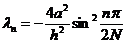 ,
, 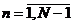 (2.45)
(2.45)
Из (2.45) видно, что все собственные значения
оператора А отрицательны, а собственные значения оператора 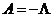 положительны,
т. е. оператор
положительны,
т. е. оператор 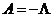 положительно
определен.
положительно
определен.
При исследовании устойчивости явной
конечно-разностной схемы (2.35) энергетическим методом воспользуемся следующими
тождествами:
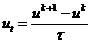 ;
;
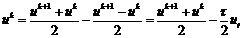 . (2.46)
. (2.46)
Умножим скалярно явную схему (2.35) на вектор 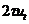 ,
получим
,
получим
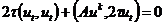 ,
,
или, после подстановки сюда тождеств (2.46),
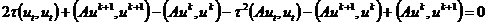 .
.
В силу самосопряженности оператора А и
коммутативности скалярного произведения, последние два слагаемых сокращаются,
после чего получим следующее энергетическое тождество:
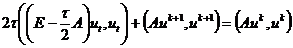 . (2.47)
. (2.47)
Если оператор
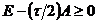 , (2.48)
, (2.48)
то из (2.47) получаем следующее энергетическое
неравенство:
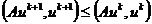 , (2.49)
, (2.49)
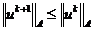 ,
,
откуда сразу следует принцип максимума
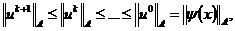
являющийся достаточным условием устойчивости.
Если теперь от неравенства (2.48) вычислить
любую норму 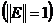 , например норму,
которая равна максимальному по модулю собственному значению оператора А, то с
использованием выражения (2.45) получим
, например норму,
которая равна максимальному по модулю собственному значению оператора А, то с
использованием выражения (2.45) получим
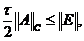
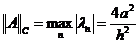 ;
;
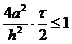 ,
,
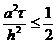 . (2.50)
. (2.50)
Таким образом, условие устойчивости Куранта
(2.33) явной конечно-разностной схемы для уравнения теплопроводности,
выведенное с помощью метода гармонического анализа, является и достаточным
условием.
Исследуем теперь устойчивость неявной
конечно-разностной схемы (2.36) энергетическим методом, для чего к тождествам
(2.46) добавим тождество
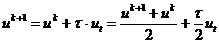 (2.51)
(2.51)
Умножим скалярно схему (2.36) на вектор 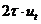 ,
получим
,
получим
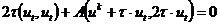 ,
,
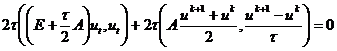 ,
,
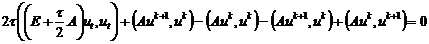 .
.
Таким образом, для неявной схемы энергетическое
тождество имеет вид
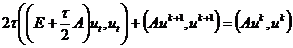 . (2.52)
. (2.52)
Здесь первое слагаемое всегда положительно
определено, поэтому энергетическое неравенство имеет вид
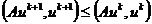 ,
,
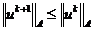 , (2.53)
, (2.53)
откуда следует принцип максимума
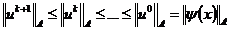 .
.
Таким образом, неявная схема (2.36) безусловно
устойчива, так как оператор 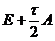 всегда
положительно определен.
всегда
положительно определен.
2.2 Конечно-разностный метод решения
задач для уравнений параболического типа
.2.1 Однородные и консервативные
конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими
производные
В задачах математической физики вообще, и в
задачах теплопроводности в частности, граничные условия 1-го рода
аппроксимируются точно в узлах на границе расчетной области и этот факт никак
не влияет на порядок аппроксимации во всей расчетной области. Этого нельзя
сказать об аппроксимации граничных условий 2-го и 3-го родов, поскольку в них
присутствует производная первого порядка искомой функции по пространственной
переменной, в результате чего порядок аппроксимации в граничных узлах может
быть ниже порядка аппроксимации во внутренних узлах расчетной области.
В этой связи необходимо ввести понятия
локального порядка аппроксимации - порядка аппроксимации в отдельно взятом
узле, и глобального порядка аппроксимации - порядка аппроксимации во всей
расчетной области. Для задач с граничными условиями 1-го рода на равномерной
сетке локальный порядок аппроксимации совпадает с глобальным.
Для задач с граничными условиями, содержащими
производные, порядок аппроксимации в граничных узлах может быть ниже порядка
аппроксимации во внутренних узлах, если конечно-разностная схема в граничных
узлах не использует дифференциальное уравнение (ниже будет показано, что в этом
случае нарушается консервативность). Тогда глобальный порядок аппроксимации
равен наименьшему относительно всех узлов сетки порядку аппроксимации.
Рассмотрим методологию сохранения на границах с
граничными условиями 2-го и 3-го родов порядка аппроксимации, который дает
аппроксимация дифференциального уравнения во внутренних узлах, т.е. получение
конечно-разностной схемы с однородной аппроксимацией. Для этого рассмотрим
третью начально-краевую задачу для уравнения теплопроводности, содержащего как
конвективные члены (пропорциональные производной 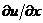 ),
так и источниковые члены, содержащие искомую функцию
),
так и источниковые члены, содержащие искомую функцию 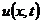 :
:
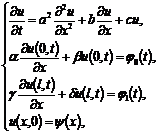
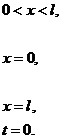
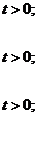
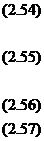
Во внутренних узлах конечно-разностной сетки
(2.2) неявная конечно-разностная схема для уравнения (2.54) имеет вид
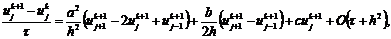
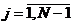 .
(2.58)
.
(2.58)
Если производные первого порядка в граничных
условиях (2.55) и (2.56) аппроксимировать по следующей схеме (с помощью
отношения конечных разностей справа и слева):
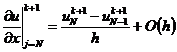 .
.
то граничные условия аппроксимируются с первым
порядком, и глобальный порядок будет равен первому порядку, несмотря на то, что
во всех остальных узлах порядок аппроксимации по пространственной переменной
равен двум. Для сохранения порядка аппроксимации, равного двум, в граничных
узлах разложим на точном решении значение 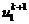 в
окрестности точки х = 0 в ряд Тейлора по переменной х до третьей производной
включительно, a
в
окрестности точки х = 0 в ряд Тейлора по переменной х до третьей производной
включительно, a 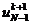 - аналогичный ряд
в окрестности точки х = l, получим (в предположении что функция
- аналогичный ряд
в окрестности точки х = l, получим (в предположении что функция 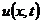 в
граничных узлах имеет первые производные по времени и вторые - по х):
в
граничных узлах имеет первые производные по времени и вторые - по х):
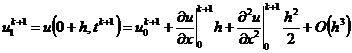 , (2.59)
, (2.59)
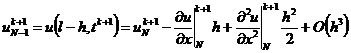 . (2.60)
. (2.60)
Подставим сюда значения второй производной в
граничных узлах, полученные из дифференциального уравнения (2.54):
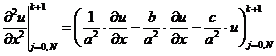 ,
,
и найдем из полученных выражений (2.59), (2.60)
значения первой производной 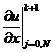 в граничных узлах
с порядком
в граничных узлах
с порядком 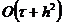 :
:
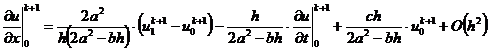 ,
,
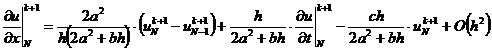 .
.
Подставляя 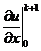 в
(2.55), а
в
(2.55), а 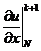 (2.56) и
аппроксимируя полученные соотношения в соответствующих граничных узлах (при
(2.56) и
аппроксимируя полученные соотношения в соответствующих граничных узлах (при 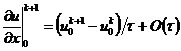 ,
,
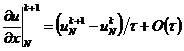 ),
получим алгебраические уравнения для граничных узлов, в каждом из которых два
неизвестных:
),
получим алгебраические уравнения для граничных узлов, в каждом из которых два
неизвестных:
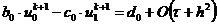 ,
, 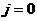 ;
(2.61)
;
(2.61)
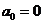 ,
, 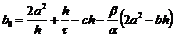 ;
;
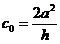 ;
;
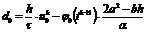 ;
;
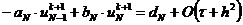 ,
,  ;
(2.62)
;
(2.62)
 ,
, 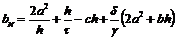 ;
;
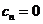 ;
;
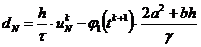 .
.
Таким образом, (2.61) - конечно-разностная
аппроксимация граничного условия 3-го рода (2.55) на левой границе х = 0, а
(2.62) - конечно-разностная аппроксимация граничного условия 3-го рода (2.56)
на правой границе х = l, которые сохраняют тот же порядок аппроксимации, что и
в конечно-разностной аппроксимации (2.58) дифференциального уравнения (2.54).
Приписывая к граничным конечно-разностным
уравнениям (2.61), (2.62), каждое из которых содержит два значения сеточной
функции, алгебраические уравнения (2.58), записанные в виде
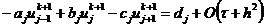 ,
, 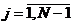 ;
(2.63)
;
(2.63)
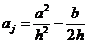 ;
; 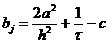 ;
;
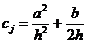 ;
;
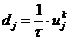 ,
,
получим СЛАУ с трехдиагональной матрицей,
решаемой методом прогонки (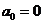 ;
;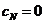 )
)
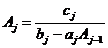 ; (2.64)
; (2.64)
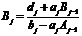
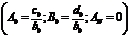 ,
,
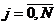 ;
;
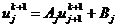
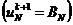 ,
,
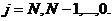 (2.65)
(2.65)
Рассмотрим более подробно метод матричной
прогонки.
Метод применим в случае, когда матрица Р -
трехдиагональная. Общая постановка задачи имеет следующий вид.
Дана система линейных алгебраических уравнений с
трехдиагональной матрицей Р. Развернутая запись этой системы имеет вид
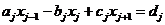 ,
, 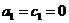 ,
,
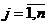 ,
(2.66)
,
(2.66)
которому соответствует расширенная матрица
 .
.
Здесь первое и последнее уравнения, содержащие
по два слагаемых, могут рассматриваться как краевые условия. Знак «минус» при
коэффициенте 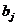 , взят для более
удобного представления расчетных формул метода.
, взят для более
удобного представления расчетных формул метода.
Требуется найти решение 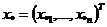 системы
(2.66) методом исключения Гаусса.
системы
(2.66) методом исключения Гаусса.
Если к (2.66) применить алгоритм прямого хода
метода Гаусса, то вместо 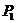 получится
получится  :
:
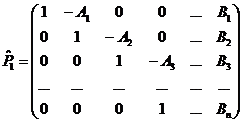
Учитывая, что последний столбец в этой матрице
соответствует правой части, и переходя к системе, включающей неизвестные,
получаем рекуррентную формулу:
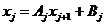 ,
, 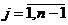 .
(2.67)
.
(2.67)
Соотношение (2.67) есть формула для обратного
хода, а формулы для коэффициентов 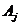 ,
,
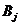 ,
которые называются прогоночными, определяются из (1.4), (2.67). Запишем (2.67)
для индекса
,
которые называются прогоночными, определяются из (1.4), (2.67). Запишем (2.67)
для индекса 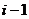 :
:
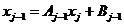
и подставим в (2.66). Получим
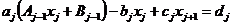 .
.
Приводя эту формулу к виду (2.67) и сравнивая
полученное выражение с (2.67), получаем рекуррентные соотношения для 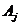 ,
,
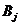 :
:
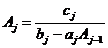 ,
, 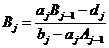 ,
,
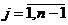 (2.68)
(2.68)
Определение прогоночных коэффициентов по
формулам (2.68) соответствует прямому ходу метода прогонки.
Обратный ход метода прогонки начинается с
вычисления хп. Для этого используется последнее уравнение, коэффициенты
которого определены в прямом ходе, и последнее уравнение исходной системы:
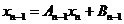 ,
,
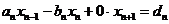
Тогда определяется хп:
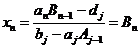 , т.е.
, т.е. 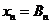 .
(2.69)
.
(2.69)
Остальные значения неизвестных находятся
рекуррентно по формуле (2.67).
Все соотношения для выполнения вычислений
получены. Тогда можно провести расчеты по методу Гаусса, используя прямой и
обратный ход.
Покажем, что изложенный метод аппроксимации
краевых условий, содержащих производные по пространственным переменным, не
только повышает порядок аппроксимации, но и сохраняет консервативность
конечно-разностной схемы, т. е. в конечно-разностной аппроксимации соблюдаются
законы сохранения, на основе которых выведены дифференциальные соотношения
задачи (2.54)-(2.57). Для этого рассмотрим вначале вывод дифференциального
уравнения теплопроводности (2.54) в случае b = с = 0 (см. рис. 2.3 а).
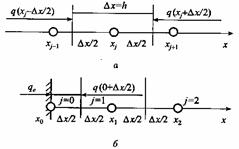
Рис. 2.3 - К аппроксимации краевых условий,
содержащих производные, с сохранением консервативности
Из физики известно, что тепловой поток, согласно
закону Фурье, в одномерном случае равен 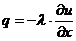 ,
где
,
где 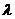 -
коэффициент теплопроводности. Для элемента длиной
-
коэффициент теплопроводности. Для элемента длиной 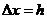 ,
в центре которого помещен узел xj, запишем сумму тепловых потоков:
,
в центре которого помещен узел xj, запишем сумму тепловых потоков: 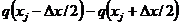 ,
подходящих к левой и правой границам элемента. По закону сохранения энергии
сумма этих тепловых потоков равна изменению энергии в этом элементе
,
подходящих к левой и правой границам элемента. По закону сохранения энергии
сумма этих тепловых потоков равна изменению энергии в этом элементе 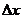 ,
которая пропорциональна массе элемента
,
которая пропорциональна массе элемента 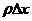 ,
теплоемкости материала с и производной первого порядка от температуры
,
теплоемкости материала с и производной первого порядка от температуры 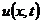 по
времени
по
времени
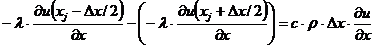 .
.
Разделив это равенство на 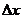 и
перейдя к пределу при
и
перейдя к пределу при 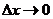 , получим
одномерное уравнение теплопроводности
, получим
одномерное уравнение теплопроводности
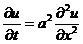 ,
, 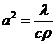 .
.
Таким образом, конечно-разностная аппроксимация
(2.58) дифференциального уравнения (2.54) учитывает и тепловые потоки, и
энергию, поглощенную элементом 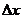 , т. е. все виды
энергии, участвующие при выводе дифференциального уравнения.
, т. е. все виды
энергии, участвующие при выводе дифференциального уравнения.
Рассмотрим теперь вывод граничного условия
(2.55) на левой границе (см. рис. 2.3 б) расчетной области (для правой границы
х = l вывод аналогичен).
К граничному узлу х=0 примыкает масса объемом 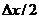 со
стороны расчетной области. При задании граничного условия 3-го рода на левой
границе х=0 осуществляется теплообмен с окружающей средой по закону Ньютона:
со
стороны расчетной области. При задании граничного условия 3-го рода на левой
границе х=0 осуществляется теплообмен с окружающей средой по закону Ньютона: 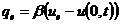 ,
где
,
где 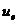 -
температура окружающей среды, а
-
температура окружающей среды, а 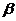 - коэффициент
теплообмена на границе х = 0, имеющей температуру
- коэффициент
теплообмена на границе х = 0, имеющей температуру 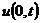 ,
с окружающей средой, имеющей температуру
,
с окружающей средой, имеющей температуру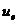 .
Справа к элементу
.
Справа к элементу 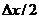 подводится
тепловой поток, описываемый законом Фурье. Тогда разность тепловых потоков,
подводимых к половине элемента, равна энергии, пошедшей на повышение
температуры элемента
подводится
тепловой поток, описываемый законом Фурье. Тогда разность тепловых потоков,
подводимых к половине элемента, равна энергии, пошедшей на повышение
температуры элемента 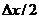 , пропорциональной
массе этого элемента
, пропорциональной
массе этого элемента 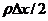 , теплоемкости с и
производной температуры по времени:
, теплоемкости с и
производной температуры по времени:
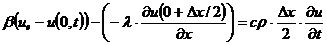 . (2.70)
. (2.70)
Переходя здесь к пределу при 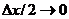 ,
получим левое граничное условие 3-го рода (2.55) (с точностью до коэффициентов)
,
получим левое граничное условие 3-го рода (2.55) (с точностью до коэффициентов)
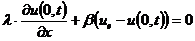 . (2.71)
. (2.71)
Таким образом, конечно-разностная аппроксимация
граничного условия (2.71) или (2.55) должна сопровождаться появлением
консервативного слагаемого, стоящего в правой части равенства (2.71). Физически
это означает, что граничные условия (2.55), (2.56) записаны для границ, не
имеющих ни массы, ни объема. В конечно-разностной аппроксимации к границе
примыкает масса с одномерным объемом, равным 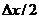 ,
в котором необходимо учитывать дифференциальное уравнение, действующее во
внутренних точках расчетной области, и не действующее на границе.
,
в котором необходимо учитывать дифференциальное уравнение, действующее во
внутренних точках расчетной области, и не действующее на границе.
В конечно-разностной аппроксимации краевого
условия, содержащего производную по переменной х, нестационарный член в правой
части выражения (2.71) с помощью дифференциального уравнения можно заменить на
дивергентный член, пропорциональный 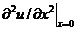 .
.
Аналогичный подход можно осуществить в краевых
задачах для дифференциальных уравнений любых типов.
2.2.2 Неявно-явная
конечно-разностная схема с весами. Схема Кранка-Николсона
Явная конечно-разностная схема (2.6), записанная
в форме
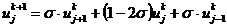 ,
, 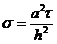 ,
,
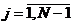 ,
,
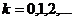 ,
(2.72)
,
(2.72)
обладает тем достоинством, что решение на
верхнем временном слое tk+1 получается сразу (без решения СЛАУ) по значениям
сеточной функции на нижнем временном слое tk , где решение известно (при k = 0
значения сеточной функции формируются из начального условия (1.18)). Но эта же
схема обладает существенным недостатком, поскольку она является условно
устойчивой с условием (2.23), накладываемым на сеточные характеристики 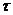 и
h.
и
h.
С другой стороны, неявная конечно-разностная
схема (2.8), записанная форме
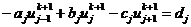 ,
, 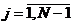 ,
,
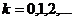 ,
(2.73)
,
(2.73)
приводит к необходимости решать СЛАУ, но зато
эта схема абсолютно устойчива.
Проанализируем схемы (2.72), (2.73). Пусть
точное решение, которое неизвестно, возрастает по времени, т.е. 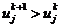 .
Тогда, в соответствии с явной схемой (2.72), разностное решение будет
заниженным по сравнению с точным, так как
.
Тогда, в соответствии с явной схемой (2.72), разностное решение будет
заниженным по сравнению с точным, так как 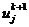 определяется
по меньшим значениям сеточной функции па предыдущем временном слое, поскольку
решение является возрастающим по времени.
определяется
по меньшим значениям сеточной функции па предыдущем временном слое, поскольку
решение является возрастающим по времени.
Для неявной схемы (2.73) на возрастающем
решении, наоборот, решение завышено по сравнению с точным, поскольку оно
определяется по значениям сеточной функции на верхнем временном слое.
На убывающем решении картина изменяется
противоположным образом: явная конечно-разностная схема завышает решения, а
неявная - занижает (см. рис. 2.4).
уравнение порядок параболический
аппроксимация
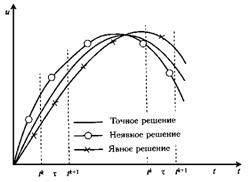
Рис. 2.4 - Двусторонний метод аппроксимации
На основе этого анализа возникла идея о
построении более точной неявно-явной конечно-разностной схемы с весами при пространственных
конечно-разностных операторах, причем при измельчении шагов  и
h точное (неизвестное) решение может быть взято в «вилку» сколь угодно узкую,
так как если явная и неявная схемы аппроксимируют дифференциальную задачу и эти
схемы устойчивы, то при стремлении сеточных характеристик
и
h точное (неизвестное) решение может быть взято в «вилку» сколь угодно узкую,
так как если явная и неявная схемы аппроксимируют дифференциальную задачу и эти
схемы устойчивы, то при стремлении сеточных характеристик  и
h к нулю решения по явной и неявной схемам стремятся к точному решению с разных
сторон.
и
h к нулю решения по явной и неявной схемам стремятся к точному решению с разных
сторон.
Рассмотрим неявно-явную схему с весами для
простейшего уравнения теплопроводности:
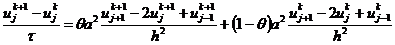 , (2.74)
, (2.74)
где 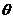 -
вес неявной части конечно-разностной схемы,
-
вес неявной части конечно-разностной схемы, 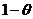 -
вес для явной части, причем
-
вес для явной части, причем 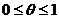 . При
. При 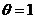 имеем
полностью неявную схему, при
имеем
полностью неявную схему, при 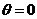 - полностью явную
схему, и при
- полностью явную
схему, и при 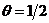 - схему
Кранка-Николсона.
- схему
Кранка-Николсона.
В соответствии с гармоническим анализом для схемы
(2.74) получаем неравенство
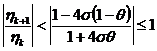 ,
,
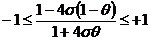 , (2.75)
, (2.75)
причем правое неравенство выполнено всегда.
Левое неравенство имеет место для любых значений
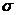 ,
если
,
если 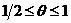 .
Если же вес
.
Если же вес 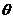 лежит в пределах
лежит в пределах 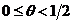 ,
то между
,
то между 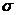 и
и
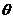 из
левого неравенства устанавливается связь
из
левого неравенства устанавливается связь
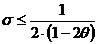 ,
, 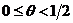 ,
(2.76)
,
(2.76)
являющаяся условием устойчивости неявно-явной
схемы с весами (6.109), когда вес находится в пределах 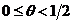 .
.
Таким образом, неявно-явная схема с весами
(2.74) абсолютно устойчива при 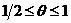 и условно
устойчива с условием (2.76) при
и условно
устойчива с условием (2.76) при 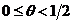 .
.
Рассмотрим порядок аппроксимации неявно-явной
схемы с весами (2.74), для чего разложим в ряд Тейлора в окрестности узла 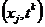 на
точном решении значения сеточных функций
на
точном решении значения сеточных функций 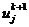 по
переменной t,
по
переменной t, 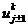 ,
, 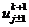 по
переменной х и полученные разложения подставим в (2.74):
по
переменной х и полученные разложения подставим в (2.74):
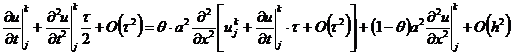 .
.
В этом выражении дифференциальный оператор 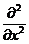 от
квадратной скобки в соответствии с дифференциальным уравнением (1.17) равен
дифференциальному оператору
от
квадратной скобки в соответствии с дифференциальным уравнением (1.17) равен
дифференциальному оператору 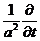 , в соответствии с
чем вышеприведенное равенство приобретает вид
, в соответствии с
чем вышеприведенное равенство приобретает вид
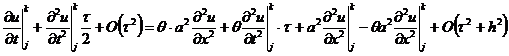
После упрощения получаем
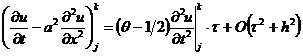
откуда видно, что для схемы Кранка-Николсона 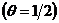 порядок
аппроксимации схемы (2.74) составляет
порядок
аппроксимации схемы (2.74) составляет 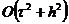 ,
т. е. на один порядок по времени выше, чем для обычных явных или неявных схем.
Таким образом, схема Кранка-Николсона (2.74) при
,
т. е. на один порядок по времени выше, чем для обычных явных или неявных схем.
Таким образом, схема Кранка-Николсона (2.74) при 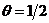 абсолютно
устойчива и имеет второй порядок аппроксимации по времени и пространственной
переменной х.
абсолютно
устойчива и имеет второй порядок аппроксимации по времени и пространственной
переменной х.
2.2.3 Метод дробных шагов Н.Н.
Яненко
В отличие от МПН, метод дробных шагов (МДШ)
использует только неявные конечно-разностные операторы, что делает его
абсолютно устойчивым в задачах, не содержащих смешанных производных. Он
обладает довольно значительным запасом устойчивости (сохранение устойчивости
при числах Куранта, значительно превышающих единицу) и в задачах со смешанными
производными.
Схема МДШ имеет вид
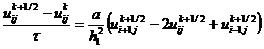 , (2.77)
, (2.77)
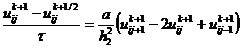 . (2.78)
. (2.78)
С помощью чисто неявной подсхемы (2.77)
осуществляются скалярные прогонки в направлении оси х в количестве, равном J-1,
в результате чего получаем сеточную функцию 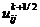 .
На втором дробном шаге по времени с помощью подсхемы (2.78) осуществляются
скалярные прогонки в направлении оси у в количестве, равном I-1, в результате
чего получаем сеточную функцию
.
На втором дробном шаге по времени с помощью подсхемы (2.78) осуществляются
скалярные прогонки в направлении оси у в количестве, равном I-1, в результате
чего получаем сеточную функцию 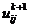 . Шаблон схемы МДШ
приведен на рис. 2.5. Для определения порядка аппроксимации схемы МДШ запишем
ее в следующей операторной форме:
. Шаблон схемы МДШ
приведен на рис. 2.5. Для определения порядка аппроксимации схемы МДШ запишем
ее в следующей операторной форме:
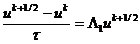 ,
, 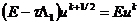 ,
,
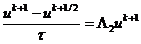 ,
, 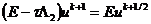 ,
,
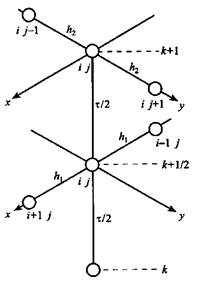
Рис. 2.5 - Шаблон схемы метода дробных шагов
Исключая здесь сеточную функцию на промежуточном
временном слое 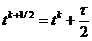 , получим
двухслойную схему
, получим
двухслойную схему 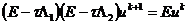 , откуда получаем
порядок аппроксимации по времени:
, откуда получаем
порядок аппроксимации по времени:
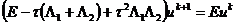 ,
,
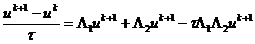 . (2.79)
. (2.79)
Из (2.79) видно, что схема МДШ (2.77), (2.78)
имеет порядок 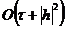 , т.е. первый
порядок по времени и второй - по переменным х и у.
, т.е. первый
порядок по времени и второй - по переменным х и у.
Для исследования устойчивости схемы МДШ (2.77),
(2.78) подставим в нее гармонику 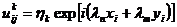 ,
получим
,
получим
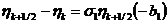 ,
, 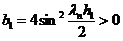 ;
;
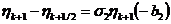 ,
, 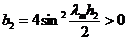 .
.
Тогда отношение амплитуд гармоник равно
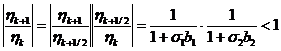 ,
,
т. е. схема метода дробных шагов абсолютно
устойчива.
Достоинства схемы МДШ: 1) проста в
алгоритмизации и программировании; 2) абсолютно устойчива с большим запасом
устойчивости даже для задач, содержащих смешанные производные.
Недостатки: 1) на каждом дробном шаге
достигается частичная аппроксимация, полная аппроксимация достигается на
последнем дробном шаге; 2) имеет первый порядок точности по времени; 3) в
задачах со смешанными производными для устойчивости МДШ на коэффициенты
накладываются жесткие ограничения, при невыполнении которых схема становится
условно устойчивой.
2.2.4 Метод переменных направлений с
экстраполяцией В. Ф. Формалева
Как видно из изложенных выше конечно-разностных
схем для многомерных задач математической физики, конечно-разностная схема
может быть либо абсолютно устойчивой, но не экономичной (метод матричной
прогонки), либо экономичной, но условно устойчивой, как схема МПН. Желание
получить схемы экономичные и одновременно абсолютно устойчивые с большим
запасом устойчивости приводит к необходимости использовать апостериорную
информацию о сеточной функции, которая получается в процессе счета. К таким
схемам относится схема метода переменных направлений с экстраполяцией (МПНЭ).
Эта схема использует распределение сеточной функции в левом (от расчетного)
пространственном сечении, уже полученное на верхнем временном слое, т. е.
неявно. В правом пространственном сечении значения сеточной функции в первом
приближении и с контролируемой точностью определяются линейной экстраполяцией
по времени с нижних временных слоев на верхний. Затем эти значения уточняются с
помощью скалярных прогонок.
Рассмотрим задачу, в которой дифференциальное
уравнение 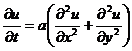 ,
, 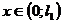 ,
,
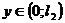 ,
,
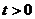 содержит
смешанные производные (наличие последних не обязательно):
содержит
смешанные производные (наличие последних не обязательно):
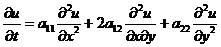 ,
, 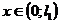 ,
,
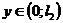 ,
,
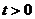 .
(2.80)
.
(2.80)
На сетке 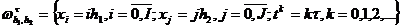 аппроксимируем
это дифференциальное уравнение с помощью следующей схемы:
аппроксимируем
это дифференциальное уравнение с помощью следующей схемы:
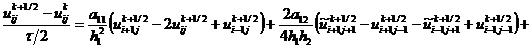
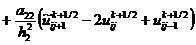 , (2.81)
, (2.81)
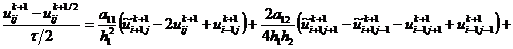
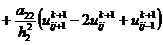 , (2.82)
, (2.82)
Здесь значения сеточной функции 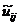 ,
помеченные волнистой чертой, определяются с помощью линейной экстраполяции:
,
помеченные волнистой чертой, определяются с помощью линейной экстраполяции:
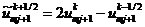 ,
, 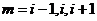 ,
,
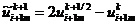 ,
, 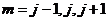 .
.
Шаблон схемы МПНЭ представлен на рис. 2.6.
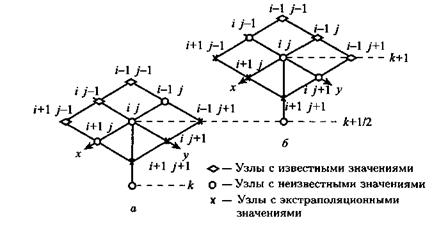
Рис. 2.6 - Шаблон схемы метода переменных
направлений с экстраполяцией: а - подсхема (2.81); б - подсхема (2.82)
В подсхеме (2.81) значения 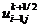 ,
,
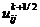 ,
,
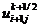 являются
искомыми, определяемыми из скалярных прогонок в направлении переменной х ,
значения
являются
искомыми, определяемыми из скалярных прогонок в направлении переменной х ,
значения 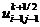 ,
,
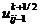 ,
,
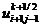 уже
известны на верхнем полуслое из прогонки вдоль координатной линии
уже
известны на верхнем полуслое из прогонки вдоль координатной линии 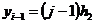 ,
а значения
,
а значения 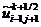 ,
, 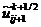 ,
,
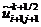 с
порядком
с
порядком 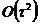 определяются
экстраполяцией по распределениям функции на двух предыдущих временных
полуслоях. При этом все конечно-разностные операторы по пространственным
переменным, за исключением оператора по переменной х, переводятся в правые
части (хотя они и являются практически полностью неявными).
определяются
экстраполяцией по распределениям функции на двух предыдущих временных
полуслоях. При этом все конечно-разностные операторы по пространственным
переменным, за исключением оператора по переменной х, переводятся в правые
части (хотя они и являются практически полностью неявными).
В подсхеме (2.82) значения 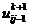 ,
,
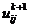 ,
,
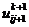 являются
искомыми, определяемыми из скалярных прогонок вдоль переменной у, значения
являются
искомыми, определяемыми из скалярных прогонок вдоль переменной у, значения 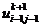 ,
,
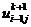 ,
,
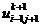 известны
как значения сеточной функции в левом пространственном сечении, а значения
известны
как значения сеточной функции в левом пространственном сечении, а значения 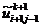 ,
,
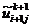 ,
,
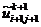 с
порядком
с
порядком  определяются
экстраполяцией по двум предыдущим временным полуслоям. При этом все
пространственные операторы, за исключением оператора по переменной у,
переводятся в правые части, хотя они практически являются полностью неявными.
определяются
экстраполяцией по двум предыдущим временным полуслоям. При этом все
пространственные операторы, за исключением оператора по переменной у,
переводятся в правые части, хотя они практически являются полностью неявными.
Аппроксимация. Для анализа аппроксимационных
свойств схемы (2.81), (2.82) прибавим и вычтем в подсхеме (2.81)
Выражения 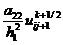 ,
,
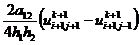 ,
получим эквивалентную схему
,
получим эквивалентную схему
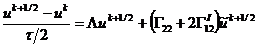 , (2.83)
, (2.83)
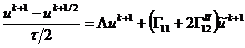 , (2.84)
, (2.84)
где 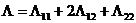 ,
,
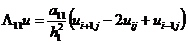 ,
,
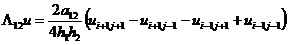 ,
, 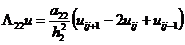 ,
,
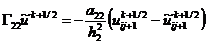 ,
, 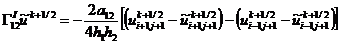 ,
,
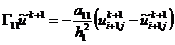 ,
, 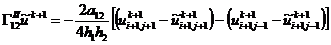 .
.
Справедлива следующая теорема.
Теорема 1. Пусть решение задачи (2.80),
(.2)-(.6)  , где
, где 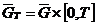 ,
,
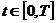 ,
,
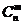 -
класс функций, т раз непрерывно дифференцируемых по t и п раз - по х, у. Тогда
схема (2.81), (2.82) и, следовательно, эквивалентная ей схема (2.83), (2.84)
аппроксимирует на точном решении дифференциальную задачу (2.80) с порядком
-
класс функций, т раз непрерывно дифференцируемых по t и п раз - по х, у. Тогда
схема (2.81), (2.82) и, следовательно, эквивалентная ей схема (2.83), (2.84)
аппроксимирует на точном решении дифференциальную задачу (2.80) с порядком 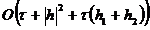 ,
где
,
где 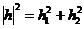 .
Доказательство. Действительно, рассматривая «осколочные» операторы
.
Доказательство. Действительно, рассматривая «осколочные» операторы  ,
,
 ,
,
 ,
,
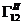 ,
можно заметить, что выполняются следующие тождества:
,
можно заметить, что выполняются следующие тождества:
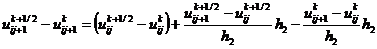 ,
,
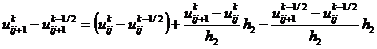 ,
,
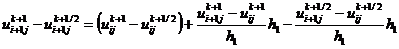 ,
,
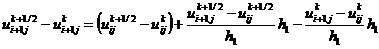 ,
,
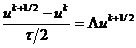 ,
, 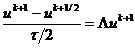 ,
,
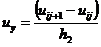 ,
, 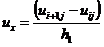 ,
,
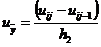 ,
,
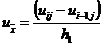 ,
, 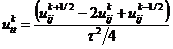 ,
,
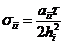 ,
,
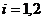 ,
,
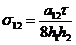 .
.
Тогда справедлива следующая цепочка равенств:
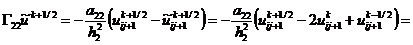
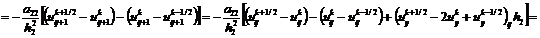
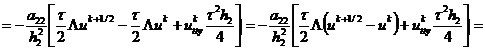
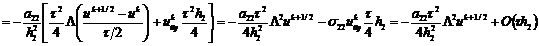 .
.
Таким образом,
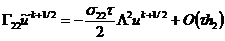 . (2.85)
. (2.85)
Аналогично,
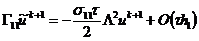 (2.86)
(2.86)
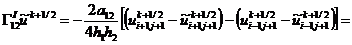
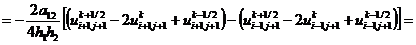
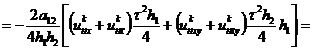
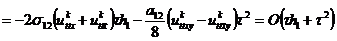 ; (2.87)
; (2.87)
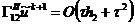 . (2.88)
. (2.88)
Подставляя выражения (2.85)-(2.88) для
«осколочных» операторов в схему (2.83), (2.84) , получим
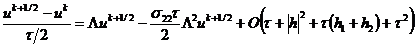 (2.89)
(2.89)
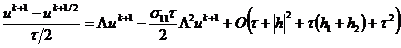 (2.90)
(2.90)
Исключение сеточной функции 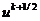 на
промежуточном временном полуслое приводит к следующей эквивалентной двухслойной
схеме:
на
промежуточном временном полуслое приводит к следующей эквивалентной двухслойной
схеме:
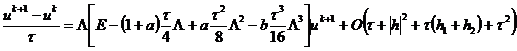 (2.91)
(2.91)
где 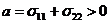 ,
,
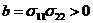 .
.
Из (2.91) следует аппроксимация с порядком 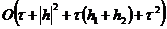 .
Теорема доказана.
.
Теорема доказана.
Устойчивость. Будем исследовать устойчивость
схемы (2.81), (2.82) методом энергетических неравенств.
Имеет место следующая теорема.
Теорема 2. Пусть выполнены условия 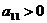 ,
,
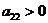 .
Тогда схема (2.81), (2.82) абсолютна устойчива по начальным условиям.
.
Тогда схема (2.81), (2.82) абсолютна устойчива по начальным условиям.
Для доказательства этой теоремы докажем
следующую лемму.
Лемма. Оператор
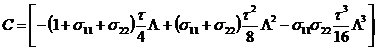
в эквивалентной схеме (2.91) является
положительно определенным и самосопряженным.
Действительно, этот оператор можно переписать в
виде
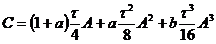 ,
,
и котором каждое слагаемое является положительно
определенным и самосопряженным оператором, поскольку 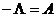 -
положительный, самосопряженный оператор, действующий в гильбертовом
пространстве Н . Следовательно, оператор С является положительно определенным,
самосопряженным оператором, что доказывает лемму.
-
положительный, самосопряженный оператор, действующий в гильбертовом
пространстве Н . Следовательно, оператор С является положительно определенным,
самосопряженным оператором, что доказывает лемму.
Таким образом, (2.91) можно переписать в виде
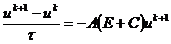 .
.
Умножая это равенство скалярно на 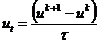 и
используя известные тождества
и
используя известные тождества
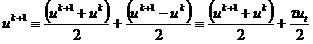 ,
,
получим следующее энергетическое тождество:
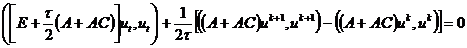 , (2.92)
, (2.92)
при выводе которого использована положительность
и самосопряженность оператора 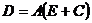 .
.
Вводя энергетическое пространство  элементов
элементов
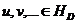 со
скалярным произведением
со
скалярным произведением 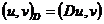 и нормой
и нормой 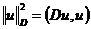 ,
в силу положительности оператора
,
в силу положительности оператора 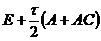 из
(2.92) получаем энергетическое неравенство
из
(2.92) получаем энергетическое неравенство
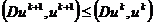
откуда следует принцип максимума
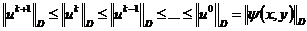 ,
,
являющийся достаточным признаком устойчивости
конечно-разностной схемы (2.81), (2.82), что доказывает теорему.
Поскольку не накладывалось никаких ограничений
на сеточные характеристики  , схема (2.81),
(2.82) является абсолютно устойчивой.
, схема (2.81),
(2.82) является абсолютно устойчивой.
По запасу устойчивости метод МПНЭ превосходит
все существующие экономичные методы расщепления для задач как содержащих, так и
не содержащих смешанные дифференциальные операторы.
К достоинствам МПНЭ можно отнести следующие: 1)
экономичность; 2) абсолютную устойчивость; 3) полную (не частичную, как в МДШ)
аппроксимацию дифференциального уравнения; 4) применимость к задачам с любой
размерностью по пространственным переменным и к задачам, содержащим смешанные
дифференциальные операторы; 5) отсутствие ограничений на величину коэффициентов
 ,
кроме ограничений
,
кроме ограничений 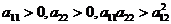 .
.
2.3 Численное решение определенных
задач
Пример 1. Пользуясь явной схемой, найти
приближенное решение начально-краевой задачи вида:
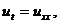
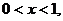
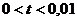 ,
,
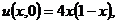
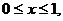 (начальное
условие)
(начальное
условие)
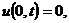
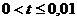 ,
(краевое условие на левой границе)
,
(краевое условие на левой границе)
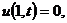
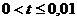 ,
(краевое условие на правой границе).
,
(краевое условие на правой границе).
Решение.
Сравнивая с общей постановкой задачи, получаем 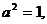
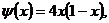
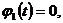
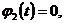
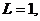
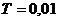 .
.
Зададим шаг по пространству: h=0,1 ,
следовательно, 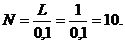 Выберем шаг по
времени из условия обеспечения устойчивости и минимизации ошибок
Выберем шаг по
времени из условия обеспечения устойчивости и минимизации ошибок 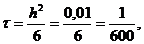 поэтому
поэтому
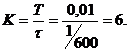 Таким
образом, получаем
Таким
образом, получаем 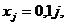
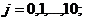
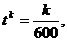
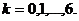
Вычислим значения решения на нулевом слое:
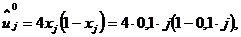
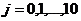 (N=10).
(N=10).
Краевые условия на левой и правой границах
записываются в виде:
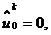
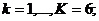
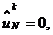
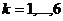 (K=6).
(K=6).
, 3. Поскольку 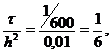 решение
на следующих слоях при k=0,1,…,5 находится по формуле
решение
на следующих слоях при k=0,1,…,5 находится по формуле
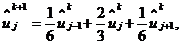 j=1,…,9,
j=1,…,9,
и занесено в таблицу
|
k
j
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
0
|
0
|
0.360
|
0.640
|
0.840
|
0.960
|
1.000
|
0.960
|
0.840
|
0.640
|
0.360
|
0
|
|
1
|
0
|
0.347
|
0.627
|
0.827
|
0.947
|
0.987
|
0.947
|
0.827
|
0.627
|
0.347
|
0
|
|
2
|
0
|
0.336
|
0.613
|
0.813
|
0.933
|
0.973
|
0.933
|
0.813
|
0.613
|
0.336
|
0
|
|
3
|
0
|
0.326
|
0.600
|
0.800
|
0.920
|
0.960
|
0.920
|
0.800
|
0.600
|
0.326
|
0
|
|
4
|
0
|
0.317
|
0.588
|
0.787
|
0.907
|
0.947
|
0.907
|
0.787
|
0.588
|
0.317
|
0
|
|
5
|
0
|
0.309
|
0.576
|
0.774
|
0.894
|
0.934
|
0.894
|
0.774
|
0.576
|
0.309
|
0
|
|
6
|
0
|
0.302
|
0.564
|
0.761
|
0.881
|
0.921
|
0.881
|
0.761
|
0.564
|
0.302
|
0
|
Полученное решение на каждом из временных слоев
является симметричным.
Решена задача параболического типа методом
сеток. При решении использовали явную схему, вычисления обработаны на MathCad и
выведены в виде кривых (Приложение 1).
Пример 2. Пользуясь явной схемой, найти
приближенное решение начально-краевой задачи вида:
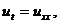
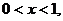
 ,
,
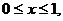 (начальное
условие)
(начальное
условие)
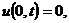
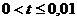 ,
(краевое условие на левой границе)
,
(краевое условие на левой границе)
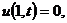
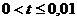 ,
(краевое условие на правой границе).
,
(краевое условие на правой границе).
Решение.
Сравнивая с общей постановкой задачи, получаем 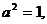
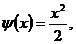
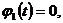
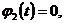
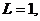
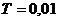 .
.
Зададим шаг по пространству: h=0,1 ,
следовательно, 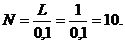 Выберем шаг по
времени из условия обеспечения устойчивости и минимизации ошибок
Выберем шаг по
времени из условия обеспечения устойчивости и минимизации ошибок 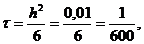 поэтому
поэтому
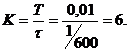 Таким
образом, получаем
Таким
образом, получаем 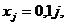
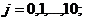
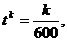
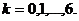
Вычислим значения решения на нулевом слое:
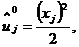
 (N=10).
(N=10).
Краевые условия на левой и правой границах
записываются в виде:
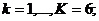
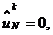
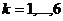 (K=6).
(K=6).
, 3. Поскольку 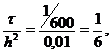 решение
на следующих слоях при k=0,1,…,5 находится по формуле
решение
на следующих слоях при k=0,1,…,5 находится по формуле
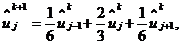 j=1,…,9,
j=1,…,9,
и занесено в таблицу
|
k
j
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
0
|
0
|
0.005
|
0.020
|
0.045
|
0.08
|
0.125
|
0.180
|
0.245
|
0.405
|
0.500
|
|
1
|
0.002
|
0.007
|
0.022
|
0.047
|
0.082
|
0.127
|
0.182
|
0.247
|
0.322
|
0.407
|
0.502
|
|
2
|
0.003
|
0.008
|
0.023
|
0.048
|
0.083
|
0.128
|
0.183
|
0.248
|
0.323
|
0.408
|
0.503
|
|
3
|
0.005
|
0.010
|
0.025
|
0.050
|
0.085
|
0.130
|
0.185
|
0.250
|
0.325
|
0.410
|
0.505
|
|
4
|
0.007
|
0.012
|
0.027
|
0.052
|
0.087
|
0.132
|
0.187
|
0.251
|
0.327
|
0.412
|
0.506
|
|
5
|
0.008
|
0.013
|
0.028
|
0.053
|
0.088
|
0.133
|
0.188
|
0.253
|
0.328
|
0.413
|
0.508
|
|
6
|
0.010
|
0.015
|
0.030
|
0.055
|
0.090
|
0.135
|
0.190
|
0.255
|
0.330
|
0.415
|
0.510
|
Решена задача параболического типа методом
сеток. При решении использовали явную схему, вычисления обработаны на MathCad и
выведены в виде кривых (Приложение 2).
Пример 3.
Дана система линейных алгебраических уравнений с
трехдиагональной матрицей А (n=4):
x1+3x2=8,
x1+6x2+x3=10,
x2+4x3-2x4 =3,-3x4 =-2
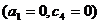 .
.
Имеем рекуррентные соотношения для 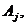
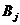 (2.68).
Определение прогоночных коэффициентов по формулам (2.68) соответствует прямому
ходу метода прогонки.
(2.68).
Определение прогоночных коэффициентов по формулам (2.68) соответствует прямому
ходу метода прогонки.
Обратный ход метода начинается с вычисления 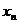 .
Для этого используется последнее уравнение, коэффициенты которого определены в
прямом ходе, и последнее уравнение исходной системы определяется известной
формулой (2.69).
.
Для этого используется последнее уравнение, коэффициенты которого определены в
прямом ходе, и последнее уравнение исходной системы определяется известной
формулой (2.69).
Результаты занесены в исходную таблицу.
|
j
|
aj
|
bj
|
cj
|
dj
|
Aj
|
Bj
|
xj
|
|
1
|
0
|
-5
|
3
|
8
|
-3/5
|
8/5
|
1
|
|
2
|
3
|
-6
|
1
|
10
|
-5/21
|
26/21
|
1
|
|
3
|
1
|
-4
|
-2
|
3
|
42/79
|
37/79
|
1
|
|
4
|
1
|
3
|
0
|
-2
|
-
|
1
|
1
|
Прямой ход Обратный
ход
Решена система методом матричной прогонки на
языке Turbo Pascal 6.0. (Приложение 3).
Заключение
Численное решение прикладных задач всегда
интересовало математиков, так как краевые задачи которые возникают в различных
областях математической физики, посвящены теплопроводности, диффузии, движению
жидкостей, акустике, электромагнетизму, волновой механике, переносу лучистой
энергии, упругим колебаниям решаются аналитически в определенных задачах.
В настоящее время с быстрым развитием
вычислительной техники позволяет многие задачи быстро решить численными
методами, даже если они решаются аналитическим способом.
В дипломной работе рассмотрены
конечно-разностные методы решения задач для дифференциальных уравнений в
частных производных параболического типа, такие как неявно-явная
конечно-разностная схема с весами; схема Кранка-Николсона; метод дробных шагов
Н.Н. Яненко; метод переменных направлений с экстраполяцией В.Ф. Формалева;
однородные и консервативные конечно-разностные схемы для задач теплопроводности
с граничными условиями, содержащими производные.
Дипломная работа состоит из двух параграфов:
первый параграф посвящен ключевым определениям
дифференциальных уравнений в частных производных, приведению уравнений второго
порядка в частности параболического типа к каноническому виду, а также
постановке задач для уравнений параболического типа;
второй параграф состоит из трех подразделов.
Первый подраздел содержит основные определения и конечно-разностные схемы для
дифференциальных уравнений параболического типа, здесь подробно описываются
понятия аппроксимации, порядка аппроксимации, сходимости, порядка сходимости,
устойчивости, а также описание различных методов исследования устойчивости. Во
втором подразделе проанализированы неявно-явные конечно-разностные схемы, как
следствие двухсторонних методов, с исследованием аппроксимации и устойчивости
для схем типа Кранка-Николсона. При численном решении многомерных задач
математической физики исключительно важным является вопрос об экономичности
используемых методов. Из экономичных конечно-разностных схем, получивших
большое распространение, в дипломной работе рассмотрена схема метода дробных
шагов Н.Н. Яненко. Данная схема при определенных условия может приводить к
неустойчивости решения, от этого недостатка свободен следующий экономичный,
абсолютно устойчивый метод переменных направлений с экстраполяцией В.Ф.
Формалева. Среди неэкономичных, полностью неявных, а потому абсолютно
устойчивых методов является метод матричной прогонки.
Для решения типовых примеров численными методами
были написаны программы на языке программирования Turbo Pascal 6.0 и в
математической системе MathCAD 7.0 Professional Edition (PRO).
Список используемой литературы
1. Бахвалов
Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: БИНОМ. Лаборатория
знаний, 2007. - 636 с.;
2. Березин
И.С., Жидков Н.П. Методы вычислений. - М.: Наука, 1960, - 524 с.;
. Данко
П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, -
М.: Высшая школа, 1997. - 486 с.;
. Демидович
Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1966. - 400 с.;
. Кабдыкайыр
К. Курс высшей математики. - Алматы, Казахский университет, 2005. - 134 с.;
. Киреев
В.И., Пантелеев А.В. Численные методы в примерах и задачах, - М.: Высшая школа,
2006. - 480 с.;
. Кошляков
Н.С., Глинер Э.Б., Смирнов М.М. Дифференциальные уравнения математической
физики, Физматлит, Москва, 1962. - 710 с.;
. Плис
А.И., Сливина Н.А. Лабораторный практикум по высшей математике. - М.: Высшая
школа, 1994. - 416 с.;
. Рихтмайер
Р.Д. Разностные методы решения краевых задач, перевод с англ., - М.: Иностранная
литература, 1960. - 262 с.;
. Рябенький
В.С. Введение в вычислительную математику. - М.: Наука, 1983.- 754 с.;
. Самарский
А.А. Теория разностных схем. - М.:Наука, 1983 - 726 с.;
. Серавайкин
С.Я., Секвенциальные модели математической физики, Алматы, 2004. - 192 с.;
. Тихонов
А.Н., Самарский А.А., Уравнения математической физики, Физматлит, Москва, 1966.
- 735 с.;
. Формалев
В.И., Ревизников Д.Л. Численные методы, - М.: ФИЗМАТЛИТ, 2004. - 400 с.
Приложение
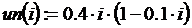 , где n=0, i=0..10
, где n=0, i=0..10
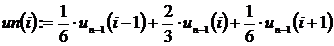
{Вычисления на нулевом слое}
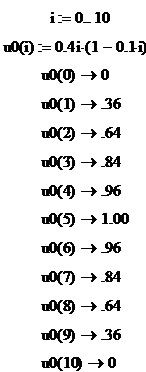
{Вычисления на последующих слоях}