Сравнительная оценка приближенных методов решения задач теории упругого режима фильтрации газа
Курсовая
работа
по
дисциплине: Подземная гидромеханика
Тема:
Сравнительная оценка приближенных методов решения задач теории упругого режима
фильтрации газа
1. Точное решение осесимметричного
притока газа к скважине
Основы теории движения газа в пористой среде
были разработаны основателем советской школы нефтегазовой гидромеханики
академиком Л.С. Лейбензоном. Он впервые получил дифференциальные уравнения
неустановившейся фильтрации совершенного газа в пласте по закону Дарси.
При выводе уравнения предполагалось, что
коэффициенты пористости и проницаемости не изменяются с давлением, т.е. пласт
недеформируем, вязкость газа также не зависит от давления, газ совершенный, а
фильтрация газа в пласте происходит при неизменных во времени температурах газа
и пласта (изотермический закон).
Для вывода дифференциального уравнения
неустановившейся фильтрации совершенного газа воспользуемся уравнением, которое
справедливо для любого сжимаемого флюида:
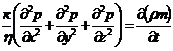 , (1)
, (1)
где коэффициенты проницаемости и
вязкости постоянны.
Функция Лейбензона для совершенного
газа определяется по формуле:
Р = ρатp2⁄(2pат)
+ С. (2)
Продифференцируем (2) по координатам
2 раза:
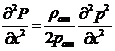 ,
, 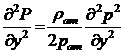 ,
, 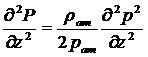 (3)
(3)
Преобразуя правую часть уравнения
(1) и считая пористость m0 постоянной и учитывая, что для совершенного газа
ρ = ρат p ⁄
pат, (4)
получим:
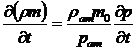 (5)
(5)
Подставив выражения (3) и (5) в
уравнение (1), получим:
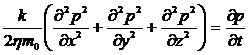 (6)
(6)
Где выражение в скобке представляет
собой оператор Лапласа относительно р2, поэтому уравнение (6) принимает вид:
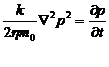 (7)
(7)
Полученное дифференциальное уравнение
неустановившейся фильтрации совершенного газа называется уравнением Лейбензона
и представляет собой нелинейное уравнение параболического типа. Оно справедливо
для совершенного газа при выполнении закона Дарси. Так как коэффициент
пористости входит в уравнение (1) в виде произведения ρm, в котором
плотность газа меняется в большей степени, чем пористость, его изменением
пренебрегают.
Уравнение Лейбензона (6) можно
записать следующим образом, умножив правую и левую части на давление р и
заменив
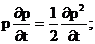
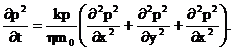 (8)
(8)
В такой записи под знаками
производных по координатам и по времени находится одна и та же функция р2, но
коэффициент в правой части kр/(ηm0)-переменный, в него входит искомая
функция p(x,y,z,t).
Неустановившаяся фильтрация
реального газа с уравнением состояния ρ = ρат p ⁄
[pатz(p)] и с учетом зависимости коэффициента вязкости от давления η=η(p)
и
недеформируемости пористой среды (m0=const, k=const) описывается следующим
нелинейным дифференциальным уравнением параболического типа:

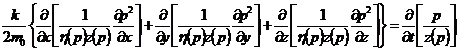 (9)
(9)
Для решения задач, связанных с
неустановившейся фильтрацией газа, дифференциальное уравнение в форме (6) или
(8) должно быть проинтегрировано по всей области газовой залежи при заданных
начальных и граничных условиях.
Так как уравнение (6) или (8)
представляет собой сложное нелинейное уравнение в частных производных, оно в
большинстве случаев не имеет точных аналитических решений. Его можно
проинтегрировать численно с помощью ЭВМ или решить приближенным способом.
Приближенные способы хорошо разработаны.
Численные методы решения различных
задач фильтрации газа на основе уравнения Л.С. Лейбензона достаточно хорошо
обоснованы в приложениях к проблемам разработки месторождений природных газов.
Наибольшее распространение получили методы конечных разностей и конечных
элементов. Вместе с тем, развитие теории фильтрации газов, вызванное
требованиями практики разработки газовых месторождений, связанных с изменением
горно-геологических условий их залегания (большие глубины, высокие давления и
температуры, многокомпонентность газа и т.д.) потребовало учета в основном
уравнении, предложенном Л.С. Лейбензоном, многих дополнительных факторов. Оказалось,
что использование функции Лейбензона в форме (2) допустимо при небольших
давлениях, в условиях недеформируемых пластов. При достаточно больших давлениях
в условиях деформируемых коллекторов под знак интеграла в формуле (2)
необходимо внести зависимости изменения проницаемости, вязкости и коэффициента
сверхсжимаемости газа от давления. При неизотермической фильтрации во многих
случаях необходимо учитывать также изменение свойств газа oт температуры.
Уравнение (6) получено с
использованием в качестве уравнения движения закона Дарси. Вместе с тем,
последующие исследования И.А. Чарного, Е.М. Минского и других показали, что при
фильтрации газов в природных пластах в большинстве случаев следует пользоваться
нелинейным (двучленным) законом фильтрации.
Одним из эффективных путей решения
уравнения Лейбензона является линеаризация, т.е. сведение его к линейному
уравнению Фурье. В некоторых практических случаях использование различных
способов линеаризации уравнения (6) позволяет получать приближенные решения, удовлетворяющие
требованиям практики.
Будем считать пласт недеформируемым,
фильтрацию изотермической и происходящей по двучленному закону. Рассмотрим
плоскорадиальный поток к осесимметрично расположенной скважине.
Воспользуемся уравнением
неразрывности для плоскорадиального движения:
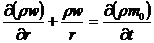 (10)
(10)
Воспользовавшись выражением для
массовой скорости ρw,
полученным
из двучленного закона фильтрации, после подстановки в них значений плотности из
уравнения состояния (4), получим:

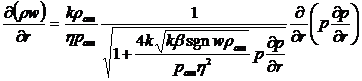 ; (11)
; (11)
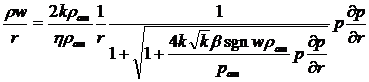 . (12)
. (12)
Подставив выражения (11), (12) и (5)
в уравнение неразрывности (10) и сократив на ρат / pат
,получим:
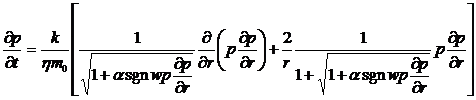 ,(13)
,(13)
где 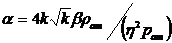 .
.
Если сделать замену 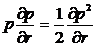 , то
дифференциальное уравнение неустановившейся фильтрации газа по двучленному
закону примет следующий вид:
, то
дифференциальное уравнение неустановившейся фильтрации газа по двучленному
закону примет следующий вид:
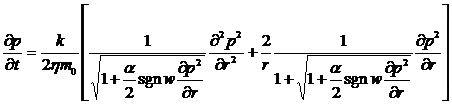 . (14)
. (14)
Аналитическое решение уравнения (14)
наталкивается на значительные трудности, однако численное решение для обычных в
подземной гидромеханике начальных и граничных условий не представляет
затруднений.
1.1 Линеаризация уравнения
Лейбензона и основное решение линеаризованного уравнения
Если заменить нелинейное
дифференциальное уравнение (8) линейным, т. е. линеаризовать его, то оно
упростится - для линейного уравнения существуют точные аналитические решения.
Ясно, что эти точные решения линеаризованного уравнения будут приближенными для
нелинейного. Оценить погрешность решения, которая возникает при замене точного
уравнения линеаризованным, можно, например, сравнивая приближенное решение с
решением на ЭВМ точного уравнения.
Были предложены различные способы
линеаризации уравнения (8). Если рассматривается плоскорадиальный приток к
скважине, то, как известно из теории установившейся фильтрации газа воронка
депрессии очень крутая, и в большей части пласта давление мало отличается от
контурного. На этом основании Леибензон предложил заменить переменное давление
p в коэффициенте уравнения (8) на постоянное давление pк, равное начальному
давлению в пласте. Тогда, обозначив 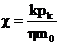 получим вместо уравнения (8)
уравнение
получим вместо уравнения (8)
уравнение
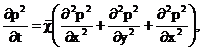 (15)
(15)
которое является линейным уравнением
пьезопроводности относительно функции р2, где χ-константа,
аналогичная коэффициенту пьезопроводности. Такой способ линеаризации, когда
переменный коэффициент χ
в
уравнении при различных значениях давления принимается константой, называется
линеаризацией по Лей6ензону. В дальнейшем различными авторами были предложены
уточнения к линеаризации по Лейбензону. Так. И. А. Чарный предложил свести
уравнение (8) к линейному заменой переменного давления в коэффициенте на
значение
ср=pmin+0,7(pmax-pmin),
где pmах и pmin - максимальное и
минимальное давления в газовой залежи на расчетный период.
Используем линеаризованное уравнение
(15) для решения конкретной задачи о притоке газа в скважину бесконечно малого
радиуса (точечный сток), расположенную в бесконечно протяженном пласте с
постоянной толщиной h. В начальный момент времени пласт невозмущен, т.е.
давление во всем пласте постоянно и равно pk. С этого момента начинается отбор
газа с постоянным дебитом Qат. Нужно найти изменение давления по пласту с
течением времени p(r, t).
Для плоскорадиальной фильтрации газа
(15) запишется следующим образом:
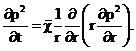 (16)
(16)
Проинтегрировав уравнение (16) при
начальном условии
= pk2 при t =0, 0 < r < ∞ (17)
и при граничном условии в удаленных
точках
р2 = рk2 при r = ∞, t > 0.
(18)
Выведем условие для давления на
забое скважины. Записав выражение для массового дебита исходя из закона Дарси в
дифференциальной форме для плоскорадиальной фильтрации:
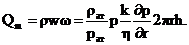
И использовав равенства 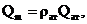
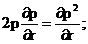
а так же сократив на рат, получим:
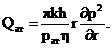
Из этого соотношения можно выразить
условие на стенке газовой скважины бесконечно малого радиуса:
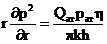 при r=0. (19)
при r=0. (19)
Таким образом, для решения
поставленной задачи уравнение (16) должно быть проинтегрировано при условиях
(17), (18), и (19).
Полученные выражения для
совершенного газа аналогичны соотношениям для упругой жидкости, только давление
входит в квадрате:
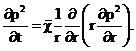 = pk2 при t = 0, 0 < r < ∞
= pk2 при t = 0, 0 < r < ∞
р2 = рk2 при r = ∞, t > 0
Решение лиеаризованного уравнения
Лейбензона для газа получим по основной формуле упругого режима для упругой
жидкости с учетом 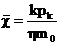 для газа и
коэффициента
для газа и
коэффициента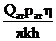 ,
аналогичных коэффициенту пьезопроводности и коэффициенту
,
аналогичных коэффициенту пьезопроводности и коэффициенту 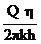 для
жидкости:
для
жидкости:
 (20)
(20)
Для малых значений аргумента 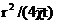 в
соответствии можно заменить интегральную показательную функцию логарифмической
в
соответствии можно заменить интегральную показательную функцию логарифмической
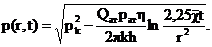 (21)
(21)
Решения (20)-(21) являются
приближенными, так как получены в результате интегрирования линеаризованного
уравнения (16), а не точного (6).
Формулы (20) и (21) определяют (при
фиксированных значениях времени t распределение давления вокруг газовой
скважины, работающей с постоянным дебитом с момента t = 0. Эти депрессионные
кривые имеют такой же характер, как при установившейся фильтрации очень крутые
вблизи скважины (рис.1,а). Если задать значение r можно найти изменение
давления в данной точке с течением времени. Можно найти изменение давления на
забое (при r=rc) после начала работы скважины (рис.1,б):
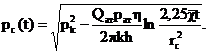 (22)
(22)
Кривые распределения давления по
пласту при неустановившемся притоке газа к скважине в разные моменты времени
(а) и динамика давлений в фиксированных точках пласта (б)


Рис. 1
Г.И. Баренблатт, применяя анализ размерностей,
показал, что нелинейное уравнение Лейбензона при определенных начальных и
граничных условиях имеет точное решение, которое может служить эталоном для
сравнения с ним приближенных решений.
Для его получения рассматривается задача о
нестационарном плоскорадиальном притоке газа с постоянным дебитом к скважине в
бесконечном пласте. Необходимо проинтегрировать нелинейное уравнение Лейбензона
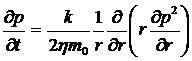 (23)
(23)
При начальных граничных условиях
= pk2 при t =0, 0 < r < ∞
р2 = рk2 при r = ∞, t > 0. 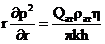 при r = 0
при r = 0
Г.И. Баренблаттом показано, что в
такой постановке давление зависит от некоторого единого комплекса, включающего
в себя обе переменные - r и t, а дифференциальное уравнение в частных
производных приводится к обыкновенному дифференциальному уравнению, которое
легко интегрируется. Чтобы установить, от каких аргументов будет зависеть
давление, проведем анализ размерностей. Распределение давления в пласте
зависит, как следует из постановки задачи, от пяти определяющих параметров
(n=5): r, t, pk, k/(2ηm0),
Qатpатη/(πkh).
Если обозначить размерность длины
через L, размерность времени Т, размерность давления [p], то размерности этих
параметров выразятся следующим образом:
[r]=L, [t]=T, [pk]=[p],
[k/(2ηm0)]=L2/[p]T, [Qатpатη/(πkh).]= [p]2.
Среди этих параметров - три с независимыми
размерностями: r, t, pk (k=3). Как следует из П-теоремы, искомая функция -
давление, приведенное к безразмерному виду F=p/pk, , будет зависеть от двух
безразмерных комплексов (n-k=5-3=2). Такими безразмерными комплексами являются
следующие:
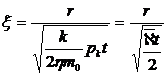 и
и 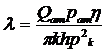 ,
,
т.е. F=p/pk=F(ξ,λ).
Дифференцируя функцию F по t и по r
как сложную функцию и подставляя производные в уравнение (23) , получим, что
функция F удовлетворяет обыкновенному дифференциальному уравнению
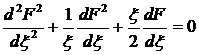 (24)
(24)
при этом начальные и граничные
условия сводятся к следующим:
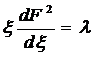 при ξ=0; F(ξ,λ)=1
при
ξ=∞ (25)
при ξ=0; F(ξ,λ)=1
при
ξ=∞ (25)
Уравнение (24) при условиях (25)
было проинтегрировано численно. Результаты расчетов приведены в табл.1 для
значений λ=0,01
и
λ=0,004994.
Через
ξ*
в
табл.1 обозначено такое значение аргумента ξ, что для ξ<
ξ* значения
ξdF2/dξ,
отличаются
от λ
меньше,
чем на 0,01%. Значит, для ξ< ξ* можно считать, что ξdF2/dξ=
λ.
Проинтегрировав это равенство,
получим:
F2=F2(ξ*, λ) + λln(ξ/
ξ*)(ξ, λ) = [F2 (ξ*, λ)-
λln(ξ*/ξ)]½ для ξ<
ξ*.
Поэтому значения F(ξ,
λ) для
ξ<
ξ* в
табл. 1 не приведены.
Таблица 1 - Результаты численного расчета
автомодельного решения
|
λ=0,01
|
λ=0,004994
|
|
ξ
|
F(ξ,
λ)
|
ξ
|
F(ξ,
λ)
|
|
ξ*=0,005787
0,01157
0,01923 0,03472 0,06553 0,09645 0,1582 0,2816 0,5285 0,7754 1,269 1,763 2,751
3,738
|
0,9701
0,9737 0,9763 0,9793 0,9825 0,9845 0,9870 0,9899 0,9930 0,9948 0,9970 0,9982
0,9994 0,9999
|
ξ*=0,.003886
0,01555
0,03109 0,06218 0,2487 0,4974 0.9949 1,492 2,498 3,482
|
0,9842
0,9877 0,9894 0,9912 0,9947 0,9964 0,9980 0,9988 0,9996 0,9999
|
1.2 Решение задачи о притоке газа к
скважине методом последовательной смены стационарных состояний
Этот метод основан на следующих предпосылках:
в каждый момент времени существует конечная
возмущенная область, в которой происходит движение газа к скважине;
движение внутри возмущенной области стационарно;
размер возмущенной области определяется из
условия материального баланса.
Решим этим методом ту же задачу о
неустановившемся притоке газа к скважине с постоянным заданным дебитом Qат, но
будем считать радиус скважины конечным и равным rc.
В любой момент времени возмущенной областью
является круговая область радиусом R(t), внутри которой давление распределено
по стационарному закону
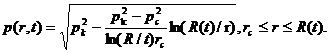 (26)
(26)
Вне возмущенной области давление
равно начальному (невозмущенное состояние):
= рk, r>R(t) (27)
В возмущенной области можно написать
также выражение для дебита для стационарной фильтрации:
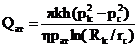 (28)
(28)
В рассматриваемой задаче забойное
давление является функцией времени.
Найдем из формулы (28) отношение
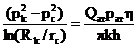
и подставим его в формулу для
давления в возмущенной области (26).
В результате получим распределение
давления, выраженное через заданный дебит и параметры пласта:
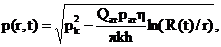 (29)
(29)
Для нахождения R(t) составляется
уравнение материального баланса.
Начальный запас газа (при р = рk) в
зоне пласта радиусом R(t):
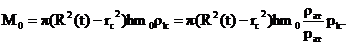 (30)
(30)
Текущий запас газа выразим через
средневзвешенное давление 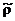 :
:
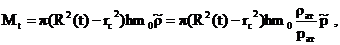 (31)
(31)
где 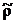 определяется по формуле
установившейся фильтрации
определяется по формуле
установившейся фильтрации
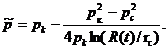 (32)
(32)
Так как отбор газа происходит с
постоянным дебитом Qат, то отобранная масса газа к моменту t равна ρатQатt.
Таким образом,
М0-мt= ρатQатt
или, с использованием (30)-(31),
найдем:
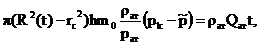 (33)
(33)
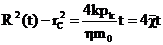 или
или 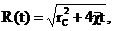 (34)
(34)
Для значений времени, для которых 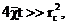 имеем:
имеем:
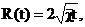 (35)
(35)
Теперь, зная закон движения границы
возмущенной области в виде (34) или (35), можно найти давление в любой точке
пласта в любой момент времени по формуле (29), а также изменение давления на
забое скважины в любой момент времени
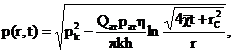
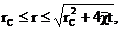 р=рк,
р=рк, 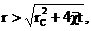 (36)
(36)
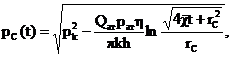 (37)
(37)
Формулы (36) пригодны как для бесконечного
пласта, так и для конечного открытого и закрытого пласта радиусом Rk. В
последнем случае они справедливы только для первой фазы движения, пока воронка
депрессии не достигнет границы пласта, т.е. для
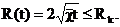
Изменение давления во второй фазе зависит от
граничных условий пласта. Если пласт закрыт, то давление будет продолжать
снижаться во всем пласте, включая границу. Если пласт открытый (р=рк или r=Rk,
т.е. режим водонапорный, то во второй фазе установится стационарный режим с
постоянной депрессией pk-pc где:
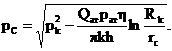
1.3 Метод усреднения
Еще одним приближенным методом,
применительно к задачам неустановившейся фильтрации газа, является метод
усреднения временной производной по пространству.
В качестве примера рассматривается
прямолинейно-параллельная фильтрация реального газа. Соответствующее этому
случаю точное дифференциальное уравнение имеет вид
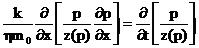 (38)
(38)
Допущением является то, что
коэффициент сверхсжимаемости z(р) можно заменить на 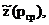 где pср -
некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р).
Тогда уравнение примет вид
где pср -
некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р).
Тогда уравнение примет вид
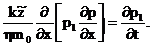 (39)
(39)
Пусть имеется первоначально невозмущенный
газонасыщенный пласт шириной В, толщиной h, длиной L. С трех сторон пласт
ограничен непроницаемыми поверхностями, а с четвертой стороны (х = 0) вскрыт
галереей. В момент t = 0 через галерею начинает отбираться газ с постоянным
массовым дебитом, который в соответствии с законом Дарси можно записать в виде:
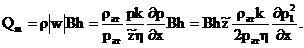
Требуется определить давление в
пласте в любой момент времени t> 0. Для этого нужно найти решение уравнения
(39) в области изменения 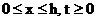 удовлетворяющее
начальному и граничным условиям:
удовлетворяющее
начальному и граничным условиям:
= p10 при t = 0 (40)
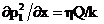 при x=0, где
при x=0, где 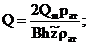 (41)
(41)
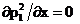 при x = L (42)
при x = L (42)
Как и в методе последовательной
смены стационарных состояний принимаем, что в каждый момент времени существует
конечная возмущенная область l(t), на границе которой выполняются условия
=p102, 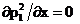 при x = l(t)
(43)
при x = l(t)
(43)
Центральным моментом в
рассматриваемом методе усреднения является принятие условия
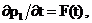
равносильного предположению, что во всей части
пласта, охваченной возмущением, давление изменяется с одинаковой скоростью;
тогда уравнение (39) принимает вид
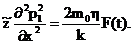 (44)
(44)
Проинтегрировав это уравнение дважды
по х получим:
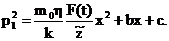 (45)
(45)
Использовав граничные условия на
галерее (41) и на границе возмущенной области (43), в результате получим
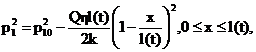 (46)
(46)
Для нахождения зависимости l(t)
проделав ряд преобразований уравнения (39) получаем
Откуда 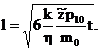 (47)
(47)
Подставив выражение l(t) в формулу
(46), получим зависимость давления, от координаты и времени.
В момент Т, когда возмущенная зона
достигнет непроницаемой границы пласта (l=L) закончится первая фаза.
Для определения ее
продолжительности:
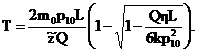 (48)
(48)
Можно найти приближенное значение T из формулы
(47) и убедиться, что погрешность не превышает 3-4%.
В течение второй фазы давление на границе x=L
падает и выполняется условие (42). Соотношения для второй фазы истощения
газового пласта строятся аналогичным образом. Проделав аналогичные выкладки,
получим закон распределения давления по пласту:
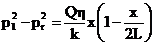 (49)
(49)
и закон изменения давления на галерее:
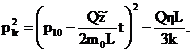 (50)2.
Расчетная часть
(50)2.
Расчетная часть
В расчетах принимаем:
k = 0,29ּ10-12 ì2,
h = 6 м,
rc=0,08 м,
Rk=300м,
- η=1,2ּ10-5Ïàּñ,
Pk=13,8МПа,
m0=0,2,
t = 1час =3600с,
дебит Qат, из условия, что λ=0,004994.
газ скважина приток уравнение
2.1 Расчет депрессии на пласт по
точной формуле и по приближенным формулам
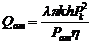
Подставив наши данные, получим:
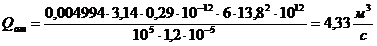
определим коэффициент
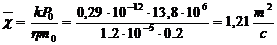
2.1.1 Точное решение
Определим безразмерную величину ξ для r = rc
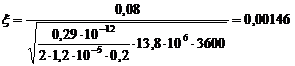
Сравнивая полученное значение ξ со
значениями в таблице 1 для λ=0,004994 заключаем, что ξ <
ξ* поэтому
безразмерное давление F определим по формуле
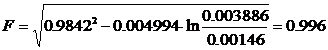 .
.
Выразив давление P=Pc, получим
= FPk = 0.996ּ13,8ּ106 = 13,7ּ106 Ïà
Депрессия на пласт через 1 час будет
равна:
∆P = Pk-Pc = (13,8-13,7)ּ106 = 0,1 ÌÏà.
Подставляя наши данные в формулу
(22), определим забойное давление Pc через 1 час
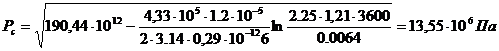
Депрессия будет равна:
∆ P= (13,8-13,55)ּ106=0,25
МПа.
2.1.3 Расчет методом
последовательной смены стационарных состояний

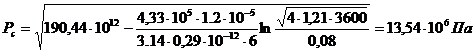
Депрессия будет равна:
∆ P = (13,8-13,54)ּ106=0,26 ÌÏà.
.2 Относительная погрешность
расчетов
. Расчет по линеаризованной формуле:
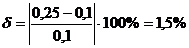
. Расчет методом последовательной
смены стационарных состояний:
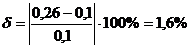
Вывод
Линеаризованная формула эффективна только в тех
случаях, когда радиус скважины очень маленький, потому что в этом случае
воронка депрессии очень крутая и давление по всему пласту в целом не сильно
отличается от начального. Но при больших радиусах скважины эта формула будет
давать большую погрешность, т.к. давление по пласту будет сильно отличаться от
начального. В отличие от линеаризованной формулы, формула последовательной
смены стационарных состояний эффективна для любых радиусов скважин, но только
для первой фазы движения, т.е. пока воронка депрессии не достигнет радиуса
контура. Как показали расчеты наиболее точной является линеаризованная формула.
Литература
1. Ê.Ñ.
Áàñíèåâ è äð. «Ïîäçåìíàÿ
ãèäðîìåõàíèêà».
Ì. Íåäðà. 1993 ã.
2. Áàñíèåâ
Ê.Ñ., Äìèòðèåâ Í.Ì.,
Ðîçåíáåðã Ã.Ä.
Íåôòåãàçîâàÿ
ãèäðîìåõàíèêà:
Ó÷åáíèê äëÿ âóçîâ.
- Ìîñêâà-Èæåâñê:
Èíñòèòóò êîìïüþòåðíûõ
èññëåäîâàíèé,
2003. - 480 ñ.
. Áàñíèåâ
Ê.Ñ., Êî÷èíà È.Í.,
Ìàêñèìîâ Â.Ì.
Ïîäçåìíàÿ ãèäðîìåõàíèêà.
- Ì.: Íåäðà, 1993. - 416 ñ.
. Äìèòðèåâ
Í.Ì., Êàäåò Â.Â., Ðàçáåãèíà
Å.Ã. Ìåòîäè÷åñêèå
óêàçàíèÿ ê âûïîëíåíèþ
êóðñîâûõ ðàáîò
ïî äèñöèïëèíå
ïîäçåìíàÿ ãèäðîìåõàíèêà.
- Ì.: íåôòü è ãàç,
1998. - 61 ñ.
. Åâäîêèìîâà
Â.À., Êî÷èíà È.Í.
Ñáîðíèê çàäà÷
ïî ïîäçåìíîé
ãèäðàâëèêå. - Ì.:
Íåäðà, 1979. - 166 ñ.
. Ïûõà÷åâ
Ã.Á., Èñàåâ Ð.Ã. Ïîäçåìíàÿ
ãèäðàâëèêà. - Ì.,
1973. - 360 ñ.
. Ùåëêà÷åâ
Â.Í., Ëàïóê Á.Á. Ïîäçåìíàÿ
ãèäðàâëèêà. - Ì.:
Ãîñòîïòåõèçäàò,
1949. - 358 ñ.
. ×àðíûé
È.À. Ïîäçåìíàÿ
ãèäðîãàçîäèíàìèêà.
- Ì.: Ãîñòîïòåõèçäàò,
1963. - 396 ñ.
. Áàðåíáëàòò
Ã.È., Åíòîâ Â.Ì., Ðûæèê
Â.Ì. Äâèæåíèå æèäêîñòåé
è ãàçîâ â ïëàñòàõ.
- Ì.: Íåäðà, 1984. -270 ñ.
. Êîëëèíç
Ð. Òå÷åíèå æèäêîñòè
÷åðåç ïîðèñòûå
ìàòåðèàëû. - Ì.:
Ìèð, 1964. - 207 ñ.
. Àçèç
Õ., Ñåòòàðè Ý. Ìàòåìàòè÷åñêîå
ìîäåëèðîâàíèå
ïëàñòîâûõ ñèñòåì.
- Ì.: Íåäðà, 1982. - 407 ñ.
Ðàçìåùåíî
íà Allbest.ru