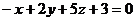Основы математики
Задание 1
Вычислить определитель,
используя правило треугольника и метод разложения по элементам ряда.
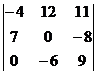
Решение:
По правилу треугольника:
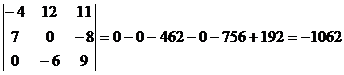
Методом разложения по элементам
ряда.
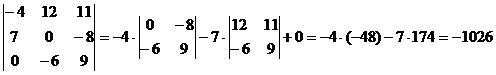
Ответ: -1026
Задание 2
Найти матрицу f(А)
по данной матрице А и функции f(x):
A=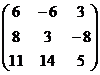 
, f(x)=6x²+7x+15
Решение:
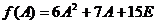
Найдем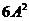 
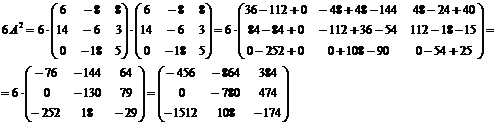
Найдем 7А
+
+
=
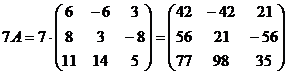
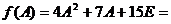
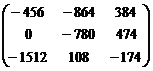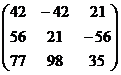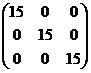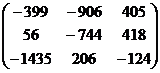
Задание 3
Для матрицы А найти обратную 
. Проверить
равенство 
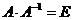
А=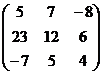 
Решение:
1) Найдем определитель матрицы по правилу
треугольника.
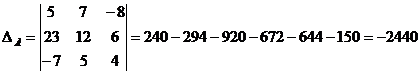
) Найдем алгебраические дополнение
всех элементов матрицы А.
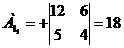
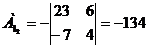
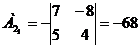
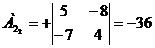
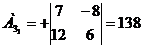
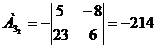
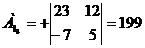
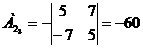
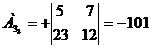
Запишем результаты в присоединенную
матрицу.
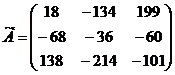
3) Транспонируем присоединенную
матрицу.
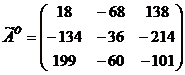
) Найдем обратную матрицу по
формуле:
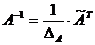
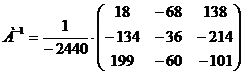
5) Проверим равенство: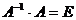 
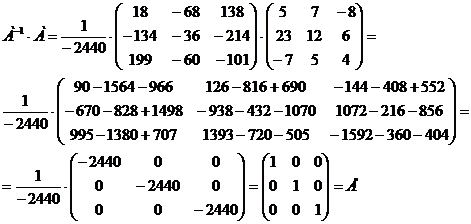
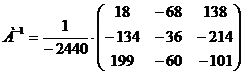
Задание 4.
Даны матрицы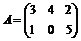 
,
,
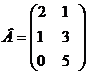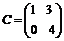. Вычислить
матрицу D
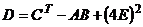
Решение:
Найдем произведение матриц А и В.
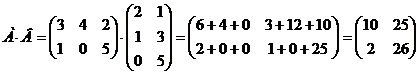
Транспонируем матрицу С
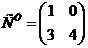
Найдем матрицу
D
.
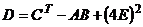
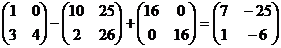
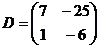
Задание 5.
Решить систему уравнений тремя
способами: методом Гаусса, методом Кремера и матричным методом.
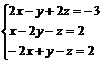
Решение:
1. Решим
систему методом Кремера.
Вычислим определитель основных коэффициентов.
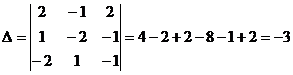
Найдем добавочные определител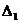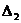и 
, 
и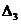 
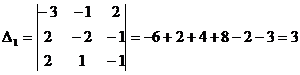
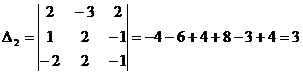
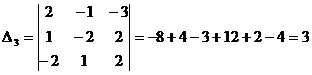
Найдем значения переменных по формулам
Кремера:
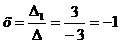
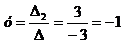
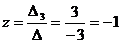
Таким образом, решение системы:
(-1;-1;-1)
2. Решим
систему матричным методом.
Запишем систему в матричном виде
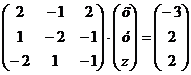
Найдем матрицу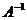 
.
1) Найдем определитель матрицы по правилу
треугольника.
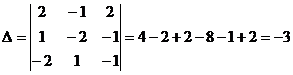
) Найдем алгебраические дополнение
всех элементов матрицы А.
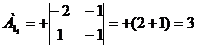
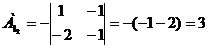
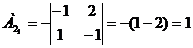
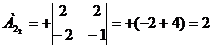
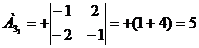
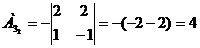
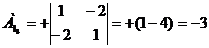
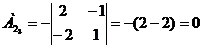
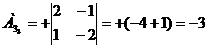
Запишем результаты в присоединенную
матрицу.
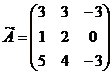
3) Транспонируем присоединенную
матрицу.
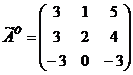
) Найдем обратную матрицу по
формуле:
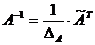
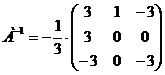
Найдем произведение этой матрицы на
матрицу свободных коэффициентов.
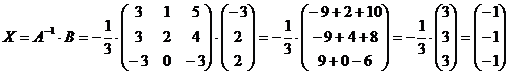
Таким образом, решение системы:
(-1;-1;-1)
3. Решим
систему методом Гаусса.
Запишем расширенную матрицу системы и приведем
ее к треугольной форме путем элементарных преобразований (они указаны справа у
каждой строки).
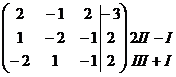
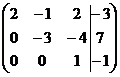
Запишем систему, соответствующую
последней расширенной матрице, и найдем неизвестные.
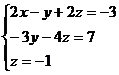
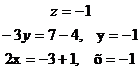
Таким образом, решение системы:
(-1;-1;-1)
Ответ: (-1;-1;-1)
Задание 6.
Даны вершины треугольника АВС.
А(2,2),
В(2,-1)
,С(-3,0)
Найти:
1)
уравнения
сторон треугольника;
2)
уравнение
медианы и высоты, проведенных из вершины В.
3)
уравнение
прямой l1через точку С, l1|| АВ;
уравнение прямой l2 через
точку В, l2
l1;
5)
точку
пересечения l1 и l2.
1. Уравнение прямой
через две точки имеет вид:
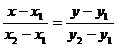
Уравнение АВ: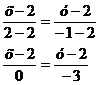 
Уравнение
АС: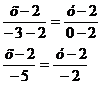 
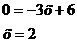
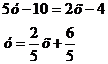
Уравнение ВС:
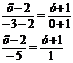
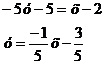
2. Составим уравнения медианы и высоты,
проведенных из вершины В.
Найдем координаты середины отрезка АС, точки М
по формуле:
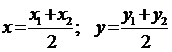
А(2;2) С(-3;0) М: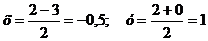 
,
следовательно, М (-0,5;1)
Составим уравнение медианы ВМ по
формуле: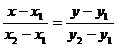
Уравнение ВМ:
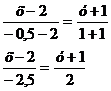
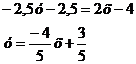
Так как ВН- высота, опущенная на АС,
то ВН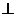АС.
Составим уравнение высоты ВH по
формуле:
,
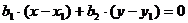где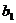 
и 
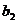- координаты вектора,
перпендикулярного прямой ВН.
Координаты вектора находим по
формуле (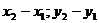
).
АС(-5;-2) и В (2;-1)
Уравнение ВН:
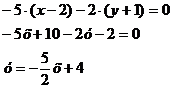
Составим уравнение прямой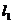 
, проходящей
через точку С, параллельно АВ.
3. Используем формулу прямой, проходящей через
точку параллельно вектору:
,
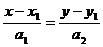где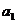 
и 
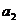- координаты вектора АВ,
параллельного прямой .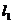
АВ(0;-3) и С (-3;0)
Уравнение :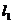
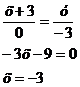
4. Составим уравнение прямой l2
, проходящей через точку В, l2 l1;
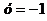
. Найдем точку пересечения прямых l1
и l2. Для этого решим систему уравнений этих прямых.
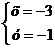
Задание 7
Даны координаты вершин пирамиды А1, А2,
А3, А4. Найти:
1) угол между ребром А1А4
и гранью А1А2А3 ;
2) площадь грани А1А2А3
;
) объем пирамиды ;
) уравнения прямой А1А2
;
) уравнение плоскости А1А2А3
;
) уравнения высоты, опущенной из вершины
А4 на грань А1А2А3 .
Сделать чертеж.
А1 (7; 7; 3), А2 (6; 5;
8), А3 (3; 5; 8), А4 (8; 4; 1) .
Решение
1. Найдем угол между ребром А1А4
и гранью А1А2А3
Составим уравнение прямой по формуле:
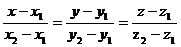
А1 (7; 7; 3), А4 (8; 4; 1)
.
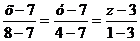, т.е. А1А4 :
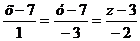
Составим уравнение плоскости А1А2А3
по формуле:
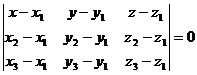
А1 (7; 7; 3), А2
(6; 5; 8), А3 (3; 5; 8),
, 
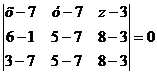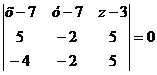
Разложив определитель по элементам
первой строки, получим уравнение:
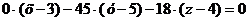
После преобразований получим А1А2А3
: 
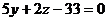
Из уравнения прямой А1А4
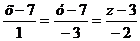: направляющий
вектор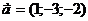 
Из уравнения плоскости А1А2А3
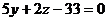: нормальный
вектор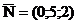 
Найдем синус угла между прямой и
плоскостью по формуле:
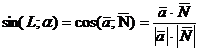
Найдем скалярное произведение
векторов по формуле:
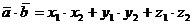
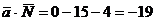
Найдем длины векторов по формуле:
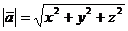
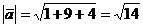
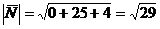
Найдем синус угла между прямой А1А4
и плоскостью А1А2А3.
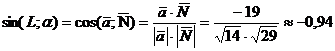
2. Найдем площадь грани А1А2А3.
Для этого достроим треугольник А1А2А3 до
параллелограмма.
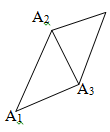
Рассмотрим векторное произведение
2-х векторов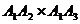 
.
Векторное произведение выражается
формулой:
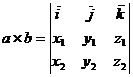
Найдем координаты векторов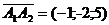 
и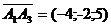 
. Вычислим
векторное произведение.
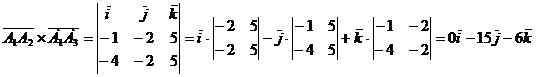
Длина (модель) векторного
произведения 
численно
равна площади параллелограмма, построенного на этих векторах. Следовательно.
Площадь треугольника равна
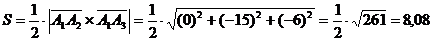
3. Объем пирамиды 
. Модуль
смешанного произведения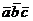 
равен
объему параллелепипеда, построенного на этих векторах. Смешанное произведение
вычисляется по формуле:
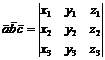
Найдем смешанное произведение
векторов
,
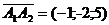
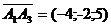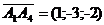
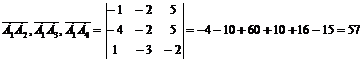
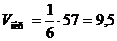
4. Составим уравнение прямой А1А2
по формуле:
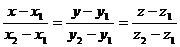
А1 (7; 7; 3), А2
(6; 5; 8),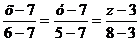 
.
Окончательно:
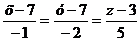
5. Составим уравнение плоскости А1А2А3
по формуле:
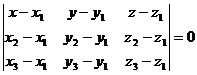
А1 (7; 7; 3), А2
(6; 5; 8), А3 (3; 5; 8),
,
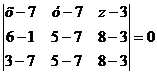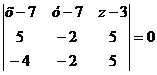
Разложив определитель по элементам
первой строки, получим уравнение:
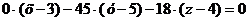
После преобразований получим А1А2А3
:
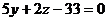
6. Составим уравнения высоты, опущенной из
вершины А4 на грань А1А2А3 .
Из уравнения плоскости А1А2А3
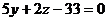: нормальный
вектор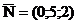
Высота проходит через точку А4
(8; 4; 1) параллельно вектору 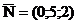. Используем формулу:
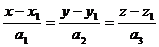
Подставим координаты точки А4
и вектора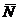 
.
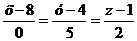
Задание 8
|
a
|
b
|
c
|
d
|
М1
|
М2
|
М3
|
М4
|
|
1.1.-5
|
-3.6.-4
|
3.6.2
|
-1.2.5
|
4.5.-3
|
-2.5.-3
|
-2.1.-1
|
-6.5.2
|
Требуется:
1) Составить уравнение
плоскости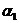 
, которая
проходит через точку М1 и имеет нормальный вектор a .
) Составить уравнение плоскости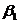 
, которая
проходит через точки М1, М2, М3.
) Составить уравнение 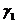плоскости 
, которая
проходит через точку М2 и параллельной плоскости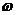 
, проходящей через точки М1, М3 и М4
) Составить уравнение плоскости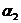 
, которая
проходит через точки М2, М3 и перпендикулярной к плоскости 
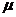, проходящей
через точку М1 с нормальным вектором b .
) Составить каноническое уравнение
прямой L1,
проходящей через точку М3 с направляющим вектором c.
) Составить общее уравнение прямой L2 в
пространстве , если она является линией пересечения плоскостей 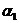(из 1-го
задания) и 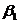(из 2-го
задания). Осуществить переход от общего уравнения к каноническому.
) Составить уравнение прямой L3,
проходящей через точки М2 и М3.
) Составить уравнение плоскости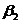 
, проходящей
через точку М1 параллельной прямым L1 (из 5-го
задания) и L2 (из 6-го
задания).
) Определить угол между прямой L1 (из 5-го
задания) и плоскостью 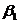(из 2-го
задания).
) Составить уравнение плоскости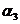 
, проходящей
через точку М2 и параллельной плоскости 
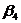, которая проходит через точку М1 с
нормальным вектором d.
Решение
1. Уравнение плоскости, проходящей
через точку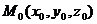 
и имеющей
нормальный вектор 
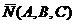, имеет вид:
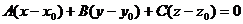
Составим уравнение плоскости 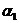, которая
проходит через точку М1(4;5;-3) и имеет нормальный вектор a (1;1;-5) .
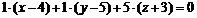
После преобразований получим:
: 
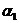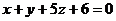
2. Составим уравнение плоскости 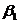по формуле:
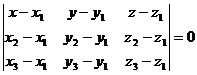
М1 (4; 5; -3), М2
(-2; 5;-3), М3 (-2; 1;-1)
, 
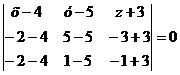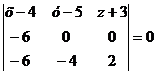
Разложив определитель по элементам
первой строки, получим уравнение:
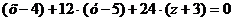
После преобразований получим
уравнение плоскости :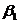 
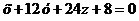
. Составим уравнение плоскости 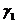, которая
проходит через точку М2 (1;-1;0) и параллельной плоскости , проходящей
через точки М1 (4; 5; -3), М3 (-2; 1;-1) и М4(-6;5;2).
Уравнение плоскости:
; 
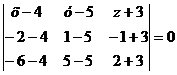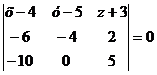
Разложив определитель по элементам первой
строки, получим уравнение:
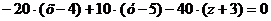
После преобразований получим
уравнение плоскости:
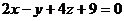
Уравнение плоскости, проходящей
через точку 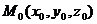и имеющей
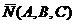нормальный вектор , имеет вид:
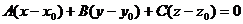
Составим уравнение 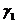плоскости , которая
проходит через точку М2 (1;-1;0) с нормальным вектором плоскости .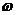 
.
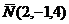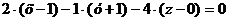
После преобразований получим
уравнение плоскости :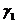 
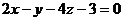
. Составим уравнение плоскости 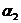, которая
проходит через точки М2 (1;-1;0) , М3 (-2; 1;-1) и
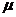перпендикулярной к плоскости , проходящей через точку М1
(4; 5; -3), с нормальным вектором b(-3;6;-4) .
Запишем уравнение плоскости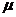
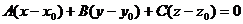
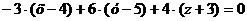
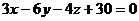
Составим уравнение плоскости .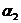
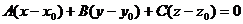
Подставим в это уравнение координаты
точек М2 (1;-1;0) , М3 (-2; 1;-1)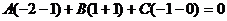 
получим: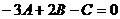 
Так как плоскость 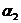перпендикулярна
к плоскости 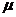, то
нормальные векторы этих плоскостей также перпендикулярны.
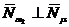, т.е. 
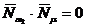, откуда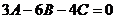 
Решим систему уравнений
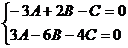
Пусть С=1, тогда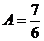 
и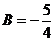 
,
следовательно 
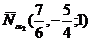
Подставим координаты точки М2
(1;-1;0) и вектора 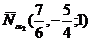в уравнение
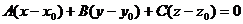
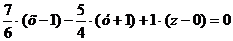
После преобразований получим
уравнение плоскости :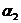
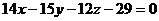
Уравнение прямой, проходящей через точку с
направляющим вектором имеет вид:
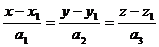
Подставим координаты и получим
уравнение прямой L1
:
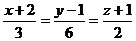
6. Составить общее уравнение прямой L2 в
пространстве , если она является линией пересечения плоскосте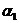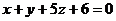й : и : .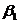
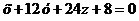Осуществить переход от общего уравнения к каноническому. Уравнение прямой L2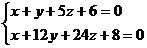 
Пусть z=0, тогда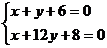 
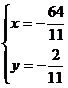
Получим точку (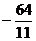
;
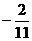;0),
принадлежащую прямой L2.
Найдем координаты направляющего
вектора по формул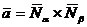е: 
, где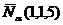 
, 
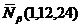. Вычислим
векторное произведение.
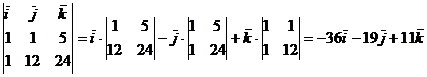
Направляющий вектор прямой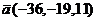 
Каноническое уравнение прямой, проходящей через
точку с направляющим вектором имеет вид:
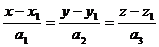
Подставим координаты точк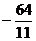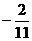и (;;0)и 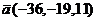и получим
уравнение прямой L2 :
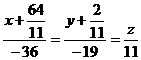
7. Составим уравнение прямой L3,
проходящей через точки М2 (1;-1;0) , М3 (-2; 1;-1)
Составим уравнение прямой по формуле:
.
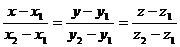
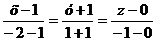Окончательно уравнение прямой L3: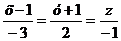 
. Составим уравнение плоскости , проходящей
через точку М1 (4; 5; -3), параллельной прямым L1 : 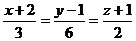и L2 : .
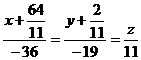Уравнение плоскости имеет вид:
; 
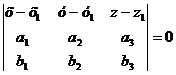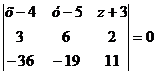
Разложив определитель по элементам первой
строки, получим уравнение:
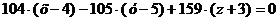
После преобразований получим
уравнение плоскости: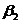
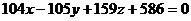
. Определим угол между прямой L1 : 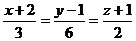и
плоскостью :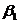
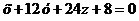
Найдем синус угла между прямой L1и плоскостью
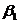
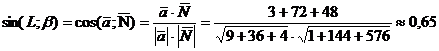
10. Составим уравнение плоскости 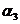, проходящей
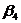через точку М2 (1;-1;0) и параллельной плоскости , которая
проходит через точку М1 (4; 5; -3), с нормальным вектором d (-1;2;5).
Так как плоскости параллельны, то
нормальный вектор плоскости 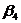является также нормальным вектором
для плоскости .
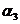Уравнение плоскости, проходящей
через точку 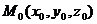и имеющей
нормальный вектор 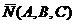, имеет вид:
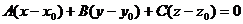
Составим уравнение плоскости 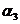, которая
проходит через точку М2 (1;-1;0) и имеет нормальный вектор d (-1;2;5).
треугольник уравнение гаусс
матричный
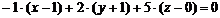
После преобразований получим:
: 
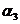