Основы высшей математики
112104
ЗФК (ЗФ)
Министерство
транспорта Российской Федерации
Федеральное
Агентство морского и речного транспорта
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
«Государственный
морской университет
имени
адмирал Ф.Ф.Ушакова»
ЗАОЧНЫЙ
ФАКУЛЬТЕТ
Специальность:
«ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ»
РАСЧЕТНО-ГРАФИЧЕСКАЯ
РАБОТА
ПО
ВЫСШЕЙ МАТЕМАТИКЕ
СТУДЕНТКИ ЗАОЧНОГО ФАКУЛЬТЕТА
КУРСА
ГОРБАТЕНКО А. П.
Г.НОВОРОССИЙСК
г.
Содержание
Часть 1
Часть 2
Часть 3
ПРИЛОЖЕНИЯ
СПИСОК ЛИТЕРАТУРЫ
Часть 1
По координатам вершин пирамиды 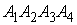 найти:
найти:
) длины ребер 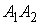 и
и 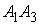 ,
,
) угол между ребрами 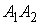 и
и 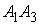 ,
,
) площадь грани  ,
,
) объем пирамиды;
) уравнения прямых 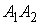 и
и 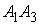 ,
,
) уравнения плоскостей  и
и 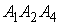 ;
;
) угол между плоскостями  и
и 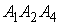 .
.
Условие:
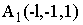 ,
, 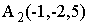 ,
, 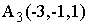 ,
, 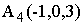 .
.
Решение:
1) Длину ребер 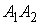 и
и 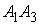 найдем по
формуле расстояний между двумя точками:
найдем по
формуле расстояний между двумя точками:
=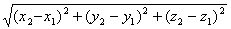
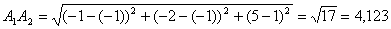

) Угол α между
ребрами А1А2 и А1А3 равен углу между векторами A1 A2 и A1 A3 . Найдем
координаты этих векторов:

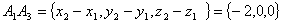
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно
найти по формуле:
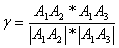
Найдем угол между ребрами  и
и 
) Площадь грани.
Площадь грани можно найти по
формуле:
где
Найдем площадь грани 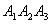
Найдем угол между ребрами  и
и :
:
Площадь грани 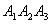
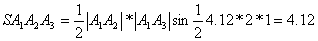
4) Объем пирамиды.
Найдем координаты векторов, описывающих
пирамиду:
А1 (-1, -1, 1)
А2 (-1, -2, 5)
А3 (-3, -1, 1)
А4 (-1, 0, 3)
Поочереди вычитая из координат точки А1
соответсятвуующие координаты остальных точек:
вектор №1 (0, 1, -4)
вектор №2 (2, 0, 0)
вектор №3 (0, -1, -2)
Запишем матрицу, найдем определитель ∆:
∆=  =0*0*(-2)+2*(-1)*(-4)+1*0*0-0*0*(-4)+(-1)*0*0+2*1*(-2)=8+4=12
=0*0*(-2)+2*(-1)*(-4)+1*0*0-0*0*(-4)+(-1)*0*0+2*1*(-2)=8+4=12
Определитель данной матрицы в 6 раз
больше объма пирамиды:
V=
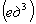
) Уравнение прямых  и
и 
Прямая, проходящая через точки
A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Уравнение прямой 
Уравнение прямой 
6) Уравнение плоскостей 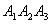 и
и 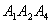
Уравнение плоскости 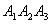
(x+1)((-1) • 0-0 • 4) - (y+1)(0 •
0-(-2) • 4) + (z-1)(0 • 0-(-2) • (-1)) = 0x - 8y - 2z + 6 = 0
Уравнение плоскости 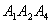
(x+1)((-1) • 2-1 • 4) - (y+1)(0 •
2-0 • 4) + (z-1)(0 • 1-0 • (-1)) = -6x + 0y + 0z + 6 = 0
) ) Угол между плоскостью 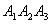 и
плоскостью
и
плоскостью 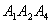
Косинус угла между плоскостью 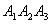 и плоскостью
и плоскостью
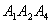 равен углу
между их нормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):
равен углу
между их нормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):
Часть 2
Дана система трех линейных уравнений с тремя
неизвестными. Найти ее решение:
1) методом Крамера
2) средствами матричного исчисления
) методом Гаусса
Проверить правильность вычисления обратной
матрицы, используя матрияное умножение.
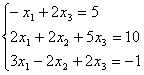
Решение:
1) методом
Крамера:
По данным системы составим определитель Δ:
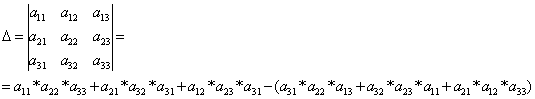
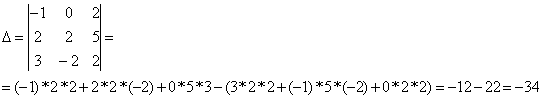
Вместо первого столбца поставим
столбец свободных коэфицентов, получим Δ1:
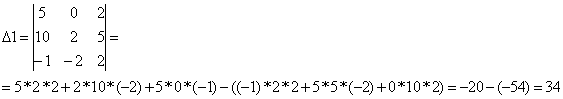
Вместо первого столбца поставим
столбец свободных коэфицентов, получим Δ2:
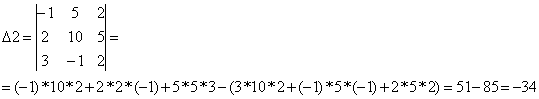
Вместо первого столбца поставим
столбец свободных коэфицентов, получим Δ3:
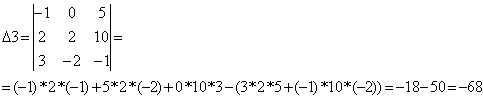
Найдем  :
:
 ;
; 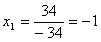 ;
;
 ;
; 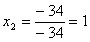 ;
;
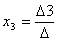 ;
;  ;
;
Ответ: (-1; 1;2).
2) Средствами матричного исчисления:
Найдем обратную матрицу по формуле:

Δ -
определитель матрицы
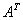 - транспонированная матрица
- транспонированная матрица
Запишем матрицу, найдем главный
определитель:
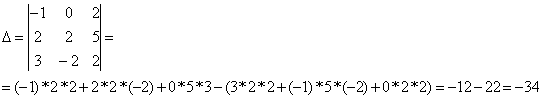
Вектор В = 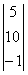
Транспонируем матрицу:
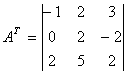
Найдем элементы матрицы: для
нахождения каждого элемента, мысленно вычеркиваем строку и столбец, в котором находится
данный элемент, оставшиеся четыре записываем в определитель, вычисляем.
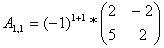
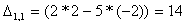
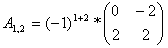
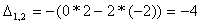
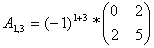
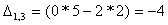
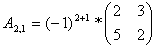
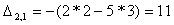

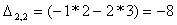
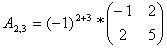
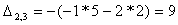
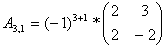
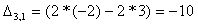
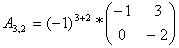
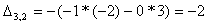

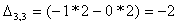
Запишем обратную матрицу:
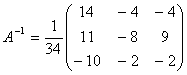
Проверим правильность обратной
матрицы, используя матричное умножение:
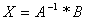
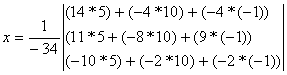
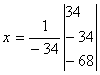
Найдем  :
:
 ;
; 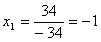 ;
;
 ;
; 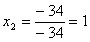 ;
;
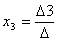 ;
;  ;
;
Проверка:
*(-1)+0*1+2*2=5
*(-1)+(-2)*1+2*2=-1
Ответ:(-1, 1, 2).
) Методом Гаусса:
Выписываем матрицу данной системы, состоящую из
коэфицентов уравнения и свободных коэфицентов:
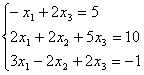
Если в каком-то уравнении на певром
месте стоит 1, то ставим это уравнение на первую строку.
С помощью этой еденицы обнуляем все
первые коэфиценты в каждом уравнении.
Приводим матрицу к ступенчатому виду:
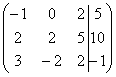
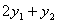
Умножаем первую строку на 2, добавим
вторую строку к первой.
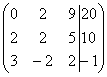
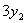 Умножаем вторую строку на 3.
Умножаем вторую строку на 3.
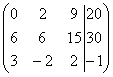

Умножаем третью строку на (-2),
добавим третью строку ко второй.
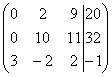
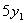
Умножим первую строку на 5.
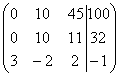

Умножим вторую строку на (-1), ко
второй строке прибавим первую.
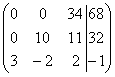
Из последнего уравнения получившейся
матрицы находим 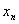 ,
подставляем его в последнее уравнение
,
подставляем его в последнее уравнение 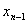 , поднимаясь выше, находим все
неизвестные.
, поднимаясь выше, находим все
неизвестные.
a)
уравнение пирамида
неизвестный система
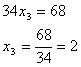
б)
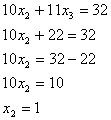
в)
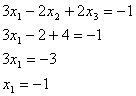
Ответ: (-1; 1; 2)
Часть 3
Привести уравнение кривой второго
порядка ƒ(x,y)=0 к
каноническому виду и найти точки пересечения ее спрямой Ax+By+C=0.
Построить графики кривой и прямой.
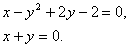
Решение:
) 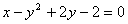
Приводим к каноническому виду:
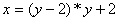
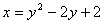
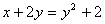
Решение для переменной у:
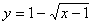

Канонический вид - парабола.
Глобальный минимум:
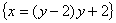 1 в у=1
1 в у=1
Неявные производных:
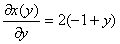
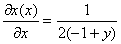
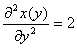
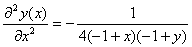
) 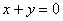
Приводим к каноническому виду:
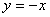
Каноническое решение:
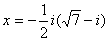
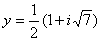
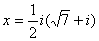
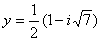
Прямая и парабола не пересекаются.
Построение графиков.
Приложение - рис.1.
Приложение
Рис.1.
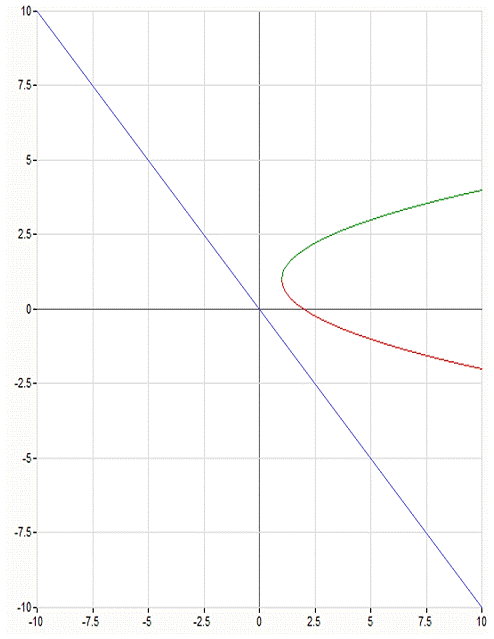
Список литературы
1. Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры: 9-е изд., перераб. М.:
Физматлит,2001. 376 с.
. Ефимов
П.В. Краткий курс аналитической геометрии: Учебник. 13-е изд., стереотип. М.:
Физ-матлит,2003.240с.
. Демидович
Б.П., Кудрявцев В.А. Краткий курс высшей математики: Учеб. пособие для вузов.
М.: Астрель,2003.656с.
. Лунгу
К.Н., Макаров Е.В. Высшая математика - Руководство к решению задач - часть 1. 2002.446с.
. Элементы
высшей математики: В. П. Григорьев, Ю. А. Дубинский - Санкт-Петербург,
Академия, 2004 г.- 320 с.