Промышленные роботы и манипуляторы
Министерство
образования и науки Российской Федерации
Федеральное
агентство по образованию
Саратовский
государственный технический университет
Контрольная
работа
по
Теории механизмов и машин
Саратов
2015
Задача 1
Определить степень свободы пространственного
манипулятора промышленного робота (рис. 1).
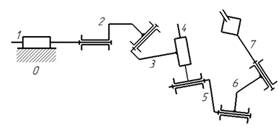
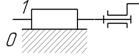
Рис. 1.Схема пространственного манипулятора.
1. Схема механизма промышленного ( рис.1)
состоит из одного неподвижного звена  стойки
0 и подвижных звеньев 1, 2, 3, 4, 5, 6, 7 Следовательно, число подвижных
звеньев равно семи, т. е.
стойки
0 и подвижных звеньев 1, 2, 3, 4, 5, 6, 7 Следовательно, число подвижных
звеньев равно семи, т. е. 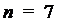 .
.
Число степеней свободы пространственного
механизма определяется формулой Малышева:
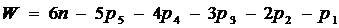 (1)
(1)
Для определения значений коэффициентов  выявим
все кинематические пары, входящие в состав схемы механизма промышленного
манипулятора. Результаты исследования заносим в таблицу 1.
выявим
все кинематические пары, входящие в состав схемы механизма промышленного
манипулятора. Результаты исследования заносим в таблицу 1.
Таблица 1
|
№
п/п
|
Номера
звеньев /название
|
Схема
|
Класс
/ подвижность
|
Вид
контакта / замыкание
|
|
1
|
0
- 1 поступательно - вращательная
|
|
4/2
|
Поверхность
(низшая) / геометрическое
|
|
2
|
1
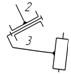
- 2 / вращательная
|
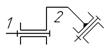
|
4/2
|
Поверхность(низшая)
/ геометрическое
|
|
3
|
2
- 3 / вращательно - поступательная
|
|
4/2
|
Поверхность(низшая)
/ геометрическое
|
|
4
|
3
- 4 / поступательно - вращательная
|
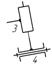
|
4/2
|
Поверхность(низшая)
/ геометрическое
|
|
5
|
4
- 5 / вращательная
|
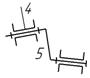
|
4/2
|
Поверхность(низшая)
/ геометрическое
|
|
6
|
5
- 6 / вращательная
|
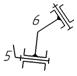
|
4/2
|
Поверхность(низшая)
/ геометрическое
|
|
7
|
6
- 7 / вращательная
|
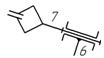
|
5/1
|
Поверхность(низшая)
/ геометрическое
|
Из анализа данных таблицы 1 следует, что
исследуемая схема механизма манипулятора промышленного робота представляет
собой разомкнутую кинематическую цепь, звенья которой образуют между собой семь
пар 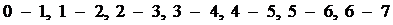
Подставив найденные значения коэффициентов в
структурную формулу Малышева (1):
робот манипулятор промышленный
рычажный
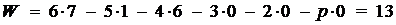
Результат свидетельствует о том, что для
однозначного описания положений звеньев механизма манипулятора промышленного
робота в пространстве необходимо семь обобщенных координат. пятого класса.
) Маневренность  это
подвижность пространственного механизма при неподвижном звене 7. Маневренность
обозначают
это
подвижность пространственного механизма при неподвижном звене 7. Маневренность
обозначают  и определяют по
формуле Малышева.
и определяют по
формуле Малышева.
Для определения маневренности необходимо
остановить (запретить перемещаться) выходное звено 7. Следовательно, число
подвижных звеньев становиться равным четырем, т.е. 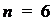 .
Значения всех остальных коэффициентов не изменяются, т.е.
.
Значения всех остальных коэффициентов не изменяются, т.е.
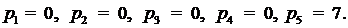
Подставив найденные значения коэффициентов в
выражение для маневренности (1), получим:
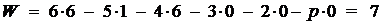
Результат говорит о том, что для однозначного
определения положений
звеньев механизма манипулятора промышленного
робота, имеющего замкнутую кинематическую цепь, достаточно семь обобщённых
координат.
Проверим полученное значение:
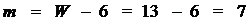
Задача 2
а) при закрепленном водиле 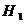 (первая
передача);
(первая
передача);
б) при закрепленном водиле 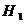 (вторая
передача).
(вторая
передача).
Известны числа зубьев колес и скорость вращения
колеса 1.
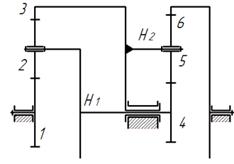
Рис.2.Схема двухскоростной планетарной коробки
передач.
Дано:
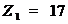 ,
, 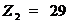 ,
,
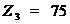 ,
,
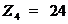 ,
,
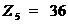 ,
,
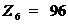 ,
,
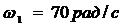
1. Рассмотрим случай при закрепленном водиле 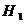 (первая
передача).
(первая
передача).
.1. Определим передаточное отношение механизма
при остановившемся водило 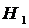 :
:
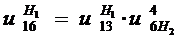
Определяем передаточное отношение от колеса 1 к
колесу 3 при остановившемся водиле 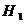 :
:
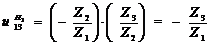
Определяем передаточное отношение от колеса 5 к
колесу 6 при остановленным колесе 4:
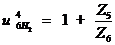
Тогда передаточное отношение от колеса 1 к
колесу 6:
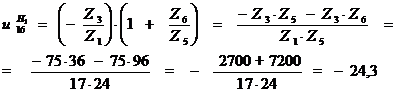
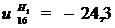
1.2. Определяем частоту вращения колеса 6:
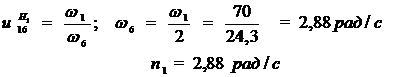
. Рассмотрим случай при закрепленном водило  (вторая
передача).
(вторая
передача).
.1. Определим передаточное отношение механизма
при остановившемся водило 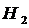 :
:
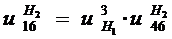
Определяем передаточное отношение от колеса 1 к
колесу 3 при остановившемся водиле 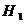 :
:
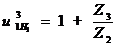
Определяем передаточное отношение от колеса 4 к
колесу 6 при остановленным водило 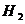 :
:
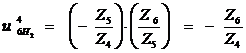
Тогда передаточное отношение от колеса 1 к
колесу 6:
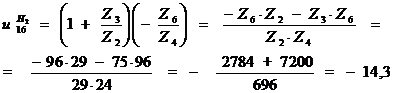
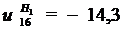
2.2. Определяем частоту вращения колеса 6:
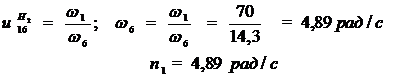
Задача 3
Для положения рычажного механизма, изображенного
на рис. 3 необходимо:
. Методом построения планов скоростей и
ускорений определить скорости и ускорения коромысла 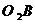 и
ползуна
и
ползуна 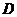 .
.
. Методом кинетостатики определить реакцию 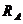 в
шарнире
в
шарнире 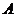 и
приведенный момент на кривошипе
и
приведенный момент на кривошипе 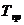 от приложенных
усилий
от приложенных
усилий 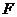 и
момента
и
момента 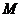 .
.
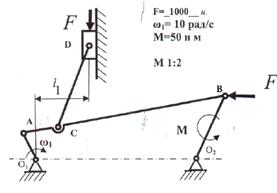
Рис. 3.Схема рычажного механизма.
Дано: 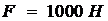 ,
,
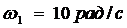 ,
,
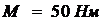 .
.
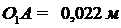 ,
, 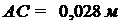 ,
,
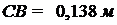 ,
,
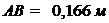 ,
,
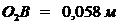 ,
,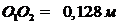 ,
,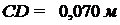 ,
,
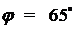 ,
,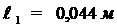 .
.
. Для механизма (рис. 4 а) выполним структурный
анализ.
Схема рычажного механизма представляет собой
замкнутую кинематическую цепь, следовательно, данный механизм является плоским
механизмом.
Подвижность рычажного механизма определяется
поструктурной формуле Чебышева:
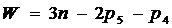
Структурная схема механизма состоит из шести
звеньев:
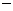 кривошипа,
кривошипа,
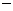 шатуна,
шатуна,
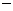 коромысла,
коромысла,
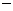 шатуна,
шатуна,
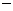 ползуна,
ползуна,
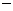 стойка.
стойка.
При этом звенья 1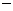 5
являются подвижными звеньями, а стойка 0 - неподвижным звеном.
5
являются подвижными звеньями, а стойка 0 - неподвижным звеном.
Следовательно, 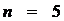 .
.
Механизм имеет 7 пар пятого класса 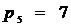 ,
четвертого класса
,
четвертого класса 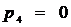 .
.
Следовательно:
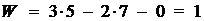
Результат говорит, что для однозначного описания
положений звеньев рычажного механизма на плоскости необходима одна обобщенная
координата  .
.
. Строим схему механизма рис.4 а:
Приняв 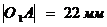 ,
определим масштабный коэффициент:
,
определим масштабный коэффициент:
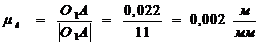
Переводим все остальные геометрические параметры
в выбранный масштабный коэффициент длин, мм:
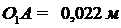 ,
,
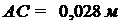 ,
,
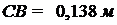 ,
,
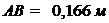 ,
,
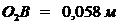 ,
,
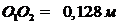 ,
,
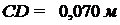 ,
,
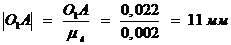 ,
, 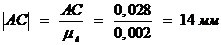 ,
,
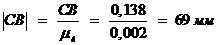 ,
, 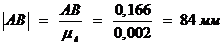 ,
,
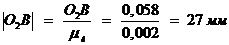 ,
, 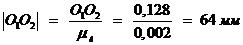 ,
,
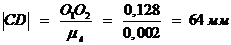 ,
, 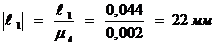 .
.
По полученным величинам в выбранном масштабном
коэффициенте выполняем чертёж рычажного механизма рис.4. а
3. Выполним кинематический анализ рычажного
механизма методом построения плана скоростей и ускорений.
.1. Построение плана скоростей.
Кривошип  вращается
с постоянной угловой скоростью
вращается
с постоянной угловой скоростью 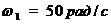 .
.
Составим векторное уравнение скорости точки 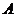 :
:
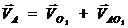 (1)
(1)
Точка 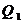 является
неподвижной точкой, следовательно, значение скорости этой точки равно нулю (
является
неподвижной точкой, следовательно, значение скорости этой точки равно нулю (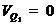 ).
).
Вектора  является
перпендикуляром к оси кривошипа 1, а направление действия совпадает с
направлением его вращения
является
перпендикуляром к оси кривошипа 1, а направление действия совпадает с
направлением его вращения
Определяем значение скорости точки 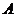 ,
м/с, равно:
,
м/с, равно:
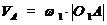
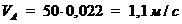 (2)
(2)
На чертеже отмечаем полюс точку 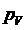 в
которой размещаем вектор скорости
в
которой размещаем вектор скорости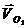 .
.
Приняв 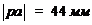 ,
принимаем масштабный коэффициент:
,
принимаем масштабный коэффициент:
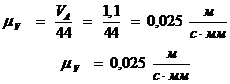
Изобразим на рис. 4.б строим вектор ра,
перпендикулярный 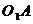 , учитывая
направление вращения звена 1.
, учитывая
направление вращения звена 1.
Составим векторное уравнение скорости точки 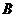 :
:
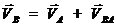
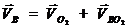
Вектор скорости точки А 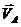 известен
по величине и направлению.
известен
по величине и направлению.
Вектор скорости точки В 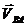 относительно
точки А, перпендикулярный звену 2 неизвестен по направлению и величине.
относительно
точки А, перпендикулярный звену 2 неизвестен по направлению и величине.
Вектор скорости точки O2 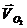 равен
нулю, располагаем его в полюсе
равен
нулю, располагаем его в полюсе 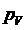 .
.
Вектор скорости точки В 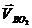 относительно
точки O2, перпендикулярны звену 3 неизвестен по направлению и величине.
относительно
точки O2, перпендикулярны звену 3 неизвестен по направлению и величине.
Строим на плане скоростей векторные уравнения.
Из точки а проводим прямую 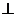
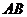 вектор
скорости точки В
вектор
скорости точки В 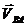 , из точки р
проводим прямую
, из точки р
проводим прямую 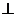
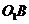 вектор
скорости точки В
вектор
скорости точки В 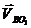 при пересечении
получаем точку b. Указываем направление скоростей
при пересечении
получаем точку b. Указываем направление скоростей 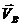 и
и
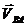 .
.
Из теоремы подобия на отрезке аb определяем
положение точки с:
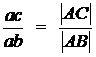
откуда:
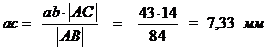
где: 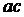 ,
,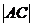 ,
,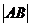 размеры с чертежа.
размеры с чертежа.
Составим векторное уравнение скорости точки 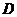 :
:
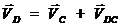
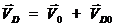
Вектор скорости точки С 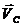 параллелен
звену 4 неизвестен по направлению и величине.
параллелен
звену 4 неизвестен по направлению и величине.
Вектор скорости точки D 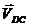 относительно
точки С, перпендикулярный звену 4 неизвестен по направлению и величине.
относительно
точки С, перпендикулярный звену 4 неизвестен по направлению и величине.
Вектор скорости точки 0 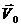 равен
нулю, располагаем его в полюсе
равен
нулю, располагаем его в полюсе 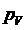 .
.
Вектор скорости точки D 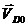 относительно
точки 0, параллелен ходу ползуна 5. Точку с соединяем с полюсом
относительно
точки 0, параллелен ходу ползуна 5. Точку с соединяем с полюсом 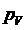 получаем
скорость точки С
получаем
скорость точки С 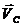 .
.
Из точки с проводим прямую 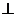
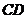 до
пересечения с вертикальной прямой проходящую через полюс
до
пересечения с вертикальной прямой проходящую через полюс 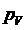 .
.
Замерив на плане скоростей рис.4. б длины
соответствующих отрезков, найдем значения скоростей характерных точек
механизма:
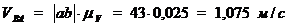
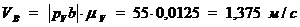
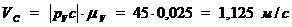
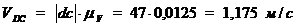
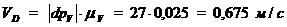
Определим угловые скорости шатунов 2, 4 и
коромысла 3.
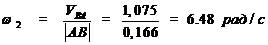
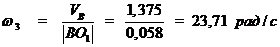
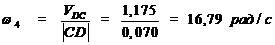
Угловая скорость ползуна 5 равна нулю, так как
совершает поступательное движение.
Направление угловых скоростей шатунов 2, 3 и
коромысла 4, соответственно, укажут вектора скоростей  ,
,
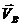 и
и
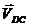 ,
взятые с плана скоростей и мысленно перенесенные в точки
,
взятые с плана скоростей и мысленно перенесенные в точки 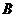 и
и
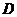 на
кинематической схеме механизма.
на
кинематической схеме механизма.
Направление угловых скоростей шатунов 2, 3 и
коромысла 4, соответственно, укажут вектора скоростей 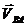 ,
,
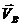 и
и
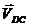 ,
взятые с плана скоростей рис.4.б и мысленно перенесенные в точки
,
взятые с плана скоростей рис.4.б и мысленно перенесенные в точки 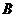 и
и
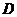 на
кинематической схеме механизма рис.4.а. При этом условно разрывается связь
звеньев 2
на
кинематической схеме механизма рис.4.а. При этом условно разрывается связь
звеньев 2 3
и звеньев 4
3
и звеньев 4 5, а точки
5, а точки 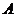 и
и
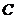 условно
закрепляются. В этом случае под действием векторов скоростей
условно
закрепляются. В этом случае под действием векторов скоростей 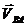 ,
,
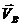 и
и
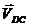 ,
соответственно, шатун 2 и коромысло 3 будут вращаться в направлении,
противоположном действию часовой стрелки, а шатун 4 в направлении, совпадающем
с действием часовой стрелки.
,
соответственно, шатун 2 и коромысло 3 будут вращаться в направлении,
противоположном действию часовой стрелки, а шатун 4 в направлении, совпадающем
с действием часовой стрелки.
Данные направления движений и есть направления
действия угловых скоростей 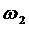 ,
,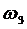 ,
и
,
и 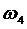 ,
соответственно.
,
соответственно.