Расчет одноконтурной системы автоматического регулирования
Курсовая работа
Расчёт одноконтурной системы автоматического регулирования
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра «Автоматизация
технологических процессов и производств»
Задание
Студенту гр. 5Б1В Степановой
Александре Олеговне
На выполнение курсовой работы по
дисциплине «Теория автоматического управления»
Тема работы: «Расчёт одноконтурной
системы автоматического регулирования».
Содержание работы
Расчётно-пояснительная записка
• титульный лист;
• задание на курсовую работу;
• аннотацию;
• введение;
• основные разделы;
• заключение;
• список литературы;
• приложение (при
необходимости);
• содержание.
Исходные данные к работе приведены в
задании на курсовую работу
Вариант задания №
Задание выдал
_______________________ «» ________________ 2005 г.
Задание принял к исполнению
студент ________________________ «»
_________________ 2005 г.
Введение
одноконтурный регулятор
автоматический инженерный
Данная курсовая работа посвящена
расчёту одноконтурной системы автоматического регулирования. Для оценки систем
регулирования с точки зрения их практической пригодности необходимо определить,
в каких условиях эти системы можно использовать, какие настроечные параметры
регулятора требуется установить, чтобы процесс регулирования, осуществляемый
при помощи различных регуляторов систем, был оптимальным.
В настоящее время системы
регулирования получили широкое применение в различных отраслях промышленности.
В связи с этим проблема определения оптимальных параметров настройки
регуляторов систем остаётся актуальной, даже несмотря на то, что разработано
большое количество приёмов и методов, позволяющих решать эти проблемы. В
частности, существует два инженерных метода расчёта систем регулирования:
корневой (с использованием РАФЧХ) и частотный по максимуму АЧХ замкнутой
системы (метод В.Я. Ротача).
Перед человеком, которому впервые
предстоит рассчитать систему регулирования, встаёт множество вопросов. Ответы
на них можно найти, решив следующие задачи: освоить указанные выше методы
расчёта систем регулирования; воспользоваться одним из них для расчёта
приведенной в задании на курсовую работу одноконтурной системы регулирования;
разобраться, какие параметры настройки регулятора считаются оптимальными и как
их определить.
В данной курсовой работе в первом
пункте приводятся исходные данные для расчёта заданноё АСР, структурная схема
которой показана во втором пункте. Третий пункт посвящен расчёту и построению
границы заданного запаса устойчивости АСР с ПИ-регулятором и объектом
регулирования корневым методом. В четвёртом пункте определяются оптимальные
параметры настройки ПИ-регулятора. Последний пункт посвящён расчётам переходных
процессов по двум каналам: по каналу регулирующего воздействия S-Y и при возмущении f, идущем по каналу регулирующего
воздействия, здесь же представлены графики этих процессов и произведены оценки
их качества.
1. Расчёт одноконтурной
системы автоматического регулирования
Исходные
данные
Дана системы регулирования с ПИ -
регулятором и объектом регулирования с передаточной функцией
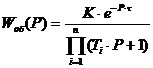 .
.
Параметры передаточной
функции объекта, требования к запасу устойчивости системы, критерий оптимальной
настройки приведены в таблице 1.
Таблица 1 - Исходные
данные по варианту
|
Номер варианта
|
K
|
n
|
T
|
ш
|
I
|
|
0.5
|
2
|
90
|
0.95
|
I1
|
|
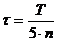 (c)=9
(с); (c)=9
(с); 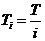 (c); (c);
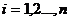 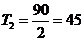 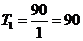
|
|
Обозначения: K
- коэффициент передачи объекта; ф
- запаздывание объекта; Ti
- i-я постоянная времени объекта; n
- порядок объекта; ш - требуемая степень затухания переходных процессов в
системе; I - заданный интегральный критерий качества работы системы 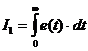 ; ;
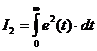 . .
|
2 Расчёт и построение
границы заданного запаса устойчивости АСР
Для расчёта и построения границы
заданного запаса устойчивости АСР с ПИ-регулятором, представленной на рисунке
1, воспользуемся корневым методом параметрического синтеза систем
автоматического регулирования с применением расширенных амплитудно-фазовых
частотных характеристик (РАФЧХ).
Используя исходные
данные, приведенные в таблице 1, можем записать, что для заданной системы
регулирования установлены следующие требования к запасу устойчивости системы:
степень затухания переходного процесса в системе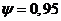 .
.
Исходя из этого, зная
зависимость между степенью затухания переходных процессов в заданной системе
регулирования ш и степенью колебательности переходных процессов в заданной
системе регулирования m,
можно определить значение заданной степени колебательности m системы по формуле:
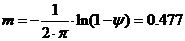 (1)
(1)
где ш - степенью
затухания переходных процессов в заданной системе регулирования.
Передаточная функция
объекта регулирования согласно исходных данных определяется по формуле:
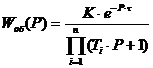 (2)
(2)
где p - оператор Лапласа.
При n=2 выражение для примет вид 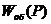 примет вид:
примет вид:
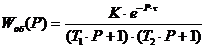 (3)
(3)
По данным таблицы 1
определяем значения неизвестных параметров: К=0.5, 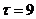 ,
T1=80, T2=40.
Тогда после подстановки значений выше приведенных параметров получаем
окончательное выражение для передаточной функции объекта регулирования:
,
T1=80, T2=40.
Тогда после подстановки значений выше приведенных параметров получаем
окончательное выражение для передаточной функции объекта регулирования:
 (4)
(4)
Определим расширенные
частотные характеристики объекта регулирования. Расширенные частотные
характеристики какого-либо звена можно получить подстановкой в передаточную
функцию этого звена W(P) оператора 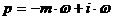 или
или
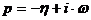 ,
в выражениях для оператора Лапласа щ - частота, с-1. В первом случае
расчётные формулы метода обеспечивают получение границы заданной степени
колебательности системы m,
а во втором - получение границы заданной степени устойчивости системы
,
в выражениях для оператора Лапласа щ - частота, с-1. В первом случае
расчётные формулы метода обеспечивают получение границы заданной степени
колебательности системы m,
а во втором - получение границы заданной степени устойчивости системы  в
пространстве параметров настройки регулятора.
в
пространстве параметров настройки регулятора.
Заменим в формуле (4) оператор
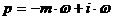 ,
в результате получаем выражение для РАФЧХ объекта регулирования:
,
в результате получаем выражение для РАФЧХ объекта регулирования:
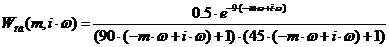 (5)
(5)
Используя математический
пакет MAthCad, предварительно задав начальное значение частоты 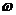 =0
с-1 и шаг по частоте
=0
с-1 и шаг по частоте 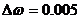 с-1,
рассчитываем расширенные частотные характеристики объекта при изменении частоты
до щ=0,20 с-1.
с-1,
рассчитываем расширенные частотные характеристики объекта при изменении частоты
до щ=0,20 с-1.
Расширенная вещественная
частотная характеристика (РВЧХ):
Reоб(m, щ)=Re(Wоб(m, iщ)) (6)
Расширенная мнимая
частотная характеристика (РМЧХ):
Imоб(m, щ)=Im(Wоб(m, iщ)) (7)
Расширенная
амплитудно-частотная характеристика (РАЧХ)
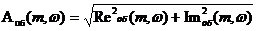 (8)
(8)
Расширенная
фазо-частотная характеристика (РФЧХ):
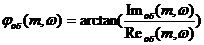 (9)
(9)
Результаты расчётов
сведём в таблицу 2, приведенную ниже.
Таблица 2 - Расширенные
частотные характеристики объекта регулирования
|
частота щ, с-1
|
Reоб(m, щ)
|
Imоб(m, щ)
|
Аоб(m,
щ)
|
цоб(m,
щ), рад
|
|
0
|
0,5
|
0
|
0,5
|
0
|
|
0,005
|
0,421
|
-0,445
|
0,613
|
-0,812
|
|
0,01
|
-0,024
|
-0,541
|
0,541
|
1,526
|
|
0,015
|
-0,244
|
-0,315
|
0,399
|
0,911
|
|
0,02
|
-0,253
|
-0,127
|
0,283
|
0,464
|
|
0,025
|
-0,201
|
-0,027
|
0,203
|
0,133
|
|
0,03
|
-0,148
|
0,018
|
0,15
|
-0,118
|
|
0,035
|
-0,108
|
0,036
|
0,114
|
-0,317
|
|
0,04
|
-0,079
|
0,041
|
0,09
|
-0,478
|
|
0,045
|
-0,058
|
0,042
|
0,072
|
-0,614
|
|
0,05
|
-0,044
|
0,04
|
0,059
|
-0,733
|
|
0,055
|
-0,033
|
0,037
|
0,05
|
-0,836
|
|
0,06
|
-0,025
|
0,034
|
0,042
|
-0,93
|
|
0,065
|
-0,019
|
0,031
|
0,037
|
-1,016
|
|
0,07
|
-0,014
|
0,028
|
0,032
|
-1,096
|
|
0,075
|
-0,011
|
0,026
|
0,028
|
-1,171
|
|
0,08
|
-0,008
|
0,024
|
0,025
|
-1,243
|
|
0,085
|
-0,005
|
0,022
|
0,023
|
-1,311
|
|
0,09
|
-0,003
|
0,020
|
0,021
|
-1,376
|
|
0,095
|
-0,002
|
0,019
|
0,019
|
-1,439
|
|
0,100
|
-0,001
|
0,017
|
0,017
|
-1,5
|
|
0,105
|
-0,000
|
0,016
|
0,016
|
-1,56
|
|
0,110
|
-0,001
|
0,015
|
0,015
|
1,524
|
|
0,115
|
-0,002
|
0,014
|
0,014
|
1,467
|
|
0,120
|
-0,0025
|
0,013
|
0,013
|
1,411
|
|
0,125
|
-0,003
|
0,012
|
0,012
|
1,356
|
|
0,130
|
-0,0034
|
0,011
|
0,011
|
1,301
|
|
0,135
|
-0,0037
|
0,01
|
0,011
|
1,248
|
|
0,140
|
-0,004
|
0,0094
|
0,01
|
1,195
|
|
0,145
|
-0,0042
|
0,0087
|
0,0096
|
1,143
|
|
0,150
|
-0,0044
|
0,0081
|
0,0092
|
1,091
|
|
0,155
|
-0,0046
|
0,0075
|
0,0087
|
1,039
|
|
0,160
|
0,0047
|
0,007
|
0,0084
|
0,989
|
|
0,165
|
0,0048
|
0,0065
|
0,008
|
0,938
|
|
0,170
|
0,0049
|
0,006
|
0,0077
|
0,888
|
|
0,175
|
0,005
|
0,0055
|
0,0074
|
0,838
|
|
0,180
|
0,0051
|
0,005
|
0,0071
|
0,788
|
|
0,185
|
0,0052
|
0,0046
|
0,0069
|
0,739
|
|
0,190
|
0,0052
|
0,0042
|
0,0067
|
0,69
|
|
0,195
|
0,0053
|
0,0038
|
0,0064
|
0,641
|
|
0,200
|
0,0053
|
0,0035
|
0,0063
|
0,592
|
Расчётные формулы корневого метода
для ПИ - регулятора имеют следующий вид:
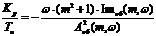 (10)
(10)
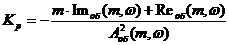 (11)
(11)
В вышеприведенных
формулах (10) и (11) 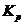 -
коэффициент передачи ПИ - регулятора,
-
коэффициент передачи ПИ - регулятора, 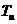 - постоянная
интегрирования ПИ - регулятора.
- постоянная
интегрирования ПИ - регулятора.
Зададим диапазон
изменения частоты 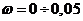 с-1
с шагом
с-1
с шагом 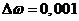 c-1,
определим настройки регулятора
c-1,
определим настройки регулятора 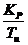 и Кр в
заданном диапазоне частот. Результаты расчётов сведём в таблицу 3.
и Кр в
заданном диапазоне частот. Результаты расчётов сведём в таблицу 3.
Таблица 3 - Результаты
расчёта настройки ПИ - регулятора в заданном диапазоне частот
|
частота щ,
с-1
|
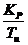 Кр Кр
|
|
|
0
|
0
|
-2
|
|
0,001
|
0,00034
|
-1,722
|
|
0,002
|
0,00131
|
-1,438
|
|
0,003
|
0,00284
|
-1,149
|
|
0,004
|
0,00485
|
-0,855
|
|
0,005
|
0,00727
|
-0,557
|
|
0,006
|
0,010
|
-0,257
|
|
0,007
|
0,0129
|
0,047
|
|
0,008
|
0,016
|
0,352
|
|
0,009
|
0,012
|
0,658
|
|
0,01
|
0,016
|
0,964
|
|
0,011
|
0,0194
|
1,27
|
|
0,012
|
0,0226
|
1,576
|
|
0,013
|
0,0258
|
1,88
|
|
0,014
|
0,0289
|
2,181
|
|
0,015
|
0,0317
|
2,48
|
|
0,016
|
0,0342
|
2,776
|
|
0,017
|
0,0364
|
3,067
|
|
0,018
|
3,354
|
|
0,019
|
0,0392
|
3,912
|
|
0,02
|
0,0398
|
4,182
|
|
0,021
|
0,0396
|
4,445
|
|
0,022
|
0,0387
|
4,701
|
|
0,023
|
0,0370
|
4,949
|
|
0,024
|
0,0343
|
5,189
|
|
0,025
|
0,031
|
5,419
|
|
0,026
|
0,0259
|
5,641
|
|
0,027
|
0,020
|
5,852
|
|
0,028
|
0,012
|
6,053
|
|
0,029
|
0,004
|
6,244
|
|
0,03
|
-0,005
|
6,423
|
Полученная кривая
является линией заданной степени затухания Ш=
Шзад=0,95 процесса регулирования, что соответствует степени
колебательности m=0.477. Таким образом,
все значения 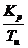 и
Kp,
лежащие на этой кривой, обеспечивают определенную степень затухания (в данном
случае Ш= Шзад=0,95).
и
Kp,
лежащие на этой кривой, обеспечивают определенную степень затухания (в данном
случае Ш= Шзад=0,95).
Значения 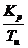 и
Kp,
лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат
процесс регулирования со степенью затухания больше заданного (Ш1> Шзад),
а лежащие вне этой области - со степенью затухания меньше заданной (Ш1<Шзад).
и
Kp,
лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат
процесс регулирования со степенью затухания больше заданного (Ш1> Шзад),
а лежащие вне этой области - со степенью затухания меньше заданной (Ш1<Шзад).
. Определение
оптимальных параметров настройки ПИ - регулятора
Поиск оптимальных
параметров настройки регулятора осуществляется вдоль границы заданного запаса
устойчивости системы регулирования, представленной на рисунке 3, до достижения
экстремума принятого критерия качества. В задании на курсовую работу в качестве
принятого критерия качества указан первый интегральный критерий.
Минимуму первого
интегрального критерия 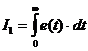 на
графике (рисунок 3) соответствует точка, в которой
на
графике (рисунок 3) соответствует точка, в которой 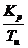 принимает
максимальное значение. Эта точка и определит оптимальные параметры настройки ПИ
- регулятора. Используя данные таблицы 3 и рисунка 3, находим, что этой точке
соответствуют значения:
принимает
максимальное значение. Эта точка и определит оптимальные параметры настройки ПИ
- регулятора. Используя данные таблицы 3 и рисунка 3, находим, что этой точке
соответствуют значения:
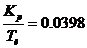 , Kp= 4.182 при щ = 0.02 с-1.
, Kp= 4.182 при щ = 0.02 с-1.
Поэтому оптимальные
параметры настройки ПИ - регулятора имеют значения:
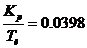 , Kp= 4.182,
, Kp= 4.182, 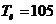 с.
Резонансная частота замкнутой системы
с.
Резонансная частота замкнутой системы
щР = 0.02 с-1.
4. Расчёт, построение и
оценка качества переходных процессов по каналу регулирующего воздействия S-Y
и при возмущении f, идущем по каналу регулирующего воздействия
Переходный процесс по
каналу регулирующего воздействия S-Y
Для одноконтурной
системы регулирования, приведенной на рисунке 1, определим передаточную функцию
замкнутой АСР по каналу S-Y по формуле:
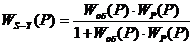 (12)
(12)
где передаточная функция
объекта регулирования
 ,
,
передаточная функция ПИ
- регулятора 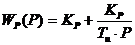 .
.
После подстановки
значения 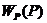 в
формулу (12), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу S-Y:
в
формулу (12), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу S-Y:
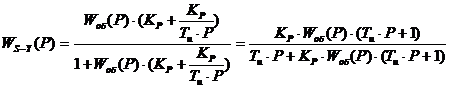 (13)
(13)
Получим выражение для
АФЧХ замкнутой системы путём замены оператора p
в формуле (13) на 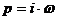 ,
в результате получаем:
,
в результате получаем:
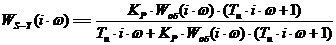 (14)
(14)
Используя математический
пакет MAthCad, предварительно задав диапазон изменения частоты 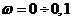 с-1
с шагом
с-1
с шагом 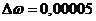 c-1,
рассчитываем вещественную частотную характеристику замкнутой АСР при
регулирующем воздействии: ReЗ.С..1(щ).
Результаты расчёта сведём в таблицу 4.
c-1,
рассчитываем вещественную частотную характеристику замкнутой АСР при
регулирующем воздействии: ReЗ.С..1(щ).
Результаты расчёта сведём в таблицу 4.
Таблица 4 - Результаты
расчёта ВЧХ замкнутой АСР при регулирующем воздействии
|
частота щ, с-1
|
ReЗ.С.1(щ)
|
|
0
|
1
|
|
5*10-5
|
0,9999986
|
|
1*10-4
|
0,9999943
|
|
1.5*10-4
|
0,9999872
|
|
2*10-4
|
0,9999772
|
|
2.5*10-4
|
0,9999644
|
|
3*10-4
|
0,9999488
|
|
3.5*10-4
|
0,9999304
|
|
4*10-4
|
0,9999091
|
|
4.5*10-4
|
0,999885
|
|
5*10-4
|
0,9998581
|
|
5.5*10-4
|
0,9998284
|
|
6*10-4
|
0,9997958
|
|
6.5*10-4
|
0,9997606
|
|
7*10-4
|
0,9997225
|
|
7.5*10-4
|
0,9996817
|
|
8*10-4
|
0,9996381
|
|
8.5*10-4
|
0,9995918
|
|
9*10-4
|
0,9995427
|
|
9.5*10-4
|
0,999491
|
|
1*10-3
|
0,9994365
|
Переходный процесс в замкнутой АСР
по каналу S-Y можно рассчитать по методу трапеций, используя график ВЧХ
замкнутой АСР, приведенный на рисунке 4.
Установлено, что переходная
характеристика какой-либо системы y(t) связана с ВЧХ этой системы Re(щ) выражением:
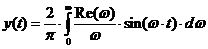 (15)
(15)
где t - время переходного процесса в замкнутой АСР.
Для более точного
расчёта в качестве верхнего предела интеграла для y(t) принимают не 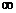 , а значение частоты,
при которой график Re(щ) стремится к
0, т.е. частоту среза щСР. По графику, приведенному на рисунке 4,
определяем, щСР =0,1 с-1. Поэтому переходный процесс в
замкнутой АСР по каналу S-Y можно рассчитать по формуле:
, а значение частоты,
при которой график Re(щ) стремится к
0, т.е. частоту среза щСР. По графику, приведенному на рисунке 4,
определяем, щСР =0,1 с-1. Поэтому переходный процесс в
замкнутой АСР по каналу S-Y можно рассчитать по формуле:
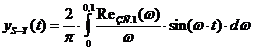 (16)
(16)
Задав диапазон изменения
времени переходного процесса 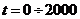 с с шагом
с с шагом 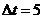 с,
рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты расчета сведём в таблицу 5.
с,
рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты расчета сведём в таблицу 5.
Таблица 5 - Результаты
расчёта переходного процесса в замкнутой АСР по каналу S-Y
|
время t,
с
|
yS-Y(t)
|
|
0
|
0
|
|
5
|
1,492*10-3
|
|
10
|
5,853*10-3
|
|
15
|
0,016
|
|
20
|
0,033
|
|
25
|
0,059
|
|
30
|
0,094
|
|
35
|
0,138
|
|
40
|
0,19
|
|
45
|
0,248
|
|
50
|
0,311
|
|
55
|
0,376
|
|
60
|
0,443
|
|
65
|
0,509
|
|
70
|
0,575
|
|
75
|
0,639
|
|
80
|
0,701
|
|
85
|
0,76
|
|
90
|
0,817
|
|
95
|
0,871
|
|
100
|
0,922
|
|
105
|
0,969
|
Переходный процесс при возмущении f,
идущем по каналу регулирующего воздействия
Для одноконтурной системы
регулирования, приведенной на рисунке 1, определим передаточную функцию
замкнутой АСР по каналу F-Y по формуле:
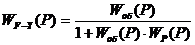 (20)
(20)
После подстановки
выражения для 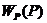 в
формулу (7), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу F-Y:
в
формулу (7), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу F-Y:
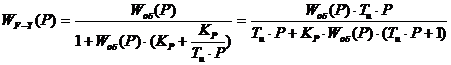 (21)
(21)
Получим выражение для
АФЧХ замкнутой системы путём замены оператора p
в формуле (18) на 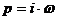 ,
в результате получаем:
,
в результате получаем:
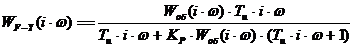 (22)
(22)
Используя математический
пакет MAthCad, предварительно задав диапазон изменения частоты 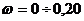 с-1
с шагом
с-1
с шагом 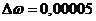 c-,
рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2(щ). Результаты расчёта сведём в таблицу 6.
c-,
рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2(щ). Результаты расчёта сведём в таблицу 6.
Таблица 6 - Результаты
расчёта ВЧХ замкнутой АСР при возмущении f
|
частота щ, с-1
|
ReЗ.С.2(щ)
|
|
0
|
9,756*10-6
|
|
5*10-5
|
3,902*10-5
|
|
1*10-4
|
8,779*10-5
|
|
1.5*10-4
|
1,56*10-5
|
|
2*10-4
|
2,437*10-5
|
|
2.5*10-4
|
3,509*10-5
|
|
3*10-4
|
4,774*10-5
|
|
3.5*10-4
|
6,233*10-5
|
|
4*10-4
|
7,885*10-5
|
|
4.5*10-4
|
9,729*10-5
|
|
5*10-4
|
1,177*10-5
|
|
5.5*10-4
|
1,399*10-5
|
|
6*10-4
|
1,641*10-5
|
|
6.5*10-4
|
1,902*10-5
|
|
7*10-4
|
1,902*10-5
|
|
7.5*10-4
|
2,181*10-5
|
|
8*10-4
|
2,48*10-5
|
|
8.5*10-4
|
2,797*10-5
|
|
9*10-4
|
3,132*10-5
|
|
9.5*10-4
|
3,486*10-5
|
|
1*10-3
|
3,859*10-5
|
Переходный процесс в замкнутой АСР
по каналу F-Y можно рассчитать по методу трапеций, используя график ВЧХ
замкнутой АСР при возмущении f.
Поэтому переходный процесс в
замкнутой АСР по каналу F-Y можно рассчитать по формуле:
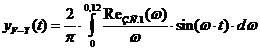 (23)
(23)
Как уже было сказана
выше, для более точного расчёта в качестве верхнего предела интеграла для yF-Y(t) принимают значение частоты среза щСР. По графику,
приведенному на рисунке 6, определяем, что щСР =0,12 с-1.
Задав диапазон изменения
времени переходного процесса 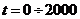 с с шагом
с с шагом 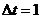 с,
рассчитываем переходный процесс в замкнутой АСР по каналу F-Y. Результаты расчета сведём в таблицу 7, приведенную ниже.
с,
рассчитываем переходный процесс в замкнутой АСР по каналу F-Y. Результаты расчета сведём в таблицу 7, приведенную ниже.
Таблица 7 - Результаты
расчёта переходного процесса в замкнутой АСР по каналу F-Y
|
время t, cyF-Y(t)
|
|
|
0
|
0
|
|
5
|
2,552*10-6
|
|
10
|
7,632*10-4
|
|
15
|
2,927*10-3
|
|
20
|
6,936*10-3
|
|
25
|
0,013
|
|
30
|
0,021
|
|
35
|
0,031
|
|
40
|
0,042
|
|
45
|
0,053
|
|
50
|
0,065
|
|
55
|
0,077
|
|
60
|
0,089
|
|
65
|
0,1
|
|
70
|
0,11
|
|
75
|
0,12
|
|
80
|
0,129
|
|
85
|
0,137
|
|
90
|
0,145
|
|
95
|
0,151
|
|
100
|
0,156
|
|
105
|
0,16
|
По данным таблицы 7 строим график
переходного процесса в замкнутой АСР по каналу F-Y.
Прямые критерии качества:
. Максимальная динамическая ошибка:
А1=0,164;
. Перерегулирование:
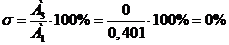 (24)
(24)
где 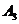 -
первое минимальное отклонение регулируемой величины;
-
первое минимальное отклонение регулируемой величины;
. Динамический
коэффициент регулирования RД:
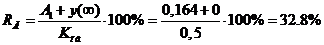 (25)
(25)
где 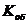 -
коэффициент передачи объекта;
-
коэффициент передачи объекта;
. Степень затухания
переходного процесса:
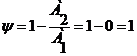 ;
;
. Статическая ошибка:
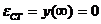 ;
;
. Время регулирования: 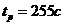 при
величине
при
величине  .
.
Так как в заданной АСР,
представленной на рисунке 2, имеется звено чистого транспортного запаздывания с
передаточной функцией 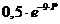 ,
то переходные процессы в этой системе имеет запаздывание на величину 9 с
относительно их начала.
,
то переходные процессы в этой системе имеет запаздывание на величину 9 с
относительно их начала.
Заключение
Определение оптимальных
параметров настройки регуляторов, расчёт различных систем автоматического
регулирования, без сомнения, являются одними из главных задач любого инженера -
конструктора. Использование современных систем регулирования требует знания
различных методов и приёмов расчёта этих систем, определения и установки
требуемых параметров настройки регулятора, основных недостатков и преимуществ
разного рода регуляторов по сравнению друг с другом.
В процессе написания
курсовой работы был изучен один из двух инженерных методов расчёта
одноконтурных систем регулирования: корневой метод (с использованием РАФЧХ).
Было выяснено, что оптимальными параметрами настройки какого-либо регулятора
считают те параметры, при которых обеспечивается близкий к оптимальному процесс
регулирования. Под оптимальным процессом регулирования обычно понимают процесс,
удовлетворяющий требованиям к запасу устойчивости системы. Автор установил, что
поиск оптимальных параметров настройки осуществляется вдоль границы заданного
запаса устойчивости системы регулирования до достижения экстремума принятого
критерия качества. В данной курсовой работе, согласно заданию, в качестве
принятого критерия качества был принят первый интегральный критерий.
В результате проделанной
работы, были получены переходные процессы по каналам S-Y и F-Y. Оценка качества этих процессов показала, что они удовлетворяют
требованиям к запасу устойчивости системы, приведенных в исходных данных.
Можно заметить, что
переходный процесс по каналу F-Y имеет прямые критерии качества лучше, чем переходный процесс по
каналу S-Y:
максимальная
динамическая ошибка: для S-Y А1=0,207, для F-Y А1=0,164;
перерегулирование: для S-Y 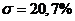 ,
для F-Y
,
для F-Y 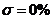 ;
;
степень затухания
переходного процесса: для S-Y 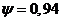 ,
для F-Y
,
для F-Y 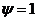 ;
;
время регулирования: для
S-Y 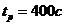 ,
для F-Y
,
для F-Y 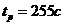 ;
;
статическая ошибка для
этих процессов равна: 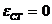 .
.
После написания курсовой
работы становится понятно, для каких целей выполняются расчёты систем
автоматического регулирования, как производится синтез различных АСР путём
замены регуляторов или изменением параметров их настройки.
Список используемой
литературы
1. Андык В.С. Теория
автоматического управления. Учебное пособие к практическим занятиям. - Томск:
Изд. ТПУ, 2005. - 108 с.
2. Стефани Е.Г. Основы
расчета настройки регуляторов теплоэнергетических процессов. - М.: ГЭИ, 1960. -
395 с.
. Ротач В.Я.
Расчет настройки промышленных систем регулирования. - М.: ГЭИ 1961. - 344 с.