Случайные физические поля и их спектральное представление

Случайные физические поля и их спектральное представление

Санкт-Петербургский государственный морской технический университет

Реферат

по дисциплине:

Многомерный анализ обработки сигналов МИИС

Тема:

Случайные физические поля и их спектральное представление

Выполнил: Шабалин К.В.

Студент 5-го курса ВЗФ (ЗО)

Специальность 180304

Санкт-Петербург - 2013 г.

Введение

В морской подводной информационной технике в качестве носителей информации широко используются различные физические поля. Многие из них по ряду причин имеют случайный характер, причем не только поля, образующие помеховый фон, но и поля-сигналы, несущие полезную информацию. По этой причине специалист-разработчик подводной информационной техники вынужден владеть методами математического анализа случайных физических полей и математического моделирования их статистических характеристик.

В структуре любого технического устройства, получающего информацию посредством физического поля, присутствует приемная антенна как преобразователь поля в электрический процесс. В антенне происходит изменение не только физической природы носителя информации, но и его структуры. Вместо поля, функции четырех переменных, им становится процесс - одномерная функция времени. Кроме того, антенна выполняет роль фильтрующего звена, выделяющего сигнал на фоне помехи. Очевидно, что специалист должен владеть методами анализа указанных преобразований и уметь оценивать изменения статических характеристик поля в выходном сигнале антенны.

Пространственная дискретизация полей, происходящая при использовании приемных антенных решеток, и временная дискретизация процессов при их цифровой обработке приводят к необходимости владеть методами математического анализа дискретных выборок из случайных полей и процессов. В основе такого анализа лежит представление выборки в виде одностолбцовой матрицы-вектора, а также использование методов матричной алгебры для получения и анализа статистических характеристик случайных матриц-векторов.

Перечисленные направления подготовки специалистов по подводной информационной технике определили назначение и содержание настоящего учебного пособия. При этом изложение методов анализа случайных полей и дискретных выборок из них, а также преобразований полей приемными антеннами ограничено в пособии рамками корреляционной теории, где рассматриваются только моментные характеристики случайных функций, причем не выше второго порядка. Эти характеристики полностью определяют статистические свойства нормальных случайных полей и выборок из них, а также являются наиболее информативными в полях и процессах, отличных от нормальных.

1. Спектральное представление стационарно-однородных случайных полей

Математическое описание физических процессов и полей функциями времени и пространственных координат во многих случаях оказывается более удобным для анализа и наглядным для понимания, если используется спектральное представление (разложение) сложных функций, т.е. их представление в виде суммы функций элементарных или базовых. Спектральное представление позволяет применять принцип суперпозиции в анализе процессов и полей, а также в анализе их преобразований линейными звеньями информационных систем.

Гармоническим спектральным представлением детерминированной функции времени называют её представление в виде суммы детерминированных временных гармоник. Многомерная функция времени и пространства, описывающая детерминированное физическое поле, также представима суммой детерминированных гармоник, но уже многомерных, пространственно-временных.

Такой же смысл имеет гармоническое спектральное представление случайных функций времени и пространства, описывающих случайные процессы и поля. При этом в качестве элементарных используются случайные временные и пространственно-временные гармоники.

Гармоническое спектральное представление особенно полезно применительно к стационарным процессам и стационарно-однородным полям ввиду того, что случайные гармоники при этом оказываются некоррелированными между собой слагаемыми. Взаимная некоррелированность суммируемых гармоник позволяет распространить принцип суперпозиции на энергетические и корреляционные характеристики стационарно-однородных полей. Обоснованием такой возможности является теорема Винера-Хинчина.

В этой статье показано, как получают формулы гармонического спектрального представления случайных полей и процессов, какой вид имеют эти формулы, какой физический смысл они в себе несут. Для лучшего понимания техники и смысла указанных процедур рассмотрим их первоначально на примере детерминированных процессов и полей.

.1 Одномерные и многомерные гармонические функции

Гармоническая функция времени, периодическая функция одной переменной t, представленная в вещественной тригонометрической форме

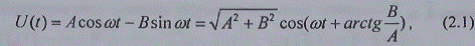
характеризуется известными параметрами:

круговой временной частотной 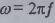 или линейной частотой f;

амплитудами квадратурных составляющих А и В или амплиту¬дой гармоники ;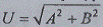

начальной фазой 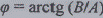гармоники;

временным периодом гармоники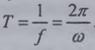

Аналогичную структуру и параметры имеет формула пространственной гармонической функции - периодической функции расстояния вдоль прямой линии. Например, гармоническая функция расстояния вдоль оси х имеет вид:

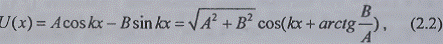
где к - круговая пространственная частота, связанная с пространственным периодом λ соотношением

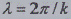
Такие же функции расстояния можно определить вдоль осей у и z:

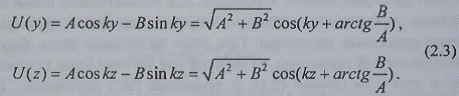
Трехмерная пространственная гармоника описывается формулой

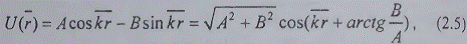
Пространственные гармоники (2.5) используются при спектральном представлении статических полей, описываемых функциями только пространственных координат. Для динамических полей необходимы гармонические функции четырех переменных, пространственно-временные гармоники. При этом желательна такая формула четырехмерной гармоники, из которой как частные виды получались бы и пространственная (2.5), и временная (2.1) гармоники. Такая функция может быть определена в четырехмерном пространстве- времени, если в нем ввести ортогональную пространственно- временную систему

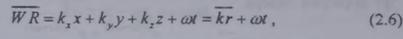
В гармоническом спектральном анализе широко используется комплексная экспоненциальная форма представления гармонических функций. Переход от тригонометрической формы к экспоненциальной выполняется при помощи формул Эйлера. Например, для временной гармоники (2.1) используют формулы

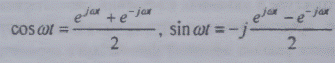
Пространственная и пространственно-временная гармоники также записываются в экспоненциальной комплексной форме. Используя формулы Эйлера

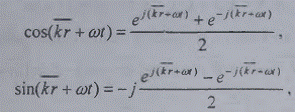
1.2 Свойства поля, описываемого пространственно-временной гармоникой

Представление функции, описывающей физическое поле, суммой пространственно-временных гармоник, с физической точки зрения эквивалентно представлению самого физического поля суперпозицией (наложением в пространстве и времени) элементарных полей, описываемых этими гармониками. В связи с этим полезно иметь ясное представление о структуре и динамике изменения элементарного поля.

Наглядное представление о пространственной структуре поля дают поверхности равных значений физического параметра U, характеризующего поле. В гармоническом поле поверхность равных значений - это поверхность равной фазы.

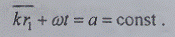
Плоские равнофазовые поверхности поля движутся с той же скоростью, но в направлении, совпадающем с направлением вектора пространственной частоты. Поле с периодической структурой, описываемое функцией

,

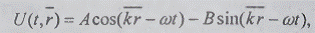называется волновым, поверхности равной фазы в нем - фронтами волн, а скорость Уф - фазовой скоростью волн. Таким образом, формулы

,

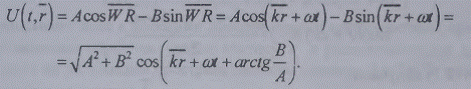
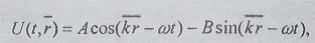
описывают поле бегущей плоской гармонической волны, причем в форме (2.16) движение волны имеет направление, совпадающее с направлением вектора пространственной частоты к.

Ввиду особой информативности вектора к относительно свойств поля плоской бегущей гармонической волны он получил название «волновой вектор». Это название мы чаще всего будем использовать в дальнейшем.

.3 Спектральное представление детерминированных полей

По аналогии с процессами, которые могут обладать либо дискретным, либо сплошным частотным спектром, поле так же может быть с дискретным или сплошным пространственно-частотным спектром. В теории волновых полей используется термин «частотно-волновой спектр» поля как синоним спектра пространственно-частотного. Такое название спектра созвучно с названием «волновой вектор

Итак, поле с дискретным частотно-волновым спектром - это поле, образованное суперпозицией конечного числа полей бегущих гармонических плоских волн разных временных и пространственных частот. Математически такое поле описывается конечной суммой пространственно-временных гармоник разных частот и амплитуд и начальных фаз (комплексных амплитуд)

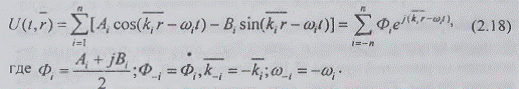
Волновой вектор к можно менять по величине и направлению, внося изменения в любую из его составляющих, поэтому в сумме (2.18) возможна более детальная структуризация, учитывающая изменения отдельных составляющих вектора к

Процесс со сплошным частотным спектром представляют в виде предела суммы бесконечно большого числа гармоник бесконечно малых амплитуд, частоты которых непрерывно заполняют некоторый интервал на частотной оси. Предел такой суммы называется интегралом Фурье. Он и является математической формой спектрального представления процесса со сплошным частотным спектром, то есть имеет место соотношение:

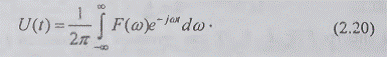
Другая функция одной переменной - функция расстояния вдоль оси х, имеющая сплошной пространственный спектр, представима таким же однократным интегралом Фурье, но по переменной кх - по пространственной частоте

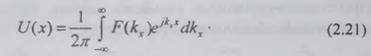
Спектральное представление произвольного поля U (х, у, z, t) как функции четырех переменных может быть получено предельным переходом от конечной суммы (2.19) к бесконечной, т.е. к кратному интегралу Фурье. Однако этот путь громоздок и менее нагляден по сравнению с формальным методом, используемым в спектральной теории полей. Он заключается в последовательном применении однократного интегрального преобразования Фурье к функции U(x,y,z,t) и ее промежуточным (параметрическим) спектрам

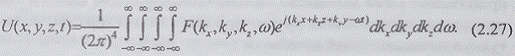
Кратный интеграл Фурье (2.27) является математической формой спектрального представления детерминированного поля U(x,y,z,t) со сплошным частотно-волновым спектром. Этот спектр описывается функцией F(kx,ky,kz,ω) которая определяет амплитуду и начальную фазу пространственно-временной гармоники с любым сочетанием четырех составляющих частот.

Компактный вид громоздкой формулы (2.27) достигается бескоординатной векторной формой записи

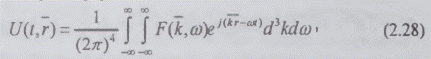
Физический смысл спектрального представления детерминированного физического поля кратным интегралом Фурье (2.28) очевиден: поле U(t,r) произвольного вида представлено в виде суперпозиции бесконечного числа полей бегущих гармонических плоских волн всех временных и пространственных частот.

Из общих свойств интеграла Фурье следует, что при наличии интегрального преобразования (2.28) существует преобразование, обратное ему. Следовательно, частотно-волновой спектр 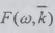поля U(t,r) определяется соотношением

где 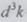 - элемент объема, выраженный через составляющие вектора г .

1.4 Случайные гармонические функции

При гармоническом спектральном представлении случайных функций в качестве элементарных используют случайные гармоники. Случайная гармоника - это функция, ансамбль реализаций которой представляет собой множество гармонических функций одной и той же частоты, отличающихся друг от друга случайным образом амплитудой и начальной фазой колебаний.

Математическая формула, описывающая случайную гармоническую функцию времени, имеет вид, аналогичный формуле (2.1) для гармоники детерминированной:

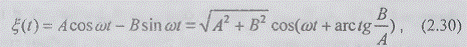
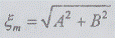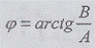однако в этой формуле амплитудные множители А и В - случайные величины. При этом условии формула (2.30) полностью соответствует определению случайной гармоники, так как её амплитуда и начальная фаза  являются случайными величинами, меняющимися от реализации к реализации случайным образом. Заметим, что случайные амплитудные множители А, В, не зависят от времени и координат пространства. Это позволяет с помощью указанных функций описывать стационарные случайные процессы и стационарно-однородные случайные поля. Правда, случайные величины А и В должны для этого обладать дополнительными статистическими свойствами

1.5 Спектральное представление случайного процесса со сплошным частотным спектром

Рассмотрим первоначально вопрос о спектральном представлении случайной функции со сплошным спектром на примере функции одной переменной - случайного процесса £(/). Получим математическую форму такого представления предельным переходом от процесса с дискретным частотным спектром. С этой целью создадим удобную математическую конструкцию, позволяющую наглядно уплотнять на частотной оси гармоники разных частот и искать предел их суммы.

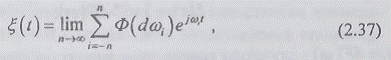
Предельное соотношение (2.37) носит название интеграла Фурье-Стилтьеса.

Более удобной для анализа и для сопоставления с привычным нам интегралом Фурье-Римана является форма записи интеграла Фурье-Стилтьеса, когда суммирование ведется по частотам 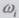, а не по номерам частотных интервалов. Чтобы перейти в (2.37) к суммированию по частотам, введем суммарную комплексную амплитуду гармоник, принадлежащих интервалам 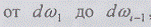, как функцию верхней граничной частоты 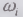 последнего в сумме интервала .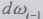

Предел (2.37) как предел суммы приращений функции 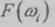на частотах со .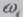

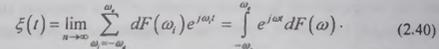
Процедура предельного перехода не изменится с увеличением верхней граничной частоты, в том числе при 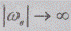, поэтому спектральное представление случайного процесса пределом бесконечной суммы случайных гармоник всех частот или интегралом Фурье- Стилтьеса принимает окончательный вид

где 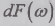- случайная комплексная амплитуда гармоники частотой .

Заметим, что интеграл Стилтьеса (2.41) переходит в интеграл Римана, если функция 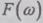 дифференцируема, т.е. имеет в каждой точке производную :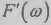

В этом случае между функциями 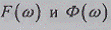имеет место соотношение спектральный частотный случайный поле

поэтому 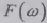можно назвать интегральным спектром функции .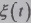

В теории случайных функций доказывается, что функция, значения которой получены суммированием большого числа взаимно некоррелированных случайных величин, недифференцируема. В нашем случае функция частоты 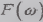получается суммированием большого числа случайных амплитуд, и эти амплитуды оказываются взаимно некоррелированными, если формируемый суммированием гармоник случайный процесс стационарен.

Из всего этого следует, что интеграл Фурье-Римана не может быть использован для спектрального представления стационарного случайного процесса ввиду недифференцируемости функци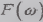и  Интеграл Стилтьеса как сумма приращений любой функции, в том числе недифференцируемой, оказывается единственно применимой интегральной формой спектрального представления стационарных случайных функций.

Этот вывод справедлив и для однородных, и для стационарно-однородных случайных полей, так как однородность - это стационарность применительно к функциям пространственных координат. Стационарные и стационарно-однородные модели полей широко используются в прикладном анализе, поэтому будем в дальнейшем использовать для спектрального представления случайных функций ин¬тегралы Фурье-Стильтьеса вида (2.41).

.6 Спектральное представление случайного поля со сплошным частотно-волновым спектром

Интегральная форма спектрального представления случайного поля 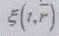может быть получена таким же формализованным методом, какой был использован при спектральном представлении детерминированного поля. Только теперь придется использовать цепочку интегральных преобразований Фурье-Стилтьеса.

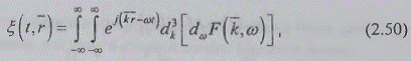
где 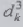 - обозначение приращения функции по трем составляющим вектора .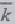

Кратный интеграл Фурье-Стилтьеса (2.50) называется стохастическим (случайным) и является математической формой спектрального представления случайного поля со сплошным частотно-волновым спектром. Подынтегральная функция 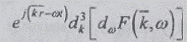 описывает случайное поле бегущей плоской гармонической волны с детерминированной текущей фазой 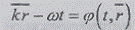и случайной амплитудой 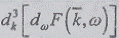 При этом случайная амплитуда волны представлена в виде приращения многомерной функции 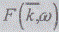по всем переменным.

Физическая трактовка равенства (2.50) такая же, как и в случае детерминированного поля: случайное поле 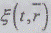произвольного вида представлено в виде суперпозиции полей случайных гармонических бегущих плоских волн всех временных и пространственных частот.

1.7 Условия стационарности случайного процесса, представленного в спектральной форме. Спектр мощности стационарного процесса

Спектральное представление случайного процесса стохастическим интегралом Фурье-Стилтьеса (2.41) позволяет получить формулу спектрального представления моментных характеристик процесса, что более важно для практических приложений. Эти формулы оказываются наиболее простыми, если случайный процесс стационарен.

Признаки стационарности случайного процесса в рамках корреляционной теории такие же, как и для стационарного случайного поля (параграф 1.4), т.е. математическое ожидание и дисперсия процесса не зависят от времени:

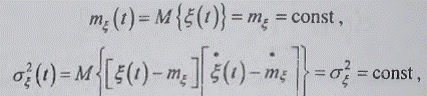
А автокорреляция зависит только от разности времен отсчета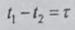

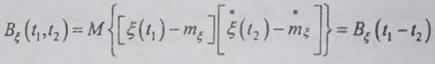
формула спектрального представления дисперсии стационарного случайного процесса (2.41) интегралом Римана:

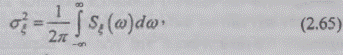
где 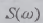 по размерности и физическому смыслу является частотной плотностью дисперсии и называется «частотной плотностью мощности», или «частотным спектром мощности» стационарного случайного процесса , представленного интегралом Фурье-Стильтьеса (2.41).

Заметим, что значение 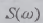- это дисперсия амплитуды случайной гармоники частотой 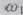 - одного из «кирпичиков», образующих процесс . Мы выяснили, что гармоники разных частот в стационарном процессе взаимно не коррелированы. Тогда выражение (2.64) является математической формулировкой следствия из теоремы о корреляции суммы взаимно некоррелированных функций, а именно: дисперсия суммы некореллированных гармоник равна сумме дисперсий слагаемых.

Спектр 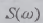 - четная функция частоты (см. задачу 2.10), поэтому

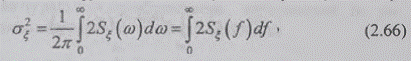
где использована функция линейной частоты, измеряемой в герцах.

формула для расчета величины дисперсии стационарного процесса, если известен его односторонний частотный спектр мощности.

1.8 Автокорреляция стационарного процесса

Теорема Винера-Хинчина

Как выяснилось в предыдущем параграфе, вторым условием стационарности случайного процесса является взаимная некоррелированность случайных амплитуд гармоник, на которые раскладывается процесс

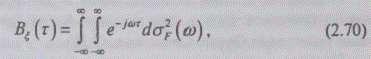
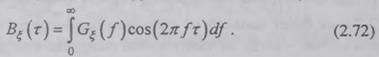
Представление автокорреляции 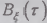интегралом Фурье-Римана

Cпектр мощности

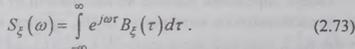
Сочетание двух интегральных формул, (2.70) и (2.72), является содержанием теоремы Винераг-Хинчина, которая формулируется следующим образом: «Автокорреляция и спектр мощности стационарного случайного процесса связаны между собой парой интегральных преобразований Фурье».

1.9 Пространственно-временная корреляция и частотно-волновой спектр мощности стационарно-однородного случайного поля. Обобщенная теорема Винера-Хинчина

Приращение функц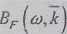ии через производную или частотную плотность дисперсии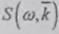

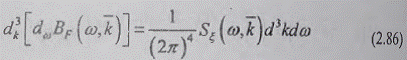
Интегральная формула для ПВК стационарно-однородного поля

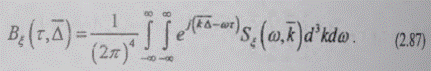
Два интегральных соотношения, (2.86) и (2.87), составляют содержание обобщенной теории Винера-Хинчина, которая формулируется следующим образом: «Пространственно-временная корреляция и частотно-волновой спектр мощности стационарно-однородного случайного поля связаны парой кратных интегральных преобразований Фурье».

1.10 Соотношения между характеристиками стационарно-однородного ноля

Теорема Винера-Хинчина устанавливает соотношение между двумя наиболее полными, наиболее информативными характеристиками стационарно-однородного случайного поля: между пространственно-временной корреляцией (ПВК) и частотно-волновым спектром (ЧВС). Эти характеристики являются функциями наибольшего числа переменных.

Кроме ПВК и ЧВС в анализе полей используются корреляционные и спектральные характеристики меньшего числа переменных. Прежде всего это пространственная и временная корреляции.

Пространственная корреляция (ПК) поля - это среднее по ансамблю реализаций произведение значений поля, наблюдаемых в двух точках пространства в один и тот же момент времени:

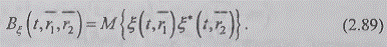
В общем случае ПК зависит от времени, но в стационарно-однородном поле она оказывается зависящей только от разности координат 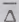. При этом формула ПК получается из формулы ПВК методом совмещения временных координат. При совмещении моментов времени их разность 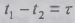равна нулю. Полагая в формуле ПВК (2.86) 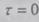, получаем интегральное выражение для расчета ПК

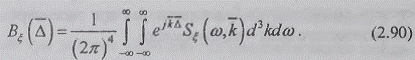
Аналогично, методом совмещения пространственных координат, т.е. при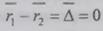, получаем из (2.86) интегральное выражение для временной корреляции (ВК) стационарно-однородного поля

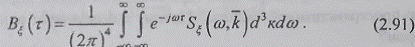
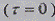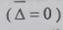Заметим, что одновременным совмещением временных  и пространственных  координат из формулы ПВК получают формулу дисперсии поля (2.80), т.е. имеет место равенство

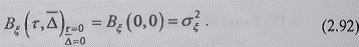
Частотный спектр мощности (ЧС) стационарно-однородного поля связан с ЧВС интегральным соотношением

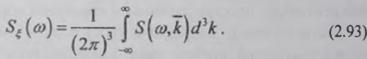
Пространственный спектр получается из ЧВС согласно равенству

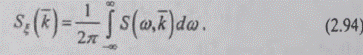
2. Дополнительные вопросы

2.1    Дайте определение случайной гармонической функции

При гармоническом спектральном представлении случайных функций в качестве элементарных используют случайные гармоники. Случайная гармоника - это функция, ансамбль реализаций которой представляет собой множество гармонических функций одной и той же частоты, отличающихся друг от друга случайным образом амплитудой и начальной фазой колебаний.

Математическая формула, описывающая случайную гармоническую функцию времени, имеет вид, аналогичный формуле (2.1) для гармоники детерминированной:

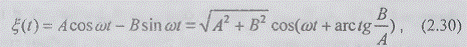
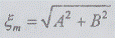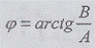однако в этой формуле амплитудные множители А и В - случайные величины. При этом условии формула (2.30) полностью соответствует определению случайной гармоники, так как её амплитуда и начальная фаза  являются случайными величинами, меняющимися от реализации к реализации случайным образом. Заметим, что случайные амплитудные множители А, В, не зависят от времени и координат пространства. Это позволяет с помощью указанных функций описывать стационарные случайные процессы и стационарно-однородные случайные поля. Правда, случайные величины А и В должны для этого обладать дополнительными статистическими свойствами

2.2 В чем различие интегральных форм спектрального представления детерминированного и случайного полей со сплошным частотно-волновым спектром?

Интегральная форма спектрального представления случайного поля 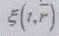может быть получена таким же формализованным методом, какой был использован при спектральном представлении детерминированного поля. Только теперь придется использовать цепочку интегральных преобразований Фурье-Стилтьеса.

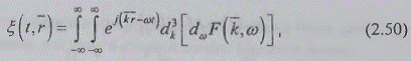
где 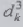 - обозначение приращения функции по трем составляющим вектора .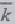

Кратный интеграл Фурье-Стилтьеса (2.50) называется стохастическим (случайным) и является математической формой спектрального представления случайного поля со сплошным частотно-волновым спектром. Подынтегральная функция 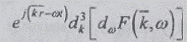 описывает случайное поле бегущей плоской гармонической волны с детерминированной текущей фазой 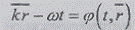и случайной амплитудой 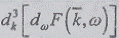 При этом случайная амплитуда волны представлена в виде приращения многомерной функции 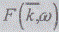по всем переменным.

Физическая трактовка равенства (2.50) такая же, как и в случае детерминированного поля: случайное поле 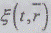произвольного вида представлено в виде суперпозиции полей случайных гармонических бегущих плоских волн всех временных и пространственных частот.

2.3 При каких условиях случайное поле, образованное суперпозицией полей случайных гармонических плоских волн, будет стационарно-однородным?

Стационарно-однородным называют случайное поле, математическое ожидание и дисперсия которого не зависят от времени и координаты пространства (постоянные величины), а пространственно-временная корреляция зависит только от разности моментов времени и разностного координатного вектора точек отсчета поля. В таком поле имеют место соотношения:

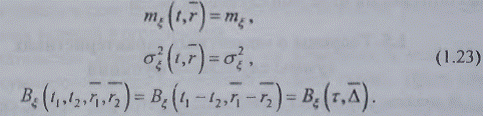
2.4 Сформулируйте обобщенную теорему Винера-Хинчина относительно корреляционной и спектральной характеристик стационарно-однородного случайного поля

Приращение функц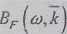ии через производную или частотную плотность дисперсии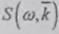

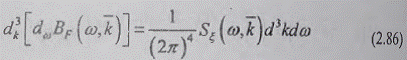
Интегральная формула для пространственно-временной корреляции стационарно-однородного поля

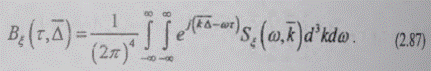
Два интегральных соотношения, (2.86) и (2.87), составляют содержание обобщенной теории Винера-Хинчина, которая формулируется следующим образом: «Пространственно-временная корреляция и частотно-волновой спектр мощности стационарно-однородного случайного поля связаны парой кратных интегральных преобразований I Фурье»

2.5 Перечислите основные корреляционные и спектральные характеристики стационарно-однородного случайного поля

Теорема Винера-Хинчина устанавливает соотношение между двумя наиболее полными, наиболее информативными характеристиками стационарно-однородного случайного поля: между пространственно-временной корреляцией (ПВК) и частотно-волновым спектром (ЧВС).