|
Параметры
|
Номер варианта
|
|
3
|
|
Длительность импульса tи1,
мс
|
3
|
|
Длительность импульса tи2,
мс
|
5
|
|
Период следования импульсов Тс, мс
|
15
|
|
Амплитуда импульсов Um,
B
|
5
|
1. Информацией называют любые сведения, являющиеся объектом
следующих операций: передачи, распределения, преобразования, хранения или
непосредственного использования. Следует заметить, что информацией являются
только новые для получателя сведения.
Форма представления информации
называется сообщением.
Передача сообщений сводится к их
переносу в пространстве на различные расстояния. Переносчиком сообщения может
быть какой-либо физический процесс, способный распространяться с определенной
скоростью от отправителя к получателю. Чтобы такой физический процесс стал
переносчиком сообщения, необходимо обеспечить изменение какого-либо его
параметра (тока, напряжения, напряженности поля) в соответствии с изменением
информационного параметра сообщения. Такой физический процесс называется электрическим
сигналом. Иначе, электрическим сигналом или просто сигналом
можно назвать электрическое колебание, содержащее сообщение.
По физической природе носителя
информации сигналы подразделяются на электрические, электромагнитные,
оптические и акустические.
По способу задания сигнала:
регулярные (детерминированные),
заданные аналитической функцией;
нерегулярные (случайные),
принимающие произвольные значения в любой момент времени.
В зависимости от функции,
описывающей параметры сигнала, выделяют аналоговые, дискретные, квантованные и
цифровые сигналы:
непрерывные (аналоговые),
описываемые непрерывной функцией;
дискретные, описываемые функцией
отсчётов, взятых в определённые моменты времени;
квантованные по уровню;
дискретные сигналы, квантованные по
уровню (цифровые).
Разнообразие форм представления
сообщений, подлежащих
передаче, привела к независимому
развитию нескольких видов
электросвязи. Каждый вид
электросвязи ориентирован на
передачу вполне определенных
сообщений:
. Телефонная связь - передача речи;
. Телеграфная связь - передача
буквенно-цифровых текстов;
3. Телевизионная связь - передача
движущегося изображения;
. Звуковое вещание - передача
звуковых программ;
. Факсимильная связь - передача
неподвижных изображений;
. Передача данных - передача
сообщений между ЭВМ.
2. Временные диаграммы периодических сигналов (рис. 1) прямоугольной
формы с параметрами, заданными в таблице 1 (рис. 1.1).

Рис. 1.1 - Временные
диаграммы периодических сигналов
Для определения
спектрального состава и построения спектральных диаграмм для заданных сигналов
необходимо рассчитать амплитуды постоянной составляющей и каждой спектральной
составляющей.
Постоянная
составляющая спектра определяется по формуле:
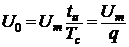
и представляет собой
среднее значение сигнала за период.
Частотный интервал между
гармониками спектра равен
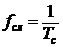 ,
,
т.е. частоте первой
гармоники.
Номер гармоники, на
которой амплитуда спектра первый раз обращается в нуль K0,
определяется из выражения:
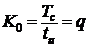 ,
,
а частота: 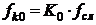
Так как за ширину
спектра принят интервал частот, содержащий 95% энергии сигнала, то ширина
спектра периодической последовательности прямоугольных импульсов
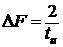 , где tu - длительность импульса.
, где tu - длительность импульса.
Для расчета
амплитуды каждой спектральной составляющей воспользуемся формулой:
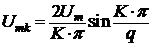 ,
,
где Um - амплитуда
импульса,
К - номер гармоники,
q - скважность периодической последовательности прямоугольных
импульсов,
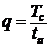 .
.
Все рассчитанные
значения сведены в таблицу 1.1
Таблица 1.1 - Рассчитанные значения
|
Дано:
|
Um = 5В, Тс = 15 мс, tи1
= 3 мс, tи2
= 5 мс
|
|
Расчитанные значения:
|
|
для tи1
= 3 мс
|
для tи2
= 5 мс
|
|
U0 = 1 В
|
U0 = 1,67 В
|
fсл
= 66,7 Гц
|
|
K0 = q = 5
|
K0 = q = 3
|
|
fk0 = 333,5
Гц
|
fk0 = 200 Гц
|
|
ΔF = 667 Гц
|
ΔF = 400 Гц
|
|
K = 1
|
1,87
В
|
K = 1
|
2,76 В
|
|
K = 2
|
1,51 В
|
K = 2
|
2,38 В
|
|
K = 3
|
1,01 В
|
K = 3
|
0
|
|
K = 4
|
0,468 В
|
K = 4
|
-0,689 В
|
|
K = 5
|
0
|
K = 5
|
-0,552 В
|
|
K = 6
|
-0,312 В
|
K = 6
|
0
|
|
K = 7
|
-0,433 В
|
K = 7
|
0,394 В
|
|
K = 8
|
-0,378 В
|
K = 8
|
0,345 В
|
|
K = 9
|
-0,208 В
|
K = 9
|
0
|
|
K = 10
|
0
|
|
|
|
K = 11
|
0,17 В
|
|
|
|
K = 12
|
0,252 В
|
|
|
|
K = 13
|
0,233 В
|
|
|
|
K = 14
|
0,134 В
|
|
|
|
K = 15
|
0
|
|
|
На основании полученных результатов
строим спектральные диаграммы заданных сигналов (рис. 1.2).

Рис. 1.2 - Спектральные диаграммы
заданных сигналов
3. Из приведенного расчета видно, что чем больше скважность
прямоугольного сигнала, тем меньше абсолютное значение имеет амплитуда
напряжения первой гармоники, но тем медленнее уменьшаются амплитуды
гармонических составляющих, т.е. тем равномернее становится спектр.
Для амплитудного спектра сигнала
можно указать огибающую, изображенную на рис. 1.2 штриховой линией. Огибающая
спектра амплитуд имеет много лепестков. Первый из них занимает интервал частот
от f = 0 до
f = fk0, второй - от f = fk0 до f = 2fk0 и т.д. Как видно из расчетов (таблица 1.1), ширина каждого
лепестка равна fk0 и определяется только
длительностью импульса. Если ширину лепестка разделить на интервал fсл между соседними спектральными линиями, то получим fk0/ fсл = K0 = Tc/tи = q, т.е. каждый лепесток огибающей
спектра содержит q спектральных линий. В свою очередь q по определению - скважность
импульса. Следовательно, вид спектра периодической последовательности
прямоугольных импульсов существенно зависит от скважности импульсов и,
соответственно, от длительности импульса tи.
Интервал между любыми соседними
спектральными линиями определяется только частотой следования импульсов и равен
fсл. Число спекральных линий в одном лепестке огибающей равно q. Спектральные линии находятся на
одинаковом расстоянии друг от друга, т.е. частоты гармоник находятся в кратных
отношениях. Такие спектры называют гармоническими. Отдельные гармоники спектра
могут отсутствовать, т.е. их амплитуды могут равняться нулю, но это не нарушает
гармоничности спектра.
Задача
2.
1. Сформулируйте
теорему В.А. Котельникова и поясните её использование для получения ИКМ
сигнала.
2. По заданным на
рисунке 2 и в таблице 2 параметрам непрерывного сигнала U(t) определите:
·интервал
дискретизации (Dt) и частоту дискретизации (fд),
·число
уровней квантования (Мкв),
·квантованные
значения дискретных отсчетов непрерывного сигнала Uкв(t) для десяти отсчетов Dt по оси времени,
·величину
ошибки квантования x(t),
·число
разрядов (п) в кодовой комбинации при кодировании двоичным кодом уровней
квантования Мкв,
·кодовые
комбинации уровней квантования дискретных отсчетов.
Таблица 2 -
Исходные данные
|
Номер варианта
|
Спектр сигнала Fmin
÷ Fmax, кГц
|
Шаг квантования DU,
мВ
|
|
3
|
0,05 - 6,3
|
2,50
|
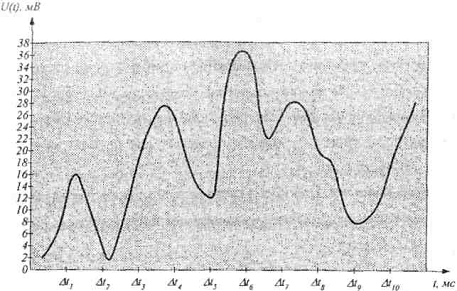
Рис. 2 - Временная
характеристика непрерывного сигнала
1. Сформулируйте теорему В.А. Котельникова и поясните её
использование для получения ИКМ сигнала.
Теорема В.А. Котельникова
формулируется следующим образом: если непрерывный сигнал u(t) имеет ограниченный спектр и наивысшая частота в спектре меньше,
чем fв герц, то сигнал u(t) полностью определяется последовательностью своих мгновенных
значений в дискретные моменты времени, отстоящие друг от друга не более чем на
1/(2fв) секунд.
Если интервал
дискретизации 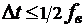 ,
то в теореме утверждается, что по значениям
,
то в теореме утверждается, что по значениям 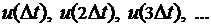 , можно определить
точное значение сигнала u(t), для любого заданного момента времени t,
находящегося между моментами отсчета. В соответствии с этой теоремой сигнал с
ограниченным спектром и верхней частотой fв
можно разложить в ряд с частотой дискретизации fд,
где
, можно определить
точное значение сигнала u(t), для любого заданного момента времени t,
находящегося между моментами отсчета. В соответствии с этой теоремой сигнал с
ограниченным спектром и верхней частотой fв
можно разложить в ряд с частотой дискретизации fд,
где 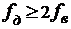 .
Для вычисления значения сигнала u(t) в момент времени t
необходимо знать значения всех отсчетов u(nΔt), как до, так и
после указанного момента t.
Если ограничиться конечным числом отсчетов, то будет получено лишь приближенное
значение сигнала u(t).
.
Для вычисления значения сигнала u(t) в момент времени t
необходимо знать значения всех отсчетов u(nΔt), как до, так и
после указанного момента t.
Если ограничиться конечным числом отсчетов, то будет получено лишь приближенное
значение сигнала u(t).
Другими словами период
дискретизации должен хотя бы в два раза меньше периода наивысшей частотной
составляющей спектра непрерывного сигнала, т.е. на каждый период наивысшей
частотной составляющей должно приходиться по крайней мере два отсчёта
(выборки). Таким образом, частота следования отсчётов должна по крайней мере в
два раза превышать наивысшую частоту в спектре непрерывного сигнала. Полученный
дискретный сигнал может быть передан по каким-либо линиям связи и из него
фильтром нижних частот на стороне приёмника может быть однозначно восстановлен
исходный аналоговый сигнал.
Таким образом, теорема
Котельникова указывает условия, при которых непрерывный сигнал может быть точно
восстановлен по соответствующему ему сигналу с дискретным временем. Реальные
непрерывные сигналы, подлежащие передаче, как правило, имеют спектры хотя и
довольно быстро стремящиеся к нулю с ростом частоты, но все же неограниченные.
Такие сигналы могут быть восстановлены по своим дискретным отсчетам лишь
приближенно. Однако, выбирая шаг дискретизации Δt
достаточно малый, можно обеспечить пренебрежимо малое значение ошибки
восстановления непрерывного сигнала по его переданным отсчетам в дискретные
моменты времени. Например, при передаче телефонного сигнала, спектр которого
неограничен, обычно принимают, что условная верхняя граничная частота fв
= 3,4 кГц. В этом случае получаем, что частота дискретизации должна
удовлетворять неравенству fд
≥ 6,8 кГц, т.е. в одну секунду должно передаваться 6,8 тысяч отсчетов.
Качество передачи речи при этом оказывается вполне удовлетворительным.
Увеличение частоты дискретизации сверх указанного значения допустимо и приводит
к незначительному повышению точности восстановления телефонного сигнала. Если
же принять fд
< 6,8 кГц, то точность восстановления телефонного сигнала заметно падает и,
соответственно, резко снижается качество принятого сигнала.
2. По заданным на рисунке 2 и в таблице 2 параметрам непрерывного
сигнала U(t) определите:
·интервал
дискретизации (Dt) и частоту дискретизации (fд),
·число
уровней квантования (Мкв),
·квантованные
значения дискретных отсчетов непрерывного сигнала Uкв(t) для десяти отсчетов Dt по оси времени,
·величину
ошибки квантования x(t),
·число
разрядов (п) в кодовой комбинации при кодировании двоичным кодом уровней
квантования Мкв,
·кодовые
комбинации уровней квантования дискретных отсчетов.
Исходные данные для
расчета:
Спектр сигнала: Fmin
÷ Fmax = 0,05 ÷ 6,3 кГц;
Шаг квантования: DU = 2,50мВ.
. Определим
интервал дискретизации
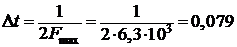 мс и частоту
дискретизации fд=
2Fmax = 2×6,3×103
= 12600Гц = 12,6кГц
мс и частоту
дискретизации fд=
2Fmax = 2×6,3×103
= 12600Гц = 12,6кГц
. Определим дискретные
значения сигнала Uаим
(t) в моменты взятия отсчетов Dt1,
Dt2,
… Dt10,
как показано на рисунке 3, а. Результаты занесем в таблицу
3.
. Определим квантованные
значения Uкв
(t) дискретного сигнала, как показано на рисунке 3, б.
Результаты занесем в таблицу 3.
. Определим величину
ошибки квантования x(t)
для каждого из десяти отсчетов сигнала. Результаты занесем в
таблицу 3. График распределения значений x(t) показан на рисунке 3, в.
5. Определим
порядковый номер уровня квантования для каждого из отсчетов по формуле:
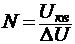 .
.
Результаты занесем в
таблицу 3.
. Определим общее число
уровней квантования
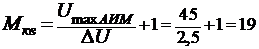
. Определим число
разрядов в кодовой комбинации:
п = log2 Мкв = log2 19 = 5
. Закодируем номера
уровней квантования N пятиразрядным двоичным
кодом. Результаты занесем в таблицу 3. График последовательности кодовых
комбинаций Uикм показан на рисунке
3, г.

Рис. 3 - Преобразование
непрерывного сигнала в цифровой ИКМ - сигнал
Таблица 3 -
Результаты расчета
|
Номер отсчета
|
DU=2,5мВ, Fmin-Fmax=0,05÷6,3кГц,
М=19, n=5
|
|
Uаим
(t), мВ
|
Uкв
(t), мВ
|
x(t),
мВ
|
Номер уровня квантования, N
|
Двоичный код U икм
|
|
1
|
15,7
|
15
|
0,7
|
6
|
00110
|
|
2
|
4,7
|
5
|
-0,3
|
2
|
00010
|
|
3
|
22,1
|
22,5
|
-0,4
|
9
|
01001
|
|
4
|
31,8
|
32,5
|
13
|
01101
|
|
5
|
14,8
|
15
|
-0,2
|
6
|
00110
|
|
6
|
45
|
45
|
0
|
18
|
10010
|
|
7
|
32,4
|
32,5
|
-0,1
|
13
|
01101
|
|
8
|
24,2
|
25
|
-0,8
|
10
|
01010
|
|
9
|
9,5
|
10
|
-0,5
|
4
|
00100
|
|
10
|
22,3
|
22,5
|
-0,2
|
9
|
01001
|
Задача
3.
1. Дайте
определение понятия «электрический фильтр», приведите классификацию фильтров по
взаимному расположению полос пропускания и задерживания. Дайте краткую
характеристику каждому типу электрического фильтра. Приведите классификацию
фильтров в зависимости от их элементной базы.
. Начертите
принципиальную схему заданного звена электрического фильтра типа «LC». Начертите примерный вид АЧХ заданного фильтра.
спектр котельников
импульс сигнал
Таблица 4 -
Исходные данные
|
Номер варианта
|
3
|
|
Тип фильтра «К»
|
ФВЧ «Т»
|
|
Частота среза, fср, кГц
|
180
|
|
Сопротивление нагрузки, Rн.,
Oм
|
200
|
. Рассчитайте
частоту среза wср, значения элементов L и С схемы фильтра
и характеристическое сопротивление Zc. Исходные данные для расчета приведены в таблице 4.
. Рассчитайте
величины входного сопротивления ZBX согласованно
нагруженного фильтра для шести произвольно выбранных значений частоты входного
сигнала в полосе пропускания, в том числе и для частоты среза fcp, и постройте график частотной зависимости входного сопротивления
заданного фильтра.
1. Электрические фильтры предназначены для выделения ряда
гармонических составляющих из спектра частот несинусоидальных колебаний.
Фильтр должен
пропускать с малым ослаблением колебания в определенном интервале частот,
называемом полосой пропускания и максимально ослаблять эти колебания на других
частотах, образующих полосу задерживания. Частота fcp
или wср, разделяющая эти полосы, называется частотой среза или граничной
частотой фильтра. В соответствии с тем, как на шкале частот расположены полосы
пропускания и задерживания, различают фильтры нижних частот (ФНЧ), фильтры
верхних частот (ФВЧ), полосовые фильтры (ПФ) и режекторные или заграждающие
фильтры (РФ или ЗФ).
Фильтры могут быть:
а) пассивными,
состоящими из катушек индуктивности и конденсаторов (пассивные LC - фильтры),
б) пассивными,
состоящими из резисторов и конденсаторов (пассивные RC - фильтры),
в) активными (ARC - фильтры),
г)
электромеханическими (кварцевые, магнитострикционные),
д) цифровыми (с
использованием ЭВМ)
и некоторыми
другими. Фильтры LC имеют широкое распространение, но в настоящее время интенсивно
вытесняются ARC-фильтрами. Кварцевые фильтры имеют очень высокую добротность на
высоких частотах, а магнитострикционные фильтры - на низких.
2. Принципиальная схема Т-образного ФВЧ типа «LC» показана на рис. 3.1
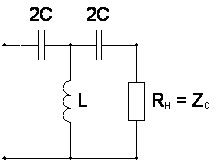
Рис. 3.1 - Принципиальная
схема ФВЧ типа LC
Примерный вид АЧХ заданного фильтра
показан на рис. 3.2
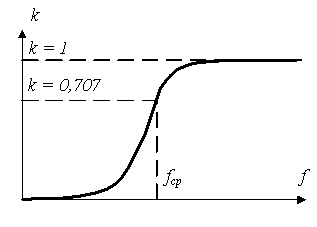
Рис. 3.2 - Примерный вид АЧХ
ФВЧ
Все пассивные фильтры
имеют одно общее свойство: произведение сопротивлений продольного плеча на
поперечное есть вещественная величина, не зависящая от частоты. Такие фильтры
называются фильтрами типа «K».
Параметр 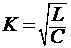 ,
называется характеристическим сопротивлением фильтра. Всем фильтрам типа «K» присущи следующие недостатки:
,
называется характеристическим сопротивлением фильтра. Всем фильтрам типа «K» присущи следующие недостатки:
значительное изменение
характеристического сопротивления в зависимости от частоты,
Фильтры типа «K» имеют и достоинства: простота конструкции, изменение фазовой
характеристики, в диапазоне частот, удаленном от частоты среза, монотонность
возрастания АЧХ. Элементы фильтров типа «K»
подбираются таким образом, чтобы их произведение на любой частоте было
постоянным, т.е. реактивные сопротивления должны иметь разные знаки.
3. Рассчитайте частоту среза wср, значения элементов L и С схемы фильтра и характеристическое сопротивление Zc.
Исходные данные для
расчета:
частота среза fср = 180 кГц
сопротивление нагрузки Rн = 200 Oм
. находим частоту среза wср:
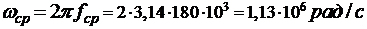
. индуктивность фильтра:
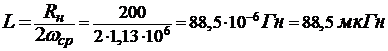
. емкость фильтра:
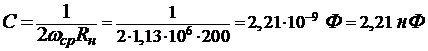
емкость каждого
конденсатора в фильтре: С = 2 · 2,21 = 4,42 нФ, величина
ближайшего значения емкости из стандартного ряда - 4,3 нФ.
. характеристическое
сопротивление:
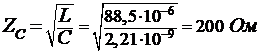
4.
Рассчитайте величины входного сопротивления ZBX согласованно
нагруженного фильтра для шести произвольно выбранных значений частоты входного
сигнала в полосе пропускания, в том числе и для частоты среза fcp,
и постройте график частотной зависимости входного сопротивления заданного
фильтра.
Для расчета величины
входного сопротивления Т-образного ФВЧ типа «LC»
воспользуемся формулой:
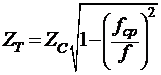
Все рассчитанные
значения занесены в таблицу 3.1
Таблица 3.1 -
Рассчитанные значения
|
№
|
f,
кГц
|
ZВХ,
Ом
|
|
1
|
180
|
0
|
|
2
|
220
|
115
|
|
3
|
260
|
144
|
|
4
|
300
|
160
|
|
5
|
340
|
170
|
|
6
|
380
|
176
|
График частотной зависимости
входного сопротивления заданного фильтра показан на рис. 3.3.

Рис. 3.3 - График частотной
зависимости входного сопротивления
Задача
4.
1. Дайте
определение понятия «длинная линия».
. Приведите
эквивалентную электрическую схему линии без потерь длиной 1 км.
. Дайте определение
бегущих, стоячих и смешанных волн в линии. Объясните условия их возникновения.
. Для заданных в
таблице 6 значений Zb и Zh рассчитайте коэффициент отражения КОТР, коэффициент
бегущей волны КБВ, коэффициент стоячей волны КСВ. Укажите режим
работы линии.
. Рассчитайте Vmin
и Umax, 1min и Imax, постройте графики изменения значений напряжения и тока вдоль
линии длиной l = l (l - длина волны) при заданном сопротивлении нагрузки ZH.
Таблица 6 -
Исходные данные
|
Номер варианта
|
3
|
|
ZB,
Ом
|
100
|
|
Zh,
Ом
|
120
|
|
Рmах,
мВт
|
15
|
6. Рассчитайте
амплитуду тока Im и амплитуду напряжения Um на входе линии без потерь в режиме согласованной нагрузки для
заданной мощности Ртaх.
1. Длинной линией называют систему проводов, геометрическая длина l которых соизмерима с
длиной волны колебаний (l) или
больше её. Параметры длинных линий (сопротивление проводов Rl,
индуктивность Ll, емкость Cl, проводимость изоляции Gl) не сосредоточены в каких-либо определенных участках линии, а
распределены вдоль всей длины проводов. Таким образом, длинные линии можно
рассматривать, как электрические цепи с распределенными параметрами.
2. По определению длинной линией называется система проводов, длина
которых соизмерима с длиной волны действующего колебания или больше её.
Например, для частоты f = 50 Гц λ = 6000 км. Для этой частоты линию длиной 1 км нельзя считать длинной,
т.к. 1 км << 6000 км. Линия длиной 1 км будет считаться длинной на
частоте f = 300 кГц, т.к. она
соизмерима с длинной волны λ = 1000 м.
Если мысленно
выделить в длинной линии участок Δx очень малой
протяженности Δx << λ, то этот участок не является длинной линией и параметры ΔR, ΔL, ΔC, ΔG можно считать сосредоточенными. Поэтому эквивалентная схема всей
линии состоит из последовательно соединенного бесконечного числа бесконечно
малых участков. Анализ процессов, протекающих в длинных линиях, значительно
упрощается, если ΔR = 0 и ΔG = 0. Такие линии называют линии без потерь. Эквивалентную
электрическую схему линии без потерь можно представить в виде Т-образного
фильтра низких частот, состоящего из n звеньев, каждое, из
которых состоит из индуктивности L и емкости С. Можно неограниченно увеличивать число звеньев
фильтра (n → ∞), не изменяя при этом общих индуктивностей nL и емкостей nC фильтра. Это можно сделать лишь за счет уменьшения L и С до
бесконечно малых величин (L → 0, C → 0), однако отношение
L/C должно оставаться конечной величиной. Такой фильтр превращается в
длинную линию, у которой любой элементарный участок длиной Δx обладает некоторой индуктивностью проводов и емкостью между проводами.
Он может быть уподоблен ФНЧ, причем число звеньев такого фильтра n → ∞. Таким
образом, эквивалентная схема линии без потерь представляет собой идеальный
многозвенный фильтр нижних частот, в котором число звеньев n → ∞ (рис.
4.1).
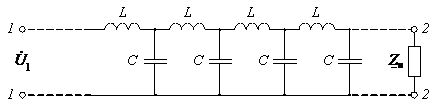
Рис. 4.1
3.
Бегущими волнами называются колебания,
фаза которых удаляется от источника возбуждения с постоянной скоростью,
зависящей от свойств среды. Бегущие волны образуются в линии, только в том
случае, когда сопротивление нагрузки будет чисто активным и равным волновому
сопротивлению линии. Такой режим еще называют согласованным. Наилучшие условия
для передачи сигналов создаются тогда, когда электромагнитная волна
распространяется вдоль линии только в одном направлении: от источника сигнала,
подключенного к входу линии, к приемнику сигнала (нагрузке), подключенному к
выходу линии. Отраженной от конца линии волны в этом случае не возникает. Такой
режим называется «Режимом бегущих волн», он образуется в согласованно нагруженной
линии, при условии ZН = ZB.
Свойства бегущих волн:
1. В каждый
фиксированный момент времени напряжение и ток распределены вдоль линии по
синусоидальному закону.
. С течением
времени синусоидальные распределения напряжения и тока как бы непрерывно перемещаются
вдоль линии слева направо, образуя так называемые падающие бегущие волны.
. В любом сечении
линии напряжение и ток бегущих волн совпадают по фазе.
4. Амплитуды напряжения и тока в
любом сечении линии постоянны, а их отношение является волновым сопротивлением
цепи.
Стоячие
волны получаются при полном отражении
энергии падающей волны к генератору. Для этого линия должна быть идеальной и на
конце либо разомкнута, либо замкнута накоротко. Если нагрузка в конце линии
отсутствует (Zh = 0 или Zh = ¥), то
электромагнитная волна полностью отражается от конца линии и образуется «Режим
стоячих волн». В таких условиях ни линия, ни нагрузка не поглощают энергии. В
конце разомкнутой линии не может быть тока, а, следовательно, и магнитного
поля. Вместе с тем, падающая волна, как и бегущая, содержит в равном количестве
энергии электрического и магнитного полей. Все это означает, что в конце
разомкнутой линии энергия магнитного поля падающей волны переходит в энергию
электрического поля, напряжение в конце линии удваивается, в связи с чем
возникает отраженная бегущая волна. Свойства отраженных волн подобны свойствам
падающих: обе волны имеют одинаковую скорость распространения и одинаковые
амплитуды. При сложении (интерференции) падающих и отраженных волн в линии
возникают колебания, называемые стоячими волнами.
Свойства стоячих
волн в разомкнутой линии:
. В каждом сечении
линии напряжение и ток изменяются синусоидально во времени.
. Амплитуда
напряжения и тока изменяются по длине линии периодически: напряжение
косинусоидально, а ток синусоидально. В результате чего вдоль линии максимумы
(пучности) напряжения и тока, а также минимумы (узлы), которые смещены вдоль
линии, т.е. образуются стоячие волны.
. Отношение
амплитуды напряжения в пучности к амплитуде тока в пучности равно ZB.
. Фаза напряжения
во всех сечениях линии одинакова.
. В любой точке
линии между напряжением и током существует
сдвиг по фазе на
90°.
Перечисленные
свойства стоячих волн показывают, что эти волны существенно отличаются от
бегущих. И в тех, и в других мгновенные значения напряжения (тока) изменяются
по длине идеальной линии, но в бегущей волне это происходит из-за изменения
фазы, а в стоячей - из-за изменения амплитуды. В бегущих волнах напряжение и
ток совпадают по фазе, а в стоячих их фазы сдвинуты на 90°. Кроме того, в
стоячих волнах имеет место пространственный сдвиг между напряжением и током на λ/4, чего нет в бегущих
волнах. Пространственный сдвиг означает, что в сечениях линии с пучностями
напряжения имеют место узлы тока, а на расстоянии λ/4 от этих сечений
находятся пучности тока при узлах напряжения.
Смешанными
волнами называется такой режим работы
линии, когда в линии одновременно существуют и бегущие, и стоячие волны. Если
сопротивление нагрузки не равно волновому сопротивлению линии (Zh > Zb или ZH < Zb), то часть
энергии, переносимой волной, поглощается нагрузкой, а часть - отражается к
началу линии. В этом случае линия работает в «Режиме смешанных волн». Такой
режим работы обычно наблюдается в реальных линиях, когда сопротивление нагрузки
на равно волновому сопротивлению. При этом оно может иметь активный или
реактивный характер. В линии, замкнутой на активное сопротивление, не равное
волновому, существуют одновременно бегущие волны и стоячие волны, причем
последние выражены тем сильнее, чем больше сопротивление нагрузки отличается от
волнового. При RН < ZВ во всех сечениях линии, расположенных на расстоянии λ/4 от её конца,
напряжение и ток совпадают по фазе, поэтому эти сечения являются резонансными.
При RН > ZВ фазы падающей и отраженной волн напряжения в конце линии
одинаковые, а волн тока - противоположные. Возникающие в линии смешанные волны
характеризуются наличием максимума напряжения на нагрузке и минимума тока в
ней. На расстоянии λ/4 от нагрузки напряжение минимальное, а ток имеет максимум.
Смешанные волны возникают в линии и в том случае, если она нагружена
комплексным сопротивлением произвольной величины. При ZН = RН + jXН коэффициент отражения может принимать любые значения в пределах
от -1 до +1 в зависимости от соотношения между RН и XН. Поэтому напряжение и
ток смешанных волн в конце линии имеют некоторые промежуточные значения между
максимальными и минимальными, а резонансные сечения линии смещены к её концу.
4. Для заданных в таблице 6 значений ZВ и ZН рассчитайте коэффициент отражения КОТР, коэффициент
бегущей волны КБВ, коэффициент стоячей волны КСВ. Укажите режим
работы линии.
Исходные данные для расчета:
Волновое сопротивление линии ZB = 100 Ом;
Сопротивление нагрузки ZН = 120 Ом;
Мощность, выделяемая в нагрузке Рmах = 15 мВт.
1. Коэффициентом
отражения (Котр) определяется по формуле:
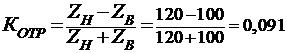 .
.
. Коэффициент бегущей
волны:
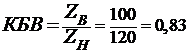 .
.
. Коэффициент стоячей
волны:
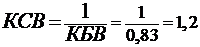 .
.
Линия работает в режиме
смешанных волн, т.к. 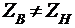 и
ZН
> ZВ.
и
ZН
> ZВ.
5. Рассчитайте Umin и Umax, 1min и Imax, постройте графики
изменения значений напряжения и тока вдоль линии длиной l = l (l -
длина волны) при заданном сопротивлении нагрузки ZH.
. Для нахождения Umax и Imax воспользуемся
формулами:
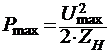 ;
; 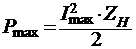
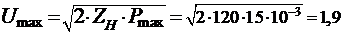 В.
В.
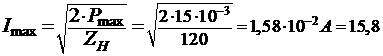 мА
мА
. Находим величины Umin и 1min:

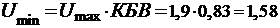 В
В
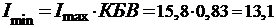 мА
мА
3. Строим график (рис.
4.2):
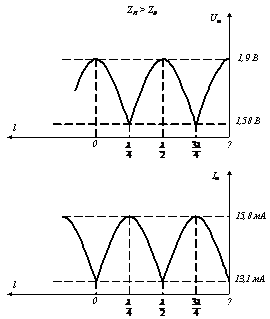
Рис. 4.2
6. Рассчитайте амплитуду тока Im и амплитуду напряжения Um на входе линии без потерь в режиме согласованной нагрузки для
заданной мощности Ртaх.
Максимальная
величина мощности Рmax выделяется в нагрузке в согласованном режиме; т.е., при ZH = ZB;
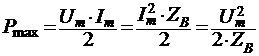
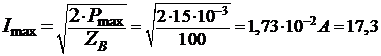 мА
мА
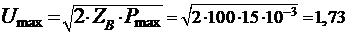 В
В
Литература
1. Шинаков Д.С., Колодежный Ю.М.
Теория передачи сигналов электросвязи. - М.: Радио и связь, 1989
2. Добротворский И.И. Теория
электрических цепей - М.; Радио и связь, 1989