|
Параметр
|
Характеристика/Величина
|
|
Минимальный уровень сигнала
amin
|
0 В
|
|
Максимальный уровень
сигнала amax
|
1,8 В
|
|
Спектральная плотность
мощности помехи сигнала N0
|
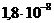 В2/Гц В2/Гц
|
|
Закон распределения помехи
сигнала
|
Равномерный
|
|
Номер уровня квантования
|
j=17
|
|
Вид модуляции
|
ЧМ (FSK)
|
|
Способ приема
|
Оптимальная когерентная
обработка сигнала
|
|
Тип ФНЧ получателя
сообщения
|
Идеальный ФНЧ
|
|
Шаг квантования по уровню
|
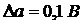
|
|
Ошибочный разряд
|
i = 7
|
|
Максимальная частота,
которой ограничен спектр реального сигнала
|
Fc=106 Гц
|
. Источник сообщения
Источник сообщений - это некий объект или система
(подразумевается либо человек, либо ЭВМ, либо автоматическое устройство или
что-либо другое), информацию о состоянии или поведении которого следует
передать на определенное расстояние.
Информация, передаваемая от источника сообщений,
является непредвиденной для получателя. Поэтому количественную меру
передаваемой по системе связи информации в теории электрической связи выражают
через вероятностные характеристики сигналов (сообщений). Сообщение - это форма представления
информации. Сообщения могут иметь непрерывный или дискретный характер.
Дискретными называются сообщения, которые
представляются последовательностью из конечного числа отдельных, резко
различимых элементов, между которыми нет промежуточных значений, т.е.
дискретная информация представляется в виде конечной совокупности символов
(печатные тексты и документы, состояния цифровых автоматов и т.д.).
Сообщение называется непрерывным, если оно является
непрерывной функцией времени (музыка, речь, изображения объемов,
телеметрические данные). Непрерывные сообщения можно преобразовать в
дискретные. Для передачи на расстояние сообщение преобразуется в сигнал [2].
Источник сообщений выдает сообщение a(t), представляющее
собой непрерывный стационарный случайный процесс, мгновенные значения которого
в интервале [amin; amax] распределены по заданному
трапециевидному закону, а мощность сосредоточена в полосе частот от 0 до Fc.
Для источника сообщений требуется:
- Записать аналитическое выражение и построить график
одномерной плотности вероятности мгновенных значений сообщения a(t).
- Найти МО, дисперсию и СКО.
- Построить график случайного процесса и на графике обозначить
максимальное и минимальное значения сигнала, МО и СКО.
Плотностью вероятности w(x) непрерывной случайной величины x называется производная ее функции
распределения F(x) (1).
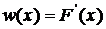 . (1)
. (1)
Плотность вероятности, как и функция распределения F(x), является одной из форм закона распределения, но в отличие
от функции распределения она существует только для непрерывных случайных
величин.
Трапециевидный закон распределения плотности вероятности задается
системой вида (2):
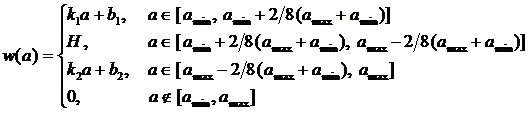 . (2)
. (2)
С
учетом, что amin= 0, система принимает вид (3):
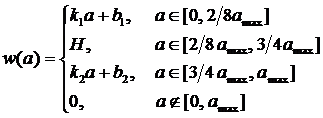 . (3)
. (3)
На
рисунке 2 изображен трапециевидный закон распределения, отрезки которого,
исходя из вышеуказанной системы, необходимо рассчитать.
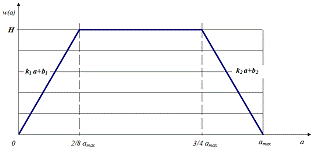
Рисунок
2 - Трапециевидный закон распределения плотности вероятности
Зададим
условие нормировки для плотности вероятности (4):
Формула
для вычисления площади трапеции, заданной трапециевидным законом распределения
плотности вероятности (5):
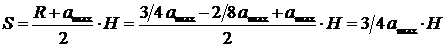 , (5)
, (5)
где
H - высота трапеции;
R - длина
верхнего основания трапеции;
amax - длина
нижнего основания трапеции.
С
учетом условия нормировки и amax =1,8
В получаем:
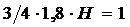 .
.
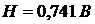 .
.
Для
записи аналитического выражения закона распределения необходимо рассчитать
функции (k1a+b1, Н, k2a+b2), которыми он задается. Для этого воспользуемся
участками трапеции рисунка 2.
Рассчитываем
первый участок. Выбираем две точки: (0;0) и (2/8 amax;
H) и составляем систему уравнений (6).
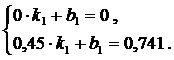 (6)
(6)
Решая
систему, получаем: k1=1,647; b1=0.
Аналогично рассчитываем третий участок. Выбираем две точки (3/4 amax; H) и (amax; 0) и составляем систему уравнений (7).
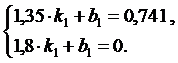 (7)
(7)
из системы получаем: k2=-1,647; b2=2,963.
Таким образом, закон распределения плотности вероятности будет иметь
следующий аналитический вид (8).
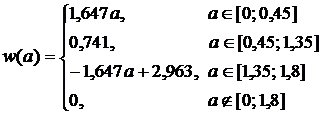 . (8)
. (8)
По полученному выражению (8) строим график одномерной плотности
вероятности сообщения a(t), мгновенные значения которого
заданны в интервале [0; 1,8]
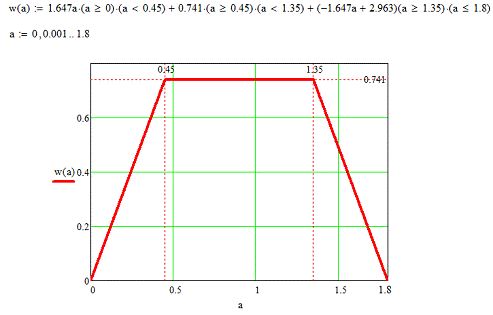
Рисунок 3 - График одномерной плотности вероятности сообщения a(t)
Числовыми характеристиками СП служат начальный момент первого порядка -
МО m(t), центральный момент второго порядка - дисперсия σ2(t) и
СКО
σ(t). Они полностью определяются
одномерным распределением и являются детерминированными функциями времени.
Применительно к нашему распределению плотности вероятностей МО (m(t)) вычисляется по формуле (9):
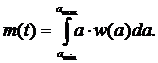 (9)
(9)
Подставляем значения в (9) и вычисляем:
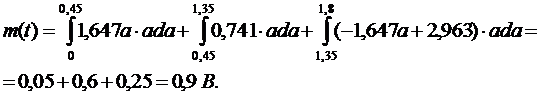
Дисперсия (σ2(t))
вычисляется по формуле (10):
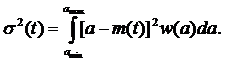 (10)
(10)
Подставляем значения в (10) и вычисляем:
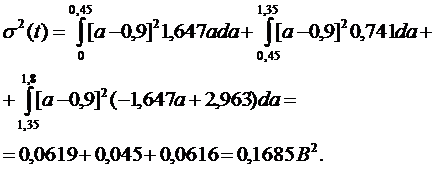
СКО (σ(t))
определяется как квадратный корень
<#"805124.files/image020.gif">. (11)
Подставляем
значение дисперсии в (11) и находим СКО:
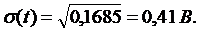
Строим
график случайного процесса и на графике обозначаем максимальное и минимальное
значения сигнала, МО и СКО.
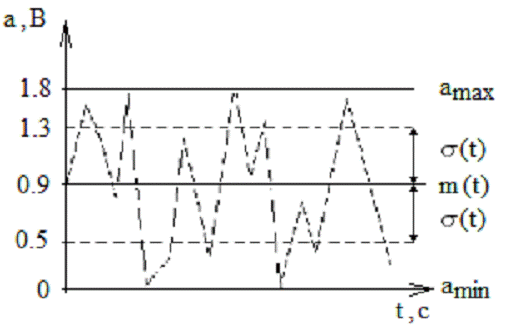
Рисунок
4 - График случайного процесса
.
Дискретизатор
Дискретизация
- это процесс перевода непрерывного аналогового сигнала в дискретный или
дискретно-непрерывный сигнал. Обратный процесс называется восстановлением. При
дискретизации только по времени, непрерывный аналоговый сигнал заменяется
последовательностью отсчётов, величина которых может быть равна значению
сигнала в данный момент времени. Возможность точного воспроизведения такого
представления зависит от интервала времени между отсчётами Δt. Дискретизатор - устройство осуществляющее
дискретизацию [2].
Передача
непрерывного процесса осуществляется дискретными методами. Для этого сообщение
а(t) дискретизируется по времени и квантуется по уровню с
равномерным шагом. Шаг квантования по уровню Dа= 0,1В.
Для
дискретизатора требуется:
- Определить шаг дискретизации по времени (Dt).
- Определить число уровней квантования (L).
- Рассчитать среднюю мощность шума квантования (Pшк).
- Рассматривая дискретизатор как источник дискретного сообщения
объемом алфавита L, определить его
энтропию и производительность (Н, Н’). Отсчеты, взятые через
интервал Dt считать независимыми.
Шаг дискретизации - интервал времени между двумя последовательными
отсчетами аналогового сигнала. Определяется исходя из теоремы Котельникова,
которая может быть записана следующим образом (12):
Fд≥2Fc, (12)
где Fд - частота дискретизации;
Fc - максимальная частота, которой ограничен спектр реального сигнала.
Исходя из частоты дискретизации, интервал дискретизации можно посчитать
по формуле (13):
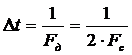 . (13)
. (13)
Подставляем
значения в (13) и вычисляем:
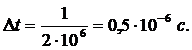
Квантование
- разбиение диапазона значений непрерывной или дискретной величины на конечное
число интервалов. Число уровней квантования можно подсчитать по формуле (14):
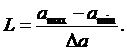 (14)
(14)
Подставляем
значения в (14) и вычисляем:
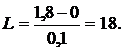
Одной
из причин, приводящих к отличию принятого сообщения от переданного цифровой
системой передачи, является шум квантования, другой - помехи в канале, которые
накладываются на передаваемые символы кодовых комбинаций и могут вызвать
ошибки. Ошибки в символах приводят к ошибочному декодированию всей кодовой
комбинации. Шум квантования не связан (не зависит) с помехами в канале и
целиком определяется выбором числа уровней квантования. Его можно сделать сколь
угодно малым, увеличивая число уровней квантования. При этом придётся
увеличивать число кодовых символов, приходящихся на каждый отсчёт, а,
следовательно, сокращать длительность символа и расширять спектр сигнала в
канале [3].
Если
считать, что ошибка квантования равномерно распределена в пределах интервала
квантования шириной 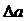 (т. е. принимает все возможные значения с равной
вероятностью), то средняя мощность шума квантования (дисперсия ошибок для
устройства квантования) определяется выражением (15)
(т. е. принимает все возможные значения с равной
вероятностью), то средняя мощность шума квантования (дисперсия ошибок для
устройства квантования) определяется выражением (15)
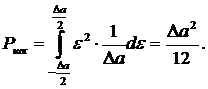 (15)
(15)
В
итоге после подстановки в (15) получаем:
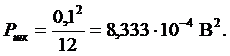
Энтропия
- средняя информативность источника на один символ, определяющая неожиданность
выдаваемых сообщений для источника без памяти. Энтропия определяется по формуле
(16) - формула Шеннона:
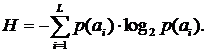 (16)
(16)
По условию задания появление любого значения сигнала равновероятно, т.е. p(a1)= p(a2)=… p(an), т.е. p=1/L.
Таким образом, формула Шеннона переходит в формулу Хартли, позволяющую
рассчитать максимальное значение энтропии (17):
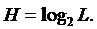 (17)
(17)
Подставляем значения в (17) и получаем:
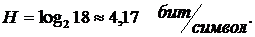
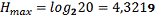
Если
источник сообщения имеет фиксированную скорость 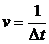 символ/с,
то производительность источника можно определить по формуле (18), как энтропию
в единицу времени (секунду):
символ/с,
то производительность источника можно определить по формуле (18), как энтропию
в единицу времени (секунду):
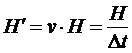 . (18)
. (18)
Подставляем
в (18) и вычисляем:
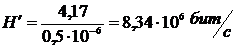 .
.
На втором этапе к полученной k-разрядной двоичной кодовой комбинации добавляются r-разрядные проверочные символы,
формируемые в соответствии с правилами кодирования по коду Хэмминга.
Для кодера требуется:
- Определить число разрядов кодовой комбинации примитивного
кода k, необходимое для кодирования всех L уровней квантованного сообщения.
- Определить избыточность кода при использовании кодирования
Хэмминга.
- Записать двоичную кодовую комбинацию, соответствующую
передаче j-го уровня, считая, что при
примитивном кодировании на первом этапе j-му уровню ставится в соответствии двоичная кодовая
комбинация, представляющая собой запись числа j в двоичной системе счисления. В полученной кодовой
комбинации указать информационные и проверочные разряды.
- Определить число двоичных символов, выдаваемых кодером в
единицу времени Vn и
длительность двоичного символа T.
Число разрядов двоичной кодовой комбинации для кодирования L уровней находим по формуле (19):
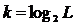 . (19)
. (19)
Так
как L=18, то получаем:
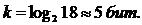
Код Хемминга - это блочный код, позволяющий исправлять одиночные и
фиксировать двойные ошибки, разработанный Ричардом Хеммингом в 40-х годах
прошлого столетия. В то время он работал в лаборатории Белла на
электромеханической счетной машине Bell Model V. Ввод данных в эту машину
осуществлялся с помощью перфокарт. Это была самая ненадежная часть
вычислительной машины. Перфокарты часто считывались неправильно. Исправление и
обнаружение ошибок ввода данных отнимало огромное количество времени, а
пропущенные ошибки могли привести к неверным результатам работы. Желая
застраховаться от возможных сбоев и ускорить процесс обработки данных, Хемминг
в 1950 году разработал способ кодирования.
Идея кодов Хемминга заключается в разбиении данных на блоки фиксированной
длины и вводе в эти блоки контрольных бит, дополняющих до четности несколько
пересекающихся групп, охватывающих все биты блока.
Хемминг рассчитал минимальное количество проверочных бит, позволяющих
однозначно исправлять однократные ошибки.
Если длина информационного блока, который требуется закодировать - k бит, количество контрольных бит,
используемых для его кодирования - r, то закодированный блок будет иметь длину: n = r+k бит. Для каждого блока такой длины возможны n различных
комбинаций, содержащих ошибку.
Если для информационных данных длиной k подобрать такое количество контрольных бит r, что максимально возможное
количество различных последовательностей длиной k+r будет больше или равно максимальному количеству различных
закодированных информационных блоков, содержащих не больше одной ошибки, то
точно можно утверждать, что существует такой метод кодирования информационных
данных с помощью r контрольных бит,
который гарантирует исправление однократной ошибки.
Следовательно, минимальное количество контрольных бит, необходимых для
исправления однократной ошибки, определяется из равенства (20):
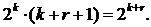 (20)
(20)
Преобразовав
(20) получаем формулу (21):
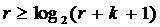 . (21)
. (21)
Первое целое число, удовлетворяющее этому условию, r = 4 бит.
Тогда полная длина кодовой последовательности: n = k + r = 9 бит.
Определим избыточность кода по формуле (22):
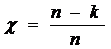 . (22)
. (22)
Получаем:
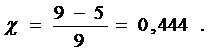
Кодированный
j=17 уровень, согласно варианту, будет иметь следующую
двоичную кодовую комбинацию, занимающую k=5 разрядов:
10 = 100012.
Все
биты, порядковые номера которых являются степенью двойки, - это контрольные
разряды (проверочные биты). Т.е. если порядковый номер бита обозначить символом
«l», то для контрольных бит должно быть справедливо
равенство (23):
l=2t
, (23)
где
t - любое положительное целое число.
Исходя
из выражения (23), для последовательности 100012 проверочными будут:
1, 2, 4 и 8 биты, т.к. 20 = 1, 21 = 2, 22 = 4,
23 = 8.
Определим
расположение проверочных бит в результирующей закодированной
последовательности. Обозначим информационные биты символом k, а
контрольные биты символом r. Индекс около этих символов будет означать их
порядковый номер в закодированной последовательности.