Анализ электрического состояния линейных и нелинейных электрических цепей

Анализ электрического состояния линейных и нелинейных электрических цепей

Учреждение образования

Минский государственный высший радиотехнический колледж

Анализ линейный и нелинейных электрических цепей

Пояснительная записка

к курсовому проекту

по дисциплине: Теоретические основы электротехники

Тема:

Анализ электрического состояния линейных и нелинейных электрических цепей

Руководитель М.А. Асаенок

Выполнила В.А. Политкина

Учащийся гр. 22291

Содержание:

Введение

. Анализ электрического состояния линейных и нелинейных электрических цепей

1.1 Расчет линейных электрических цепей постоянного тока

1.2 Расчет нелинейных электрических цепей постоянного тока

. Анализ электрического состояния Линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов

2.1 Расчет однофазных линейных электрических цепей переменного тока

2.2 Расчет трехфазных линейных электрических цепей переменного тока

2.3 Исследование переходных процессов в электрических цепях

Заключение

Список используемой литературы

Введение

Главной задачей расчёта электрических цепей является определение токов отдельных элементов цепи (источников, приёмников, приборов). Определив значение тока легко найти напряжение, мощность. Значение этих величин необходимо для того, чтобы правильно выбрать или оценить условие работы элементов цепи, расчёты проводят по схемам электрических цепей.

Электрическая цепь - совокупность устройств, элементов <#"803086.files/image001.jpg">

1) Составим систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.

Метод узловых и контурных уравнений основан на первом и втором законах Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.

При расчете данным методом произвольно задаемся направлением токов в ветвях I₁, I₂, I₃, I₄, I₅, I₆ .

Составим систему, в системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).

В заданной цепи шесть ветвей, значит, в системе должно быть 6 уравнений (m=6). Сначала составим уравнения узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n-1) независимых уравнений. В нашей цепи 4 узла (A,B,C,D), значит, число уравнений: n-1=4-1=3. Составим 3 уравнения для любых 3-х узлов, например, для узлов A,B,C.

Узел A: I₅= I₄+ I₃

Узел B: I₆ + I₁ =I₅

Узел C: I₂ +I₃ = I₆

Так как всего в системе должно быть шесть уравнений, три уже есть. Три недостающих мы составим для линейно независимых контуров. Чтоб они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.

Задаемся обходом каждого контура и составим уравнения по второму закону Кирхгофа.

Первый контур - обход по часовой стрелке.

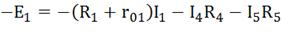
Второй контур - обход по часовой стрелке.

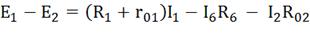
Третий контур - обход по часовой стрелке.

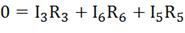
ЭДС в контуре берется со знаком “+“, если направление ЭДС совпадает с обходом контура. ЭДС в контуре берется со знаком “-”, если направление ЭДС не совпадает с обходом контура.

Падение напряжения на сопротивлении контура берется со знаком “+“, если направление тока в нем совпадает с обходом контура, со знаком “-“, если не совпадает.

Получим систему из шести уравнений с шести неизвестными.

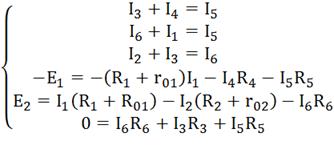
Решив систему, определим величину и направление тока во всех ветвях схемы.

Если при решении системы ток получается со знаком “ - “, значит его действительное направление обратно тому направлению, которым мы задались.

)   Определить токи во всех ветвях схемы, используя метод контурных токов.

Метод контурных токов основан только на втором законе Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.

Достигается это распределением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока - контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи можно рассмотреть три контура-ячейки и ввести для них контурные токи I_к1, I_к2, I_к3.

Контуры - ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определимое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

Стрелками указываем направления контурных токов I_к1, I_к2, I_к3 в контурах - ячейках. Направление обхода контуров принимаем таким же;

Составим уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.

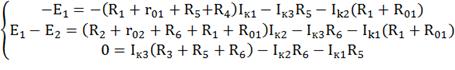
Подставим в уравнение численные значения ЭДС и сопротивлений.

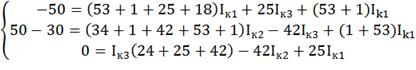
Или

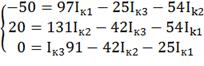
Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители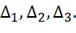

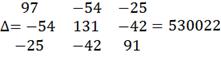
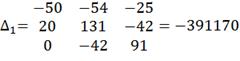
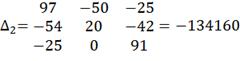
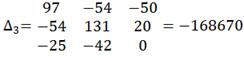
Вычислим контурные токи:

Действительные токи ветвей:

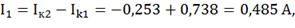
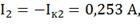
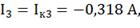
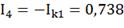
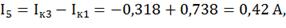
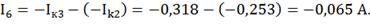
3) Определим токи во всех ветвях схемы на основании метода наложения.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

а) определим частные токи от ЭДС Е₁ при отсутствии ЭДС Е₂, т.е. рассчитываем цепь по рисунку 1.21(1).

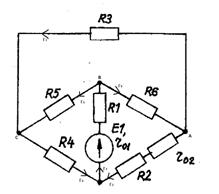
Рисунок 1.21(1)

Показываем направление частных токов от ЭДС Е₁ и обозначаем буквой I с одним штрихом (I^’). Решаем задачу методом звезды. Преобразуем треугольник сопротивлений 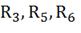в звезду.

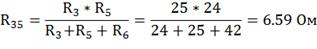
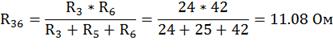
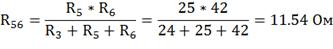
Ток источника

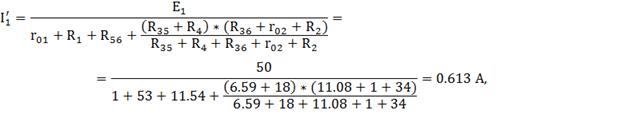
По формуле разброса:

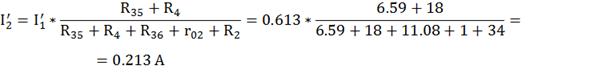
Из первого закона Кирхгоффа:

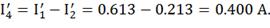
Для нахождения остальных токов, находим падения напряжения из второго закона Кирхгоффа.

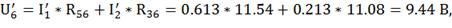
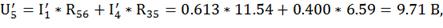
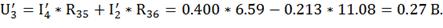
По закону Ома находим оставшиеся токи:

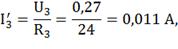
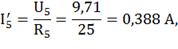
б) определим частные токи от ЭДС Е₂ при отсутствии ЭДС Е₁, т.е. рассчитываем цепь по рисунку 1.21(2).

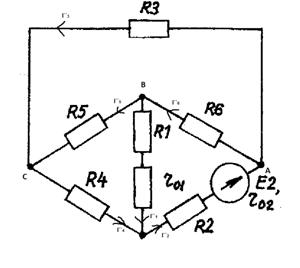
Рисунок 1.21(2)

Показываем направление частных токов от ЭДС Е₂ и обозначаем буквой I с двумя штрихами (I^’’). Решаем задачу также как и в первом случае методом звезды. Преобразуем треугольник сопротивлений 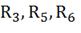в звезду.

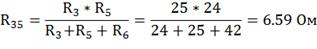
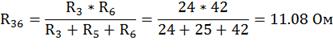
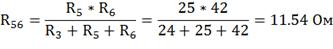
Ток источника

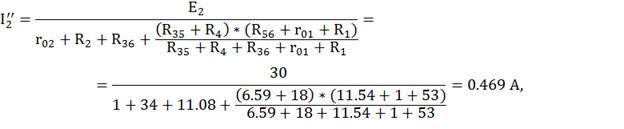
По формуле разброса:

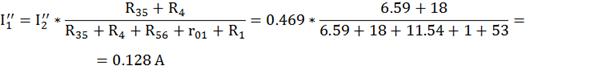
Из первого закона Кирхгоффа:

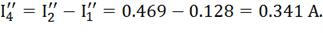
Для нахождения остальных токов, находим падения напряжения из второго закона Кирхгоффа.

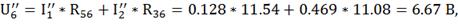
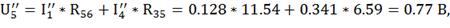
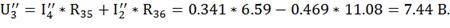
По закону Ома находим оставшиеся токи:

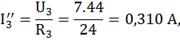
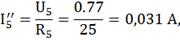
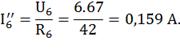
Вычислим токи исходной цепи, выполняя алгебраическое сложение частных токов, учитывая их направление.

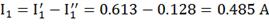
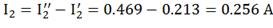
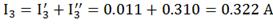
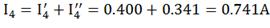
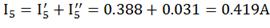
4) Составим баланс мощностей для заданной схемы.

Источники Е₁ и Е₂ вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадает. Баланс мощностей для заданной цепи запишется так:

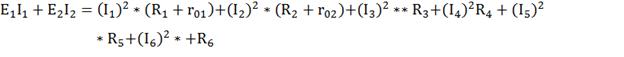
Подставим числовые значения и вычисляем

*0,485 + 30*0,253 = (0,485)² * 54 + (0,253)² * 35 + (0,318)² * 24 +

(0,738)²*18 + (0,42)²* *25 + (0,065)² * 42 31.84Вт = 31.76Вт

5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.

Расчет токов ветвей методами с учетом ошибок вычислений практически одинаков.

)   Определим ток во второй ветви методом эквивалентного генератора.

Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.

Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R₂, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R₂ служит источником электрической энергии, т.е. генератором). Получается схема замещения.

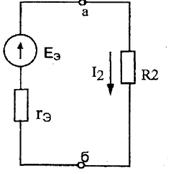
На схеме искомый ток I₂ определим по закону Ома для замкнутой цепи:

Где Е_Э - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах холостого хода,

r_Э - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.

Изобразим схему эквивалентного генератора в режиме холостого хода (рисунок - 1.21(2)).

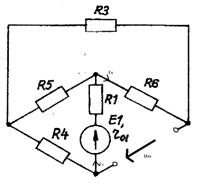
Рисунок 1.21(2)

Для нахождения U_хх, определим вспомогательные токи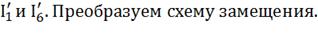

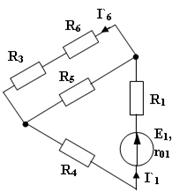
По формуле разброса:

По формуле разброса:

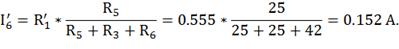
Из второго закона Кирхгоффа:

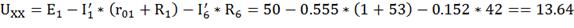
Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный, при этом ЭДС Е₁ и Е₂ из схемы исключается, внутреннее сопротивление этих источников r₀₁ и r₀₂ остаются (рисунок - 1.21(6).

Вычислим эквивалентное сопротивление относительно зажимов а и б.

Для нахождения 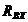, преобразуем треугольник сопротивлений R₃, R₅, R₆ в звезду

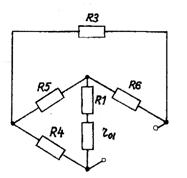
Рисунок - 1.21(6)

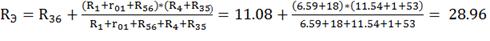Ом

Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:

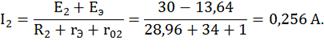
Т.е. ток в этой ветви с учетом ошибок получился практически таким же, как и в пунктах 2 и 3.

) Построим потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Изобразим контур (рисунок 1.21(7), зададимся обходом контура против часовой стрелки. Заземлим одну из точек контура (нулевую точку). Потенциал этой точки будет равен нулю..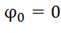

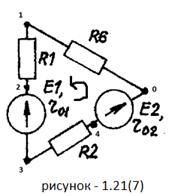
Зная величину и направление токов ветвей ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу.

Найдем ток в заданном контуре:

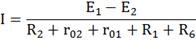
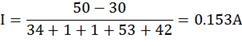
Начнем обход с нулевой точки.

;

;

;

;

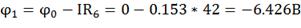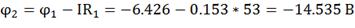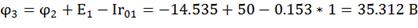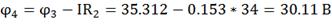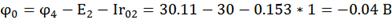
- проверочная точка.

Потенциальная диаграмма представлена в приложении 1,где по оси абсцисс откладываем сопротивления контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака.

1.2 Расчет нелинейных электрических цепей постоянного тока

Задание

Построить входную вольтамперную характеристику схемы (рис 1.32). Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.

Использовать вольтамперные характеристики элементов “в”.

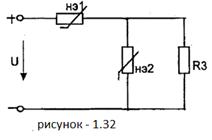
Дано:

U=80 В,

R₃=32 Oм,

R₄=48 Ом

Определить:I₁, I₂, I₃, U₁, U₂, U₃

ВАХ линейного элемента строим по уравнению 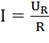. Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, U_R= 64В, тогда соответствующее значение тока 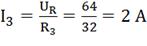. Соединив полученную точку с началом координат, получим ВАХ линейного элемента.

Далее строим общую ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически «сворачиваем» цепь. Начнем с разветвленного участка. Линейный и нелинейный элементы соединены параллельно, их ВАХ 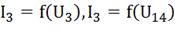. С учетом этого строим общую для них ВАХ. Для этого задаемся напряжением и складываем токи при этом напряжении 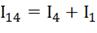. Точка пересечения этих значений тока и напряжения дает одну из точек из общей ВАХ. В результате получим множество точек и по ним строим ВАХ .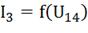

Далее мы имеем характеристики первого нелинейного элемента 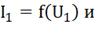общую характеристику линейного и нелинейного элементов 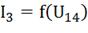, которые соединены между собой последовательно. Строим общую для них ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи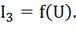

Дальнейший расчет цепи производим по полученным графикам.

Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 80В (точка «а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ 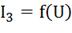, получим точку «b». Из точки «b» опускаем перпендикуляр на ось тока (точка «с»). Отрезок «ос» дает нам искомое значение общего тока 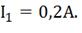Когда опускаем перпендикуляр из точки «b» на ось тока, то пересекаем ВАХ 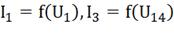 в точках «f» и «d» соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получим напряжения на каждом участке цепи: 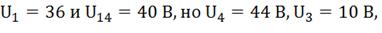т.к. линейный и нелиненый элементы соединены параллельно. Чтобы найти токи 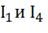при U₁₄= 40В, опустим перпендикуляр с точки «d» на ось напряжений до пересечения с ВАХ 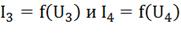 в точках «N» и «M». Опустив из этих точек перпендикуляры на ось токов, получим . В результате имеем следующие значения токов и напряжений на всех элементах цепи:.

линейный нелинейный постоянный переменный

2. АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА: ОДНОФАЗНЫХ, ТРЕХФАЗНЫХ. ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

2.1 Расчет однофазных электрических цепей переменного тока

Задание

К зажимам электрической цепи подключен источник синусоидального напряжения 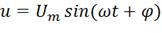В и частотой .

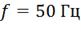Выполнить следующее:

)   Начертить схему замещения электрической цепи, соответвующую варианту, рассчитать реактивные сопротивления элементов цепи;

2)      Определить действующее значение токов во всех ветвях цепи;

)        Записать уравнение мгновенного значения тока источника;

)        Составить баланс активных и реактивных мощностей;

)        Построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений.

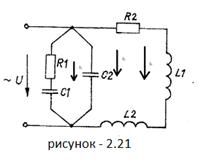
Дано:

U_m=180 В,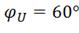, R₁=25 Ом, R₂=50 Ом, L₁=79.5 мГн, L₂=127.2 мГн, С₁=318 мкФ, С₂=79.5 мкФ .

Определить:, I₁, I₂, I₃, X_L1, X_L2, X_C1, X_C2

1) Реактивные сопротивления цепи:

X_L1=

X_L2 =

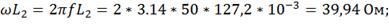
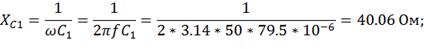
2) Расчет токов в ветви выполним методом эквивалентных преобразований.

Представим схему в следующем виде:

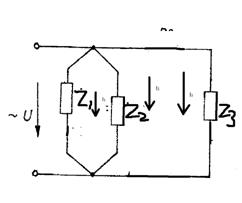
Находим комплексные сопротивления ветвей, зачем участков цепи и всей цепи:

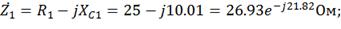
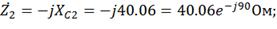
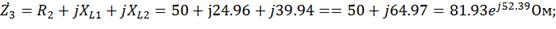
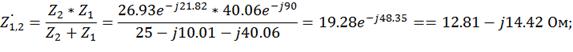
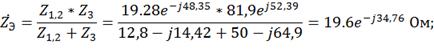
Выразим действующее значение напряжения в комплексной форме:

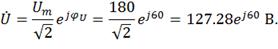
Вычислим токи ветвей и общий ток цепи:

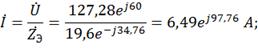
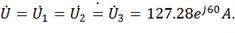
Определения токи параллельных ветвей I₁, I₂, I₃:

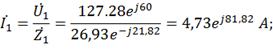
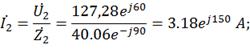
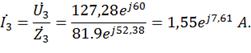
3) Составим уравнение мгновенного значения тока источника:

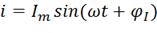
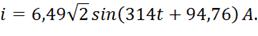
4) Составляем баланс активных и реактивных мощностей приемника.

Находим полную мощность цепи в комплексном виде:

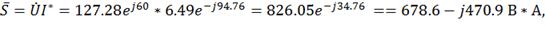
Где S_ист. = 826.05 В*А,

Р_ист. = 678.6 Вт,_{ист .}= -470.9 Вар(знак «-» определяет емкостной характер нагрузки в целом).

Находим активную Р_пр. и реактивную Q_пр. мощности приемников:

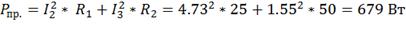
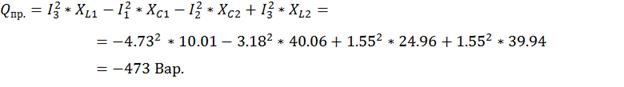
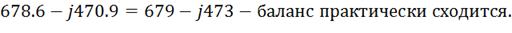
5) Находим напряжение на элементах схемы замещения цепи:

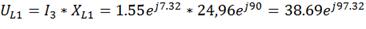
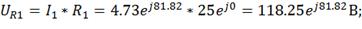
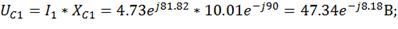
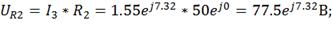
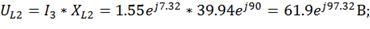
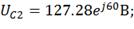
6) Строим топографическую векторную диаграмму на комплексной плоскости. Выбираем масштаб: М_I=1 А/см., М_U=30 В/см.

I₁=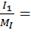4,73А/см;

I₂=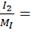3,18А/см;₃= 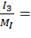1,55А/см;_L1=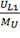=1.29 В/см;_С1=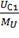=1.58 В/см;_R1=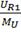=3.94 В/см;_L2=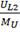=2.06 В/см;_R2=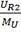=2.58 В/см;_C2=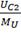=4.24 В/см;

На комплексной плоскости в масштабе откладываем векторы токов и напряжений в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелки, а отрицательные по часовой стрелке. Итак, вектор тока I₁=4.73e^j81.82 A повернут относительно оси (+1) на угол 81.82^○, а его длина 4,73 см. Вектор тока I₂=3.18e^j150 A повернут относительно оси (+1) на угол 150^○, а его длина 3,18 см. Вектор тока I₃=1.55e^j7.61A повернут относительно оси (+1) на угол 7.61^○, а его длина 1,55 см. Соединяем векторы токов в соответствие с соединением элементов цепи, получаем общий ток, равный по числовому значению и фазе с первым током.

Аналогичным образом откладываем векторы напряжений. Соединяем векторы напряжений в соответствие с соединение элементов цепи, получаем напряжение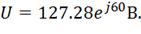

2.2 Расчет трехфазных линейных электрических цепей переменного тока

Задание

)   Начертить схему соединения сопротивлений в трехфазной цепи;

)   Фазные токи;

3)      Ток в нулевом проводе (при соединении звездой);

)        Активную, реактивную и полную мощность каждой фазы и всей трехфазной цепи;

)        Полные сопротивления фаз;

Дано: U_л=220 В; R_A=50 Ом;

R_B=72 Ом; Х_LB=32 Ом; Х_LC=90 Ом;

Х_СA=72 Ом.

Определить:Z_A; Z_B; Z_C; I_A; I_B; I_C; I_N; P; Q; S

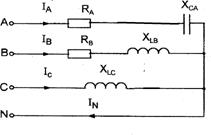
Рисунок - 2.21.3

1) Выразим в комплексной форме фазные напряжения:

U_Ф =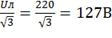

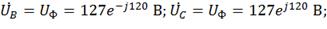
2) Выразим сопротивления фаз в комплексной форме:

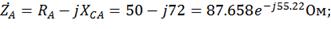
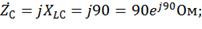
3) Находим комплексы фазных токов:

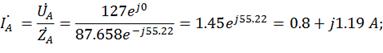
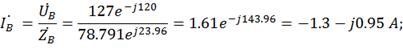
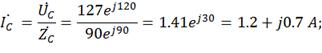
4) Вычисляем ток в нейтральном проводе:

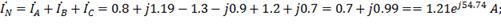
5) Вычисляем мощности фаз и всей цепи:

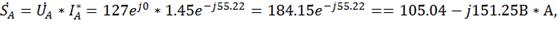
Где S_A=184.15 В*А, Р_А=105.04 Вт, Q_A= −151.25 Вар;

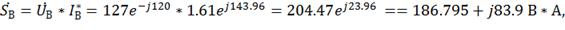
Где S_В=204.47В*А, Р_В=186.79 Вт, Q_В=83.01 Вар;

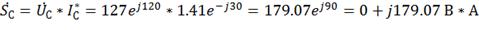
Где S_С=179.07 В*А, Р_С=0 Вт, Q_С=179.07 Вар;

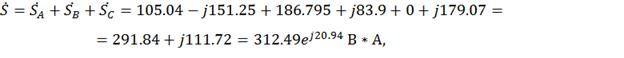
Где S=312.49 В*А, Р =291.84 Вт, Q=111.72 Вар.

.3 Исследование переходных процессов в переходных цепях

Определить закон изменения тока и ЭДС самоиндукции в цепи. определить практическую длительность переходного процесса и энергию магнитного поля при .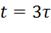

Дано: R=70 Ом, L=0.8 Гн,

U=70 В,

Определить: i=f(t), t, e_L=f(t),W_M.

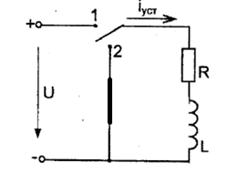
Рисунок - 2.31

1. Устанавливаем переключатели в положение 1 (под включения катушки к источнику постоянного напряжения)

До замыкания переключателя в положение 1 ток в цепи был равен нулю. В первый момент после замыкания переключателя в положение 1, т.е. в момент начала переходного процесса (t=0), ток в цепи будет таким же, как и в последний момент до начала коммутации, т.е. i₀=0.

После коммутации ток стремится достигнуть величины установившегося тока (i_уст), но на основании первого закона коммутации изменяется не скачком, а постепенно.

Согласно схеме

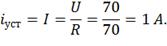
Чтобы найти закон изменения переходного тока, запишем уравнение в общем виде:

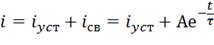
В этой формуле

Где 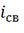- свободная составляющая тока;

А - постоянная интегрирования;

е = 2,71 - основание натурального логарифма;

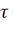- постоянная времени переходного процесса;

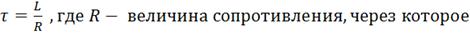 проходит переходной процесс;- текущее время.

Определяем постоянную интегрирования, полагая t=0, тогда уравнение 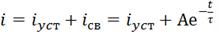примет вид:

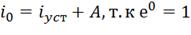
Значит,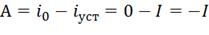

Запишем уравнение(закон изменения переходного тока) при включении катушки:

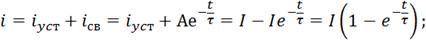
В нашем случае

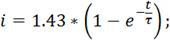
Находим постоянную времени переходного процесса:

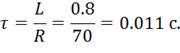
Практическая длительность переходного процесса:

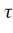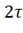Строим график переходного процесса i=f(t), задавшись моментом времени t=0, t=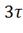, t=, t=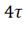, t=, t=.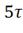

Значения для переходного процесса для заданных значений времени:

t=0, i₀=1*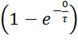=1*(1-1) = 0 A;=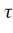, i₁=1*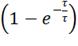=1*(1-0.367) = 0.633 A;=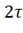, i₂=1*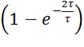=1*(1-0.135) = 0.865A;=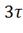, i₃=1*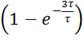=1*(1-0.049) = 0.951 A;=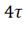, i₄=1*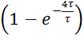=1*(1-0.018) = 0.982 A;=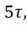 i₅=1*=1*(1-0.007) = 0.993 A;

Строим график i=f(t)

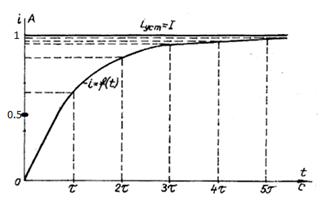
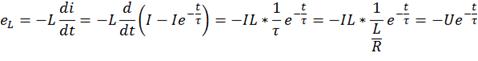
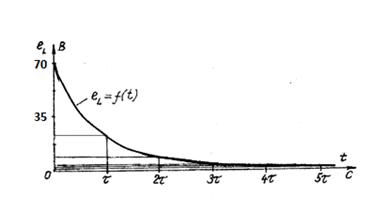
В нашем случае e_L= - 70.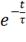

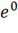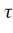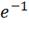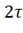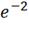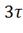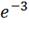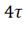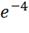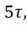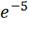t=0, e₀= -70*= -70*1 = -70 В;=, e₁= -70*= -70*0.367 = -25.69 В;=, e₂= -70*= -70*0.135 = -9.45В;=, e₃= -70*= -70*0.049= -3.43 В;=, e₄= -70*= -70*0.018 = -1.26В;= e₅= -70*= -70*0.007 = -0.49В;

Строим график е_L=f(t)

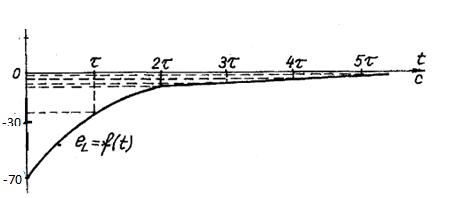
Энергию магнитного поля при 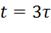 можно вычислить так:

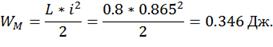
2. Переключаем переключатель из положения 1 в положение 2 (отключаем катушку от источника постоянного при одновременном ее замыкании на сопротивление).

В этом случае отключаем цепь от источника и при переключении в положение 2. В образовавшемся контуре ток поддерживается за счет энергии, накопленной в магнитном поле катушки. Энергия магнитного поля непрерывно уменьшается, так как в активном сопротивлении контура идет необратимый процесс превращения электрической энергии в тепловую.

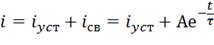
В этом случает i_уст=0, т.к. при отключении цепи от источника ток в цепи будет равен нулю. Тогда

,

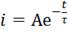где 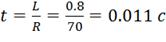 -постоянная времени переходного процесса.

Определим постоянную интегрирования, полагая, что t=0, тогда уравнение 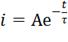 примет вид:

но 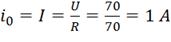 - согласно первому закону коммутации ток в первый момент коммутации будет таким, каким был в последний момент до коммутации.

Значит, А=1 А,.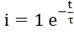

Длительность переходного процесса:

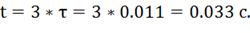
Строим график переходного процесса i=f(t), задавшись моментом времени t=0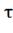, t=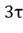, t=, t=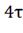, t=, t=.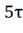

Значения для переходного процесса для заданных значений времени:

t=0, i₀=1* =1*1 = 1 A;=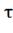, i₁=1* 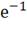=1*0.367 = 0.367 A;=, i₂=1*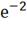 =1*0.135 = 0.135A;=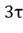, i₃=1*=1*0.049 = 0.049A;=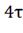, i₄=1*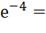1*0.018 = 0.018A;

t=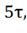 i₅=1*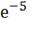=1*0.007 = 0.007A;

Строим график i=f(t)

Закон изменения самоиндукции можно получить по закону:

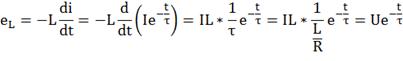
В нашем случае e_L= 70.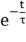

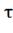t=0, e₀= 70*= 70*1 =70 В;=, e₁= 70*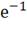=70*0.367 =25.69 В;=, e₂= 70*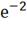=70*0.135 = 9.45В;=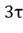, e₃= 70*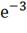=70*0.049= 3.43В;=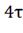, e₄= 70*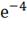= 70*0.018 = 1.26В;=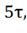 e₅= 70*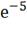= 70*0.007 = 0.49 В;

Строим график е_L=f(t)

Заключение:

В данном курсовом проекте мы рассматривали разветвленные и не разветвленные, линейные и нелинейные электрические цепи переменного и постоянного тока, для расчета которых применяются законы Кирхгофа и Ома. А так же метод контурных токов, метод наложения, метод эквивалентного генератора, метод непосредственного применения законов Кирхгофа, метод комплексных амплитуд, а для расчета нелинейных электрических цепей применяется графический метод.

Проверка расчетов осуществлялась с помощью баланса мощностей, а в методе комплексных амплитуд - с помощью топографической векторной диаграммы токов и напряжений.

Список используемой литературы:

1. Г.И. Атабеков «Теоретические основы электротехники». М.: 1978 год.

2.      Ю.В. Буртаев, П.Н. Овсянников «Теоритические основы электротехники». М.: 1984 год

.        И.А. Данилов, П.М. Иванов «Общая электротехника с основами электроники». М.: 1989 год.

.        Ф.Е. Евдокимов «Теоретические основы электротехники». М.: 1981 год

.        Л.А. Частоедов «Электротехника». М.: 1989 год

.        В.С. Попов «Теоритическая электротехника». М.: 1978 год.