Анализ электрического состояния линейных и нелинейных цепей постоянного и переменного токов
КУРСОВАЯ РАБОТА
Анализ электрического состояния
линейных и нелинейных цепей постоянного и переменного токов
Содержание
Введение
1. Решение линейной электрической цепи постоянного тока
1.1 Составление на основании законов Кирхгофа системы уравнений для
определения токов схемы
1.2 Определение токов схемы методом контурных токов
1.3 Определение токов схемы методом наложения
1.4 Составление баланса мощностей схемы
1.5 Определение тока во второй ветви методом эквивалентного
генератора
1.6 Построение потенциальной диаграммы для контура, включающего обе
ЭДС
2. Решение нелинейных электрических цепей постоянного тока
3. Решение однофазной линейной электрической цепи переменного тока
3.1 Схема замещения электрической цепи, определение реактивных
сопротивлений элементов цепи
3.2 Определение действующего значения токов цепи
3.3 Составление уравнения мгновенного значения тока источника
3.4 Составление баланса активных и реактивных мощностей
3.5 Построение векторной диаграммы токов и напряжений
4. Решение трехфазной линейной электрической цепи переменного тока
4.1 Нахождение фазных токов
4.2 Вычисление токов в нулевом проводе
4.3 Определение активной, реактивной и полной мощности каждой фазы
и всей трехфазной цепи
4.4 Определение угла сдвига фаз между током и напряжением в каждой
фазе. Построение векторной диаграммы трехфазной цепи
Заключение
Список использованных источников
Введение
Целью данного курсового проекта является формирование у
учащегося навыков по решению различных типов задач.
Задача анализа электрического состояния цепей
постоянного/переменного тока заключается в определении токов в отдельных
ветвях, напряжения между двумя любыми узлами цепи или конкретно на отдельном
элементе, а также построение необходимых диаграмм. Расчеты производятся различными
методами: по I и II закону Кирхгофа, методом наложения, методом эквивалентного
генератора, используется метод расчета электрической цепи с помощью комплексных
чисел. При этом задаются: конфигурация и параметры цепи, параметры элементов
включенных в цепь, а также параметры источников питания. Если цепь содержит
хотя бы один нелинейный элемент, то к ней применяется графический метод
решения. Если исследуются переходные процессы в электрической цепи, то
необходимо знать начальные значения токов на индуктивностях и напряжения на
емкостях.
Работа над данным курсовым проектом позволяет решить
следующие задачи:
закрепление теоретических знаний, полученных на лекционном
курсе;
развитие творческого технического мышления;
усвоение методики выполнения расчетов;
развитие навыков по работе со справочной литературой;
развитие умения составления и оформления пояснительной
записки и графической части проекта;
Курсовое проектирование по предмету "Теоретические
основы электротехники” является завершающим этапом изучения данного предмета и
занимает важное место в процессе подготовки будущего специалиста к работе на
производстве.
линейная нелинейная электрическая цепь
1. Решение
линейной электрической цепи постоянного тока
.1
Составление на основании законов Кирхгофа системы уравнений для определения
токов схемы
Для электрической цепи (рис.1.1) выполнить следующее:
) Составить на основании законов Кирхгофа систему уравнений
для определения токов во всех ветвях схемы;
) определить токи во всех ветвях схемы, используя метод контурных
токов;
) определить токи во всех ветвях схемы на основании метода
наложения;
) составить баланс мощностей для заданной схемы;
) определить ток во второй ветви методом эквивалентного
генератора;
) построить потенциальную диаграмму для любого замкнутого
контура, включающего обе ЭДС.
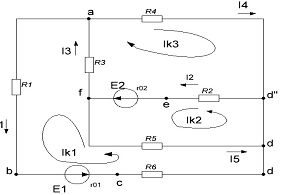
Рис. 1.1
Дано:
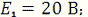
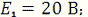
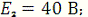
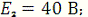
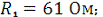
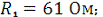
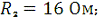
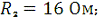
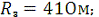
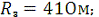
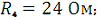
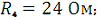
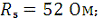
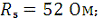
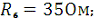
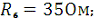
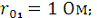
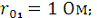
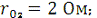
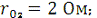
Определить: 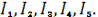
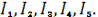
1) Cоставить систему уравнений, применяя
законы Кирхгофа для определения токов во всех ветвях. Метод узловых и контурных
уравнений основан на применении первого и второго законов Кирхгофа. Он не
требует никаких преобразований схемы и пригоден для расчёта любой цепи.
При расчёте данным методом произвольно задаём направления токов в
ветвях 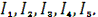
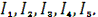
Составляем систему уравнений. В системе должно быть столько
уравнений, сколько в цепи ветвей (неизвестных токов). В заданной цепи пять
ветвей, значит, в системе должно быть пять уравнений 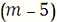
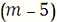 . В схеме n=3 узла. Значит
должно быть n-1=3-1=2 уравнения по первому закону
Кирхгофа:
. В схеме n=3 узла. Значит
должно быть n-1=3-1=2 уравнения по первому закону
Кирхгофа:
m- (n-1) =5-2=3.
Составляем уравнения узлов, например, для узлов a и f
Узел
a: I3=I1+I4;
Узел
f: I2=I3+I5
Задаёмся обходом каждого контура и составляем уравнения по второму
закону Кирхгофа.
Контур add`fa -
обход против часовой стрелки:
E1=I1 (R1+r01+R6) - I5 R5+I3 R3;
Контур d``f d` − обход
против часовой стрелки:
E2=I2 (R2+r02) +I5 R5;
Контур add’fa -
обход по часовой стрелке:
E2=I2 (R2+r02) I3 R3+I4 R4.
1.2
Определение токов схемы методом контурных токов
Определить токи во всех ветвях схемы, используя метод контурных
токов. Метод контурных токов основан на использовании только второго закона
Кирхгофа. Это позволяет уменьшить число уравнений в схеме на n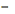
 1. Достигается это разделением схемы на ячейки (независимые
контуры) и введением для каждого контура-ячейки своего тока - контурного тока,
являющегося расчётной величиной. Итак, в заданной цепи (рис.1.1) можно
рассмотреть три контура-ячейки и ввести для них контурные токи Ik1 Ik2 Ik3.
1. Достигается это разделением схемы на ячейки (независимые
контуры) и введением для каждого контура-ячейки своего тока - контурного тока,
являющегося расчётной величиной. Итак, в заданной цепи (рис.1.1) можно
рассмотреть три контура-ячейки и ввести для них контурные токи Ik1 Ik2 Ik3.
Контуры-ячейки имеют ветвь, не входящую в другие контуры - это
внешние ветви. В этих ветвях контурные токи являются действительными токами
ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными
ветвями. В них действительный ток равен алгебраической сумме контурных токов
смежных контуров, с учётом их направления.
На основании вышеизложенного порядок расчёта цепи методом
контурных токов будет следующим: стрелками указываем выбранные направления
контурных токов Ik1 Ik2 Ik3 в контурах-ячейках. Направление обхода контура выбираем таким же;
составляем уравнения и решаем систему или методом подстановки, или с помощью
определителей.
E1= (R1+r01+R3+R5+R6)
Ik1-R5 Ik2+R3 Ik3
E2= (R2+r01+R5)
Ik2-R5 Ik1+ (R2+r02) Ik3
E2= (R2+r02+R3+R4)
Ik3+R3 Ik1+ (R2+r02) Ik2
Подставляем в уравнения численные значения ЭДС и сопротивлений
20= (61+1+41+52+35) Ik1-52Ik2+43Ik3
40= (16+2+52) Ik2-52k1+
(16+2) Ik3
40= (16+2+41+24) Ik3+41Ik1+
(16+2) Ik2
20=190Ik1-52Ik2+41Ik3
40=-52Ik1+70Ik2+18Ik3
=41Ik1+18Ik2+83Ik3
Решим систему с помощью определителей. Вычислим определитель
системы дельта и частные определители дельта 1, дельта 2, дельта 3.
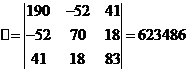
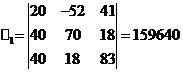
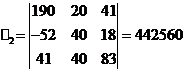
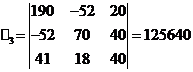
Вычисляем контурные токи:

Вычисляем реальные токи:

1.3
Определение токов схемы методом наложения
Определить токи во всех ветвях схемы методом наложения.
По методу наложения ток в любом участке цепи рассматривается
как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
а) определяем частные токи от 
 при отсутствии
при отсутствии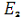
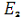 , то есть рассчитываем цепь по рис. 1.3.1
, то есть рассчитываем цепь по рис. 1.3.1
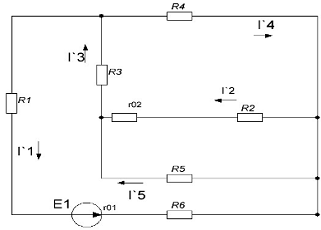
Рис. 1.3.1
Показываем направление частных токов от 
 и обозначаем буквой
и обозначаем буквой 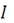
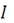 c одним штрихом (I'). Решаем задачу методом свёртывания.
c одним штрихом (I'). Решаем задачу методом свёртывания.
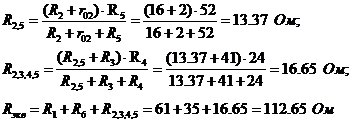
Вычисляем ток источника:
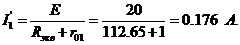
Применяем формулу разброса и 1 закон Кирхгофа, вычисляем токи
ветвей
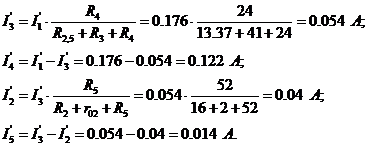
б) Определяем частные токи от 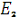
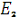 при отсутствии
при отсутствии 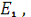
 то есть рассчитываем цепь на рис. 1.3.2
то есть рассчитываем цепь на рис. 1.3.2
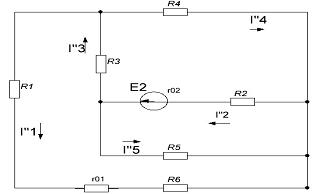
Рис. 1.3.2
Показываем направление частных токов от Е2 и обозначаем
их буквой 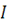
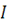 c двумя штрихами
(
c двумя штрихами
(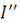
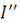 ). Рассчитываем общее сопротивление цепи:
). Рассчитываем общее сопротивление цепи:
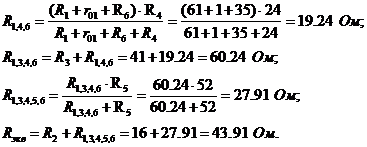
Применяем формулу разброса и 1 закон Кирхгофа, вычисляем токи
ветвей

Вычисляем токи ветвей исходной цепи (рис 1.1), выполняя
алгебраическое сложение частных токов, учитывая их направление:

1.4
Составление баланса мощностей схемы
Составить баланс мощностей для заданной схемы.
Источники 
 и
и 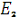
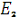 вырабатывают электрическую энергию, так как направление ЭДС и
тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи
запишется так:
вырабатывают электрическую энергию, так как направление ЭДС и
тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи
запишется так:
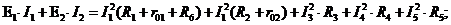
Подставляем числовые значения и вычисляем:
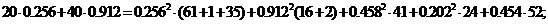
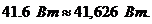
С учётом погрешности расчётов баланс мощностей практически
сошёлся.
.5
Определение тока во второй ветви методом эквивалентного генератора
Метод эквивалентного генератора используется для исследования
работы какого-либо участка в сложной электрической цепи. Определим ЭДС
эквивалентного генератора Еэ (рис. 1.5.1)
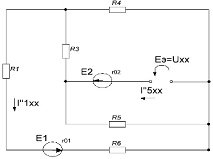
Рис. 1.5.1
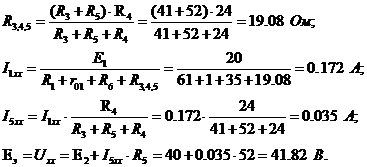
Для расчета внутреннего сопротивления эквивалентного генератора
необходимо преобразовать активный двухполюсник в пассивный (рис.1.5.2) при этом
ЭДС
 и
и
 из схемы исключается, а внутренние сопротивления этих источников
в схеме остаются.
из схемы исключается, а внутренние сопротивления этих источников
в схеме остаются.
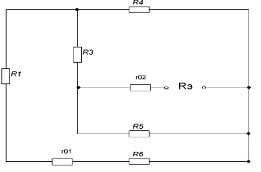
Рис.1.5.2
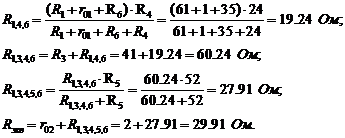
Зная ЭДС и внутреннее сопротивление эквивалентного генератора
вычисляем ток исследуемой ветви:
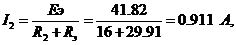
т.е. ток во второй ветви получился таким же, как и в пунктах 1.2 и
1.3.
.6 Построение
потенциальной диаграммы для контура, включающего обе ЭДС
Построить потенциальную диаграмму для любого замкнутого
контура, включающего обе ЭДС.
Возьмем контур "abcdefa”. Зададимся обходом
контура против часовой стрелки. Заземлим одну из точек контура, пусть это будет
точка "a”.
Потенциал этой точки равен нулю.
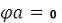
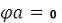 (рис. 1.6.1).
(рис. 1.6.1).
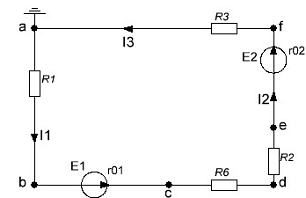
Рис. 1.6.1
Зная величину и направление токов ветвей и ЭДС, а также величины
сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента
к элементу. Начнем обход от точки "a”.

Строим потенциальную диаграмму. По оси абсцисс откладываем
сопротивления контура в той последовательности, в которой производим обход
контура, прикладывая сопротивления друг к другу, по оси ординат
 потенциалы
точек с учетом их знака.
потенциалы
точек с учетом их знака.
2. Решение
нелинейных электрических цепей постоянного тока
Построить входную вольт-амперную характеристику схемы
(рис.2.1). Определить токи во всех ветвях схемы и напряжения на отдельных
элементах, используя полученные вольтамперные характеристики.
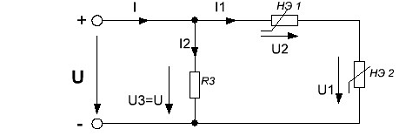
Рис 2.1
Использовать вольтамперные характеристики элементов
"а" и "б" (рис 1.37) в методическом указании.
ВАХ нэ1 U1 (I1) и нэ2
U2 (I1) на рис. 2.2
Определить: 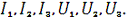
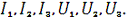
Расчёт производим графическим методом.
Построим ВАХ U (I2) тангенс угла наклона который к оси токов численно равен R3=38 Ом. Суммируя ВАХ U1 (I1) и U2 (I1) по оси напряжений получим ВАХ U (I1). Суммируя ВАХ U (I1) и U (I2) по оси
токов, получим входную ВАХ U (I). Из ВАХ U (I), U (I1) и U (I2) при U=220 В находим:
I=9.9 A; I1=4.1 A; I2=5.8
A; или 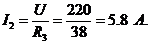
Из ВАХ U (I1) и U2 (I1) при I1=4.1 A находим: U1=130 B; U2=90 B.
Поверка:
I=I1+I2 9.9=4.1+5.8
9.9=9.9
=>
=>
U=U1+U2
220=130+90 220=220
Таким образом, токи и напряжения найдены верно.
3. Решение
однофазной линейной электрической цепи переменного тока
3.1 Схема
замещения электрической цепи, определение реактивных сопротивлений элементов
цепи
К зажимам электрической цепи, схема замещения которой приведена на
(рис. 3.1.1), подключен источник синусоидального напряжения 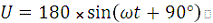
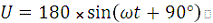 В, с частотой
В, с частотой 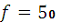
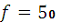 Гц.
Гц.
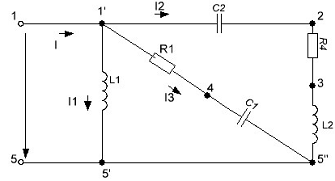
Рис. 3.1
Дано:
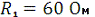
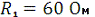 ;
; 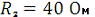
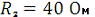 ;
;
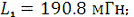
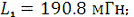
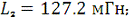
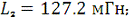
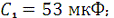
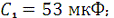
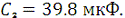
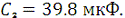
Определить: 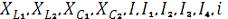
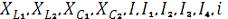 .
.
Рассчитаем реактивные сопротивления элементов цепи
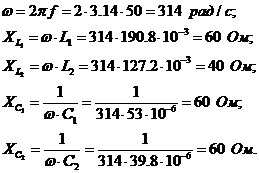
Находим комплексные сопротивления ветвей, затем участков цепи и
всей цепи (рис. 3.2)
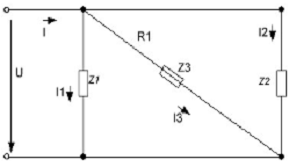
Рис 3.2
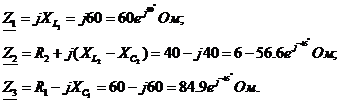
Комплекс действующего значения напряжения на входе цепи:
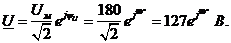
3.2
Определение действующего значения токов цепи
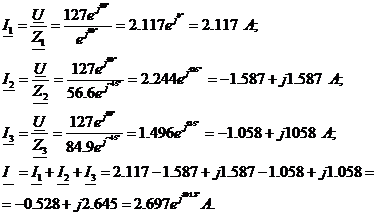
3.3
Составление уравнения мгновенного значения тока источника
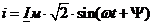
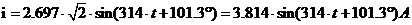
3.4
Составление баланса активных и реактивных мощностей
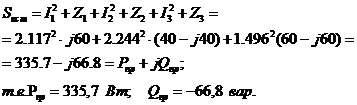
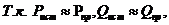
то баланс мощностей практически сходится.
3.5 Построение
векторной диаграммы токов и напряжений
Для построения топографической диаграммы напряжений определим
напряжения на сопротивлениях цепи:
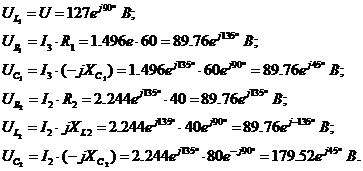
Векторная диаграмма токов, совмещенная с топографической
диаграммой напряжения построена на рис.3.3.
4. Решение
трехфазной линейной электрической цепи переменного тока
Расчет трехфазной линейной электрической цепи переменного
тока.
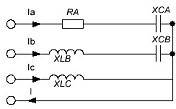
Дано: Uф=220 В;
RA=36 Ом;
XLB=20 Ом;
XLC=50 Ом;
XCA=48 Ом;
XCB=65 Ом;
Схема соединения -
4.1
Нахождение фазных токов
Выразим в комплексной форме, фазные напряжения:
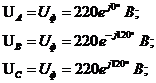
Выразим сопротивление фаз в комплексной форме:
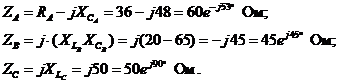
Находим комплексы фазных токов:
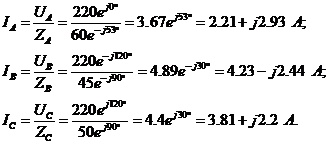
4.2
Вычисление токов в нулевом проводе
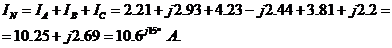
4.3
Определение активной, реактивной и полной мощности каждой фазы и всей
трехфазной цепи
Вычисляем мощности фаз и всей цепи:
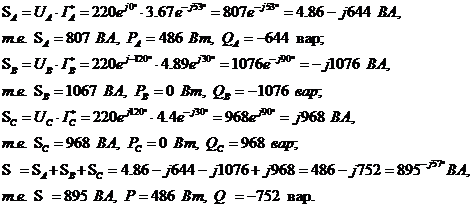
4.4
Определение угла сдвига фаз между током и напряжением в каждой фазе. Построение
векторной диаграммы трехфазной цепи
Углы сдвига фаз между током и напряжением равны:
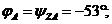
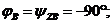
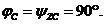
Векторная диаграмма построена на рис 4.4.1.
Заключение
В данном курсовом проекте я проводил:
анализ электрического состояния линейных электрических цепей
постоянного тока
анализ электрического состояния нелинейных электрических
цепей постоянного тока
анализ электрического состояния однофазных нелинейных
электрических цепей переменного тока
анализ электрического состояния трехфазных нелинейных
электрических цепей переменного тока
исследование переходных процессов в электрических цепях
Список
использованных источников
1)
Атабеков Г.И. Теоретические основы электротехники. - М., 2009.
)
Буртаев Ю.В., Овсянников П.Н. Теоретические основы электротехники. - М., 2009.
)
Данилов И.А., Иванов П.М. Общая электротехника с основами электроники. - М.,
2009.
)
Евдокимов Ф.Е. Теоретические основы электротехники. - М., 2011.
)
Зайчик М.Ю. Сборник задач и упражнений по теоретической электротехнике. - М.,
1989.
)
Мельников А.К. Сборник контрольных заданий и программ для решения задач с
использованием ЭВМ по теоретическим основам электротехники. - Мн., 1992.
)
Попов В.С. Теоретическая электротехника. - М., 2008. _
)
Шебес М.О. Сборник задач по теории электрических цепей. - М., 2010.
)
Государственные стандарты Республики Беларусь.