Оценка погрешностей результатов измерений
Министерство
образования и науки Российской Федерации
Факультет
дистанционного обучения (ФДО)
Томский
государственный университет систем управления и радиоэлектроники (ТУСУР)
Контрольная
работа
по
дисциплине "Метрология и радиоизмерения"
1. Систематические и случайные погрешности
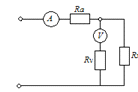
2) Методом амперметра-вольтметра измеряется
сопротивление 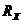 (см. рисунок).
(см. рисунок).
При этом 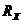 определяется
в соответствии с законом Ома по показаниям амперметра
определяется
в соответствии с законом Ома по показаниям амперметра 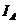 и
вольтметра
и
вольтметра 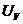 . Известно, что
. Известно, что 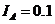 А,
А,
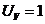 В,
В,
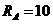 Ом,
Ом,
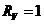 кОм.
Определить абсолютную погрешность измерения, величину поправки, исправленный
результат измерения, относительную погрешность измерения
кОм.
Определить абсолютную погрешность измерения, величину поправки, исправленный
результат измерения, относительную погрешность измерения 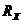 .
Классифицировать вид измерения, погрешность измерения, метод устранения
погрешности.
.
Классифицировать вид измерения, погрешность измерения, метод устранения
погрешности.
Решение
Измерения 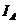 и
и
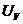 -
прямые (их значения устанавливаются по индикаторам соответствующих приборов
непосредственно в ходе измерительного эксперимента), однократные (измерения
проводятся один раз), статические (ЭДС источника и сопротивление постоянны),
абсолютные (результаты измерений получаются в соответствующих единицах ФВ).
-
прямые (их значения устанавливаются по индикаторам соответствующих приборов
непосредственно в ходе измерительного эксперимента), однократные (измерения
проводятся один раз), статические (ЭДС источника и сопротивление постоянны),
абсолютные (результаты измерений получаются в соответствующих единицах ФВ).
Измерение 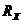 -
косвенное (определяется на основании известной зависимости по результатам
прямых измерений других величин
-
косвенное (определяется на основании известной зависимости по результатам
прямых измерений других величин 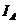 и
и 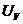 ),
однократное, статическое, абсолютное.
),
однократное, статическое, абсолютное.
Так как измерения не связаны с передачей размера
единицы ФВ и производятся рабочими СИ, то все измерения технические.
Напряжение и ток измеряются методом непосредственной
оценки, т.к. результаты измерений определяются непосредственно по отсчетным
устройствам приборов.
Погрешность измерения является в данном случае
методической, т.к. обусловлена неидеальностью метода измерения (по условию
задачи амперметр измеряет силу тока абсолютно точно, т.е. инструментальные
погрешности отсутствуют); систематической (т.к. при многократных измерениях
погрешность остается постоянной).
Результат измерения в соответствии с указанным
методом определяется на основании закона Ома по показаниям приборов:
погрешность измерение метрология
интервал
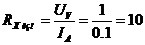 Ом.
Ом.
Определим ток через сопротивление 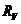 :
:
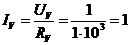 мА.
мА.
Тогда ток через сопротивление 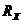 :
:
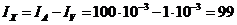 мА.
мА.
Зная ток  и
напряжение
и
напряжение 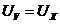 , определим
сопротивление
, определим
сопротивление 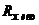 :
:
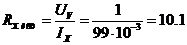 Ом.
Ом.
Абсолютная методическая погрешность измерения:
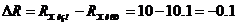 Ом.
Ом.
Относительная методическая погрешность
измерения:
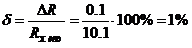 .
.
Поправка 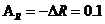 Ом,
необходимая для устранения систематической погрешности, представляет собой
абсолютную погрешность, взятую с противоположным знаком.
Ом,
необходимая для устранения систематической погрешности, представляет собой
абсолютную погрешность, взятую с противоположным знаком.
. Суммирование погрешностей
4) При измерении индуктивности получены
следующие результаты: 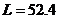 мкГн; составляющие
случайной погрешности
мкГн; составляющие
случайной погрешности 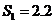 мкГн,
мкГн, 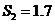 мкГн;
составляющие систематической погрешности
мкГн;
составляющие систематической погрешности 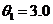 мкГн,
мкГн,
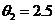 мкГн,
мкГн,
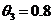 мкГн.
Записать результаты измерения при
мкГн.
Записать результаты измерения при 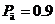 .
.
Решение
Для определения общей погрешности измерения
необходимо просуммировать отдельно составляющие систематической погрешности 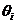 ,
отдельно составляющие случайной погрешности
,
отдельно составляющие случайной погрешности 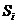 и
затем сложить полученные суммарные значения НСП и случайной погрешности в
соответствии с правилами суммирования погрешностей. Тогда границы
систематической погрешности:
и
затем сложить полученные суммарные значения НСП и случайной погрешности в
соответствии с правилами суммирования погрешностей. Тогда границы
систематической погрешности:
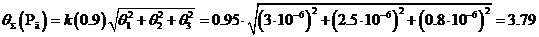 мкГн.
мкГн.
а СКП систематической погрешности:
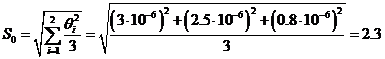 мкГн.
мкГн.
В условии задачи отсутствует указание величин
коэффициента корреляции, следовательно, составляющие случайной погрешности
некоррелированы (независимы) и суммарная СКП:
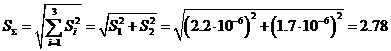 мкГн.
мкГн.
Границы доверительного интервала случайной
погрешности 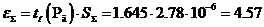 мкГн, где
мкГн, где 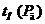 -
коэффициент нормального закона распределения.
-
коэффициент нормального закона распределения.
Далее необходимо сложить систематическую и
случайные составляющие погрешности. Сначала определяем соотношение:
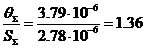 , т.е.
, т.е. 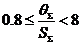 .
.
Тогда:
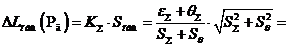
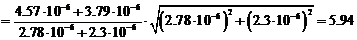 мкГн.
мкГн.
Результат измерения с учетом правил округления
погрешности и результата запишется в следующем виде:
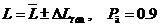 , т.е.
, т.е. 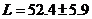 мкГн,
мкГн,
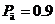 .
.
3.
Обработка однократных прямых измерений
9) Определить величину измеряемого тока, если
известно, что погрешность измерения 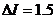 мА,
а измерения проводились амперметром с пределом шкалы 100 мА, класса точности
2.0/1.0. Повторить решение этой задачи для прибора с классом точности
мА,
а измерения проводились амперметром с пределом шкалы 100 мА, класса точности
2.0/1.0. Повторить решение этой задачи для прибора с классом точности  .
.
Решение
Для первого амперметра с классом точности
2.0/1.0 относительная погрешность определяется выражением:
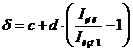 ,
,
где (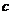 и
и 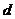 имеют
размерность %).
имеют
размерность %).
Абсолютная погрешность:
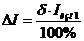 .
.
Решая совместно эти два уравнения, определим
измеренное значение тока:
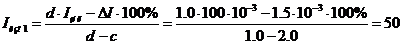 мА.
мА.
Результат измерения 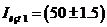 мА.
мА.
Для второго амперметра с классом точности  погрешность:
погрешность:
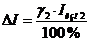 ,
,
откуда измеренное значение тока:
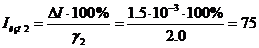 мА.
мА.
Результат измерения 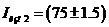 мА.
мА.
. Обработка многократных измерений
2) При многократных измерениях ёмкости получены
следующие результаты:
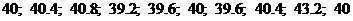 пФ.
пФ.
Записать результат измерения при доверительной
вероятности 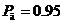 .
.
Решение
Из условия задачи следует, что полученная
совокупность результатов представляет собой выборку равноточных нормально
распределенных данных. Используя формулу:
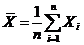 .
.
. Найдем оценку действительного значения
измеряемой величины 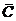 .
.
. Оценка средней квадратичной погрешности
экспериментальных данных.
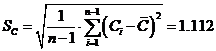 пФ.
пФ.
. В получений совокупности экспериментальных
данных девятый результат 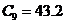 пФ существенно
отличается от остальных. Проверим, не содержит ли он грубую погрешность.
пФ существенно
отличается от остальных. Проверим, не содержит ли он грубую погрешность.
Определим
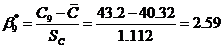 .
.
Далее найдем значение нормированных отклонений 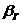 для
доверительной вероятности
для
доверительной вероятности 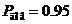 и числа выборки
равной 10 из таблицы. Имеем
и числа выборки
равной 10 из таблицы. Имеем 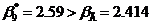 , следовательно,
результат
, следовательно,
результат 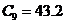 пФ содержит грубую
погрешность и должен быть отброшен.
пФ содержит грубую
погрешность и должен быть отброшен.
. Уточняем значения 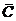 и
и
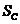 .
.
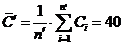 пФ;
пФ;
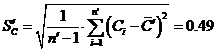 пФ.
пФ.
В оставшейся совокупности результатов следует
проверить еще результат 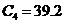 пФ. При той же
доверительной вероятности
пФ. При той же
доверительной вероятности 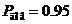 для выборки из 9
результатов находим табличное значение
для выборки из 9
результатов находим табличное значение 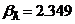 .
Определяем
.
Определяем
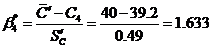 .
.
Так как 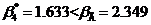 ,
результат измерения
,
результат измерения 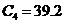 пФ должен быть
оставлен.
пФ должен быть
оставлен.
. Определим СКП результата измерения (за
результат измерения принимается уточненное значение 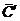 ):
):
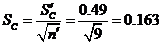 пФ.
пФ.
. Определим границы доверительного интервала для
результата измерений. Так как число обрабатываемых результатов 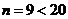 ,
то при определении коэффициента
,
то при определении коэффициента 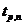 пользуемся
табличными значениями распределения Стьюдента. Задаем доверительную вероятность
пользуемся
табличными значениями распределения Стьюдента. Задаем доверительную вероятность
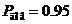 и
для выборки из 9 наблюдений находим
и
для выборки из 9 наблюдений находим 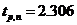 .
.
Границы доверительного интервала для результата
измерения:
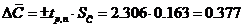 пФ.
пФ.
. Запишем результат измерения с указанием
доверительной погрешности (соблюдая все правила метрологии при округлении
значения погрешности и значения результата):
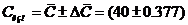 кГц;
кГц; 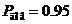 ;
;
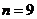
Или
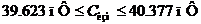 ;
; 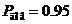 ;
;
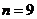 .
.
5. Обработка косвенных измерений
3) Измерение сопротивления осуществляется в
соответствии с выражением 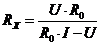 . Известно, что
. Известно, что 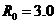 кОм;
кОм;
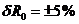 .
Показание вольтметра класса точности
.
Показание вольтметра класса точности 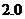 с
пределом измерения
с
пределом измерения 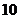 В,
В, 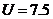 В.
Показания амперметра с классом точности с пределом
В.
Показания амперметра с классом точности с пределом  измерения
измерения 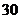 мА,
мА,
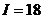 мА.
мА.
Решение
Определим оценку результата косвенных измерений 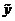 путем
подстановки оценок аргументов
путем
подстановки оценок аргументов 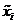 :
:
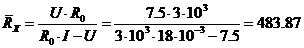 Ом.
Ом.
Вычислим числовое значение каждого коэффициента
влияния 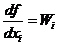 :
:
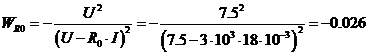 ;
;
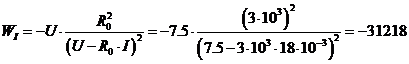 ;
;
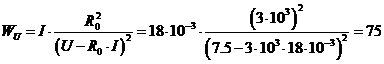 .
.
Используя 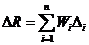 ,
абсолютную погрешность косвенного измерения
,
абсолютную погрешность косвенного измерения 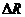 находим
по общему правилу:
находим
по общему правилу:
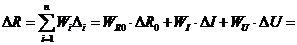
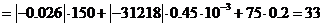 Ом.
Ом.
где - 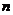 количество
аргументов, от которых зависит
количество
аргументов, от которых зависит 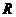 ;
;
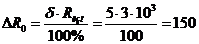 Ом;
Ом;
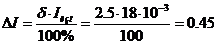 мА;
мА;
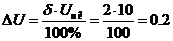 В.
В.
Соблюдая правила метрологии, запишем результат
косвенного измерения в окончательном виде:
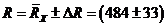 Ом,
Ом,
Или
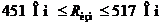 .
.