Численные методы
КАЗАНСКИЙ
ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра
прикладной математики
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
по курсу
"Информатика"
для
самостоятельной работы студентов
всех
специальностей
ЧИСЛЕННЫЕ
МЕТОДЫ
ЧАСТЬ 2
Казань
Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов,
И.Н.Гатауллин,
Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов.
УДК 621.313: 518.6
Методические указания по курсу
"Информатика" для самостоятельной работы студентов всех
специальностей. Численные методы. Часть 2. /Казанский государственный
архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов,
И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. -Казань, 2008. -35с.
Методические указания состоят из двух частей и
предназначены для самостоятельной работы студентов всех специальностей 2-го
курса дневного и заочного отделений. В данной работе приводятся численные
методы решения нелинейных уравнений, систем линейных и нелинейных
алгебраических уравнений, дифференциальных уравнений, определенных интегралов,
методы аппроксимации дискретных функций и методы решения задач линейного
программирования.
Табл. 6, библиогр. назв. 6.
Рецензент - Р.Б.Салимов, доктор физ.-мат. наук,
профессор
Казанский государственный
ã архитектурно-строительный
университет, 2008г.
5. Численное интегрирование
Требуется вычислить определенный интеграл:
I=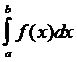 (5.1)
(5.1)
Выберем на отрезке интегрирования [а,b] n различных
узлов
a=x0<x1<x2<...xn-1< xn = b
и интерполируем функцию f(x) по ее
значениям в этих узлах некоторым полиномом Pm(x).
Тогда определенный интеграл (5.1)
приближенно можно вычислять по формуле
I´} =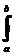 Pm(x)dx , (5.2)
Pm(x)dx , (5.2)
которая называется квадратурной
формулой интерполяционного типа.
5.1 Метод
прямоугольников
На каждом отрезке [xi, xi+1], i=0,1,2,...,n-1 функция f(x) заменяется
полиномом нулевой степени P0(x)=f(xi).
Поэтому приближенно I вычисляется
по формуле (см. рис. 5.1):
I´´ = f(x i) (xi+1- x i). (5.3)
f(x i) (xi+1- x i). (5.3)
Величина ошибки½I´-I½
определяется ошибкой интерполирования ½f(x)-Pm(x)½ на отрезке [а,b] и может
быть представлена в форме
R(f)=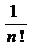
 (x-x1)(x-x2)...(x-xn)f(n)(x)dx,
(5.4)
(x-x1)(x-x2)...(x-xn)f(n)(x)dx,
(5.4)
Нахождение точного значения R(f) затрудняет
то обстоятельство, что не известна зависимость x от x. Однако,
если известна производная порядка n, то ее
всегда можно оценить
½ f(n)(x)½£
Mn , x Î [а,b].
(b-a)2
½I-I´½£ ¾¾¾ M1, (5.5)
n
где M1=max½f×(x)½- наибольшее
значение модуля первой производной f(x) на отрезке
[a, b].
y
=f(x)
(x0) f(x1)
x0=a x1 x2
... xn-1 xn=b x
Рис. 5.1. Метод прямоугольников.
Для равноотстоящих узлов формула
(5.5) имеет следующий вид:
I´
= h 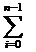 f(xi), h =
xi+1- x i (5.6)
f(xi), h =
xi+1- x i (5.6)
или I´ = h 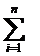 f(xi). (5.7)
f(xi). (5.7)
Формулу (5.6) называют формулой
левых прямоугольников, а (5.7) правых прямоугольников.
Программа вычисления интеграла
методом прямоугольников представлена на рис. 5.2.
REM LR-5-1,
m=13, n=5FNF(X)=2*X^2+.10,1,8A,B,N=(B-A)/N=0: X=A
S=S
+FNF(X)*H=X+HX<B
THEN 1²S=²;
S
Рис. 5.2. Программа вычисления
интеграла методом прямоугольников.
5.2 Метод
трапеций
В этом методе на каждом отрезке [xi ,xi+1] функция f(x) заменяется
полиномом 1-й степени P1(x).
По формуле Лагранжа:
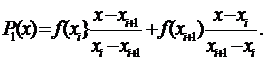 (5.9)
(5.9)
Интегрируя P1(x) на отрезке
[ xi ,xi+1], получим:
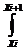 P1(x)dx =
P1(x)dx = 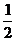 (f(xi)+f(xi+1))(xi+1-
xi) (5.10)
(f(xi)+f(xi+1))(xi+1-
xi) (5.10)
Суммируя по всем i (i =
0,1,...,n-1), получим формулу трапеций (см. рис. 5.3):
I´
= 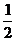
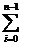 (f(xi)+f(xi+1))(xi+1-xi)
(5.11)
(f(xi)+f(xi+1))(xi+1-xi)
(5.11)
Для равноотстоящих узлов x0, x1=x0+h,...,xn=x0+nh формула
(5.11) принимает следующий вид:
I´
= h [(f(x0)+f(xn))/2+
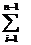 f(xi)]
(5.12)
f(xi)]
(5.12)
y(x0)
(x1)=f(x)
x0=a x1 x2
... xn-1 xn=b
Рис. 5.3. Метод трапеций.
Погрешность этого метода оценивается
следующим выражением:
½I-I´ ½£ 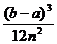 M2 , (5.13)
M2 , (5.13)
где M2=max½f²(x)½- наибольшее
значение модуля второй производной f²(x) на отрезке
[a,b].
Программа вычисления интеграла
методом трапеций представлена на рис. 5.4.
REM LR-5-2,
m=13, n=5FNF(X)=2*X^2+0.10,1,8A,B,N=(B-A)/N=(FNF(A)+FNF(B))/2= A+H
S=S+FNF(X)=X+HX<B
THEN 1=S*H²S=²;
S
Рис. 5.4. Программа вычисления
интеграла методом трапеций.
Метод парабол (Симпсона)
Интервал [a,b] разделим
на 2n отрезков.
Группируя узлы тройками xi-1,xi,xi+1, на
каждом отрезке [xi-1,xi+1] i=1,3,...,2n-1
интерполируем функцию f(x) полиномом
2-й степени P2(x):
По формуле Лагранжа:
P2(x)=f(xi-1)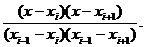 +f(xi)
+f(xi)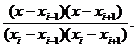 +
+
+ f(xi+1) 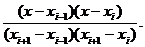 .
.
Интегрируя P2(x) на отрезке
[xi-1 ,xi+1], получим:
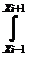 P2(x)dx =
P2(x)dx = 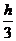 [f(xi-1)+4f(xi)+f(xi+1)]
. (5.14)
[f(xi-1)+4f(xi)+f(xi+1)]
. (5.14)
Суммируя формулу (5.14) по всем n блокам,
получаем формулу для приближенного интегрирования (см. рис.5.5):
´
= 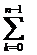
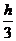 [(f(x2k)+4f(x2k+1)+f(x2k+2)] (5.15)
[(f(x2k)+4f(x2k+1)+f(x2k+2)] (5.15)
Погрешность метода Симпсона
оценивается формулой:
½I-I´ ½£ 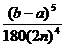 M4 , (5.16)
M4 , (5.16)
где M4=max½fIV(x)½- наибольшее
значение модуля четвертой производной fIV(x) на отрезке
[a,b].
y(x0)
(x1)(x2)
y=f(x)
x0=a x1 x2
... x2n-1 x2n=b
Рис. 5.3. Метод
парабол (Симпсона).
Пример: Требуется вычислить
определенный интеграл методами прямоугольников, трапеций и парабол:
I = 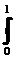 (2x2+0,1) dx
(2x2+0,1) dx
Решение: Выберем на отрезке
интегрирования [0,1] n=8 различных
узлов
=x0<x1<x2<...x7< x8 =1
Шаг разбиения для равноотстоящих
узлов h = xi+1-x i определяем
по формуле
h = (b-a)/n = (1-0)/8
=0,125
Тогда определенный интеграл
приближенно можно вычислять по формуле левых прямоугольников
I´ = h 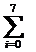 (2xi2+0,1)
(2xi2+0,1)
или по формуле правых
прямоугольников
I´ = h 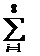 (2xi2+0,1)
(2xi2+0,1)
Определенный интеграл вычислим по
формуле трапеций
I´
= h [(f(x0)+f(xn))/2+
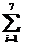 f(xi)]
f(xi)]
Определенный интеграл вычислим по
формуле парабол
I´
= 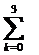
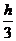 [(f(x2k)+4f(x2k+1)+f(x2k+2)]
[(f(x2k)+4f(x2k+1)+f(x2k+2)]
Результаты решения приводятся в
таблице 5.3
Таблицы 5.3
|
i
|
xi
|
f(xi)
|
h
f(xi)
|
Метод
левых прямоуголь-ников
|
Метод правых
прямоуголь-ников
|
Метод
трапеций
|
Метод
парабол
|
|
0
|
0
|
0,1
|
0,0125
|
0,0125
|
0
|
0,00625
|
0,004167
|
|
1
|
0,125
|
0,13125
|
0,016406
|
0,016406
|
0,016406
|
0,016406
|
0,021875
|
|
2
|
0,25
|
0,225
|
0,028125
|
0,028125
|
0,028125
|
0,028125
|
0,01875
|
|
3
|
0,375
|
0,38125
|
0,047656
|
0,047656
|
0,047656
|
0,047656
|
0,063542
|
|
4
|
0,5
|
0,6
|
0,075
|
0,075
|
0,075
|
0,075
|
0,05
|
|
5
|
0,625
|
0,88125
|
0,110156
|
0,110156
|
0,110156
|
0,110156
|
0,146875
|
|
6
|
0,75
|
1,225
|
0,153125
|
0,153125
|
0,153125
|
0,153125
|
0,102083
|
|
7
|
0,875
|
1,63125
|
0,203906
|
0,203906
|
0,203906
|
0,203906
|
0,271875
|
|
8
|
1
|
2,1
|
0,2625
|
0
|
0,2625
|
0,13125
|
0,0875
|
|
Ответ
|
|
|
0,646875
|
0,896875
|
0,771875
|
0,766667
|
Программа вычисления интеграла методом парабол
(Симпсона) представлена на рис. 5.6.
CLSLR-5-3, m=13,
n=5FNF(X)=2*X^2+0.10,1,4A,B,N=(B-A)/N/2=0=A
S=S+H*(FNF(X)+4*FNF(X+H)+FNF(X+2*H))/3=X+2*HX<B-H
THEN 1²S=²;
S
Рис. 5.6. Программа
вычисления интеграла методом парабол (Симпсона).
6. Решение задачи Коши
для обыкновенных дифференциальных уравнений
В зависимости от числа независимых переменных
дифференциальные уравнения делятся на две категории:
обыкновенные дифференциальные уравнения,
содержащие одну независимую переменную;
уравнения с частными производными, содержащие
несколько независимых переменных.
Обыкновенными дифференциальными уравнениями
называются такие уравнения, которые содержат одну или несколько производных от
искомой функции y=y(x):
F(x,y,y¢,...,y(n))=0
, (6.1)
где х - независимая переменная, n
- порядок дифференциального уравнения.
Уравнения первого и второго порядков
записываются в виде:
F(x,y,y¢)=0,
F(x,y,y¢,y¢¢)=0.
Записи: y¢=f(x,y),
y¢¢=f(x,y,y¢)
(6.2)
называются уравнениями, разрешенными
относительно старшей производной.
Линейным дифференциальным уравнением называется
уравнение, линейное относительно искомой функции и ее производных. Например,
y¢-
x2 y
= sin(x)
- линейное уравнение первого порядка.
Решением дифференциального уравнения (6.1)
называется всякая функция y=j(x),
которая после ее подстановки в уравнение превращает ее в тождество.
Общее решение обыкновенного дифференциального
уравнения n-го порядка
содержит n произвольных
постоянных c1,c2,...,cn
y=j(
c1,c2,...,cn)
(6.3)
Частное решение дифференциального уравнения
получается из общего, если произвольным постоянным придать определенные
значения.
Для уравнения первого порядка общее решение
зависит от одной произвольной постоянной:
y=j(x,c).
(6.4)
Если постоянная принимает определенное значение
с=с0, то получим частное решение: y=j(x,c0).
Дадим геометрическую интерпретацию
дифференциального уравнения первого порядка (6.2).
Поскольку производная y¢
характеризует наклон касательной k интегральной
кривой в данной точке, то при y¢=k=const
из (6.2) получим f(x,y)=k
- уравнение линии постоянного наклона, называемой изоклиной. Меняя k,
получаем семейство изоклин.
Приведем геометрическую интерпретацию общего
решения (6.4). Это решение описывает бесконечное множество интегральных кривых
с параметром c, а частному
решению соответствует одна кривая из этого семейства. Через каждую точку из
области решения проходит одна интегральная кривая.
Для выделения некоторого частного решения
уравнения первого порядка достаточно задать координаты (x0,y0)
произвольной точки на данной интегральной кривой.
Для уравнений высших порядков для выделения
частного решения из общего нужно задавать столько дополнительных условий,
сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения.
Если эти условия задаются в одной точке, то
такая задача называется задачей Коши. Дополнительные условия в задаче Коши
называются начальными условиями х = x0,
в которой они задаются, - начальной точкой.
Если же дополнительные условия задаются при различных
значениях независимой переменной, то такая задача называется краевой. Сами
дополнительные условия называются граничными условиями.
Наиболее распространенным и универсальным
численным методом решения дифференциальных уравнений является метод конечных
разностей. Его сущность состоит в следующем. Область непрерывного изменения
аргумента, заменяется дискретным множеством точек, называемых узлами, и задача
считается решенной, если найдены неизвестные значения функции в этих точках.
Численные методы решения дифференциальных уравнений методом конечных разностей
проводятся в два этапа:
1 Аппроксимация
дифференциального уравнения системой линейных и нелинейных разностных уравнений;
2 Решение
полученной системы разностных уравнений.
Разностные методы позволяют находить только
конкретное (частное) решение, однако необходимо подчеркнуть, что эти методы в
настоящее время являются основными при решении дифференциальных уравнений с
помощью ЭВМ.
Одним из простейших разностных методов решения
обыкновенного дифференциального уравнения является одношаговый метод Эйлера.
Пусть требуется решить задачу Коши для уравнения
первого порядка:
y¢=f(x
,y), y(x0)=
y0 (6.5)
на отрезке [а,b].
На данном отрезке выбираем некоторую
совокупность узловых точек a=x0<
x1<x2<
...<x
n=b
и разложим искомую функцию y(x)
в ряд Тейлора в их окрестностях.
6.1 Метод Эйлера
Если отбросить все члены, содержащие производные
второго и более высоких порядков, и считать узлы равностоящими, т.е. Dxi=xi+1-xi=h,
то это разложение можно записать в виде:
y(xi+1) = yi+1 = yi + h f(xi,yi), i
=0,1,...,n-1. (6.6)
Соотношения (6.6) имеют вид рекурентных формул,
с помощью которых значение сеточной функции yi+1
в любом узле xi+1
вычисляется по ее значению yi
в предыдущем узле xi.
На каждом шаге погрешность имеет порядок O(h2).
На рис. 6.1 дана геометрическая интерпретация метода Эйлера. В силу невысокой
точности формулой Эйлера редко пользуются в практических расчетах и используют
более точные методы. Например, модифицированный метод Эйлера.
y
y2
y0
y1
x0 x1
x2 x
Рис. 6.1. Метод Эйлера.
Пример: Решить задачу Коши методом Эйлера для
дифференциального уравнения
y¢=x2+y,
y(0)= 1 на отрезке [0;0,3]
с шагом 0,1.
Решение: По формуле (6.6) вычислим значение y1
y1 = y0
+ h f(x0,y0)
= 1 +0,1 (02 +1) = 1,1
Аналогично вычисляются последующие значения
функции в узловых точках
y2 = y1 + h
f(x1,y1)=1,1+0,1·(0,12+1,1) = 1,211= y2 + h f(x2,y2)=1,211+0,1·(0,22+1,211) =
1,3361
Сеточную функцию записываем в виде таблицы
x 0 0,1 0,2 0,3
y 1 1,1 1,211 1,3361
Программа решения задачи Коши методом Эйлера
дана на рис. 6.2.
CLSLR-6-1, m=13, n=5FNY(X,Y)=X^2+Y0,
0.3, 1, 0.1A, B, Y0, HA;Y0=A: Y=Y0
Y=Y+ FNY(X,Y)*H=X+HX;YX<B THEN 1
Рис. 6.2. Программа решения задачи Коши методом
Эйлера.
6.2 Модифицированный метод Эйлера
Модифицированный метод Эйлера позволяет
уменьшить погрешность на каждом шагу до величины O(h3)
вместо O(h2)
в обычном методе (6.6). Запишем разложение функции в ряд Тейлора в виде:
yi+1 = yi
+ h y¢i
+ h2/2 y¢¢i
+ O(h3).
(6.7)
Аппроксимируем вторую производную с помощью
отношения конечных разностей: y¢¢i
= (y¢i+1
- y¢i)
/ h.
Подставляя это соотношение в (6.7) и пренебрегая
членами порядка O(h3),
получаем:
yi+1 = yi + h/2 [f(xi,yi) +
f(xi+1,yi+1)]. (6.8)
Полученная схема является неявной, поскольку
искомое значение yi+1
входит в обе части соотношения (6.8) и его нельзя выразить явно. Если имеется
хорошее начальное приближение yi,
то можно построить решение с использованием двух итераций следующим образом.
Сначала по формуле (6.6) вычисляют первое приближение y}i+1
y}i+1=
yi + h
f(yi,xi).
(6.9)
Найденное значение подставляется вместо yi+1
в правую часть соотношения (6.8) и находится окончательное значение
yi+1 = yi + h[f(xi,yi) + f(xi+1, y}i+1)]/2,
i=0,1,...,n-1. (6.10)
На рис. 6.3 дана геометрическая интерпретация
первого шага вычислений при решении задачи Коши модифицированным методом
Эйлера.
y
}1
x0 h/2 h/2 x1 x
Рис. 6.3. Модифицированный
метод Эйлера.
Пример: Решить задачу Коши модифицированным
методом Эйлера для дифференциального уравнения
y¢=x2+y,
y(0)= 1 на отрезке [0;0,3]
с шагом 0.1.
Решение: По формуле (6.9) вычислим первое
приближение y}1
y}1
= y0 + h
f(x0,y0)
= 1 +0,1 (02 +1) = 1,1
Используя формулу (6.10), находим окончательное
значение в точке x1=0.1
y1=y0+h
[f(x0,y0)+f(x1,
y}1)]/2=1+0,1·
(02+1+0,12+1,1)/2=1,1055
Аналогично вычисляются последующие значения
функции в узловых точках
y}2
= y1 + h f(x1,y1)=1,1055+0,1· (0,12+1,1055) = 1,21705=y1+h[f(x1,y1)+f(x2,y}2)]/2=
=1,1055+0,1·
(0,12+1,1055+0,22+1,21705)/2=1,224128}3
= y2 + h f(x2,y2)=1,224128+0,1· (0,22+1,224128) = 1,350541=y2+h[f(x2,y2)+f(x3,y}3)]/2=
=1,224128+0,1·
(0,12+1,224128+0,22+1,350541)/2=1,355361
Сеточную функцию записываем в виде таблицы
x 0 0.1 0.2 0.3
y 1 1.1055 1,224128
1,355361
Программа решения задачи Коши модифицированным
методом Эйлера дана на рис. 6.4.
CLSLR-6-2, m=13, n=5FNY(X,Y)=X^2+Y0,
0.3, 1, 0.1A, B, Y0, HA;Y0=A: Y=Y0
Y1=Y+
FNY(X,Y)*H=Y+H*(FNY(X,Y)+FNY(X+H,Y1))/2=X+HX;YX<B THEN 1
Рис. 6.4. Программа решения задачи Коши
модифицированным методом Эйлера.
Существуют и другие одношаговые методы. Наиболее
распространенным из них является метод Рунге-Кутта.
6.3 Метод Рунге-Кутта
На основе метода Рунге-Кутта могут быть
построены разностные схемы разного порядка точности. Наиболее употребительной
является следующая схема четвертого порядка:
yi+1 = yi
+ (k0 + 2k1
+ 2k2 + k3)
/6. (6.11)
где
k0 = h
f(xi,
yi),
k1 = h f(xi+h/2, yi+ k0 /2),= h
f(xi+h/2, yi+ k1 /2), (6.12)3= h
f(xi+h,
yi+ k2).
Таким образом, метод Рунге-Кутта требует на
каждом шаге четырехкратного вычисления правой части уравнения. Однако это
окупается повышенной точностью, что дает возможность проводить счет с
относительно большим шагом.
Пример: Решить задачу Коши методом Рунге-Кутта
для дифференциального уравнения
y¢=x2+y,
y(0)= 1 на отрезке [0,0.3]
с шагом 0.1.
Решение: По формулам (6.12) вычислим значения k0
, k1, k2,
k3
k0=h f(x0,y0)=0,1·(02+1)=0,1=h
f(x0+h/2, y0+k0 /2)=0,1· ((0+0,1/2)2+1+0,1/2)=0,10525=h f(x0+h/2,y0+k1 /2)=0,1·
((0+0,1/2)2+1+0,10525/2)=0,105513= h f(x0+h, y0+ k2)=0,1· ((0+0,1)2+1+0,105513)=
0,111551
Используя формулу (6.11), находим значение y1
в точке x1=0.1
y1=y0+(k0+2k1+2k2+k3)/6=
=1+(0,1+2·0,10525+2·0,105513+0,111551)/6=1,105513
Аналогично вычисляются последующие значения
функции в узловых точках
k0=h f(x1,y1)=0,1· (0,12+1,105513)=0,111551=h
f(x1+h/2,y1+k0/2)=0,1· ((0,1+0,1/2)2+1,105513+0,111551/2)=0,118379=h
f(x1+h/2,y1+k1/2)=0,1· ((0,1+0,1/2)2+1,105513+0,118379/2)=0,11872= h
f(x1+h,y1k2)=0,1· ((0,1+0,1)2+1,105513+0,11872)=0,126423=y1+(k0+2k1+2k2+k3)/6=
=1,105513+(0,111551+2·0,118379+2·0,11872+0,126423)/6=1,224208=h
f(x2,y2)=0,1· (0,22+1,224208)=0,126421=h f(x2+h/2, y2+k0 /2)=0,1·
((0,2+0,1/2)2+1,224208+0,126421/2)=0,134992=h f(x2+h/2,y2+k1 /2)=0,1·
((0,2+0,1/2)2+1,224208+0,134992/2)=0,13542=h f(x2+h,y2+k2)=0,1· ((0,2+0,1)2+1,224208+0,13542)=0,144963=y2+(k0+2k1+2k2+k3)/6=
=1,224208+(0,126421+2·0,134992+2·0,13542+0,144963)/6=1,359576
Сеточную функцию записываем в виде таблицы
x 0 0.1 0.2 0.3
y 1 1,105513
1,224208 1,359576
Программа решения задачи Коши методом
Рунге-Кутта дана на рис. 6.5.
CLSLR-6-3, m=13, n=5FNY(X,Y)=X^2+Y0,
0.3, 1, 0.1A, B, Y0, HA;Y0=A: Y=Y0
K0 = H*FNY(X,Y)=
H*FNY(X+H/2,Y+K0/2)= H*FNY(X+H/2,Y+K1/2)=
H*FNY(X+H,Y+K2)=Y+(K0+2*K1+2*K2+K3)/6=X+HX;YX<B THEN 1
Рис. 6.5. Программа решения задачи Коши методом
Рунге-Кутта.
.4 Разностные
методы решения краевой задачи для обыкновенного дифференциального уравнения
Линейная краевая задача имеет вид:
y¢¢+
p(x) y¢+ q(x) y = f(x)
(6.12)
a1y(a) + a2
y¢(a) = a3
,
(6.13)
b1 y(b)+ b2
y¢(b) = b3
,
при |a1|+|a2|
¹ 0 |b1|+|b2|
¹ 0 xÎ[a,b].
Решение задачи (6.12)-(6.13)
проводится в следующей последовательности:
1 Определение
сетки:
Отрезок [a,b]
делится на конечное число частей:
y1 y2 . .
.
yk .
.
.
.
.
yn-1 yn yn+1
| |
| |
| |=a
x2 .
.
.
xk .
.
.
.
.
xn-1 xn xn+1=b x
____
xk=x1
+
(k -
1)h;
k=1,n+1;
h=(b-a)/n.
x1, xn+1 - краевые точки, x2, x3, .
.
.
, xn-1, xn - внутренние точки.
2 Определение
сеточной функции yi = y(xi):
|
x1
|
x2
|
x3
|
...
|
xn+1
|
|
у1
|
у2
|
у3
|
...
|
у
n+1
|
3
Аппроксимация
уравнения:
Aппроксимация производных y¢(x)
и y¢¢(x)
центральными конечноразностными аналогами имеет вид:
¢(xk)=(y(xk+h)-y(xk-h))/2h+O(h2),
(6.14)¢¢(xk)=(y(xk+h)-2y(xk)+y(xk-h))/h2+O(h2).
(6.15)
Подстановка полученных соотношений (6.14)¾(6.15)
в уравнение (6.12) дает
(yk+1-2yk+yk-1)/h2+pk(yk+1-yk-1)/2h+qkyk=fk,
(6.16)
где yk=y(xk), pk=p(xk),
qk=q(xk),
fk=f(xk).
yk+1-2yk+yk-1+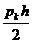 yk+1-
yk+1- 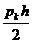 yk-1+qkh2yk=fkh2,
yk-1+qkh2yk=fkh2,
(1-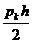 )
yk-1+(qkh2-2)yk+(1+
)
yk-1+(qkh2-2)yk+(1+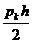 ) yk+1=fkh2.
) yk+1=fkh2.
После этих преобразований уравнение
(6.16) можно
представить в виде:
+ckyk+bkyk+1=dk, k=2,n (6.17)
где ak= 1-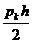 , bk= 1+
, bk= 1+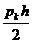 , ck=gkh2-2, dk= fkh2.
, ck=gkh2-2, dk= fkh2.
Для краевых условий применяем следующие
разностные формулы:
или
¢(а)=(y¢(x1)=(y(x2)-y(x1))/h=(y2-y1)/h
,
y¢(b)=y¢(x
n+1)=(y(x
n+1)-y(x
n))/h=(y
n+1-y
n)/h
.
Подставляя в краевые условия (8.2)-(8.3)
получим:
a1y1 + a2
(y2-y1)/h
= a3 ,
b1 y(b)+ b2
(y n+1-y
n)/h
= b3 .
После преобразований краевые условия (6.13)
запишем в виде:
c1y1 + b1y2 = d1 , (6.18)+1yn + c
n+1yn+1 = d n+1 , (6.19)
где c1 = a1
h -
a2; b1 = a2;
d1 = a3 h;+1 = - b2;
cn+1 = b1 h + b2;
d n+1 = b3 h.
Таким образом, для определения (n+1)
неизвестных величин yk
составляется (n+1) уравнений вида:
c1y1
+ b1y2
= d1 ,
k=1+ckyk+bkyk+1=dk, k=2,n (6.20)
an+1yn + c n+1yn+1 = d n+1 , k=n+1.
Система (n+1)
уравнений (8.10) решается методом прогонки.
Пример: Решить краевую задачу методом конечных
разностей с шагом h = 0,1:
y¢¢
- xy¢+ 2xy
= 0,8
y(1,2) - 0,5y¢(1,2)
= 1
y¢(1,5)
= 2.
Решение. Решение проводим в следующей
последовательности:
1 Определение
сетки:
| |
| |=1,2
x2=1,3 x3=1,4 x4=1,5 x
, x4 - краевые точки, x2, x3 - внутренние точки.
2 Определение
сеточной функции yi = y(xi):
3. Аппроксимация уравнения:
при x1=1,2: у1-0,5(y2-y1)/0,1
= 1 (6.21)
при x2=1,3: (у3-2у2+у1)/0,01-1,3(y3-y1)/0,2+2*1,3y2=0,8
(6.22)
при x3=1,4: (у4-2у3+у2)/0,01-1,4(y4-y2)/0,2+2*1,4y3=0,8
(6.23)
при x4=1,5: (y4-y3)/0,1
= 2. (6.24)
Полученная система четырех линейных уравнений с
четырьмя неизвестными у1, у2, у3 и у4 решается методом прогонки.
у1-5(y2-y1) = 1
(у3-2у2+у1) -6,5(y3-y1)+2*1,3y2=0,8
(у4-2у3+у2) -7(y4-y2)+2*1,4y3=0,8
(y4-y3) = 2
у1 - 5y2 = 1
,5у1 - 197,4у2 + 93,5у3 = 0,8
у2 -197,2у3+93у4 = 0,8
-10y3+10y4 = 2
Значения ai;
bi; ci;
di; i=1,
2, 3, 4 записываем в виде таблицы 6.1.
Таблица 6.1
|
i
|
ai
|
bi
|
ci
|
di
|
|
1
|
0
|
6
|
- 5
|
1
|
|
2
|
106,5
|
-
197,4
|
93,5
|
0,8
|
|
3
|
107
|
-197,2
|
93
|
0,8
|
|
4
|
-10
|
10
|
0
|
2
|
Прямой ход прогонки. Определяем прогоночные
коэффициенты Ui и Vi
(i=1,2,3,4)
U1=-c1/b1=5/6=0,833333=d1/b1=1/6=0,166667=-c2
/(b2 + a2U1)=- 93,5/(-197,4+106,5*0,833333)= 0,860561=(d2-a2V1)/(b2+a2U1)=
=(0,8-106,5·0,166667)/(-197,4+106,5·0,833333)=0,156006=-c3
/(b3+a3U2)=-93/(-197,2+107·0,860561)=0,884703=(d3-a3V2)/(b3+a3U2)=(0,8-107·0,156006)/(-197,2+107·0,860561)=0,151186=-c4
/(b4+a4U3)=0=(d4-a4V3)/(b4+a4U3)=(2+10·0,151186)/(10-10·0,884703)=3,045925
Обратный ход прогонки. По формулам (2.7)
вычисляем все xi; i=4,3,2,1).
Поскольку cn
= 0, то y4 = V4
= 3,045925.
Далее вычисляем y3,
y2, y1
y3 = U3
y4 + V3
= 0,884703·3,045925+0,151186=2,845925
y2 = U2
y3 + V2
=0,860561·2,845925+0,156006=2,605098
y1 = U1
y2 + V1
=0,833333·2,605098+0,166667=2,337581
Сеточную функцию yi
= y(xi) записываем в виде
таблицы
|
xi
|
1,2
|
1,3
|
1,4
|
1,5
|
|
yi
|
2,337581
|
2,605098
|
2,845925
|
3,045925
|
интеграл дифференциальный уравнение
программирование
7. Задачи линейного
программирования
Общая постановка задачи ЛП включает целевую
функцию
f(x1,x2,x3,...,xn)=c1x1+c2x2+...+cnxn
® max (min) (7.1)
ограничения типа равенств
gi=ai1x1+ai2x2+...+ain
xn+bi=0
i=1,2,...,k
(7.2)
и ограничения типа неравенств
gi=ai1x1+ai2x2+...+ain
xn+bi£0
i=k+1,k+2,...,n
(7.3)
В задачах ЛП в число ограничений очень часто
входит условие положительности переменных:
xj
³ 0, i
= 1, ..., n (7.4)
Обычно оно связано с тем, что xi
в этих задачах означает количество объектов i-того
типа (производимых, перевозимых, потребляемых и т.п.).
7.1 Графический метод
решения задач линейного программирования
Пусть дана задача:
=С1Х1+С2Х2 ®
max
а11Х1 + а12Х2 £
а1
а21Х1 + а22Х2 £
а2 (7.5)
...
аm1Х1
+ аm2Х2 £
аm.
Введем на плоскости декартову прямоугольную
систему координат и сопоставим каждой паре чисел (Х1,Х2) точку плоскости с
координатами Х1 и Х2. Выясним, прежде всего, что будет представлять собой
множество точек, соответствующих допустимым решениям данной задачи.
Рассмотрим сначала одно линейное неравенство с
двумя переменными:
а11Х1 + а12Х2 £
а2.
Оно, как известно, определяет на плоскости одну
из двух частей (полуплоскостей), на которые прямая а11Х1+а12Х2=а1, разбивает
плоскость. При этом соответствующая полуплоскость включает и граничную прямую
а11Х1+а12Х2=а1 (замкнутая полуплоскость). Чтобы определить, какую именно из
двух замкнутых полуплоскостей определяет данное неравенство, достаточно
подставить в него координаты одной какой- нибудь точки, не лежащей на граничной
прямой. Если неравенство удовлетворяется, то искомая полуплоскость та, в
которой лежит взятая точка, а если не удовлетворяется- то противоположная ей.
Пусть допустимая область задачи линейного
программирования (7.1) оказалась непустой (многоугольник MNP0
на рис. 7.1).
Как геометрически найти оптимальные точки?
Оптимальными являются те точки допустимой области, координаты которых
доставляют целевой функции наибольшее значение.
Определяем градиент функции ®grad
f:
®grad
f={C1,
C2}.
x2
M
С1Х1+ С2Х2=c
Af
x1
P
Рис. 7.1
Линия f(x,y)=c
при любом значении постоянной c
представляет собою прямую, перпендикулярную вектору grad
f. Считая c
параметром, получаем семейство параллельных прямых (называемых линиями
постоянного значения, или линиями уровня функции). Нас интересуют, в
соответствии с нашей задачей, те точки допустимой обласи, которые принадлежать
линии уровня с наибольшим значением c
по сравнению с его значениями для всех других линей уровня, пересекающихся с
допустимой областью. Увеличение c
соответствует перемещению линии уровня вдоль ®grad
f. Следовательно,
чтобы найти оптимальные точки допустимого множества задачи на максимум, нужно
перемещать линии уровня в направлении вектора ®grad
f, начиная с какого
- нибудь фиксированного положения, при котором она пересекается с допустимой
областью (точка А на рис. 7.1) до тех пор, пока она не перестанет пересекаться
с ней. В точке области допустимых значений, в которой функция f
достигает максимума, линия уровня покидает D.
Поэтому, если мы найдем проекцию D
на направление ®grad
f, то точка
максимума будет проектироваться на конец полученного отрезка. Пересечение
допустимой области с линией уровня в том ее положении, когда дальнейшее
перемещение дает пустое пересечение, и будет множеством оптимальных точек
задачи линейного программирования (на рис. 7.1 это единственная точка N).
Аналогично, при уменьшении c
соответствующая линия уровня покинет D
в точке минимума f, и эта
точка проектируется на начало отрезка-проекции D
на направление grad
f.
В качестве примера рассмотрим задачу о
распределении ресурсов.
Пример. Имеется 300 кг металла, 100 м2 стекла и
160 - человеко-часов рабочего времени; из них изготавливают изделия двух
наименований А и Б; стоимость одного изделия А равна 10 $, для его изготовления
нужно 4 кг металла, 2 м2 стекла и 2 человеко-часа рабочего времени; стоимость
одного изделия Б равна 12 $, для его изготовления нужно 5 кг металла, 1 м2
стекла и 3 человеко-часа рабочего времени; требуется спланировать производство
так, чтоб произвести изделия с максимальной стоимостью.
Решение. Допустим, что предприятие выпускает x1
единиц продукции вида A и x2 единиц продукции вида B. Для этого потребуется
4*x1+ 5*x2 единиц металла. Так как в наличии имеется всего 300 единиц металла, то
должно выполняться неравенство
*x1+ 5*x2£ 300
Аналогичные рассуждения, проведенные для
остальных видов сырья и рабочего времени, позволяют записать следующие
неравенства
*x1+ x2£ 100
*x1+ 3*x2£ 160
При этих условиях доход Z, получаемый
предприятием, составит
= f(x1, x2) = 10*x1 + 12*x2 ®
max (7.6)
Таким образом, математически задачу можно
сформулировать так:
Найти max Z = 10*x1 + 12*x2
при ограничениях
*x1+ 5*x2£ 300
*x1+ x2£ 100 (7.7)
*x1+ 3*x2£ 160³
0; x2 ³
0.
Введем на плоскости прямоугольную декартову
систему координат x10x2. Известно, что геометрическое место точек на плоскости,
координаты которых удовлетворяют системе линейных неравенств, образуют выпуклый
многоугольник.
Этот многоугольник называется многоугольником
решений данной системы неравенств. Стороны этого многоугольника располагаются
на прямых, уравнения которых получаются, если в неравенствах системы знаки
неравенств заменить на знаки равенств. А сам этот многоугольник есть общая
часть полуплоскостей, на которые делит плоскость каждая из указанных прямых.
Вычертим эти прямые (рис 7.2).
x2
100 -
90 - (2)
80 -
70 -
60 - (1)
50 - P
40 -
30 - •
M R
20 -
10 - ®grad
f F (3)
0 ¹
¹
¹
¹
¹
¹
¹
¹
¹
¹
x1
10
20 30 40 50 60 70 80 90 100
Рис. 7.2
Полуплоскости в пересечении дают многоугольник
решений 0PRF. При этом, любая точка из внутренности многоугольника
удовлетворяет всем неравенствам (7.7).
Рассмотрим линейную форму (7.6)
(x1, x2) = 10*x1 + 12*x2.
Выберем внутреннюю точку M0(x1,x2), например
x1=10, x2=30, и вычислим значение целевой функции Z0=F(10,30)=10*10+12*30=460.
Уравнение 10*x1+12*x2=Z0 определяет на плоскости
геометрическое место точек, в которых прямая f(x1,x2) принимает постоянное
значение Z0. Меняя значение Z0, получаем различные прямые, однако все они
параллельны между собой, т.е. образуют семейство параллельных прямых. Эти
прямые перпендикулярны вектору ®grad f=10®e1+12®e2.
Вектор ®grad
f указывает направление, двигаясь в котором, мы переходим от меньших значений
формы к большим. Теперь должно быть ясным, что оптимальное решение определяется
точкой R(35,30) (рис.7.2), и наибольшее значение формы f равно 10*35+12*35=710.
Итак, оптимальное решение задачи найдено x1=30,
x2=35.
7.2 Симплекс метод
решения задач линейного программирования
На практике в задачах планирования приходится
решать задачи линейного программирования с очень большим числом переменных. При
большом числе переменных мы не можем воспользоваться графическим методом, и
нужны иные способы решения задачи.
Канонический вид задачи ЛП. Прежде всего задачу
линейного программирования (ЛП) приводят к некоторому стандартному виду,
называемому каноническим.
Как мы знаем, общая постановка задачи ЛП
включает целевую функцию
f(x1,x2,x3,...,xn)=c1x1+c2x2+...+cnxn
® max (min)
ограничения типа равенств
gi=ai1x1+ai2x2+...+ain
xn+bi=0
i=1,2,...,k
и ограничения типа неравенств
gi=ai1x1+ai2x2+...+ain
xn+bi£0
i=k+1,k+2,...,n
Всюду ниже мы будем считать, что на переменные
наложено условие
xj
³ 0, i
= 1, ..., n
Прежде всего отметим, что при разработке методов
решения задач ЛП достаточно рассматривать задачи минимизации, поскольку любая
задача на максимум сводится к задаче на минимум путем замены целевой функции f
на новую целевую функцию F=
-f.
Далее, мы можем исключить из состава ограничений
неравенства. Для этого вводятся l
дополнительных положительных переменных xn+1,xn+2,...,xn+l,
и задача приобретает вид
min
f(x1,...,xn,xn+1,...,xn+l)=c1*x1+c2*x2+...+cn+l*xn+l
(7.8)
(здесь cn+1=
cn+2= ... = cn+l
= 0),
a11x1+ a12x2+ ... + a1,n xn = b1
.............x1+ ak2x2+ ... + ak,n
xn = bk (7.9)+1,1x1+ ak+1,2x2+ ... + ak+1,n+1xn+1= bk+1
.............+l,1x1+ ak+l,2x2+ ... +
ak+l,n+lxn+l = bk+l ³
0, j = 1, ..., n
+ l . (7.10)
Как мы видим, каноническая форма задачи ЛП
(7.8)-(7.10) есть частный случай ее общей постановки, который отличается от
общего тем, что здесь нет ограничений типа неравенств, кроме условий
положительности, и отыскиваются лишь точки минимума целевой функции.
Из общей теории разрешимости задач ЛП нам
известно, что одним из решений такой задачи является вершина многогранника
допустимых значений. Поэтому мы можем найти решение путем перебора всех вершин,
вычисляя там целевую функцию и выбирая ту вершину, где ее значение минимально.
Но при большом числе переменных и ограничений число вершин такого многогранника
огромно, и перебор всех вершин приводит к большому объему вычислений.
Желательно организовать этот перебор так, чтобы не рассматривать вершины, где
значение целевой функции заведомо больше, чем в уже рассмотренных вершинах.
Одним из способов такого рационального перебора вершин является так называемый
симплекс-метод.
Симплекс размерности n
- это простейший многогранник этой размерности. Так, 2-симплекс - это любой
треугольник, 3-симплекс - это любой тетраэдр и т. п. Слово симплекс означает
«простейший».
Идея симплекс-метода такова. Найдем какую-либо
одну (начальную) вершину многогранника допустимых значений. Будем перебирать
все ребра, выходящие из этой вершины, пока не найдем ребра, при перемещении вдоль
которого целевая функция убывает. Если такого ребра нет, то начальная вершина
есть точка минимума. Если же ребро с указанным свойством найдется, то мы
переходим вдоль этого ребра к следующей вершине, и начинаем перебор ребер,
выходящих из нее.
Таким образом, мы движемся по ребрам
многогранника, всякий раз переходя к вершине с меньшим значением целевой
функции, пока не прибудем в точку ее минимума.
Опишем численную реализацию этой идеи для задачи
ЛП в канонической форме.
Отметим, что среди ограничений (7.9) могут быть
взаимозависимые (скажем, одно из равенств равно сумме двух других).
Ограничения, являющиеся следствиями других ограничений, необходимо отбросить,
поскольку они не содержат никакой дополнительной информации о значениях
неизвестных. Пусть после такого отбрасывания осталось m
ограничений типа равенств:
a11x1+
a12x2+
... + a1nxn = b1x1+ a22x2+ ... + a2nxn =
b2 (7.11)
. . . . . . . . . . . .
am1x1+
am2x2+
... + amnxn = bm
Здесь n
- это общее число неизвестных, включая дополнительные (балансовые) переменные.
Коэффициенты aij, bj
- заданные числа (но, вообще говоря, новые, полученные после приведения к
каноническому виду и отбрасывания зависимых уравнений). Поскольку любая система
из m > n
линейных уравнений с n
неизвестными, либо зависима, либо несовместна, то мы должны считать, что m<n.
Случай m=n
не относится к теории оптимизации: в этом случае решение системы (7.11)
единственно, т. е. многогранник допустимых значений состоит из единственной
точки, проблемы выбора между различными точками этого многогранника не стоит.
Поэтому мы должны рассматривать лишь случай m<n.
Алгоритм симплексного метода состоит из
следующих пяти шагов: 1. Выразим первые m
переменных x1,x2,x3,...,xm
через остальные с помощью уравнений (7.11):
x1= p1+ q1,m+1 xm+1+ q1,m+2 xm+2+
... + q1n xn= p2 + q2,m+1 xm+1 + q2,m+2 xm+2 + ... + q2n xn (7.12)
................= pm + qm,m+1xm+1+
qm,m+2xm+2+ ... + qmnxn.
Для этого достаточно решить систему (7.11)
относительно неизвестных x1,x2,x3,...,xm,
считая переменные xm+1,xm+2,...,xn
фиксированными.
Свободные члены p1,p2,...,pm
неотрицательные. Переменные x1,x2,x3,...,xm
называют базисными (зависимыми), а xm+1,xm+2,...,xn-
небазисными (свободными).
Представление (7.12) позволяет найти начальную
вершину (опорное решение). Для этого достаточно положить xm+1=xm+2=...=xn=0
и вычислить переменные x1,x2,x3,...,xm
по формулам (7.12). Тем самым мы находим одно из неотрицательных базисных
решений: (p1,p2,...,pm,0,...,0).
. Кроме того, мы можем подставить правые части
(7.12) в выражение целевой функции вместо x1,x2,x3,...,xm,
и получить ее выражение через свободные переменные:
F = d0+ dm+1·xm+1+ ... + dn·xn. (7.13)
Поскольку в начальной вершине xm+1=...=xn=0,
то функция F принимает в этой
вершине значение d0.
Выясним, не является ли начальная вершина
оптимальной, т.е. не дает ли она решение задачи минимизации F.
Она является точкой минимума, если при любом изменении свободных переменных
значение F только
увеличивается. Поскольку xj³0,
то это произойдет при условии dj³0,
j=m+1,...,n.
Итак, если все коэффициенты при свободных
неизвестных в представлении (7.13) неотрицательны, то точка минимума уже
найдена.
. Допустим, что это не так, и среди этих
коэффициентов имеются отрицательные коэффициенты. Пусть для конкретности dm+1
<0. Тогда, при увеличении xm+1
значение F уменьшается.
Увеличение переменной xm+1
(с сохранением нулевых значений остальных свободных переменных) соответствует
перемещению из начальной вершины вдоль некоторого ребра.
Такое перемещение можно совершать до тех пор,
пока базисные переменные в соответствии с уравнениями (7.12) остаются
положительными. При xm+1=
x(1)m+1,
xm+2=0,...,xn=0.
Формула (7.12) дает
xi = pi
+ qi,m+1x(1)m+1,
i=1,2,...,m.
Если все коэффициенты qi,m+1
положительны, то базисные переменные положительны при любом x(1)m+1³0.
Это значит, что в этом случае x(1)m+1
можно увеличивать безгранично (это возможно, если многогранник допустимых
значений неограничен). Тогда F
неограниченно убывает, т. е. задача минимизации не имеет решения.
. Но на практике этот случай встречается редко.
Обычно решение существует, и, соответственно, среди коэффициентов qi,m+1
имеются отрицательные коэффициенты. Если qi,m+1,
то условие положительности xi
приводит к условию:
x*m+1
< -pi/qi,m+1
(правая часть этого неравенства положительна).
Возможное наибольшее значение xm+1
есть, таким образом,
x*m+1= min { -pi/qi,m+1} qi<0.
Этому значению соответствует вершина, в которую
мы попадаем, двигаясь вдоль ребра. Значение F
в этой вершине меньше, чем в начальной вершине.
. Здесь мы выбираем в качестве новых базисных
переменных x1,x2,...,xm-1,xm+1,
выражаем их и целевую функцию F
через свободные переменные, и повторяем все вычисления и рассуждения,
приведенные выше. В результате мы либо обнаружим, что эта вершина дает решение,
либо перейдем в новую вершину. В конце концов, мы получим решение. Можно
доказать, что количество вершин, которые придется перебрать при использовании
этого метода, имеет порядок O(n),
в то время как общее количество вершин имеет порядок O(2n).
В качестве примера рассмотрим задачу о распределении
ресурсов.
Пример. Имеется 300 кг металла, 100 м2 стекла и
160 - человеко-часов рабочего времени; из них изготавливают изделия двух
наименований А и Б; стоимость одного изделия А равна 10 $, для его изготовления
нужно 4 кг металла, 2 м2 стекла и 2 человеко-часа рабочего времени; стоимость
одного изделия Б равна 12 $, для его изготовления нужно 5 кг металла, 1 м2
стекла и 3 человеко-часа рабочего времени; требуется спланировать производство
так, чтоб произвести изделия с максимальной стоимостью.
Решение. Если x1,
x2 есть количество
изделий А и Б соответственно, то задача такова:
f(x1,
x2) = 10·x1
+ 12·x2 ®
max
при ограничениях
·x1+
5·x2£
300
·x1+
x2£
100
·x1+
3·x2£
160
Приводим задачу к каноническому виду. Для этого
нужно ввести 3 балансовых переменных (по числу неравенств) x3,
x4, x5,
и записать ограничения в виде
·x1
+ 5·x2 + x3
= 300
·x1+
x2 + x4=
100 (7.14)
·x1+
3·x2+ x5=
160
x1,2,3,4,5³
0
и заменить целевую функцию f
на F:
F(x1,x2)=-f(x1,x2)=-10·x1- 12·x2-
0·x3 - 0·x4 - 0·x5 ® min (7.15)
Мы должны выбрать 3 базисных переменных. Здесь
удобно взять в качестве базисных балансовых пеpеменные
x3,x4,x5,
поскольку они легко выражаются из ограничений (7.14):
x3= 300 - 4x1-
5x2
x4= 100 - 2x1-
x2 (7.16)
x5= 160- 2x1-
3x2
Полагая свободные переменные x1,
x2 равными нулю,
находим начальную вершину (первое опорное решение)
x(0)1=0, x(0)2=0,
x(0)3=300, x(0)4=100,
x(0)5=160.
Значение F
в этой вершине равна 0. Подставляя (7.16) в (7.15) находим, что вид выражения
(7.15) не меняется. Поскольку коэффициенты при свободных переменных
отрицательны, то это решение не оптимальное: значение F
может быть уменьшено путем увеличения как x1,
так и x2.
Положим x2=0
и будем увеличивать x1. Во всех
соотношениях (7.16) коэффициенты при x1
отрицательны, что приводит к оценкам
x1<300/4=75, x1<100/2=50,
x1<160/2=80.
Таким образом, x1
можно увеличивать до 50, и при x1=50,
x2=0 мы находим
новую вершину (второе опорное решение).
x(1)1= 50, x(1)2=
0, x(1)3= 100, x(1)4=
0, x(1)5 = 60.
Значения x3,
x4, x5
здесь найдены из (7.16). Целевая функция F
в этой вершине равно -500; как и следовало ожидать, оно меньше, чем в
предыдущей вершине.
Теперь выберем в качестве нового базиса
ненулевые переменные x1,x3,x5.
Их необходимо выразить через свободные переменные x2
и x4. Это можно
сделать так. Считая x2 и x4
фиксированными, перенесем их в правую часть (7.14). Получим систему из трех
уравнений с тремя неизвестными x1,x3,x5:
x1+ x3=
300 - 5x2
x1= 100 - x2
- x4
x1+ x5=
160 - 3x2
Ее легко разрешить: из второго уравнения
x1= 50 - 0,5x2
- 0,5x4,
и подставляя это выражение в первое и третье
уравнения, окончательно получаем
x1= 50 - 0,5x2
- 0,5x4
x3= 100 - 3x2+
2x4 (7.17)
x5= 60 - 2x2+
x4
Подставляя эти выражения в (7.15), имеем
F = -500- 7x2+
5x4.
Поскольку коэффициент при x2
отрицателен, то и эта вершина не является оптимальной. Теперь мы должны
увеличивать x2, положив x4=0.
Из (7.17) имеем ограничения,
x2<50/(1/2)=100, x2<100/3=33.33,
x2<60/2=30,
т.е. мы можем увеличить x2
до 30 и получить очередную вершину
x(2)1=35, x(2)2=30,
x(2)3=10, x(2)4=0,
x(2)5=0.
в этой вершине F
= -710.
Теперь мы выбираем ненулевые переменные x1,
x2, x3
в качестве базисных, и выражаем их через свободные переменные x4,
x5. Из (7.14)
получаем
x1+ 5x2+
x3= 300
x1+ x2
= 100 - x4
x1+ 3x2
= 160 - x5
Вычитая из третьего уравнения второе, получаем
x2=60+x4-x5,
x2=30+0,5x4
- 0,5x5
Подставляя это все во второе уравнение, имеем
x1= 100-x4-x2=100-x4-30-0,5x4+0,5x5=70-0,5*x4+0,5x5,
x1=35-0,75x4+0,25x5
Теперь первое уравнение дает
x3=300-4x1-5x2=300-140+3x4-x5-150-2.5*x4+2.5*x5=10+0,5x4+1,5x5,
Подставляя эти выражения в (7.15) находим
F=-10(35-0,75x4+0,25x5)
-12(30+0,5x4 -0,5x5)=
-710+1,5x4+3,5x5.
Здесь коэффициенты при x4,
x5 положительны, т.
е. найденная вершина есть точка минимума.
Итак, оптимальный план производства получается
при x1=35, x2=30.
Поскольку в исходной задаче две переменные, то
ее можно было решить графически.
Наше решение симплекс-методом соответствует
движению по границе многоугольника из вершины A1(0,0)
в вершину A2(50,0) и затем в
вершину A3(35,30).
7.3 Симплекс-таблица
Все математические методы линейного
программирования основаны на нахождении неотрицательных базисных решений. Итак,
перед нами стоит задача определения неотрицательного базисного решения. Пусть в
системе линейных уравнений свободные члены всех уравнений - числа
неотрицательные (в противном случае умножением обеих частей уравнения на -1
можно сделать свободный член положительным). Будем решать систему методом
полного исключения переменных.
Исходная таблица:
x1
x2 ... xj ... xn
a11
a12 ... a1j ... a1n b1
......................
ai1
ai2 ... aij ... ain bi
......................
am1
am2 ... amj ... amn
bm
Решение начинается с выбора разрешающего
элемента. Сделаем это следующим образом:
) за разрешающий столбец примем такой столбец, в
котором имеется хотя бы один положительный элемент (Если все коэффициенты при
переменных отрицательные, а свободные члены неотрицательные, то неотрицательное
решение единственно: это (0,...,0));
) пусть в разрешающем столбце несколько
положительных элементов. Найдем отношения соответствующих свободных членов к
этим элементам и за разрешающий элемент возьмем тот из них, для которого это отношение
наименьшее (если в столбце один положительный элемент, то он и будет
разрешающим). Затем осуществим пересчет элементов таблицы. Такое преобразование
носит название симплексного.
Добавим, что если найдено хотя бы одно
неотрицательное базисное решение, то с помощью симплексного преобразования
можно перейти к другому неотрицательному базисному решению (если такое есть).
Правило прямоугольника. Правило для нахождения
элемента преобразованной таблицы, не принадлежащего разрешающим столбцу или
строке, называют правилом прямоугольника.
Алгоритм преобразования:
) элементы разрешающей строки получаются из
соответствующих элементов прежней строки делением на разрешающий элемент;
) все элементы разрешающего столбца
преобразованной таблицы, кроме разрешающего элемента, равны нулю;
3 все
остальные элементы пересчитываются по правилу прямоугольника: выделяем
прямоугольник в таблице 7.2 так, что элемент подлежащий пересчету (5), и
разрешающий элемент (2) образуют одну из диагоналей. А затем из произведения
этих элементов вычитаем произведение элементов, образующих другую диагональ, и
полученную разность делим на разрешающий элемент.
Пример. С помощью Симплекс-таблицы найти
минимальное значение
целевой функции (7.15):
F(x1,x2)=
-f(x1,x2)=
-10·x1- 12·x2-
0·x3 - 0·x4
- 0·x5 ®
min
при данных ограничениях (7.14)
·x1
+ 5·x2 + x3
= 300
·x1+
x2 + x4=
100
·x1+
3·x2+ x5=
160
x1,2,3,4,5³
0
Решение. Коэффициенты при переменных
переписываем в симплексные таблицы (Табл. 7.2). В данной задаче исходным
базисным решением является: (0;0;300;100;160). Целевую функцию запишем в
следующем виде:
+10·x1+12·x2+0·x3+0·x4+0·x5 ®
min.
Таблица 7.2
Базисные х1 х2 х3
х4 х5 Свободные
переменные члены
х3 4 5 1 0
0 300
х4 2 1 0 1
0 100
х5 2 3 0 0
1 160
F 10 12 0 0 0 0
Разрешающий элемент таблицы есть а12=2. Для
нахождения разрешающего элемента в столбце с положительным значением
коэффициента целевой функций с1=10 выбираются положительные элементы a11=4,
a12=2, а13=2; составляются отношения b1/a11=300/4, b2/a12=100/2 и b3/a13=160/2;
из полученных отношений выбирается наименьшее.
Переменная х1 должна заменить в исходном базисе
переменную х4. После соответствующих преобразований таблица будет иметь
следующий вид:
Таблица 7.3
Базисные х1 х2 х3
х4 х5 Свободные
переменные члены
х3 0 3 1 0
0 100
х1 1 0,5 0 0,5
0 50
х5 0 2 0 -1
1 60
F 0 7 0 -5 0 -500
В строке коэффициентов целевой функций F таблицы
7.3 элемент c2=7 положительный. Разрешающий элемент таблицы есть а23=2. Для
нахождения разрешающего элемента в столбце выбираются положительные элементы
a21=3, a22=0,5, а23=2; составляются отношения b1/a21=100/3, b2/a22=50/0,5 и
b3/a23=60/2; из полученных отношений выбирается наименьшее. Переменная х2
должна заменить в исходном базисе переменную х5. После соответствующих
преобразований таблица будет иметь следующий вид:
Таблица 7.4
Базисные х1 х2 х3
х4 х5 Свободные
переменные члены
х3 0 0 1 1,5
-1,5 10
х1 1 0 0 0,75
-0,25 35
х2 0 1 0 -0,5
0,5 30
F 0 0 0 -1,5 -3,5 -710
В строке коэффициентов целевой функции нет
положительных элементов. Таблица 7.4 является последней в решении поставленной
задачи. Из этой таблицы видно, что при базисном решении (35;30;10;0;0) целевая
функция F имеет значение F=-710. Значение F=-710 является наименьшим в данной
задаче при x1=35, x2=30.
ЛИТЕРАТУРА
.
Калиткин Н.П. Численные методы. М.: Наука, 1978. - 512 с.
.
Солодовников А.С. Введение в линейную алгебру и линейное программирование. М.:
Просвещение, 1966. - 183 с.
.
Химмельблау Д. Прикладное нелинейное программирование.
М.:
Мир, 1975. - 534 с.
.
Попов В.И. Численные методы расчета мостовых конструкций на ЭВМ. М.: 1981. - 78
с.
.
Монахов В.М. и др. Методы оптимизации. Применение математических методов в
экономике. М., Просвещение, 1978. - 175 с.
.
Информатика. Методические указания к лабораторным работам. «Численные методы
решения задач строительства на ЭВМ» для студентов специальности
2910.//Казанская государственная архитектурно-строительная академия; Сост.:
Габбасов Ф.Г., Гатауллин И.Н., Киямов Х.Г. - Казань:, 1998. -50 с.