Контрольная работа по математике
Задание №1
Вычислить предел функции, не используя правило Лопиталя
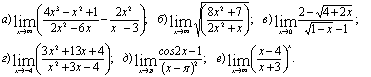
Решение:
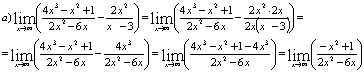
Вычислим
предел подставив в него 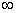 :
:
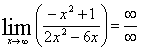 -
неопределенность.
-
неопределенность.
Для
устранения неопределенности воспользуемся свойством:
Значение
дроби не изменится если ее числитель и знаменатель разделить на одно и тоже
ненулевое число.
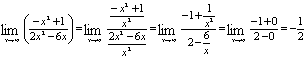
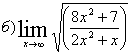
Вычислим
предел подкоренного выражения:
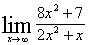
Вычислим
предел подставив в него 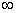 :
:
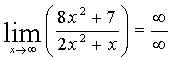 -
неопределенность.
-
неопределенность.
Для
устранения неопределенности воспользуемся свойством:
Значение
дроби не изменится если ее числитель и знаменатель разделить на одно и тоже
ненулевое число.
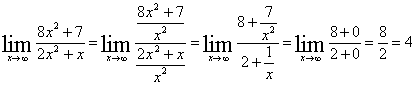
Получаем:
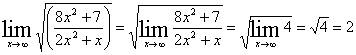
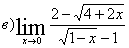
Вычислим
предел подставив в него 0:
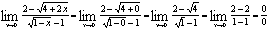 -
неопределенность.
-
неопределенность.
Для
устранения неопределенности умножим и разделим выражение на сопряженные
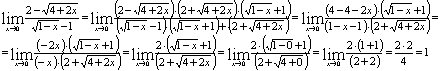
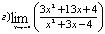
Вычислим
предел подставив в него (-4):
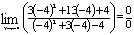 -
неопределенность
-
неопределенность
Для
устранения неопределенности разложим числитель и знаменатель дроби на множители
по формулам:
ах2
+ bx + с = 0

ах2
+ bx + с = а(х-х1)(х-х2)
Тогда
получим:
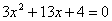
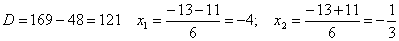
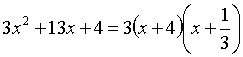
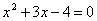
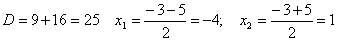

Получаем:
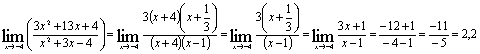
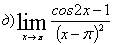
Вычислим
предел подставив в него 0:
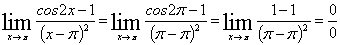 -
неопределенность.
-
неопределенность.
Произведем
тождественные преобразования:
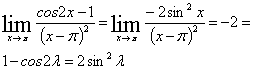
Для
устранения неопределенности применим формулы 1-го замечательного предела:

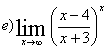
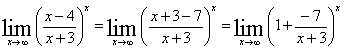
Сделаем
замену
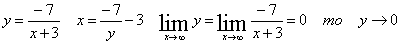

Используя
второй замечательный предел 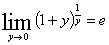

Задание №2
Найти производные функций
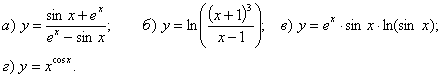
Решение:
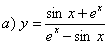
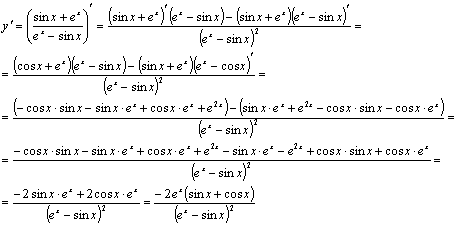
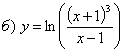
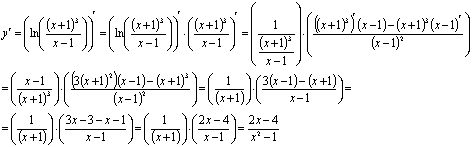
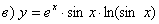
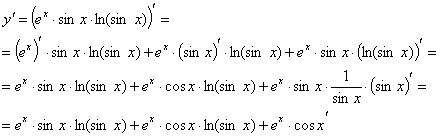
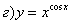
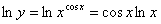
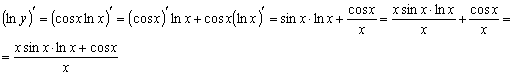
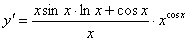
Задание №3
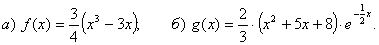
Решение:
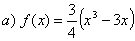
1)Область
определения:
Функция
определена и непрерывна на всей числовой прямой т.к. f(x) -
многочлен. 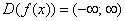
)Точки
пересечения с осями координат:
С
осью ОХ т.е. у=0:
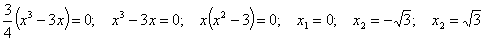
 - точки
пересечения с осою ОХ.
- точки
пересечения с осою ОХ.
С
осью ОУ т.е. х=0: 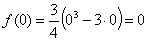
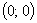 - точка
пересечения с осою ОУ.
- точка
пересечения с осою ОУ.
)
Исследуем на четность нечетность. Проверим выполнимость равенств: если f(-x) = f(x),
то функция четная, если f(-x) = -f(x), то функция нечетная, при х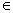 D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
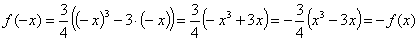
Функция
нечетная.
)Исследуем
на наличие асимптот.
Вертикальных
асимптот нет т.к. нет точек разрыва.
Наклонные
асимптоты:
y = kx + b -
уравнение наклонной асимптоты.

тогда
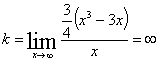
Значит
и наклонных асимптот тоже нет.
)Исследуем
функцию на наличие точек экстремума (точек максимума и минимума), промежутки
возрастания и убывания функции.
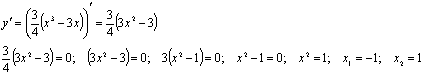
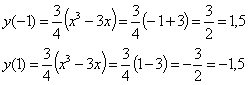
(-1;
1,5); (1; -1,5) - точки подозрительные на экстремум.
Исследуем
поведение функции справа и слева от каждой критической точки.
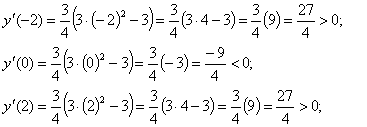
Значит
на промежутке [-1; 1] функция убывает, а на промежутке (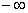 ; -1) и (1;
; -1) и (1;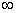 ) функция
возрастает.
) функция
возрастает.
Занесем
полученные данные в таблицу:
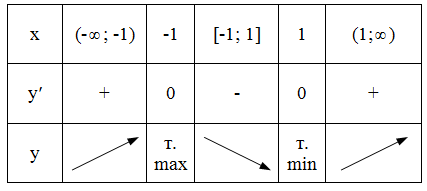
(-1;
1,5) - точка максимума.
(1;
-1,5) - точка минимума.
)Исследуем
функцию на наличие точек перегиба, промежутки выпуклости и вогнутости функции.
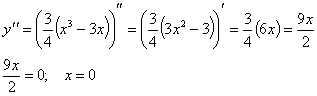
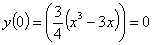
Точка
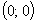 подозрительная на перегиб.
подозрительная на перегиб.

Точка
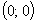 подозрительная на перегиб.
подозрительная на перегиб.

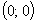 -
координата точки перегиба.
-
координата точки перегиба.
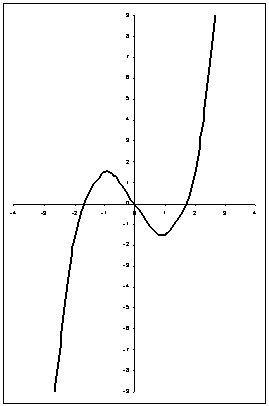
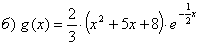
1)Область определения:
Функция определена и непрерывна на всей числовой прямой т.к.
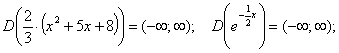 Значит
Значит 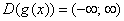
)Точки
пересечения с осями координат:
С
осью ОХ т.е. у=0: 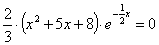 так как
так как 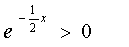 то
получаем
то
получаем 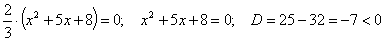
С
осью ОХ не пересекается. С осью ОУ т.е. х=0: 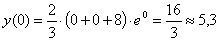
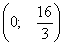 - точка
пересечения с осою ОУ.
- точка
пересечения с осою ОУ.
)
Исследуем на четность нечетность. Проверим выполнимость равенств: если f(-x) = f(x),
то функция четная, если f(-x) = -f(x), то функция нечетная, при х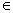 D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
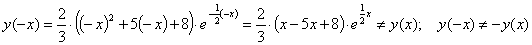
Функция
ни четная ни нечетная
)Исследуем
на наличие асимптот.
Вертикальных
асимптот нет т.к. нет точек разрыва.
Наклонные
асимптоты:
y = kx + b -
уравнение наклонной асимптоты.
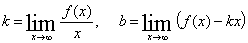 , тогда
, тогда 
Наклонных
асимптот нет.
)Исследуем
функцию на наличие точек экстремума (точек максимума и минимума), промежутки
возрастания и убывания функции.
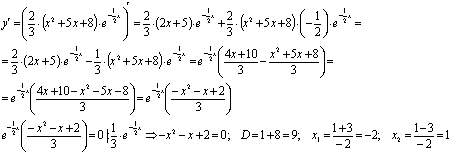
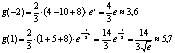
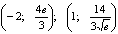 - точки
подозрительные на экстремум.
- точки
подозрительные на экстремум.
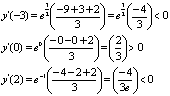
На
промежутке (-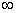 ; -2), (1;
; -2), (1; 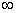 ) функция
убывает.
) функция
убывает.
На
промежутке [-2; 1] функция возрастает.

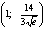 - точка
максимума.
- точка
максимума.
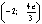 - точка
минимума.
- точка
минимума.
)Исследуем
функцию на наличие точек перегиба, промежутки выпуклости и вогнутости функции.
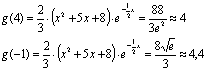
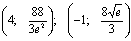 -
точки подозрительные на перегиб.
-
точки подозрительные на перегиб.
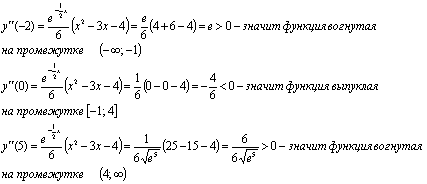
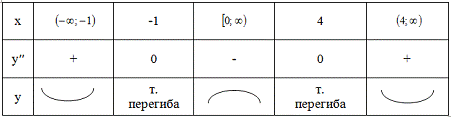
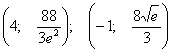 -
координаты точек перегиба.
-
координаты точек перегиба.
Задание №4
Найти неопределенные интегралы и выполнить проверки дифференцированием.
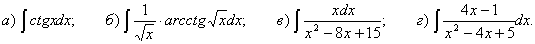
Решение:
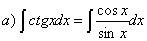
Вычислим
получившиеся интегралы по отдельности:
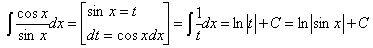
Проверка
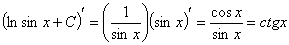
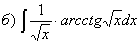
Воспользуемся
формулой интегрирования по частям.
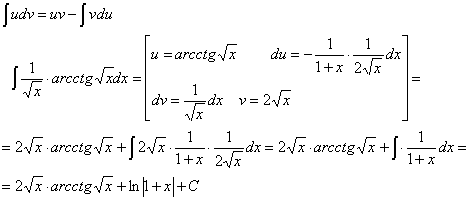
Проверка:
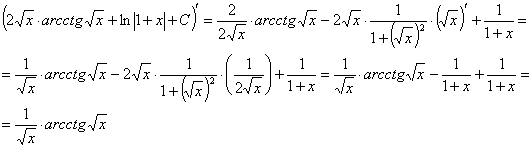
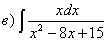
Разложим знаменатель на множители

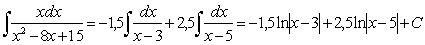
Проверка:

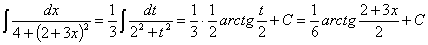
Проверка:
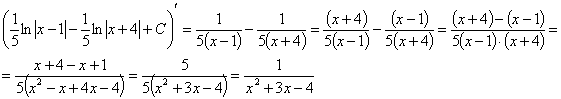
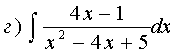
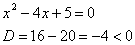
Значит,
можем воспользоваться формулой:
Воспользуемся
формулой интегрирования по частям.
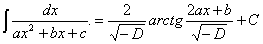
Для
последующей замены переменных вычислим производную знаменателя
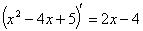
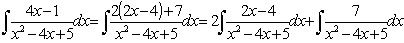
Вычислим получившиеся интегралы по отдельности
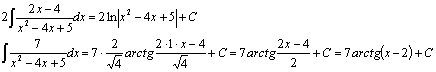
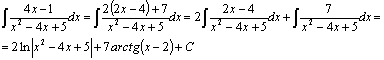
Проверка:
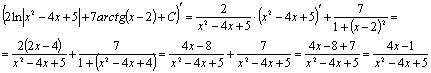
функция производная интеграл дифференцирование
Задание
№5
Найти
площадь фигуры, ограниченной графиками функций 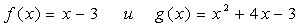
Решение:
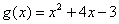 -
графиком функции является парабола, ветви которой направлены вверх.
-
графиком функции является парабола, ветви которой направлены вверх.
Найдем
координаты вершины параболы
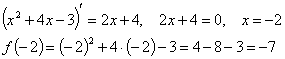
(-2; -7) - координаты вершины параболы.
 -
графиком функции является прямая.
-
графиком функции является прямая.
Найдем
точки пересечения f(x) и g(x)
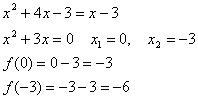
(0;
-3) и (-3; -6) - координаты точек пересечения графиков функций.
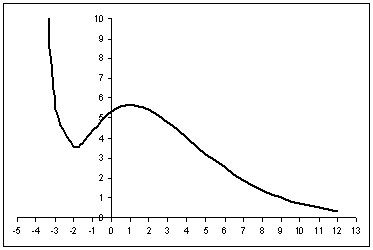
Сделаем
чертеж:
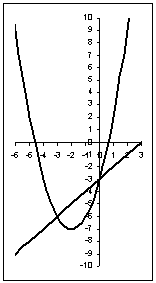
На
промежутке [-3; 0] 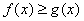
Вычислим площадь фигуры с пределами интегрирования а=-1 и b=0,5.

Ответ:

Задание №6
Найти
общее решение дифференциального уравнения и построить графики двух различных
решений этого уравнения 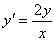
Решение:
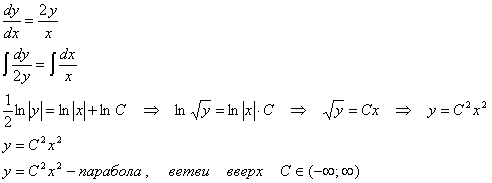
Найдем частные решения
Пусть С1=1 С2= 2
у1 = х2 у2 = 4х2
Построим графики двух частных решений.
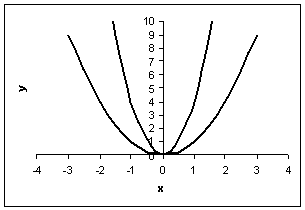
Задание №7
Решение:
Разделим обе
части уравнения на х
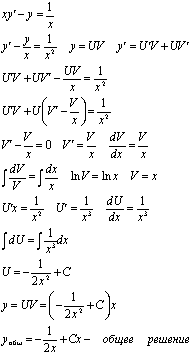
Для
отыскания частного решения найдем С
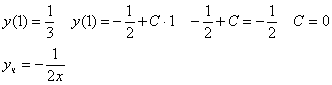
Ответ:
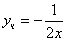
Задание №8
Найти
частное решение дифференциального уравнения, удовлетворяющее данным указанным
условиям 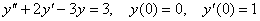
Решение:
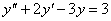
Составим
характеристическое уравнение
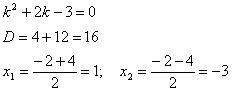
Общее
решение однородного уравнения
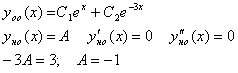
Общее
решение дифференциального уравнения

Частное решение дифференциального уравнения

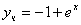
Ответ:
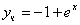
Задание
№9
Исследовать
ряд на сходимость
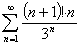
Решение:
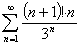
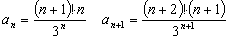
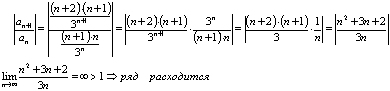
Ответ: ряд расходится
Задание №10
Найти
радиус и интервал сходимости степенного ряда и исследовать его сходимость на
концах интервала 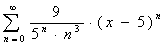
Решение:
Найдем радиус сходимости
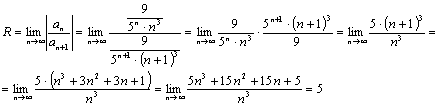
Найдем
интервал сходимости
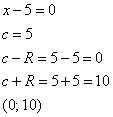
Ответ:
радиус сходимости R = 5; интервал сходимости (0; 10).
Список
использованной литературы
1.Выгодский М. Я. Справочник по высшей математике. - М.: АСТ:
Астрель, 2006. - 991с.
.Зимина О. В., Кириллов А. И., Сальникова Т. А. Высшая
математика. Под ред. А. И. Кирилова. - 3-е изд., испр. - М.: ФИЗМАТЛИТ, 2006. -
368с.
.Выгодский М. Я. Справочник по элементарной математике. - М.:
АСТ: Астрель, 2007. - 509с.
.Красс М. С., Чупрыков Б. П. Математика для экономистов. -
СПб.: Питер 2007. - 464с.