Теория автоматического управления. Линейные системы

Министерство образования Российской Федерации

Санкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ)

Кафедра электротехники, вычислительной техники и автоматизации

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЛИНЕЙНЫЕ СИСТЕМЫ

Методические указания

к выполнению лабораторных работ

для студентов всех специальностей

Санкт-Петербург 2004г.

Теория автоматического управления. Линейные системы. Методические указания к выполнению лабораторных работ по курсу для студентов всех специальностей. СПб, 2004.

Методические указания предназначены для выполнения лабораторного практикума по курсу "Теория автоматического управления. Линейные системы", составленного в целях практического закрепления знаний об основных свойствах линейных систем во временной и частотной областях. Практикум выполняется на персональных компьютерах с использованием системы MATLAB - Simulink.

Указания включают краткое изложение вопросов теории и пояснения к экспериментальному этапу работ.

Составители: канд. техн. наук, доц. О. П. Томчина,

канд. техн. наук, доц. О. Л. Шарякова,

канд. техн. наук, А. Е. Епишкин,

ст.преп. В. А. Шаряков

Методические указания утверждены на заседании кафедры

© Санкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ), 2004

© Томчина О. П., Шарякова О. Л., Епишкин А. Е., Шаряков В. А., 2004

ВВЕДЕНИЕ

Настоящие методические указания служат пособием для студентов института, выполняющих лабораторные и курсовые работы по теории линейных систем автоматического управления и автоматизированному электроприводу. Целью практикума является закрепление теоретического материала по дифференциальным уравнениям, передаточным функциям, временным и частотным характеристикам звеньев и автоматических систем, их устойчивости, влиянию параметров и структуры систем на показатели качества процессов управления в переходном и установившемся режимах функционирования, исследованию систем с запаздыванием.

Особенностью данного практикума является его выполнение на персональных компьютерах с использованием системы MATLAB - Simulink, позволяющей автоматизировать процесс анализа систем управления, представленных в виде структурных динамических схем.

Практикум предусматривает выполнение шести лабораторных работ для приобретения практических навыков при анализе основных свойств линейных систем управления во временной и частотной областях.

ЛАБОРАТОРНАЯ РАБОТА № 1. ИЗУЧЕНИЕ СИСТЕМЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ MATLAB - SIMULINK

Цель работы

Ознакомление с системой MATLAB, приобретение практических навыков исследования систем автоматического управления (САУ) с помощью приложения MATLAB - системой имитационного моделирования Simulink.

1.1 Основные сведения

MATLAB - это язык программирования сверхвысокого уровня, предназначенный для технических вычислений. Он включает в себя вычисления, визуализацию и программирование в легкой для использования среде, где задачи и решения представлены в общей математической форме. MATLAB является интерактивной системой, в которой основные элементы данных представлены массивами, не требующими предварительного задания размерности. Это позволяет решать множество технических задач, особенно в матричной и векторной форме, а также писать программу на традиционных скалярных языках, таких как Си или Фортран.

Название "MATLAB" произошло от сокращения слов "matrix laboratory". Система MATLAB состоит из пяти основных частей:

. Язык программирования MATLAB. Это матрично-массивный язык высокого уровня с управлением состоянием, функциями, структурами данных, входом/выходом, и объектно-ориентированным программированием.

. Рабочая среда MATLAB. Это графический интерфейс, с которым работает пользователь. Включает рабочий стол MATLAB, командное окно, редактор и отладчик файлов MATLAB, справочный броузер.

. Графическая система MATLAB. Содержит команды высокого уровня для двухмерного и трехмерного представления данных, обработки изображений, анимации. Также содержит набор команд низкого уровня, позволяющих пользователю построить собственный интерфейс.

. Библиотека математических функций MATLAB. Содержит набор вычислительных алгоритмов, начиная с элементарных арифметических функций (сложение/вычитание, тригонометрические функции) и заканчивая сложными функциями, такими как обращение матриц и преобразования Фурье.

. Интерфейс прикладных программ MATLAB. Эта библиотека позволяет писать программы на языках Си и Фортран, взаимодействующие с MATLAB. Включает в себя устройства вызова из MATLAB (динамической связи), вызова MATLAB как вычислительного механизма, и для работы с MAT-файлами.

Simulink является программой для имитационного моделирования и анализа динамических систем, входящей в состав пакета MATLAB. Simulink позволяет производить построение модели в виде унифицированных блоков на экране компьютера и может работать с линейными, нелинейными, непрерывными, дискретными моделями или их сочетаниями с большим числом переменных.

.2 Порядок выполнения работы

. Включите компьютер.

. Находясь в ОС Windows, запустите MATLAB двойным щелчком левой кнопки "мыши" по соответствующей иконке на рабочем столе. В результате открывается основное окно MATLAB.

. Для запуска Simulink нажмите в основном окне MATLAB на кнопку с всплывающей подписью Simulink Library Browser. В результате открывается окно библиотеки блоков Simulink.

. Для построения новой модели в окне Simulink Library Browser нажмите на кнопку с всплывающей подписью New model. Программа откроет окно с "чистым листом" без имени (untitled). Для открытия существующей модели в окне библиотеки блоков или в командном окне нажмите на кнопку с всплывающей подписью Open a model, и в появившемся окне выберите требуемый файл (файлы, созданные в Simulink, имеют расширение .mdl).

. Создайте структурную схему, приведенную на рис. 1.1 и задайте указанные преподавателем значения ее параметров.

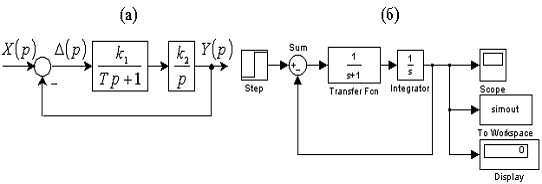
Рис. 1.1 Структурная схема (а) и модель в Simulink (б) исследуемой системы

Набор структурной схемы осуществляется путем выбора требуемых блоков в окне Simulink Library Browser и перетаскивания их при помощи мыши в окно, где осуществляется построение модели. Для удобства пользования все блоки разделены на группы. В данной лабораторной работе использованы блоки группы Simulink с подгруппами Continuous (непрерывные звенья), Math Operations (математические блоки), Sinks (приемники данных), Sources (источники сигналов). Имена блоков указаны на рис. 1.1,б.

Редактирование параметров блока осуществляется двойным щелчком левой кнопки мыши по требуемому блоку. При этом открывается окно параметров блока, вид которого зависит от вида блока.

Для соединения блоков достаточно указать курсором мыши на выход блока-источника сигнала и затем при нажатой кнопке мыши протянуть соединение на вход блока-приемника сигнала. Соединение блоков можно также осуществлять выделением левой кнопкой мыши требуемых блоков при нажатой клавише Ctrl. Для создания отвода необходимо указать правой кнопкой мыши на место отвода соединения и при нажатой кнопке протянуть отвод на вход требуемого блока.

Для вывода результатов моделирования к выходам требуемых блоков необходимо присоединить блоки-приемники сигналов (см. п. 9).

Удаление ненужных блоков и соединений происходит путем выделения соответствующего объекта и нажатия клавиши Delete клавиатуры. Дополнительную информацию по построению моделей, а также по работе с MATLAB в целом можно найти в меню Help Desk, а также в [3, 4].

. Сохраните созданную модель.

. Задайте параметры для процесса численного интегрирования модели. Для этого в меню окна модели откройте Simulation - Parameters. В появившемся окне выставляются указанные преподавателем время начала и окончания расчета, точность расчета и метод.

. Рассчитайте полученную модель. Запуск расчета (интегрирования) модели в меню Simulation кнопкой Start. Процесс расчета модели отображается прогрессивной шкалой в нижней части окна. При необходимости вернитесь на предыдущий этап и поменяйте время окончания расчета так, чтобы обеспечить стабилизацию выходной переменной (окончание переходного процесса).

. По окончании расчета получите требуемые результаты с помощью блоков-приемников данных. Просмотр и печать графиков переходных процессов осуществляется с помощью блока Scope. Просмотр численных значений переменной в ходе моделирования осуществляется блоком Display. Для редактирования полученных графиков или сохранения их в формате графического файла, необходима установка выходных блоков То Workspace. В параметрах этих блоков указывается имя выводимой переменной Variable name и формат данных Save format (Array). Далее в командном окне MATLAB или редакторе М-файлов, вызываемого командой меню New M-file, записывается команда построения графиков. В простейшем случае она имеет вид:

plot(x,y)

где x, y - имена выводимых переменных.

При построении нескольких графиков в одних осях команда примет вид:

plot(x,y,x,z,..)

где x - имя общей (независимой) переменной, y,z - зависимые переменные.

Примечание: команды, набранные в командной строке, выполняются после нажатия клавиши Enter. Для выполнения команд, набранных в редакторе М-файлов, необходимо сохранить и запустить их на выполнение командой Save and Run меню Debug или клавишей F5.

Вывод нескольких переменных в один блок-приемник данных, осуществляется с помощью блока объединения сигналов в общую шину Mux.

Переменная времени в MATLAB обозначена как tout. После сохранения (редактор генерирует файл с расширением .m) и запуска программы (команда Run меню Tools редактора), последняя строит график в окне Figure, который может быть обработан имеющимися в меню окна инструментами. Сохранение графика происходит либо как файла с расширением .fig (команда Save меню File окна графика), в этом случае он будет доступен только из MATLAB, либо как графического файла с расширениями .bmp, .jpg и прочими по выбору (команда Export меню File окна графика). В последнем случае график может быть вставлен в документ отчета по лабораторной работе, написанного, например, в редакторе Word.

. Для построения логарифмических частотных и амплитудно-фазовых частотных характеристик (ЛЧХ и АФЧХ) по полиному передаточной функции необходимо в командном окне или в М-файле ввести соответственно команды

bode(tf(nym,den)); или nyquist(tf(nym,den))

где nym и den - коэффициенты полинома соответственно числителя и знаменателя передаточной функции системы, записываемые через пробел. В случае наличия двух и более коэффициентов в полиноме, последние записываются в квадратных скобках через пробел. Например, для построения ЛЧХ колебательного звена с передаточной функции

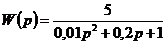, необходимо набрать следующую команду:

bode(tf(5,[0.01 0.2 1]));

Для построения частотных характеристик по модели, в Simulink с помощью блоков In и Out необходимо указать соответственно вход и выход исследуемой системы. Далее в командном окне MATLAB или в М-файле с помощью команд linmod, bode и nyquist производится соответственно линеаризация исследуемой модели и построение её ЛЧХ или АФЧХ. Синтаксис команд:

[A,B,C,D]=linmod('имя файла модели')

bode(A,B,C,D) или nyquist(A,B,C,D)

где A, B, C, D - матрицы пространства состояний системы, полученные при выполнении команды linmod; grid - команда нанесения на график координатной сетки.

. После окончания работы выйдите из MATLAB, закрыв все окна.

1.3 Содержание отчета по работе

. Цель работы.

. Схема исследованной системы с числовыми значениями параметров.

. Ответы на контрольные вопросы.

.4. Контрольные вопросы

1. Что из себя представляет система MATLAB и какова область его применения?

2. С какими видами моделей может работать Simulink?

3. Каким образом осуществляется построение структурной схемы в Simulink?

4. Как в Simulink осуществляется ввод и редактирование параметров блоков?

5. Как в MATLAB осуществляется построение ЛЧХ и АФЧХ системы?

6. Как осуществляется печать графиков переходных процессов?

ЛАБОРАТОРНАЯ РАБОТА № 2. ИССЛЕДОВАНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ

Цель работы

Исследование переходной функции, амплитудно-фазовых и логарифмических частотных характеристик апериодического, реального дифференцирующего и колебательного звеньев.

2.1 Основные сведения

Типовыми динамическими звеньями САУ являются звенья, процессы в которых описываются линейными дифференциальными уравнениями первого и второго порядков с постоянными коэффициентами и в общем случае имеют следующий вид:

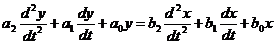,                                               (2.1)

где 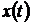,  - соответственно входной и выходной сигналы звена; 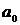, , 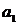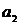; 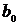, , 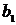 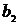- постоянные коэффициенты.

Данное уравнение дает возможность определить передаточную функцию типового звена в виде

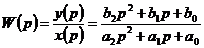                                                     (2.2)

Анализ возможных вариантов задания коэффициентов передаточной функции (2.2) показывает, что к типовым звеньям нулевого и первого порядка, т.е. к звеньям, описываемым уравнениями вида (2.1) при 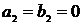, относятся следующие

. Безынерционное звено (при )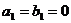

.

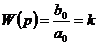. Дифференцирующее звено (при )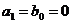

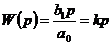, где .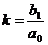

. Форсирующее звено (при )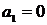

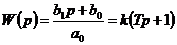, где , .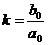

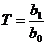. Интегрирующее звено (при )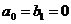

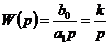, где .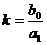

. Апериодическое звено первого порядка (при )

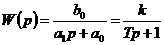, где , .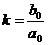

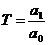. Реальное дифференцирующее звено (при )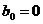

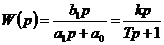, где , .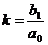

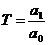Из типовых звеньев второго порядка наибольшее применение нашло колебательное звено при 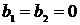 с передаточной функцией следующего вида:

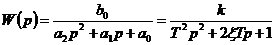, где ; ; .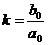

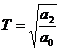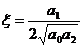Рассмотренная совокупность типовых динамических звеньев первого и второго порядков оказывается достаточной для построения структуры практически любой линейной САУ. При этом сложные реальные звенья могут заменяться последовательным или параллельным соединением нескольких типовых звеньев.

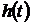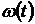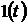Временными характеристиками являются взаимосвязанные переходная  и весовая  функции, представляющие собой реакции исследуемых звеньев на типовые воздействия в виде единичной ступенчатой функции  и 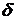-функции 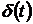. При этом переходная функция дает возможность оценить устойчивость и качество процессов управления, происходящих в исследуемых звеньях при скачкообразных входных воздействиях.

Частотные характеристики, основанные на использовании преобразования Фурье, позволяют оценить происходящие в звеньях процессы управления не только при скачкообразных, но и при любых других входных сигналах, действующих в реальных условиях.

При этом любой входной с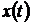игнал  представляется в виде суммы гармоник различных частот с определенными, соответствующими данному сигналу амплитудами и фазами, а реакция на сумму входных гармоник, т.е. выходной сигнал  равен сумме реакций на каждую из них.

Для отдельной гармоники на входе линейного звена 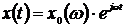 реакцией будет совокупность вынужденной и переходной составляющих, последняя из которых по истечении некоторого времени затухает, и на выходе звена установится синусоидальный сигнал той же частоты, что и на входе, т.е. .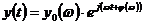

Реакция звена на гармоники различных частот характеризуется его комплексным коэффициентом передачи, который представляет собой амплитудно-фазовую частотную характеристику (АФХ) звена определяется следующим образом:

,

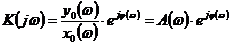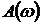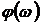где  и  - соответственно амплитудная (АЧХ) и фазовая (ФЧХ) частотные характеристики исследуемого звена.

Подставляя выражение для входного и выходного сигналов звена в (2.1), получим уравнение

,

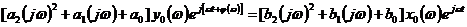дающее возможность рассчитать АФХ звена через коэффициенты дифференциального уравнения (2.1) следующим образом:

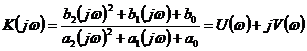,                                         (2.3)

где 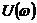,  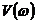- соответственно вещественная (ВЧХ) и мнимая (МЧХ) частотные характеристики исследуемого звена.

При этом очевидны следующие соотношения:

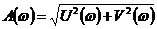, .                                            (2.4)

Из (2.2) и (2.3) видно, что для получения АФХ исследуемого звена достаточно использовать соотношения (2.4) и его передаточную функцию

, .

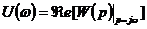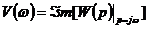Таким образом, АФХ, вид которой иллюстрируется рис. 2.1, представляет собой годограф конца вектора 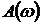, положение которого определяется фазой  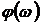в декартовой системе координат  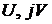при изменении частоты .

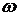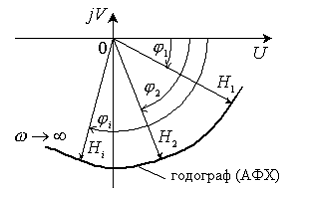
Рис. 2.1. Вид амплитудно-фазовой частотной характеристики

Кроме АФХ звеньев в теории автоматического управления широкое распространение нашли логарифмические амплитудные (ЛАХ) и фазовые (ЛФХ) частотные характеристики (ЛЧХ). При их построении по оси абсцисс откладывается частота в логарифмическом масштабе, а по оси ординат - величина 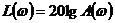 в децибелах и 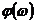. При этом наибольшее применение получили асимптотические ЛАХ.

.2 Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемых типовых звеньев.

1. Исследование основных характеристик апериодического звена первого порядка

а) Определение 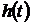 при отрицательных начальных условиях. В пакете расширения Simulink создайте структуру, соответствующую подаче ступенчатой функции с коэффициентом 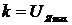 (табл. 2.1.) на вход исследуемого звена, задайте требуемые значения параметров. Для задания передаточной функции звена с начальными условиями используйте блок Transfer Fcn (with initial states), находящийся в дополнительной группе блоков Simulink Extras, подгруппе Additional Linear. В параметрах моделирования задайте время моделирования не менее 5Т. Проведите имитационное моделирование, получите на экране график переходной функции и напечатайте его. Отрицательные начальные условия соответствуют значению 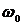 со знаком "минус" (табл. 2.1).

б) Определение 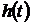 при положительных начальных условиях. Отредактируйте значения параметров исследуемого звена и повторите моделирование. Нанесите на полученный в предыдущем пункте график новые значения переходной функции в узловых точках, постройте график.

в) Определение 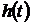 при нулевых начальных условиях. Выполните п. 1,б.

г) Определение частотных характеристик при номинальных значениях параметров. Постройте и распечатайте ЛЧХ и АФХ исследуемого звена. На полученной ЛАХ постройте асимптотическую ЛАХ, определите ошибку сопряжения.

. Исследование основных характеристик реального дифференцирующего звена. Задайте на входе ступенчатую функцию с коэффициентом усиления 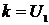 (табл. 2.1).

а) Определение 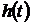 при номинальных значениях параметров. Выполните п. 1,а при 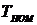, задав время моделирования не менее .

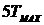б) Определение 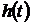 при увеличенной постоянной времени. Выполните п. 1,б.

в) Определение частотных характеристик при номинальных значениях параметров. Отредактируйте значения параметров исследуемого звена и выполните п. 1,г.

г) Определение частотных характеристик при увеличенной постоянной времени. Отредактируйте значения параметров исследуемого звена и получите на экране требуемые частотные характеристики. Используя их, нанесите на полученные в предыдущем пункте графики новые значения характеристик в узловых точках, постройте графики.

. Исследование основных характеристик колебательного звена

а) Определение 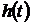 при отрицательных начальных условиях и 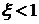. Выполните п. 1,а. Отрицательные начальные условия выбираются из табл. 2.1 для положения 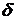 и скорости 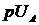 со знаком "минус".

б) Определение 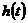 при положительных начальных условиях и 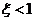. Выполните п. 1,б.

в) Определение 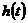 при нулевых начальных условиях и 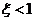. Выполните п. 1,б.

г) Определение 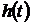 при нулевых начальных условиях и 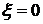. Выполните п. 1,а.

д) Определение 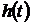 при нулевых начальных условиях и 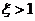. Выполните п. 1,б.

ж) Определение частотных характеристик при 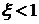. Выполните п. 1,г.

з) Определение частотных характеристик при удвоенном 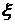. Выполните п. 2,г, положив 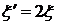, где .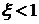

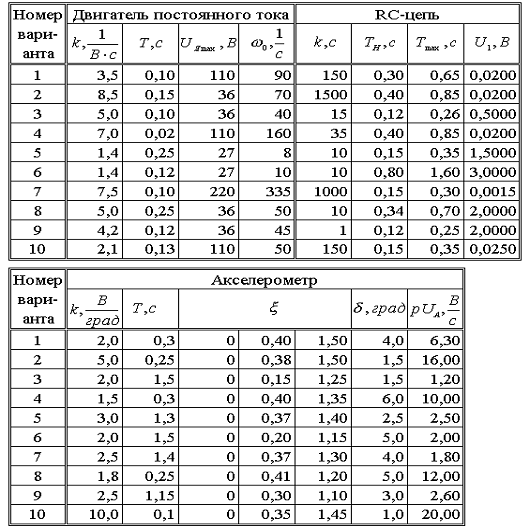
2.3 Варианты заданий

В данной работе исследуются основные временные и частотные характеристики апериодического, реального дифференцирующего и колебательного звеньев, т.к. характеристики безынерционного и интегрирующего звеньев очевидны, а реализация операции идеального дифференцирования средствами цифровой вычислительной техники невозможна.

При этом с помощью апериодического звена 1-го порядка описывается двигатель постоянного тока, реального дифференцирующего звена - дифференцирующая RC-цепь, колебательного звена - акселерометр для измерения угловых ускорений. Схемы исследуемых звеньев приведены на рис. 2.2.

Исходные данные для моделирования указанных звеньев приведены в табл. 2.1.

.4 Содержание отчета по работе

. Цель работы.

. Схемы исследованных типовых звеньев, их передаточные функции с числовыми значениями параметров и экспериментально полученные графики.

. Ответы на контрольные вопросы.

2.5 Контрольные вопросы

. Как зависит характер переходной функции в апериодическом звене от начальных условий?

. Чему равна ошибка на сопрягающей частоте при использовании асимптотической ЛАХ?

. Как влияют параметры апериодического звена на вид АФХ?

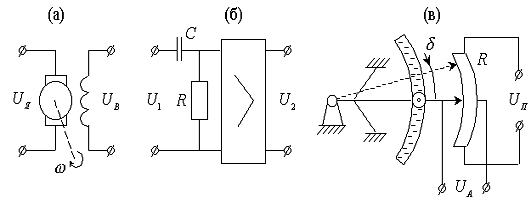
Рис. 2.2. Исследуемые типовые звенья САУ: а - двигатель постоянного тока; б - дифференцирующая цепь; в - акселерометр угловых ускорений

Таблица 2.1.

4. Как зависит характер переходной функции от параметров k и Т реального дифференцирующего звена?

. Зависит ли вид ЛЧХ от параметра k реального дифференцирующего звена?

. Как зависит вид АФХ от параметра Т реального дифференцирующего звена?

. Как сказывается введение ненулевых начальных условий по первой производной выходной величины колебательного звена на характер переходной функции?

8. Как зависит характер переходной функции колебательного звена от параметра .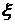

. Как зависит вид ЛЧХ колебательного звена от параметра ?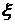

10. Как зависит вид АФХ колебательного звена от его параметров?

ЛАБОРАТОРНАЯ РАБОТА № 3. АНАЛИЗ УСТОЙЧИВОСТИ САУ ЧАСТОТНЫМИ МЕТОДАМИ

Цель работы

Изучение и приобретение практических навыков применения критерия Найквиста и метода ЛЧХ для анализа устойчивости САУ.

.1 Основные сведения

Процессы управления в линейных разомкнутых САУ описываются уравнениями вида:

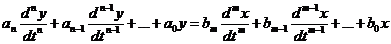                         (3.1)

Общее решение однородного уравнения

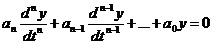
имеет вид 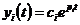, , 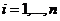где 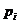 являются корнями характеристического уравнения

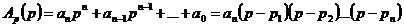                       (3.2)

и определяют устойчивость системы, т.е. способность возвращаться в установившееся состояние после прекращения действия, которое вывело её из этого состояния.

Система является устойчивой, если все корни располагаются в левой полуплоскости комплексной переменной, т.е. являются отрицательными или имеют отрицательные вещественные части. Для определения устойчивости используются различные критерии, позволяющие определять знаки корней без их вычисления.

Наибольшее применение нашли частотные критерии устойчивости, а среди них критерий Найквиста и метод ЛЧХ, основанные на принципе аргумента. При переходе в частотную область анализа заменой 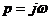, изменение аргумента каждого сомножителя  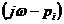в уравнении (3.2) при  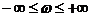определяется в среднем следующим выражением:

,

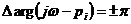где знак "+" соответствует корню 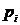 левой, а "-" - правой полуплоскости (рис. 3.1).

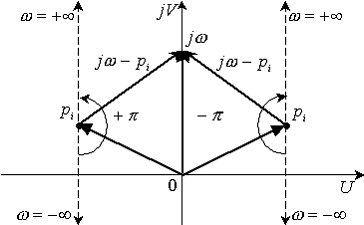
Рис. 3.1. Изменение аргумента 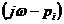 для корней левой и правой полуплоскости

Если характеристическое уравнение имеет 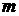 корней в правой и 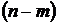 в левой полуплоскости, то

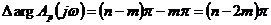 при .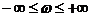

Для устойчивой разомкнутой системы 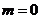 и принцип аргумента с учетом симметрии 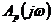 определяется выражением

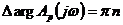 при .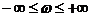

Анализ устойчивости замкнутых САУ основывается на применении принципа аргумента к выражению

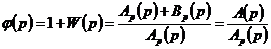,                                                (3.3)

где 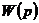 - передаточная функция разомкнутой системы,  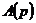- характеристический полином замкнутой системы.

Согласно данному принципу изменение аргумента определяется выражением

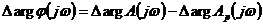 при .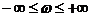

При наличии 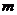 корней в характеристическом уравнении замкнутой системы, расположенных в правой полуплоскости комплексной переменной, и при условии устойчивости разомкнутой системы справедливо равенство

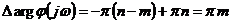 при .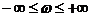

Отсюда очевидно, что для систем, устойчивых в разомкнутом и замкнутом состояниях, выполняется условие критерия Найквиста

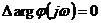 при .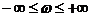

Графическая интерпретация этого условия для статической системы показана на рис. 3.2,а.

Переход к АФХ САУ, т.е. к её комплексному коэффициенту передачи, полученному из (3.3) по выражению

,

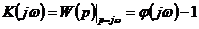дает возможность сформулировать критерий Найквиста следующим образом.

САУ, устойчивая в разомкнутом состоянии, устойчива в замкнутом состоянии в том и только в том случае, если АФХ разомкнутой системы, построенная при 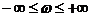, не охватывает критическую точку с координатами  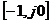(рис. 3.2,б).

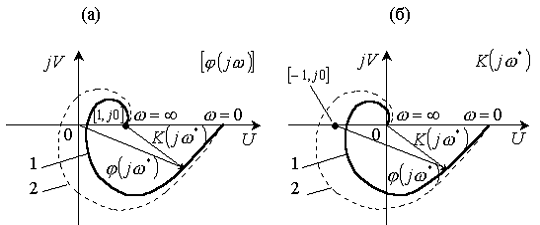
Рис 3.2. Критерий устойчивости Найквиста: а - в плоскости 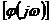; б - в плоскости 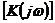; 1 - устойчивая САУ; 2 - неустойчивая САУ

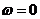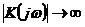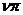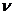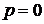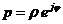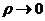Следует отметить, что при  АФХ астатических систем претерпевает разрыв. При этом , а фаза меняется на , где  - порядок астатизма, за счет того, что нулевой корень  относят к левой полуплоскости (рис. 3.3,а), т.е. производят замену , где , а 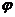 меняется от  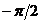до .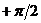

Следовательно, для интегратора справедливо выражение

,

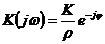объясняющее вид его АФХ, приведенный на рис. 3.3,б.

Критерий Найквиста, интерпретированный в область ЛЧХ, получил название метода ЛЧХ. Согласно этому методу САУ, устойчивая в разомкнутом состоянии в том и только в том случае, когда на частоте среза разомкнутой системы, т.е. частоте, при которой 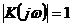, , 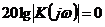фазовый сдвиг 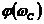 не превосходит значения .

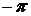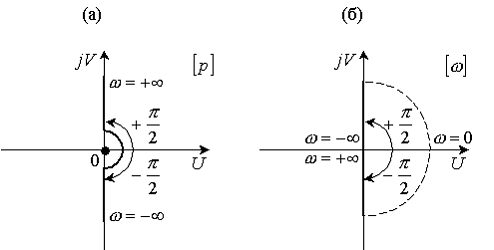
Рис. 3.3 АФХ интегратора: а - в плос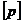кости ; б - в плоскости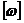

Применение метода ЛЧХ к анализу устойчивости астатической системы первого порядка показано на рис. 3.4. На этом же рисунке показано определение запасов устойчивости по фазе 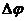 и по модулю .

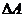Рис. 3.4. Интерпретация критерия Найквиста в области ЛЧХ: а - устойчивая астатическая система первого порядка; б - метод ЛЧХ

.2 Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемых САУ.

1. Анализ устойчивости статической системы

а) Определение устойчивости методом ЛЧХ

Создайте структуру замкнутой системы с единичной обратной связью, на вход которой подается единичное ступенчатое воздействие, а передаточная функция прямой цепи соответствует заданной передаточной функции разомкнутой системы. Задайте требуемые значения параметров.

Получите ЛЧХ исследуемой системы, подобрав диапазон изменения частоты таким образом, чтобы в него входили все сопрягающие частоты.

На полученной ЛАХ постройте асимптотическую ЛАХ, определите частоту среза и фазовый сдвиг на этой частоте.

Сделайте вывод об устойчивости исследуемой системы. Для устойчивой системы определите запасы устойчивости по фазе 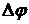 и модулю .

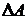б) Определение устойчивости по критерию Найквиста

Получите качественный вид АФХ, исследуемой системы при изменении частоты от верхней границы выбранного диапазона частот до минимально необходимого значения.

Путем изменения нижней границы частоты найдите критическую точку на мнимой оси и напечатайте АФХ исследуемой системы вблизи этой точки.

По полученной АФХ определите фазовый сдвиг на частоте среза.

Сделайте вывод об устойчивости исследуемой системы. Для устойчивой системы определите запасы устойчивости по фазе и по модулю. Сравните результаты с п. 1,а.

в) Проверка устойчивости методом моделирования

Проведите имитационное моделирование. Получите график переходной функции, подобрав экспериментально время моделирования, исходя из возможности вывода об устойчивости исследуемой системы. Напечатайте график.

. Анализ устойчивости астатической системы первого порядка

Выполните операции п. 1.

. Анализ устойчивости астатической системы второго порядка

Выполните операции п. 1.

3.3 Варианты заданий

В данной работе применяются критерий Найквиста и метод ЛЧХ для анализа устойчивости статических и астатических систем первого и второго порядка.

Передаточные функции исследуемых систем в общем виде определяются следующим образом:

.

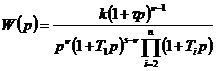Исходные данные для моделирования указанных систем приведены в табл. 3.1.

Таблица 3.1

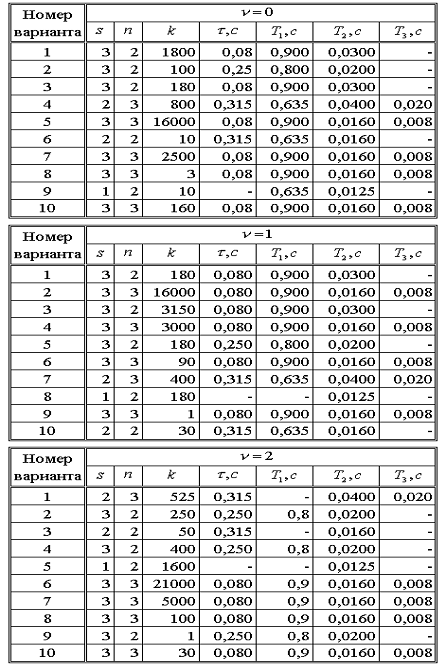
3.4 Содержание отчета по работе

. Цель работы.

. Структурные динамические схемы исследованных систем, их передаточные функции с числовыми значениями параметров и экспериментально полученные графики АФХ, ЛЧХ и переходных функций.

. Ответы на контрольные вопросы.

.5 Контрольные вопросы

. На каком принципе основан частотный критерий устойчивости Найквиста?

. Как формулируется критерий устойчивости Найквиста?

. Чему равны координаты критической точки?

. В чем особенность построения АФХ для астатических систем?

. Чему равен фазовый сдвиг вблизи нулевой частоты для статических и астатических систем?

6. К чему стремится АФХ статических и астатических систем при бесконечно большом увеличении частоты ?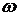

. Как определяются запасы по фазе и модулю с помощью АФХ исследуемой системы?

. Как определяются запасы по фазе и модулю с помощью ЛЧХ исследуемой системы?

. В чем заключается связь между АФХ и ЛЧХ САУ?

10. В чем физический смысл запасов устойчивости по модулю и фазе?

амплитудный фазовый колебательный звено

ЛАБОРАТОРНАЯ РАБОТА № 4. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОКАЗАТЕЛЕЙ КАЧЕСТВА В ПЕРЕХОДНОМ РЕЖИМЕ ОТ ИЗМЕНЕНИЯ ПАРАМЕТРОВ СЛЕДЯЩЕЙ СИСТЕМЫ

Цель работы

Практическое освоение методики исследования переходных режимов функционирования САУ на структурных моделях и приобретение соответствующих знаний о влиянии параметров исследуемой системы на основные показатели качества управления.

4.1 Основные сведения

Исследование САУ заданной структуры в переходном режиме соответствующем реакции на одно из типовых воздействий, проводится с целью оценки показателей качества процессов управления и определения зависимости этих показателей от вариации параметров.

К типовым воздействиям при исследовании САУ относятся следующие функции:

- ступенчатая ,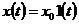

линейная ,

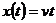квадратичная ,

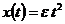гармоническая .

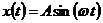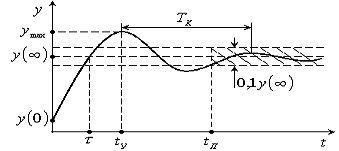
Рис. 4.1. Определение показателей качества по переходной функции

Обычно качество процессов управления оценивается по реакции системы на ступенчатое воздействие, т.е. по переходной функции, которая в общем случае имеет вид, показанный на рис. 4.1. При этом качество управления в переходном режиме характеризуется следующими показателями:

1. Начальное значение 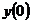, определяемое выражением

.

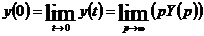. Установившееся значение 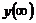, определяемое выражением

.

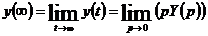. Перерегулирование 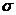, определяемое выражением

,

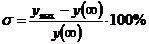где 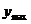 - максимальное значение регулируемой величины.

. Время первого согласования 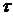, исчисляемое от начала процесса до момента, когда регулируемая величина впервые становится равной установившемуся значения.

. Время установления 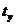, определяемое как время достижения переходной функции первого максимума.

. Время переходного процесса 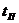, отсчитываемое с момента приложения к системе воздействия до момента, после которого в интервале 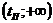 выполняется условие

.

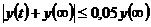. Частота колебаний 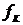, определяемая выражением

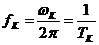
где 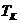 - "период" колебаний.

. Колебательность системы 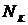, определяемая числом максимумов или минимумов в течение переходного процесса, т.е.

.

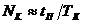Основными показателями качества в рассматриваемом режиме функционирования САУ являются перерегулирование 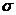 и время переходного процесса .

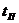аналитические, графические и графоаналитические методы решения дифференциальных уравнений САУ, из которых наибольшее распространение получил операторный метод на основе преобразования Лапласа;

частотные методы, наиболее известным из которых является метод использования вещественных частотных характеристик;

метод математического моделирования.

Рассматриваемый в данной работе, метод математического моделирования, реализуемый средствами цифровой вычислительной техники, при наличии развитого программного обеспечения значительно снижает трудоемкость и повышает эффективность проводимых исследований.

4.2 Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемой системы.

. Получение переходной функции при заданных значениях параметров исследуемой системы

а) Создайте структуру исследуемой системы, на вход которой подается единичное ступенчатое воздействие. Задайте требуемые значения параметров.

б) Проведите имитационное моделирование, подобрав время решения, исходя из получения на экране переходной функции исследуемой системы. Напечатайте график и определите по нему показатели качества процесса управления.

в) Получите и напечатайте график изменения указанных преподавателем промежуточных величин моделируемой системы.

. Получение зависимости основных показателей качества от изменения добротности исследуемой системы

а) Изменяя коэффициент передачи прямой цепи 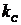 и оставляя неизменными прочие параметры системы, установите такое его значение, при котором визуально наблюдается заметное изменение переходной функции.

По полученной переходной функции определите основные показатели качества, т.е. перерегулирование 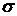 и время переходного процесса 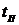. Время  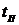удобно определять, пользуясь выводом результатов моделирования в таблицу.

б) Проанализируйте качественно влияние изменения параметра 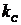 на указанные преподавателем промежуточные величины моделируемой системы.

в) Подобным образом получите три - пять переходных функций, отличающихся друг от друга и дающих представление основных показателей качества и промежуточных величин от изменяемого параметра 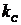 системы.

г) Постройте зависимость перерегулирования и времени переходного процесса от изменяемого параметра.

д) Установите номинальное значение изменяемого параметра, обеспечивающее исходный вид переходной функции.

. Получение зависимости основных показателей качества от изменения коэффициента передачи цепи положительной прямой связи. Выполните п.2, изменяя коэффициент передачи демпфирующего трансформатора 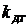 аналогично изменению коэффициента передачи .

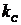. Получение зависимости основных показателей качества от изменения коэффициента передачи 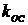 цепи гибкой обратной связи.

Выполните п.2, изменяя коэффициент передач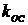и  аналогично изменению коэффициента передачи прямой цепи .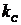

4.3 Варианты заданий

В данной работе исследуются переходные режимы работы следящей системы копировально-фрезерного станка, структурная схема которой приведена на рис. 4.2. Исходные данные для моделирования указанной системы приведены в табл. 4.1.

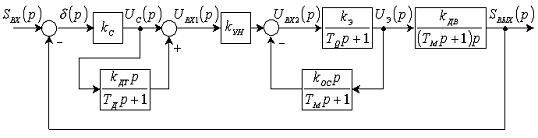
Рис. 4.2. Структурная схема исследуемой системы

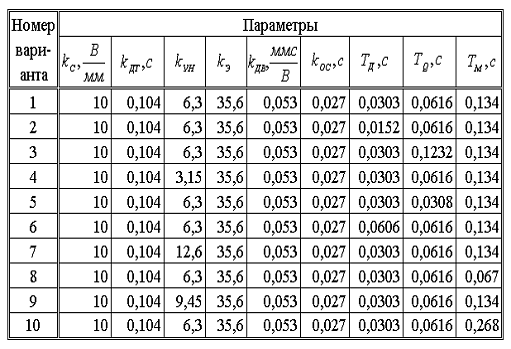
Таблица 4.1

.4 Содержание отчета по работе

. Цель работы.

. Схема исследованной системы с числовыми значениями параметров и экспериментально полученные графики.

. Ответы на контрольные вопросы.

.5 Контрольные вопросы

. Какие воздействия являются типовыми при исследовании САУ?

. По реакции на какое воздействие оценивается качество процессов управления?

. Какими показателями характеризуется качество процессов управления в переходных режимах работы САУ?

. Какие показатели качества являются основными?

. Какими методами можно получить переходную функцию исследуемой системы для анализа качества процессов управления?

. Как зависит вид переходной функции исследуемой системы от изменения её добротности?

. Как зависят основные показатели качества исследуемой системы от коэффициента передачи цепи положительной прямой связи?

. Как зависят основные показатели качества исследуемой системы от коэффициента передачи цепи гибкой обратной связи?

. Как зависит вид указанных преподавателем промежуточных величин моделируемой системы от изменения добротности и коэффициентов передачи положительной и отрицательной обратной связи?

. Изменение какого из исследуемых параметров системы оказывается наиболее сильно на её устойчивости?

ЛАБОРАТОРНАЯ РАБОТА № 5. ОЦЕНКА ТОЧНОСТИ УСТАНОВИВШЕГОСЯ РЕЖИМА В ЗАВИСИМОСТИ ОТ ПОРЯДКА АСТАТИЗМА СИСТЕМ УПРАВЛЕНИЯ

Цель работы

Исследование точности установившихся режимов функционирования САУ в зависимости от порядка их астатизма экспериментальным методом цифрового имитационного моделирования и аналитическим расчетом.

.1 Основные сведения

Исследование САУ в установившемся режиме, соответствующем реакции на одно из типовых воздействий после затухания переходного процесса, проводится с целью вычисления ошибки, характеризующей точность функционирования, а следовательно и качество процессов управления в рассматриваемом режиме.

При этом, в зависимости от вида типового воздействия, установившиеся режимы делятся на:

- статические, обусловленные постоянными во времени воздействиями вида 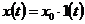, под действием которых система приходит в состояние покоя.

динамические, при которых приложенные к системе воздействия изменяются по некоторому закону вида 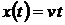, , 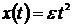 и обуславливают режим установившего вынужденного движения.

Искомое значение ошибки для рассмотренных типовых воздействий, за исключением гармонического, можно определить, пользуясь теоремой о конечном значении

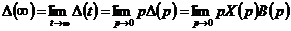,                                            (5.1)

где 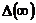, , 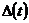 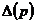- соответственно оригиналы и изображение ошибки,  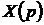- изображение воздействия 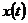,  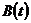- передаточная функция исследуемой системы по ошибке.

Передаточная функция по ошибке САУ, структура которой в общем виде приведена на рис. 5.1, определяется выражением

,

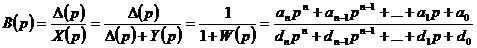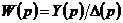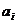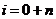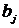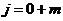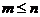где  - передаточная функция разомкнутой системы, полученная через коэффициенты , , , ,  дифференциального уравнения при ; , .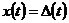

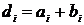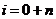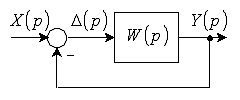
Рис. 5.1. Общий вид структуры исследуемой системы

После подстановки этого выражения в (5.1), имеем

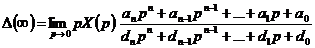.                                       (5.2)

Анализ полученной зависимости позволяет оценить качество процессов управления статических и астатических САУ в статическом, при изображении ступенчатого воздействия 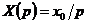, и динамическом, при изображениях степенных функций времени 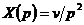, , 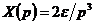режимах. Эта оценка дает следующие значения статических 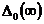 и динамических 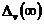,  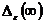ошибок:

для статических систем ()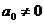

, , ;

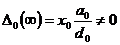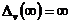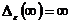для астатических систем первого порядка (, )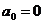

, , ;

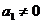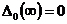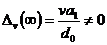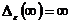для астатических систем второго порядка (, )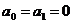

, , .

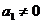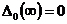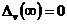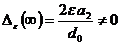Возможные случаи изменения ошибок иллюстрируются рис. 5.2.

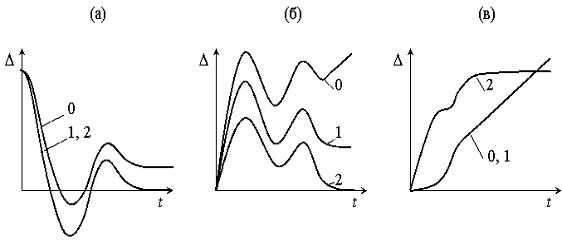
Рис. 5.2. Графики ошибок при ступенчатом (а), линейном (б) и квадратичном (в) воздействиях: 0 - нулевой астатизм; 1 - астатизм первого порядка; 2 - астатизм второго порядка

Для определения значения расходящейся ошибки в любой момент времени из интервала (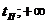) передаточную функцию по ошибке представим в виде ряда 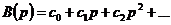, что позволяет определить ошибку в следующем виде:

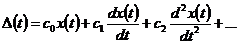                                                        (5.3)

При этом коэффициенты разложения 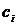 определяются, исходя из выражения для передаточной функции по ошибке

или рекуррентной формулой через коэффициенты передаточной функции разомкнутой системы

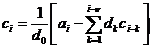,                                                                        (5.5)

где 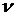 - порядок астатизма.

Динамическая ошибка при гармоническом воздействии 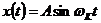, где 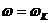 - частота качки, изменяется по закону воздействия, т.е. имеет периодический характер. Поэтому при оценке качества процессов управления в установившемся гармоническом режиме достаточно оценить амплитудное значение искомой динамической ошибки. Это наиболее просто осуществляется по частотным характеристикам исследуемой САУ, исходя из выражения

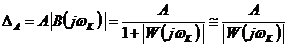,                                             (5.6)

где 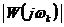 - модуль передаточной функции разомкнутой системы на частоте 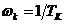,  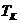- период качки.

Очевидно, что 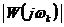 определяется либо аналитически, либо из ЛАХ разомкнутой системы.

Приведенные выше выражения для статических и динамических ошибок в установившемся режиме позволяют сделать заключение о зависимости точности функционирования САУ в рассматриваемом режиме от величина воздействий, структуры и параметров исследуемой системы. При этом повышение порядка астатизма системы управления увеличивает её точность, снижает устойчивость.

5.2 Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемых САУ.

. Анализ точности функционирования статической системы

а) В Simulink создайте структуру замкнутой САУ (с единичной обратной связью), на вход которой подаётся заданное ступенчатое воздействие, а передаточная функция прямой цепи соответствует заданной передаточной функции разомкнутой системы. Задайте требуемые значения параметров.

б) Проведите имитационное моделирование, подобрав время решения исходя из полученных на экране графиков ошибки выходной величины исследуемой системы в установившемся режиме.

в) Напечатайте график ошибки и определите по нему ошибку установившегося режима, пользуясь выводом результатов моделирования в таблицу.

г) Отредактируйте структуру исследуемой системы, подав на её вход заданное линейно возрастающее воздействие.

д) Выполните п. "б".

е) Нанесите на полученный в п. "в" график новые значения ошибки в узловых точках, постройте график.

ж) Отредактируйте структуру исследуемой системы, подав на её вход заданную квадратичную функцию времени. Следует иметь в виду, что при подаче данного воздействия величину скачка по ускорению устанавливают равной удвоенному значению 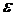, приведенного в табл. 5.1 для выполняемого варианта.

з) Выполните п.п. "б" и "е".

и) Используя выражение (5.2), рассчитайте аналитически значение ошибки в установившемся режиме. В случае расходящейся ошибки определите коэффициенты ошибок по (5.4) или (5.5) и, используя (5.3), определите значение ошибки в произвольный момент времени. Сравните полученные результаты с экспериментальным данными.

к) Отредактируйте структуру исследуемой системы, подав на её вход заданное гармоническое воздействие.

л) Выполните п.п. "б" и "в".

м) Получите и напечатайте ЛЧХ исследуемой системы.

н) Используя выражение (5.6), рассчитайте значение ошибки в установившемся режиме, определив 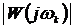 сначала аналитически, а затем по ЛАХ, полученной в предыдущем пункте. Сравните полученные результаты с экспериментальными данными.

. Анализ точности функционирования астатической системы первого порядка

Выполните п. 1 для структуры, соответствующей исследуемой системы с астатизмом первого порядка.

. Анализ точности функционирования астатической системы второго порядка

Выполните п. 1 для структуры, соответствующей исследуемой системе с астатизмом второго порядка.

5.3 Варианты заданий

В данной работе исследуется точность установившихся режимов статической, а также астатических систем первого и второго порядка.

Передаточные функции исследуемых систем в общем виде определяются следующим образом:

.

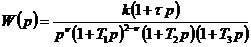Исходные данные для моделирования указанных систем приведены в табл. 5.1.

Таблица 5.1

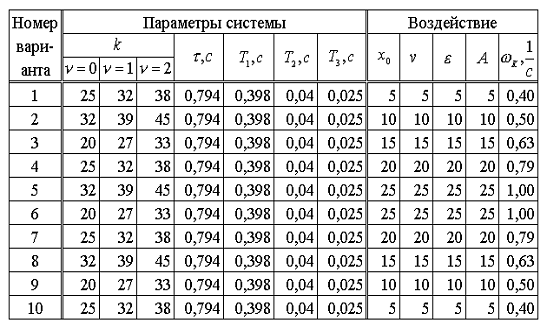
5.4 Содержимое отчета по работе

. Цель работы.

. Структурные динамические схемы исследованных систем, их передаточные функции с числовыми значениями параметров, экспериментально полученные графики и результаты аналитических расчетов.

. Ответы на контрольные вопросы.

5.5 Контрольные вопросы

. Какие виды установившихся режимов имеют место в САУ?

. Какая теорема позволяет определить конечное значение ошибки в установившемся режиме?

. Как определяется установившееся значение расходящейся ошибки в произвольный момент времени?

. Каким образом связаны между собой передаточная функция разомкнутой САУ и её передаточная функция по ошибке?

. Какими способами можно определить коэффициенты ошибок?

. Какие системы обладают большей точностью в статическом установившемся режиме?

. Каков необходимый порядок астатизма САУ для обеспечения нулевой динамической ошибки при воздействии в виде квадратичной функции времени?

. Каков порядок астатизма САУ, обеспечивающий устойчивый динамический режим функционирования при линейно возрастающем воздействии?

. Какими способами можно определить динамическую ошибку при гармоническом воздействии?

. В каком соотношении находятся точность САУ в установившемся режиме и её устойчивость?

ЛАБОРАТОРНАЯ РАБОТА № 6. ИССЛЕДОВАНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ЗАПАЗДЫВАНИЕМ

Цель работы

Определение влияния величины запаздывания на устойчивость систем управления на основе структурных преобразований исследуемой системы в зависимости от места нахождения звена с запаздыванием.

.1 Основные сведения

Системы с запаздыванием отличаются от обычных линейных САУ отличием одного или нескольких звеньев, величина на выходе которых 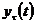 начинает меняться при изменении величины на входе 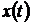 с некоторой постоянной временной задержкой 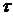, т.е. .

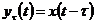Подобные звенья с "чистым" запаздыванием имеют передаточную функцию вида

,

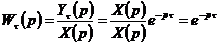которой соответствует комплексный коэффициент передачи

,

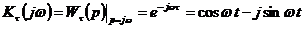а частотные характеристик определяются выражениями

, , .

, .

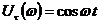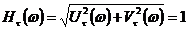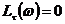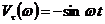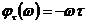Таким образом, АФХ звена с запаздыванием представляет собой круг единичного радиуса на комплексной плоскости 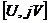 с центром в начале координат, ЛАХ имеет нулевое значение и инвариантна к изменениям частоты, а ЛФХ неограниченно убывает с увеличением частоты.

При последовательном включении звена с запаздыванием вместе с обычными динамическими звеньями передаточная функция и комплексный коэффициент передачи разомкнутой системы будут

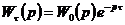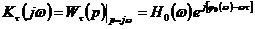, ,                       (6.1)

где 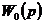, , 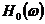 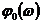- соответственно передаточная функция, амплитудная и фазовая частотные характеристики разомкнутой системы без учета запаздывания.

Следовательно, системы, отличающиеся друг от друга лишь величиной запаздывания, имеют одинаковые амплитудные и различные фазовые характеристики. При этом большей величине запаздывания 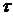 соответствует больший фазовый сдвиг на частоте среза системы, что приводит к ухудшению её устойчивости.

Устойчивость системы с запаздыванием определяется с помощью критерия Найквиста по передаточной функции и комплексному коэффициенту передачи исследуемой системы в виде (6.1). Это требует структурных преобразований исходной системы в зависимости от места нахождения звеньев с запаздыванием.

Так, если данное звено включено в прямую цепь, то при размыкании главной обратной связи (см. рис. 6.1,а)

,

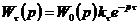Если же звено запаздывания включено в местную обратную связь, то (см. рис. 6.1,б)

,

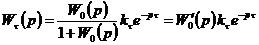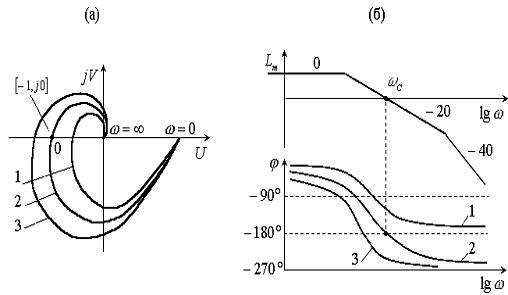
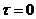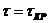Рис. 6.1. АФХ (а) и ЛЧХ (б) САУ: 1 - ; 2 -; 3 -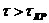

что соответствует размыканию местной обратной связи.

Формулировка критерия Найквиста для систем с запаздыванием меняется. Однако в рассматриваемых системах явления устойчивости и неустойчивости чередуются при непрерывном изменении .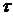

Для определения условий устойчивости вводится понятие критического времени запаздывания 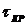, которое определяется из равенства фазовой частотной характеристики разомкнутой системы на частоте среза 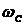 величине 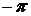, т.е. (см. рис. 6.2)

.

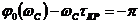Отсюда определяем

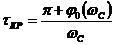,                                                                               (6.2)

где 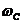 определяется из условия .

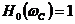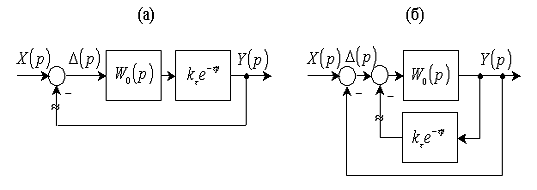
Рис. 6.2 Структурные преобразования исследуемой системы с размыканием главной (а) и местной (б) обратной цепи

6.2 Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемой САУ (табл. 6.1).

. Определение критического времени запаздывания

а) В Simulink создайте структуру, соответствующую рис. 6.2,а при 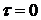, т.е. при отсутствии звена с запаздыванием. Задайте требуемые значения параметров.

б) Проведите имитационное моделирование, подобрав время решения исходя из полученного на экране графика переходного процесса. Напечатайте его.

в) Получите и напечатайте ЛЧХ и АФХ исследуемой разомкнутой структуры, по которой определите частоту среза и запас по фазе на этой частоте. При этом график АФХ напечатайте вблизи критической точки.

г) По выражению (6.2) рассчитайте критическое время запаздывания.

д) Определите критическое время запаздывания аналитическим путём, используя экспериментально полученное значение 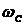. Сравните результаты.

. Определение временных и частотных характеристик исследуемой САУ при наличии звена с запаздыванием в прямой цепи

а) Введите звено с запаздыванием в исследуемую структуру в соответствии с рис. 6.2,а.

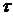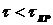б) Изменяя значение  при , подберите такое его значение, при котором визуально наблюдается заметное изменение переходной функции. Нанесите на полученный в п. 1,б график новые значения переходной функции в узловых точках. Постройте график.

в) Нанесите на полученные в п. 1,в в характеристики новые значения частотных характеристик. Постройте графики.

г) Выполните п. "б" и "в" для .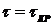

д) Выполните п. "б" и "в" для .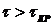

. Определение временных и частотных характеристик исследуемой САУ при наличии звена с запаздыванием в цепи местной обратной связи

Выполните п. 1 и п. 2 для структуры, изображенной на рис. 6.2,б.

.3 Варианты заданий

В данной работе исследуется влияние величины запаздывания на устойчивость системы управления при наличии в ней звена с запаздыванием как в прямой цепи, так и в цепи местной обратной связи.

При этом исходная разомкнутая система без запаздывания представляет собой последовательное соединение двух апериодических звеньев, т.е. имеет передаточную функцию

.

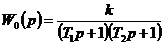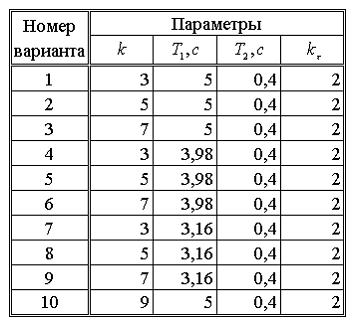
Исходные данные для моделирования данной передаточной функции приведены в табл. 6.1.

Таблица 6.1

6.4 Содержание отчета по работе

. Цель работы.

. Схемы исследованных систем, их передаточные функции с числовыми значениями параметров, экспериментально полученные графики и результаты аналитических расчетов.

. Ответы на контрольные вопросы.

6.5 Контрольные вопросы

. Чем отличаются системы с запаздыванием от обычных линейных систем?

. Какова зависимость выходной величины звена с "чистым" запаздыванием от его входной величины?

. Как записывается передаточная функция звена с запаздыванием?

4. Какой вид имеют частотные характеристики звена с запаздыванием?

. Каково влияние запаздывания на ЛЧХ исследуемой САУ?

. Каково влияние запаздывания на АФХ исследуемой САУ?

. С помощью какого критерия определяется устойчивость систем с запаздыванием?

. Зависит ли устойчивость САУ от расположения звена запаздывания в исследуемой структуре?

. Что называется критическим временем запаздывания?

10. Как определяется критическое время запаздывания?

СПИСОК ЛИТЕРАТУРЫ

1.   Бесекерский В. А., Попов Е. П. Теория систем автоматического управления. - СПб.: Изд-во "Профессия", 2003. - 752 с.

2.       Воронов А. А. Основы теории автоматического управления. - М.: Высшая школа. - Часть I. - 1986.

3.   Дьяконов В. Simulink 4. Специальный справочник. - СПб: Питер, 2002.

4.       Епишкин А. Е. Исследование динамических процессов в системе MATLAB - Simulink. Методические указания. СПб., 2004. - 32 с.

.        Первозванский А. А. Курс теории автоматического управления. - М.: Наука, 1986. - 616 с.

.        Цыпкин Я. З. Основы теории автоматических систем. - М.: Наука, 1977. - 559 с.