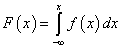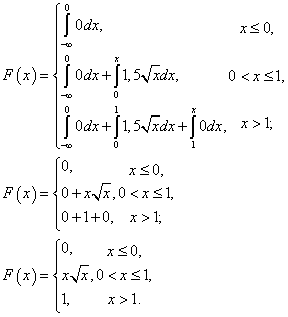Теория вероятности
Задача 1
Вероятность появления события 
в
каждом из 
испытаний 
.
Найти вероятность того, что в испытаниях событие
появится:
а) ровно 
раз;
б) не более 
раз;
в) не меньше 
раз.
РЕШЕНИЕ
а) Вероятность того, что событие произойдет
ровно 2 раза из 5, найдем по формуле Бернулли.
где 
-
общее количество испытаний, 
- количество
появлений события , 
-
вероятность появления события , 
-
вероятность появления события 
.
б) Вероятность того, что событие произойдет не
более 2х раз равносильно сумме событий 
.
Вероятность указанных событий найдем по формуле
Бернулли.
б) Вероятность того, что событие произойдет не
меньше 4х раз равносильно сумме событий 
.
Вероятность указанных событий найдем по формуле
Бернулли.
Задача 2
Задана дискретная случайная величина 
.
Найти функцию распределения случайной величины .
Построить ее график. Найти 
.
РЕШЕНИЕ
Найдем функцию распределения
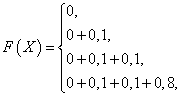
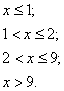
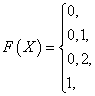
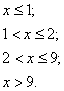
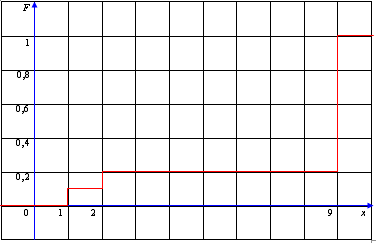
Построим график функции распределения.
Математическое ожидание дискретной случайной
величины 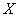найдем
по формуле
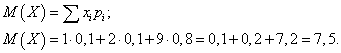
Дисперсию дискретной случайной величины 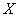найдем
по формуле
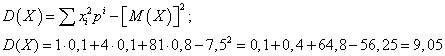
Найдем среднее квадратическое отклонение
.
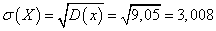Задача 3
Исходя из свойств интегральной функции
распределения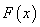 
, определить
неизвестные параметры. Найти плотность распределения 
.
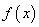Построить графики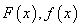 
. Найти
.
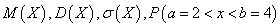РЕШЕНИЕ
Функция 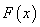является
непрерывной по определению. Чтобы в точках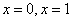 
не
было разрыва должны выполняться следующие условия:
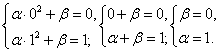
Т.о. интегральная функция распределения равна
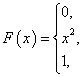
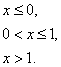
Найдем плотность распределения .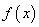
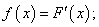
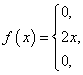
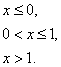
По свойству плотности вероятности:
.
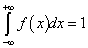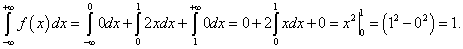
Значит параметр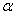 
найден
верно.
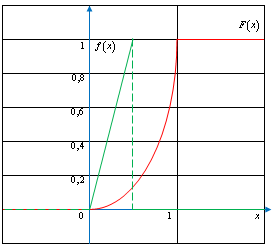
Построим графики функци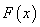и распределения и
плотности распределения .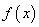
Математическое ожидание находим по формуле:
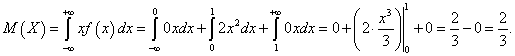
Найдем дисперсию:
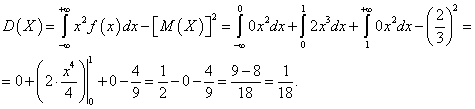
Среднее квадратическое отклонение:
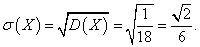
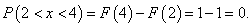
Задача 4
Непрерывная случайная величина 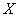распределена
по нормальному закону:
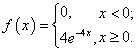
Найти функцию распределения,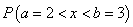 
.
РЕШЕНИЕ
Найдем функцию распределения непрерывной
случайной величины.
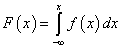
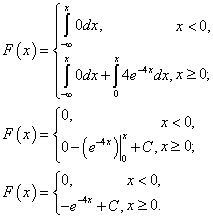
Найдем параметр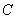 
.
По определению функция распределения является непрерывной, следовательно,
должно выполняться следующее условие:
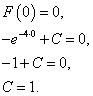
Тогда функция распределения приобретает вид:
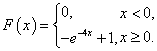
Найдем вероятность попадания в интервал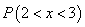 
.
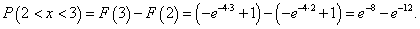
Задача 5
Исходя из свойств плотности распределения,
определить параметр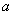 
, построить график .
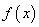Найти функцию распределения .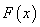
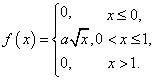
РЕШЕНИЕ
По свойству плотности распределения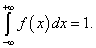 
Плотность распределения имеет вид:
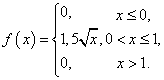
Построим график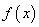
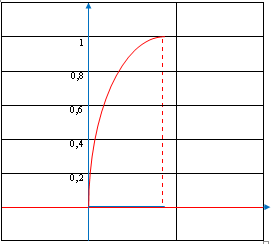
Найдем функцию распределения по формуле:
событие дискретный
интегральный распределение
