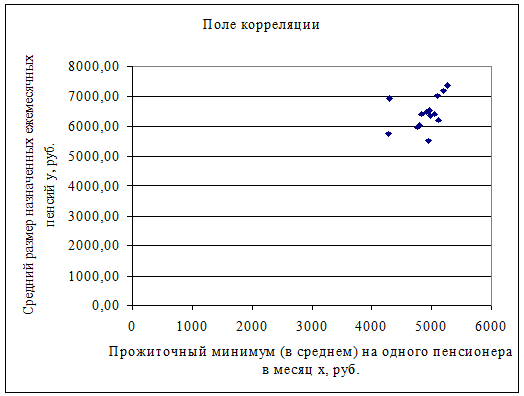
Поле корреляции
1. Поле корреляции
В соответствии с условием задачи средний размер пенсий будет
результативным признаком (у), а прожиточный минимум факторным признаком.
Отсортируем исходные данные по возрастанию факторного
признака:
|
Прожиточный
минимум (в среднем) на одного пенсионера в месяц x, руб.
|
Средний размер
назначенных ежемесячных пенсий y, руб.
|
|
x
|
y
|
|
4184
|
5426,00
|
|
4272
|
5906,00
|
|
4282
|
5748,00
|
|
4302
|
6920,00
|
|
4756
|
5966,00
|
|
4794
|
6032,00
|
|
4838
|
6404,00
|
|
4906
|
6466,00
|
|
4942
|
5494,00
|
|
4958
|
6518,00
|
|
4980
|
6334,00
|
|
5048
|
6416,00
|
|
5104
|
7020,00
|
|
5122
|
6202,00
|
|
5200
|
7196,00
|
|
5272
|
7372,00
|
Построим поле корреляции
2. Параметры уравнений парных регрессий
Составим
уравнение линейной регрессии.
Найдем коэффициенты регрессии по формулам:
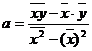 ;
; 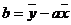
Построим таблицу для вычисления коэффициентов регрессии:
|
№
|
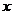 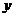 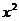 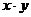 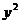 
|
|
|
|
|
|
|
1
|
4184,00
|
5426,00
|
17505856
|
22702384
|
29441476
|
5759,96
|
|
2
|
4272,00
|
5906,00
|
18249984
|
25230432
|
34880836
|
5841,32
|
|
3
|
4282,00
|
5748,00
|
18335524
|
24612936
|
33039504
|
5850,57
|
|
4
|
4302,00
|
6920,00
|
18507204
|
29769840
|
47886400
|
5869,06
|
|
5
|
4756,00
|
5966,00
|
22619536
|
28374296
|
35593156
|
6288,82
|
|
6
|
4794,00
|
6032,00
|
22982436
|
28917408
|
36385024
|
6323,96
|
|
7
|
4838,00
|
6404,00
|
23406244
|
30982552
|
41011216
|
6364,64
|
|
8
|
4906,00
|
6466,00
|
24068836
|
31722196
|
41809156
|
6427,51
|
|
9
|
4942,00
|
5494,00
|
24423364
|
27151348
|
30184036
|
6460,80
|
|
10
|
4958,00
|
6518,00
|
24581764
|
32316244
|
42484324
|
6475,59
|
|
11
|
4980,00
|
6334,00
|
24800400
|
31543320
|
40119556
|
6495,93
|
|
12
|
5048,00
|
6416,00
|
25482304
|
32387968
|
41165056
|
6558,80
|
|
13
|
5104,00
|
7020,00
|
26050816
|
35830080
|
49280400
|
6610,58
|
|
14
|
5122,00
|
6202,00
|
26234884
|
31766644
|
38464804
|
6627,22
|
|
15
|
5200,00
|
7196,00
|
27040000
|
37419200
|
51782416
|
6699,34
|
|
16
|
5272,00
|
7372,00
|
27793984
|
38865184
|
54346384
|
6765,91
|
|
сумма
|
76960,00
|
101420,00
|
372083136,00
|
489592032,00
|
647873744,00
|
101420,00
|
|
среднее
|
4810,00
|
6338,75
|
23255196,00
|
30599502,00
|
40492109,00
|
6338,75
|

Уравнение линейной регрессии имеет вид:
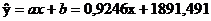
Дадим экономическую интерпретацию полученным результатам. На
основании коэффициента регрессии 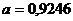 можно сделать вывод: при увеличении прожиточного минимума на 1
рубль, средний размер пенсий увеличивается в среднем на 0,9246 рубля. По
полученному значению коэффициента
можно сделать вывод: при увеличении прожиточного минимума на 1
рубль, средний размер пенсий увеличивается в среднем на 0,9246 рубля. По
полученному значению коэффициента 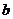 делаем вывод, что при нулевом уровне прожиточного минимума (
делаем вывод, что при нулевом уровне прожиточного минимума ( ) прогнозируемое значение среднего размера
пенсий равно 1891,491 рублей. При увеличении прожиточного минимума возрастает
средний размер пенсий.
) прогнозируемое значение среднего размера
пенсий равно 1891,491 рублей. При увеличении прожиточного минимума возрастает
средний размер пенсий.
График линейной зависимости:
Составим
уравнение логарифмической регрессии.
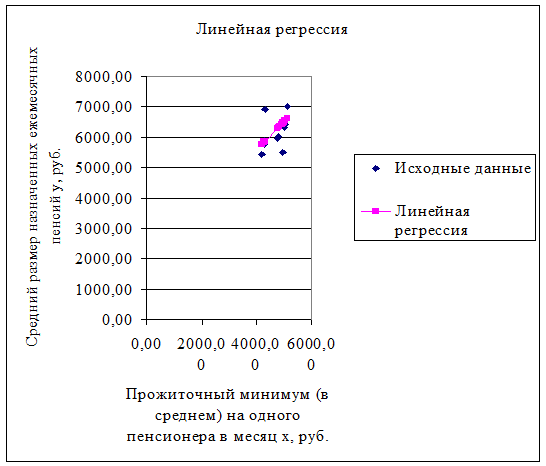
Уравнение логарифмической регрессии представлено следующим
уравнением:
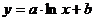
Значения параметров логарифмической регрессии определяются по
формулам:
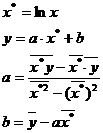
Расчетные значения параметров
|
№
|
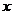 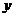 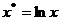 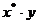 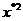 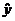
|
|
|
|
|
|
|
1
|
4184
|
5426
|
8,34
|
45247,54
|
69,54
|
5757,59
|
|
2
|
4272
|
5906
|
8,36
|
49373,20
|
69,89
|
5846,04
|
|
3
|
4282
|
5748
|
8,36
|
48065,78
|
69,93
|
5855,98
|
|
4
|
4302
|
6920
|
8,37
|
57898,50
|
70,00
|
5875,78
|
|
5
|
4756
|
5966
|
8,47
|
50515,09
|
71,69
|
6302,12
|
|
6
|
4794
|
6032
|
8,48
|
51121,93
|
71,83
|
6335,94
|
|
7
|
4838
|
6404
|
8,48
|
54333,18
|
71,98
|
6374,77
|
|
8
|
4906
|
6466
|
8,50
|
54949,45
|
72,22
|
6434,08
|
|
9
|
4942
|
5494
|
8,51
|
46729,36
|
72,34
|
6465,15
|
|
10
|
4958
|
6518
|
8,51
|
55460,08
|
72,40
|
6478,88
|
|
11
|
4980
|
6334
|
8,51
|
53922,51
|
72,47
|
6497,70
|
|
12
|
5048
|
6416
|
8,53
|
54707,61
|
72,71
|
6555,33
|
|
13
|
5104
|
7020
|
8,54
|
59935,21
|
72,89
|
6602,22
|
|
14
|
5122
|
6202
|
8,54
|
52973,14
|
72,95
|
6617,18
|
|
15
|
5200
|
7196
|
8,56
|
61571,95
|
73,21
|
6681,40
|
|
16
|
5272
|
7372
|
8,57
|
63179,26
|
73,45
|
6739,84
|
|
сумма
|
76960
|
101420
|
135,61
|
859983,81
|
1149,51
|
101420,00
|
|
среднее
|
4810,00
|
6338,75
|
8,48
|
53748,99
|
71,84
|
6338,75
|
Параметры уравнения регрессии:
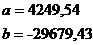
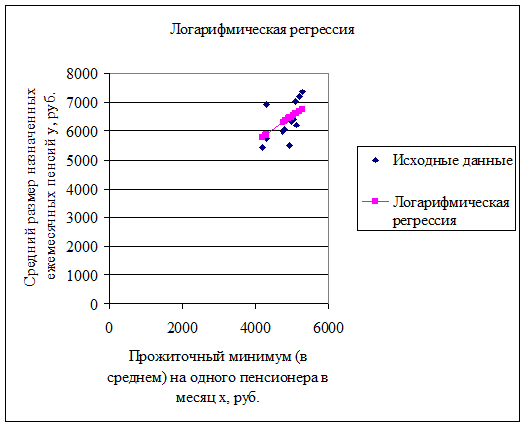
Уравнение логарифмической регрессии:
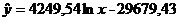
С экономической точки зрения результаты можно объяснить следующим
образом. По полученному значению коэффициента  делаем вывод, что средний размер пенсий в среднем изменится на
4249,54 рублей при увеличении прожиточного минимума на 1 рубль. По полученному
значению
делаем вывод, что средний размер пенсий в среднем изменится на
4249,54 рублей при увеличении прожиточного минимума на 1 рубль. По полученному
значению 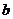 делаем вывод, что при нулевом уровне
прожиточного минимума (
делаем вывод, что при нулевом уровне
прожиточного минимума (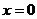 ) прогнозируемое значение среднего размера
пенсий равно -29679,43 рублей.
) прогнозируемое значение среднего размера
пенсий равно -29679,43 рублей.
График логарифмической зависимости:
Составим
уравнение показательной регрессии
Уравнение показательной регрессии выглядит следующим образом: 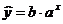 . Данное уравнение нормализуется и
приводится к виду
. Данное уравнение нормализуется и
приводится к виду 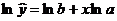 . Произведем замену
. Произведем замену 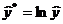 ,
, 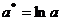 ,
, 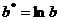 . Уравнение принимает вид:
. Уравнение принимает вид: 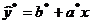 , т.е. обычное линейное уравнение.
Относительно новых параметров имеем следующую систему уравнений:
, т.е. обычное линейное уравнение.
Относительно новых параметров имеем следующую систему уравнений:
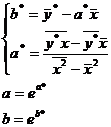
Расчетные значения параметров
|
№
|
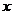 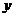 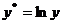 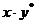 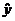
|
|
|
|
|
|
1
|
4184
|
5426
|
8,60
|
35978,04
|
5760,90
|
|
2
|
4272
|
5906
|
8,68
|
37096,87
|
5835,66
|
|
3
|
4282
|
5748
|
8,66
|
37067,59
|
5844,21
|
|
4
|
4302
|
6920
|
8,84
|
38039,02
|
5861,36
|
|
5
|
4756
|
5966
|
41347,86
|
6264,47
|
|
6
|
4794
|
6032
|
8,70
|
41730,97
|
6299,44
|
|
7
|
4838
|
6404
|
8,76
|
42403,51
|
6340,18
|
|
8
|
4906
|
6466
|
8,77
|
43046,78
|
6403,65
|
|
9
|
4942
|
5494
|
8,61
|
42557,60
|
6437,52
|
|
10
|
4958
|
6518
|
8,78
|
43542,76
|
6452,62
|
|
11
|
4980
|
6334
|
8,75
|
43593,36
|
6473,46
|
|
12
|
5048
|
6416
|
8,77
|
44253,55
|
6538,27
|
|
13
|
5104
|
7020
|
8,86
|
45203,67
|
6592,13
|
|
14
|
5122
|
6202
|
8,73
|
44728,52
|
6609,54
|
|
15
|
5200
|
7196
|
8,88
|
46182,66
|
6685,50
|
|
16
|
5272
|
7372
|
8,91
|
46949,50
|
6756,39
|
|
сумма
|
76960
|
101420
|
140,01
|
673722,26
|
101155,28
|
|
среднее
|
4810,00
|
6338,75
|
8,75
|
42107,64
|
6322,21
|
Параметры уравнения регрессии:
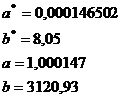
Уравнение показательной регрессии:
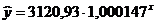
График показательного уравнения регрессии:
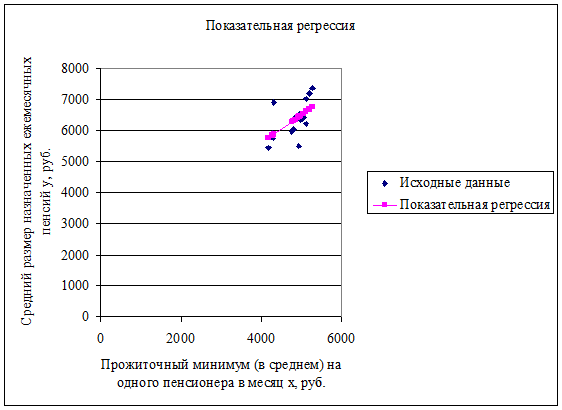
Составим
уравнение степенной регрессии.
Уравнение степенной регрессии имеет вид: 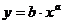 , после логарифмирования уравнения и
замены
, после логарифмирования уравнения и
замены 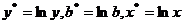 уравнение принимает следующий вид:
уравнение принимает следующий вид: 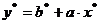 . Запишем коэффициенты для уравнения
степенной регрессии, путем следующей замены:
. Запишем коэффициенты для уравнения
степенной регрессии, путем следующей замены: 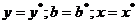 . Получаем формулы:
. Получаем формулы:
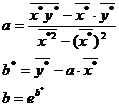
Расчетные значения параметров
|
№
|
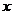 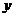 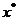 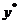 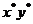 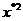 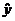
|
|
|
|
|
|
|
|
1
|
4184
|
5426
|
8,34
|
8,60
|
71,71
|
69,54
|
5757,83
|
|
2
|
4272
|
5906
|
8,36
|
8,68
|
72,59
|
69,89
|
5839,23
|
|
3
|
4282
|
5748
|
8,36
|
8,66
|
72,39
|
69,93
|
5848,45
|
|
4
|
4302
|
6920
|
8,37
|
8,84
|
73,98
|
70,00
|
5866,86
|
|
5
|
4756
|
5966
|
8,47
|
8,69
|
73,61
|
71,69
|
6277,62
|
|
6
|
4794
|
6032
|
8,48
|
8,70
|
73,77
|
71,83
|
6311,41
|
|
7
|
4838
|
6404
|
8,48
|
8,76
|
74,36
|
71,98
|
6350,42
|
|
8
|
4906
|
6466
|
8,50
|
8,77
|
74,57
|
72,22
|
6410,49
|
|
9
|
4942
|
5494
|
8,51
|
8,61
|
73,24
|
72,34
|
6442,18
|
|
10
|
4958
|
6518
|
8,51
|
8,78
|
74,73
|
72,40
|
6456,24
|
|
11
|
4980
|
6334
|
8,51
|
8,75
|
74,52
|
72,47
|
6475,55
|
|
12
|
5048
|
6416
|
8,53
|
8,77
|
74,75
|
72,71
|
6535,06
|
|
13
|
5104
|
7020
|
8,54
|
8,86
|
75,62
|
72,89
|
6583,87
|
|
14
|
5122
|
6202
|
8,54
|
8,73
|
74,59
|
72,95
|
6599,53
|
|
15
|
5200
|
7196
|
8,56
|
8,88
|
75,99
|
73,21
|
6667,15
|
|
16
|
5272
|
7372
|
8,57
|
8,91
|
76,32
|
73,45
|
6729,27
|
|
сумма
|
76960
|
101420
|
135,61
|
140,01
|
1186,74
|
1149,51
|
101151,18
|
|
среднее
|
4810,00
|
6338,75
|
8,48
|
8,75
|
74,17
|
71,84
|
6321,95
|
Параметры уравнения степенной регрессии:
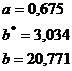
Уравнение степенной регрессии:

График степенного уравнения регрессии:
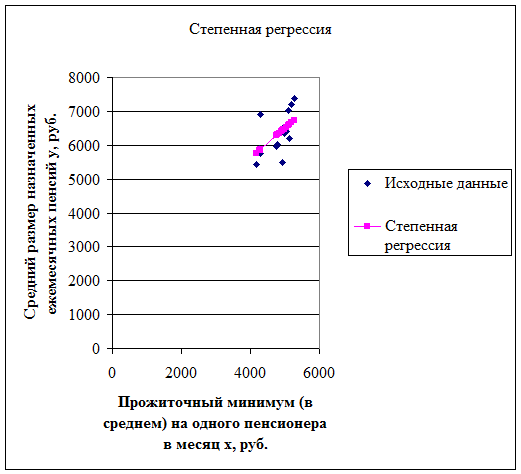
В степенных функциях коэффициент регрессии 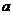 имеет экономическое истолкование - он
является коэффициентом эластичности. Это означает, что величина коэффициента
показывает, на сколько процентов изменится в среднем результат, если фактор
измениться на 1%. В данном случае, с увеличением прожиточного минимума на 1%,
средний размер пенсий возрастет в среднем на 0,675%.
имеет экономическое истолкование - он
является коэффициентом эластичности. Это означает, что величина коэффициента
показывает, на сколько процентов изменится в среднем результат, если фактор
измениться на 1%. В данном случае, с увеличением прожиточного минимума на 1%,
средний размер пенсий возрастет в среднем на 0,675%.
Уравнение регрессии имеет вид: 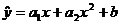 . Для определения коэффициентов используются формулы:
. Для определения коэффициентов используются формулы:
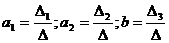
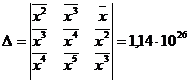
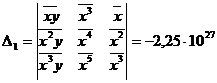
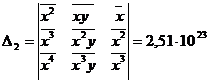
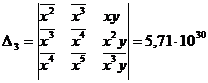
Рассчитаем значения параметров уравнения:
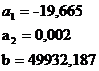
Уравнение регрессии в виде многочлена второй степени имеет вид
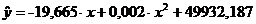
Расчетные значения параметров
|
№
|
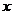 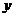 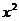 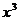 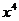 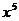 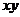 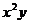 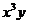 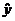
|
|
|
|
|
|
|
|
|
|
|
1
|
4184
|
5426
|
1,75E+07
|
7,32E+10
|
3,06E+14
|
1,28E+18
|
2,27E+07
|
9,50E+10
|
3,97E+14
|
6041,54
|
|
2
|
4272
|
5906
|
1,82E+07
|
7,80E+10
|
3,33E+14
|
1,42E+18
|
2,52E+07
|
1,08E+11
|
4,60E+14
|
5942,79
|
|
3
|
4282
|
5748
|
1,83E+07
|
7,85E+10
|
3,36E+14
|
1,44E+18
|
2,46E+07
|
1,05E+11
|
4,51E+14
|
5933,72
|
|
4
|
4302
|
6920
|
1,85E+07
|
7,96E+10
|
3,43E+14
|
1,47E+18
|
2,98E+07
|
1,28E+11
|
5,51E+14
|
5916,89
|
|
5
|
4756
|
5966
|
2,26E+07
|
1,08E+11
|
5,12E+14
|
2,43E+18
|
2,84E+07
|
1,35E+11
|
6,42E+14
|
6006,78
|
|
6
|
4794
|
6032
|
2,30E+07
|
1,10E+11
|
5,28E+14
|
2,53E+18
|
2,89E+07
|
1,39E+11
|
6,65E+14
|
6055,30
|
|
7
|
4838
|
6404
|
2,34E+07
|
1,13E+11
|
5,48E+14
|
2,65E+18
|
3,10E+07
|
1,50E+11
|
7,25E+14
|
6119,40
|
|
8
|
4906
|
6466
|
2,41E+07
|
1,18E+11
|
5,79E+14
|
2,84E+18
|
3,17E+07
|
1,56E+11
|
7,64E+14
|
6235,15
|
|
9
|
4942
|
5494
|
2,44E+07
|
1,21E+11
|
5,97E+14
|
2,95E+18
|
1,34E+11
|
6,63E+14
|
6304,65
|
|
10
|
4958
|
6518
|
2,46E+07
|
1,22E+11
|
6,04E+14
|
3,00E+18
|
3,23E+07
|
1,60E+11
|
7,94E+14
|
6337,36
|
|
11
|
4980
|
6334
|
2,48E+07
|
1,24E+11
|
6,15E+14
|
3,06E+18
|
3,15E+07
|
1,57E+11
|
7,82E+14
|
6384,17
|
|
12
|
5048
|
6416
|
2,55E+07
|
1,29E+11
|
6,49E+14
|
3,28E+18
|
3,24E+07
|
1,63E+11
|
8,25E+14
|
6542,27
|
|
13
|
5104
|
7020
|
2,61E+07
|
1,33E+11
|
6,79E+14
|
3,46E+18
|
3,58E+07
|
1,83E+11
|
9,33E+14
|
6687,71
|
|
14
|
5122
|
6202
|
2,62E+07
|
1,34E+11
|
6,88E+14
|
3,53E+18
|
3,18E+07
|
1,63E+11
|
8,33E+14
|
6737,37
|
|
15
|
5200
|
7196
|
2,70E+07
|
1,41E+11
|
7,31E+14
|
3,80E+18
|
3,74E+07
|
1,95E+11
|
1,01E+15
|
6969,02
|
|
16
|
5272
|
7372
|
2,78E+07
|
1,47E+11
|
7,73E+14
|
4,07E+18
|
3,89E+07
|
2,05E+11
|
1,08E+15
|
7206,52
|
|
сумма
|
76960
|
101420
|
3,72E+08
|
1,81E+12
|
8,82E+15
|
4,32E+19
|
4,90E+08
|
2,38E+12
|
1,16E+16
|
101420,64
|
|
среднее
|
4810,00
|
6338,75
|
2,33E+07
|
1,13E+11
|
5,51E+14
|
2,70E+18
|
3,06E+07
|
1,48E+11
|
7,24E+14
|
6338,79
|
Построим график полученного уравнения регрессии:
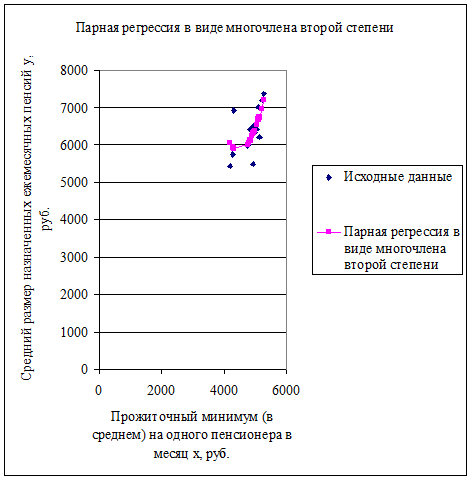
Составим
уравнение регрессии в виде многочлена третьей степени.
Уравнение регрессии имеет вид:
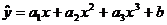 .
.
Для определения коэффициентов используются формулы:
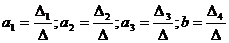
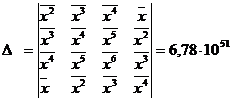
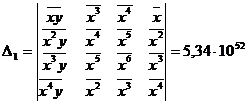
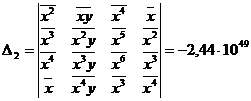
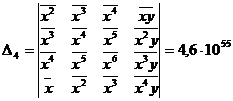
Рассчитаем значения параметров уравнения:
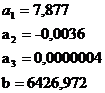
Уравнение регрессии в виде многочлена третьей степени имеет вид
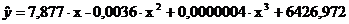
|
№
|
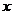 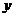 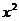 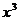 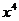 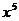 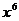 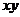 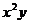 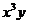 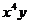 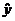
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
4184
|
5426
|
1,75E+07
|
7,32E+10
|
3,06E+14
|
1,28E+18
|
5,36E+21
|
2,27E+07
|
9,50E+10
|
3,97E+14
|
1,66E+18
|
6022,17
|
|
2
|
4272
|
5906
|
1,82E+07
|
7,80E+10
|
3,33E+14
|
1,42E+18
|
6,08E+21
|
2,52E+07
|
1,08E+11
|
4,60E+14
|
1,97E+18
|
5947,00
|
|
3
|
4282
|
5748
|
1,83E+07
|
7,85E+10
|
3,36E+14
|
1,44E+18
|
6,16E+21
|
2,46E+07
|
1,05E+11
|
4,51E+14
|
1,93E+18
|
5939,98
|
|
4
|
4302
|
6920
|
1,85E+07
|
7,96E+10
|
3,43E+14
|
1,47E+18
|
6,34E+21
|
2,98E+07
|
1,28E+11
|
5,51E+14
|
2,37E+18
|
5926,91
|
|
5
|
4756
|
5966
|
2,26E+07
|
1,08E+11
|
5,12E+14
|
2,43E+18
|
1,16E+22
|
2,84E+07
|
1,35E+11
|
6,42E+14
|
3,05E+18
|
6017,23
|
|
6
|
4794
|
6032
|
2,30E+07
|
1,10E+11
|
5,28E+14
|
2,53E+18
|
1,21E+22
|
2,89E+07
|
1,39E+11
|
6,65E+14
|
3,19E+18
|
6062,29
|
|
7
|
4838
|
6404
|
2,34E+07
|
1,13E+11
|
5,48E+14
|
2,65E+18
|
1,28E+22
|
3,10E+07
|
1,50E+11
|
7,25E+14
|
3,51E+18
|
6122,49
|
|
8
|
4906
|
6466
|
2,41E+07
|
1,18E+11
|
5,79E+14
|
2,84E+18
|
1,39E+22
|
3,17E+07
|
1,56E+11
|
7,64E+14
|
3,75E+18
|
6232,92
|
|
9
|
4942
|
5494
|
2,44E+07
|
1,21E+11
|
5,97E+14
|
2,95E+18
|
1,46E+22
|
2,72E+07
|
1,34E+11
|
6,63E+14
|
3,28E+18
|
6300,16
|
|
10
|
4958
|
6518
|
2,46E+07
|
1,22E+11
|
6,04E+14
|
3,00E+18
|
1,49E+22
|
3,23E+07
|
1,60E+11
|
7,94E+14
|
3,94E+18
|
6332,03
|
|
11
|
4980
|
6334
|
2,48E+07
|
1,24E+11
|
6,15E+14
|
3,06E+18
|
1,53E+22
|
3,15E+07
|
1,57E+11
|
7,82E+14
|
3,90E+18
|
6377,88
|
|
12
|
5048
|
6416
|
2,55E+07
|
1,29E+11
|
6,49E+14
|
3,28E+18
|
1,65E+22
|
3,24E+07
|
1,63E+11
|
8,25E+14
|
4,17E+18
|
6534,68
|
|
13
|
5104
|
7020
|
2,61E+07
|
1,33E+11
|
6,79E+14
|
3,46E+18
|
1,77E+22
|
3,58E+07
|
1,83E+11
|
9,33E+14
|
4,76E+18
|
6681,34
|
|
14
|
5122
|
6202
|
2,62E+07
|
1,34E+11
|
6,88E+14
|
3,53E+18
|
1,81E+22
|
3,18E+07
|
1,63E+11
|
8,33E+14
|
4,27E+18
|
6731,92
|
|
15
|
5200
|
7196
|
2,70E+07
|
1,41E+11
|
7,31E+14
|
3,80E+18
|
1,98E+22
|
3,74E+07
|
1,95E+11
|
1,01E+15
|
5,26E+18
|
6970,88
|
|
16
|
5272
|
7372
|
2,78E+07
|
1,47E+11
|
7,73E+14
|
4,07E+18
|
2,15E+22
|
3,89E+07
|
2,05E+11
|
1,08E+15
|
5,69E+18
|
7220,74
|
|
сумма
|
76960
|
101420
|
3,72E+08
|
1,81E+12
|
8,82E+15
|
4,32E+19
|
2,13E+23
|
4,90E+08
|
2,38E+12
|
1,16E+16
|
5,67E+19
|
101420,62
|
|
среднее
|
4810,00
|
6338,75
|
2,33E+07
|
1,13E+11
|
5,51E+14
|
2,70E+18
|
1,33E+22
|
3,06E+07
|
1,48E+11
|
7,24E+14
|
6338,79
|
Построим график полученного уравнения регрессии:
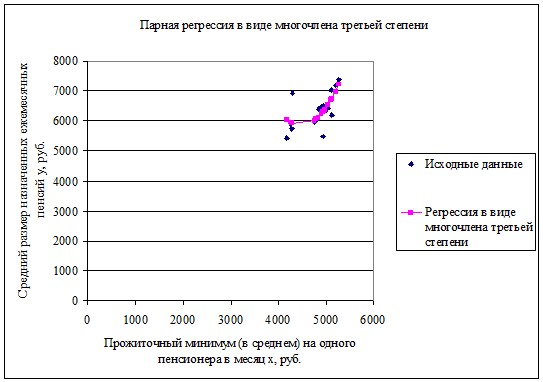
3. Оценка гетероскедастичности
Проверим все полученные уравнения регрессии на
гетероскедастичность с помощью теста ранговой корреляции Спирмена при 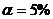
Оценка гетероскедастичности линейного уравнения регрессии методом
Спирмена
|
№
|
 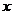 Ранг ( Ранг (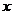 ) )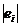 Ранг ( Ранг (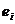 ) )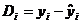 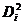
|
|
|
|
|
|
|
1
|
4184
|
1
|
596,17
|
14
|
-13
|
169
|
|
2
|
4272
|
2
|
41,00
|
2
|
0
|
0
|
|
3
|
4282
|
3
|
191,98
|
8
|
-5
|
25
|
|
4
|
4302
|
4
|
993,09
|
16
|
-12
|
144
|
|
5
|
4756
|
5
|
51,23
|
4
|
1
|
1
|
|
6
|
4794
|
6
|
30,29
|
1
|
5
|
25
|
|
7
|
4838
|
7
|
281,51
|
11
|
-4
|
16
|
|
8
|
4906
|
8
|
233,08
|
10
|
-2
|
4
|
|
9
|
4942
|
9
|
806,16
|
15
|
-6
|
36
|
|
10
|
4958
|
10
|
185,97
|
7
|
3
|
9
|
|
11
|
4980
|
11
|
43,88
|
3
|
8
|
64
|
|
12
|
5048
|
12
|
118,68
|
5
|
7
|
49
|
|
13
|
5104
|
13
|
338,66
|
12
|
1
|
1
|
|
14
|
5122
|
14
|
529,92
|
13
|
1
|
1
|
|
15
|
5200
|
15
|
225,12
|
9
|
6
|
36
|
|
16
|
5272
|
16
|
151,26
|
6
|
10
|
100
|
|
сумма
|
76960
|
136
|
4818,01
|
136
|
0
|
680
|
|
среднее
|
4810
|
8,5
|
301,13
|
8,5
|
0
|
42,5
|
Вычисляем коэффициент ранговой корреляции по формуле:
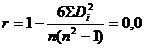
Вычисляем тестовую статистику по формуле:
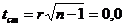
Значение 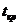 при
при 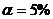 и числе степеней свободы, равном
и числе степеней свободы, равном 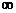 составляет 1,96.
составляет 1,96.
Так как 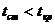 , то гипотеза об отсутствии
гетероскедастичности подтверждается.
, то гипотеза об отсутствии
гетероскедастичности подтверждается.
Оценка гетероскедастичности логарифмического уравнения регрессии
методом Спирмена
|
№
|
 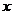 Ранг ( Ранг (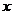 ) )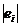 Ранг ( Ранг (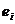 ) )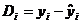 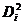
|
|
|
|
|
|
|
1
|
4184
|
1
|
331,59
|
9
|
-8
|
64
|
|
2
|
4272
|
2
|
59,96
|
4
|
-2
|
4
|
|
3
|
4282
|
3
|
107,98
|
5
|
-2
|
4
|
|
4
|
4302
|
4
|
1044,22
|
16
|
-12
|
144
|
|
5
|
4756
|
5
|
336,12
|
10
|
-5
|
25
|
|
6
|
4794
|
6
|
303,94
|
8
|
-2
|
4
|
|
7
|
4838
|
7
|
29,23
|
1
|
6
|
36
|
|
8
|
4906
|
8
|
31,92
|
2
|
6
|
36
|
|
9
|
4942
|
9
|
971,15
|
15
|
-6
|
36
|
|
10
|
4958
|
10
|
39,12
|
3
|
7
|
49
|
|
11
|
4980
|
11
|
163,70
|
7
|
4
|
16
|
|
12
|
5048
|
12
|
139,33
|
6
|
6
|
36
|
|
13
|
5104
|
13
|
417,78
|
12
|
1
|
1
|
|
14
|
5122
|
14
|
415,18
|
11
|
3
|
9
|
|
15
|
5200
|
15
|
514,60
|
13
|
2
|
4
|
|
16
|
5272
|
16
|
632,16
|
14
|
2
|
4
|
|
сумма
|
76960
|
136
|
5537,98
|
136
|
0
|
472
|
|
среднее
|
4810,00
|
8,5
|
346,12
|
8,5
|
0
|
29,5
|
корреляция уравнение регрессия гетероскедастичность
Вычисляем коэффициент ранговой корреляции по формуле:
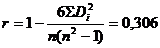
Вычисляем тестовую статистику по формуле:
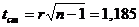
Cписок источников:
1.
Годин А.М. Статистика: Учебник. - 2-е изд., перераб. - М.: Издательско-торговая
корпорация «Дашков и К», 2003. - 472 с.
.
Гусаров В.М. Теория статистики. - М.: Аудит, ЮНИТИ, 2000.
.
Беляевский И.К., Ряузов Н.Н., Ряузов Д.Н. Эконометрика. - М.: Финансы и
статистика, 1999. - 400 с.