Множественная линейная регрессия
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (СИБСТРИН)
Кафедра
прикладной математики
Индивидуальное
задание
По
дисциплине «Математическое моделирование»
Тема: «Множественная
линейная регрессия»
Студент: Филиппов А.В.
Специальность «Экспертиза, оценка и
управление недвижимостью»
группа 115-маг-з
Руководитель работы: Воскобойников
Ю.Е.
Новосибирск
2013
Исходные данные
регрессия дисперсия детерминация
интервал
Имеются следующие данные о потреблении
некоторого продукта У (в условных единицах). В зависимости от уровня
урбанизации (доли городского населения) - переменная X1,
относительного образовательного уровня - X2,
относительного заработка - переменная X3,
для девяти географических районов.
Конкретные значения представлены в таблице 1.
Таблица 1.
|
Номер
района
|
xi1
|
xi2
|
xi3
|
yi
|
|
1
|
42,2
|
11,2
|
31,9
|
197
|
|
2
|
48,6
|
10,6
|
13,2
|
204
|
|
3
|
42,6
|
10,6
|
28,7
|
130
|
|
4
|
39
|
10,4
|
26,1
|
193
|
|
5
|
34,7
|
9,3
|
30,1
|
110
|
|
6
|
44,5
|
10,8
|
8,5
|
144
|
|
7
|
39,1
|
10,7
|
24,3
|
193
|
|
8
|
40,1
|
10
|
18,6
|
144
|
|
9
|
45,9
|
12
|
20,4
|
215
|
Решение
1. Для данного задания может быть построена
линейная множественная регрессия вида:
Y=β0+β1xi1+
β2xi2+
β3xi3+εi,
(1)
Тогда оценка для данной регрессии имеет вид:
ŷ=b0+b1x1+
b2x2+
b3x3,
(2)
где b0,
b1,
b2, b3
- коэффициенты уравнения регрессии.
Введем матричные обозначения и матричные
вычисления, тогда справедливы следующие формулы
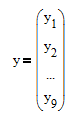 (3)
(3)
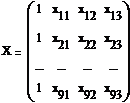 (4)
(4)
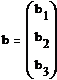 (5)
(5)
Коэффициенты уравнения множественной регрессии
находятся по формуле:
b=(XT*X)-1*(XT*y),
(6)
Решение представлено на рисунке 1.

Рисунок 1 - Расчет коэффициентов линейной
множественной регрессии
Таким образом уравнение регрессии имеет вид:
ŷ=-241.085+1,14xi1+
33.422xi2+
0.373xi3,
где i
= 1,2 …9.
2. Для определения дисперсий найденных
коэффициентов уравнения регрессии нужно рассчитать оценку дисперсии случайной
составляющей s2:
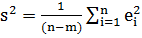 , (7)
, (7)
где n-
объем выработки (n=9), m-число
оцениваемых параметров (m=k+1=4),
ei-невязка i-го
измерения.
ei=yi-
ŷi,
(8)
Тогда оценка дисперсии коэффициента уравнения
регрессии bj,
рассчитывается по формуле:
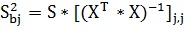 (9)
(9)
где 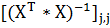 -
j-й диагональный
элемент матрицы
-
j-й диагональный
элемент матрицы 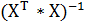 .
.
Отсюда следует, что коэффициент bjзначим
(принимается гипотеза H1:
bj≠0), если
выполняется условие:
|Tbj|=|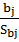 |
>t(1-α,
n-m),
|
>t(1-α,
n-m),
где m
- количество коэффициентов регрессии, α
- уровень значимости (0,05).
Решение представлено на рисунке 2.

Рисунок 2 - Расчет дисперсий коэффициентов
уравнения регрессии и проверка их значимости.
Как видно из расчетов, неравенство значимости
коэффициента не выполняется для всех коэффициентов (x1,x2,x3,x4).
3. Коэффициент детерминации рассчитывается по
формуле:
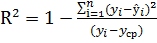 , (10)
, (10)
где (yi-
ŷi)2
- вектор, состоящий из квадратов невязки 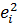 можно
взять из предыдущего расчета, yср
- вектор размерности n=9,
составленный из средних значений.
можно
взять из предыдущего расчета, yср
- вектор размерности n=9,
составленный из средних значений.
Если известен коэффициент детерминации, то
скорректированный коэффициент детерминации:
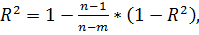 (11)
(11)
Расчет представлен на рисунке 3.
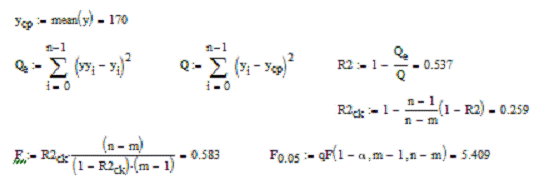
Рисунок 3 - Расчет коэффициента детерминации,
скорректированного коэффициента детерминации и значение коэффициента F.
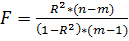 , (12)
, (12)
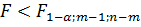 ,
,
то есть уравнение множественной регрессии
статистически не значимо (гипотеза H0).
. 95%-ный доверительный интервал для
коэффициентов βj:
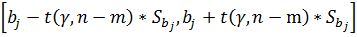 , (13)
, (13)
Результаты представлены на рисунке 4.
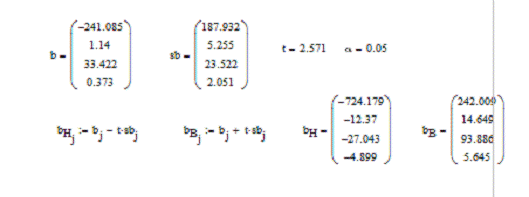
Рисунок 4 - Интервальная оценка коэффициентов
уравнения регрессии.
Интервалы:
для β0
- [-724,179; 242,009];
для β1
- [-12.37;14.649];
для β2
- [-27,043; 93.886];
для β3
- [-4,899; 5.645].
5. Доверительный интервал для f(x)
= M(Y/x):
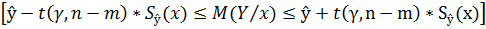 , (14)
, (14)
где Sŷ(x)
рассчитывается по формуле:
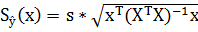 , (15)
, (15)
где 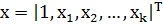 -вектор,
координаты которого определяют значения объясняющих переменных, при которых
вычисляется значение регрессии ŷ. Расчет представлен на рисунке 5 (ун
- нижняя граница, ув - верхняя граница).
-вектор,
координаты которого определяют значения объясняющих переменных, при которых
вычисляется значение регрессии ŷ. Расчет представлен на рисунке 5 (ун
- нижняя граница, ув - верхняя граница).
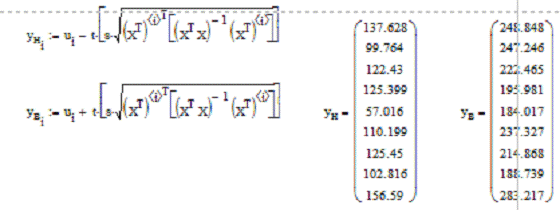
Рисунок 5 - Доверительный интервал для f(x)
= M(Y/x).
. Рассматриваемая классическая модель
множественной линейной регрессии в данном случае не отражает в должной мере
количественную зависимость между экономическими явлениями. Построенное
уравнение регрессии с помощью существующих независимых переменных объясняет
изменение зависимой переменной на 53,7%, а в скорректированном виде - на 25,9%.
Таким образом, получаем не значимость уравнения регрессии, и не значимость всех
коэффициентов, что может быть вызвано недостатком объясняющих переменных и
мультиколлинеарностью (стохастической) - наличием высокой взаимной
коррелированности между объясняющими переменными.
. Для исключения мультиколлинеарности и
повышения точности построенной регрессионной модели проводим пошаговое введение
наиболее информативных объясняющих моделей с построением корреляционной таблицы
и расчетом обыкновенного и скорректированного коэффициентов детерминации для
каждого шага. Расчет представлен на рисунке 6. На рисунке 7 представлен расчет
коэффициентов детерминации на втором шаге.
Выбирается та переменная, которая больше другой
коррелированна с у. В нашем случае это x2.
Выбираем ее для того, чтобы в дальнейших расчетах получить большее значение
скорректированного коэффициента детерминации чем в исходной модели. Для
построенной модели рассчитываются обыкновенный и скорректированный коэффициенты
детерминации. Причем для парной регрессии обыкновенный коэффициент детерминации
равен квадрату соответствующего коэффициента корреляции.
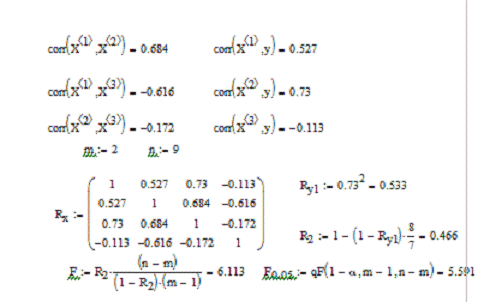
Рисунок 6 - Отбор объясняющих переменных
регрессионной модели.
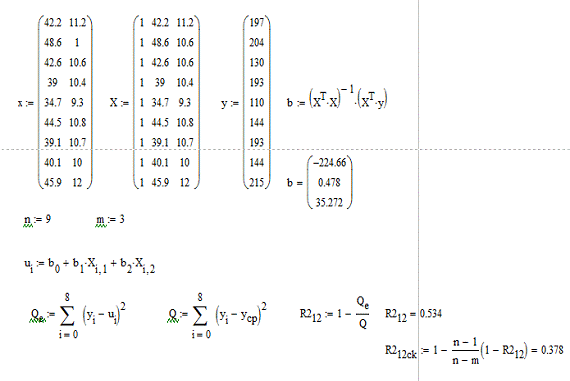

Рисунок 7 - Построение регрессионной модели на
шаге 2 отбора объясняющих переменных и расчет коэффициентов уравнения регрессии
для новой модели.
8. На втором шаге в модель попеременно
добавляются переменныеx1
и x3.
Для этих уравнений рассчитываются коэффициенты уравнения (рисунок 7), коэффициенты
детерминации, скорректированные коэффициенты детерминации, F-критерии.
Оценивая найденные значения можно сказать, что
введение дополнительных переменных на втором шаге снижает значение коэффициента
детерминации и уравнение регрессии становится статически не значимо.
Расчет всех необходимых параметров для уравнения
регрессии с переменной x2
приведен на рисунке 8.

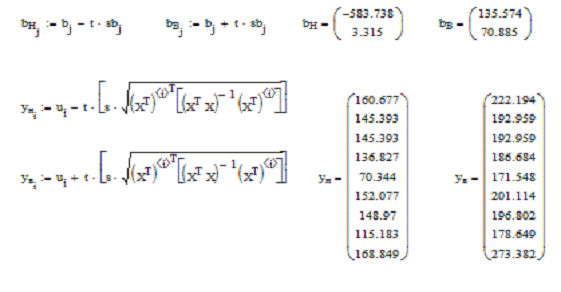
Рисунок 8 - Расчет параметров уравнения парной
регрессии
Согласно расчета, только второй коэффициент
уравнения регрессии является значимыми, как и само уравнение регрессии.
Произведены расчеты для определения доверительных интервалов βjи
доверительного интервала f(x)
= M(Y/x).
. Скорректированный коэффициент
детерминации для второго уравнения больше, чем для первого, что говорит о
большей адекватности второго варианта, предпочтительность второй регрессии
можно доказать и через F-критерий.
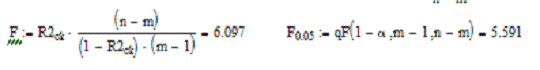
То есть неравенство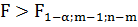 выполняется, можно сделать вывод о значимости построенного уравнения регрессии,
следовательно, исследуемая зависимость у достаточно хорошо описывается
включенной в регрессионную модель переменной x1.
В первой же модели это условие не выполняется, поэтому первое регрессионное
уравнение незначимо.
выполняется, можно сделать вывод о значимости построенного уравнения регрессии,
следовательно, исследуемая зависимость у достаточно хорошо описывается
включенной в регрессионную модель переменной x1.
В первой же модели это условие не выполняется, поэтому первое регрессионное
уравнение незначимо.
. Прогноз с использованием второго
уравнения регрессии:
при x1=34
x2=10,3
x3=26,2.
ŷ=37,1xi1,
= 382,13.
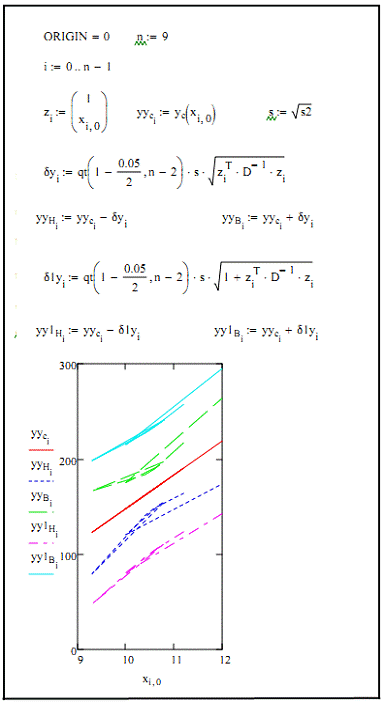
Рисунок 9 -Построение интервальной оценки для M(Y/x).
Общий вывод
Классическая линейная модель в рамках
множественного регрессионного анализа не всегда адекватно и точно отражает
зависимость между переменными. В случае наличия мультиколлинеарности,
недостатка или переизбытка объясняющих переменных, попадая в уравнение
регрессии случайной составляющей, применяют специальные методы выявления и
устранения проблем. В итоге с упором на принцип наименьшей сложности и высокой
информативности может быть построена эффективная регрессионная модель.