Поверхностные свойства воды: численное и теоретическое исследование
Введение
Вода играет важную роль в функционировании многих физико-химических и
биологических процессов на Земле. Однако, несмотря на многочисленные как
экспериментальные, так и теоретические исследования, многие структурные и
динамические свойства, а также природа аномального поведения параметров и
характеристик воды остаются не выясненными до сих пор.
Среди необычных свойств воды трудно обойти вниманием ее исключительно
высокое поверхностное натяжение 0,073 Н/м (при 20°С). Из всех жидкостей более
высокое поверхностное натяжение имеет только ртуть. Оно проявляется в том, что
вода постоянно стремится стянуть, сократить свою поверхность, хотя она всегда
принимает форму емкости, в которой находится в данный момент. Вода лишь кажется
бесформенной, растекаясь по любой поверхности. Сила поверхностного натяжения
заставляет молекулы ее наружного слоя сцепляться, создавая упругую внешнюю
пленку. Свойства пленки также определяются замкнутыми и разомкнутыми
водородными связями, ассоциатами различной структуры и разной степени
упорядоченности. Благодаря пленке некоторые предметы, будучи тяжелее воды, не
погружаются в воду (например, осторожно положенная плашмя стальная иголка).
Многие насекомые (водомерки, ногохвостки и др.) не только передвигаются по
поверхности воды, но взлетают с нее и садятся, как на твердую опору. Более
того, живые существа приспособились использовать даже внутреннюю сторону водной
поверхности. Личинки комаров повисают на ней с помощью не смачиваемых щетинок,
а маленькие улитки - прудовики и катушки - ползают по ней в поисках добычи.
Высокое поверхностное натяжение позволяет воде принимать шарообразную
форму при свободном падении или в состоянии невесомости: такая геометрическая
форма имеет минимальную для данного объема поверхность. Струя химически чистой
воды сечением 1см2 по прочности на разрыв не уступает, стали того же сечения.
Водную струю как бы цементирует сила поверхностного натяжения. Поведение воды в
капиллярах подчиняется и более сложным физическим закономерностям. Сент -
Дьердьи отмечал, что в узких капиллярах возникают структурно упорядоченные слои
воды вблизи твердой поверхности. Структурирование распространяется в глубь
жидкой фазы на толщину слоя порядка десятков и сотен молекул (ранее
предполагали, что упорядоченность ограничивается лишь мономолекулярным слоем
воды, примыкающим к поверхности). Особенности структурирования воды в
капиллярных системах позволяют с определенным основанием говорить о капиллярном
состоянии воды. В природных условиях это состояние можно наблюдать у так называемой
поровой воды. В виде тончайшей пленки она устилает поверхность полостей, пор,
трещин пород и минералов земной коры. Развитые межмолекулярные контакты с
поверхностью твердых тел, особенности структурной упорядоченности, вероятно, и
являются причиной того, что поровая вода замерзает при более низкой
температуре, чем обычная - свободная - вода. Исследования показали, что при
замерзании связанной воды проявляются не только изменения ее свойств, - иными
становятся и свойства тех горных пород, с которыми она непосредственно
соприкасается.
Цель и задачи
выпускной квалификационной работы
Цель:
· Исследование поверхностных свойств воды с помощью методов моделирования.
Задачи:
· Разработка алгоритмов моделирования молекулярной динамики воды и
выполнение соответствующих численных экспериментов;
· Исследование структурных свойств воды при быстром
переохлаждении;
· Разработка алгоритмов по нахождения (вычислению)
поверхностного натяжения и поверхностной энтропии.
Глава I.
Методы и подходы к определению поверхностного натяжения
§ 1.1
Поверхностное натяжение
Согласно термодинамическому определению, поверхностное натяжение -
термодинамическая характеристика поверхности раздела двух находящихся в
равновесии фаз, определяемая работой обратимого изотермокинетического образования
единицы площади этой поверхности раздела при условии, что температура, объём
системы и химические потенциалы всех компонентов в обеих фазах остаются
постоянными. Основываясь на методах статистической физики, Фаулер в работе [1]
предложил формулу, связывающую поверхностное натяжение и потенциал
межмолекулярного взаимодействия
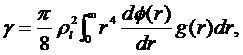 (1.1.1)
(1.1.1)
здесь ρl -
плотность жидкости, g(r) -
радиальная функция распределения частиц и φ(r) - потенциал межчастичного
взаимодействия.
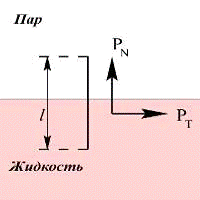
Рис. 1.1.1. Схематическое изображение компонент тензора напряжений вблизи
поверхности раздела фаз
Данная формула удовлетворительно работает при низких температурах, но
вблизи критической точки здесь наблюдаются значительные погрешности. Первые
попытки выразить поверхностное натяжение в величинах потенциала межчастичного
взаимодействия и радиальной функции распределения частиц были выполнены в
работе [2] Кирквудом и Бафом. Они вычислили тензор напряжения в области вблизи поверхности
раздела и получили выражения для компонент тензора напряжений PT и PN. В соответствии с их теорией нормальная составляющая тензора
напряжений определяется давлением пара
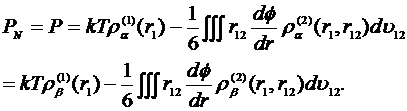 (1.1.2)
(1.1.2)
Тангенциальная компонента тензора напряжений выражается следующим образом
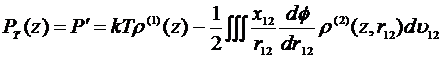 . (1.1.3)
. (1.1.3)
Тогда поверхностное натяжение будет определяться как
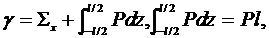 (1.1.4)
(1.1.4)
здесь
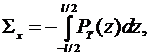 (1.1.5)
(1.1.5)
или в пределе при 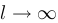 , получим
, получим
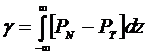 . (1.1.6)
. (1.1.6)
1.2 Метод
пробной поверхности
Недавно в работе [3] был предложен новый метод определения поверхностного
натяжения - Test-Area Method (Метод пробной поверхности). В
соответствии с этим подходом выражение для поверхностного натяжения принимает
вид
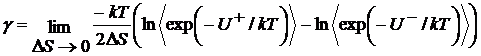 . (1.2.1)
. (1.2.1)
В данной работе было вычислено поверхностное натяжение для различных
моделей воды (Tip3P, SPC, SPC/E, Tip4P, и для нового поколения моделей,
подобных Tip4P, Tip4P/Ew, Tip4P/Ice, Tip4P/2005). Использовалось
термодинамическое направление, предложенное Глуром [3]. Согласно ему для
определения поверхностного натяжения оценивалось изменение свободной энергии за
счет небольшого изменения межфазной области при постоянном объеме. Значения
поверхностного натяжения, полученные данным методом, соответствуют данным,
полученным стандартным механическим направлением, основанным на оценке
компонент тензора давления.
В
данном подходе рассматривается плоскость, состоящая из 1024 частиц воды, заключенная
между двумя пустыми областями. Моделирование выполнялось при постоянной
температуре и объеме в орторомбической ячейке (30,30,100) 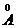 . С помощью пакета GROMACS (версия
3.3) были получены компоненты тензора давления, с помощью которых было
вычислено поверхностное натяжение.
. С помощью пакета GROMACS (версия
3.3) были получены компоненты тензора давления, с помощью которых было
вычислено поверхностное натяжение.
В
таблице 1.2.1 представлены значения поверхностного натяжения, полученные
методом моделирования для различных моделей воды (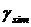 - значение, полученное в данной работе,
- значение, полученное в данной работе, 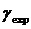 - экспериментальные данные) [4].
- экспериментальные данные) [4].
Таблица
1.2.1. Значения поверхностного натяжения, полученные методом моделирования для
различных моделей воды (- значение, полученное в данной работе, -
экспериментальные данные)
|
Модель воды
|
Т, К
|
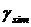 , мДж/м² , мДж/м²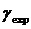 ,
мДж/м² ,
мДж/м²
|
|
|
Tip3P
|
300 450
|
52.3 24.7
|
71.73 42.88
|
|
SPC
|
300 450
|
54.7 28.1
|
71.73 42.88
|
|
SPC/E
|
300 350 367 450
500 550
|
63.6 54.1 51.6
36.7 25.9 13.8
|
71.73 63.22
63.22 42.88 31.61 19.69
|
|
Tip4P
|
300 350 400 450
500
|
59.0 48.8 38.6
27.5 17.1
|
71.73 63.22
53.33 42.88 31.61
|
|
Tip4P/2005
|
300 350 400 450
500 550
|
69.3 61.9 52.3
41.8 30.9 19.2
|
71.73 63.22
53.33 42.88 31.61 19.69
|
|
Tip4P/Ew
|
300 350 400 450
500 550
|
65.2 57.1 47.5
37.3 26.1 15.3
|
71.73 63.22
53.33 42.88 31.61 19.69
|
|
Tip4P/Ice
|
300 450 550 600
|
80.1 56.3 33.8
22.8
|
71.73 42.88
19.69 8.37
|
1.3 Метод
термодинамического интегрирования
В работе [5] был предложен совершенно новый подход к определению
поверхностного натяжения при капельной нуклеации воды. Данный метод основывается
на термодинамическом интегрировании величин, которые являются результатами
компьютерного моделирования молекулярной динамики.
Согласно этому методу поверхностная энергия может быть определена как
избыточная энергия на единицу площади поверхности, что обуславливается
недостатками «соседей» для частиц при поверхности по сравнению с частицами в
объеме (Рис. 1.3.1).
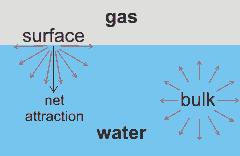
Рис. 1.3.1 Поверхностные силы на
границе вода - пар
Если
ограничиться рассмотрением ближайших соседей с взаимодействием 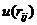 , тогда можно записать следующее соотношение
, тогда можно записать следующее соотношение
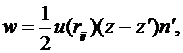 (1.3.1)
(1.3.1)
где
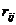 - среднее расстояние между соседями в новой фазе,
величина
- среднее расстояние между соседями в новой фазе,
величина 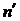 обозначает число поверхностных частиц на единицу
площади,
обозначает число поверхностных частиц на единицу
площади, 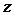 и
и 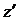 - первые
координационные числа объемных и поверхностных частиц, соответственно. Тогда
поверхностное натяжение может быть вычислено следующим образом
- первые
координационные числа объемных и поверхностных частиц, соответственно. Тогда
поверхностное натяжение может быть вычислено следующим образом
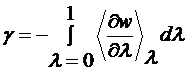 . (1.3.2)
. (1.3.2)
Координата
реакции 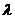 или, так называемое,
или, так называемое, 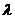 -масштабирование
связано с нормированными размерами кластеров
-масштабирование
связано с нормированными размерами кластеров 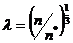 , которая
равна нулю при отсутствии ядер, и имеет значении единица, если размер ядер
равен критическому
, которая
равна нулю при отсутствии ядер, и имеет значении единица, если размер ядер
равен критическому 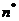 . Обозначение
. Обозначение 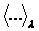 значит
среднее по ансамблю при конкретном значении
значит
среднее по ансамблю при конкретном значении 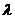 .
Значения, представленные в работе [5] хорошо описываются следующей формулой
.
Значения, представленные в работе [5] хорошо описываются следующей формулой
где
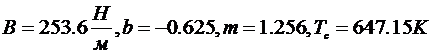
1.4 Подход по
определению поверхностного натяжения с учетом кривизны поверхности
В работе [6] был продемонстрирован метод определения поверхностного
натяжения системы с искривленной поверхностью. В этом методе, давление
подмножества системы определялось применением локальных (виртуальных)
механических деформаций, в результате чего был найден отклик жидкости и
вычислено поверхностное натяжения через уравнение Юнга - Лапласа. Поверхностное
натяжение искривленной поверхности октан-вода было вычислено с помощью данного
метода и результаты были сравнены с данными для плоской поверхности (≈
46,7 дин / см).
В
соответствии с уравнением Юнга - Лапласа для системы с изогнутой поверхностью
(радиусом 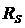 ), внутреннее давление может отличаться от внешнего
давления системы
), внутреннее давление может отличаться от внешнего
давления системы
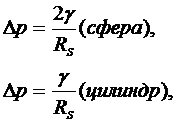 (1.4.1)
(1.4.1)
где
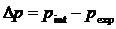 - есть разность между внутренним
- есть разность между внутренним 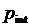 и внешним
и внешним 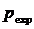 давлением.
давлением.

Рис. 1.4.1 Гексагональная фаза
жидкости. Цилиндры заполнены водой и испытываю давление
Для плоской поверхности поверхностное натяжение оценивается следующим
образом
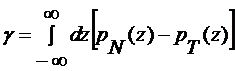 , (1.4.2)
, (1.4.2)
где
нормаль к поверхности направлена вдоль 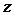 ,
, 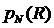 - нормальное давление,
- нормальное давление, 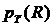 -
тангенциальное давление.
-
тангенциальное давление.
Для
цилиндра поверхностное натяжение вычисляется
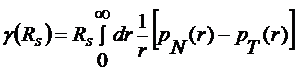 , (1.4.3)
, (1.4.3)
где
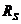 - площадь поверхности.
- площадь поверхности.
При
деформации поверхность изменяется, тогда
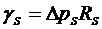 . (1.4.4)
. (1.4.4)
Учитывая,
что размеры ячейки флуктуируют, что определяет некоторую равновесную высоту
ячейки 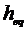 .
.
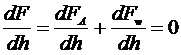 , (1.4.5)
, (1.4.5)
где
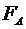 - свободная энергия вдоль направления xy, а
- свободная энергия вдоль направления xy, а
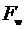 - свободная энергия поверхности воды.
- свободная энергия поверхности воды.
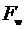 может
быть представлена в виде зависимости от h
может
быть представлена в виде зависимости от h
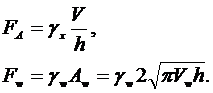 (1.4.6)
(1.4.6)
Учитывая
условие равновесия (1.4.5), получаем
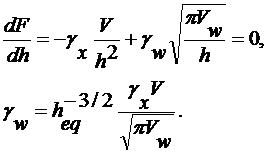 (1.4.7)
(1.4.7)
В
таблице 1.4.1 представлены значения поверхностного натяжения 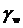 , где
, где 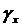 - внешнее
натяжение:
- внешнее
натяжение:
Таблица
1.4.1. Значения поверхностного натяжения при различных высотах ячейки
|
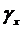 , дин/м , дин/м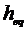 , Аº , Аº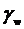 , дин/м , дин/м
|
|
|
|
8
|
24.2
|
48.1
|
|
10
|
29.1
|
45.7
|
|
12
|
31.7
|
48.1
|
|
14
|
35.8
|
46.7
|
|
16
|
37.8
|
49.4
|
Глава II. Методы компьютерного моделирования
§ 2.1 Метод
молекулярной динамики
Жидкости,
расплавы, плотная плазма и ряд других конденсированных систем, не имеющих
упорядоченной структуры, характеризуются тем, что средняя кинетическая энергия,
приходящаяся на одну частицу, E, по порядку величины равна потенциальной энергии U.
Отсутствие малого параметра, по которому было бы удобно проводить разложение,
приводит к тому, что в жидкостях и расплавах нет такой же строгой теории, как,
например, в твердом теле (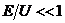 ) или в газе (
) или в газе (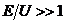 ) [7].
) [7].
Несмотря
на то, что в последнее время в изучении плотных неупорядоченных систем
достигнуты большие успехи, что особенно относится к исследованию физики явлений
в простых жидкостях, теоретические исследования в этой области еще далеки от
завершения. Многие качественные результаты, полученные в физике простых
жидкостей, как правило, опираются на количественные данные молекулярной
динамики (МД). Метод МД - принципиально новый метод исследования сильно
коррелированных многочастичных систем. Он основан на математическом
моделировании движения достаточно большого числа частиц с известными изначально
законами взаимодействия. В результате численного решения уравнений движения
определяются динамические траектории частиц, а затеи с помощью эргодической
гипотезы гиббсовские средние от любых динамических переменных.
Метод
МД впервые предложен Олдером и Вайнрайтом для изучения движения системы твердых
сфер. В течение ряда лет этот метод интенсивно развивался и в последние годы
широко применяется для исследования термодинамических и транспортных свойств
конденсированных сред. При этом он удачно дополняет метод Монте-Карло.
В
настоящее время общепринятой является следующая схема выполнения МД.
Рассматривается классическая система из нескольких десятков или сотен частиц с
заданным потенциалом взаимодействия. Классические уравнения движения частиц
численно решаются с помощью разностных методов, например
 (2.1.1)
(2.1.1)
где
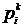 - импульс i-й частицы на k-м шаге,
- импульс i-й частицы на k-м шаге, 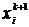 - координата i-й частицы на k-м шаге,
- координата i-й частицы на k-м шаге, 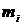 - масса i-й частицы,
- масса i-й частицы, 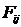 - сила,
действующая на i-ю частицу со стороны j-й частицы. Для простоты формулы
приведены для одномерной системы. При решении уравнений движения налагаются
периодические граничные условия, реализуемые следующем образом. Рассматривается
периодическая решетка с элементарной кубической ячейкой V, заполненная N
частицами. Если какая-либо частица выходит через грань куба с импульсом
- сила,
действующая на i-ю частицу со стороны j-й частицы. Для простоты формулы
приведены для одномерной системы. При решении уравнений движения налагаются
периодические граничные условия, реализуемые следующем образом. Рассматривается
периодическая решетка с элементарной кубической ячейкой V, заполненная N
частицами. Если какая-либо частица выходит через грань куба с импульсом 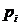 , то другая частица входит через противолежащую грань
с тем же импульсом, симметрично относительно плоскости, проходящей через центр
куба. При расчете сил, действующих на частицу, последняя окружается кубическим
объемом V и учитывается взаимодействие только с частицами, находящимися в
объеме V. Исключением являются лишь системы с дальнодействующем кулоновским
потенциалом взаимодействия, где в некоторых случаях для расчета энергии
взаимодействия обычно используется метод Эвальда.
, то другая частица входит через противолежащую грань
с тем же импульсом, симметрично относительно плоскости, проходящей через центр
куба. При расчете сил, действующих на частицу, последняя окружается кубическим
объемом V и учитывается взаимодействие только с частицами, находящимися в
объеме V. Исключением являются лишь системы с дальнодействующем кулоновским
потенциалом взаимодействия, где в некоторых случаях для расчета энергии
взаимодействия обычно используется метод Эвальда.
Найденные
траектории частиц 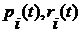 позволяют получить информацию о термодинамических и
кинетических свойствах системы многих частиц путем усреднения по времени вдоль
классической траектории системы соответствующих функций динамических переменных
позволяют получить информацию о термодинамических и
кинетических свойствах системы многих частиц путем усреднения по времени вдоль
классической траектории системы соответствующих функций динамических переменных
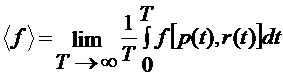 , (2.1.2)
, (2.1.2)
где
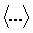 обозначает среднее по Гиббсу от какой-либо функции
динамических переменных p и r. При этом предполагается, что изучаемая система
является эргодической.
обозначает среднее по Гиббсу от какой-либо функции
динамических переменных p и r. При этом предполагается, что изучаемая система
является эргодической.
В
работе [8] на основе анализа экспериментальных данных была получена следующая
эмпирическая формула для поверхностного натяжения
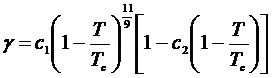 , (2.1.3)
, (2.1.3)
где коэффициенты для некоторых модельных потенциалов для воды
представлены в следующей таблице 2.1.1.
Таблица 2.1.1. Коэффициенты для некоторых модельных потенциалов для воды
|
Модель воды
|
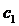 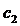 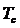 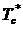
|
|
|
|
|
SPC/E TIP4P
TIP4P/2005 TIP4P/Ew TIP4P/Ice
|
205.32 172.90
227.86 208.37 256.24
|
0.6132 0.3929
0.6413 0.5878 0.6684
|
625.7 593.9
641.4 628.3 704.7
|
630 639 588 640
628 705
|
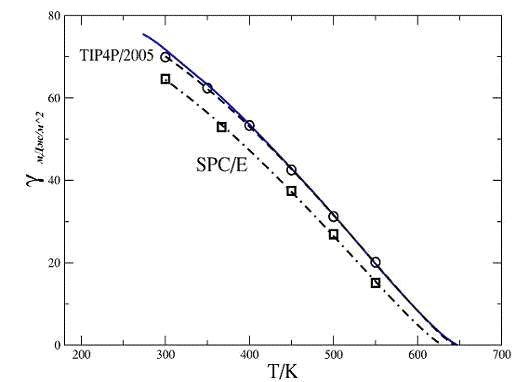
Рис. 2.1.1 Температурная зависимость поверхностного натяжения для воды:
сплошная линия - экспериментальные данные
.1.1 Детали
моделирования
Моделирование выполнялось в пакете Lammps - свободный пакет для классической молекулярной
динамики. Пакет может применяться для крупномасштабных расчётов (до десятков
миллионов атомов).
В LAMMPS реализована поддержка большинства двухчастичных и многочастичных
короткодействующих потенциалов (потенциалы Леннарда-Джонса, Морзе, Юкавы, EAM,
AI-REBO). Есть возможность записи атомных конфигураций в текстовый или бинарный
файл. Начальная конфигурация атомов для расчета может быть как сгенерирована в
программе, так и прочитана из бинарного/текстового файла.
Есть встроенные возможности анализа атомной конфигурации: построение
парной корреляционной функции, определение координационного числа, параметра
центральной симметрии и др. реализованы встроенные термостаты, баростаты,
методы добавления внешних сил и потенциальных стенок. Предусматривается
возможность использования графических процессоров для расчета.
В нашем случае моделирование было выполнено в NpT-ансамбле при давлении p=1.0 атм. для области значений температур от 273 до 373 К.
При этом система состояла из 8000 атомов. Взаимодействие между частицами
осуществлялось с помощью модельного mW-потенциала. При моделировании использовались термостат и баростат с
параметром 10 фс, т.е. термостат и баростат включался через каждые 10 фс.
Временной шаг моделирования составляет 50 фс.
.2 Метод
Монте-Карло
Применение строгих методов статистической физики к классическим
конденсированным системам, как хорошо известно, сталкивается с затруднениями в
связи с необходимостью подсчета или асимптотической оценки (при N, V→∞)
конфигурационного интеграла
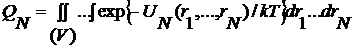 , (2.2.1)
, (2.2.1)
где
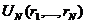 - энергия взаимодействия частиц системы, которая
предполагается известной, и N очень велико. При изучении интегральных уравнении
для корреляционных функций, возникает эквивалентная трудность в виде
необходимости решать систему N интегро-дифференциальных уравнений для N
неизвестных функций при N→∞. В современных теориях жидкого
состояния эти затруднения преодолеваются или приближенной оценкой
- энергия взаимодействия частиц системы, которая
предполагается известной, и N очень велико. При изучении интегральных уравнении
для корреляционных функций, возникает эквивалентная трудность в виде
необходимости решать систему N интегро-дифференциальных уравнений для N
неизвестных функций при N→∞. В современных теориях жидкого
состояния эти затруднения преодолеваются или приближенной оценкой 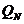 по методу теории свободного объема, или же путем
обрыва цепочки уравнений для корреляционных функций с помощью «суперпозиционного
приближения». В обоих случаях получаются приближенные теории.
по методу теории свободного объема, или же путем
обрыва цепочки уравнений для корреляционных функций с помощью «суперпозиционного
приближения». В обоих случаях получаются приближенные теории.
Существенно
новые идеи и новые результаты появились в последние годы в связи с развитием
методов моделирования, в первую очередь - «метода Монте- Карло». Идея метода в
применении к задачам статистической физики была высказана впервые Майером и
вначале применена для очень упрощенных моделей систем частиц, а затем, после
значительного усовершенствования метода, к более сложным и интересным системам.
Полученные
до сих пор по методу Монте- Карло результаты хотя и очень интересны для
статистической физики, но все же остаются довольно скромными. Однако надо
учесть, что опубликованные пока первые работы преследовали главным образом цель
проверки пригодности самого метода и его усовершенствования, а не получение
новых результатов. В настоящее время следует признать, что метод себя вполне
оправдал и после дальнейшего усовершенствования может оказаться весьма
перспективным не только для задач теории жидкостей, но и для многих других
задач статистической физики. Если учесть бурный рост технических средств
методов вычислительной математики, то эти надежды оказываются тем более реальными
я оправданными. Нам представляется, что именно в этом направлении в ближайшем
будущем следует ожидать наибольших успехов статистической физики, по крайней
мере, в области классической теории. Кроме того, многие из идей, возникших в
новом методе (например, идея о введении периодических граничных условий для
неупорядоченной системы, см. ниже), могут оказаться полезными в статистической
физике вне зависимости от данного метода.
В
существующем варианте новый метод применим только к классическим системам, так
как в нем явно используются численные значения энергии системы в различных ее
состояниях. В квантовых системах отыскание собственных значений энергии как раз
и представляет главную трудность.
В
настоящем обзоре мы кратко изложим основные идеи метода Монте-Карло и
полученные им к настоящему времени результаты в применении к теории кристаллов,
жидкостей и плотных газов. Вопросы обоснования метода еще нуждаются в более
тщательной разработке, и на них мы остановимся лишь очень бегло. Последний
раздел обзора не связан с методом Монте-Карло. Но его содержание также целиком
основано на применении современной машинной математики к статистической физике
и по многим пунктам соприкасается с содержанием остальной части обзора.
Основная
идея нового метода состоит в замене прямого многократного интегрирования в
(2.2.1) или в аналогичных интегральных выражениях, определяющих средние
значения функций от координат усреднением по множеству случайных событий
(конфигураций), образующих цепь Маркова с постоянными вероятностями переходов
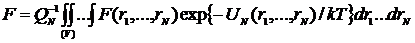 . (2.2.2)
. (2.2.2)
Рассмотрим
3N-мерное конфигурационное пространство изучаемой системы и сделаем его
дискретным путем подразделения на произвольно большое число s равных по объему
ячеек. Пусть все ячейки в каком - либо порядке занумерованы. Пусть, сама
система находится в i-м состоянии, если ее изображающая точка находится в i-й
ячейке. В каждом состоянии можно приписать системе определенное численное
значение 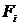 любой функции координат системы
любой функции координат системы 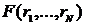 , взяв значения
, взяв значения 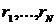 ,
соответствующие, например, центрам ячеек. В частности, и энергия взаимодействия
частиц системы теперь изображается набором ее возможных значений
,
соответствующие, например, центрам ячеек. В частности, и энергия взаимодействия
частиц системы теперь изображается набором ее возможных значений 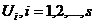 . Ясно, что если s достаточно
велико, то замена непрерывного конфигурационного пространства дискретным
практически не отразится на оценке средних значений функции от координат. Тогда
вместо (2.2.1) имеем
. Ясно, что если s достаточно
велико, то замена непрерывного конфигурационного пространства дискретным
практически не отразится на оценке средних значений функции от координат. Тогда
вместо (2.2.1) имеем
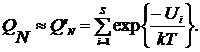 , (2.2.3)
, (2.2.3)
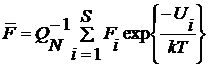 (2.2.4)
(2.2.4)
Далее
будем рассматривать совокупность всех s возможных состояний системы как
набор случайных событий 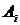 , образующих цепь Маркова с постоянными вероятностями
переходов
, образующих цепь Маркова с постоянными вероятностями
переходов 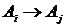 , равными
, равными 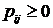 и
удовлетворяющими условию нормировки
и
удовлетворяющими условию нормировки
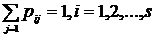 . (2.2.5)
. (2.2.5)
В
дальнейшем нам нужны будут некоторые простые сведения из теории однородных
марковских цепей. Обозначим через 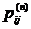 вероятность
реализации перехода
вероятность
реализации перехода 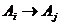 за n шагов. Если все
за n шагов. Если все 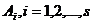 ,
образуют один эргодический класс, т.е. все состояния
,
образуют один эргодический класс, т.е. все состояния 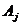 не периодические, и из любого состояния
не периодические, и из любого состояния 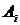 достижимо любое состояние
достижимо любое состояние 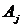 при некотором конечном числе переходов n, то
существуют предельные вероятности
при некотором конечном числе переходов n, то
существуют предельные вероятности
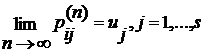 , (2.2.6)
, (2.2.6)
для всех i, и при этом
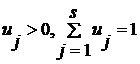 , (2.2.7)
, (2.2.7)
и
что 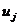 реализуют некоторое распределение вероятностей для
реализуют некоторое распределение вероятностей для 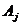 . Кроме того, в теории цепей Маркова доказывается, что
величины
. Кроме того, в теории цепей Маркова доказывается, что
величины 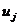 однозначно определяются при соблюдении нормировки
(2.2.7) знамениями величин
однозначно определяются при соблюдении нормировки
(2.2.7) знамениями величин 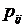 из
системы линейных уравнений
из
системы линейных уравнений
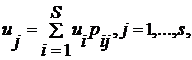 , (2.2.8)
, (2.2.8)
и
что распределение, определяемое числами 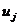 , есть
стационарное распределение вероятностей событий
, есть
стационарное распределение вероятностей событий 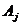 , т.е.
такое их распределение, которое, будучи принятое за начальное, не изменялось бы
в ходе изучаемого марковского процесса. Уравнение (2.1.6) выражают собой
стремление системы к стационарному состоянию независимо от выбора начального
состояния.
, т.е.
такое их распределение, которое, будучи принятое за начальное, не изменялось бы
в ходе изучаемого марковского процесса. Уравнение (2.1.6) выражают собой
стремление системы к стационарному состоянию независимо от выбора начального
состояния.
Обратимся
теперь к конкретным физическим системам и рассмотрим для них вопрос о
соблюдении требования эргодичности. Пусть для простоты полная энергия
взаимодействия частиц системы может быть представлена в виде суммы парных
взаимодействий
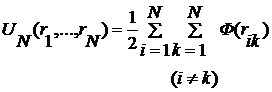 , (2.2.9)
, (2.2.9)
где
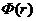 - взаимный потенциал двух частиц,
- взаимный потенциал двух частиц, 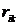 - расстояние между i-й к k-й
частицами. Если потенциал
- расстояние между i-й к k-й
частицами. Если потенциал 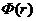 нигде не обращается в
нигде не обращается в 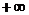 , то
величины
, то
величины 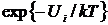 нигде не обращаются в нуль, так что все
нигде не обращаются в нуль, так что все 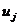 (2.2.6) также отличны от нуля. Поэтому для любого
перехода
(2.2.6) также отличны от нуля. Поэтому для любого
перехода 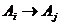 между состояниями в дискретном конфигурационном
пространстве существует ненулевая вероятность реализации
между состояниями в дискретном конфигурационном
пространстве существует ненулевая вероятность реализации 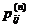 при некотором конечном числе шагов n. Все состояния
системы оказываются, таким образом, достижимыми друг из друга, и их
совокупность образует один эрг одический класс. В таком случае любая цепь
Маркова с вероятностями переходов, определенными сходится к каноническому
ансамблю в (2.2.9).
при некотором конечном числе шагов n. Все состояния
системы оказываются, таким образом, достижимыми друг из друга, и их
совокупность образует один эрг одический класс. В таком случае любая цепь
Маркова с вероятностями переходов, определенными сходится к каноническому
ансамблю в (2.2.9).
В
приложениях статистической физики часто используются модельные межмолекулярные
потенциалы 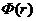 , обращающиеся при r = 0 в
, обращающиеся при r = 0 в 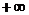 . Допущение о парности межмолекулярных сил в системе
(2.2.9) не является обязательным. Изложенный выше метод Монте- Карло справедлив
при любом законе взаимодействия частиц, зависящем только от конфигураций
частиц, если при этом соблюдено требование эргодичности.
. Допущение о парности межмолекулярных сил в системе
(2.2.9) не является обязательным. Изложенный выше метод Монте- Карло справедлив
при любом законе взаимодействия частиц, зависящем только от конфигураций
частиц, если при этом соблюдено требование эргодичности.
Следует
также отметить, что если отбросить сомнительные случаи, где, возможно,
нарушается условие эргодичности, то эквивалентность предельного поведения
наученных выше цепей Маркова и канонического ансамбля Гиббса оказывается
точной. Поэтому конкретные физические результаты, которые могут быть получены
на этой основе (при достаточно точной практической реализации метода), помимо
обычных статистических ошибок, никаких других неточностей не будут содержать.
Этим изложенный новый метод принципиально отличается, например, от методов
теории свободного объема или теории, основанной на суперпозиционном
приближении. Обе эти теории являются приближенными по своему существу, и притом
так, что степень приближения наперед даже невозможно оценить [10].
2.3
Моделирование с помощью ансамбля Гиббса
Рассмотрим
сплошную систему с сильным внутримолекулярным взаимодействием [11]. Для такой
системы удобно выделить два вклада: связанную межмолекулярную энергию (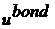 ) и «внешнюю» несвязнунную межмолекулярную энергию (
) и «внешнюю» несвязнунную межмолекулярную энергию (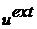 ), которые, соответственно, содержат межмолекулярное
взаимодействие и несвязывающее межмолекулярное взаимодействие. Согласно
реализации ансамблей Гиббса, мы пытаемся обменять молекулы между двумя
коробками. Однако изначально молекулы помещались случайным образом.
Воспользуемся следующей процедурой роста молекул атом за атомом в случайно
выбранной коробке. Допустим, эта коробка 1 с объемом
), которые, соответственно, содержат межмолекулярное
взаимодействие и несвязывающее межмолекулярное взаимодействие. Согласно
реализации ансамблей Гиббса, мы пытаемся обменять молекулы между двумя
коробками. Однако изначально молекулы помещались случайным образом.
Воспользуемся следующей процедурой роста молекул атом за атомом в случайно
выбранной коробке. Допустим, эта коробка 1 с объемом 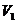 . Номер частицы в этой коробке обозначим за
. Номер частицы в этой коробке обозначим за 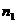 .
.
. Первый
атом вставляется случайным образом, и (внешняя) энергия 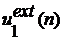 вычисляется следующим образом
вычисляется следующим образом
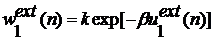 . (2.3.1)
. (2.3.1)
2. Вставляем
следующий атом i, сформировалась k пробная
ориентация. Набор k пробных ориентаций обозначим, как 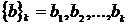 . Эти ориентации генерируются не случайно, но с
вероятностью того, что есть функция от связанной части межмолекулярной энергии
. Эти ориентации генерируются не случайно, но с
вероятностью того, что есть функция от связанной части межмолекулярной энергии
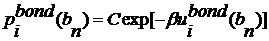 . (2.3.2)
. (2.3.2)
Каждая
из этих пробных ориентаций внешней энергии вычисляется как 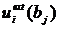 совместно с коэффициентом
совместно с коэффициентом
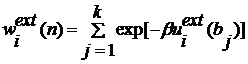 . (2.3.3)
. (2.3.3)
Из этого k пробные позиции
выбираются с вероятностью
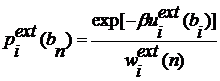 . (2.3.4)
. (2.3.4)
3. Шаг 2 повторяется через время (l-1) и коэффициент Розенблюта молекул можно найти
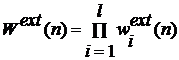 . (2.3.5)
. (2.3.5)
Для другой коробки, выбираем молекулу случайным образом и, определяя
коэффициент Розенблюта, получаем следующую процедуру:
1. Частицы выбираются случайно.
2. (Внешняя)
энергия первого атома определяется как 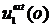 совместно
с
совместно
с
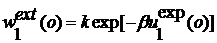 . (2.3.6)
. (2.3.6)
. Для
следующих атомов, (k-1) пробная ориентация выбирается с вероятностью,
получаемой по формуле (2.3.2). Эти пробные ориентации совместно с
действительной позицией атома 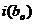 образуют
множество
образуют
множество 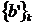 , для которого определяем коэффициент
, для которого определяем коэффициент
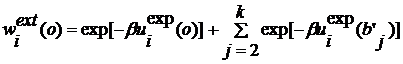 . (2.3.7)
. (2.3.7)
4. Шаг 2 повторяется через время (l-1),прослеживаем всю цепь и подсчитываем коэффициент
Розенблюта
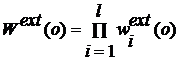 . (2.3.8)
. (2.3.8)
Затем принимаем этот шаг с вероятностью
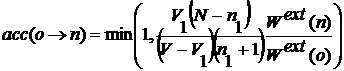 . (2.3.9)
. (2.3.9)
Комбинация техники ансамблей Гиббса с методом Монте - Карло была
использована для определения кривой жидкость - пар сосуществования частиц
Леннард - Джонса и алканов.
§ 2.4
Термодинамический подход
Рассмотрим другой подход к определению поверхностного натяжения для
плоской поверхности, не связанный с механическим определением [12]. Введем в
межфазной области жидкость-газ поверхность разделения нулевой толщины. После
того, как введена разделяющая поверхность, объем системы, может определяться
следующим образом
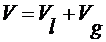 , (2.4.1)
, (2.4.1)
где
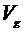 - объем газа,
- объем газа, 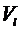 - объем
жидкости.
- объем
жидкости.
Если
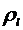 - плотность жидкости,
- плотность жидкости, 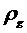 - плотность
газа, то сумма
- плотность
газа, то сумма 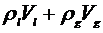 отличается от количества частиц двухфазной системы
отличается от количества частиц двухфазной системы
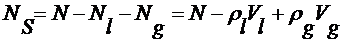 . (2.4.2)
. (2.4.2)
Аналогично для энтропии и внутренней энергии
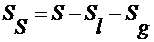 . (2.4.3)
. (2.4.3)
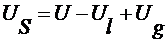 . (2.4.4)
. (2.4.4)
Значения
избыточных количеств 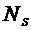 ,
, 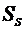 и
и 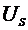 зависят от выбранной поверхности раздела. Запишем
основное уравнение термодинамики для двухфазной системы с учетом (2.4.2) -
(2.4.4)
зависят от выбранной поверхности раздела. Запишем
основное уравнение термодинамики для двухфазной системы с учетом (2.4.2) -
(2.4.4)
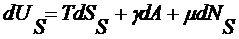 (2.4.5)
(2.4.5)
Это есть фундаментальное уравнение тории капиллярности Гиббса для плоской
границы.
Для потенциала свободной энергии
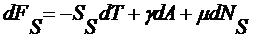 . (2.4.5)
. (2.4.5)
В соответствии с теоремой Эйлера
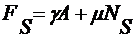 . (2.4.7)
. (2.4.7)
Наряду с избыточными количествами, будем рассматривать плотности
избыточных количеств
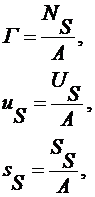 (2.4.8)
(2.4.8)
где
Г - адсорбция, 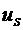 - плотность внутренней энергии,
- плотность внутренней энергии, 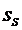 - плотность энтропии.
- плотность энтропии.
С
учетом (2.4.6) и (2.4.7) получаем
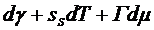 . (2.4.9)
. (2.4.9)
В случае эквимолекулярной поверхности, т.е. Г=0
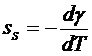 . (2.4.10)
. (2.4.10)
Подставляя (2.4.10) в (2.4.5), получаем
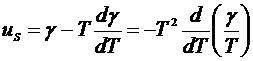 . (2.4.11)
. (2.4.11)
Интегрируя (2.4.11)
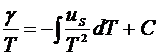 . (2.4.12)
. (2.4.12)
Процесс определения поверхностного натяжения с помощью (2.4.12) состоит в
расчете температурной зависимости плотности поверхностной энергии. Для
нахождения температурной зависимости, температурная зависимость была
аппроксимирована с помощью следующей функции
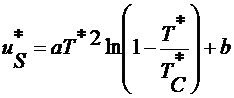 , (2.4.13)
, (2.4.13)
где a=0.286±0.006, b=2.783±0.008.
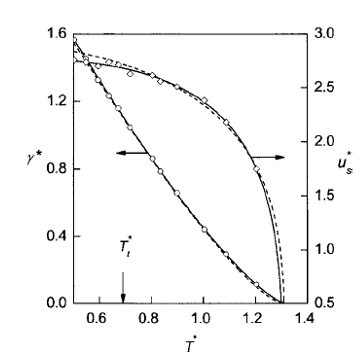
Рис. 2.4.1 Температурная зависимость
поверхностного натяжения и плотности поверхностной внутренне энергии
Глава III. Исследование поверхностных явлений
Две фазы (например, жидкость - кристалл, жидкость - газ, кристалл - газ)
в состоянии равновесия характеризуются следующими условиями в рамках
термодинамики
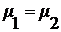 -
равенство химических потенциалов,
-
равенство химических потенциалов,
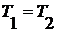 -
равенство температур,
-
равенство температур,
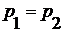 -
равенство давлений.
-
равенство давлений.
Эти условия указывают на то, что обе фазы могут сосуществовать. При этом
имеется некоторый граничный слой - так называемая граница раздела.
Рассмотрим, для примера, фазовое равновесие жидкость - газ. В
поверхностном слое, граничащим с газом, будут появляться, так называемые, силы
поверхностного натяжения, масштаб действия которых определяется масштабом
действия потенциала межмолекулярного взаимодействия.
Рассмотрим следующий рисунок (Рис 3.1).
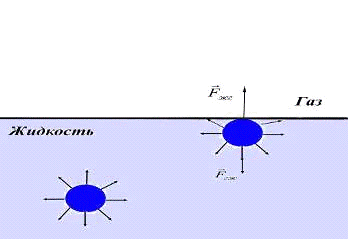
Рис. 3.1. Силы, действующие на
молекулы внутри жидкости и на ее поверхности
На этом рисунке сравниваются силы, действующие на молекулу в объеме
жидкости с силами, действующими на молекулу при поверхности. Так, в случае
молекулы в объеме, силы, оказывающие влияние со стороны соседних молекул
компенсируются. Таким образом, в этом случае результирующая сил будет равна
нулю.
В случае поверхностной молекулы она будет испытывать избыточное
притяжение, которое формирует результирующую силу, направленную в объем. Такая
результирующая сила объясняется тем фактом, что соседей в жидкой фазе больше,
чем в фазе пара, т.к. плотнить жидкости больше плотности пара.
Запишем условие механического равновесия для поверхности, изображенной на
рис. 3.1
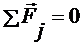 , (3.1)
, (3.1)
где
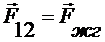 ,
, 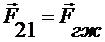 ,
, 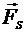 - силы поверхностного натяжения, которые
- силы поверхностного натяжения, которые 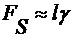 ,
, 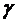 -
коэффициент поверхностного натяжения,
-
коэффициент поверхностного натяжения, 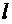 -
пространственный параметр, характеризующий контур поверхности.
-
пространственный параметр, характеризующий контур поверхности.
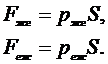 (3.2)
(3.2)
Тогда из (3.1.1) получаем:
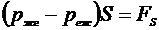 , (3.3)
, (3.3)
молекулярный
водяной пар температурный
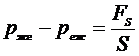 . (3.4)
. (3.4)
Предположим, что поверхность имеет сферическую форму радиуса R. Тогда из (3.1.4) получаем
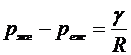 . (3.5)
. (3.5)
Формула (3.5) является знаменитой формулой Лапласа для давления. Она
имеет очень интересное следствие: чем меньше разность давлений, тем больше
параметр R. Это указывает на то, что
равновесная фаза жидкости имеет макроскопический размер.
Расчет поверхностного натяжения с помощью методов моделирования
молекулярной динамики является непростой задачей. Существуют различные методы,
которые позволяют оценить поверхностное натяжение для различных межфазных
границ.
3.1 Расчет
поверхностного натяжения через компоненты тензора давления
Как было показано Ирвингом и Кирквудом локальное поверхностное натяжение
может быть определено с помощью следующего выражения
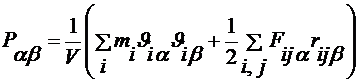 , (3.1.1)
, (3.1.1)
здесь
V - объем системы, 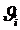 -
скорость i-ой частицы,
-
скорость i-ой частицы, 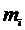 - масса i-ой
частицы,
- масса i-ой
частицы, 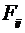 - сила, действующая на i-ую частицу со
стороны j-ой,
- сила, действующая на i-ую частицу со
стороны j-ой, 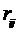 -
расстояние между частицами i и j,
-
расстояние между частицами i и j, 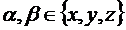 .
.
Очевидно,
что если рассматривать поверхность, ортогональную направлению z
(рис. 3.1.1)
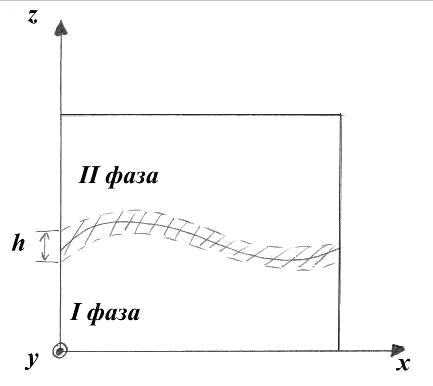
Рис. 3.1.1 Двухфазная поверхность с
поверхностью, ортогональной оси z. h - толщина межфазного слоя
При моделировании эта величина определяется положениями частиц одной
фазы, которые взаимодействуют с частицами другой фазы.
Поверхностный слой будет характеризоваться анизотропией давления. Тогда
поверхностное натяжение для геометрии, изображенной на рисунке, можно
определить следующим образом
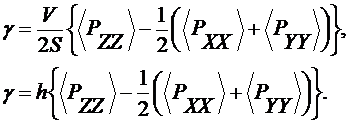 (3.1.2)
(3.1.2)
Следует отметить, что выражение (3.1.2) позволяет выполнить оценку
коэффициента поверхностного натяжения при любых межфазных комбинаций [13].
3.2
Капиллярно - флуктуационный метод
Данный подход основан на оценке равновесных флуктуаций высоты границы
раздела. Отсюда, поверхностные свойства могут быть изучены в рамках капиллярной
теории. Упрощенно основную физическую идею этого метода можно сформулировать
следующим образом: искривление плоской межфазной границы непосредственным
образом определяется силами сцепления молекул в поверхностном слое или
поверхностное натяжение.
Рассмотрим вариант этого метода, адаптированный к численному эксперименту
по моделированию молекулярной динамики.
В данном методе ключевым моментом является геометрия ячейки
моделирования. Согласно работе [14] наиболее
оптимальной должна являться следующая геометрия:
1. Ячейка моделирования представляет из себя сэндвич из трех слоев
(рис.3.2.1) - кристалл - жидкость.
2. Длина направления, по которому будет оцениваться поверхность
должно быть много больше толщины моделируемой ячейки, b<<d.
. В случае трехслойного сэндвича можно использовать периодические
граничные условия по всем трем направлениям.
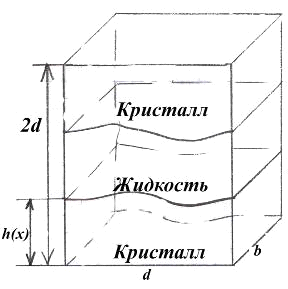
Рис. 3.2.1 Ячейка моделирования -
сэндвич. b<<d
Эта система будет уравновешиваться при выбранных температуре и давлении.
Ключевой величиной, которая возникает в данном методе, является, так
называемая, жесткость поверхности, которая определяется следующим образом
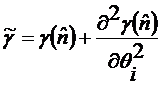 , (3.2.1)
, (3.2.1)
где
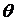 - есть угол между нормалью к поверхности и
усредненной ориентацией плоской исходной поверхности (Рис. 3.2.2).
- есть угол между нормалью к поверхности и
усредненной ориентацией плоской исходной поверхности (Рис. 3.2.2).
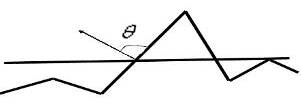
Рис.
3.2.2 Угол между нормалью к поверхности и усредненной ориентацией плоской
поверхности
Жесткость
непосредственно связывается со спектром равновесной статистической флуктуации
высоты поверхности 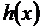 .
.
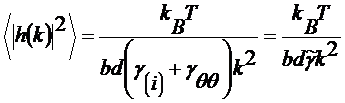 , (3.2.2)
, (3.2.2)
где
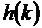 - есть одномерное Фурье - преобразование величины
- есть одномерное Фурье - преобразование величины 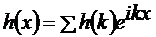 .
.
С
другой стороны, величина 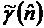 воспроизводиться в рамках кубического гармонического
разложения следующим образом
воспроизводиться в рамках кубического гармонического
разложения следующим образом
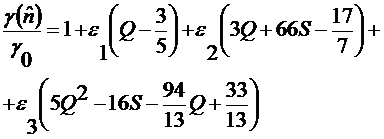 , (3.2.3)
, (3.2.3)
где
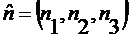 ,
, 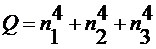 ,
, 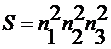 .
.
Очевидно,
что при параметризации (3.2.3) появляется четыре подгоночных параметра 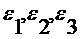 . Тогда, рассматривая производные (3.2.3) линии радела
по трем различным направлениям
. Тогда, рассматривая производные (3.2.3) линии радела
по трем различным направлениям 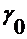 .
.
Данный
метод является пригодным для оценки поверхностного натяжения двухфазных систем,
одной из которых является кристаллическая фаза.
Следует
также отметить, что кроме коэффициента поверхностного натяжения данный метод
позволяет получать поправочные константы 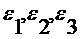 , которые
оценивают анизотропию поверхностных свойств.
, которые
оценивают анизотропию поверхностных свойств.
3.3 Модельный
mW-потенциал
В работе [15] рассмотрена кристаллизация воды при 180К через
крупномасштабное молекулярно - динамическое моделирование модели воды mW (monatomic water).
В
работе использовался mW-потенциал воды, состоящий из парной суммы 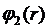 и суммы трех частей
и суммы трех частей 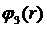
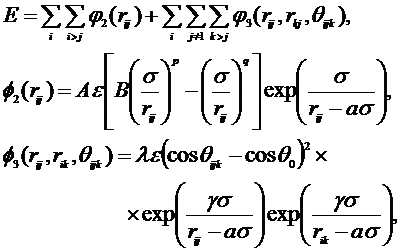 (3.3.1)
(3.3.1)
где А=7.09556277, В=0.6022245584, p=4,
q=0, 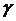 =1.2, a=1.8,
=1.2, a=1.8, 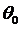 =109.47°,
=109.47°,
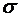 =2.3925A°,
=2.3925A°, 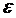 =6.189
kcal mol-1,
=6.189
kcal mol-1, 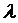 =23.15.
=23.15.
Система,
состоящая из 32768 частиц, мгновенно охлаждалась от 300К до 110К, данные
записывались через 0,3 пс.
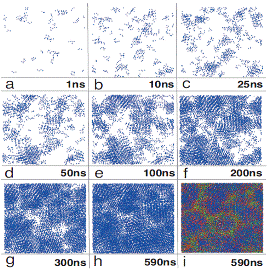
Рис. 3.3.1 Снимки кристаллизации воды
при мгновенном охлаждении
Также
в работе [15] была вычислена радиальная функция распределения 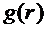 , формула (3.3.2), между молекулами воды для выбранной
формы моделирования (с помощью пакета LAMMPS).
, формула (3.3.2), между молекулами воды для выбранной
формы моделирования (с помощью пакета LAMMPS).
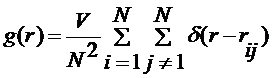 (3.3.2)
(3.3.2)
Даже когда количество кластеров льда значительно, пики едва заметны
(Рис.3.3.2), наличие льда не заметно до ступени е) - 16%.
Рис. 3.3.2 Радиальная функция распределения при 180К. Уровни
соответствуют долям льда на снимках Рис.3.3.1
В работе [16] на основе следующих соотношений оценивается поверхностная
энтропия (3.3.3), энергия поверхности раздела двух сред (3.3.4) и поверхностная
теплоемкость для воды - пара (3.3.5)
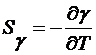 (3.3.3)
(3.3.3)
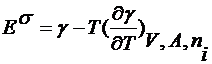 (3.3.4)
(3.3.4)
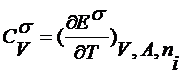 (3.3.5)
(3.3.5)
На основе данных формул, также с помощью формулы (3.3.5) была рассчитана
поверхностная теплоемкость. Зависимость данной величины от температуры
представлена на рисунке 3.3.3:
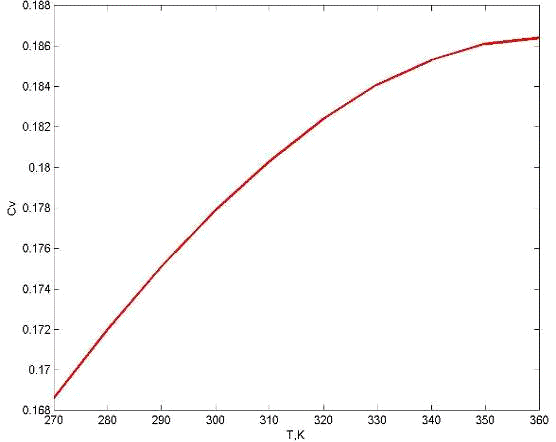
Рис. 3.3.3 Зависимость поверхностной
теплоемкости от температуры
Из графика видно, что при увеличении температуры поверхностная
теплоемкость тоже увеличивается.
3.4
Результаты расчета поверхностного натяжения
В работе [5] недавно были получены результаты моделирования для конденсации
паров водяного пара. При этом моделирование было выполнено с помощью модельного
mW-потенциала, определяемого формулой
(3.3.1).
А.В. Мокшин Б.Н. Галимзянов в работе [5] рассчитали значения
координационных чисел для жидкой фазы и фазы пара. При этом данные были
получены для целого ряда экспериментов моделирования. Зная явный вид
взаимодействия потенциала U(r), на основе §1.3 и с помощью формулы
(3.3.1) в данном случае можно получить следующее значения для поверхностной
энергии
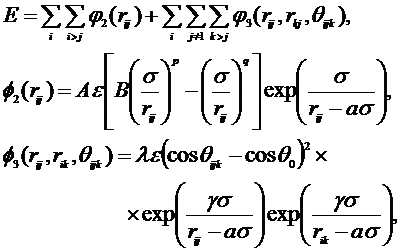 (3.4.1)
(3.4.1)
где А=7.09556277, В=0.6022245584, p=4,
q=0, 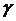 =1.2, a=1.8,
=1.2, a=1.8, 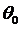 =109.47°,
=109.47°,
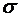 =2.3925A°,
=2.3925A°, 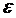 =6.189
kcal mol-1,
=6.189
kcal mol-1, 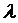 =23.15.
=23.15.
Тогда
для коэффициента поверхностного натяжения будем иметь следующее выражение
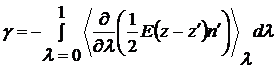 . (3.4.2)
. (3.4.2)
Тогда поверхностная энтропия может быть вычислена с помощью следующей
формулы
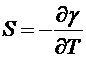 . (3.4.3)
. (3.4.3)
На рисунке 3.4.1 представлено распределение координационных чисел,
полученных в работе [5] через моделирование конденсации воды.
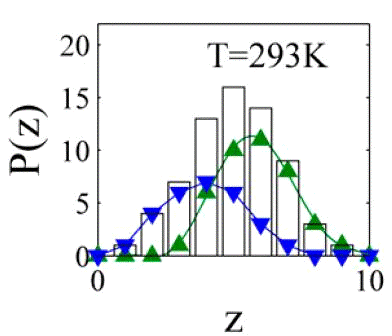
Рис. 3.4.1 Распределение первых координационных чисел для молекул воды
критического размера при температуре 293 К. Зеленая линия показывает
воздействие объемных молекул, а синяя - поверхностные молекулы. Данные
усреднены по шагам
На основе данного распределения, получаем с помощью уравнения (3.4.2)
следующую температурную зависимость поверхностного натяжения, представленную на
рисунке 3.4.2:
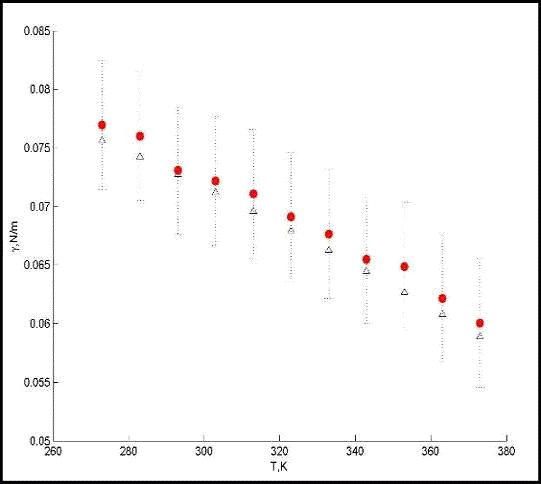
Рис. 3.4.2 Температурная зависимость поверхностного натяжения
Экспериментальные данные показаны треугольными маркерами, а результаты
моделирования - круглыми маркерами. Пунктирная линия показывает погрешности
[5].
Полученные
результаты свидетельствуют об уменьшении поверхностного натяжения  с увеличением температуры.
с увеличением температуры.
Причем
результаты согласуются с хорошо известными экспериментальными данными. Такое
согласие несколько удивительно, потому что экспериментальные данные получены
для плоской границы раздела, в то время как значения поверхностного натяжения,
рассчитанные нами, определены для случая сферической жидкой капли. Тем не
менее, области погрешностей, полученных нами результатов, покрывают
экспериментальные данные.
3.5
Поверхностная энтропия
Как известно, вода обладает рядом аномалий (структурных, динамических,
энергетических и др.).
Так,
одной из интегрирующих особенностей воды, которое интенсивно обсуждается в
современной научной литературе [5], является аномалия в поверхностном натяжении
(жидкая капля - пары воды) при температурах - чуть выше температуры плавления 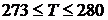 .
.
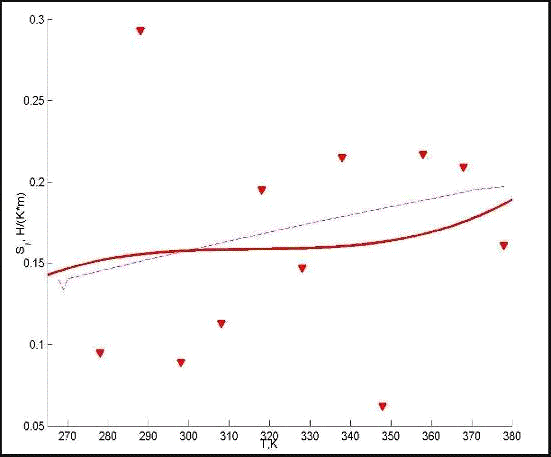
Рис. 3.5.3 Температурная зависимость поверхностной энтропии
Пунктирной
линией показана температурная зависимость 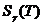 для
плоской границы раздела, маркерами - температурная зависимость
для
плоской границы раздела, маркерами - температурная зависимость 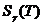 для случая сферической жидкой капли, сплошной линией
- кубическая интерполяция температурной зависимости
для случая сферической жидкой капли, сплошной линией
- кубическая интерполяция температурной зависимости 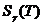 для случая сферической жидкой капли.
для случая сферической жидкой капли.
С
другой стороны, наличие такой сингулярности можно проверить математически,
рассчитав первую производную по температуре от поверхностного натяжения, т.е.
определив температурную зависимость поверхностной энтропии. Это можно выполнить
с помощью уравнения (3.4.3). На рисунке 3.5.1 представлены результаты
вычисления температурной зависимости 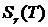 .
.
Из
рисунка 3.5.3 ясно видно, что возможная аномалия в температурной зависимости
поверхностного натяжения воды может быть в температурной области 270 - 290К,
также в температурной области 345 - 365К. данные численного эксперимента
наглядно свидетельствуют об этом. В области температур 300 - 335К в зависимости
поверхностного натяжения, каких - либо ярко выраженных изменений не
наблюдается, хотя и результат моделирования показывает завышенные значения по
сравнению с данными из справочника [16]. Тем не менее, необходимо отметить, что
если данные из справочника приводятся для плоской границы раздела (между жидкой
фазой и водяным паром), то результаты наших вычислений выполнены для жидкой
капли конечного размера. Поэтому такая нетривиальная зависимость, наблюдаемая
на рисунке 3.5.3, вполне может быть связана с различными эффектами.
Выводы
На основании проведенных исследований были получены следующие выводы и
результаты:
· выполнено компьютерное моделирование молекулярной динамики
воды для области температур 273 - 373К;
· в соответствии с разработанным алгоритмом выполнен расчет
температурной зависимости поверхностного натяжения капель воды в водяного пара;
· был разработан алгоритм по моделированию молекулярной
динамики воды на основе модельного mW-потенциала;
· выполнен расчет температурной зависимости поверхностной
энтропии и рассмотрена возможность существования аномалий в поверхностном
натяжении. Возможная аномалия в температурной зависимости поверхностного
натяжения воды может быть в температурной области 270 - 290К, также в
температурной области 345 - 365К. данные численного эксперимента наглядно
свидетельствуют об этом. В области температур 300 - 335К в зависимости
поверхностного натяжения, каких - либо ярко выраженных изменений не
наблюдается, хотя и результат моделирования показывает завышенные значения по
сравнению с данными из справочника [16]. Тем не менее, необходимо отметить, что
если данные из справочника приводятся для плоской границы раздела (между жидкой
фазой и водяным паром), то результаты наших вычислений выполнены для жидкой
капли конечного размера. Поэтому такая нетривиальная зависимость, наблюдаемая,
вполне может быть связана с различными эффектами.
Благодарность
Выражаю
глубокую признательность и благодарность за неоценимую помощь в постановке цели
и задач, организации теоретических и практических исследований, обсуждении
полученных результатов и за моральную поддержку научному руководителю, доценту,
кандидату физико-математических наук Мокшину А.В., а также рецензенту доктору
физико-математических наук, профессору Нефедьеву Л.А
<http://kpfu.ru/main?p_id=28733>.
Выражаю
благодарность за действенную помощь в проведении численных расчетов кандидату
физико-математических наук Хуснутдинову Р.М.
Список
литературы
1. J. D. Bernal, R.H. Fowler. A Theory
of Water and Ionic Solution, with ParticularReference to Hydrogen and Hydroxyl
Ions // J. Chem. Phys.,
- 1933 - 1, 515.
.
J. G. Kirkwood, F. P. Buff. The statistical mechanical theory of surface
tension// J. Chem. Phys., - 1949 - 17(3): 338-343.
3. G. J. Gloor, G. Jackson,
F. J. Blas, E. de Miguel. Test-area simulation method for the direct
determination of the interfacial tension of systems with continuous or
discontinuous potentials// J. Chem. Phys. - 2005 - 123, 134703.
4. C. Vega, E. de Miguel.
Surface tension of the most popular models of water by using the test-area
simulation method// J. Phys. Chem. - 2007 - 126, 154707.
. Anatolii V. Mokshin, Bulat
N. Galimzyanov. Steady-State Homogeneous Nucleation and Growth of Water
Droplets: Extended Numerical Treatment// J. Phys. Chem. - 2012 - 116, 11959−11967.
. Alexander J. Sodt, Richard
W. Pastor. The tension of a curved surface from simulation// J. Chem. Phys. - 2012 - 137, 234101.
7. А.Н.
Лагарьков, В.М. Сергеев. Метод молекулярной динамики в статистической физике//
Успехи физических наук - 1978 - Т.125 - с.409-448.
8. G. W. Robinson, S. Singh, S. B. Zhu,
and M. W. Evans. Water in Biology, Chemistry and Physics: Experimental
Overviews and Computational Methodologies// World Scientific, Singapore - 1996.
9. H. J. White, J. V.
Sengers, D. B. Neumann, J. C. Bellows. IAPWS Release on the Surface Tension of
Ordinary Water Substance// Physical Chemistry of Aqueous Systems - 1995 - А139.
10. И.З.
Фишер. Применение методов Монте-Карло в статистической физике// Успехи
физических наук -1959 - вып.3.
. D. Frenkel, B. Smit.
Understanding Molecular Simulation. // Academic press. - 2002. - 638p.
. V.G. Baidakov, S.P.
Protsenko, Z.R. Kozlova, G.G. Chernykh. Metastable extension of the liquid -
vapor equilibrium and surface tension// J. Chem. Phys. - 2007 - 126, 214505.
. F. Varnik, J. Baschnagel,
K. Binder. Molecular dynamics results on the pressure tensor of polymer films//
J. Chem. Phys. - 2000 - 113, 4444.
14. .J. Hoyt, M. Astra, A.
Karma. Matrices Science and Engineering// 2003 - R41, 121-163 (2003).