Система передачи дискретной информации
Содержание
Введение
.
Обработка результатов измерений искажений
.
Программное (теоретическое) кодирование
.1
Общие сведения
.2
Программное (теоретическое) кодирование
.
Разработка схемы кодирующего устройства
.
Разработка схемы декодирующего устройства
Заключение
Введение
Система передачи дискретной информации (ПДИ) как
и любая система связи включает в себя в общем виде передатчик, канал связи и
приемник. Передатчик обеспечивает преобразование сообщения-оригинала в сигнал,
канал переносит этот сигнал из одной точки пространства в другую в
помехоактивной среде, приемник выполняет обратное преобразование сигнала в
сообщение-копию, выдавая его получателю сообщения.
В системах ПДИ преобразование сообщения в
электрический сигнал и обратное преобразование выполняются в два этапа, что
является их характерной особенностью.
К дискретной информации относятся все
буквенно-цифровые текстовые сообщения (телеграммы), потоки цифр в системах
телеобработки (данные), команды и извещения систем автоматики, телемеханики,
телесигнализации (сообщения ТУ-ТС). Такие сообщения отображаются дискретными
сигналами, представляющими собой дискретную функцию дискретного времени, или
последовательностью прямоугольных импульсов. Это накладывает свои особенности
на методы формирования сигналов, передачи и различения их в пункте приема, на
построение оконечных, каналообразующих и коммутационных устройств и на
применяемую при анализе и синтезе таких сигналов теорию.
Одним из важных требований, предъявляемых к
устройствам передачи дискретной информации, является обеспечение высокой
верности, характеризующейся вероятностью появления ошибок. Особенно это
относится к системам передачи данных, в которых вероятность появления ошибки в
символах должна быть не более 106- 108 (для сравнения: в обычной телеграфной
связи - 3-105).
Методы повышения верности передачи информации
различны, важное место среди них отводится корректирующим кодам и системам с
обратной связью. Использование некоторых корректирующих кодов, в частности
циклического, позволяет обнаруживать и исправлять ошибки в принимаемой
информации. При этом можно достичь практически любой верности передачи
информации. Однако с целью упрощения схем кодирующих и декодирующих устройств
возможности корректирующих кодов часто используются не полностью - ошибки
только обнаруживаются, а исправление происходит путем повторения неправильно
принятых информационных блоков. Это становится возможным при наличии обратной
связи приемника и передатчика.
Корректирующие коды строят таким образом, что
все используемые для передачи информации комбинации (разрешенные кодовые
комбинации) отличаются друг от друга не менее чем в двух разрядах. Комбинации,
не используемые для передачи информации, принадлежат к числу неразрешенных
(запрещенных), поэтому один неправильно принятый разряд приводит к замене
разрешенной кодовой комбинации неразрешенной.
Обнаружение и исправление определенного
количества ошибок в кодовой комбинации осуществляются за счет введения
избыточности в передаваемую информацию, т. е. дополнительно к информационным
символам в процессе кодирования добавляют несколько проверочных символов,
полученных из информационных, по определенной для данного кода системе.
Передача данных - область электросвязи,
предназначенная для передачи информации между электронными вычислительными
машинами. Под термином “данные” понимают формализованную цифровую информацию,
циркулирующую между объектами управления и управляющим центром какой-либо
автоматизированной системы управления.
Устройства, обеспечивающие передачу данных,
являются составной частью комплекса технических средств автоматизированной
системы управления железнодорожным транспортом (АСУЖТ), которая позволяет
автоматизировать управление подразделениями транспорта, быстрее решать многие
технологические задачи, что ведет к улучшению качественных показателей работы в
целом.
1.
Обработка результатов измерения искажений
искажение кодирование комбинация
информация
Высокая верность - важное требование для
передачи дискретной информации. Термин «верность» означает защищенность от
появления ошибок. Для оценки этого параметра используется вероятность ошибок по
знакам (кодовым комбинациям, блокам, кадрам) или единичным элементам (символам
кода).
Конкретные значения допустимой вероятности
ошибок зависят от назначения информации и методов ее обработки. Например, при
передаче статистических данных по погрузке и выгрузке вагонов достаточно, чтобы
вероятность ошибок не превышала 10-4 - 10-5 на знак; при передаче данных,
связанных с управлением сложными технологическими процессами, - 10-6, бухгалтерских
данных по денежным расчетам - 10-7-10-8, для телеграфной связи -3-10-5.
Верность можно повысить разными методами:
а) улучшением качественных показателей каналов
связи, каналообразующей аппаратуры и оконечных устройств передачи и приема
дискретной информации;
б) введением различного рода избыточности
(например, использованием систем с обратными связями, корректирующих кодов и т.
д.).
Основными причинами появления ошибок являются
искажения дискретных сигналов, нарушение синхронности и синфазности работы
передающих и приемных устройств. В курсовом проекте следует произвести расчет
вероятности ошибок, обусловленных искажениями сигналов, и выбрать способы
защиты, при которых будет обеспечена заданная верность передачи данных.
Искажения дискретных сигналов могут быть
регулярными и случайными. К регулярным относятся искажения, обусловленные
несоблюдением норм технического обслуживания аппаратуры (отклонение напряжения
источников питания от номинала, регулировка входных и выходных реле с
преобладанием), плавными изменениями уровня в системах тонального
телеграфирования с амплитудной модуляцией, сдвигом частот в системах с
частотной модуляцией, несоответствием ширины спектра канала скорости модуляции
и др. Причинами искажений случайного характера являются аддитивные и
мультипликативные помехи и кратковременные прерывания канала связи.
Изучение искажений можно вести двумя путями:
а) аналитически - на основе зависимостей между
первичными характеристиками каналов (амплитудно- и фазочастотными
характеристиками, скачками уровня, шумами и др.) и величиной искажений;
б) экспериментально - непосредственным
измерением искажений.
Первый путь сложен и не всегда дает точные
результаты вследствие невозможности учета всех факторов, влияющих на
передаваемые сигналы. На действующих каналах связи целесообразно использовать
второй путь. Результаты измерения отражают не только наличие и интенсивность
помех в канале, но и качество настройки аппаратуры, позволяя в ряде случаев
установить причины появления искажений.
Для определения статистической структуры краевых
искажений применяют анализатор искажений. Используя результаты измерений таким
прибором, необходимо рассчитать оценки математического ожидания α
и
среднеквадратического отклонения σ:
|
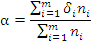
|
(1.1)
|
|
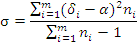
|
(1.2)
|
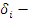
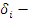 среднее значение смещения значащего
момента восстановления (ЗМВ), т. е. искажение для i-ro интервала;- количество
смещений в i-м интервале (частота смещений);- количество интервалов.
среднее значение смещения значащего
момента восстановления (ЗМВ), т. е. искажение для i-ro интервала;- количество
смещений в i-м интервале (частота смещений);- количество интервалов.
Подставив данные из таблицы 1
задания в формулы (1.1), (1.2) для расчета математического ожидания α и
среднеквадратического отклонения σ получим:
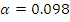
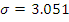
Построим гистограмму результатов
измерения искажений. По оси абсцисс отложим результаты измерений величин
искажений, а по оси ординат - значения 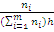
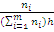 где h - шаг шкалы измерителя (h = 2
%). Также построим график нормального закона распределения с вычисленными
параметрами
где h - шаг шкалы измерителя (h = 2
%). Также построим график нормального закона распределения с вычисленными
параметрами 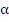
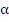 и
и 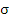
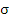 , определяемому по выражению:
, определяемому по выражению:
|
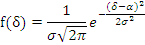
|
(1.3)
|
Таблица 1.1 - Результаты расчетов измерения
искажений.
|
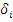
|
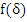
|
|
-29,5
|
0
|
|
-8
|
0.004
|
|
-6
|
0.02
|
|
-4
|
0.053
|
|
-2
|
0.102
|
|
0
|
0.125
|
|
2
|
0.11
|
|
4
|
0.061
|
|
6
|
0.02
|
|
8
|
0.004
|
|
29,5
|
0
|
Гистограмма и график представлены на рисунке 1 и
на рисунке 2 соответственно.
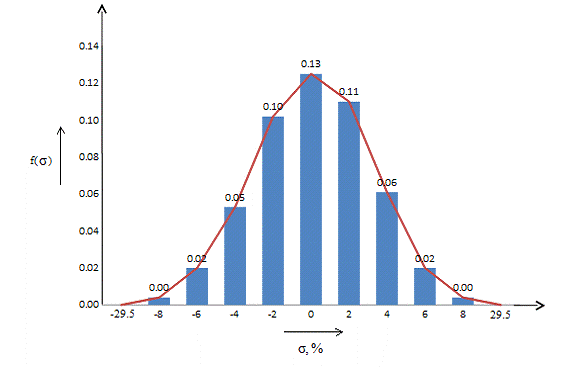
Рисунок 1 - Гистограмма результатов измерения
искажений
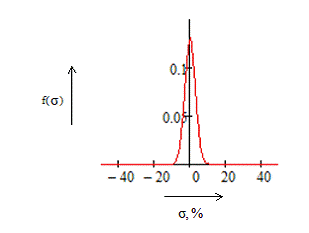
Рисунок 2 - график нормального закона
распределения.
Определим теоретические значения
частности смещений границ импульсов 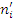
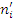 по следующей формуле:
по следующей формуле:
|
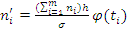 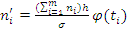 ,(1.4) ,(1.4)
|
|
где h - шаг выборки (интервал смещений ЗМВ),
равный двум, кроме крайних членов, где он равен 41;
|
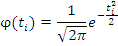
|
(1.5)
|
|
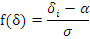
|
(1.6)
|
По полученным данным рассчитаем критерий Пирсона
по формуле:
|
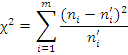
|
(1.7)
|
А также рассчитаем количество степеней свободы
m2 по формуле (1.8):
где b - число параметров теоретического
распределения; b = 2, так как нормальный закон является двухпараметрическим.
Результаты расчетов 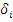
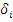 ,
, 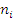
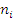 ,
, 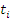
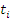 ,
, 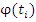
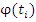 ,
, 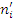
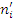 ,
, 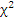
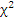 и m2 приведены в таблице 1.2.
и m2 приведены в таблице 1.2.
Таблица 1.2 - Результаты расчетов 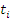
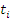 ,
, 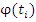
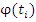 ,
, 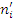
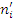 ,
, 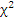
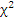 и m2.
и m2.
-29,5 0 -9.702 1.448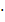
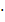 10-211.197
10-211.197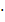
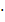 10-17
10-17
.064
|
|
|
|
|
|
-8
|
5
|
-2.654
|
0.012
|
4.747
|
|
|
|
-6
|
25
|
-1.999
|
0.054
|
21.822
|
|
|
|
-4
|
65
|
-1.343
|
0.162
|
65.262
|
|
|
|
-2
|
125
|
-0.688
|
0.315
|
126.988
|
|
|
|
0
|
155
|
-0.032
|
0.399
|
160.769
|
|
|
|
2
|
135
|
0.624
|
0.328
|
132.427
|
|
|
|
4
|
75
|
1.279
|
0.176
|
70.972
|
|
|
|
6
|
25
|
1.935
|
0.061
|
24.747
|
|
|
|
8
|
5
|
2.59
|
0.014
|
5.614
|
|
|
|
29,5
|
0
|
9.638
|
2.688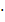 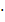 10-212.222 10-212.222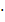 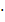 10-17 10-17
|
|
|
|
Сравним вероятность P(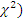
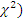 c 0.01. P(
c 0.01. P(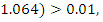
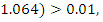 т.е. можно утверждать, что
эмпирическое распределение краевых искажений соответствует нормальному закону с
параметрами
т.е. можно утверждать, что
эмпирическое распределение краевых искажений соответствует нормальному закону с
параметрами 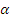
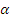 и
и 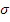
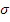 .
.
Рассчитаем вероятность ошибки в
элементе Рэ, которая зависит от параметров распределения искажений и допустимой
величины искажений μ:
|
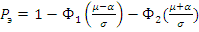 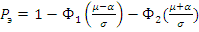 ,(1.9) ,(1.9)
|
|
где Ф1 и Ф2 - функции распределения
типа 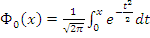
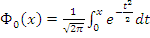 нормированного центрированного
нормального распределения, численные значения которых принимаются по данным
справочника
нормированного центрированного
нормального распределения, численные значения которых принимаются по данным
справочника
Для определения графика зависимости
Рэ = f(μ),
где
μ
- допустимое
значение искажений в пределах от 14 до 18 %. График зависимости Рэ = f(μ) представлен
на рисунке 3.
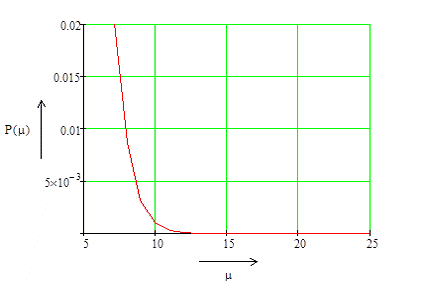
Рисунок 3 - График зависимости Рэ =
f(μ)
Выберем несколько μ по графику и
данные зависимости Рэ = f(μ) занесем в таблицу 1.2.
Таблица 1.3 - Значения зависимости
Рэ = f(μ)
взятое
в нескольких точках.
|
μ
|
Рэ
= f(μ)
|
|
17
|
2.551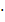 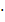 10-8 10-8
|
|
20
|
5.652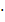 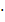 10-11 10-11
|
Рассчитаем вероятность ошибки в комбинации из n
элементов при μ=17 по следующей
формуле:
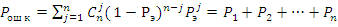
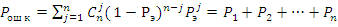 , где
, где
j - кратность ошибки, т. е.
количество неправильных разрядов в комбинации (блоке);- общее количество
разрядов; n = k - для простого кода; n = k + r - для корректирующего кода (k и
r - количество информационных и проверочных разрядов соответственно);
Р1, Р2, Рn - вероятности
однократной, двукратной, n-кратной ошибки.
Пример расчета:

А также рассчитаем вероятность
ошибки в комбинации из n элементов с исключением из общей суммы вероятностей
вероятности однократной ошибки. Данные занесем в таблицу 1.3.
Таблица 1.4 - значения вероятностей
ошибок в комбинации.
|
Вероятности
ошибок
|
Значение
вероятностей ошибок
|
|
P1
|
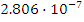
|
|
P2
|
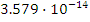
|
|
P3
|
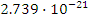
|
|
P4
|
0
|
|
P5
|
0
|
|
P6
|
0
|
|
P7
|
0
|
|
P8
|
0
|
|
P9
|
0
|
|
P10
|
0
|
|
P11
|
0
|
|
P11
|
0
|
|
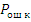
|
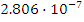
|
Важным параметром корректирующего кода является
минимальное кодовое (хэммингово) расстояние d0, которое определяется как
минимальное количество отличающихся разрядов при попарном сравнении всех
разрешенных комбинаций кода. Для простых (некорректирующих) кодов d0 = 1, для
избыточных (корректирующих) d0 ≥ 2.
Корректирующие коды могут использоваться в двух
режимах - исправления или обнаружения ошибок. Во втором режиме декодер
приемного устройства формирует сигнал наличия ошибок, не определяя точно
ошибочные разряды. Исправление при этом должно осуществляться другим методом,
например, повторной передачей ошибочной комбинации (блока) в системах с
решающей обратной связью (РОС).
Кратность гарантированно обнаруживаемых ε
и
исправляемых t ошибок связана с минимальным кодовым расстоянием соотношениями:
d0 = ε
+ 1 и
do = 2t+l.
Для определения значения ε
или
t поочередно исключают из общей суммы вероятность однократной (P1), двукратной
(Р2), ... ошибок, пока оставшаяся сумма не окажется меньше допустимого
значения. Количество исключенных членов и означает необходимую кратность
исправляемых (t) или обнаруживаемых (ε) ошибок.
Так как по заданию наш код должен исправлять
однократную ошибку (P1), то t =1, из чего следует, что do = 3.
При построении циклических кодов кодовые
комбинации принято представлять в виде полиномов:

где аn-1, а0 - коэффициенты, принимающие
значения, равные нулю или единице;
х - основание кода, х = 2.
Циклическими (n, k)-кодами называются коды,
каждая кодовая комбинация которых, выраженная в виде полинома, имеет степень,
не превышающую n - 1, и нацело делится на некоторый полином g(x) степени r.
Полином g(x) называется образующим (производящим, порождающим), от его выбора
зависит обнаруживающая и исправляющая способность циклического кода.
Выбор образующего полинома является
ответственной задачей, так как корректирующие возможности разрабатываемого
кода, алгоритмы и схемы кодирования и декодирования определяются этим
полиномом. Общий вид образующего полинома: 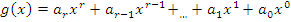
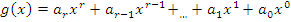
В качестве образующих полиномов
используются неприводимые многочлены или их произведения.
Степень образующего полинома,
численно равная количеству проверочных элементов, определяется из соотношений:
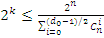
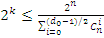 - при нечетном d0; (1.10)
- при нечетном d0; (1.10)
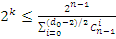
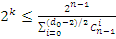 при четном d0; (1.11)
при четном d0; (1.11)
где i = 0, 1, 2,…
Методом подбора находим решение
неравенства 1.10. Получаем, что n=11, k=7, r=4.
Следовательно, необходимый нам
неприводимый полином имеет четвертую степень.
2. Программное
(теоретическое) кодирование
.1 Общие сведения
Кодирование и декодирование
циклическим кодом могут быть выполнены алгебраическими операциями (программный
метод) либо в результате работы специально разработанных схем (схемный метод).
При программном методе преобразование комбинаций, обнаружение и исправление
ошибок производятся алгебраическими операциями над многочленами, для выполнения
которых программируется вычислительная система устройств связи. Особенностью
алгебраических действий в теории кодирования является замена операций сложения
и вычитания одной - сложением по модулю два. При этом четное число одинаковых
членов дает ноль, а нечетное - единицу.
Поскольку заданием предполагается
выполнение только алгебраических операций без составления программы, назовем
этот способ теоретическим. Теоретическое кодирование в свою очередь может быть
выполнено двумя способами:
а) умножением k-элементной
комбинации простого кода на образующий полином g(x) (в результате получают
комбинацию неразделимого циклического кода);
б) умножением кодовой комбинации
простого кода на одночлен хr и добавлением к этому произведению остатка от
деления произведения хr Р(х) на g(x). В результате получают комбинацию
разделимого циклического кода.
Неразделимость кода значительно
усложняет процесс декодирования, поэтому на практике чаще используется второй
способ построения кодовых комбинаций.
Одним из свойств циклического кода
является деление разрешенной кодовой комбинации на образующий полином без
остатка. Следовательно, появление остатка от деления говорит о наличии ошибки.
В кодах, работающих в режиме исправления ошибок, вид остатка однозначно
определяет порядковые номера ошибочных разрядов. Поэтому для декодирования
предварительно следует составить таблицу синдромов ошибок (остатков от деления)
для всех вариантов ошибочных разрядов. Повторение синдромов в этой таблице
означает невозможность исправления, так как появляется неопределенность, и это
соответствует режиму обнаружения ошибок.
Составим таблицу синдромов ошибок,
приведенную в таблице 2.1, для всех вариантов ошибочных разрядов для
разделимого кода из n = 11 элементов с исправлением однократной ошибки .
Таблица 2.1 - Таблица синдромов
ошибок.
|
Ошибочный
разряд
|
Полином
ошибки
|
Синдром
ошибки
|
|
1
|
x10
|
x
3+x
|
|
2
|
x9
|
x2+1
|
|
3
|
x8
|
x3+x2+x
|
|
4
|
x7
|
x2+x+1
|
|
5
|
x6
|
x3+x2+x+1
|
|
6
|
x5
|
x3+x+1
|
|
7
|
x4
|
x3+1
|
|
8
|
x3
|
x3
|
|
9
|
x2
|
x2
|
|
10
|
x1
|
x1
|
|
11
|
x0
|
x0
|
.2 Программное (теоретическое) кодирование
По заданию задан разделимый код, который следует
составить для комбинации 0001111 по выбранному в предыдущем пункте образующему
полиному. Из этого следует, что:
а) P(x)= x3+x2+x+1
б) g(x)= x4+ x3+1
Рассчитаем кодовую комбинацию неразделимого
циклического кода умножением k-элементной комбинации простого кода на
образующий полином g(x).
F(x)=x4( x3+x2+x1 +1)+остаток от (x4(
x3+x2+x1+1)/ (x4+ x3+1))= x7+x6+x5+x4+x3+x
Отсюда следует, что кодовая комбинация
00011111010.
.3 Программное (теоретическое) декодирование
Произведем теоретическое декодирование кодовой
комбинации с пятым ошибочным элементом, путем деления ее полинома F(x)=
x7+x6+x5+x4+x3+x на образующий полином g(x) = x4+x3 +1.
F(x)/ g(x) = (x7+x6+x5+x4+x3+x)/(
x4+x3 +1) = x3+x2+1+( x3+x2+x+1)/( x4+x3 +1)
В результате получаем остаток от деления равный
(x3+x2+x+1), что соответствует синдрому ошибки в пятом разряде, следовательно,
декодирование выполнено верно.
3.
Разработка схемы кодирующего устройства
Схемный способ предполагает разработку
кодирующих и декодирующих устройств, вид которых определяется образующим
многочленом. Эти устройства должны обеспечить аппаратную реализацию описанных
выше процессов, определяющих формирование кодовых комбинаций и синдромов ошибок
в кодирующем и декодирующем устройствах соответственно. Основой схем являются
регистры сдвига с обратными связями, выполняющими операции умножения и деления
многочленов.
В состав кодера входят логические элементы И и
ИЛИ, r-раздядный регистр сдвига и двухвходовые сумматоры по модулю два (М2),
число последних на единицу меньше числа ненулевых элементов членов образующего
полинома g(x). Включаются сумматоры в схеме кодирующего устройства перед ячейками
регистра, обозначенными ненулевыми коэффициентами образующего полинома, начиная
с низшего разряда.
Тактовые импульсы ТИ1, поступающие в вход
элемента И в течение первых k-тактов, необходимы для осуществления обратной
связи между входом и выходом регистра и для формирования в нем остатка от
деления. Этот остаток затем в течение r тактов (действуют тактовые импульсы
ТИ2) поступает на выход схемы.
Функциональная схема кодирующего устройства
приведена на рисунке 4, а принципиальная схема - на рисунке 5.
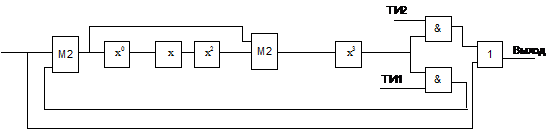
Рисунок 4 - Функциональная схема
кодирующего устройства.

Рисунок 5 - Принципиальная схема
кодирующего устройства.
Таблица 3.1 - Потактовая работа
схемы кодирующего устройства.
|
Такт
|
Вход
|
RG
|
ТИ
|
&1
|
&2
|
Выход
|
|
1
|
0
|
0000
|
ТИ1
|
0
|
0
|
0
|
|
2
|
0
|
0000
|
ТИ1
|
0
|
0
|
0
|
|
3
|
0
|
0000
|
ТИ1
|
0
|
0
|
0
|
|
4
|
1
|
1001
|
ТИ1
|
0
|
0
|
1
|
|
5
|
1
|
0100
|
ТИ1
|
1
|
0
|
1
|
|
6
|
1
|
1011
|
ТИ1
|
0
|
0
|
1
|
|
7
|
1
|
0101
|
ТИ1
|
1
|
0
|
1
|
|
8
|
0
|
0010
|
ТИ2
|
0
|
1
|
1
|
|
9
|
0
|
0001
|
0
|
0
|
0
|
|
10
|
0
|
0000
|
ТИ2
|
0
|
1
|
1
|
|
11
|
0
|
0000
|
ТИ2
|
0
|
0
|
0
|
4 Разработка схемы декодирующего устройства
В каждом из устройств имеется по два регистра -
RG1 и RG2. В регистре RG1 для разделимых кодов число ячеек равно числу
информационных элементов k.
Места включения инверторов в схемах для
исправления ошибок определяются состоянием регистра RG2 в момент поступления
ошибочного элемента на верхний вход выходного сумматора по модулю два.
Для исправления ошибочного разряда на нижний
вход этого сумматора должен быть подан сигнал логической единицы. Этим и
определяется положение инверторов в схеме при потактовом анализе ее работы и
подаче на вход комбинации с заранее известным ошибочным разрядом.
Схема декодирующего устройства приведена на
рисунке 6.
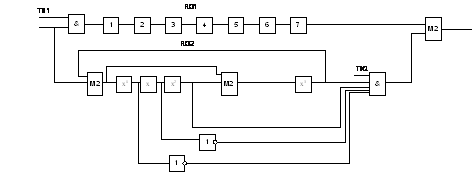
Рисунок 6 - Схема декодирующего
устройства.
Таблица 4.1 - Потактовая работа
схемы декодирующего устройства при приеме правильной комбинации.
|
Такт
|
Вход
|
RG1
|
RG2
|
ТИ
|
Вход
выходного сумматора
|
Выход
|
|
1
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
2
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
3
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
4
|
1
|
1000000
|
1001
|
ТИ1
|
-
|
-
|
|
5
|
1
|
1100000
|
0100
|
ТИ1
|
-
|
-
|
|
6
|
1
|
1110000
|
1011
|
ТИ1
|
-
|
-
|
|
7
|
1
|
1111000
|
0101
|
ТИ1
|
-
|
-
|
|
8
|
1
|
1111000
|
0010
|
-
|
-
|
-
|
|
9
|
0
|
1111000
|
0001
|
-
|
-
|
-
|
|
10
|
1
|
1111000
|
0000
|
-
|
-
|
-
|
|
11
|
0
|
1111000
|
0000
|
-
|
-
|
-
|
|
12
|
0
|
0111100
|
0000
|
ТИ2
|
0⊕0
|
0
|
|
13
|
0
|
0011110
|
0000
|
ТИ2
|
0⊕0
|
0
|
|
14
|
0
|
0001111
|
0000
|
ТИ2
|
0⊕0
|
0
|
|
15
|
0
|
0000111
|
0000
|
ТИ2
|
0⊕1
|
1
|
|
16
|
0
|
0000011
|
0000
|
ТИ2
|
0⊕1
|
1
|
|
17
|
0
|
0000001
|
0000
|
ТИ2
|
0⊕1
|
1
|
|
18
|
0
|
0000000
|
0000
|
ТИ2
|
0⊕1
|
1
|
Таблица 4.2 - Потактовая работа схемы
декодирующего устройства при приеме комбинации с ошибкой на первом разряде.
|
Такт
|
Вход
|
RG1
|
RG2
|
ТИ
|
Вход
выходного сумматора
|
Выход
|
|
1
|
1
|
1000000
|
1001
|
ТИ1
|
-
|
-
|
|
2
|
0
|
0100000
|
1101
|
ТИ1
|
-
|
-
|
|
3
|
0
|
0010000
|
1111
|
ТИ1
|
-
|
-
|
|
4
|
1
|
1001000
|
0111
|
ТИ1
|
-
|
-
|
|
5
|
1
|
1100100
|
0011
|
ТИ1
|
-
|
-
|
|
6
|
1
|
1110010
|
0001
|
ТИ1
|
-
|
-
|
|
7
|
1
|
1111001
|
0000
|
ТИ1
|
-
|
-
|
|
8
|
1
|
1111001
|
1001
|
-
|
-
|
-
|
|
9
|
0
|
1111001
|
1101
|
-
|
-
|
-
|
|
10
|
1
|
1111001
|
0110
|
-
|
-
|
-
|
|
11
|
0
|
1111001
|
0011
|
-
|
-
|
-
|
|
12
|
0
|
0111100
|
1000
|
ТИ2
|
1⊕1
|
0
|
|
13
|
0
|
0011110
|
0100
|
ТИ2
|
0⊕0
|
0
|
|
14
|
0
|
0001111
|
0010
|
ТИ2
|
0⊕0
|
0
|
|
15
|
0
|
0000111
|
0001
|
ТИ2
|
1⊕0
|
1
|
|
16
|
0
|
0000011
|
1001
|
ТИ2
|
1⊕0
|
1
|
|
17
|
0
|
0000001
|
1101
|
ТИ2
|
1⊕0
|
1
|
|
18
|
0
|
0000000
|
1111
|
ТИ2
|
1⊕0
|
1
|
Таблица 4.3 - Потактовая работа схемы
декодирующего устройства при приеме комбинации с ошибкой на пятом разряде.
|
Такт
|
Вход
|
RG1
|
RG2
|
ТИ
|
Вход
выходного сумматора
|
Выход
|
|
1
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
2
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
3
|
0
|
0000000
|
0000
|
ТИ1
|
-
|
-
|
|
4
|
1
|
1000000
|
1001
|
ТИ1
|
-
|
-
|
|
5
|
0
|
0100000
|
1101
|
ТИ1
|
-
|
-
|
|
6
|
1
|
1010000
|
0110
|
ТИ1
|
-
|
-
|
|
7
|
1
|
1101000
|
1010
|
ТИ1
|
-
|
-
|
1
|
1101000
|
1100
|
-
|
-
|
-
|
|
9
|
0
|
1101000
|
0110
|
-
|
-
|
-
|
|
10
|
1
|
1101000
|
1010
|
-
|
-
|
-
|
|
11
|
0
|
1101000
|
0101
|
-
|
-
|
-
|
|
12
|
0
|
0110100
|
1011
|
ТИ2
|
0⊕0
|
0
|
|
13
|
0
|
0011010
|
1100
|
ТИ2
|
0⊕0
|
0
|
|
14
|
0
|
0001101
|
0110
|
ТИ2
|
0⊕0
|
0
|
|
15
|
0
|
0000110
|
0011
|
ТИ2
|
1⊕0
|
1
|
|
16
|
0
|
0000011
|
1000
|
ТИ2
|
0⊕1
|
1
|
|
17
|
0
|
0000001
|
0100
|
ТИ2
|
1⊕0
|
1
|
|
18
|
0
|
0000000
|
0010
|
ТИ2
|
1⊕0
|
1
|
Заключение
В ходе выполнения данной курсовой работы на
основании анализа результатов измерения краевых искажений выбран образующий
полином циклического кода, произведено теоретическое кодирование, разработаны
схемы кодирования/декодирования.
В качестве мер повышения верности при передаче
дискретной информации введена избыточность, которой является применение
корректирующего кода.