Пошук резервів. Ділова гра
МІНІСТЕРСТВО ОСВІТИ І НАУКИ
УКРАЇНИ
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ
ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
імені Вадима Гетьмана
Пошук резервів: Ділова гра
(практикум)
Навчальний посібник
Терещенко
Т.О. Романюк Т.П. Кузубова В.В.
Київ - 2009
ЗМІСТ
АНОТАЦІЯ
ВСТУП
Розділ 1. ЕКОНОМІЧНІ УМОВИ ЗАДАЧІ
.1 ПОСТАНОВКА ЗАДАЧІ
.2 ІНФОРМАЦІЯ ТА СТРУКТУРА ПІДРОЗДІЛІВ ФІРМИ
Розділ 2. ПРОЦЕС ВИКОНАННЯ ДІЛОВОЇ ГРИ
.1 ОРГАНІЗАЦІЙНІ ПИТАННЯ
.2 ЗАВДАННЯ ДЛЯ ВИКОНАННЯ ДІЛОВОЇ ГРИ
Розділ 3. МЕТОДИЧНІ ПОРАДИ ДО РОЗВ’ЯЗАННЯ ЗАДАЧ
ДІЛОВОЇ ГРИ
.1 ЗАДАЧА ОПТИМАЛЬНОГО РОЗКРОЮ МАТЕРІАЛІВ ФІРМИ
.2 ЗАДАЧА ОПТИМАЛЬНОГО ВИКОРИСТАННЯ ОБЛАДНАННЯ ФІРМИ
“SUCCESS”
.3 ЗАДАЧА ОПТИМІЗАЦІЇ ВИРОБНИЧОЇ ПРОГРАМИ ФІРМИ
“SUCCESS”
РОЗДІЛ 4. ВИРОБНИЧА ФУНКЦІЯ ФІРМИ «SUCCESS»
.1 ПОБУДОВА ВИРОБНИЧОЇ ФУНКЦІЇ 1МНК
.2 ПЕРЕВІРКА НАЯВНОСТІ МУЛЬТИКОЛІНЕАРНОСТІ
ПОЯСНЮВАЛЬНИХ ЗМІННИХ
.3 ПЕРЕВІРКА НАЯВНОСТІ АВТОКОРЕЛЯЦІЇ ЗАЛИШКІВ
.4 ПОБУДОВА ВИРОБНИЧОЇ ФУНКЦІЇ МЕТОДОМ ЕЙТКЕНА
РОЗДІЛ 5. АНАЛІЗ ВИКОРИСТАННЯ ВИРОБНИЧИХ РЕСУРСІВ
ЛІТЕРАТУРА
Анотація
Навчальний посібник “Пошук резервів: Ділова гра” є
практикумом для виконання ділової гри “Пошук резервів”. Ділова гра розроблена
колективом викладачів кафедри економіко-математичного моделювання для
проведення тренінгових занять з дисципліни “Економіко-математичне моделювання”
для усіх спеціальностей. Навчальний посібник включає формування цілей і завдань
навчання за даною діловою грою, її організацію та методи розв’язання комплексу
задач оптимального планування виробничої програми підприємства. Велика увага
приділена аналізу ефективності використання основних виробничих ресурсів.
Ділова гра “Пошук резервів” може бути використана як
підсумкове тренінгове заняття для комплексу навчальних дисциплін: економіка
підприємства, економіко-математичного моделювання та економічного аналізу.
Вступ
Підготовка фахівців у вищих навчальних закладах базується на
отриманні знання та вміння за кожною дисципліною навчального плану. З кожним
роком кількість цих знань та вмінь збільшується. Тому щоб підвищити рівень
освіти в Україні необхідно удосконалювати методи навчання за умови постійного
удосконалення навчальних планів.
Система методів навчання, її рівень та структура у кожному
вищому навчальному закладі є різною і не досконалою. Удосконалення системи
методів навчання може бути здійснено, перш за все, за рахунок розширення частки
тренінгових методів, оскільки саме вони дозволять більш успішно набувати вмінь
з кожної дисципліни навчального плану. У межах вирішення даної проблеми
пропонується більш широке застосування ділових ігор. Нами розроблена ділова гра
«Пошук резервів», яка присвячена математичному моделюванню економічних і
технологічних задач фінансово-господарської діяльності підприємства.
Мета ділової гри: побудувати систему економіко-математичних
моделей оптимального планування виробничої програми та застосувати їх для
ефективного використання виробничих ресурсів підприємства
Суб’єкт підприємницької діяльності - фірма “Success”, що
виготовляє чотири види світильників за типорозмірами основного матеріалу 1,5м,
2м, 0,9м, 0,7м.
Виробничі ресурси:
· взаємозамінювані групи обладнання
трьох видів;
· фактичний фонд робочого часу за рік;
· матеріальні ресурси, які включають
перш за все, металеві прутки, довжиною 6м та 8м;
· грошові кошти, що інвестуються у
підприємницьку діяльність.
Предмет дослідження - методи побудови та використання системи
економіко-математичних моделей для оптимального планування виробничої програми
фірми при заданих обсягах ресурсів та попиту на кожний вид світильників.
Зміст та реалізація цієї ділової гри може бути використана
для отримання певних вмінь з різних дисциплін. Це, перш за все,
економіко-математичне моделювання, економіка підприємств, економічний аналіз.
Розділ1. Економічні умови задачі
1.1 Постановка задачі
Необхідно визначити оптимальний обсяг виробництва світильників
за рік, виходячи із основних виробничих ресурсів фірми та проаналізувати рівень
ефективності їх використання. Критерієм оптимальності виробничої програми
використаємо максимум річного доходу фірми.
.2 Інформація та структура підрозділів фірми
Для розв’язання поставленої задачі необхідно використати
інформацію, що є результатом роботи певних структурних підрозділів фірми.
. а) підготовчий відділ (відділ використання матеріальних
ресурсів) складає варіанти розкрою прутків довжиною 6 та 8 метрів, на чотири
деталі довжиною 1,5м, 1,2м, 0,9м та 0,7м, що відповідають типорозмірам
світильників фірми.
б) підготовчий відділ розв’язує задачу оптимального розкрою
матеріалів, яка дозволяє визначити ефективні способи крою. Розрахувати таку
кількість типорозмірів матеріалу, що забезпечить випуск світильників у
відповідності з попитом на них на ринку при мінімальних відходах матеріалу.
. Відділ маркетингу вивчає ринок світильників, прогнозує
попит на всі типи світильників і надає цю інформацію у підготовчий та фінансово-виробничий
відділ.
Визначено, що річний попит на світильники складає:
· Першого типу - 400 одиниць;
· Другого типу - 600 одиниць;
· Третього типу - 500 одиниць;
· Четвертого типу - 300 одиниць.
. Відділ праці та заробітної плати визначає фактичний фонд
робочого часу та нормативи витрат робочого часу на виготовлення одного
світильника кожного виду.
Оскільки фірма має 30 робітників, які працюють 290-300 днів
на рік із семигодинним робочим днем, то календарний річний фонд робочого часу
складає 67 тис. люд-год. Врахувавши відпустки та лікарняні, інші невиробничі
ресурси часу, фактичний фонд робочого часу складає 49 тис.люд-год.
Нормативи витрат робочого часу, що встановлені відділами
праці та заробітної плати, складають:
Таблиця 1
Витрати часу на виготовлення одного світильника
|
Світильник
|
І вид
|
ІІ вид
|
ІІІ вид
|
ІV вид
|
|
Витрати часу
(люд.-год.)
|
22
|
28
|
34
|
18
|
. Технологічний відділ забезпечує безперебійну роботу
обладнання, а також визначає режимний фонд роботи кожної групи обладнання та
норми витрат часу на обробку кожного із світильників на кожній групі
обладнання. Ці дані наведені в таблиці 2.
Таблиця 2
Норми витрат часу на обробку деталей кожного світильника на
кожному типі обладнання
|
Типи обладнання
|
Витрати часу на
один світильник (маш.-год.)
|
Режимний фонд
роботи обладнання (маш.-год.)
|
|
1
|
2
|
3
|
4
|
|
|
І
|
10,5
|
11,1
|
0
|
9
|
3500
|
|
ІІ
|
0
|
5,7
|
4,8
|
6,0
|
3800
|
|
ІІІ
|
3,8
|
3,2
|
3,0
|
0
|
3020
|
На основі даних таблиці 2 будується математична модель задачі
оптимального використання взаємозамінюваних груп обладнання, яка дозволяє мінімізувати
витрати часу на обробку всіх деталей на всіх групах обладнання за умов, що
витрати часу по кожній з груп обладнання не будуть перевищувати режимного фонду
часу роботи та буде оброблено така кількість деталей, яка відповідає ринковому
попиту продукції.
. Фінансово-виробничий відділ розраховує оптимальний обсяг
виробництва світильників кожного виду, який при заданих виробничих ресурсах
забезпечить максимальний дохід фірми за рік. Одночасно визначає грошові кошти,
які фірма може вкласти у виробничу програму світильників та встановлює середні
ціни реалізації їх у відповідності з кон’юнктурою ринку. Кон’юнктура ринку
визначається відділом маркетингу. Ці дані наведено в таблиці 3.
Таблиця 3
|
Показники
|
Середня сума коштів
на 1 світильник (грн.)
|
Загальний обсяг
коштів (тис.грн.)
|
|
1
|
2
|
3
|
4
|
|
|
Грошові кошти
|
38
|
44
|
61
|
24
|
80
|
|
Середня ціна
реалізації (грн.)
|
200
|
250
|
300
|
100
|
|
. Фінансово-виробничий відділ також аналізує рівень
використання виробничих ресурсів щомісячно у динаміці за два роки на основі
економетричного моделювання. Для цього необхідно побудувати виробничу функцію
фірми “Success”, яка буде характеризувати залежність між доходом фірми та
основними виробничими ресурсами, що використовуються на фірмі. Функцію
залежності (економетричну модель доходу) необхідно побудувати на основі
інформації, що наведена в таблиці 4.
Таблиця 4
|
Період часу, t
|
Доходи (тис.грн.),
V
|
Інвестиції
(тис.грн.), I
|
Фонд робочого часу
обладнання (тис.маш.-год.), K
|
Фактичний фонд
робочого часу (тис. люд.-год.), L
|
|
1
|
30
|
5
|
0,8
|
4,2
|
|
2
|
32
|
5,5
|
0,9
|
4,5
|
|
3
|
35
|
6
|
1,1
|
4,8
|
|
4
|
34
|
5,8
|
0,92
|
4,64
|
|
5
|
33
|
5,6
|
0,95
|
4,9
|
|
6
|
32
|
5,4
|
0,88
|
4,3
|
|
7
|
35
|
6,1
|
1,11
|
4,7
|
|
8
|
36
|
6,2
|
1,13
|
4,85
|
|
9
|
38
|
6,5
|
1,2
|
4,88
|
|
10
|
35
|
5,97
|
1,12
|
4,8
|
|
11
|
34
|
5,85
|
0,93
|
4,68
|
|
12
|
37
|
6,5
|
1,15
|
4,75
|
|
13
|
32
|
5,5
|
1
|
4,4
|
|
14
|
35
|
6,2
|
1,14
|
4,81
|
|
15
|
37
|
6,5
|
1,17
|
5
|
|
16
|
38
|
6,8
|
1,23
|
5,15
|
|
17
|
39
|
6,9
|
1,27
|
5,24
|
|
18
|
40
|
7
|
1,31
|
5,5
|
|
19
|
41
|
7,2
|
1,4
|
5,8
|
|
20
|
37
|
6,6
|
1,16
|
4,95
|
|
21
|
39
|
6,95
|
1,25
|
5,25
|
|
22
|
35
|
6,5
|
1,13
|
4,85
|
|
23
|
36
|
6,8
|
1,14
|
4,98
|
|
24
|
42
|
7,5
|
1,35
|
5,9
|
Перелік питань, на які необхідно відповісти за даною інформацією
включає:
1) ідентифікацію змінних;
2) специфікацію економетричної моделі на основі лінійної
та степеневої функцій;
) оцінку параметрів моделі 1МНК;
) перевірку статистичної значущості моделі та оцінок
її параметрів;
) перевірити наявність мультиколінеарності
пояснювальних змінних (χ2, хі-квадрат);
) перевірку наявності автокореляції залишків (критерій
Дарбіна-Уотсона, коефіцієнт автокореляції);
) за наявності автокореляції застосувати метод
Ейткена;
8) визначення точкового та інтервального прогнозу доходу
фірми на наступний місяць, якщо інвестиції збільшаться на 10%, а фактичний фонд
робочого часу зменшиться на 10% у порівнянні з останнім місяцем другого року;
9) розрахунок показників ефективності використання
виробничих ресурсів (оцінки параметрів моделі, мультиплікатори);
10) висновок щодо ефективності використання виробничих
ресурсів на фірмі.
Розділ2. Процес виконання ділової гри
2.1 Організаційні питання
Групу студентів необхідно поділити на чотири підгрупи, у
кожну з яких буде входити 5-6 студентів.
Перша підгрупа студентів - це співробітники підготовчого
відділу матеріальних ресурсів фірми.
Друга підгрупа входить до технологічного відділу фірми.
Третя підгрупа студентів буде представляти
фінансово-виробничий відділ фірми.
Четверта підгрупа студентів може також представляти
фінансово-виробничий відділ, або входити до фахівців обліку та аудиту фірми
У першому розділі, де зроблена постановка задачі,
розглядаються основні взаємозв’язки названих вище підрозділів підприємницької
діяльності з відділами маркетингу, праці та заробітної плати і інформація, яку
повинні підготовити ці відділи.
2.2 Завдання для виконання ділової гри
Перша підгрупа (підготовчий відділ):
1) складає варіанти розкрою;
2) виконує постановку початкової та двоїстої задач
оптимального розкрою матеріалів;
) розв’язує поставлені задачі за допомогою програмного
пакету Excel «Поиск решения»
) виконує аналіз розв’язку початкової та двоїстої
задачі раціонального розкрою матеріалів, формує потребу в основних матеріальних
ресурсах. Ці ресурси використовуються відділами маркетингу для укладення угод з
постачальниками та фінансово-виробничим відділом для оптимізації виробничої
програми
Друга підгрупа (технологічний відділ):
1) виконує постановку задачі оптимального використання
взаємозамінюваного обладнання;
2) будує двоїсту задачу до побудованої, дає економічне
тлумачення двоїстих оцінок;
) розв’язує поставлені задачі за допомогю програмного
пакету Excel «Поиск решения»
) виконує аналіз розв’язку початкової та двоїстої
задач оптимального використання обладнання; готує інформацію по режимному фонду
роботи обладнання та нормах витрат часу на обробку деталей кожного світильника,
яка передається фінансово-виробничому відділу для використання при оптимізації
виробничої програми фірми.
Третя підгрупа студентів (фінансово-виробничий відділ):
1) виконує математичну постановку задачі оптимізації
виробничої програми фірми;
2) будує двоїсту задачу до побудованої раніше задачі
оптимізації виробничої програми, дає економічне тлумачення двоїстих оцінок;
) розв’язує поставлені задачі за допомогою програмного
пакету Excel «Поиск решения»
) виконує аналіз розв’язку початкової та двоїстої
задач оптимальної виробничої програми, аналізує використання виробничих
ресурсів фірми та їх вплив на фінансові результати.
Четверта підгрупа студентів (фінансово-виробничий відділ):
1) будує економетричну модель (виробничу функцію доходу
фірми) 1МНК, методом Ейткена, використовуючи функцію «ЛИНЕЙН» в Excel;
2) розраховує систему статистичних характеристик
достовірності економетричної моделі та застосовує їх для перевірки статистичної
значущості моделі доходу та оцінок її параметрів;
) перевіряє гіпотези щодо наявності
мультиколінеарності пояснювальних змінних та автокореляції залишків;
) виконує точковий та інтервальний прогноз доходу
фірми на основі побудованої економетричної моделі, враховуючи запропоновані
зміни виробничих ресурсів;
) розраховує основні економічні характеристики
взаємозв’язку, на основі яких можна прогнозувати зміну доходу фірми при
граничній зміні кожного з виробничих ресурсів фірми та зворотні зв’язки
динаміки виробничих ресурсів від зміни доходу.
Розділ 3. Методичні поради до розв’язання задач
ділової гри
.1 Задача оптимального розкрою матеріалів фірми
)
Загальна математична постановка початкової та двоїстої задач.
Відповідно до загальної постановки ділової гри, перша група
студентів має розв’язати задачу оптимального розкрою металевих прутків довжиною
відповідно 6м і 8м на деталі чотирьох типорозмірів - 1,5м; 1,2м; 0,9м і 0,7м,
котрі будуть використані фірмою “Success” для випуску світильників.
Метою розв’язку даної задачі є знаходження оптимального плану
розкрою, тобто потрібно з розроблених варіантів розкрою відшукати таку їх
множину, щоб потреба в деталях всіх типорозмірів була задоволена повністю і
загальні відходи ресурсів були б найменшими
Наведемо загальну модель задачі :
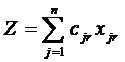 (min)
(1)
(min)
(1)
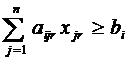 ;
;
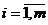 ,
,  ,
,
 (2)≥ 0, цілі числа. (3)
(2)≥ 0, цілі числа. (3)
В моделі використані наступні індекси і позначення:
і - номер типорозміру деталей, 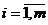 ;-
кількість типорозмірів деталей;- номер варіанту,
;-
кількість типорозмірів деталей;- номер варіанту,  ;-
кількість варіантів розкрою;- номер виду ресурсу,
;-
кількість варіантів розкрою;- номер виду ресурсу,  ;- кількість видів ресурсів;- вихід деталей i-го
типорозміру за j-м варіантом розкрою з одиниці ресурсу r-ого виду;- відходи по
j-ому варіанту з одиниці ресурсу r-ого виду;- шукані змінні, котрі визначають
інтенсивність j-го варіанту розкрою, або кількість ресурсів r-го виду, що
розкраюється за j-м варіантом розкрою.
;- кількість видів ресурсів;- вихід деталей i-го
типорозміру за j-м варіантом розкрою з одиниці ресурсу r-ого виду;- відходи по
j-ому варіанту з одиниці ресурсу r-ого виду;- шукані змінні, котрі визначають
інтенсивність j-го варіанту розкрою, або кількість ресурсів r-го виду, що
розкраюється за j-м варіантом розкрою.
Таким чином, загальна модель задачі складається з трьох частин (1) -
(3)
Економічний зміст моделі:
цільова функція (1) виражає те, що загальні відходи матеріалів в
процесі розкрою мають бути мінімальними;
обмеження (2) відповідають кожному типорозміру деталей і показують, що
вихід деталей і-го типорозміру з усіх варіантів розкрійного плану має бути не
меншим їх потреби;
обмеження (3) виражають умову того, що змінні, котрі в сукупності після
розв’язку задачі складатимуть оптимальний план розкрою, мають бути невід’ємними
і цілочисельними.
До початкової задачі потрібно побудувати двоїсту, котра буде мати
наступний загальний вигляд:
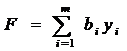 (max),
(4)
(max),
(4)
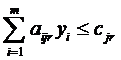 ;
;
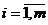 ,
,  ,
,
 (5)≥0. (6)
(5)≥0. (6)
Шуканими змінними двоїстої задачі є yi, котрі визначають
об’єктивно-обумовлені оцінки одиниці і-го типорозміру деталей.
Цільова функція (4) визначає максимальну загальну ефективну оцінку
потреби деталей всіх типорозмірів;
обмеження (5) визначають умови того, що загальна оцінка виходу деталей
для кожного варіанту розкрою одиничної інтенсивності має бути не більше
величини відходу за цим варіантом;
обмеження (6) виражають умову невід’ємності двоїстих оцінок як умова,
котра має місце для симетричних взаємо-спряжених задач.
2)
Формування варіантів розкрою матеріалів.
Отже, перш за все для розв’язку задачі потрібно розробити
варіанти розкрою. В таблиці 5 наведено 20 варіантів, з них - 10 варіантів для
першого виду ресурсу (6м) і 10 для другого виду ресурсу (8м).
Таблиця 5
Варіанти розкрою
|
Типороз-мір деталей
|
Перший вид ресурсу
(r1 = 6м)
|
Другий вид ресурсу
(r2 = 8м)
|
|
p11
|
p21
|
p31
|
p41
|
p51
|
p61
|
p71
|
p81
|
p91
|
p10,1
|
p12
|
p22
|
p32
|
p42
|
p52
|
p62
|
p72
|
p82
|
p92
|
p10,2
|
|
r1=1,5
|
4
|
3
|
2
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
4
|
3
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
r2=1,2
|
0
|
1
|
2
|
3
|
3
|
1
|
1
|
0
|
0
|
1
|
2
|
3
|
0
|
2
|
1
|
1
|
0
|
0
|
0
|
|
r3=0,9
|
0
|
0
|
0
|
0
|
0
|
2
|
3
|
2
|
5
|
1
|
0
|
1
|
1
|
8
|
3
|
5
|
1
|
7
|
6
|
0
|
|
r4=0,7
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
2
|
0
|
7
|
1
|
0
|
5
|
1
|
0
|
2
|
5
|
2
|
3
|
11
|
|
Відходи
|
0
|
0,3
|
0,6
|
0
|
0,2
|
0,6
|
0,6
|
0,1
|
0
|
0,2
|
0,1
|
0,1
|
0
|
0,1
|
0,2
|
0,1
|
0,1
|
0,3
|
0,5
|
0,3
|
Кожен варіант позначений pjr і їм відповідають змінні - xjr,
їх інтенсивності.
Варіанти розкрою будуються шляхом послідовного перебору всіх
можливих сполук типорозмірів деталей на одиниці ресурсу відповідного типу.
Наприклад, побудуємо перший варіант розкрою p11 на довжині
матеріалу довжиною 6м. За цим варіантом деталь типорозміру 1,5м. може укластись
на довжині прутка чотири рази і відход буде рівним нулю.
Дійсно: 4·1,5м+0 = 6м.
За другим варіантом p21 передбачається вихід три типорозміри
деталей 1,5м. і одна деталь типорозміру 1,2м. з відходом рівним 0,3м:
,5м·3+1,2м·1+0,3 = 4,5м +1,2м +0,3м = 6м.
Отже, загальний вихід деталей за цим варіантом склав:
4,5м+1,2м = 5,7м.
Тоді відход дорівнює 6м-5,7м = 0,3м.
Варіанти розкрою, котрі побудовані на другому виді матеріалу
довжиною 8м, мають позначення pj2 і розраховуються таким же чином.
Наприклад, за першим варіантом розкрою p12 на одиниці
матеріалу довжиною 8м укладається чотири деталі типорозміру 1,5м, одна деталь
довжиною1,2м і одна деталь - 0,7м. Тоді загальний вихід всіх типорозмірів
деталей складає:
,5м·4+1,2м·1+0,7м·1= 6м+1,2м+0,7м = 7,9м.
Отже, відход дорівнює : 8м-7,0м = 0,1м.
Перебираючи довільно різні сполучення типорозмірів деталей на
одиниці ресурсу відповідної довжини, будуються й інші варіанти розкрою.
Таким чином, маючи побудовані варіанти розкрою і потребу у
деталях різних типорозмірів, побудуємо початкову і двоїсту числові моделі
задачі оптимального розкрою ресурсів.
3)
Постановка початкової та двоїстої задачі раціонального розкрою фірми,
економічний зміст двоїстих оцінок
Модель початкової задачі:
Цільова
функція=0·x11+0,3·x21+0,6·x31+0·x41+0,2·x51+0,6·x61+0,6·x71+0,1·x81+
+0·x91+0,2·x10,1+0,1·x12+0,1·x22+0·x32+0,1·x42+0,2·x52+0,1·x62+
+0,1·x72+0,3·x82+0,5·x92+0,3·x10,2 ( min ).
Обмеження за потребою в деталях відповідних типорозмірів:
для деталей довжиною 1,5м:
·X11+3·X21+2·X31+0·X41+1·X51+0·X61+1·X71+1·X81+1·X91+0·X10,1+4·X12+3·X22+0·X32+0·X42+0·X42+1·X52+0·X62+1·X72+0·X82+0·X92+0·X10,2≥400;
для деталей довжиною1,2м:
·X11+1·X21+2·X31+5·X41+3·X51+3·X61+1·X71+1·X81+0·X91+0·X10,1+1·X12+2·X22+3·X32+0·X42+2·X52+1·X62+1·X72+0·X82+0·X92+0·X10,2
≥ 600;
для деталей довжиною 0,9м:
·X11+0·X21+0·X31+0·X41+0·X51+2·X61+3·X71+2·X82+5·X91+1·X10,1+0·X12+1·X22+1·X32+8·X42+3·X52+5·X62+1·X72+7·X82+6·X92+0·X10,2
≥ 500;
для деталей довжиною 0,7м:
·X11+0·X21+0·X31+0·X41+1·X51+0·X61+0·X71+2·X81+0·X91+7·X10,1+1·X12+0·X22+5·X32+1·X42+0·X52+2·X62+5·X72+2·X82+3·X92+11·X10,2
≥ 300;
умови невід’ємності змінних : Xjr ≥ 0, цілі числа;  ,
,  .
.
Модель двоїстої задачі
В моделі двоїстої задачі буде стільки змінних, скільки обмежень має
модель початкової задачі. Отже, введемо чотири змінних y1, y2, y3 і y4, котрі
відповідають обмеженням за потребою в деталях відповідних типорозмірів.
Використовуючи правила побудови двоїстих задач, запишемо її модель.
Цільова функція
= 400y1+600y2+500y3+300y4 (max)
Обмеження:
·y1+0·y2+0·y3+0·y4 ≤ 0 4·y1+1·y2+0·y3+1·y4 ≤ 0,1
·y1+1·y2+0·y3+0·y4 ≤0,3 3·y1+2·y2+1·y3+0·y4 ≤ 0,1
·y1+2·y2+0·y3+0·y4 ≤ 0,6 0·y1+3· y 2+1·y3+0·y4 ≤ 0
·y1+5·y2+0·y3+0·y4 ≤ 0 0·y1+0·y2+8·y3+1·y4 ≤ 0,1
·y1+3·y2+0·y3+1·y4 ≤ 0,2 1·y1+2·y2+3·y3+0·y4 ≤ 0,2
·y1+3·y2+2·y3+0·y4 ≤ 0,6 0·y1+1·y2+5·y3+2·y4 ≤ 0,1
·y1+1·y2+3·y3+0·y4 ≤ 0,6 1·y1+1·y2+1·y3+5·y4 ≤ 0,1
·y1+1·y2+2·y3+2·y4 ≤ 0,1 0·y1+0·y2+7·y3+2·y4 ≤ 0,3
·y1+0·y2+5·y3+0·y4 ≤ 0 0·y1+0·y2+6·y3+3·y4 ≤ 0,5
·y1+0·y2+1·y3+7·y4 ≤ 0,2 0·y1+0·y2+0·y3+11·y4 ≤ 0,3
Умови невід’ємності змінних
≥ 0, 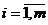
)
Підготовка інформації для розв’язку задач на ПК
Розв’язок моделі початкової задачі здійснюється в Excel
(Сервис, Поиск решения).
Вихідною інформацією є: планова потреба в деталях певних
типорозмірів і множина варіантів розкрою з визначенням виходу тих чи інших
типорозмірів деталей та величини відходів з кожного варіанту одиничної
інтенсивності.
Сукупність побудованих варіантів надається в таблиці (табл.5)
і заноситься в поле Excel.
Пошук розв’язку відбувається в наступній послідовності:
1) виділяємо діапазон комірок для шуканих змінних моделі. Цей
діапазон має складатись з 20-ти комірок, кожна з яких відповідає інтенсивності
того чи іншого варіанту розкрою (краще всього цей діапазон розмістити в таблиці
№1 над варіантами розкрою. Ці комірки до розв’язку задачі можна заповнити
довільними числами, тобто всі змінні xjr (початковий план) є довільними;
2)в окремій комірці знаходимо значення цільової функції з
використанням вбудованої математичної функції СУММПРОИЗВ (перший масив - рядок
таблиці №1, котрий відповідає відходам; другий масив - діапазон комірок
відповідний шуканим змінним, котрі в період підготовки моделі до розв’язку є
довільними). Після реалізації цієї функції у виділеній комірці з’явиться
результат початкової цільової функції задачі. послідовно в окремих комірках за
допомогою вбудованої математичної функції МУМНОЖ аналогічно знаходимо значення
лівих частин обмежень за потребою в деталях 4-х типорозмірів;
) в окремі комірки заносимо числа, які відповідають плановій
потребі в деталях відповідних типорозмірів (це значення вільних членів обмежень
моделі початкової задачі : 400, 600, 500 і 300);
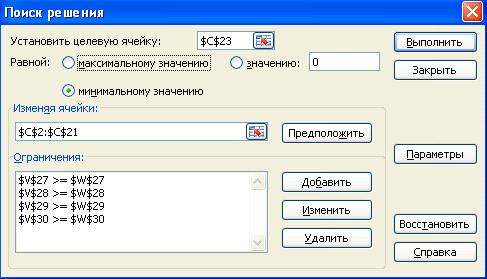
5) вибираємо команду «Сервіс → Поиск решения» і
вводимо інформацію у вікно «Поиска» (рис.1); далі активізуємо
клавішу«Выполнить» і, якщо з’явиться інформація «Pешение найдено» (рис. 2) -
перейти до аналізу оптимального плану;
) у вікні «Результаты» пакету програм «Поиск решений»
активізуємо команди «Результати» і «Устойчивость».
Інформація для розв’язку задачі записується так:
|
Інтенсивн.
|
Початковий
|
Відходи
|
|
способів
|
довільний
|
при
|
|
крою
|
план
|
розкрою
|
|
x11
|
2,0
|
0
|
|
х21
|
2,0
|
0,3
|
|
x31
|
2,0
|
0,6
|
|
x41
|
2,0
|
0
|
|
x51
|
2,0
|
0,2
|
|
x61
|
2,0
|
0,6
|
|
x71
|
2,0
|
0,6
|
|
x81
|
2,0
|
0,1
|
|
x91
|
2,0
|
0
|
|
x10,1
|
2,0
|
0,2
|
|
x12
|
2,0
|
0,1
|
|
x22
|
2,0
|
0,1
|
|
x32
|
2,0
|
0
|
|
x42
|
2,0
|
0,1
|
|
x52
|
2,0
|
0,2
|
|
x62
|
2,0
|
0,1
|
|
x72
|
2,0
|
0,1
|
|
x82
|
2,0
|
0,3
|
|
x92
|
2,0
|
0,5
|
|
x10,2
|
2,0
|
0,3
|
|
Z0=
|
8,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x11
|
х21
|
х31
|
x41
|
x51
|
x61
|
x71
|
x81
|
x91
|
x10,1
|
х12
|
х22
|
|
4
|
3
|
2
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
4
|
3
|
|
0
|
1
|
2
|
5
|
3
|
3
|
1
|
1
|
0
|
0
|
1
|
2
|
|
0
|
0
|
0
|
0
|
0
|
2
|
3
|
2
|
5
|
1
|
0
|
1
|
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
2
|
0
|
7
|
1
|
0
|
|
х32
|
х42
|
х52
|
х62
|
х72
|
х82
|
х92
|
х10,2
|
Ліва частина
обмеження
|
Права частина
обмеження
|
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
44
|
400
|
|
3
|
0
|
2
|
1
|
1
|
0
|
0
|
0
|
52
|
600
|
|
1
|
8
|
3
|
5
|
1
|
7
|
6
|
0
|
90
|
500
|
|
5
|
1
|
0
|
2
|
5
|
2
|
3
|
11
|
80
|
300
|
Наведена інформація заноситься до вікна пакету програми
«Поиск решения»
Зауважимо, що розв’язок даної задачі є цілочисловим , тому її
потрібно розв’язати в «Поиске решений», задавши додаткову умову для шуканих
змінних - «Целые значения», або розв’язати як задачу лінійного програмування,
округлюючи дробові значення xjr до цілих чисел. В цьому випадку в «Отчете по
устойчивости» програми «Поиск решений» буде розрахований оптимальний план
двоїстої задачі (див. «Теневые цены»)
Аналіз оптимального плану розкрою
Аналіз проводиться в такій послідовності:
)визначаємо, яка кількість ресурсів кожного виду має бути
розкроєна по тому чи іншому варіанту; знаходимо загальну кількість кожного виду
ресурсів для виготовлення планової потреби в деталях відповідних типорозмірів;
2)розраховуємо значення цільової функції  ,
тобто визначаємо мінімальні загальні відходи ресурсів за всіма варіантами
розкрою, що увійшли в оптимальний план;
,
тобто визначаємо мінімальні загальні відходи ресурсів за всіма варіантами
розкрою, що увійшли в оптимальний план;
)визначаємо вихід деталей кожного типорозміру з усіх варіантів розкрою
оптимального плану і порівнюємо його з плановою потребою;
)знаходимо оптимальний план моделі двоїстої задачі (Поиск решения -
Отчет по устойчивости; Теневые цены);
)перевіряємо рівність цільових функцій за першою теоремою двоїстості:
 ;
;
)перевіряємо, як виконуються обмеження двоїстої задачі, котрі
відповідають змінним 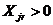 і
і 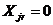 (застосування
другої теореми двоїстості).
(застосування
другої теореми двоїстості).
3.2 Задача оптимального використання обладнання фірми
“Success”
) Загальна математична модель задачі
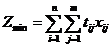
За умов:
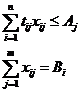
Подамо економічний зміст застосованих символів у задачі:
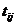 -
витрати часу на обробку одиниці деталі і-го виду на j-ій групі обладнання (
-
витрати часу на обробку одиниці деталі і-го виду на j-ій групі обладнання (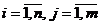 );
);
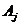 -
режимний фонд часу роботи j-тої групи обладнання;
-
режимний фонд часу роботи j-тої групи обладнання;
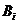 -
необхідна кількість деталей і-го виду, які необхідно обробити;
-
необхідна кількість деталей і-го виду, які необхідно обробити;
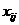 -
невідомі величини, що характеризують кількість деталей і-го виду, які необхідно
обробити на j-ій групі обладнання.
-
невідомі величини, що характеризують кількість деталей і-го виду, які необхідно
обробити на j-ій групі обладнання.
Отже, у цільовій функції задачі мінімізуються сумарні витрати часу на
обробку всіх деталей на всіх групах обладнання.
Перша система обмежень вимагає, щоб витрати часу на обробку всіх
деталей на одному типі обладнання не перевищували режимного фонду часу його
роботи.
Друга система обмежень вимагає, щоб кількість деталей кожного виду, яка
обробляється на різних типах обладнання, відповідала потребі цих деталей для
формування попиту світильників.
Виконаємо математичну постановку задачі фірми “Success”, яка випускає
чотири види світильників, що обробляються на чотирьох типах взаємозамінюваного
обладнання. Для цього запишемо всю необхідну інформацію спочатку у таблиці 6.
діловий гра автокореляція фірма
Таблиця 6
|
Типи обладнання
|
Норми витрат часу
на обробку одиниці продукції, маш.-год.
|
Режимний фонд часу
роботи обладнання, маш.-год
|
|
1
|
2
|
3
|
4
|
10,5
|
x11
|
11,1
|
x12
|
0
|
x13
|
9
|
x14
|
3500
|
|
ІІ
|
0
|
x21
|
5,7
|
x22
|
4,8
|
x23
|
6,0
|
x24
|
3800
|
|
ІІІ
|
3,8
|
x31
|
3,2
|
x32
|
3,0
|
x33
|
0
|
x34
|
3020
|
|
Попит на
світильники, шт.
|
400
|
600
|
500
|
300
|
|
) Математична модель задачі оптимального використання
обладнання
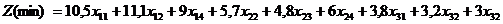
за умов:

Двоїста задача:
Щоб правильно побудувати двоїсту задачу до записаної вище необхідно
спочатку привести знак нерівності обмежень у відповідність до екстремуму
цільової функції задачі. Цільова функція на «мінімум» вимагає тип нерівності «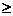 ». Запишемо систему обмежень:
». Запишемо систему обмежень:
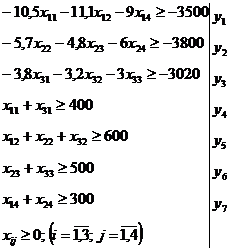

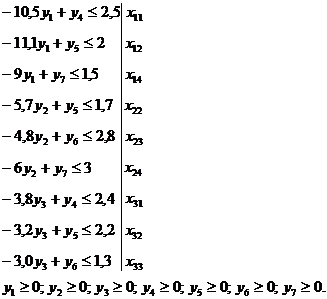
Щоб економічно тлумачити двоїсту задачу, необхідно дати економічний
зміст її змінних, які називаються двоїстими оцінками або тіньовими цінами:-
двоїста оцінка одиниці часу роботи обладнання першого типу;- двоїста оцінка
одиниці часу роботи обладнання другого типу;- двоїста оцінка одиниці часу
роботи обладнання третього типу;- двоїста оцінка одного світильника першого
виду;- двоїста оцінка одного світильника другого виду;- двоїста оцінка одного
світильника третього виду;- двоїста оцінка одного світильника четвертого виду.
У цільовій функції двоїстої задачі максимізується різниця між оцінкою
світильників усіх видів та оцінкою режимного фонду часу роботи усіх типів
обладнання.
Кожне обмеження двоїстої задачі відноситься до певної змінної вихідної
задачі. Навпроти кожного із них записана відповідна змінна. Відсутні лише ті
змінні, які за умовою задачі дорівнюють нулю. У кожному обмеженні двоїстої
задачі порівнюється різниця між оцінкою одного світильника, деталі якого
оброблюються на даній групі обладнання, і оцінкою робочого часу обладнання, що
витрачається на обробку одного світильника, з часом обробки деталей даного
світильника. Якщо ця різниця дорівнює часу обробки (виконується рівняння), то
деталі даного світильника доцільно обробляти на даній групі обладнання, у
протилежному випадку така обробка неефективна (виконується нерівність)
) Підготовка інформації для розв’язку задач на ПК
Обидві задачі (вихідна та двоїста) оптимального використання
взаємозамінюваних типів обладнання розв’язуються одночасно. Для використання
пакету «Поиск решения» умови задачі повинні бути записані так:
а) формування довільного початкового плану задачі:
|
Змінні моделі
|
Кількісне значення
змінних початкового плану
|
Коефіцієнти при
змінних у цільовій функції задачі
|
|
x11
|
10
|
10,5
|
|
x12
|
10
|
11,1
|
|
x13
|
10
|
0
|
|
x14
|
10
|
9
|
|
x21
|
10
|
0
|
|
x22
|
10
|
5,7
|
|
x23
|
10
|
4,8
|
|
x24
|
10
|
6,0
|
|
x31
|
10
|
3,8
|
|
x32
|
10
|
3,2
|
|
x33
|
10
|
3,0
|
|
x34
|
10
|
0
|
|
 572 572
|
|
б) визначення обмежень задачі:
|
x11
|
x12
|
x13
|
x14
|
x21
|
x22
|
x23
|
x24
|
x31
|
x32
|
x33
|
x34
|
Ліва частина
обмеження
|
Права частина
обмеження
|
|
10,5
|
11,1
|
0
|
9,0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
306
|
3800
|
|
0
|
0
|
0
|
0
|
0
|
5,7
|
4,8
|
6
|
0
|
0
|
0
|
0
|
165
|
3500
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
3,8
|
3,2
|
3,0
|
100
|
3020
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
20
|
400
|
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
30
|
600
|
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
20
|
500
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
20
|
300
|
Програма «Поиск решения» знаходиться у зовнішній пам’яті ПК.
Для роботи у оперативній пам’яті необхідно скористатись такими кроками:
Меню «Сервис» → «Надстройки» → «Поиск решения» →
Enter.
Щоб відкрити програму для роботи у оперативній пам’яті
необхідно зробити такі кроки:
Меню «Сервис» → «Поиск решения» → Enter.
З’являється вікно програми «Поиск решения», куди заноситься
інформація, що наведена вище :

3.3 Задача оптимізації виробничої програми фірми
“Success”
) Загальна математична модель задачі

За умов:
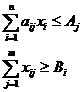 ;
;
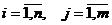
Подамо економічний зміст символів, що використані у записаній моделі
задачі:
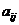 -
норми витрат j-го ресурсу на випуск одиниці продукції i-го виду;
-
норми витрат j-го ресурсу на випуск одиниці продукції i-го виду;
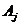 -
обсяг j-го ресурсу на підприємстві;
-
обсяг j-го ресурсу на підприємстві;
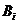 -
попит на продукцію i-го виду;
-
попит на продукцію i-го виду;
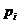 -
середня ринкова ціна одиниці i-го виду продукції;
-
середня ринкова ціна одиниці i-го виду продукції;
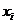 -
кількість продукції i-го виду, невідомі величини.
-
кількість продукції i-го виду, невідомі величини.
Звідси можна дати економічне тлумачення записаної вище задачі.
У цільовій функції максимізується загальний дохід підприємства. Перша
система обмежень вимагає, щоб витрати кожного з виробничих ресурсів на випуск
усіх видів світильників не перевищували наявність ресурсів на підприємстві.
Друга система обмежень вимагає, щоб випуск світильників кожного виду
відповідав їх попиту (у крайньому разі був не нижчий, якщо збільшений попит не
затримує термін їх реалізації).
) Математична модель задачі оптимального випуску продукції фірми
“Success”

за умов:
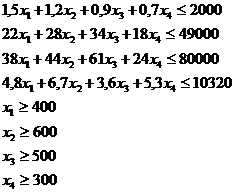
Обмеження по ресурсах включають:
· обмеження матеріальних ресурсів;
· обмеження робочої сили;
· обмеження інвестицій;
· обмеження режимному фонду часу роботи
обладнання.
Зауважимо, що обсяг матеріальних ресурсів у даній задачі розраховано на
основі оптимального плану задачі раціонального розкрою матеріалів. Оптимальний
розв’язок цієї задачі включає 228 прутків довжиною 6м і 87 прутків довжиною 8м.
Це означає, що для виробничої програми світильників необхідно мати матеріалу 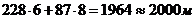 .
.
Оскільки деталі світильників обробляються на трьох взаємозамінюваних
групах обладнання, то для задачі оптимізації виробничої програми використано
загальний фонд часу роботи всіх трьох груп разом:
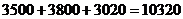 (маш.-год)
(маш.-год)
Нормативи витрат часу на обробку кожної деталі усереднені на основі
даних задачі оптимального використання обладнання.
)Двоїста задача:
Для побудови двоїстої задачі необхідно узгодити знак нерівності
обмежень із екстремумом цільової функції задачі, записаної вище. Оскільки
цільова функція задачі на максимум, то система обмежень повинна мати знак
нерівності «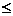 ».
».
Запишемо систему обмежень:
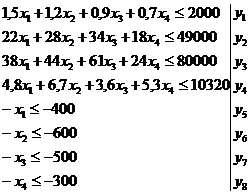
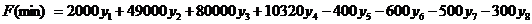
За умов:

Економічний зміст змінних двоїстої задачі:- двоїста оцінка 1м
матеріалів;- двоїста оцінка 1 люд.-год робочого часу;- двоїста оцінка 1 грн.
інвестицій;- двоїста оцінка 1 маш.-год роботи обладнання;- двоїста оцінка
одного світильника першого виду;- двоїста оцінка одного світильника другого
виду;- двоїста оцінка одного світильника третього виду;- двоїста оцінка одного
світильника четвертого виду.
Подамо економічний зміст двоїстої задачі:
У цільовій функції мінімізується різниця між оцінкою використовуваних
виробничих ресурсів та оцінкою продукції, що випускається.
Кожне обмеження двоїстої задачі відноситься до відповідної змінної
початкової задачі виробничої програми. Так, у першому обмеженні двоїстої задачі
порівнюється різниця між оцінкою усіх ресурсів на один світильник першого виду
з ціною цього світильника. Якщо ця різниця перевищує ціну, то світильник
випускати недоцільно. Інші обмеження двоїстої задачі мають те ж саме
тлумачення, але воно відноситься до другого, третього та четвертого
світильників.
) Підготовка інформації для розв’язування задач на ПК
Для розв’язання задачі в Excel, пакет «Поиск решения», умови задачі
повинні бути записані так:
а) формування довільного початкового плану задачі:
|
Змінні моделі
|
Кількісне значення
змінних початкового плану
|
Коефіцієнти при
змінних цільової функції задачі
|
|
x1
|
20
|
200
|
|
x2
|
20
|
250
|
|
x3
|
20
|
300
|
|
x4
|
20
|
100
|
|
Z0=
|
1700
|
б) визначення обмежень задачі
|
x1
|
x2
|
x3
|
x4
|
Ліва частина
обмеження
|
Права частина
обмеження
|
|
1,5
|
1,2
|
0,9
|
0,7
|
86
|
2000
|
|
22
|
28
|
34
|
18
|
2040
|
49000
|
|
3,8
|
44
|
61
|
24
|
3340
|
80000
|
|
4,8
|
6,7
|
3,6
|
5,3
|
408
|
10320
|
|
1
|
0
|
0
|
0
|
20
|
400
|
|
0
|
1
|
0
|
0
|
20
|
600
|
|
0
|
0
|
1
|
0
|
20
|
500
|
|
0
|
0
|
0
|
1
|
20
|
300
|
Програма «Поиск решения» знаходиться у зовнішній пам’яті ПК.
Для роботи у оперативній пам’яті необхідно скористатись такими кроками:
Меню «Сервис» → «Надстройки» → «Поиск решения» →
Enter.
Щоб відкрити програму для роботи у оперативній пам’яті
необхідно зробити такі кроки:
Меню «Сервис» → «Поиск решения» → Enter.
З’являється вікно програми «Поиск решения», куди заноситься
інформація, що наведена вище:

Розділ 4. Виробнича функція фірми «Success»
Рівень використання виробничих ресурсів щомісячно у динаміці
за два роки аналізується на основі економетричного моделювання. Для цього необхідно
побудувати виробничу функцію фірми «Success», яка буде характеризувати
залежність між доходами фірми та основними виробничими ресурсами, що
використовуються на фірмі. Функцію залежності (економетричну модель доходу)
необхідно побудувати на основі інформації, що наведена у таблиці 7.
Таблиця 7
|
Період часу, t
|
Доходи (тис.грн.),
V
|
Інвестиції
(тис.грн.), I
|
Фонд робочого часу
обладнання (тис.маш.-год.), K
|
Фактичний фонд
робочого часу (тис. люд.-год.), L
|
|
1
|
30
|
5
|
0,8
|
4,2
|
|
2
|
32
|
5,5
|
0,9
|
4,5
|
|
3
|
35
|
6
|
1,1
|
4,8
|
|
4
|
5,8
|
0,92
|
4,64
|
|
5
|
33
|
5,6
|
0,95
|
4,9
|
|
6
|
32
|
5,4
|
0,88
|
4,3
|
|
7
|
35
|
6,1
|
1,11
|
4,7
|
|
8
|
36
|
6,2
|
1,13
|
4,85
|
|
9
|
38
|
6,5
|
1,2
|
4,88
|
|
10
|
35
|
5,97
|
1,12
|
4,8
|
|
11
|
34
|
5,85
|
0,93
|
4,68
|
|
12
|
37
|
6,5
|
1,15
|
4,75
|
|
13
|
32
|
5,5
|
1
|
4,4
|
|
14
|
35
|
6,2
|
1,14
|
4,81
|
|
15
|
37
|
6,5
|
1,17
|
5
|
|
16
|
38
|
6,8
|
1,23
|
5,15
|
|
17
|
39
|
6,9
|
1,27
|
5,24
|
|
18
|
40
|
7
|
1,31
|
5,5
|
|
19
|
41
|
7,2
|
1,4
|
5,8
|
|
20
|
37
|
6,6
|
1,16
|
4,95
|
|
21
|
39
|
6,95
|
1,25
|
5,25
|
|
22
|
35
|
6,5
|
1,13
|
4,85
|
|
23
|
36
|
6,8
|
1,14
|
4,98
|
|
24
|
42
|
7,5
|
1,35
|
5,9
|
Позначимо:
– часовий період - t ;
– доходи фірми - V;
– інвестиції у виробництво - І;
– фонд робочого часу обладнання - K;
– фактичний фонд робочого часу - L,
де V визначає залежну змінну економетричної моделі;, L, K -
пояснюючі фактори або регресори моделі.
Для визначення специфікації моделі висунемо наступні гіпотези
про вид зв’язку між залежною змінною Vt та пояснювальними змінними It, Lt, Kt:
1) лінійна залежність: 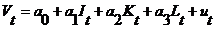 ;
;
) степенева залежність: 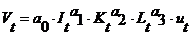 .
.
Візьмемо зліва та справа логарифми даних степеневої функції та
перейдемо до лінійно-логарифмічного виду:
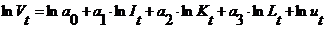 .
.
Результати логарифмування наведено в таблиці 8:
Таблиця8
|
lnV
|
lnI
|
lnK
|
lnL
|
|
3,4011974
|
1,609438
|
-0,22314
|
1,435085
|
|
3,4657359
|
1,704748
|
-0,10536
|
1,504077
|
|
3,5553481
|
1,791759
|
0,09531
|
1,568616
|
|
3,5263605
|
1,757858
|
-0,08338
|
1,534714
|
|
3,4965076
|
1,722767
|
-0,05129
|
1,589235
|
|
3,4657359
|
1,686399
|
-0,12783
|
1,458615
|
|
3,5553481
|
1,808289
|
0,10436
|
1,547563
|
|
3,5835189
|
1,824549
|
0,122218
|
1,578979
|
|
3,6375862
|
1,871802
|
0,182322
|
1,585145
|
|
3,5553481
|
1,786747
|
0,113329
|
1,568616
|
|
3,5263605
|
1,766442
|
-0,07257
|
1,543298
|
|
3,6109179
|
1,871802
|
0,139762
|
1,558145
|
|
3,4657359
|
1,704748
|
0
|
1,481605
|
|
3,5553481
|
1,824549
|
0,131028
|
1,570697
|
|
3,6109179
|
1,871802
|
0,157004
|
1,609438
|
|
3,6375862
|
1,916923
|
0,207014
|
1,638997
|
|
3,6635616
|
1,931521
|
0,239017
|
1,656321
|
|
3,6888795
|
1,94591
|
0,270027
|
1,704748
|
|
3,7135721
|
1,974081
|
0,336472
|
1,757858
|
|
3,6109179
|
1,88707
|
0,14842
|
1,599388
|
|
3,6635616
|
1,938742
|
0,223144
|
1,658228
|
|
3,5553481
|
1,871802
|
0,122218
|
1,578979
|
|
3,5835189
|
1,916923
|
0,131028
|
1,60543
|
|
3,7376696
|
2,014903
|
0,300105
|
1,774952
|
.1 Побудова виробничої функції 1МНК
Приймемо гіпотези про можливість застосування методу
найменших квадратів до оцінки параметрів виробничої функції. За допомогою
стандартної функції Ecxel «ЛИНЕЙН» у категорії «Статистичні» отримаємо
кількісні характеристики взаємозв’язку. Запишемо лінійну модель виробничої
функції на основі абсолютних значень показників (таблиця 4):
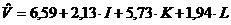 (1)
(1)
Степенева виробнича функція має вигляд:
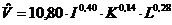 (2)
(2)
Необхідно:
а) оцінити достовірність отриманих параметрів моделей (1) і (2) та
статистичну значущість в цілому;
б) дати економічне тлумачення оцінок параметрів моделі в обох
виробничих функціях.
Зауважимо, що для виконання поставлених вимог необхідно ще раз
застосувати функцію «ЛИНЕЙН».
Визначимо розрахункові значення доходу фірми на основі отриманих
функцій та знайдемо залишки моделі за формулами:
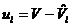 ;
;
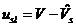 ,
,
де 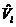 - розрахункові значення доходу, що отримані на основі
лінійної виробничої функції;
- розрахункові значення доходу, що отримані на основі
лінійної виробничої функції;
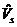 -
розрахункові значення доходу фірми, що отримані на основі степеневої функції;
-
розрахункові значення доходу фірми, що отримані на основі степеневої функції;
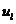 -
залишки за лінійною функцією;
-
залишки за лінійною функцією;
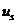 -
залишки за степеневою функцією. Представимо ці характеристики у таблиці 9:
-
залишки за степеневою функцією. Представимо ці характеристики у таблиці 9:
Таблиця 9
|
V
|
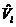 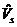 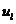 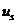 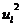 
|
|
|
|
|
|
|
30
|
29,99403
|
29,92971
|
0,005965
|
0,07029
|
3,558E-05
|
0,004941
|
|
32
|
32,21649
|
32,24621
|
-0,21649
|
-0,24621
|
0,0468659
|
0,060618
|
|
35
|
35,01165
|
34,99522
|
-0,01165
|
0,004777
|
0,0001358
|
2,28E-05
|
|
34
|
33,24327
|
33,33124
|
0,756726
|
0,668761
|
0,5726342
|
0,447241
|
|
33
|
33,49234
|
33,52914
|
-0,49234
|
-0,52914
|
0,2423993
|
0,279991
|
|
32
|
31,50042
|
31,49993
|
0,499584
|
0,500075
|
0,2495842
|
0,250075
|
|
35
|
35,0885
|
35,06435
|
-0,0885
|
-0,06435
|
0,0078316
|
0,004141
|
|
36
|
35,70757
|
35,69942
|
0,292427
|
0,300585
|
0,0855136
|
0,090351
|
|
38
|
36,80734
|
36,76022
|
1,192663
|
1,239775
|
1,4224447
|
1,537043
|
|
35
|
35,06213
|
35,01503
|
-0,06213
|
-0,01503
|
0,0038603
|
0,000226
|
|
34
|
33,48492
|
33,57923
|
0,515082
|
0,420769
|
0,2653099
|
0,177047
|
|
37
|
36,2688
|
36,25959
|
0,731203
|
0,740412
|
0,5346577
|
0,548209
|
|
32
|
32,59522
|
32,52835
|
-0,59522
|
-0,52835
|
0,3542853
|
0,279155
|
|
35
|
35,68725
|
35,66087
|
-0,68725
|
-0,66087
|
0,4723134
|
0,436743
|
|
37
|
36,8683
|
36,87969
|
0,131696
|
0,120313
|
0,0173439
|
0,014475
|
|
38
|
38,14358
|
38,13965
|
-0,14358
|
-0,13965
|
0,0206148
|
0,019501
|
|
39
|
38,76081
|
38,72859
|
0,271414
|
0,0572129
|
0,073665
|
|
40
|
39,70781
|
39,66476
|
0,292188
|
0,335243
|
0,0853738
|
0,112388
|
|
41
|
41,23232
|
41,11048
|
-0,23232
|
-0,11048
|
0,0539748
|
0,012207
|
|
37
|
36,92759
|
36,95557
|
0,072405
|
0,044429
|
0,0052425
|
0,001974
|
|
39
|
38,77244
|
38,77373
|
0,22756
|
0,226273
|
0,0517835
|
0,0512
|
|
35
|
36,34824
|
36,3823
|
-1,34824
|
-1,3823
|
1,8177473
|
1,910751
|
|
36
|
37,29836
|
37,3715
|
-1,29836
|
-1,3715
|
1,6857307
|
1,881004
|
|
42
|
41,78062
|
41,77356
|
0,219384
|
0,226437
|
0,0481292
|
0,051274
|
|
Cума
|
|
|
|
|
8,1010248
|
8,244243
|
Як свідчать дані таблиці 9, розрахункові значення доходу фірми за
побудованими функціями дуже наближені до фактичного щомісячного рівня доходу
фірми, і сума квадратів залишків за обома моделями відрізняється несуттєво (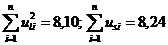 ). Це означає, що обидві функції можуть бути
використані для моделювання залежності доходу від виробничих ресурсів. Зроблені
висновки підтвержують графіки, що представлені на рис. 2.
). Це означає, що обидві функції можуть бути
використані для моделювання залежності доходу від виробничих ресурсів. Зроблені
висновки підтвержують графіки, що представлені на рис. 2.
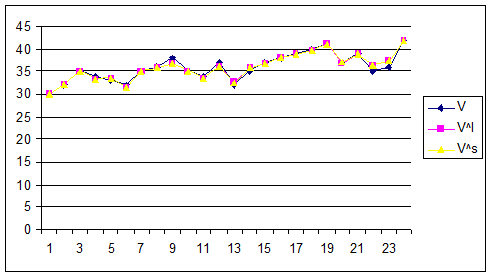
Рис. 2. Криві зміни фактичного доходу та доходу за функціями
Розподіл залишків за лінійною та степеневою функціями представлені на
рис. 3 та 4.
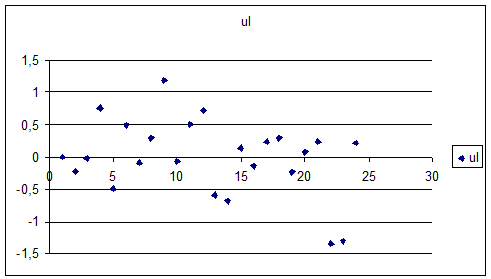
Рис. 3. Залишки за лінійною функцією

Рис. 4. Залишки за степеневою функцією
Як видно з цих рисунків, розподіли залишків практично не відрізняються
між собою.
.2 Перевірка наявності мультиколінеарності
пояснювальних змінних
Якщо пояснювальні змінні мультиколінеарні, то метод найменших квадратів
може зумовити зміщення оцінок параметрів виробничих функцій. Тому виникає
необхідність перевірити рівень тісноти зв’язку між векторами  . Для цього потрібно зробити такі кроки:
. Для цього потрібно зробити такі кроки:
1) побудувати матрицю коефіцієнтів парної кореляції
пояснювальних змінних;
2) визначити детермінант матриці коефіцієнтів парної
кореляції;
3) розрахувати критерій  (хі-квадрат),
на основі якого оцінити наявність мультиколінеарності.
(хі-квадрат),
на основі якого оцінити наявність мультиколінеарності.
Вказівка:
· для побудови матриці коефіцієнтів
парної кореляції потрібно скористатись функцією Excel «Корреляция», зробивши
такі кроки: Сервис → Надстройки → Пакет анализа → Корреляция;
· Детермінант
матриці визначається за допомогою функції «МОПРЕД», категорія «Математичні»,
вставка функції ( )
)
· Критерій
 розраховується за формулою:
розраховується за формулою: 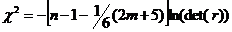 , де m - кількість пояснювальних змінних; n -
кількість спостережень; r - матриця коефіцієнтів парної кореляції.
, де m - кількість пояснювальних змінних; n -
кількість спостережень; r - матриця коефіцієнтів парної кореляції.
За наявності мультиколінеарності використати найпростіші
методи звільнення від неї:
) перетворити пояснювальні змінні, застосувавши перші
та другі різниці (від кожного наступного значення відповідної змінної
віднімається попереднє). До перетворених змінних застосувати пропозиції по
визначенню наявності мультиколінеарності, що наведені вище;
) використати рідж-регресію.
.3
Перевірка наявності автокореляції залишків
Оскільки виробничі функції були побудовані на основі часових
рядів, то можна очікувати автокореляцію пояснювальних змінних, яка зумовлює
автокореляцію залишків. Якщо існує автокореляція залишків, то оцінки параметрів
потрібно оцінити методом Ейткена
Для визначення автокореляції залишків побудуємо критерій
Дарбіна-Уотсона:
 ,
,
та циклічний коефіцієнт автокореляції:
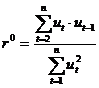 .
.
Використаємо дані таблиць 9 і 10 та розрахуємо зазначені вище
характеристики взаємозв’язку:
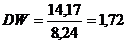 ;
; 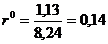 .
.
Таблиця 10
|
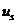 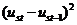 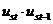
|
|
|
|
0,07029
|
|
|
|
-0,24621
|
0,10017
|
-0,01731
|
|
0,004777
|
0,062993
|
-0,00118
|
|
0,668761
|
0,440874
|
0,003195
|
|
-0,52914
|
1,43497
|
-0,35387
|
|
0,500075
|
1,059286
|
-0,26461
|
|
-0,06435
|
0,318574
|
-0,03218
|
|
0,300585
|
0,133177
|
-0,01934
|
|
1,239775
|
0,882079
|
0,372658
|
|
-0,01503
|
1,574526
|
-0,01863
|
|
0,420769
|
0,189918
|
-0,00632
|
|
0,740412
|
0,102171
|
0,311543
|
|
-0,52835
|
1,60976
|
-0,3912
|
|
-0,66087
|
0,01756
|
0,349169
|
|
0,120313
|
0,61024
|
-0,07951
|
|
-0,13965
|
0,067578
|
-0,0168
|
|
0,271414
|
0,16897
|
-0,0379
|
|
0,335243
|
0,004074
|
0,09099
|
|
-0,11048
|
0,198674
|
-0,03704
|
|
0,044429
|
0,023998
|
-0,00491
|
|
0,226273
|
0,033067
|
0,010053
|
|
-1,3823
|
2,587505
|
-0,31278
|
|
-1,3715
|
0,000117
|
1,895819
|
|
0,226437
|
2,553393
|
-0,31056
|
|
Сума
|
14,17367
|
1,129298
|
Необхідно: порівняти отримані критерії з табличним значенням за
вибраного рівня значущості 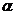 ,
та зробити висновки щодо наявності автокореляції.
,
та зробити висновки щодо наявності автокореляції.
.4
Побудова виробничої функції методом Ейткена
) побудувати матрицю перетворення вихідної інформації, яка
має вигляд:

Це квадратна матриця розміром 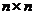 (
( ), де
), де 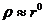
) помножити дану матрицю (функція «МУМНОЖ») на вихідну інформацію, яка
включає такі вектори: Y, X0, X1, X2, X3, де X0 - вектор n одиниць.
) записати натуральні логарифми скоригованої вихідної інформації, яка
включає вектори: 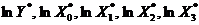 ;
;
) побудувати лінійну та степеневу функції на основі отриманих масивів
скоригованої вихідної інформації за допомогою стандартної функції «ЛИНЕЙН»
Увага: у віконці «Константа» необхідно поставити «0»
) Порівняти отримані функції із функціями, що розраховані раніше 1МНК,
зробити висновки.
4.5 Прогноз доходу фірми “Success” та аналіз
використання ресурсів
) дати точковий прогноз доходу фірми “Success” на основі
побудованих виробничих функцій, якщо вектор очікуваних пояснювальних змінних на
січень місяць наступного року буде задано так:
 **
**
Прогноз доходу визначається так:
· За
лінійною функцією: 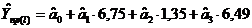
· За
степеневою функцією: 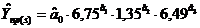
2) зробити висновки щодо рівня використання виробничих
ресурсів фірми, використавши оцінки параметрів побудованих виробничих функцій.
Розділ 5. Аналіз використання виробничих ресурсів
Проаналізувати рівень дефіцитності виробничих ресурсів,
виходячи з перевірки системи обмежень задачі оптимальної виробничої програми.
Визначити граничні межі можливих змін обсягів дефіцитних
виробничих ресурсів, які не будуть змінювати двоїсті оцінки ресурсів.
Визначити граничні межі можливих змін рівня цін (або
прибутку) на продукцію за умови, що двоїсті оцінки не зміняться.
Визначити, за яких виробничих умов доцільно випускати
п’ятий вид світильників, ціна яких буде складати 400грн.
Порівняти двоїсті оцінки оптимального плану обсягу
виробництва та оцінки параметрів економетричної моделі, зробити висновки.
Наведемо приклад розв’язку задачі раціонального розкрою
матеріалів на основі пакету «Поиск решения». Результати розв’язку наведені у
таких таблицях:
Таблиця 11
|
Целевая ячейка
(Минимум)
|
|
|
|
Ячейка
|
Имя
|
Исходное значение
|
Результат
|
|
|
$C$23
|
Z0=
|
8,8
|
0
|
|
|
Изменяемые ячейки
|
|
|
|
Ячейка
|
Имя
|
Исходное значение
|
Результат
|
|
|
$C$2
|
x11
|
2
|
78
|
|
|
$C$3
|
X21
|
2
|
0
|
|
|
$C$4
|
x31
|
2
|
0
|
|
|
$C$5
|
x41
|
2
|
84
|
|
|
$C$6
|
x51
|
2
|
0
|
|
|
$C$7
|
x61
|
2
|
0
|
|
|
$C$8
|
x71
|
2
|
0
|
|
|
$C$9
|
x81
|
2
|
0
|
|
|
$C$10
|
x91
|
2
|
88
|
|
|
$C$11
|
x10,1
|
2
|
0
|
|
|
$C$12
|
x12
|
2
|
0
|
|
|
$C$13
|
x22
|
2
|
0
|
|
|
$C$14
|
x32
|
2
|
60
|
|
|
$C$15
|
x42
|
2
|
0
|
|
|
$C$16
|
x52
|
2
|
0
|
|
|
$C$17
|
x62
|
2
|
0
|
|
|
$C$18
|
x72
|
2
|
0
|
|
|
$C$19
|
x82
|
2
|
0
|
|
|
$C$20
|
x92
|
2
|
0
|
|
|
$C$21
|
x10,2
|
2
|
0
|
|
|
Ограничения
|
|
|
Ячейка
|
Имя
|
Значение
|
Формула
|
Статус
|
Разница
|
|
$V$27
|
|
400
|
$V$27>=$W$27
|
связанное
|
0
|
|
$V$28
|
|
600
|
$V$28>=$W$28
|
связанное
|
0
|
|
$V$29
|
|
500
|
$V$29>=$W$29
|
связанное
|
0
|
|
$V$30
|
|
300
|
$V$30>=$W$30
|
связанное
|
0
|
З даної таблиці видно, що початкові відходи матеріалів
складали 8,8м, а в оптимальному плані вони склали 0м, тобто відсутні. При цьому
оптимальна інтенсивність способів розкрою визначається:
х11=78;
х41=84;
х91=88;
х32=60.
Цей розв’язок свідчить про те, що першого матеріалу фірма
повинна закупити (78+84+88), а другого лише 60. При цьому кожне із обмежень
задачі по отриманню певних розмірів матеріалу для випуску світильників
виконується як строге рівняння, тобто відповідає попиту світильників на ринку.
Таблиця 12
|
Изменяемые ячейки
|
|
|
|
|
|
|
Результ.
|
Нормир.
|
Целевой
|
Допустимое
|
Допустимое
|
|
Ячейка
|
Имя
|
значение
|
стоимость
|
Коэффициент
|
Увеличение
|
Уменьшение
|
|
$C$2
|
x11
|
78
|
0
|
0
|
0
|
0
|
|
$C$3
|
X21
|
0
|
0,3
|
0,3
|
1E+30
|
0,3
|
|
$C$4
|
x31
|
0
|
0,6
|
0,6
|
1E+30
|
0,6
|
|
$C$5
|
x41
|
84
|
0
|
0
|
0
|
0
|
|
$C$6
|
x51
|
0,2
|
0,2
|
1E+30
|
0,2
|
|
$C$7
|
x61
|
0
|
0,6
|
0,6
|
1E+30
|
0,6
|
|
$C$8
|
x71
|
0
|
0,6
|
0,6
|
1E+30
|
0,6
|
|
$C$9
|
x81
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$10
|
x91
|
88
|
0
|
0
|
0
|
0
|
|
$C$11
|
x101
|
0
|
0,2
|
0,2
|
1E+30
|
0,2
|
|
$C$12
|
x12
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$13
|
x22
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$14
|
x32
|
60
|
0
|
0
|
0,1
|
0
|
|
$C$15
|
x42
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$16
|
x52
|
0
|
0,2
|
0,2
|
1E+30
|
0,2
|
|
$C$17
|
x62
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$18
|
x72
|
0
|
0,1
|
0,1
|
1E+30
|
0,1
|
|
$C$19
|
x82
|
0
|
0,3
|
0,3
|
1E+30
|
0,3
|
|
$C$20
|
x92
|
0
|
0,5
|
0,5
|
1E+30
|
0,5
|
|
$C$21
|
x102
|
0
|
0,3
|
0,3
|
1E+30
|
0,3
|
У таблиці 12 наведений оптимальний розв’язок задачі
раціонального розкрою матеріалів та допустимі межі зміни інтенсивностей
способів розкрою. Ці результати свідчать про стійкість оптимального плану.
Таблиця 13
|
Ограничения
|
|
|
|
|
|
|
|
|
Результ.
|
Теневая
|
Ограничение
|
Допустимое
|
Допустимое
|
|
Ячейка
|
Имя
|
значение
|
Цена
|
Правая часть
|
Увеличение
|
Уменьшение
|
|
$V$27
|
|
400
|
0
|
400
|
1E+30
|
312
|
|
$V$28
|
|
600
|
0
|
600
|
1E+30
|
420
|
|
$V$29
|
|
500
|
0
|
500
|
1560
|
440
|
|
$V$30
|
|
300
|
0
|
300
|
700
|
300
|
У таблиці 13 наведені тіньові ціни (двоїсті оцінки) різних типорозмірів
світильників фірми. Оскільки обмеження по типорозмірах матеріалів виконуються
як строгі рівняння, то двоїсті оцінки є нульовими. Допустиме збільшення та
зменшення відноситься до типорозмірів світильників і свідчить про можливу зміну
їх обсягу за виробничої необхідності.
Таблиця 14
|
Изменяемое
|
|
|
Нижний
|
Целевой
|
|
Верхний
|
Целевой
|
|
Ячейка
|
Имя
|
Значение
|
|
предел
|
результат
|
|
предел
|
результат
|
|
$C$2
|
x11
|
78
|
|
78
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$3
|
X21
|
0
|
|
0
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$4
|
x31
|
0
|
|
0
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$5
|
x41
|
84
|
|
84
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$6
|
x51
|
0
|
|
1,19257E-09
|
2,38515E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$7
|
x61
|
0
|
|
1,97363E-09
|
1,18418E-09
|
|
#Н/Д
|
#Н/Д
|
|
$C$8
|
x71
|
0
|
|
1,31575E-09
|
7,89453E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$9
|
x81
|
0
|
|
1,97363E-09
|
1,97363E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$10
|
x91
|
88
|
|
88
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$11
|
x101
|
0
|
|
3,94726E-09
|
7,89453E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$12
|
x12
|
0
|
|
1,19257E-09
|
1,19257E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$13
|
x22
|
0
|
|
3,94726E-09
|
3,94726E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$14
|
x32
|
60
|
|
60
|
0
|
|
#Н/Д
|
#Н/Д
|
|
$C$15
|
x42
|
0
|
|
1,19257E-09
|
1,19257E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$16
|
x52
|
0
|
|
1,31575E-09
|
2,63151E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$17
|
x62
|
0
|
|
7,89453E-10
|
7,89453E-11
|
|
#Н/Д
|
#Н/Д
|
|
$C$18
|
x72
|
0
|
|
3,94726E-09
|
3,94726E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$19
|
x82
|
0
|
|
5,96287E-10
|
1,78886E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$20
|
x92
|
0
|
|
6,57877E-10
|
3,28939E-10
|
|
#Н/Д
|
#Н/Д
|
|
$C$21
|
x102
|
0
|
|
1,08416E-10
|
3,25248E-11
|
|
#Н/Д
|
#Н/Д
|
Загалом, у наведених таблицях подано оптимальний розв’язок
задачі раціонального розкрою матеріалів та характеристики аналізу оптимального
плану. Такі ж таблиці отримуються при знаходженні оптимального плану по
використанню обладнання на фірмі та оптимізації виробничої програми.
Література
1. Анурейчиков
А.В., Анурейчикова О.Н. Аналіз, синтез, планирование решений в экономике //
Учебник. - М.: 2000.
2. Вітлінський
В.В. Моделювання економіки // Навчальний посібник. - К.: КНЕУ, 2003. - 408с.
. Вітлінський
В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування //
Навчально-методичний посібник для самостійного вивчення дисципліни. - К.: КНЕУ,
2001. - 248с.
. Наконечний
С.І., Терещенко Т.О., Романюк Т.П. Економетрія // Підручник. - К.: КНЕУ, 2006.
-520с.