Поиск экстремума в нелинейных моделях

Поиск экстремума в нелинейных моделях

Контрольная работа

Поиск экстремума в нелинейных моделях

1. Математическое программирование (поиск экстремума в нелинейных моделях)

Определение 0. Математическое программирование (МП) - раздел математики (теории оптимизации), в котором изучаются методы отыскания экстремума (max или min) функций, зависящих от нескольких переменных, на некотором множестве.

Формальная постановка задачи МП

а) Управляющие переменные - совокупность векторов с n компонентами (координатами): 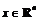, то есть 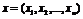. (Внимание! При вычислениях векторы считаются векторами-столбцами, запись в строку используется для экономии бумаги.)

б) В качестве целевой функции выступает какая-либо функция многих переменных .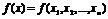

в) Допустимое множество X расположено в 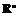, любой элемент 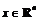называется допустимым вектором, или допустимой точкой, или допустимым планом, или допустимым управлением.

Краткая (символическая) запись задачи МП:

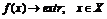.(1.1)

2. Необходимые определения и пояснения в задаче МП

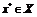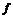Определение 1. Точка  называется точкой глобального минимума (максимума) функции  на 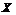, если

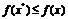для всех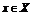 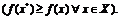 (1.2)

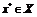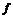Определение 2. Точка  называется точкой локального минимума (максимума) функции  на 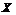, если найдется такая константа 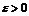 такая, что  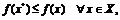удовлетворяющих условию

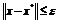
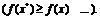   (1.3)

Определение 3. Точка 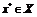 называется точкой строгого минимума (максимума) в локальном или глобальном смысле, если соответствующие неравенства в (1.2), (1.3) выполняются как строгие (при ).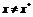

В дальнейшем будем использовать следующие обозначения, обычно применяемые для записи того факта, что 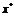 - точка минимум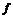а  на :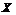

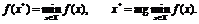
Если пишут 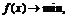то имеют ввиду поиск безусловного минимума функции  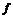(для максимума обозначения аналогичные).

Будем считать синонимами выражения: точка экстремума, решение, оптимальное решение, оптимальный план, оптимальное управление, .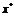

Замечание. Задача на min легко превращается в задачу на max (и наоборот):

Технология решения задачи МП:

·   постановка задачи;

·   приведение её к удобному для решения виду;

·   поиск подозрительных на решение (критических) точек (векторов);

·   проверка условий оптимальности (т.е. применение соответствующих теорем).

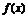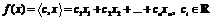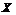Замечание. Случай, когда целевая функция  линейна (т.е. ) и  сформировано линейными условиями, будем рассматривать особо. Поэтому до начала главы "Линейное программирование" будем рассчитывать на нелинейность целевой функции.

Задание. Законспектировать в тетради с лекциями три примера задачи МП, включая транспортную задачу (см. рекомендованные учебники и учебные пособия).

3. Поиск безусловного экстремума

Рассмотрим более простую по отношению к (1.1) задачу (безусловного экстремума)

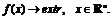(1.4)

Обозначим градиент целевой функции символом "набла":

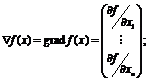
а матрицу вторых производных - символом "набла в квадрате":

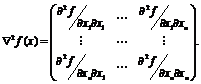
Для поиска решения задачи (1.4) будем пользоваться следующими теоремами (первая из них применяется для обнаружения подозрительных на экстремум точек, а вторая - для определения характера экстремальности найденных критических точек).

Теорема 1 (необходимое условие первого порядка экстремальности 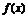). Пусть функция n переменных  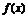дифференцируема в точке  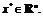Тогда, если  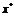- локальное решение задачи (1.4), то

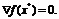(1.5)

Запись 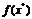 означает, что целевая функция вычисляется в точке 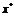. Решения системы уравнений (1.5) называются критическими (стационарными, подозрительными на экстремум) точками.

Теорема 2 (условия второго порядка экстремальности 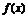). Для того, чтобы дважды дифференцируемая функция n переменных 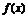 имела в стационарной точке  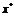безусловный локальный min (max), необходимо, чтобы матрица ее вторых производных 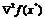 была неотрицательно (неположительно) определенной, и достаточно, чтобы она была положительно (отрицательно) определенной.

Замечание. Теоремы 1 и 2 справедливы и для задачи условной оптимизации (1.1), если решение 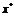 лежит внутри множества .

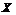При исследовании на знакоопределенность матриц вторых производных целесообразно применять известный из алгебры критерий Сильвестра.

Определение 4. Главным угловым минором k-го порядка некоторой квадратной матрицы называется определитель матрицы, составленной из первых k строк и первых k столбцов исходной матрицы.

Критерий Сильвестра. Квадратная матрица является:

а) положительно определенной тогда и только тогда, когда все ее главные угловые миноры положительны;

б) отрицательно определенной, когда все ее главные угловые миноры нечетного порядка отрицательны, а четного - положительны;

в) неотрицательно определенной тогда и только тогда, когда все миноры, полученные из исходной матрицы вычеркиванием строк и столбцов с одинаковыми номерами, неотрицательны;

г) неположительно определенной, когда все миноры, полученные из исходной матрицы вычеркиванием строк и столбцов с одинаковыми номерами, нечетного порядка - неположительны, а четного - неотрицательны.

Таким образом, будем использовать следующую схему поиска безусловных экстремумов функций многих переменных:

·   составляется и решается система алгебраических уравнений (1.5) - ищутся критические точки;

·   в критических точках исследуется на знакоопределенность матрица вторых производных: те точки, в которых матрица положительно определена, являются точками строгого локального минимума; стационарные точки, в которых матрица отрицательно определена, - точками строгого локального максимума;

·   анализируются критические точки, в которых матрица вторых производных не является строго знакоопределенной. Если матрица неотрицательно (неположительно) определена, то соответствующая точка подозрительна на локальный минимум (максимум). Иногда, непосредственно изучая поведение функции в окрестности подозрительной точки, удается выяснить, является или нет она экстремальной. Наконец, если в критической точке матрица вторых производных вообще не является знакоопределенной, то такая точка заведомо не может быть экстремальной.

Заметим, что исследование найденных точек локального экстремума на глобальный экстремум весьма затруднительно. Мы будем ограничиваться проверкой частного случая, когда матрица вторых производных неотрицательно (неположительно) определена на всем пространстве 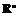(в простейшем случае компоненты матрицы просто не зависят от x), - тогда все критические точки функции являются точками глобального минимума (максимума). В остальных случаях будем делать вывод: глобальный характер экстремума установить не удалось, требуется дополнительное исследование.

Пример 1. Исследовать на экстремум

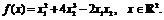
Составляем систему уравнений, приравняв градиент целевой функции нулю:

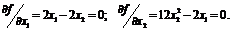
Решив данную систему, найдем критические точки: 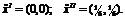 Матрица вторых производных в первой из этих точек 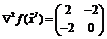 не является знакоопределенной, т.к. главный угловой минор 2-го порядка отрицателен. Следовательно, точка 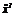 заведомо не является экстремальной. Во второй критической точке 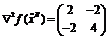 является положительно определенной, а значит 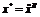- точка строгого локального минимума. Можно ли установить глобальный характер найденного минимума? Матрица вторых производных не является знакоопределенной на всем пространстве, поэтому мы не можем сразу ответить на данный вопрос. Зато мы легко замечаем, что, например, в точке (0, -1) целевая функция равна -4, что меньше значения функции в точке локального минимума -1/108. Значит, рассматриваемая точка не может быть точкой глобального минимума.

Ответ:

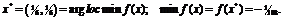
Пример 2. Исследуем на экстремум

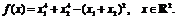
Приравняв градиент целевой функции нулю, решим систему уравнений - найдем три критические точки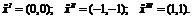

Рассмотрим первую подозрительную на экстремум точку. 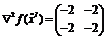 неположительно определена, а значит, - точка (0,0) подозрительна на локальный максимум, требуется дополнительное исследование.

Для второй и третьей критических точек вычисления совпадают:

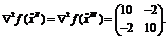
Данная матрица положительно определена, поэтому точки (-1,-1) и (1,1) являются точками строгого локального минимума. Для установления глобальности найденного минимума требуется дополнительное исследование.

Ответ. (0,0) подозрительна на локальный максимум, требуется дополнительное исследование.

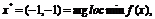
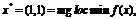
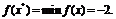
Для установления глобальности минимума требуется дополнительное исследование.

Заметим, что во втором примере мы столкнулись с необходимостью применения более глубоких математических знаний, чем анонсировано в лекции. Обойти эту проблему и провести исследование до конца можно (а так обычно и делают), если заметить, что исследуемая функция зависит только от двух переменных, а значит - можно построить либо ее график, либо семейство линий уровня и по ним провести пресловутое "дополнительное исследование". Это легко сделать при помощи персонального компьютера.

а) найденный ответ в примере 1 верный;

б) первая критическая точка в примере 2 не является экстремальной; точки локального минимума в примере 2 являются точками глобального минимума.

Исследуйте самостоятельно на безусловный экстремум функции

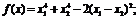
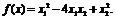
4. Поиск условного экстремума. Метод множителей Лагранжа

В качестве задачи на условный экстремум рассмотрим так называемую "классическую" задачу с ограничениями типа равенства (уравнениями):

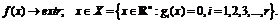 (1.6)

Обычно предполагается, что 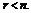 Это предположение естественно, поскольку в противном случае система уравнений в (1.6) либо вообще не имеет решений (т.е. 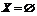), либо имеет решения в виде изолированных точек (тогда достаточно вычислить 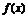 в этих точках и выбрать точки экстремума простым сравнением нескольких чисел). Уравнения в (1.6) обычно называют уравнениями связи.

Исторически первым методом решения задачи (1.6) выступает так называемый "метод исключения". Он применим, когда из уравнений связи удается выразить r переменных 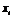 и подставить их в  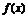- тем самым получаем задачу безусловной оптимизации с n - r переменными. Этот метод прост по сути, но зачастую трудно реализуем (далеко не всегда удается разрешить систему уравнений связи). Поэтому основное внимание уделим другому, чрезвычайно распространенному и универсальному, методу, также сводящему (1.6) к задаче безусловной оптимизации, но уже с большим количеством переменных.

Речь идет о методе множителей Лагранжа.

Рассмотрим функцию n + r переменных (ее называют либо функцией Лагранжа, либо лагранжианом):

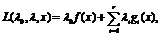(1.7)

где 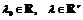 - набор множителей Лагранжа.

Имеет место

Теорема 3 (необходимое условие первого порядка условного экстремума). Пусть 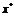- точка локального экстремума в задаче математического программирования (1.6); функции 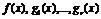 непрерывно дифференцируемы в окрестности 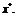 Тогда существуют такие число 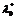 и вектор 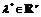, не равные нулю одновременно, такие, что

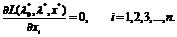(1.8)

Смысл теоремы 3 прозрачен - вместо задачи (1.6) мы занимаемся безусловной оптимизацией лагранжиана.

Заметим, что каждой точке локального экстремума 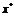 соответствует бесконечное множество наборов множителей Лагранжа. Ситуацию с 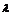 проясняют следующие определения и утверждения.

Определение 5. Если среди наборов 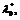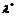, соответствующих точке локального экстремума, нет наборов с 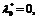 то такая точка называется нормальной (регулярной) точкой экстремума. В противном случае 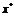 нерегулярна, или анормальна.

Нас интересует с конструктивной точки зрения как раз регулярные (нормальные) 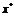, так как имеют место

Утверждение. Для нормальной точки локального экстремума соответствующие множители Лагранжа определяются единственным образом с точностью до постоянного множителя.

Утверждение. Точка локального экстремума 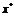 в задаче (1.6) является нормальной тогда и только тогда, когда векторы градиентов 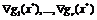 линейно независимы.

Теперь сформулируем правило поиска условно-критических точек в задаче (1.6):

а) составляется функция Лагранжа (1.7);

б) выписываются необходимые условия оптимальности (1.8), к ним добавляются ограничения-равенства из (1.6) (а это частные производные лагранжиана по компонентам набора множителей Лагранжа, приравненные нулю!). Из полученной системы находятся стационарные (условно-критические) точки, для которых существует нетривиальный (т.е. не равный нулю) набор 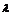. Рассматриваются обычно 2 случая:

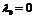·  (анормальная точка). Как правило, это предположение приводит к несовместности уравнений связи либо к тривиальности набора ;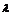

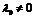·  , тогда можно назначить 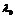 любым действительным числом (удобнее - единицей).

Пример 3. Рассмотрим "дефектную" задачу МП - с анормальной точкой экстремума ("дефект" появился из-за особенностей допустимого множества 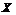- решения уравнения ):

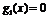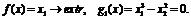
Лагранжиан выглядит следующим образом: 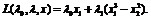 Запишем систему для поиска условно-критических точек и наборов множителей Лагранжа:

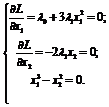
Рассмотрим два случая:

а) 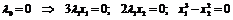 и для 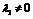 находим !

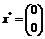б) 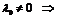ни при каких значениях  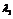мы не обнаружим !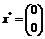

Задание. Рассмотрите экономический смысл множителей Лагранжа и геометрическую интерпретацию метода множителей Лагранжа.

Для выяснения характера экстремальности условно-стационарной точки следует привлекать производные функци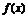й  и 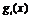 более высокого порядка, чем первый: нас будет интересовать знакоопределенность матрицы вторых производных 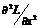 лагранжиана по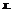

Будем использовать для решения классических задач МП следующую теорему.

Теорема 4 (достаточное условие второго порядка оптимальности в задаче (1.6)). Пусть: 1) функции 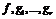 дважды дифференцируемы в точке  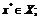2) для некоторого нетривиального набора 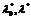,  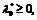выполнено условие (1.8); 3) квадратичная форма

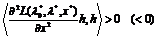
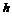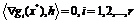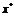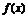для всех ненулевых векторов , определяемых условиями  и  Тогда - точка строгого локального минимума (максимума) функции  на .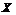

(Заметим, что иногда достаточно проверить матрицу вторых производных лагранжиана по x на строгую знакоопределенность на всем пространстве.)

Пример 4. Применим правило множителей Лагранжа к решению задачи

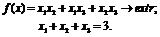
Результат проверим с помощью метода исключения.

Составляем лагранжиан:

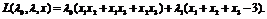
Заметим, что в данном примере присутствует только одно ограничение, поэтому "набор" множителей Лагранжа оказался скаляром, а не вектором, и можно было не нумеровать множитель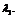

Продифференцируем построенную функцию Лагранжа по компонентам вектора 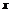и запишем систему алгебраических уравнений для определения условно-критических точек:

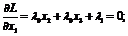
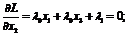
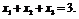
Прежде всего проанализируем нормальность исследуемых стационарных точек, для чего рассмотрим два случая:

а) Пусть 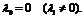Данное предположение сразу приводит к противоречию: из первых трех уравнений следует, что множитель Лагранжа тоже должен равняться нулю, что невозможно.

б) Пусть 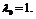 Тогда система линейных уравнений легко разрешается: мы получили в качестве подозрительной на экстремум условно-критическую точку 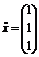 и соответствующий ей множитель Лагранжа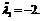

Для определения характера экстремальности найденной стационарной точки исследуем знакоопределенность матрицы вторых производных лагранжиана по 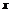на всем пространстве:  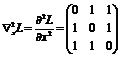не является строго знакоопределенной, т.к. главный угловой минор первого порядка равен нулю. Придется проверить знак квадратичной формы (см. пункт 3 теоремы 4) 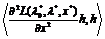, рассчитывая на знакоопределенность матрицы вторых производных лагранжиана по 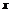 в допустимом множестве - множестве решений уравнения 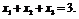Векторы 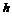получаем, решая систему уравнений 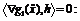 так как 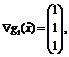то 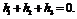 Это недоопределенная система, она имеет множество решений. Будем считать параметрами вторую и третью компоненты искомого вектора, тогда решение системы можно записать как

.

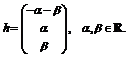Тогда

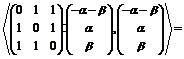
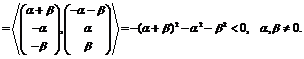
Таким образом, 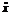 является точкой строгого локального максимума функции 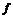 на множестве, заданном ограничением  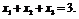При этом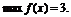

Для проверки полученного результата применим метод исключения. Выразив из уравнения 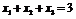 переменную 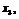подставим ее в целевую функцию. В итоге получим вспомогательную задачу исследования на безусловный экстремум функции двух переменных:

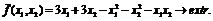
Для ее решения применим теорию пункта 1.3: приравняв градиент нулю, найдем стационарные (критические) точки, экстремальность которых затем проверим при помощи матрицы вторых производных.

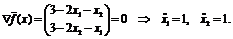
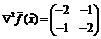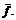 является строго отрицательно определенной (главный угловой минор первого порядка отрицателен, а минор второго порядка положителен), поэтому найденная критическая точка является точкой строгого локального максимума функции  А значит, мы нашли и строгий локальный максимум исходной функции 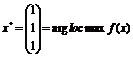на допустимом множестве, заданном уравнением 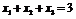. Более того, мы можем утверждать, что найденный экстремум является глобальным, т.к. матрица вторых производных 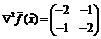 строго отрицательно определена на всем пространстве.

Задание. Самостоятельно ознакомьтесь с графо-аналитическим методом решения задач нелинейного программирования (см., например, пособие В.И. Кустовой "Математическое программирование (сборник задач и упражнений)", часть 1, стр.33-37 или материалы практических занятий).

Исследуйте самостоятельно тремя способами (методом исключения, методом множителей Лагранжа, графо-аналитическим методом) следующие задачи:

а)

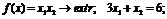
б)

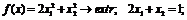
в)

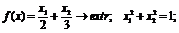
5. Задачи выпуклого и квадратичного программирования. Теорема Куна-Таккера

Заметим, что пока мы познакомились с методами решения только двух классов задач математического программирования: безусловных и классических, с ограничениями типа равенства. Если же рассматривать более общие задачи, включающие и ограничения типа неравенств, то можно утверждать, что для их решения не существует универсальных методов (поэтому вот уже в течение полувека бурно развивается так называемая "вычислительная математика", в которой разрабатываются многочисленные методы приближенного решения задач оптимизации при помощи компьютера).

Однако существуют еще два класса задач нелинейного программирования со специфическими свойствами целевой функции и функций, задающих ограничения, для которых разработаны эффективные методы их аналитического исследования - обычно их называют "задачи выпуклого программирования" и "задачи квадратичного программирования". В этом параграфе мы обзорно с ними познакомимся - это задачи, имеющие 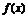 вогнутую, выпуклую или даже квадратичную, а 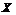- выпуклое или, в самом простом случае, - линейное. Выделение данных задач в отдельные классы произошло благодаря чрезвычайно широкому их распространению при моделировании экономических систем.

Конкретности ради остановимся на задаче

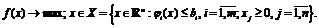(1.9)

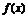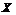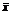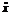Определение 6. Функция , заданная на выпуклом множестве , называется выпуклой (вогнутой), если для любых двух точек  и  из 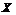и любого числа  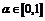выполняется неравенство

().

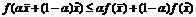
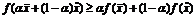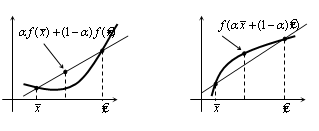
Рис. 1.1

а) график выпуклой функции б) график вогнутой функции

Геометрический смысл понятий выпуклости и вогнутости для случая функции одной переменной представлен на рис. 1.1. Из него, в частности, видно, что график выпуклой функции лежит ниже отрезка, соединяющего точк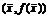и  и 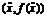, а график вогнутой - выше.

В курсе математического анализа доказано, что достаточным условием выпуклости функции 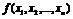 является положительная определенность во всех точках  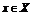так называемой матрицы Гессе (матрицы вторых производных, выше мы обозначали ее )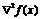

.

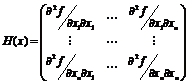Соответственно, достаточным условием вогнутости является отрицательная определенность матрицы Гессе. В частности, для функций одной переменной достаточным условием выпуклости (вогнутости) является выполнение неравенства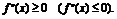

Как следует из геометрической интерпретации, для выпуклой (или вогнутой) функции локальный экстремум, если он существует, совпадает с глобальным. Справедлива теорема.

Теорема 5. Если 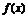 выпуклая (вогнутая) на  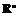функция и 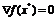, то 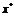 - точка глобального минимума (максимума) .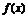

Поскольку выпуклые функции обладают столь "полезными" оптимизационными качествами, они занимают исключительно важное место в математическом программировании. Соответствующий раздел получил название выпуклого программирования, а общая задача выпуклого программирования формулируется как проблема поиска максимума вогнутой (минимума выпуклой) функции на выпуклом множестве.

Определение 7. Задача (1.9) называется задачей выпуклого программирования, если функция 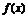 является вогнутой (выпуклой в случае минимизации), а функции 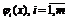 - выпуклыми.

Для задачи выпуклого программирования справедлив аналог теоремы 5.

Теорема 6. Любой локальный максимум (минимум) задачи выпуклого программирования является глобальным максимумом (минимумом).

Остановимся кратко на фундаментальном результате выпуклого программирования - теореме Куна-Таккера, позволяющей распространить метод Лагранжа для решения задач математического программирования с ограничениями в форме неравенств, в частности - задач вида (1.9).

Определим функцию Лагранжа (при моделировании реальных экономических процессов мы вправе рассчитывать на нормальность экстремальных точек, поэтому определим множитель при целевой функции равным единице)

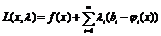,(1.10)

где 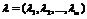 - набор множителей Лагранжа.

Введем также новый в данной главе объект - так называемую седловую точку.

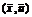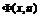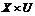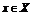Определение 8. Пара векторов  называется седловой точкой функции  в некоторой области , если для любых  и 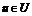 справедливы неравенства:

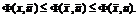(1.11)

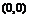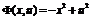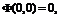
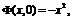
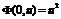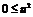Неравенства (1.11) часто называют неравенствами седловой точки, смысл их прозрачен: в седловой точке по одной переменной функция достигает своего максимума, а по другой - минимума. В качестве примера седловой точки может быть приведена точка  для функции , определенной на плоскости. В самом деле,   , а для любых  и  выполняются неравенства и . На рис.1.2 изображен график указанной функции (гиперболический параболоид), и, как видно, в окрестности начала координат он действительно по форме напоминает седло, чем и объясняется происхождение соответствующего термина.

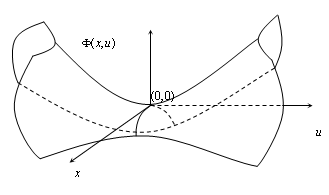
Рис. 1.2

Основная теорема данного параграфа оказывается верной только при выполнении дополнительных условий, которым должна удовлетворять задача выпуклого программирования (1.9). Важнейшим из них является так называемое условие регулярности Слейтера.

Определение 9. Говорят, что функция 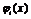, задающая ограничение в задаче (1.9), удовлетворяет условию регулярности Слейтера, если существует такая точка 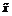, принадлежащая области допустимых планов 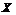, что 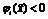, т.е.  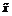является внутренней точкой относительно выбранного ограничения (данное условие часто называют условием телесности множества допустимых планов).

Теперь мы готовы сформулировать основной результат.

Теорема 7. (необходимое и достаточное условие наличия экстремума в задаче выпуклого программирования - теорема Куна-Таккера). Для задачи выпуклого программирования (1.9), в которой целевая функция 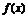 и функции ограничений 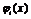- дифференцируемы, нелинейные ограничения в форме неравенств удовлетворяют условию регулярности Слейтера, вектор 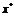 является оптимальным планом тогда и только тогда, когда существует такой неотрицательный вектор 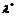, что 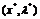 - седловая точка функции Лагранжа (1.10).

Значение теоремы Куна-Таккера состоит в том, что она позволяет связать процесс решения оптимизационной задачи с поиском седловых точек функции Лагранжа, т.е., грубо говоря, с максимизацией лагранжиана по 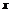 и его минимизацией по 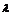. В результате можно сформулировать пару так называемых двойственных задач, обладающих больших набором полезных свойств и активно используемых математиками при анализе моделируемых систем. Ниже, при изучении задач линейного программирования, мы рассмотрим двойственность подробно (в нелинейных задачах соответствующие выкладки слишком сложны для студентов экономических специальностей).

Заметим, что формулировка теоремы 7 пока не дает нам возможности построить конструктивный алгоритм решения задачи, подобно предыдущим параграфам. Поэтому, чтобы продемонстрировать эффективность условий Куна-Таккера, рассмотрим частный случай задачи выпуклого программирования - задачу квадратичного программирования. В такой задаче можно предположить, что целевая функция и функции ограничений непрерывно дифференцируемы, и теорему Куна-Таккера можно дополнить аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка 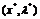 была седловой точкой функции Лагранжа, т.е. являлась решением задачи выпуклого программирования. Эти выражения имеют следующий вид:

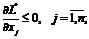(1.12)

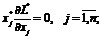(1.13)

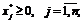(1.14)

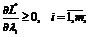(1.15)

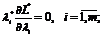(1.16)

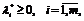(1.17)

где 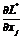 и 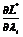 - значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.

Прежде чем сформулировать задачу квадратичного программирования, дадим некоторые определения.

Определение 10. Квадратичной формой относительно переменных 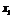, , 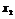…,  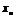называется числовая функция от этих переменных, имеющая вид

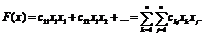
Определение 11. Квадратичная форма 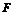 называется положительно (отрицательно)-определенной, если 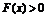 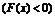 для всех значений переменных, кроме .

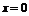Определение 12. Квадратичная форма 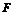 называется неотрицательно(неположительно)-определенной, если 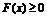 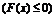 для любого набора значений переменных и, кроме того, существует такой набор переменных 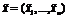, где не все значения переменных одновременно равны нулю, что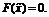

Справедлива

Теорема 8. Квадратичная форма является выпуклой функцией, если она неотрицательно-определена, и вогнутой функцией, если она неположительно-определена.

Определение 13. Задача, состоящая в определении максимального (минимального) значения функции

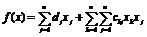(1.18)

при ограничениях

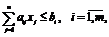(1.19)

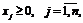(1.20)

где 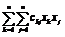 - неположительно (неотрицательно)-определенная квадратичная форма, называется задачей квадратичного программирования.

Для сформулированной задачи квадратичного программирования (1.18)-(1.20) функция Лагранжа запишется в виде

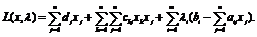
Если лагранжиан 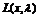 имеет седловую точку 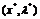, то в этой точке выполняются соотношения (1.12)-(1.17). Вводя теперь дополнительные неотрицательные переменные 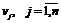 и 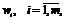 обращающие неравенства (1.12) и (1.15) в равенства, перепишем выражения (1.12)-(1.17) для задачи квадратичного программирования следующим образом:

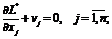(1.21)

(1.22)

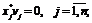(1.23)

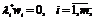(1.24)

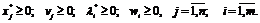(1.25)

Таким образом, чтобы найти решение задачи квадратичного программирования (1.18)-(1.20), нужно определить неотрицательное решение систем линейных уравнений (1.21) и (1.22), удовлетворяющее условиям (1.23) и (1.24).

Пример 5. Найдем максимальное значение функции

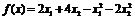
при условиях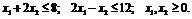

Функция 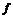 является вогнутой, так как представляет собой сумму линейной функции 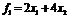 (которую можно рассматривать как вогнутую) и квадратичной формы 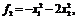 которая является отрицательно определенной и, следовательно, также вогнутой. Система ограничений задачи только лишь линейные неравенства. Следовательно, можно воспользоваться теоремой Куна-Таккера. Составим лагранжиан

и запишем в виде выражений (1.21)-(1.25) необходимые и достаточные условия существования седловой точки построенной функции:

(1.26)

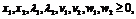(1.27)

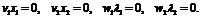(1.28)

Если теперь найти базисное решение системы линейных уравнений (1.26) с учетом выполнения равенств (1.28), то будет получена седловая точка функции Лагранжа 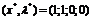 для исходной задачи, т.е. определено оптимальное решение 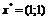 и

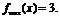
Задание. Проделайте все необходимые вычисления в примере 5 и убедитесь в правильности предъявленного решения.

Исследуйте самостоятельно следующие задачи:

а)

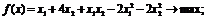
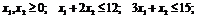
б)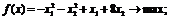

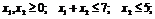
в)

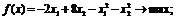
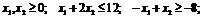
г)

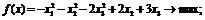
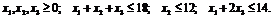
условный экстремум множитель квадратичный

Литература

1.       Абчук В.А. Экономико-математические методы. - СПб.: Союз, 1999.

2.       Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие. - М.: Высшая школа, 1986.

.         Аргучинцев А.В. Методы оптимизации: Часть 1. Математическое программирование. - Иркутск: Изд-во ИГУ, 1993.

.         Беников А.И. Симплекс-метод решения задач линейного программирования: Учебное пособие по практическим занятиям. - Иркутск: Изд-во ИИНХ, 1993

.         Беников А.И., Лямзина Н.И. Элементы линейного программирования (Симплекс-метод): Методические указания. - Иркутск: Изд-во ИГУ, 1991.

.         Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. - СПб.: Издательство "Лань", 2000.

.         Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике: Учебник. - М.: МГУ им.М.В.Ломоносова, Изд-во "Дело и Сервис", 1999.

.         Интрилигатор М. Математические методы оптимизации и экономическая теория. - М.: Айрис-пресс, 2002. - 576 с.

.         Экономико-математическое моделирование: Учебник / Под общ.ред. И.Н. Дрогобыцкого, - М.: Издательство "Экзамен", 2004, - 800 с.

.         Конюховский П.В. Математические методы исследования операций в экономике. - СПб.: Питер, 2000 (Серия "Краткий курс").

.         Косоруков О.А., Мищенко А.В. Исследование операций: Учебник. - М.: "Экзамен", 2003. - 448 с.

.         Кремер Н.Н., Путко Б.А., Тришин И.М., Фридман М.Н. Исследование операций в экономике: Учебное пособие для вузов. - М.: Банки и биржи, ЮНИТИ, 1997.

.         Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика: Математическое программирование. - Мн.: Выш.шк., 1994.

.         Кузнецов А.В., Сакович В.А., Холод Н.И., Дежурко Л.Ф. и др. Сборник задач и упражнений по высшей математике: Математическое программирование. - Мн.: Выш.шк., 1995.

.         Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. - М.: Высшая школа, 1990.

.         Кустова В.И. Математическое программирование: Сборник задач и упражнений. Часть 1. Часть 2. Часть 3. - Иркутск: Изд-во ИГЭА

.         Срочко В.А. Основы линейного программирования: Учебное пособие. - Иркутск: Изд-во ИИНХ, 1993.

.         Таха Х. Введение в исследование операций. - М.:Мир, 1985.

.         Трояновский В.М. Математическое моделирование в менеджменте: Учебное пособие. - М.: Изд-во РДЛ, 2000.

.         Тятюшкин А.И., Деренко Н.В. Решение и анализ задач линейного программирования: Методические указания. - Иркутск: Изд-во ИГЭА, 1996.