Основные методы решения задач нелинейного программирования
Содержание
Введение
1. Классический метод решения задач нелинейного программирования
1.2 Экстремум функции одной переменной
1.3 Экстремумы функций многих переменных
1.4 Метод неопределенных множителей Лагранжа
1.4.1 Основные положения
1.4.2 Геометрическая интерпретация метода множителей Лагранжа
1.4.3 Экономическая трактовка метода множителей Лагранжа
1.4.4 Особые случаи
1.5 Особенности реальных задач
2. Численные методы решения задач нелинейного программирования
2.1 Общая характеристика методов решения задач нелинейного
программирования
2.2 Методы одномерной оптимизации
2.2.1 Метод прямого сканирования
2.2.2 Метод половинного деления
2.2.3 Метод "золотого сечения"
2.2.4 Метод Фибоначчи
2.3 Методы многомерной оптимизации
2.3.1 Метод Гаусса-Зайделя
2.3.2 Метод градиента
2.3.3 Метод наискорейшего спуска
2.3.4 Метод квантования симплексов
2.3.5 Поиск при наличии "оврагов" целевой функции
2.4 Методы поиска условного экстремума
2.4.1 Метод проектирования вектора-градиента
2.4.2 Метод ажурной строчки
2.5 Проблемы поиска глобального экстремума
3. Численные методы решения задач нелинейного программирования
3.1 Графический метод решения задач нелинейного программирования
3.2 Метод множителей Лагранжа
3.3 Компьютерная реализация решений задач нелинейного
программирования
3.3.1 Решение задач нелинейного программирования в среде приложения
Excel
3.3.2 Решение задач нелинейного программирования в среде приложения
Matlab
Выводы
Перечень ссылок
Введение
Задача нелинейного программирования встречается в
естественных науках, технике, экономике, математике, в сфере деловых отношений
и в науке управления государством.
Нелинейное программирование, например, связано с основной
экономической задачей. Так в задаче о распределении ограниченных ресурсов
максимизируют либо эффективность, либо, если изучается потребитель, потребление
при наличии ограничений, которые выражают условия недостатка ресурсов. В такой
общей постановке математическая формулировка задачи может оказаться
невозможной, но в конкретных применениях количественный вид всех функций может
быть определен непосредственно. Например, промышленное предприятие производит
изделия из пластмассы. Эффективность производства здесь оценивается прибылью, а
ограничения интерпретируются как наличная рабочая сила, производственные площади,
производительность оборудования и т.д.
Метод "затраты - эффективность" также укладывается
в схему нелинейного программирования. Данный метод был разработан для
использования при принятии решений в управлении государством. Общей функцией
эффективности является благосостояние. Здесь возникают две задачи нелинейного
программирования: первая - максимизация эффекта при ограниченных затратах,
вторая - минимизация затрат при условии, чтобы эффект был выше некоторого
минимального уровня. Обычно эта задача хорошо моделируется с помощью
нелинейного программирования.
Результаты решения задачи нелинейного программирования
являются подспорьем при принятии государственных решений. Полученное решение
является, естественно, рекомендуемым, поэтому необходимо исследовать
предположения и точность постановки задачи нелинейного программирования, прежде
чем принять окончательное решение.
нелинейное программирование метод решение
Задачи нелинейного программирования часто возникают и в
других отраслях науки. Так, например, в физике целевой функцией может быть
потенциальная энергия, а ограничениями - различные уравнения движения. В
общественных науках и психологии возникает задача минимизации социальной
напряженности, когда поведение людей ограничено определенными законами.
Целью дипломного проекта является решение задач нелинейного
программирования различными методами для проведения анализа поведения этих
методов на выбранных математических моделях нелинейного программирования.
Для достижения поставленной цели необходимо выполнить
следующее
решить выбранные задачи нелинейного программирования
графическим методом;
решить выбранные задачи нелинейного программирования методом
множителей Лагранжа;
представить компьютерную реализацию выбранных задач
нелинейного программирования в среде пакетов Excel и Matlab.
Общая характеристика диплома: количество страниц - ____,
количество таблиц - 1, количество рисунков - 33, количество ссылок - 6.
1.
Классический метод решения задач нелинейного программирования
Математическая формулировка задачи принятия решения часто
эквивалентна задаче отыскания экстремума функции одной или многих переменных.
Поэтому для решения подобных задач могут быть использованы различные методы
исследования функций классического анализа, в частности, методы поиска экстремума.
Эти методы применяют в тех случаях, когда известен аналитический вид
зависимости оптимизируемой функции Q от независимых переменных uι.
1.1
Постановка задачи
В задаче нелинейного программирования требуется найти значение
многомерной переменной х= (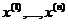 ), минимизирующее целевую функцию f (x) при условиях, когда на
переменную х наложены ограничения типа неравенств
), минимизирующее целевую функцию f (x) при условиях, когда на
переменную х наложены ограничения типа неравенств  , i=1,2,…,m, а переменные
, i=1,2,…,m, а переменные 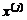 , т.е. компоненты вектора х,
неотрицательны:
, т.е. компоненты вектора х,
неотрицательны: 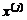
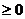 .
.
Иногда в формулировке задачи ограничения имеют противоположные
знаки неравенств. Учитывая, однако, что если 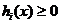 , то
, то 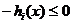 , всегда можно свести задачу к
неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком
равенства, например
, всегда можно свести задачу к
неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком
равенства, например 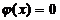 , то их можно представить в виде пары
неравенств
, то их можно представить в виде пары
неравенств 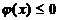 ,
, 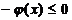 , сохранив тем самым типовую формулировку задачи.
, сохранив тем самым типовую формулировку задачи.
1.2 Экстремум
функции одной переменной
Большинство простейших задач принятия решений эквивалентно
задачам отыскания экстремума функции одной переменной.
Пусть требуется найти экстремум функции одной переменной Q
(u) при отсутствии ограничений на диапазон изменения переменной u.
Необходимым условием существования экстремума непрерывной
функции Q (u) является равенство нулю первой производной (dQ /du
= 0) или ее отсутствие. Графически равенство нулю производной означает, что
касательная к кривой Q (u) в этой точке параллельна оси абсцисс
(рис.1.1, а), на рис.1.1, б изображен случай, когда производные в
точках экстремума не существуют.
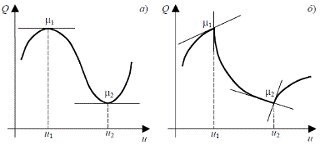
Рисунок 1.1 - Различные типы экстремума функции одной
переменной:
а - производная в точке экстремума существует;
б - производная в точке экстремума не существует.
Названные условия являются лишь необходимыми условиями. Их
выполнение не означает еще, что в данных точках функция имеет экстремум
(рис.1.2).
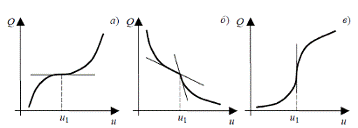
Рисунок 1.2 - Функции Q (u), удовлетворяющие
необходимым условиям экстремума: а - производная равна нулю; б - производная
не существует; в - производная равна бесконечности.
Для того, чтобы определить, действительно ли в исследуемой
точке существует экстремум, необходимо проверить выполнение достаточных условий
одним из методов, приведенных ниже.
1) Сравнение значений функций. Этот способ сводится к определению
значений функции в точках, расположенных слева и справа в достаточной близости
от исследуемой точки, т.е. в точках 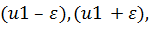
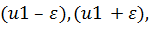 где
где 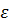
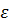 - малая положительная величина. Если
- малая положительная величина. Если 
 то в точке u1 существует максимум (рис.1.3).
то в точке u1 существует максимум (рис.1.3).
Если 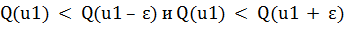
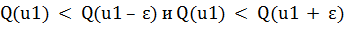 , то в точке u1 существует минимум (рис.1.3, б). Если же Q (u1)
будет занимать промежуточное между положение
, то в точке u1 существует минимум (рис.1.3, б). Если же Q (u1)
будет занимать промежуточное между положение 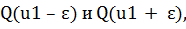
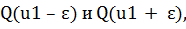 например,
например,
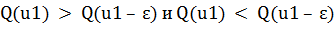
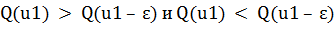 , то в точке u1 экстремума не будет (рис.1.3, в).
, то в точке u1 экстремума не будет (рис.1.3, в).
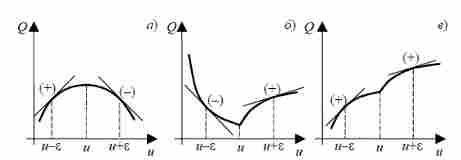
Рисунок 1.3 - Проверка достаточных условий экстремума:
) Сравнение знаков производной. При этом способе определяется знак
первой производной функции 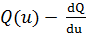
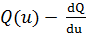 в точках
в точках 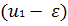
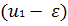 и
и 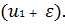
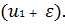 Если знаки производных различны, то в точке u1 имеется
экстремум функции Q (u), причем, если при переходе от точки
Если знаки производных различны, то в точке u1 имеется
экстремум функции Q (u), причем, если при переходе от точки 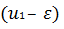
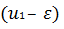 к точке
к точке 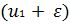
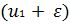 знак производной изменяется с "+" на "-", то
в точке u1 - максимум (рис.1.3, а). Если же знак меняется с
"-" на "+", то в точке u1 - минимум (рис.1.3, б).
знак производной изменяется с "+" на "-", то
в точке u1 - максимум (рис.1.3, а). Если же знак меняется с
"-" на "+", то в точке u1 - минимум (рис.1.3, б).
Если же знаки производных в точках 
 и
и 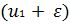
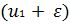 одинаковы, то в точке u1 экстремума нет (рис.1.3, в).
одинаковы, то в точке u1 экстремума нет (рис.1.3, в).
) Исследование знаков высших производных. Этот способ применяется
в тех случаях, когда исследуемая функция имеет производные высших порядков.
Если в точке u1 выполняется необходимое условие экстремума, т.е. 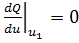
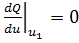 и существует вторая производная -
и существует вторая производная - 
 , значение которой вычисляется в "подозреваемой" точке
u1, то точка u1 является точкой максимума, если
, значение которой вычисляется в "подозреваемой" точке
u1, то точка u1 является точкой максимума, если 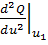
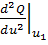 < 0, и точкой минимума, если
< 0, и точкой минимума, если 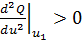
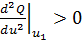 .
.
Если же 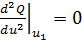
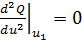 , то для дальнейших исследований вычисляются
, то для дальнейших исследований вычисляются 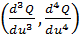
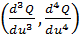 и т.д.
и т.д.
При решении практических задач, как правило, приходится
исследовать функции, имеющие несколько экстремумов. В этом случае говорят о
нахождении наибольшего и наименьшего значения функции, которые называют
глобальными экстремумами. Остальные экстремумы называются локальными. Также в
практических задачах диапазон изменения переменной u часто бывает ограничен
заданным интервалом [a, b], поэтому в число "подозреваемых" точек
должны быть включены и крайние точки этого интервала, так как в них может
достигаться глобальный экстремум.
1.3
Экстремумы функций многих переменных
В большинстве задач оптимизации критерий оптимальности является
функцией нескольких независимых переменных - 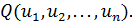
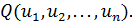 Если он является непрерывной функцией, имеющей непрерывные
частные производные первого и второго порядка по всем переменным uι (ι = 1, n), то необходимым условием
экстремума в точке
Если он является непрерывной функцией, имеющей непрерывные
частные производные первого и второго порядка по всем переменным uι (ι = 1, n), то необходимым условием
экстремума в точке 
 является
равенство нулю в этой точке первых производных по всем переменным, т.е. точки,
в которой функция
является
равенство нулю в этой точке первых производных по всем переменным, т.е. точки,
в которой функция 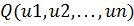
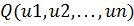 может достигать экстремума, определяются решением системы
уравнений
может достигать экстремума, определяются решением системы
уравнений
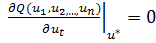
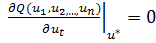 , t=
, t=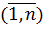
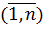 .
.
Достаточные условия существования экстремума определяются в
результате анализа знака квадратичной формы B=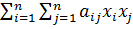
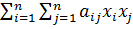 , коэффициенты которой определяются соотношениями
, коэффициенты которой определяются соотношениями
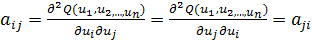
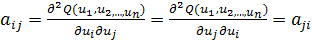 ; i,j=
; i,j=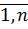
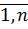 .
.
Квадратичная форма может быть положительно определенной и
отрицательно определенной. Ответ о знаке квадратичной формы дает теорема,
которая формулируется следующим образом: для положительной определенности
квадратичной формы необходимо и достаточно, чтобы были выполнены условия
Сильвестра
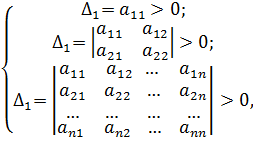
т.е. все главные миноры матрицы
=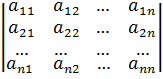
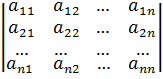
должны быть строго положительны.
Квадратичная форма будет отрицательно определенной, если все
главные миноры матрицы A, имеющие нечетный порядок, отрицательны, а,
имеющие четный порядок, положительны, т.е. 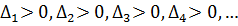
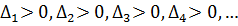
Если квадратичная форма является положительно определенной, то
исследуемая точка является точкой минимума, если же квадратичная форма будет
отрицательно определенной, то в точке {uι} имеет место максимум.
Возможен случай, когда все главные миноры отличны от нуля, но
условия положительной или отрицательной определенности квадратичной формы не
выполняются, в этом случае в исследуемой точке функция не имеет ни максимума,
ни минимума. В случае обращения в нуль главных миноров матрицы A, вопрос
о наличии экстремума в исследуемой точке решается более сложно с использованием
производных более высокого порядка.
Пусть в реакторе идеального смешения протекает реакция первого
порядка (A → P). Требуется определить оптимальные условия -
время пребывания и температуру, при которой себестоимость продукта P будет
минимальной.
Критерий оптимальности - себестоимость задается функцией
(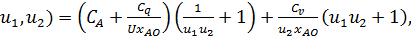
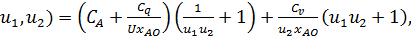
где u1 - время пребывания, u2 - константа скорости
химической реакции, связанная с температурой уравнением Аррениуса u2 =
exp ( - E / RT), E и R - константы; СА - стоимость
единицы расходуемого сырья; Сq - стоимость дополнительного оборудования
реактора, исчисляемая с учетом амортизации; Сv - стоимость единицы
объема реактора, исчисляемая с учетом его амортизации; U - нагрузка
реактора по исходному сырью; xA0 - начальная концентрация вещества А.
Необходимые условия экстремума функции Q (u1, u2)
дают систему уравнений:

Последнее уравнение не удовлетворяет ни каким значениям u1,
u2, поэтому разумно выдерживать максимально возможную температуру
ведения процесса, что определит значение u2. Оптимальное значение
времени пребывания, соответствующее принятому значению температуры в этом
случае определится как

Минимальная себестоимость составит
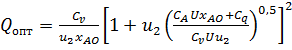
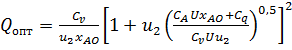 .
.
Найти экстремум функции Q (u1, u2) = 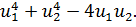
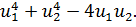 Необходимые условия экстремума записываются в виде системы:
Необходимые условия экстремума записываются в виде системы:
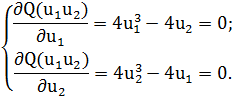
Решение полученной системы уравнений дает три подозрительные точки
на экстремум: (0, 0); (1, 1); (-1, - 1). Для определения существования
экстремума в найденных точках требуется проверить достаточные условия. С этой
целью составляется матрица
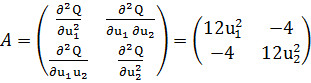
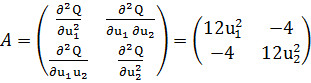 .
.
В найденных точках
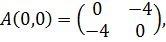
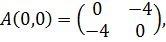
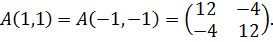
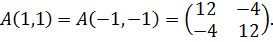
Матрица 
 - знаконеопределенна, следовательно, точка (0, 0) не является
экстремальной. Матрицы
- знаконеопределенна, следовательно, точка (0, 0) не является
экстремальной. Матрицы 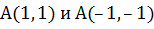
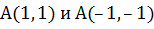 положительно определенные
положительно определенные 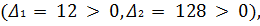
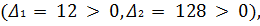 поэтому в точках (1, 1) и (-1,-1) будет минимум -
поэтому в точках (1, 1) и (-1,-1) будет минимум - 
 .
.
1.4 Метод
неопределенных множителей Лагранжа
Условия экстремума функции, которые рассмотрены выше,
позволяют найти, так называемый, безусловный экстремум. Однако, в большинстве
практических задач принятия решения требуется принять решение - определить
экстремум критерия оптимальности при условии, что на независимые переменные
наложены ограничения, имеющие вид равенств. Типичными примерами подобных задач
служат задачи, в которых требуется оптимальным образом распределить заданное
количество ресурсов, чтобы принятая оценка эффективности процесса имела при
этом максимальное или минимальное значение. Для решения таких задач в
классическом анализе используется метод неопределенных множителей Лагранжа.
Сами задачи получили название задач на условный экстремум.
1.4.1
Основные положения
Пусть требуется найти экстремум функции, например, минимум
Q (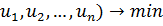
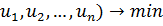 , при условии
, при условии
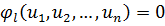
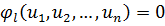 ,
, 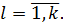
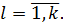
Согласно методу Лагранжа для решения задач на условный экстремум
функции составляется вспомогательная функция Лагранжа, которая определяется
соотношением
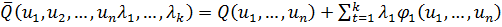
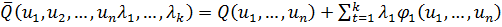 ,
,
где 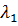
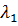 ,
,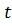
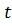 =
= 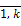
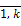 - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа.
Таким образом, задача нахождения условного экстремума функции
сводится к задаче нахождения безусловного экстремума функции, но число
неизвестных в ней n + k (uι, ι = 1, n; λj, j = 1, k).
Как известно из п.1.2 необходимым условием безусловного экстремума
функции является равенство нулю частных производных, которые для данного конкретного
случая записываются в виде
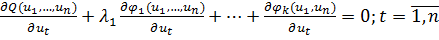
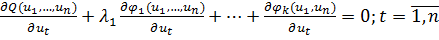 .
.
и дает n уравнений для определения неизвестных. Эта система
уравнений дополняется к уравнениям и, следовательно, получается (n + k)
неизвестных и (n + k) уравнений.
Метод множителей Лагранжа дает лишь необходимые условия
существования условного экстремума для непрерывных функций, имеющих также
непрерывные производные, поэтому найденные значения переменных могут и не
давать экстремума функции Q (u1,., un), их надо проверить с
использованием достаточных условий экстремума функции многих переменных.
В окончательном решении задачи фактически множители Лагранжа не
известны, поэтому задача совместного решения системы, иногда ставится как
задача исключения "k" неизвестных переменных uι с последующим решением остающейся системы
n уравнений с n неизвестными.
Задача Лагранжа имеет "n - k" степеней свободы.
1.4.2
Геометрическая интерпретация метода множителей Лагранжа
Интерес представляют геометрический смысл множителей
Лагранжа. Для такой интерпретации лучше рассмотреть задачу с двумя неизвестными
и одним ограничением.
Пусть требуется найти минимум функции 
 при условии
при условии 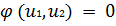
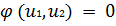 . Если минимум существует, то в пространстве функция Q должна
иметь вид воронки, а условие связи - это некоторая поверхность.
. Если минимум существует, то в пространстве функция Q должна
иметь вид воронки, а условие связи - это некоторая поверхность.
На рис.4, б изображены на плоскости переменных u1, u2
линии уровня функции Q (u1, u2) и ограничение φ (u1, u2) = 0,
представляющее собой линию. Составляется вспомогательная функция Q (u1, u2)
= Q (u1, u2) + λφ (u1, u2). Необходимое
условие экстремума дает:

Рисунок 1.4 - Геометрический смысл множителей Лагранжа:
а - пространственное
изображение;
б - изображение
проекции на плоскость u2 - u1

 или
или 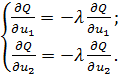
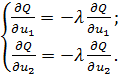
В точке А - точке касания линии 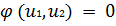
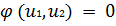 с линией равного уровня функции
с линией равного уровня функции 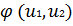
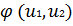 и
и 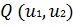
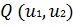 имеют общую касательную и необходимое условие минимума
представляет собой условие пропорциональности двух векторов: вектора
имеют общую касательную и необходимое условие минимума
представляет собой условие пропорциональности двух векторов: вектора 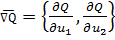
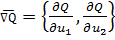 - градиента
функции
- градиента
функции 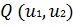
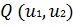 и вектора
и вектора 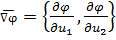
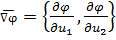 - градиента функции
- градиента функции 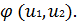
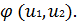
Два вектора пропорциональны друг другу лишь в том случае, если они
коллинеарные. Так как градиент функции перпендикулярен касательной к линии
уровня, то в точке А выполняется условие, и множитель 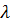
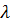 является коэффициентом пропорциональности между векторами
является коэффициентом пропорциональности между векторами 
 и
и 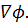
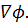
1.4.3
Экономическая трактовка метода множителей Лагранжа
В некоторых задачах множители Лагранжа допускают и экономическое
толкование. Если толковать целевую функцию Q (u1,., un) как прибыль,
получаемую некоторым предприятием при использовании ресурсов, а условия 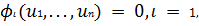
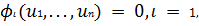 k ограничения на дефицит ресурсов, то при
k ограничения на дефицит ресурсов, то при 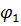
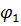 (u1,., un) < 0 прибыль, то максимум целевой
функции будет расти.
(u1,., un) < 0 прибыль, то максимум целевой
функции будет расти.
Экономист такую задачу будет решать следующим образом. Он назначит
некоторые цены 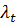
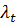 на единицы ресурсов
на единицы ресурсов 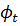
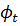 и предложит потребителю купить их по этой цене. Последний,
максимизируя чистую прибыль
и предложит потребителю купить их по этой цене. Последний,
максимизируя чистую прибыль 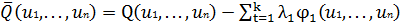
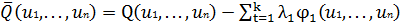 , найдет (u1,., un) и скажет, сколько ресурсов он
хотел бы купить. В экономике почти всегда бывает так, что чем больше
, найдет (u1,., un) и скажет, сколько ресурсов он
хотел бы купить. В экономике почти всегда бывает так, что чем больше 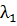
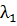 , тем меньше
, тем меньше 
 (u1,., un), и чем меньше
(u1,., un), и чем меньше 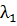
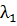 , тем больше
, тем больше 
 (u1,., un). Если окажется, что
(u1,., un). Если окажется, что 
 (u1,., un) > 0, то экономист повысит цену, если
(u1,., un) > 0, то экономист повысит цену, если 
 (u1,., un) < 0 - понизит. Так будет происходить
до тех пор, пока при некоторой цене, называемой равновесной, потребителю будет
выгодно, чтобы дефицит ресурсов
(u1,., un) < 0 - понизит. Так будет происходить
до тех пор, пока при некоторой цене, называемой равновесной, потребителю будет
выгодно, чтобы дефицит ресурсов 
 (u1,., un) был равен нулю, при этом чистая прибыль
будет максимальна, т.е. будут выполняться условия
(u1,., un) был равен нулю, при этом чистая прибыль
будет максимальна, т.е. будут выполняться условия

Таким образом, равновесная цена с точностью до знака равна
множителю Лагранжа.
1.4.4 Особые
случаи
В заключение следует отметить особые случаи, когда градиент
функции 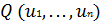
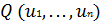 равен нулю
равен нулю 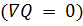
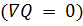 и когда градиент φ1 (u1,., un) равен нулю
и когда градиент φ1 (u1,., un) равен нулю 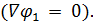
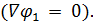
В первом случае решение может достигаться в точке экстремума
функции 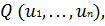
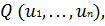 множители
множители 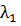
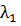 равны нулю, и задача сводится к задаче безусловного экстремума и
условия
равны нулю, и задача сводится к задаче безусловного экстремума и
условия 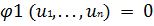
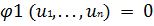 роли не играют. Во втором случае подозрительные на экстремум
точки находятся из уравнений
роли не играют. Во втором случае подозрительные на экстремум
точки находятся из уравнений 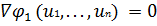
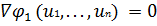 , в которых затем вычисляется значение критерия
, в которых затем вычисляется значение критерия 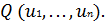
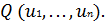
Для того, чтобы условия экстремума были справедливы и в особых
случаях, функцию Лагранжа записывают в виде
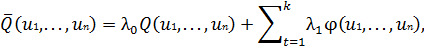
тогда можно утверждать, что для условного экстремума Q (u1,.,
un) необходимо существование таких чисел 
 ,
, 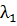
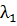 , одновременно не равных нулю, что в точке предполагаемого решения
выполнены условия
, одновременно не равных нулю, что в точке предполагаемого решения
выполнены условия 
 ≥ 0
≥ 0


 (u1,., un) =0.
(u1,., un) =0.
Требуется найти минимум функции 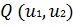
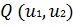 =
=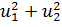
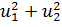 при условии
при условии
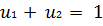
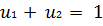 .
.
Для решения записывается функция Лагранжа

 ,
,
для которой уже необходимо определить безусловный экстремум. Необходимое
условие экстремума даст следующую систему уравнений:
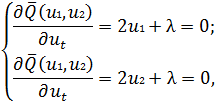
откуда 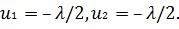
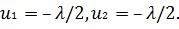 Используя уравнение связи
Используя уравнение связи 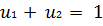
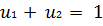 , получают
, получают 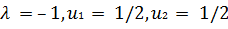
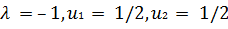 и соответственно
и соответственно 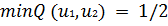
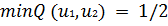 . По плану производства продукции предприятию необходимо
изготовить 180 изделий. Эти изделия могут быть изготовлены двумя
технологическими способами. При производстве u1 изделий первым способом
затраты равны (4u1 +
. По плану производства продукции предприятию необходимо
изготовить 180 изделий. Эти изделия могут быть изготовлены двумя
технологическими способами. При производстве u1 изделий первым способом
затраты равны (4u1 + 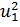
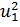 ), а при изготовлении u2 изделий вторым способом они
составляют (8u2+
), а при изготовлении u2 изделий вторым способом они
составляют (8u2+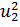
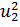 ). Определить, сколько изделий каждым из способов следует
изготовить, так чтобы общие затраты на производство продукции были
минимальными.
). Определить, сколько изделий каждым из способов следует
изготовить, так чтобы общие затраты на производство продукции были
минимальными.
Математическая постановка задачи состоит в определении
минимального значения функции 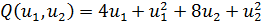
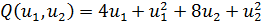 при
условиях
при
условиях
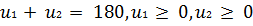
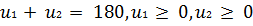 .
.
Задача может быть решена методом множителей Лагранжа. Для этого
без учета требования неотрицательности переменных составляется функция Лагранжа
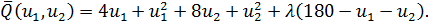
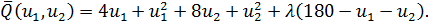
Необходимое условие экстремума функции Лагранжа дает
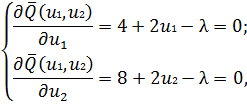
откуда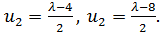
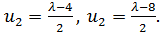
Подстановка найденных значений в условие u1 + u2 =
180 дает 

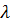
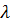 − и,
следовательно,
− и,
следовательно,
 =186 и, соответственно, u1 = 91,u2 = 89. По вторым
частным производным можно показать, что найденная точка доставляет минимум
функции Q (u1, u2), т.е. если будет изготовлено 91 изделие первым
технологическим способом и 89 изделий вторым технологическим способом, общие
затраты будут минимальны и составят Qmin = 17 278.
=186 и, соответственно, u1 = 91,u2 = 89. По вторым
частным производным можно показать, что найденная точка доставляет минимум
функции Q (u1, u2), т.е. если будет изготовлено 91 изделие первым
технологическим способом и 89 изделий вторым технологическим способом, общие
затраты будут минимальны и составят Qmin = 17 278.
1.5
Особенности реальных задач
Рассмотренные классические методы анализа предполагают
известное аналитическое выражение критерия оптимальности, имеющего производные
по всем переменным, и позволяют найти экстремум только внутри области изменения
независимых переменных. Реальные задачи решать этими методами практически
невозможно, так как они имеют ряд особенностей.
) Целевая функция не является гладкой, она может быть
"колючей" (рис.1.5), и тогда применять необходимые условия экстремума
не представляется возможным.
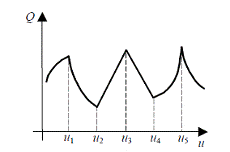
Рисунок 1.5 - "Колючая" целевая функция
) При наличии ограничений на независимые переменные минимум
целевой функции может быть на границе (рис.1.6). Необходимое условие
оптимальности позволяет найти минимум только внутри допустимой области, и в
этом случае механизм нахождения экстремума (определение первых производных и
приравнивание их нулю) теряет смысл, так как минимум таким образом определен не
будет.
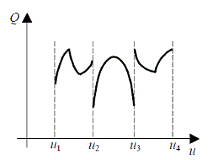
Рисунок 1.6 - Целевая функция с минимумом на границе
) Критерий оптимальности задается алгоритмически, производные
тогда можно рассчитывать только численными методами. Примером такого критерия
является прибыль, которую нельзя аналитически связать с капиталовложениями.
) Метод множителей Лагранжа предполагает наличие связей в
виде равенств. В реальных задачах существуют ограничения и в виде неравенств.
Во всех перечисленных случаях экстремум целевой функции может
быть определен, но другими методами, которые рассматриваются далее.
2. Численные
методы решения задач нелинейного программирования
Математическая формулировка задачи принятия решения эквивалентна
задаче отыскания наибольшего или наименьшего значения функции одной или нескольких
переменных. В большинстве практических задач критерий оптимальности Q (u),
где u - вектор управляющих переменных, не может быть записан в
явном виде, его значение обычно находится в результате решениясистемы уравнений
математического описания оптимизируемого объекта. На независимые переменные 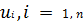
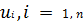 могут быть
наложены связи и ограничения как в виде равенств
могут быть
наложены связи и ограничения как в виде равенств 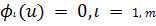
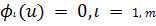 , так и в
виде неравенств
, так и в
виде неравенств 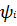
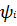

 , которые, как правило, являются нелинейными и трудно вычислимыми
соотношениями. Задачи такого типа являются предметом рассмотрения специального
раздела математики, называемого нелинейным программированием. Обычно, решения
задач нелинейного программирования могут быть найдены только численными
методами.
, которые, как правило, являются нелинейными и трудно вычислимыми
соотношениями. Задачи такого типа являются предметом рассмотрения специального
раздела математики, называемого нелинейным программированием. Обычно, решения
задач нелинейного программирования могут быть найдены только численными
методами.
2.1 Общая
характеристика методов решения задач нелинейного программирования
Нередко методы нелинейного программирования могут быть охарактеризованы
как многошаговые методы или методы улучшения исходного решения. Разнообразие
методов решения задач нелинейного программирования объясняется стремлением
найти оптимальное решение за наименьшее число шагов, чтобы избежать
необходимости многократного вычисления значений целевой функции.
В большинстве методов нелинейного программирования
используется идея движения в n-мерном пространстве в направлении
оптимума. При этом из некоторого исходного или промежуточного состояния ui
осуществляется переход в следующее состояние ui+1
изменением вектора ui на величину Δ ui, называемую шагом.
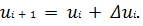
При поиске минимума целевой функции 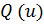
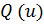 для удачно выбранного шага должно выполняться условие
для удачно выбранного шага должно выполняться условие 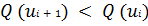
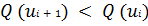 , в противном случае переход в состояние ui+1
нецелесообразен.
, в противном случае переход в состояние ui+1
нецелесообразен.
В значительной части методов шаг определяется как некоторая
функция состояния 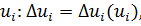
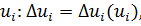 и, следовательно, новое состояние можно
рассматривать как функцию исходного состояния
и, следовательно, новое состояние можно
рассматривать как функцию исходного состояния
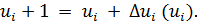
В этом смысле шаговые методы поиска оптимума называются
итеративными.
Методы нелинейного программирования в зависимости от способа
задания шага 
 подразделяются на три основных класса:
подразделяются на три основных класса:
) градиентные методы;
) безградиентные методы;
) методы случайного поиска. Некоторые методы организуются как
комбинированные алгоритмы, использующие достоинства методов различных классов.
Кроме того различают методы одномерной оптимизации (u-скаляр) и
многомерной оптимизации (u-вектор).
Задача нелинейного программирования в общем случае рассматривается
в n-мерном пространстве, где наглядное графическое изображение
отсутствует, в связи с этим используется следующий прием графического
представления.
Если целевая функция 
 непрерывна в области U, то вокруг точки uопт
всегда можно провести в данной плоскости замкнутую линию, вдоль которой
значение Q (u) постоянно (рис.2.1, а). Эти замкнутые линии называются
линиями равного уровня функции
непрерывна в области U, то вокруг точки uопт
всегда можно провести в данной плоскости замкнутую линию, вдоль которой
значение Q (u) постоянно (рис.2.1, а). Эти замкнутые линии называются
линиями равного уровня функции 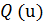
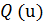 и отвечают различным значениям
и отвечают различным значениям 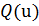
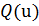 =qι. Вокруг
точки uопт можно провести сколько угодно линий уровня, причем
каждая из них будет целиком охватывает любую линию, для которой значение
целевой функции
=qι. Вокруг
точки uопт можно провести сколько угодно линий уровня, причем
каждая из них будет целиком охватывает любую линию, для которой значение
целевой функции 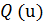
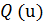 меньше (или больше).
меньше (или больше).
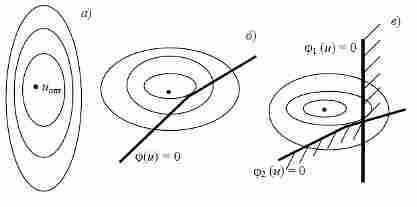
Рисунок 2.1 - Геометрическое представление целевой функции: а -
линии равного уровня; б - линии равного уровня и связи типа
равенств; в - линии равного уровня и ограничения типа неравенств
При наличии связи 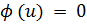
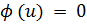 , что в n-мерном пространстве определяет (n-1) -
мерную поверхность, пересечение которой с рассматриваемой поверхностью
определяет область (рис.2.1, б), в которой и ищется оптимальное решение.
, что в n-мерном пространстве определяет (n-1) -
мерную поверхность, пересечение которой с рассматриваемой поверхностью
определяет область (рис.2.1, б), в которой и ищется оптимальное решение.
Ограничения типа неравенств независимо от их числа наглядно
представлены на рис.2.1, в. Здесь заходить в заштрихованную область
нельзя.
Особенностями целевой функции являются седловые точки, так
называемые "овраги" и многоэкстремность. В седловых точках функция 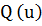
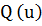 по одному или нескольким направлениям имеет минимум, в то время
как по остальным - максимум. При наличии оврагов вдоль определенных направлений
величина функции
по одному или нескольким направлениям имеет минимум, в то время
как по остальным - максимум. При наличии оврагов вдоль определенных направлений
величина функции 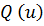
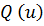 изменяется очень слабо. Целевая функция может иметь не один, а
несколько оптимумов. Оптимум называется глобальным, если для него справедливо
условие
изменяется очень слабо. Целевая функция может иметь не один, а
несколько оптимумов. Оптимум называется глобальным, если для него справедливо
условие 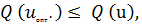
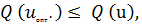
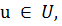
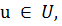 которое выполняется для любых допустимых значений u. Если
существуют другие оптимумы, то они называются локальными, и соотношения типа
которое выполняется для любых допустимых значений u. Если
существуют другие оптимумы, то они называются локальными, и соотношения типа 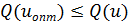
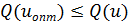 выполняется только в окрестностях точек
выполняется только в окрестностях точек 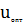
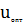 . Для отыскания глобального оптимума необходимо найти и проверить,
вообще говоря, все без исключения локальные оптимумы, имеющейся целевой
функции. Среди методов, применяемых для решения задач нелинейного
программирования значительное место занимают методы поиска решения, основанные
на анализе производных оптимизируемой функции. Эта функция должна быть
непрерывно дифференцируемой. Для этого вводится понятие производной по
направлению l
. Для отыскания глобального оптимума необходимо найти и проверить,
вообще говоря, все без исключения локальные оптимумы, имеющейся целевой
функции. Среди методов, применяемых для решения задач нелинейного
программирования значительное место занимают методы поиска решения, основанные
на анализе производных оптимизируемой функции. Эта функция должна быть
непрерывно дифференцируемой. Для этого вводится понятие производной по
направлению l
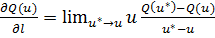
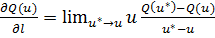 ,
,
где u, u* - точки, расположенные на прямой l.
Эта производная характеризует скорость изменения функции Q (u) в точке и
в направлении l, она может быть выражена через производные по
координатам, число которых конечно и равно размерности n. Согласно
правилу дифференцирования сложных функций, можно записать
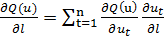
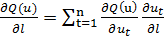 .
.
Рассмотрим расчет ∂uι /∂l в пространстве двух
переменных (рис.2.2).
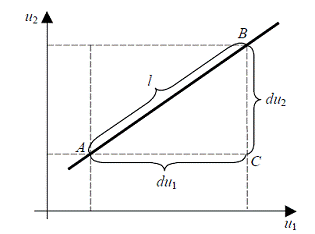
Рисунок 2.2 - К определению направляющих косинусов
Из прямоугольного треугольника АВС можно записать
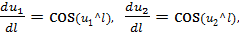
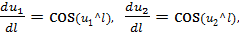
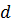
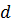 l=
l=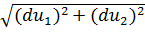
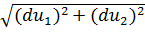 .
.
Таким образом, величины 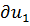
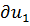 /dl есть не что иное, как направляющие косинусы выбранного
направления l по отношению к осям координат. Следовательно, можно
переписать следующим образом
/dl есть не что иное, как направляющие косинусы выбранного
направления l по отношению к осям координат. Следовательно, можно
переписать следующим образом
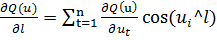
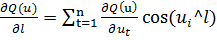 .
.
Если теперь рассмотреть поверхность равного уровня, которая имеет
(n-1) независимых переменных, то в каждой точке этой поверхности,
называемой гиперповерхностью, можно провести (n-1) взаимно
перпендикулярных касательных в соответствии с числом измерений этой
поверхности. Кроме того, в этой же точке можно провести ось, перпендикулярную
всем касательным и, следовательно, направленную по нормали к поверхности.
Подобное построение для случая (n = 3) изображено на рис.2.3
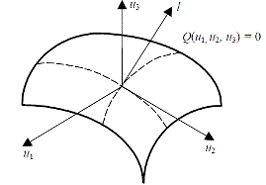
Рисунок 2.3 - Система координат, связанная с произвольной точкой
поверхности постоянного уровня
Касательные и нормаль могут рассматриваться как система координат
с началом в выбранной точке поверхности. Данная система координат обладает тем
важным свойством, что частные производные от
функции Q (u) по направлениям осей равны нулю, так
как вдоль этих направлений функция Q (u) сохраняет постоянное
значение. В соответствии со сказанным производная по произвольному направлению l
запишется как
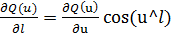
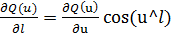 ,
,
что следует из, где производные по всем осям, за исключением
нормали, оказываются равными нулю.
Максимальное значение 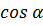
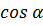 по абсолютной величине не превышает единицы, аргумент при этом
равен нулю, следовательно, направление, по которому производная
по абсолютной величине не превышает единицы, аргумент при этом
равен нулю, следовательно, направление, по которому производная 
 имеет
максимальное значение, совпадает с направлением нормали к поверхности
постоянного уровня функции
имеет
максимальное значение, совпадает с направлением нормали к поверхности
постоянного уровня функции 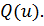
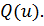 Если теперь по направлению нормали отложить вектор длиной равной,
Если теперь по направлению нормали отложить вектор длиной равной,
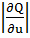
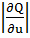 то полученный вектор называется градиентом скалярной функции
то полученный вектор называется градиентом скалярной функции 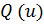
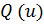 в точке u и обозначается
в точке u и обозначается 
 (u) (читается "набла ку") или (
(u) (читается "набла ку") или (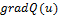
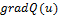 ).
).
Формулу можно записать как 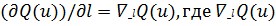
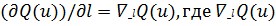 - проекция градиента функции
- проекция градиента функции 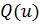
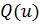 по направлению l. Отсюда следует, что проекции вектора
градиента на оси координат равны производным функции Q (u) по
соответствующим переменным, т.е.
по направлению l. Отсюда следует, что проекции вектора
градиента на оси координат равны производным функции Q (u) по
соответствующим переменным, т.е. 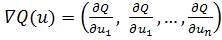
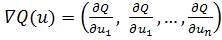 .
.
Основным свойствам градиента целевой функции является то, что
вектор градиента по направлению совпадает с направлением наискорейшего
возрастания этой функции. Именно это свойство обусловило применение градиентных
методов при решении задач нелинейного программирования.
2.2 Методы
одномерной оптимизации
Задача поиска экстремума функции одной переменной возникает при
оптимизации целевой функции, зависящей от одной скалярной переменной. Такие задачи
входят составной частью во многие итерационные методы решения задач многомерной
оптимизации. Например, численные методы поиска экстремума имеют особенность в
том, что их применение не позволяет определить точное значение
координат, при котором достигается экстремум функции. В этом случае определяют
интервал неопределенности, в котором локализуется экстремум функции. Величина
этого интервала - 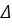
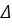 , определяется исходя из требований точности результата решения
при постановке задачи (быстродействие, точность и пр.). Таким образом,
численное решение задачи поиска экстремума функции сводится к уменьшению
интервала неопределенности от исходного до
, определяется исходя из требований точности результата решения
при постановке задачи (быстродействие, точность и пр.). Таким образом,
численное решение задачи поиска экстремума функции сводится к уменьшению
интервала неопределенности от исходного до 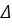
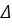 .
.
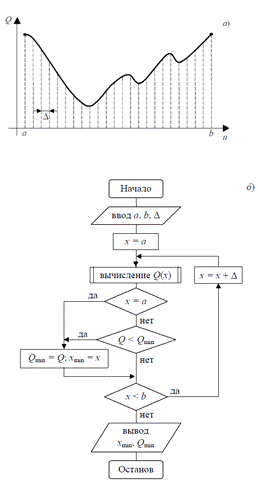
Рисунок 2.4 - Локализация экстремума методом сканирования:
а - геометрическая
интерпретация; б - блок-схема алгоритма
.2.2 Метод
половинного деления
Естественным и наиболее распространенным на практике методом
поиска экстремума функции одной переменной является метод последовательного
деления отрезка пополам. Этот метод был известен еще в древней Греции как метод
дихотомии.
Пусть требуется определить экстремум унимодальной функции Q (u)
на отрезке 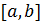
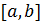 с точностью
с точностью 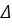
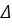 . Отрезок
. Отрезок 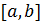
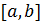 делится пополам и вычисляются значения функции Q (x1) = F1
и Q (x2) = F2 в точках
делится пополам и вычисляются значения функции Q (x1) = F1
и Q (x2) = F2 в точках
1,2=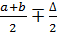
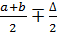 .
.
На основе анализа значений 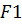
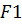 и
и 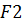
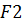 вдвое уменьшается интервал неопределенности и процесс повторяется
пока
вдвое уменьшается интервал неопределенности и процесс повторяется
пока 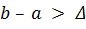
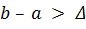 . Блок-схема этого метода приведена на рис.2.5, б.
. Блок-схема этого метода приведена на рис.2.5, б.
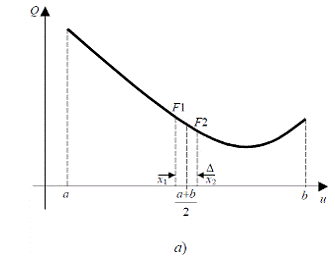
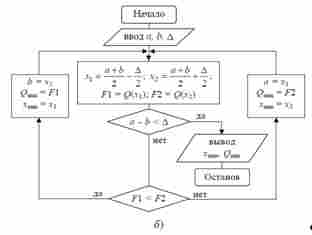
Рисунок 2.5 - Метод деления отрезка пополам: а - геометрическая
интерпретация; б - блок-схема
2.2.3 Метод
"золотого сечения"
Гораздо эффективнее, с точки зрения уменьшения затрат на
вычисления, метод "золотого сечения": интервал неопределенности
делится не пополам, как в методе дихотомии, а в определенном иррациональном
соотношении
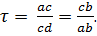
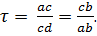
Это соотношение выполняется при
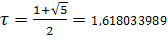
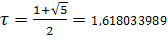 .
.
Метод заключается в том, что по заданным a и b как
можно точнее определяется значение внутренней точки x1 (см. рис.2.6, б)
по формуле
1 = b - (b - a) / 1,618033989…
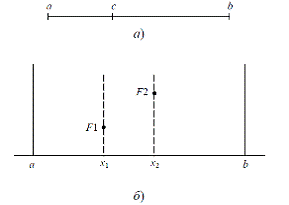
Рисунок 2.6 - Метод "золотого сечения": а - золотое
сечение; б - геометрическое представление
Точка x2 определяется как точка, симметричная точке x1
на отрезке (a-b).
На основе анализа значений F1 = Q (x1) и F2 =
Q (x2) интервал неопределенности сокращается путем отбрасывания из
рассмотрения отрезка в котором экстремум исключен, исходя из условий
уни-модальности Q (u). Далее мы определим симметричную точку внутри
новых границ, вычисляем значение Q в этой точке, проводим анализ и т.д.
до тех пор, пока разность между симметричными точками внутри интервала
неопределенности больше 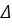
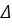 . Блок-схема алгоритма метода "золотого сечения"
представлена на рис.2.7.
. Блок-схема алгоритма метода "золотого сечения"
представлена на рис.2.7.
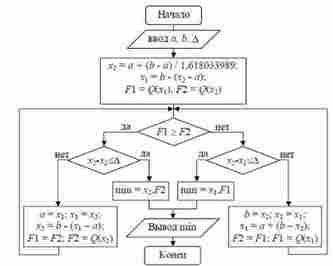
Рисунок 2.7 - Блок-схема метода "золотого сечения"
2.2.4 Метод
Фибоначчи
Метод, использующий числа Фибоначчи, позволяет наиболее
эффективно достичь заданной точности в поиске экстремума функции Q (u).
Числа Фибоначчи определяются соотношением
0 = F1 = 1; Fk = Fk-1 + Fk-2; k = 2,
3, …
При большом "k" отношение соседних чисел
Фибоначчи близко к отношению "золотого сечения".
Этот метод делит интервал неопределенности не в постоянном
соотношении, а в переменном и предполагает некоторое, вполне определенное,
зависящее от 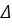
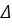 , число вычислений значений функции Q (u).
, число вычислений значений функции Q (u).
По заданному 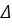
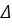 определяется количество вычислений n и соответствующее ему
число Фибоначчи Fn, исходя из соотношения
определяется количество вычислений n и соответствующее ему
число Фибоначчи Fn, исходя из соотношения
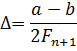
В остальном схема метода близка к методу "золотого
сечения" в котором значение x1 и x2 (см. рис.2.8)
определяются отношением соответствующих чисел Фибоначчи.
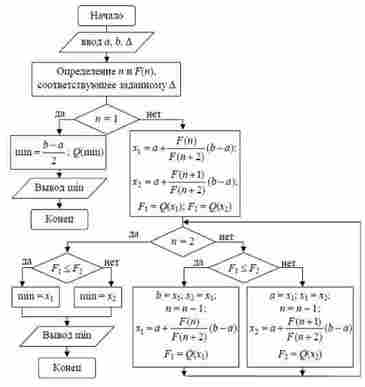
Рис.2.8 - Блок-схема метода Фибоначчи
2.3 Методы
многомерной оптимизации
В настоящее время разработано огромное число методов
многомерной оптимизации, охватывающие почти все возможные случаи. Здесь
рассматривается лишь несколько основных, считающихся классическими, методов поиска
экстремума функции многих переменных.
Смысл всех методов нахождения безусловного экстремума функции
нескольких переменных заключается в том, что по определенному правилу
выбирается последовательность значений {uι} вектора u такая, что 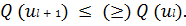
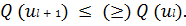 Так как целевая функция предполагается ограниченной, то такая
последовательность ее значений стремится к пределу.
Так как целевая функция предполагается ограниченной, то такая
последовательность ее значений стремится к пределу.
В зависимости от принятого алгоритма и выбора начальной точки этим
пределом может быть локальный или глобальный экстремум функции Q (u).
2.3.1 Метод
Гаусса-Зайделя
Метод заключается в последовательном определении экстремума
функции одной переменной с точностью до ε вдоль каждой координаты,
т.е. фиксируются все координаты, кроме одной, по которой и осуществляется поиск
экстремума Q. Потом та же процедура осуществляется при фиксации
следующей координаты.
После рассмотрения всех n координат выполняется
возврат к первой и вновь производится поиск локального экстремума вдоль каждой
из n координат до тех пор, пока экстремум не будет локализован с
заданной точностью (см. рис.2.9).
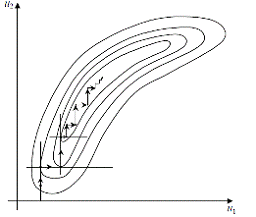
Рисунок 2.9 - Характер движения к оптимуму в методе
Гаусса-Зейделя
2.3.2 Метод
градиента
В этом методе используется градиент целевой функции, шаги
совершаются по направлению наибыстрейшего уменьшения целевой функции, что,
естественно, ускоряет процесс поиска оптимума.
Идея метода заключается в том, что находятся значения частных
производных по всем независимым переменным 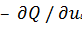
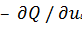 ,
, 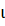
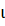 = 1, n, которые определяют направление градиента в
рассматриваемой точке
= 1, n, которые определяют направление градиента в
рассматриваемой точке 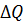
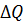 =
=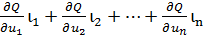
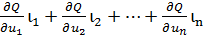 , и осуществляется шаг в направлении обратном направлению
градиента, т.е. в направлении наибыстрейшего убывания целевой функции (если
ищется минимум). Итерационный процесс имеет вид
, и осуществляется шаг в направлении обратном направлению
градиента, т.е. в направлении наибыстрейшего убывания целевой функции (если
ищется минимум). Итерационный процесс имеет вид 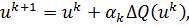 где параметр
где параметр 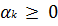
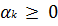 задает длину шага.
задает длину шага.
Алгоритм метода градиента при непосредственном его применении
включает в себя следующие этапы: 1) Задается начальное значение вектора
независимых переменных (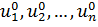
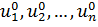 ), определяющего точку, из которой начинается движение к минимуму.
2) Рассчитывается значение целевой функции в начальной точке
), определяющего точку, из которой начинается движение к минимуму.
2) Рассчитывается значение целевой функции в начальной точке 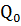
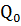 (
(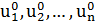
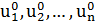 ). 3) Определяется направление градиента в начальной точке
(рис.2.10).
). 3) Определяется направление градиента в начальной точке
(рис.2.10).
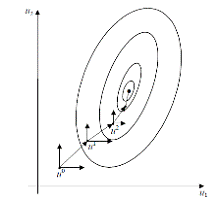
Рисунок 2.10 - Характер движения к оптимуму в методе градиента
) Делается шаг в направлении антиградиента при поиске минимума, в
результате чего попадают в точку 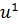
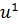 .
.
) Процесс поиска продолжается, повторяя все этапы с п.2, т.е.
вычисляется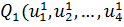
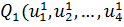 ) определяется направление градиента в точке u1,
делается шаг и т.д.
) определяется направление градиента в точке u1,
делается шаг и т.д.
Важной задачей в этом методе является выбор шага. Если размер шага
слишком мал, то движение к оптимуму будет долгим из-за необходимости расчета
целевой функции и ее частных производных в очень многих точках. Если же шаг
будет выбран слишком большим, то в районе оптимума может возникнуть
"рыскание", которое либо затухает слишком медленно, либо совсем не
затухает. На практике сначала шаг выбирается произвольно. Если окажется, что
направление градиента в точке u1 существенно отличается от направления в
точке u2, то шаг уменьшают, если отличие векторов по
направлению мало, то шаг увеличивают. Изменение направления градиента можно
определять по углу поворота градиента рассчитываемого на каждом шаге по
соответствующим выражениям.
Итерационный процесс поиска обычно прекращается, если выполняются
неравенства 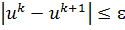
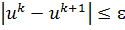 ,
, 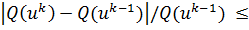
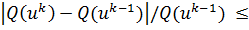 ∂,
∂, 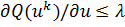
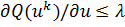 , где
, где 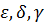
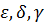 - заданные числа. Недостатком градиентного метода является то,
что при его использовании можно обнаружить только локальный минимум целевой
функции. Для нахождения других локальных минимумов поиск необходимо производить
из других начальных точек.
- заданные числа. Недостатком градиентного метода является то,
что при его использовании можно обнаружить только локальный минимум целевой
функции. Для нахождения других локальных минимумов поиск необходимо производить
из других начальных точек.
2.3.3 Метод
наискорейшего спуска
При применении метода градиента на каждом шаге вычисляются
значения всех частных производных оптимизируемой функции Q по всем
независимым переменным U, что при большом числе этих переменных приводит
к весьма большому времени поиска оптимума. Сократить время поиска позволяет
метод наискорейшего спуска, блок-схема, где 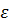
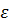 - точность вычисления, H - величина шага, n - размерность
вектора u, Q - алгоритм вычисления целевой функции Q (u), L
- количество шагов по конкретному направлению градиента функции Q. Таким
образом, в начальной точке u0 определяется градиент целевой функции
- точность вычисления, H - величина шага, n - размерность
вектора u, Q - алгоритм вычисления целевой функции Q (u), L
- количество шагов по конкретному направлению градиента функции Q. Таким
образом, в начальной точке u0 определяется градиент целевой функции 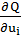
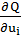 и, следовательно, направление ее наибыстрейшего убывания; далее
делается шаг спуска в этом направлении. Если значение целевой функции
уменьшились, то делается следующий шаг в этом же самом направлении.
и, следовательно, направление ее наибыстрейшего убывания; далее
делается шаг спуска в этом направлении. Если значение целевой функции
уменьшились, то делается следующий шаг в этом же самом направлении.
Процедура повторяется до тех пор, пока в этом направлении не будет
найден минимум, после чего только вычисляется градиент и определяется новое
направление наибыстрейшего убывания целевой функции.
По сравнению с методом градиента метод наискорейшего спуска
оказывается более выгодным из-за сокращения объема вычислений. Чем менее резко
изменяется направление градиента целевой функции, тем выгоднее использовать
метод наискорейшего спуска, т.е. вдали от оптимума. Вблизи оптимума
рассматриваемый метод автоматически переходит в метод градиента. Окончание
поиска происходит в соответствии с теми же критериями, что и в методе
градиента.
2.3.4 Метод
квантования симплексов
Симплексный метод относится к группе безградиентных методов
детерминированного поиска. Основная идея метода заключается в том, что по
известным значениям функции в вершинах выпуклого многогранника, называемого
симплексом, находится направление, в котором требуется сделать следующий шаг,
чтобы получить наибольшее уменьшение (увеличение) критерия оптимальности. Примером
симплекса на плоскости является треугольник, в трехмерном пространстве -
четырехгранная пирамида, в n-мерном пространстве - многогранник с n +
1 вершиной. Основным свойством симплекса является то, что против любой из
вершин симплекса расположена только одна грань, на которой можно построить
новый симплекс, отличающийся от прежнего расположением новой вершины, остальные
вершины обоих симплексов - совпадают.
Наглядную иллюстрацию симплексного метода удобнее
рассматривать на примере задачи отыскания минимального значения целевой функции
двух независимых переменных (рис.2.11).
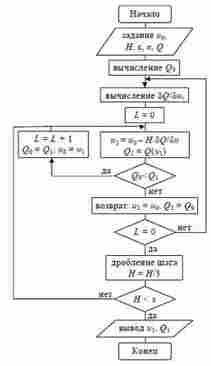
Рисунок 2.11 - Блок-схема метода наискорейшего спуска
Алгоритм поиска заключается в следующем.
) Определяются значения целевой функции в трех точках S10,
S20, S30, соответствующих вершинам симплекса. Из найденных
значений выбирается наибольшее. В рассматриваемом примере - это S10
(рис.2.12).
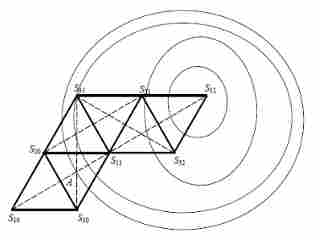
Рисунок 2.12 - Поиск оптимума симплексным методом
) Строится новый симплекс, для этого вершина S10
исходного симплекса заменяется вершиной S11, расположенной симметрично
вершине S10 относительно центра грани, расположенной против вершины S10.
Построение нового симплекса S20 S30 S11 осуществляется
определением центра А стороны S20 S30 треугольника S10
S20 S30, после чего проводится прямая S10A, на
продолжении которой откладывается отрезок АS11 равный S10А.
) Вычисляется значение целевой функции в вершине S11,
которое сравнивается с известными значениями в вершинах S20 и S30.
В результате определяется вершина S30 с наибольшем значением целевой
функции, подлежащая исключению при построении следующего симплекса S11 S20
S31.
Исключение из рассмотренных вершин симплексов с наибольшим
значением целевой функции приводит к сходимости процесса к минимальному
значению.
При использовании симплексного метода возможно зацикливание
вблизи оптимума, которое приводит к тому, что при исключении вершины образуется
не новый, а предыдущий симплекс. Для устранения зацикливания достаточно
изменить размеры симплекса в сторону его уменьшения, т.е. уменьшить шаг спуска
в районе оптимума. Если зацикливание возникает вновь, то размеры симплекса
уменьшаются до тех пор, пока не будет достигнута требуемая точность определения
оптимума.
Критерием окончания поиска могут служить размеры симплекса.
Поиск можно прекратить, если все ребра симплекса станут меньше заданной
достаточно малой величины.
2.3.5 Поиск
при наличии "оврагов" целевой функции
Если целевая функция имеет "овраги", то
рассмотренные методы поиска экстремума этой функции малоэффективны, так как
будет найдено дно "оврага", и далее применяемые методы застрянут на
этом дне. Поэтому для решения оптимальных задач, в которых целевая функция
имеет особенности типа "оврагов" разработаны специальные методы. Одним
из таких методов является метод шагов по "оврагу", алгоритм которого
заключается в следующем.
) Все независимые переменные разбиваются на две группы:
первая группа включает в себя переменные, изменение которых существенно влияет
на значение целевой функции, вторая группа содержит переменные, при изменении
которых значение целевой функции изменяется не столь значительно.
) Выбирается начальная точка u0, из которой
производится поиск, будем считать для определенности, минимума любым методом
локального поиска. Этот поиск закончится на дне "оврага", в
результате чего будет найдена некоторая критическая точка u1….
(рис.2.13).

Рисунок 2.13 - Метод "оврагов"
) Из состояния 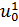
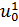 производится поиск минимума, в результате которого определяется
еще одна критическая точка u2, расположенная на дне "оврага"
(рис.2.13).
производится поиск минимума, в результате которого определяется
еще одна критическая точка u2, расположенная на дне "оврага"
(рис.2.13).
) Две найденные критические точки u1 и u2 соединяются
прямой и выполняется "шаг по оврагу" в направлении убывания целевой
функции. Это дает новое исходное состояние 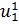
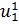 .
.
) Из состояния 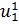
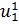 производится спуск на "дно оврага" и находится
критическая точка u3. Далее определяется состояние
производится спуск на "дно оврага" и находится
критическая точка u3. Далее определяется состояние 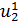
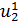 и т.д. (рис.2.13).
и т.д. (рис.2.13).
Процесс поиска продолжается до тех пор, пока значение целевой
функции во вновь найденной критической точке 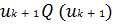
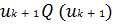 не окажется больше, чем в предыдущей точке
не окажется больше, чем в предыдущей точке 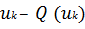
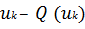 . Минимум в этом случае находится между точками uk-1 и uk+1.
Далее процесс поиска можно повторить, но уже с меньшими "шагами по
оврагу", пока не будет достигнута требуемая точность.
. Минимум в этом случае находится между точками uk-1 и uk+1.
Далее процесс поиска можно повторить, но уже с меньшими "шагами по
оврагу", пока не будет достигнута требуемая точность.
В результате поиска могут возникнуть различные ситуации. Например,
когда все переменные примерно одинаково влияют на значение оптимизируемой
функции, но, тем не менее, "овраг" существует. В этом случае для
поиска состояния 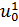
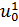 можно сделать любой шаг из начального состояния u0, далее
поиск продолжается по описанному выше алгоритму.
можно сделать любой шаг из начального состояния u0, далее
поиск продолжается по описанному выше алгоритму.
2.4 Методы
поиска условного экстремума
При рассмотрении реальных задач оптимизации на переменные
состояния накладываются условия типа равенств или неравенств, которые задают
область изменения независимых переменных.
Задача нелинейного программирования в этом случае формулируется
следующим образом: требуется найти оптимум (минимум) функции Q (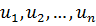
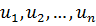 ) при
) при 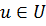
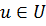 и условия,
что
и условия,
что 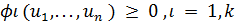
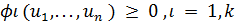 .
.
Число условий типа неравенств может быть любым, т.е. меньше или
больше числа независимых переменных. Если при решении такой задачи экстремум
целевой функции будет находится внутри допустимой области изменения независимых
переменных 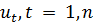
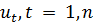 ,
ограниченной неравенствами
,
ограниченной неравенствами 
 , то в некоторых случаях эту задачу можно решить рассмотренными
выше методами поиска без учета ограничений. Вести поиск подобным образом при
наличии условий типа равенств обычно невозможно. Если же экстремум целевой
функции будет расположен на границе допустимой области, то для его отыскания
применяют специальные методы.
, то в некоторых случаях эту задачу можно решить рассмотренными
выше методами поиска без учета ограничений. Вести поиск подобным образом при
наличии условий типа равенств обычно невозможно. Если же экстремум целевой
функции будет расположен на границе допустимой области, то для его отыскания
применяют специальные методы.
2.4.1 Метод
проектирования вектора-градиента
При решении задач поиска максимума функции 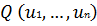
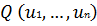 с ограничениями типа неравенств вида
с ограничениями типа неравенств вида 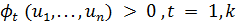
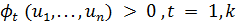 часто
используется метод проектирования вектора-градиента. Согласно этому методу
движение к оптимуму происходит вдоль границы допустимой области. Степень
нарушения ограничений определяется функцией H (u) =
часто
используется метод проектирования вектора-градиента. Согласно этому методу
движение к оптимуму происходит вдоль границы допустимой области. Степень
нарушения ограничений определяется функцией H (u) =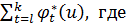
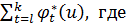 ,
, 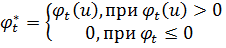
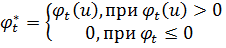 , т.е. внутри допустимой области U функция H (u)
тождественно равна нулю. При таком подходе к решению задачи положение точки при
выполнении очередного шага должны оставаться за пределами области U, где
градиент функции H (u) отличен от нуля. Если в результате выполнения
очередного шага произойдет слишком большое нарушение ограничений, то коррекция
этого нарушения должна осуществляться до того положения, пока функция H (u)
еще отлична от нуля.
, т.е. внутри допустимой области U функция H (u)
тождественно равна нулю. При таком подходе к решению задачи положение точки при
выполнении очередного шага должны оставаться за пределами области U, где
градиент функции H (u) отличен от нуля. Если в результате выполнения
очередного шага произойдет слишком большое нарушение ограничений, то коррекция
этого нарушения должна осуществляться до того положения, пока функция H (u)
еще отлична от нуля.
Движение вдоль границы ограничений будет продолжаться до тех пор,
пока не будет выполняться условие 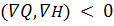
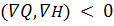 , т.е. пока искомый оптимум находится за пределами касательной
плоскости, проведенной через рассматриваемую точку, расположенную на границе.
Иллюстрация метода представлена на рис.2.14.
, т.е. пока искомый оптимум находится за пределами касательной
плоскости, проведенной через рассматриваемую точку, расположенную на границе.
Иллюстрация метода представлена на рис.2.14.
Если условие 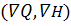
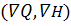 < 0 оказывается нарушенным, то происходит "отрыв" от
границы области U и дальнейший подъем будет происходить уже без влияния
ограничений (рис.2.14, точка u3).
< 0 оказывается нарушенным, то происходит "отрыв" от
границы области U и дальнейший подъем будет происходить уже без влияния
ограничений (рис.2.14, точка u3).
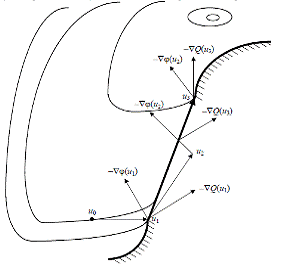
Рисунок 2.14 - Поиск оптимума методом проектирования
вектора-градиента при наличии ограничений типа неравенств
2.4.2 Метод
ажурной строчки
Этот метод заключается в зигзагообразном движении вдоль
границы. Идея этого метода при использовании его в задачах с ограничениями типа
неравенств, а также равенств заключается в следующем.
Без учета ограничений ищется оптимум любым методом спуска до
тех пор пока некоторые неравенства не будут нарушены. Как только произойдет
нарушение одного или нескольких ограничений спуск прекращается и осуществляется
возврат в допустимую область изменения переменных ui по направлению
антиградиентов к тем гиперповерхностям, ограничения которых оказались нарушенными.
Таким образом, выбирая в качестве поискового метода метод
градиента, движемся до границы и попадаем в запрещенную точку. Далее забываемо
целевой функции и движемся вдоль границы (рис.2.15).
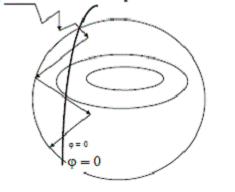
Рисунок 2.15 - Поиск оптимума методом ажурной строчки
Вычисляется градиент функции ? (u) и осуществляется возврат в допустимую область.
Следующий шаг делается опять по градиенту целевой функции Q (u) и т.д.
Сложность метода заключается в выборе алгоритма уменьшения шага и правила
остановки. Это зависит от опыта и способностей программиста и определяется его
творчеством.
2.5 Проблемы
поиска глобального экстремума
Исследуемая функция может иметь несколько экстремумов. Если
для всех значений независимых переменных выполняется условие
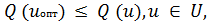
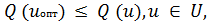 то экстремум в точке uопт называется глобальным, другие
экстремумы называются локальными.
то экстремум в точке uопт называется глобальным, другие
экстремумы называются локальными.
Поскольку заранее число экстремумов функции Q (u)
неизвестно, то для нахождения глобального экстремума необходимо, вообще говоря,
найти и проверить все без исключения локальные экстремумы, имеющиеся у целевой
функции решаемой задачи. С этой целью осуществляется поиск из различных
начальных точек, для чего область изменения независимых переменных ui покрывается
сеткой и начальная точка ui0 выбирается из областей, полученных в
результате проведенного сканирования.
Также для поиска глобального экстремума используют случайный
поиск, в частности, методы Мон-те-Карло. Здесь экстремум находится с какой-то
вероятностью. В заключение следует отметить, что большое разнообразие методов
нелинейного программирования свидетельствует, прежде всего, о сложности
проблемы поиска и трудностях в оценке эффективности использования того или
иного метода при решении конкретной задачи. Следует сопоставлять практическую
эффективность вычислительных возможностей разных методов. Методы нелинейного
программирования служат не только для решения специфических задач, но являются
также необходимым средством, к которому обращаются при решении оптимальных
задач, а также задач вычислительной математики. По мере развития
математического моделирования роль этих методов будет несомненно вырастать, что
приведет к более глубокой разработке существующих и созданию новых алгоритмов
поиска экстремума в задачах нелинейного программирования.
3. Численные
методы решения задач нелинейного программирования
3.1
Графический метод решения задач нелинейного программирования
Рассмотрим задачу нелинейного программирования, содержащую
только две переменные, записанную в виде
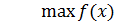
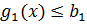
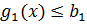 ,…………….
,…………….
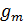
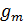 (x) <
(x) <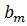
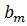 , x = (
, x = (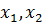
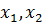 )
) 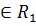
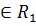 .
.
Как уже отмечалось, функция f (x) называется целевой функцией, а
неравенства 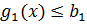
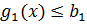 , i= 1,.,m называются ограничениями задачи. Множество точек,
удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.
, i= 1,.,m называются ограничениями задачи. Множество точек,
удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.
Решить задачу нелинейного программирования графически - значит
найти такую точку из допустимого множества, через которую проходит линия уровня
f (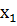
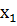 ,
,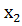
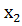 ) = С, имеющая максимальное значение величины С из всех линий
уровня, проходящих через допустимые точки задачи.
) = С, имеющая максимальное значение величины С из всех линий
уровня, проходящих через допустимые точки задачи.
Как и в случае задач линейного программирования, для задач
нелинейного программирования, содержащих только две переменные, возможна
графическая интерпретация.
Наиболее существенное отличие задачи нелинейного программирования
от линейных задач заключается в том, что оптимальное решение может находиться
как на границе допустимого множества, так и являться его внутренней точкой.
Этапы графического решения задач нелинейного программирования можно
сформулировать следующим образом.
Этап 1. На плоскости наносятся геометрические места точек,
соответствующих каждому уравнению из ограничений задачи 
 (x) =
(x) =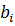
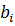 , i= 1,.,m. Строится допустимое множество задачи. Если допустимое
множество задачи пусто, то задача не имеет решения.
, i= 1,.,m. Строится допустимое множество задачи. Если допустимое
множество задачи пусто, то задача не имеет решения.
Этап 2. Строятся линии уровня целевой функции f (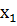
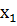 ,
,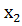
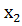 ) = С при различных значениях параметра С.
) = С при различных значениях параметра С.
Этап 3. Определяется направление возрастания (для задачи
максимизации) или убывания (для задачи минимизации) линий уровня целевой
функции.
Этап 4. Определяется точка допустимого множества, через которую
проходит линия уровня с максимальным (для задачи максимизации) или минимальным
(для задачи минимизации) значением параметра С. Если целевая функция не
ограничена сверху (для задачи максимизации) или не ограничена снизу (для задачи
минимизации) на допустимом множестве, то задача не имеет решения.
Этап 5. Для найденной точки определяют ее координаты 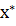
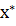 = (
= (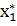
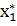 ,
,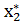
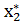 )
) 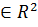
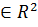 и значение целевой функции в данной точке f= (
и значение целевой функции в данной точке f= (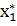
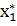 ,
,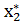
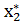 )
)
Решим следующую задачу нелинейного программирования, используя
геометрическую интерпретацию
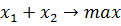
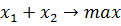 ,
,

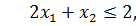
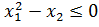
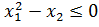 .
.
Построим линии, соответствующие ограничениям задачи и вычислим
область определения функции (рис.3.1).
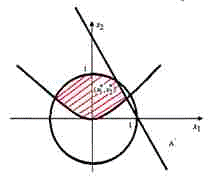
Рисунок 3.1 - Область определения функции
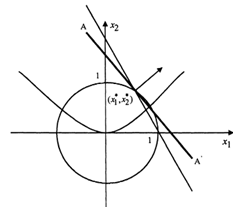
Рисунок 3.2 - Линия уровня функции
Линия уровня, соответствующая максимальному параметру С и
проходящая через какую-либо точку допустимого множества, изображена на рисунке
3.2 АА’. Координаты оптимальной точки находятся из системы уравнений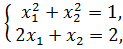
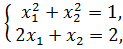 откуда
откуда 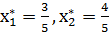
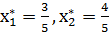 .
.
.2 Метод
множителей Лагранжа
Пусть требуется решить задачу нелинейного программирования
следующего вида:
F (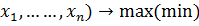
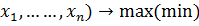 ,
,
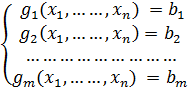
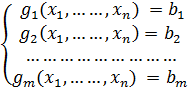 ,
,
где функции f и 
 , i=
, i=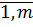
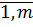 непрерывны, и непрерывны их частные производные по
непрерывны, и непрерывны их частные производные по 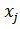
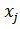 , l=
, l=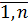
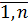 .
.
Для решения поставленной задачи может быть применен метод
множителей Лагранжа. Объясним идею метода на примере задачи нелинейного
программирования, зависящей от двух переменных и имеющие только одно
ограничение:
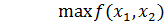
g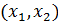
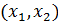 =b.
=b.
Будем исходить из геометрической интерпретации задачи. А именно,
заметим, что линия уровня с максимальным значением параметра С будет касаться
линии границы в точке, являющейся оптимальным решением задачи (рис.3.3).

Рисунок 3.3 - Геометрическая интерпретация задачи
Поскольку две гладкие линии (имеющие непрерывные частные
производные) касаются друг друга в точке 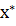
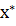 , то их векторы-нормали сонаправлены. Поскольку вектор-нормаль
есть градиенты функций (вектор частных производных), то справедливо векторное
соотношение f’ (
, то их векторы-нормали сонаправлены. Поскольку вектор-нормаль
есть градиенты функций (вектор частных производных), то справедливо векторное
соотношение f’ (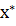
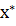 ) =λg’ (
) =λg’ (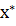
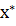 ), где λ есть
некоторый коэффициент пропорциональности. Координаторами векторов f’ (
), где λ есть
некоторый коэффициент пропорциональности. Координаторами векторов f’ (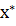
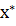 ) и g’ (
) и g’ (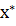
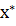 ), являются значения частных производных функций f и g
соответственно в точке
), являются значения частных производных функций f и g
соответственно в точке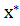
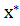 .
.
’ (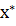
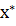 ) =
) =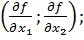
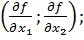 ’ (
’ (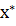
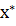 ) =
) =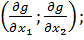
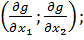
Из условия пропорциональности в точке 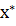
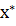 имеем
имеем
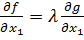
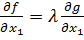 ;
;
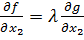
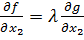 .
.
Для определения значений 
 и
и 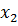
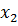 в которых функция f достигает максимума, к этим уравнениям надо
добавить условие принадлежности точки
в которых функция f достигает максимума, к этим уравнениям надо
добавить условие принадлежности точки 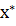
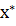 графику функции g (
графику функции g (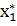
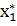 ,
,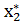
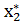 ) =b.
) =b.
Окончательно получаем систему уравнений, определяющую оптимальное
решение поставленной задачи
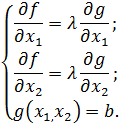
Введем новую функцию
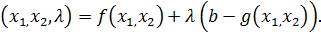
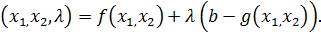
Тогда последняя система перепишется в виде
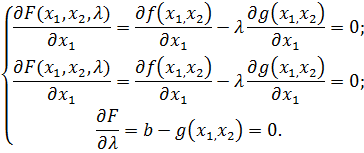
Функцию F называют функцией Лагранжа.
Этап 1. Составляют функцию Лагранжа
(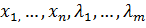
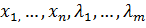 ) =f (
) =f (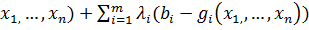
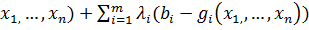 .
.
Этап 2. Находят частные производные функции Лагранжа по 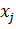
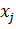 и
и 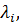
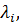 i=1,n; j=1,m и приравнивают их к нулю
i=1,n; j=1,m и приравнивают их к нулю
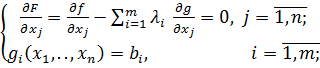
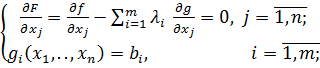 .
.
Этап З. Решают систему и определяют точки, в которых функция 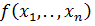
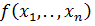 может иметь экстремум.
может иметь экстремум.
Этап 4. Проверяют полученные на этапе 3 точки на экстремум и определяют
экстремальное значение функции f найденной точки.
Рассмотрим применение изученных методов на примере решения задачи
оптимальной реализации продукции, в частности для расчета
экономико-математической модели при нелинейных затратах на производство. Фирма
реализует автомобили двумя способами: через магазин и через торговых агентов.
При реализации 
 автомобилей через магазин расходы на реализацию составляют 4
автомобилей через магазин расходы на реализацию составляют 4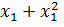
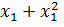 усл. ед., а при продаже
усл. ед., а при продаже 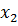
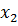 автомобилей через торговых агентов расходы составляют
автомобилей через торговых агентов расходы составляют 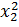
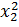 усл. ед. Найти оптимальный способ реализации автомобилей,
минимизирующий суммарные расходы, если общее число предназначенных для продажи
автомобилей составляет 200 шт. Составим математическую модель задачи. Целью
является минимизация суммарных расходов R =4
усл. ед. Найти оптимальный способ реализации автомобилей,
минимизирующий суммарные расходы, если общее число предназначенных для продажи
автомобилей составляет 200 шт. Составим математическую модель задачи. Целью
является минимизация суммарных расходов R =4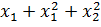
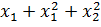 . Управляющие переменные - это число автомобилей, реализуемых
первым и вторым способом:
. Управляющие переменные - это число автомобилей, реализуемых
первым и вторым способом: 
 и
и 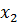
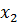 соответственно (200 шт.). Окончательно математическая модель имеет
следующий вид:
соответственно (200 шт.). Окончательно математическая модель имеет
следующий вид:
=4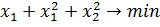
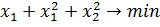 ,
,
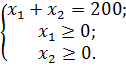
Для ее расчета применим метод множителей Лагранжа. Функция
Лагранжа имеет вид
(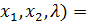
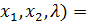 4
4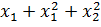
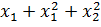 +λ (200-
+λ (200-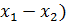
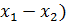 .
.
Найдем частные производные функции F по 
 ,
, 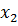
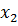 и λ и
приравняем их к нулю.
и λ и
приравняем их к нулю.
Получим следующую систему уравнений:

Решая систему, найдем 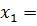
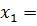 99,
99, 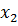
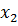 = 101,
= 101, 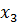
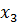 = 202, f (
= 202, f (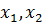
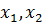 ) = 20 398.
) = 20 398.
Таким образом, для получения минимальных расходов, нужно
реализовать 99 автомобилей через магазин и 101 автомобиль через торговых
агентов. При этом расходы на реализацию составят 20 398 усл. ед.
.3
Компьютерная реализация решений задач нелинейного программирования
3.3.1 Решение
задач нелинейного программирования в среде приложения Excel
Рассмотрим примеры нелинейной оптимизационной экономической
задачи, её экономико-математическую модель и метод компьютерной реализации в
среде пакета Excel.
Особенности компьютерной реализации
Задача (модель) нелинейного программирования формулируется так же,
как и общая задача оптимального программирования со следующими требованиями к
целевой функции и допустимой области: целевой функции f (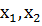
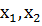 ,.,
,., 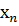
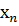 ) и (или) одна из функций
) и (или) одна из функций 
 (
(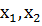
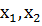 ,.,
,., 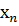
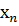 ) являются нелинейными: min (max)
) являются нелинейными: min (max)
(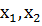
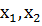 ,.,
,., 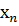
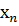 ),
),

 (
(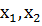
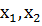 ,.,
,., 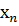
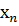 ) {
) {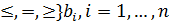
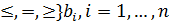 .
.
У произвольной задачи нелинейного программирования некоторые или
все свойства, характерные для задач линейного программирования, отсутствуют.
Вследствие этого задачи нелинейного программирования несравнимо сложнее задач
линейного программирования, и для них не существует общего универсального
метода их решения (аналогично симплексному методу).
Есть целый ряд методов решения задач нелинейного программирования.
В пакете Excel реализован метод множителей Лагранжа, идея которого заключается
в преобразовании задачи условной оптимизации в задачу безусловной оптимизации,
решение которой производится методами поиска - градиентными методами (методы
первого порядка) или методами Ньютона (методы второго порядка). Наиболее
распространенными являются градиентные методы.
Необходимо помнить, что существующие методы дают возможность
находить только локальные оптимумы (помимо случаев, когда задачи обладают
соответствующими свойствами выпуклости и вогнутости). Если же есть подозрение,
что в допустимой области целевой функции может иметь несколько оптимумов, то
эту область следует разбить на ряд областей и в каждой из них определить свои
локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В
таком практическом подходе задача поиска глобального оптимума сводится к
решению ряда задач, в которых ищется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач
оптимизации существует только один оптимум.
Решение задачи нелинейного программирования (реализация модели
нелинейной оптимизации) средствами Excel отличается от решения линейного
программирования следующим:
назначаются начальные значения искомых переменных так, чтобы ЦФ в
начальной точке не была равна нулю, 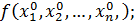
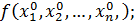
в диалоговом окне Поиск решения в режиме Параметры не надо вводить
Линейная модель.
В Excel признаком достижения оптимума является величина
относительного приращения целевой функции на каждой итерации 
 . Оптимум считается достигнутым, если выполняется условие
. Оптимум считается достигнутым, если выполняется условие 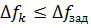
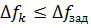 , где
, где 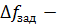
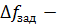 точность, назначаемая при решении задачи (Параметры).
точность, назначаемая при решении задачи (Параметры).
Примером задачи нелинейного программирования является модель
оптимального формирования портфеля ценных бумаг (модель Марковица минимального
риска).
В этой модели приняты следующие обозначения:
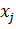
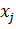 , - доля капитала, потраченная на покупку ценных бумагу j-го вида
(весь выделенный капитал принимается за 1);
, - доля капитала, потраченная на покупку ценных бумагу j-го вида
(весь выделенный капитал принимается за 1);
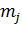
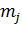 - средняя ожидаемая доходность j-й ценной бумаги, (mj называют
эффективностью j-й ценной бумаги);
- средняя ожидаемая доходность j-й ценной бумаги, (mj называют
эффективностью j-й ценной бумаги);
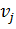
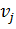 - дисперсия случайной доходности j-й ценной бумаги, (называют
риском j-й ценной бумаги).
- дисперсия случайной доходности j-й ценной бумаги, (называют
риском j-й ценной бумаги).
В предположении о некоррелированности ценных бумаг (их
независимости) модель Марковица имеет вид:
Найти 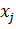
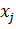 ,j=1,…,n, минимизирующие риск портфеля ценных бумаг
,j=1,…,n, минимизирующие риск портфеля ценных бумаг
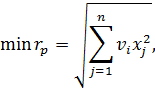
при условии, что обеспечивается заданное значение эффективности
портфеля mp, т.е.
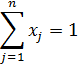
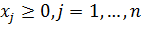
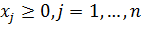 .
.
Нелинейной является целевой функции.
Задачи оптимизации, в результате решения которых искомые значения
переменных должны быть целыми числами, называются задачами (моделями)
целочисленного (дискретного) программирования:
(max) f (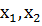
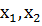 ,.,
,., 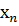
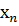 )
)

 (
(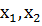
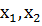 ,.,
,., 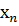
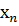 ) {
) {


Если множество индексов 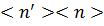
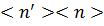 ={1,2,.,n}, то задачу называют полностью целочисленной, если
={1,2,.,n}, то задачу называют полностью целочисленной, если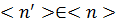
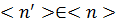 , то - частично целочисленной.
, то - частично целочисленной.
Рассмотрим задачу оптимального формирования портфеля ценных бумаг.
Необходимо сформировать оптимальный портфель Марковица (минимального риска)
трех ценных бумаг с эффективностями и рисками: (4,10), (10, 40), (40, 80).
Нижняя граница доходности портфеля задана равной 15. Построим
экономико-математическая модель. Введем необходимые обозначения, пусть хj
(j =1, 2,3) - число предметов j-го типа, которое следует
погрузить на баржу. Тогда математическая модель задачи о подборе для баржи
допустимого груза максимальной ценности запишется следующим образом:
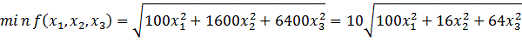
4x1 + 10x2 + 40х3
≥ 15
x1 + x2 + x3
= 1
xj
≥ 0, j = 1, 2, 3.
Заполняем рабочий лист данными.
x1 = 0,5213, х2 = 0, 2078,
х3 = 0,2709,т.е. доли ценных бумаг оказались равными 52,13 %;
20,78 % и 27,09 %. При этом минимальный риск - 23,79, доходность портфеля
оказалась равной заданной - 15.
3.3.2 Решение
задач нелинейного программирования в среде приложения Matlab
Метод покоординатного спуска (Гаусса - Зейделя)
На каждом шаге метод "приближается" к решению
последовательно по каждой из координат. Переход от точки 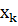
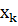 к точке
к точке 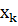
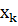 +1 назовем "внешней" итерацией. Внутри каждой
"внешней" итерации находятся n "внутренних" для
последовательного вычисления координат точки
+1 назовем "внешней" итерацией. Внутри каждой
"внешней" итерации находятся n "внутренних" для
последовательного вычисления координат точки 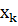
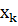 +1.
+1.
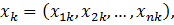
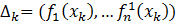
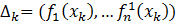 .
.
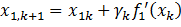
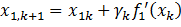 ,
,
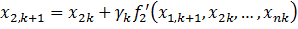
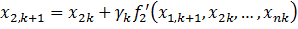 ,
,
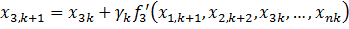
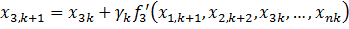 ,
,
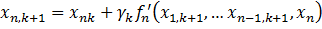
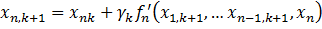 .
.
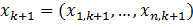
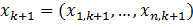 ,
,
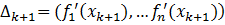
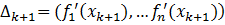 .
.
Блок-схема алгоритма метода покоординатного спуска с постоянным
шагом и программа приведены в Приложении 1. Графическая
иллюстрация решения приведена на Рис.3.9.
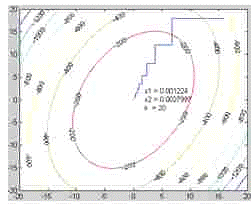
Рисунок 3.9 - Графическая иллюстрация движения к максимуму методом
покоординатного спуска.
На каждой итерации метод "приближается" к решению,
вычисляя новое значение каждой координаты в соответствии с формулой. Блок-схема
алгоритма метода с постоянным шагом и программа приведены в Приложении.
Графическая иллюстрация решения приведена на Рис.3.10.
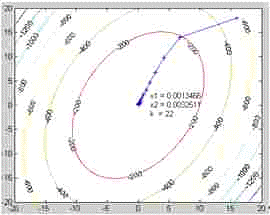
Рисунок 3.10 - Движение к максимуму с постоянным шагом.
В примере Рис.3.11 происходит дробление шага на первой итерации
алгоритма. В этом можно убедиться, поставив точку останова на строке 56.
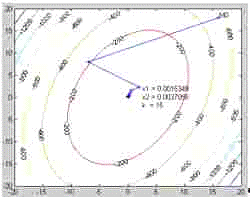
Рисунок 3.11 - Графическая иллюстрация метода с дроблением шага
Градиентный метод наискорейшего спуска.
На каждой итерации вычисляется значение шага γ, максимизирующее значение целевой функции:
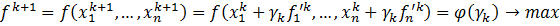
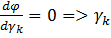
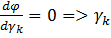 .
.
Новые координаты вычисляются с помощью этого значения:
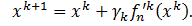
Скалярное произведение векторов-градиентов на двух смежных
итерациях равно нулю:

Это означает, что движение от точки к точке происходит по
взаимно-ортогональным направлениям. (Рис.3.12).

Рис.3.12 - Движение к экстремуму по взаимно-ортогональным
направлениям в методе наискорейшего спуска.
Сравнение методов.
Для сравнения точности и быстродействия методов в данной работе
используется следующий простой прием. В вышеприведенных примерах решалась
простейшая задача, точное решение которой находится из системы линейных
уравнений.
(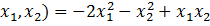
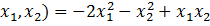
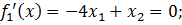
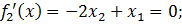
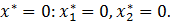
В таблице 3.1 для каждого метода приводится число итераций к, за
которое из одной и той же начальной точки алгоритм приходит в точку хк, норма
вектора-градиента в которой становится меньше заданного числа δ =0,01 - точности метода. Точка хк
является решением задачи. Методы сравниваются по значению отклонения этой точки
от точки х*=0 - точного безусловного максимума.
Таблица 3.1 - Сравнения точности и быстродействия методов
|
Метод
|
Отклонение
|
Число итераций
|
|
Покоординатный
спуск
|
0.0030555
|
20
|
|
"По всем
координатам сразу" с постоянным шагом
|
0.0035189
|
22
|
|
"По всем
координатам сразу" с дроблением шага
|
0.0040109
|
14
|
|
Метод
наискорейшего спуска
|
0.0013446
|
12
|
Выводы
В данном дипломном проекте я представила решение задач
нелинейного программирования различными методами для проведения анализа
поведения этих методов на выбранных математических моделях нелинейного
программирования.
Для достижения поставленной цели были выполнены следующие
действия
решены выбранные задачи нелинейного программирования
графическим методом;
решены выбранные задачи нелинейного программирования методом
множителей Лагранжа
представлена компьютерная реализация выбранных задач
нелинейного программирования в среде пакетов Excel и Matlab.
Перечень
ссылок
Монографии
и учебники (один, два или три автора)
1. Акулич
И.Л. Математическое программирование в примерах и задачах. Изд. "Высшая
школа", 1986.
2. Гершкович
Ю.Б. Методы оптимизации и их применение для управления процессами в нефтяной
промышленности. М. МИНГ им. И.М. Губкина, 1988.
. Моисеев
Н.Н., Иванилов Ю.П. Методы оптимизации. М. Наука, 1978.
. Новгородцев
А. Расчет электрических цепей в "MATLAB”. Изд. Питер, 2004.
. В.И.
Бодров, Т.Я. Лазарева, Ю.Ф. Мартемьянов " Математические методы принятия
решений".
. Косоруков
О. А, Мищенко А.В. "Исследование операций".