Метод проекции антиградиента
Метод проекции антиградиента
Курсовая работа
Оглавление
Введение
. Численные методы нелинейного программирования
.1 Виды численных методов нелинейного программирования
.2 Оценка численных методов нелинейного программирования
. Метод проекции антиградиента
.1 Задача
Заключение
Список использованной литературы
Введение
Проникновение количественных методов в экономику, технику и другие
области человеческой деятельности, которое в последние десятилетия неуклонно
возрастает, усиливает внимание специалистов в области прикладных наук к
математическому аппарату, используемому в интересующих их областях, и
привлекает все большее число математиков к разработке математической
проблематики прикладного характера. В последнее время все чаще возникают задачи,
сводящиеся к схеме нелинейного программирования. Вместе с тем имеющаяся на
русском языке монографическая литература по нелинейному программированию (в
отличие от линейного программирования) совершенно недостаточна. Нелинейное
программирование в определенном смысле подобно линейному программированию, в
нем отсутствует лишь требование линейности функций, хотя, конечно теория
нелинейного программирования охватывает и линейный случай.
Методы оптимизации - это методы поиска лучшего результата, оптимального
решения, лучшего пути. Задачей оптимизации называется задача о поиске
экстремума функции или функционала на заданном множестве допустимых решений. А
постановка задачи - это определенные действия для выполнения конкретной задачи.
Сама по себе постановка задачи оптимизации проста и естественна: заданы
множество Ω и функция ƒ(x), определенная на Ω; требуется найти точки минимума
или максимума функции ƒ на Ω. Запишем задачу на минимум в виде:
ƒ(x)→min, x 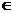 Ω (1)
Ω (1)
При
этом ƒ
будем называть целевой функцией, Ω
- допустимым множеством, любой элемент x 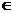 Ω - допустимой точкой задачи ƒ(x)→min.
Ω - допустимой точкой задачи ƒ(x)→min.
Нелинейное
программирование, охватывая весьма широкий круг задач, является одним из
основных разделов в теории методов оптимизации.
Существует
множество методов поиска локального экстремума. В данной курсовой работе будут
рассмотрены численные методы нелинейного программирования и наиболее подробно
метод проекции антиградиента.
Таким
образом, целью данной курсовой работы является подробно изучить метод проекции
антиградиента. Задачи:
· ознакомиться с задачей нелинейного программирования;
· рассмотреть численные методы нелинейного программирования;
· изучить метод проекции антиградиента;
· решить тестовые задачи в MS Excel;
· сделать выводы.
1. Численные
методы нелинейного программирования
Задача нелинейного программирования встречается в естественных и
физических науках, технике, экономике, математике, в сфере деловых отношений и
в науке управления государством. В наиболее абстрактной форме задача
нелинейного программирования ставится так: что-то должно быть максимизировано
(или минимизировано); однако ограничения лимитируют действия, которые мы можем
принять для достижения максимума (или минимума).
Задачи оптимизации (экстремальные задачи)
На минимум:
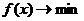
при
ограничениях
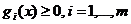
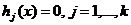
На максимум:
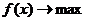
при
ограничениях
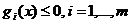
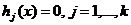
называются
задачами нелинейного программирования (сокращенно задачами НЛП), если среди
функцийƒ,g1...gm,h1...,hk имеется хотя бы одна нелинейная функция. Задачи НЛП,
как и любые другие задачи оптимизации, являются математическими моделями
некоторых практических задач принятия решения.
Как
и в любой теории принятия решения, перед теорией нелинейной оптимизации стоят
следующие три основные проблемы:
)
проблема существования оптимального решения;
)
проблема установления необходимых и достаточных признаков оптимальности
(характерных свойств, присущих точкам минимума и максимума);
)
разработка способов вычисления оптимальных решений (методов решения задач НЛП).
Известно достаточно много численных методов решения общей задачи
нелинейного программирования. Во многих из них реализованы идеи, реализованные
в численных методах безусловной минимизации. Основное отличие состоит в том,
что при решении этой задачи необходимо учитывать ограничения, задающие
допустимое множество Х Є Rⁿ,
на котором нужно найти точку x* Є X минимума целевой функции ƒ(x). Далее представлены наиболее часто
применяемые на практике численные методы решения такой задачи.
.1 Виды
численных методов нелинейного программирования
Метод условного градиента или метод линейной аппроксимации (линеаризации)
целевой функции. Применение данного метода оправдано лишь в том случае, когда
задача вида ƒ(x)→min, x Є X ,
т.е. задача минимизации линейной функции на X, решается достаточно просто. Но если множество X имеет сложную структуру, то задача
трудна.
Метод приведенного градиента основан на сокращении размерности задачи с
помощью представления всех переменных через подмножество независимых
переменных.
Метод возможных направлений основан на движении из одной допустимой точки
к другой с лучшим значением целевой функции.
Проективные методы образуют целое семейство. Иногда их называют методами
допустимых направлений или градиентными методами с большой длиной шага.
Сущность этих методов заключается в следующем : линейные и линеаризированные
ограничения образуют линейное многообразие (определяемое пересечением
ограничений), на которое можно спроектировать выбранное направление поиска S в пространстве решений. То, что в
методах подразумевается под проекцией, ассоциируется с понятием проекции
вектора, описывающего локальное приращение функции при перемещении в заданном
направлении.
.2 Оценка
численных методов нелинейного программирования
нелинейный программирование антиградиент проекция
На вопрос о том, какой из методов нелинейного программирования наилучший
можно сказать при оценивании «качества» того или иного алгоритма. Критерии
оценивания:
1) время необходимое для реализации серии вычислительных процедур
(число операций и время их выполнения);
2) степень сложности задачи (размерность, число ограничений в виде
равенств, число ограничений в виде неравенств);
3) точность
решения по отношению к оптимальному значению х* или по отношению к ƒ(х*), h(x*), g(x*) и 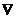 ƒ(х*);
ƒ(х*);
) простота
практического использования алгоритма (время, необходимое для ввода исходных
данных и записи функций в память ЭВМ);
) простота
машинной программы, реализующей рассматриваемый алгоритм;
) алгоритм
должен позволять решать задачи, которые представляют практический интерес
(нельзя полагать, что какой-либо из алгоритмов окажется эффективным при решении
любой задачи).
2. Метод
проекции антиградиента
Антиградиент дает только направление минимизации, но не длину шага.
Направление проекции антиградиента является локально наилучшим направлением
движения к условному минимуму целевой функции. При поиске условного максимума
используют проекцию градиента. Вместе с градиентом можно определить вектор
антиградиента, равный по модулю вектору градиента, но противоположный по
направлению. Он указывает сторону наибольшего убывания функции в данной точке.
Все проективные методы предполагают реализацию на каждом k-ом этапе указанной ниже
последовательности шагов:
1) алгоритм
начинает работу в допустимой точке х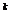 ;
;
) определяется
допустимое направление s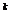 ;
;
) в
допустимом направлении выбирается шаг длиной 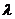
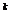 ,
минимизирующий ƒ(х), но в то же время сохраняющий вектор х
,
минимизирующий ƒ(х), но в то же время сохраняющий вектор х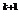 =х
=х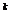 +
+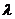
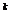 s
s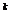 допустимым.
допустимым.
Целевая
функция метода проекции антиградиента имеет вид 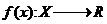 .
И задача оптимизации задана следующим образом
.
И задача оптимизации задана следующим образом 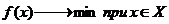 .
Основная идея метода заключается в том, чтобы идти в направлении наискорейшего
спуска, а это направление задается антпградиентом
.
Основная идея метода заключается в том, чтобы идти в направлении наискорейшего
спуска, а это направление задается антпградиентом 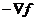 :
:
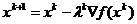 (2)
(2)
Где
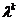 выбирается
выбирается
· постоянной, в этом случае метод может расходиться;
· дробным шагом, то есть длина шага в процессе спуска делится на некое
число;
· наискорейшим спуском.
Алгоритм:
1) вычислить
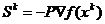 .
.
) если
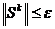 , то вычислить
, то вычислить 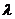 по
формуле
по
формуле 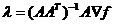 и закончить вычисления. В противном случае -
продолжить вычисления, переходя к пункту 3.
и закончить вычисления. В противном случае -
продолжить вычисления, переходя к пункту 3.
) определить
максимальную длину шага:
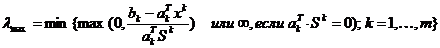
4) решить задачу одномерного поиска:

Критерии остановки процесса приближенного нахождения минимума могут быть
основаны на различных соображениях. Некоторые из них:
1. 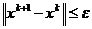
. 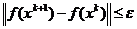
Здеcь
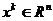 - значение, полученное после
- значение, полученное после 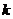 -го шага оптимизации.
-го шага оптимизации. 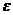 - наперед
заданное положительное число
- наперед
заданное положительное число
Данный
алгоритм можно легко распространить на неравенства, используя либо
дополнительные переменные, либо активные ограничения.
Рисунок
1
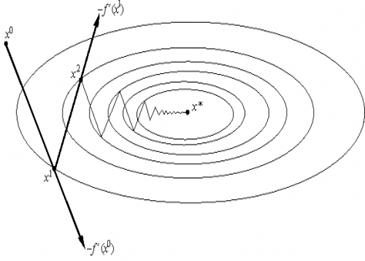 <#"785431.files/image028.gif">раз".
<#"785431.files/image028.gif">раз".
Линейные
ограничения типа равенства. Пусть в задаче оптимизации допустимое множество Ω
определено ограничениями типа равенства, то есть имеет вид
Ω={x Є Rⁿ : (ai;x) = bi, i=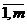 } (3)
} (3)
а
целевая функция ƒ(х) дифференцируема в Rⁿ.
Предположим, что известна точка х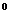
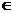 Ω.
Рассмотрим функцию
Ω.
Рассмотрим функцию 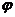 (у)=ƒ(х
(у)=ƒ(х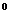 +P*y), y
+P*y), y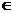 Rⁿ где
матрица P определена соотношением
Rⁿ где
матрица P определена соотношением
P= А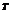 (АА
(АА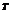 )
)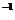 А (4)
А (4)
Для этой функции в силу правила дифференцирования сложной функции и
симметричной матрицы Р справедливо равенство
grad 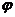 (y)=P*
grad ƒ
(y)=P*
grad ƒ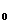 (x) (5)
(x) (5)
Прежде
всего убедимся, что х*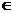 Ω. Используя представление
Ω. Используя представление
х*=х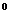 +Р*у* (6)
+Р*у* (6)
и
условие х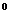
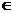 Ω,
заключаем, что (а
Ω,
заключаем, что (а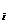 ,х*)=( а
,х*)=( а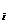 ,х
,х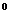 )+( а
)+( а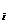 ,Р*у*)=(
а
,Р*у*)=(
а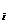 ,х
,х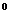 )=b
)=b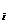 , i=
, i=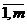 . Поскольку вектор Р*у* ортогонален каждому вектору
линейного подпространства ₤
. Поскольку вектор Р*у* ортогонален каждому вектору
линейного подпространства ₤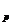 , в том
числе и векторам а
, в том
числе и векторам а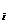 . Следовательно, х*
. Следовательно, х*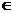 Ω.
Ω.
Так
как у* является стационарной точкой функции 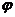 (у), то grad
(у), то grad 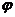 (y*)=0, и поэтому, учитывая grad
(y*)=0, и поэтому, учитывая grad 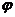 (y)=P* grad ƒ
(y)=P* grad ƒ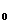 (x) и P= А
(x) и P= А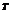 (АА
(АА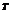 )
)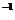 А при х=х* и у=у*, находим
А при х=х* и у=у*, находим
Р*
grad ƒ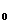 (x*)= grad ƒ
(x*)= grad ƒ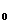 (x*)-
А
(x*)-
А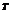 (АА
(АА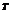 )
)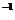 grad ƒ
grad ƒ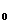 (x*)= grad ƒ
(x*)= grad ƒ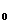 (x*)+
А
(x*)+
А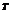
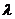 = grad ƒ
= grad ƒ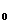 (x*)+
(x*)+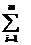
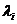 а
а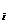 =0, (7)
=0, (7)
где
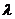 = -(АА
= -(АА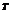 )
)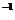 А grad ƒ
А grad ƒ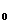 (x*),
а
(x*),
а 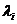 - координаты вектора
- координаты вектора 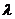
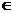 Rⁿ. Представив ограничения (3) в виде ƒ
Rⁿ. Представив ограничения (3) в виде ƒ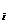 (х)=(а
(х)=(а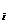 ,х)-b
,х)-b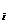 =0, i=
=0, i=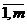 ,и учитывая равенства gradƒ
,и учитывая равенства gradƒ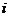 (x*)=а
(x*)=а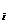 , заключаем, что точка х* является стационарной точкой
функции Лагранжа
, заключаем, что точка х* является стационарной точкой
функции Лагранжа
L(x,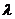 )=ƒ(x)+
)=ƒ(x)+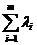 ((a
((a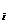 ,x)-b
,x)-b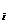 ) (8)
) (8)
то есть удовлетворяет необходимому условию минимума целевой функции ƒ(х) на множестве Ω.
Стационарные
точки целевой функции
ƒ(х) на допустимом множестве можно
определять, решая задачу безусловной минимизации функции 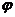 (у). В общем случае функция
(у). В общем случае функция 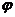 (у) может иметь несколько стационарных точек, причем
каждой ее стационарной точке у* будет соответствовать стационарная точка (6)
функции Лагранжа (8). Через минимизацию функции
(у) может иметь несколько стационарных точек, причем
каждой ее стационарной точке у* будет соответствовать стационарная точка (6)
функции Лагранжа (8). Через минимизацию функции 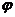 (у) можно
найти все стационарные точки целевой функции. Однако, если целевая функция
является выпуклой функцией на выпуклом множестве Ω, то для решения задачи
минимизации такой функции достаточно найти хотя бы одну стационарную точку
целевой функции в Ω, поскольку в любой стационарной точке выпуклая
функция достигает наименьшего значения. Строго выпуклая функция может иметь
лишь одну стационарную точку, так как она может достигать наименьшего значения
на выпуклом множестве только в одной точке.
(у) можно
найти все стационарные точки целевой функции. Однако, если целевая функция
является выпуклой функцией на выпуклом множестве Ω, то для решения задачи
минимизации такой функции достаточно найти хотя бы одну стационарную точку
целевой функции в Ω, поскольку в любой стационарной точке выпуклая
функция достигает наименьшего значения. Строго выпуклая функция может иметь
лишь одну стационарную точку, так как она может достигать наименьшего значения
на выпуклом множестве только в одной точке.
Нелинейные
ограничения. Если среди ограничений в задаче оптимизации есть нелинейные, то
поиск минимума целевой функции ƒ(х) на
допустимом множестве усложняется. Пусть для определенности Ω={х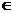 Rⁿ: g
Rⁿ: g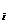 (x)≤0,
i=
(x)≤0,
i=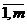 }, где g
}, где g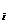 (x)- дифференцируемые функции на k-ой
итерации известна точка х
(x)- дифференцируемые функции на k-ой
итерации известна точка х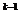
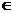 Ω,
для которой активными являются ограничения с индексами i
Ω,
для которой активными являются ограничения с индексами i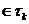 ={i
={i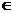 N: g
N: g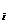 (x
(x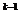 )=0}.
Составим матрицу
)=0}.
Составим матрицу 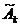 , строками которой являются матрицы-строки (grad g
, строками которой являются матрицы-строки (grad g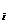 (x
(x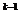 ))
))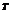 , i
, i ,
предполагая, что они линейно независимы. Тогда проекционная матрица
,
предполагая, что они линейно независимы. Тогда проекционная матрица 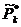 =I
=I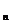 -
- 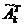 (
(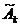
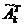 )
)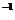
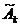 спроектирует антиградиент w
спроектирует антиградиент w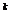 = -grad ƒ(x
= -grad ƒ(x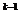 ) целевой
функции в точке x
) целевой
функции в точке x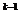 на направление, ортогональное градиентам всех функций
g
на направление, ортогональное градиентам всех функций
g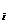 (x), i
(x), i , задающих в этой точке активные ограничения. Но в
общем случае может оказаться, что это направление будет направлением спуска,
поскольку оно может лишь касаться в точке x
, задающих в этой точке активные ограничения. Но в
общем случае может оказаться, что это направление будет направлением спуска,
поскольку оно может лишь касаться в точке x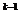
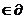 Ω
границы
Ω
границы 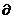 Ω множества Ω.
Ω множества Ω.
.1 Задача
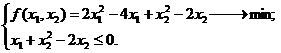
В
данном случае целевая функция является квадратичной и ее можно записать в виде 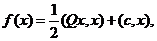 где
где
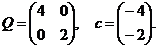
Единственное
ограничение задачи имеет вид 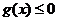 , где
, где 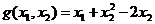 . В качестве начальной возьмем точку
. В качестве начальной возьмем точку 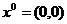 , а в условии прекращения поиска
, а в условии прекращения поиска 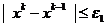 положим
положим 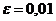 .
.
Вычислим
антиградиент
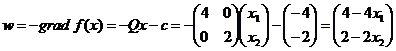
И
градиент левой части ограничения
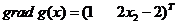 .
.
Рассмотрим
подробнее первую (k=1) итерацию при решении этой задачи методом проекции
антиградиента.
) поскольку
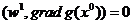 , то антиградиент
, то антиградиент 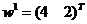 и
градиент
и
градиент 

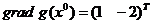 в
начальной точке
в
начальной точке 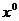 ортогональны. Следовательно, нет необходимости
вычислять проекционную матрицу
ортогональны. Следовательно, нет необходимости
вычислять проекционную матрицу 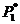 , которая
в данном случае является единичной
, которая
в данном случае является единичной 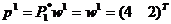 .
.
) при
помощи исчерпывающего спуска из точки 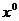 в
направлении вектора р
в
направлении вектора р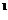 находим значение
находим значение
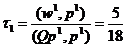
И
точку 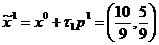 . Ясно, что продвижение точки
. Ясно, что продвижение точки 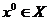 в направлении вектора
в направлении вектора 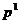 выводит
за пределы допустимого множества, то есть
выводит
за пределы допустимого множества, то есть 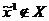 , так
как
, так
как 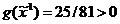 . Точка
. Точка 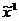 лежит на
касательной кривой
лежит на
касательной кривой 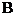 , заданной уравнением
, заданной уравнением  , в точке
, в точке
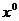 .
.
) проектируем
точку 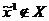 на допустимое множество Х, то есть найдем точку
на допустимое множество Х, то есть найдем точку 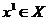 кривой В, наименее удаленную от точки
кривой В, наименее удаленную от точки 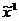 . Так как функция
. Так как функция 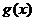 дифференцируемая,
то точка
дифференцируемая,
то точка 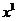 будет основанием кратчайшего перпендикуляра,
опущенного из
будет основанием кратчайшего перпендикуляра,
опущенного из 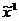 на кривую В. Эту точку можно найти методом последовательных
приближений.
на кривую В. Эту точку можно найти методом последовательных
приближений. 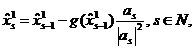 где
где 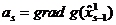 . В
качестве нулевого приближения при s=1 можно принять
. В
качестве нулевого приближения при s=1 можно принять 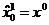 , а условием прекращения последовательных приближений
можно считать выполнение неравенства
, а условием прекращения последовательных приближений
можно считать выполнение неравенства 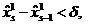 где
где 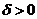 - заданный параметр точности. При выполнении этого
неравенства полагаем
- заданный параметр точности. При выполнении этого
неравенства полагаем 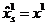 и
и 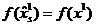 . Выбирая
. Выбирая
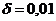 получаем
получаем 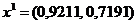 , при
этом
, при
этом 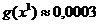 .
.
) проверяем
условие прекращения итераций: 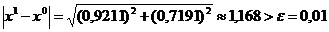 . Так как
требуемая точность еще не достигнута, поиск точки
. Так как
требуемая точность еще не достигнута, поиск точки 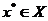 минимума целевой функции
минимума целевой функции  на множестве Х следует продолжить. Для этого
переходим к пункту 1, заменив точку
на множестве Х следует продолжить. Для этого
переходим к пункту 1, заменив точку 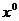 на
найденную на первой итерации точку
на
найденную на первой итерации точку 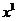 .
.
Таблица 1. Результаты расчетов на четырех итерациях.
|
k
|
|
|
|
|
1
|
(0,9211, 0,7191)
|
-2,9086
|
1,168
|
|
2
|
(0,9976, 0,9512)
|
-2,9976
|
0,244
|
|
3
|
1,0000, 0,9995)
|
-3,0000
|
0,048
|
|
4
|
(1,0000, 1,0000)
|
-3,0000
|
0,0005
|
Таким
образом, результат четвертой итерации с заданной точностью совпал с точным
решением задачи 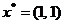 .
.
Заключение
Практика порождает все новые и новые задачи оптимизации, причем их
сложность растет. Требуются новые математические модели и методы, которые
учитывают наличие многих критериев, проводят глобальный поиск оптимума. Другими
словами, жизнь заставляет развивать математический аппарат оптимизации.
В данной курсовой работе была описана задача нелинейного программирования
и рассмотрены некоторые численные методы. Наиболее подробно был изучен метод
проекции антиградиента. Его алгоритм был реализован при решении задачи. Также
тестовые задачи были решены в среде MS Excel. Подводя
итоги, можно сказать, что направление проекции антиградиента является локально
наилучшим направлением движения к условному минимуму целевой функции. При
поиске условного максимума используют проекцию градиента.
Список
использованной литературы
1. Аттетков,
А.В. Методы оптимизации/ А.В. Аттетков, С.В. Галкин, В.С. Зарубин. - М., МГТУ
им. Н.Э. Баумана, 2010, 371 с.
2. Банди,
Б Методы оптимизации. Вводный курс/ Б. Банди. - М., Радио и связь, 1988, 51 с.
. Зангвил,
У.И. Нелинейное программирование/ У.И. Зангвил; под общ. ред. В.М. Гальперина;
- М., Советское радио, 2008, 11 с.
. Интрилигатор,
М. Математические методы оптимизации и экономическая теория/ М. Интрилигатор. -
М., Айрис пресс, 2012, 57 с.
. Сухарев,
А.В. Курс методов оптимизации/ А.Г. Сухарев, А.В. Тимохов, В.В. Федоров. - М.,
ФИЗМАТЛИТ, 2009, 256 с.
. Харчистов,
Б.Ф Методы оптимизации/ Б.Ф. Харчистов. - Таганрог, ТРТУ, 56 с.
. Химмельблау,
Д. Прикладное нелинейное программирование/ Д. Химмельблау; под общ. ред.
Быховского М.Л. - М., Мир, 2006, 72 с.
. Википедия
[Электронный ресурс]/ Градиентный метод; 2009. URL: http://ru.wikipedia.org/wiki, свободный