Проектирование редуктора
1. Выбор двигателя.
Кинематический и силовой расчёты привода
Принимаем КПД элементов привода: КПД
муфты соединительной  ; КПД
закрытой в корпусе конической зубчатой передачи с учетом потерь в подшипниках
валов передачи
; КПД
закрытой в корпусе конической зубчатой передачи с учетом потерь в подшипниках
валов передачи 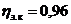 ; КПД
закрытой в корпусе цилиндрической зубчатой передачи с учетом потерь в
подшипниках валов передачи
; КПД
закрытой в корпусе цилиндрической зубчатой передачи с учетом потерь в
подшипниках валов передачи 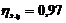 . Тогда
общий КПД привода от двигателя до приводного вала:
. Тогда
общий КПД привода от двигателя до приводного вала:
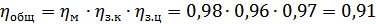
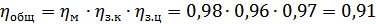 .
.
Требуемую мощность двигателя Pтреб определяем по формуле:
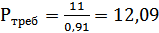
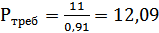 кВт.
кВт.
Для выбора двигателя, кроме мощности
Pтреб, необходимо ориентировочно определить его синхронную частоту
вращения nсинхр=1000 мин-1.
Выбираем асинхронный двигатель серии
АИ типоразмера АИР160М6 со следующими техническими данными:
Pном=15 кВт; nном=960 мин-1; Tmax/Tном=2,0.
Общее передаточное отношение привода
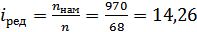
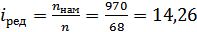 .
.
Распределяем iред между быстроходной ступенью с передаточным отношением iБ и тихоходной ступенью с передаточным отношением iТ:
а) передаточное отношение тихоходной
ступени
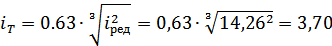
б) передаточное отношение
быстроходной ступени:
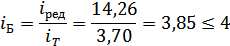
Полученные передаточные отношения 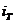 и
и 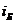 находятся
в рекомендуемом диапазоне передаточных отношений для цилиндрической и
конической зубчатых передач, установленных в закрытом корпусе.
находятся
в рекомендуемом диапазоне передаточных отношений для цилиндрической и
конической зубчатых передач, установленных в закрытом корпусе.
Определим частоты вращения валов
редуктора, а также вращающий Т и крутящий МК моменты в различных
сечениях этих валов.
Частоты вращения валов редуктора:
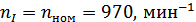
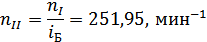
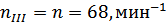
Определим вращающий момент на
деталях передач редуктора.
Требуемый вращающий момент на
выходном конце тихоходного вала (III) редуктора:
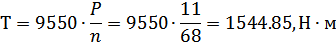
Обозначим Т2Т - вращающий
момент на колесе тихоходной ступени.
Условие равновесия вала III:
Т2Т=Т=1544,85, Н м
Вращающий момент на шестерни
тихоходной ступени:
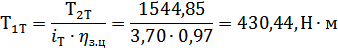
Т2Б=Т1Т=430,44,
Н м
Т2Б - вращающий момент
колеса быстроходной ступени.
Вращающий момент на шестерни
быстроходной ступени:
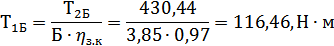
. Расчёт тихоходной
ступени редуктора
Исходные данные:
а) передаточное
отношение передачи 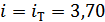
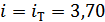 (здесь индекс
(здесь индекс 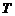 -
тихоходная ступень);
-
тихоходная ступень);
б) частота вращения
шестерни ступени 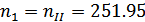
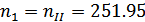
 ;
;
в) частота вращения
колеса ступени 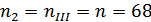
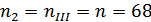
 ;
;
г) вращающий момент на
колесе ступени 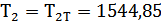
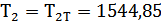
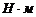 ;
;
д) остальные данные
указаны в техническом задании.
Порядок расчета
. Выбор варианта
термообработки зубчатых колес и определение средней твердости активной
поверхности зубьев.
Принимаем вариант
термообработки II:
а) термообработка
шестерни - улучшение + закалка ТВЧ, твёрдость поверхности зубьев 45…50 HRCэ.
б) для колеса
термообработка улучшение, твёрдость поверхности 269…302 HB.
В) материалы зубчатых
колёс 40Х; 40ХН; 35ХМ…
Средние твёрдости
поверхностей зубьев:
Шестерни 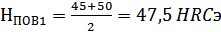
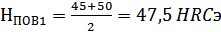
Колесо 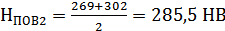
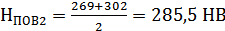 .
.
2. Допускаемые
контактные напряжения 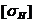 при
расчете зубчатой передачи на сопротивление контактной усталости активных
поверхностей зубьев.
при
расчете зубчатой передачи на сопротивление контактной усталости активных
поверхностей зубьев.
Предел контактной
выносливости активных поверхностей зубьев  , соответствующий
абсциссе точки перелома кривой усталости для контактных напряжений:
, соответствующий
абсциссе точки перелома кривой усталости для контактных напряжений:
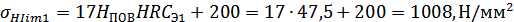
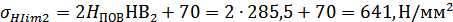
Коэффициент безопасности
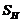 :
:
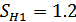
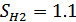
Определяем коэффициент
долговечности Zn:
Эквивалентное число
циклов нагружения 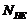 для
шестерни и колеса при числе зацеплений за один оборот зуба шестерни
для
шестерни и колеса при числе зацеплений за один оборот зуба шестерни 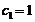 и
зуба колеса
и
зуба колеса 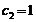 :
:
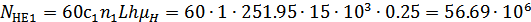
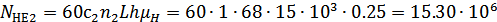
Базовое число циклов
нагружения 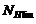 (абсцисса
точки перелома кривой усталости для контактных напряжений) для варианта т.о. II:
(абсцисса
точки перелома кривой усталости для контактных напряжений) для варианта т.о. II:
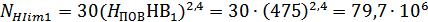
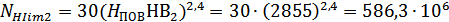
Так как 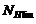 не
должно превышать
не
должно превышать 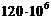 .
А мы получили
.
А мы получили 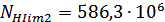
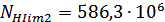 , то принимаем
, то принимаем 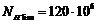 .
.
Для определения
коэффициента долговечности 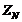 при расчёте на
сопротивление контактной усталости сопоставляем полученные величины
при расчёте на
сопротивление контактной усталости сопоставляем полученные величины 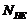 и
и
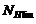 .
.
В нашем случае для
шестерни 
 и коэффициент
долговечности
и коэффициент
долговечности  рассчитываем
по формуле:
рассчитываем
по формуле:
Для шестерни:
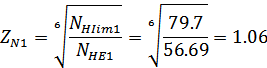
Для колеса:
Тогда допускаемые
контактные напряжения 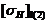 согласно
формуле для принятого варианта т.о. II:
согласно
формуле для принятого варианта т.о. II:
Для шестерни:
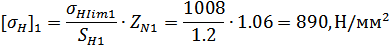
Для колеса:
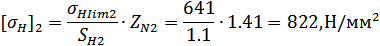
Минимальная величина
допускаемых контактных напряжений 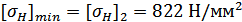
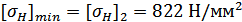 .
.
Для цилиндрической
косозубой передачи при известных допускаемых контактных напряжениях для шестерни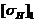 и колеса
и колеса 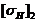 допускаемые
контактные напряжения
допускаемые
контактные напряжения 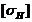 для
передачи в сборе, т.е. для сопряжённой зубчатой пары, ГОСТ 21354-87 рекомендует
определять по формуле:
для
передачи в сборе, т.е. для сопряжённой зубчатой пары, ГОСТ 21354-87 рекомендует
определять по формуле:
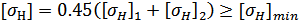
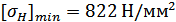
Окончательно для
дальнейших расчётов принимаем 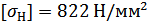
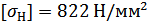
3. Межосевое расстояние
передачи.
Передаточное число
ступеней:
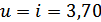
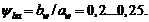
Примем коэффициент 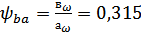
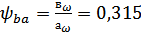 .
.
Тогда коэффициент
рабочей ширины передачи относительно делительного диаметра шестерни
(предварительно):
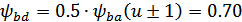
Коэффициент концентрации
нагрузки 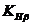 при
расчёте по контактным напряжениям для кривой 5 для:
при
расчёте по контактным напряжениям для кривой 5 для: 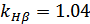
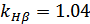 .
.
Коэффициент внешней
динамической нагрузки 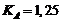 .
.
При приведенном модуле
упругости для стали 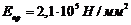 и
вращающем моменте на колесе передачи
и
вращающем моменте на колесе передачи 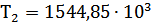
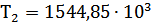 Н*мм, межосевое
расстояние рассчитываемой косозубой цилиндрической передачи:
Н*мм, межосевое
расстояние рассчитываемой косозубой цилиндрической передачи:
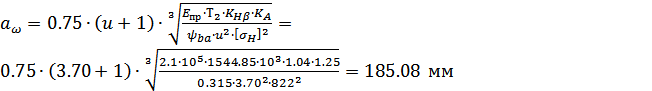
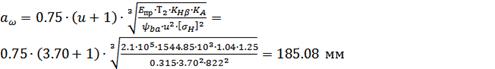 ,
,
где 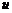 -
передаточное число; для понижающей передачи.
-
передаточное число; для понижающей передачи.
По ряду 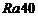 ГОСТ
6636-69 принимаем
ГОСТ
6636-69 принимаем 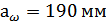
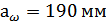 .
.
4. Модуль передачи, угол
наклона зубьев, числа зубьев шестерни и колеса.
Ориентировочно величина
модуля 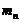 для
косозубой передачи может быть определена по соотношению:
для
косозубой передачи может быть определена по соотношению:
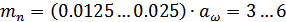
Принимаем стандартное
значение 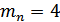
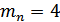 .
.
Угол наклона зуба 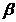 на
делительном цилиндре составляет в нераздвоенной косозубой передаче
на
делительном цилиндре составляет в нераздвоенной косозубой передаче 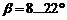 .
.
В нашем примере
косозубая передача является нераздвоенной и для нее предварительно принимаем 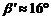 .
.
Тогда число зубьев
шестерни
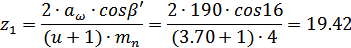
Принимаем 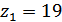
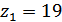 .
.
Число зубьев колеса
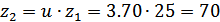
Принимаем 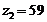 .
.
Уточняем окончательно
значение угла наклона зуба 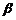 :
:
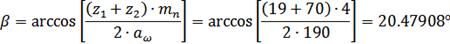
что находится в
рекомендуемом диапазоне 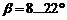 для
нераздвоенных косозубых передач.
для
нераздвоенных косозубых передач.
Фактическое передаточное
число рассчитываемой передачи
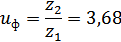
Отклонение 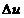 передаточного
числа
передаточного
числа 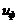 и
и
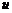 :
:

В нашем случае это
условие выполняется: 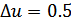
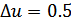 .
.
5. Основные размеры
шестерни и колеса.
Диаметры делительные
(точность расчетов-два знака после запятой):
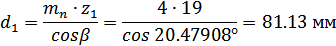
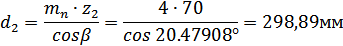
Диаметры начальные
(передача без смещения): 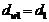 ,
,
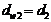 .
.
Проверка:
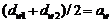 ;
; 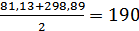
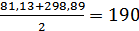 мм
мм
Выполненная проверка
справедлива для косозубой передачи без смещения и при высотной коррекции.
При коэффициентах высоты
головки зуба 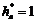 и
радиального зазора
и
радиального зазора 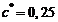 высоты
головки
высоты
головки 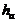 и
ножки
и
ножки 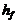 зуба
(для передачи без смещения):
зуба
(для передачи без смещения):
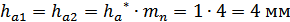

Диаметры окружностей
вершин зубьев:
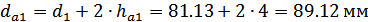
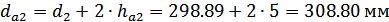
Диаметры окружностей
впадин зубьев:
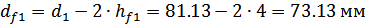

Рабочая ширина передачи
(округляется до целого числа):
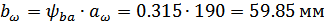
Ширина венца колеса
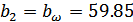
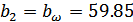 мм
мм
Ширина венца шестерни
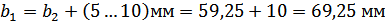
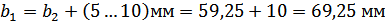 .
.
Окончательно коэффициент
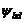 :
:
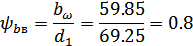
6. Выбор марки стали для
изготовления зубчатых колес.
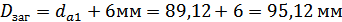
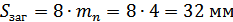
Принимаем для
изготовления шестерни и колеса легированную хромистую сталь 40Х. При этом
выполняются условия:
а) для шестерни (т.о.
улучшение + закалка ТВЧ)
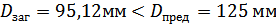
б) для колеса (т.о.
улучшение + цементация + закалка)
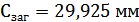
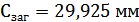 и
и 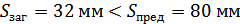
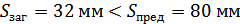 .
.
При выполнении выше
записанных условий для шестерни и колеса гарантируется получение твердости
активной поверхности зубьев при данном варианте термообработки в диапазоне
45…50HRCЭ.
7. Степень точности
передачи.
Окружная скорость
шестерни и колеса в полюсе зацепления
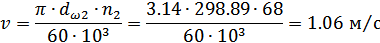
Принимаем 8-ю степень
точности.
8. Определение сил,
действующих в косозубом зацеплении.
Окружная сила 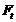 на
начальном цилиндре в торцовом сечении косозубой цилиндрической передачи при
на
начальном цилиндре в торцовом сечении косозубой цилиндрической передачи при 
 :
:
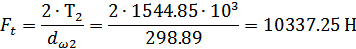
При этом для шестерни и
колеса:
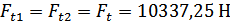
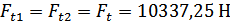 .
.
Радиальная сила  для
шестерни и колеса:
для
шестерни и колеса:
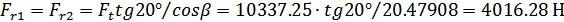
Осевая сила 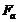 для
шестерни и колеса:
для
шестерни и колеса:
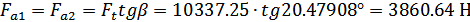
Направления сил 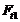 ,
,
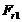 и
и
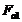 на
шестерне противоположны направлениям соответствующих сил
на
шестерне противоположны направлениям соответствующих сил 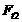 ,
,
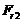 и
и
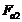 на
колесе.
на
колесе.
9. Проверочный расчет
передачи на сопротивление контактной усталости активных поверхностей зубьев.
Коэффициент
неравномерности нагрузки одновременно зацепляющихся пар зубьев
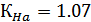
Коэффициент торцового
перекрытия
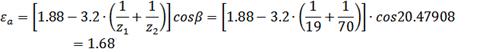
Коэффициент уменьшения
контактных напряжений в косозубой передаче в сравнении с прямозубой:
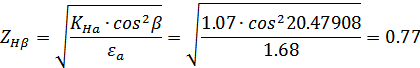
Коэффициент 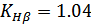
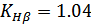
Коэффициент 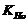 ,
учитывающий внутреннюю динамическую нагрузки передачи при расчете по контактным
напряжениям, для окружной скорости
,
учитывающий внутреннюю динамическую нагрузки передачи при расчете по контактным
напряжениям, для окружной скорости 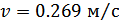
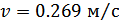 ,
, 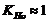 .
Тогда расчетные контактные напряжения в полюсе зацепления
.
Тогда расчетные контактные напряжения в полюсе зацепления
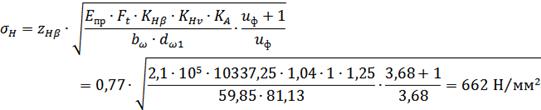
Сопротивление контактной
усталости активных поверхностей зубьев обеспечивается, так как выполняется
условие:
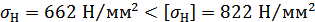
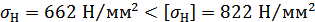 .
.
10. Допускаемые
напряжения изгиба 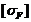 при
расчете на сопротивление усталости зубьев при изгибе.
при
расчете на сопротивление усталости зубьев при изгибе.
Предел выносливости
зубьев по напряжениям изгиба 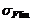 , соответствующий
абсциссе точки перелома кривой усталости для напряжений изгиба, для принятого
вида термообработки:
, соответствующий
абсциссе точки перелома кривой усталости для напряжений изгиба, для принятого
вида термообработки:
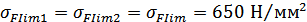
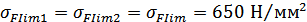 .
.
Коэффициент безопасности
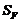 :
:


Коэффициент приведения  :
:
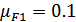
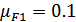 для
для 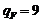 (так
как Н1>350HB);
(так
как Н1>350HB);

 для
для 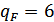
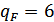 (так как Н2<350HB).
(так как Н2<350HB).
Эквивалентное число
циклов нагружения 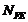 для
шестерни и колеса при числе зацеплений за один оборот зуба шестерни
для
шестерни и колеса при числе зацеплений за один оборот зуба шестерни 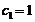 и
зуба колеса
и
зуба колеса 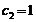 :
:
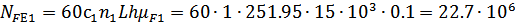
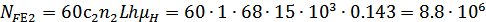
Базовое число циклов
нагружения  (абсцисса
точки перелома кривой усталости для напряжений изгиба) для всех видов
термообработки:
(абсцисса
точки перелома кривой усталости для напряжений изгиба) для всех видов
термообработки: 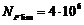 .
Тогда
.
Тогда
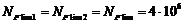 .
.
Для определения
коэффициента долговечности 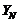 при расчете на
сопротивление усталости зубьев при изгибе сопоставляем полученные величины
при расчете на
сопротивление усталости зубьев при изгибе сопоставляем полученные величины 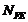 и
и
 .
.
Для шестерни 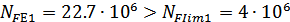
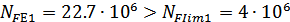 и коэффициент
долговечности
и коэффициент
долговечности 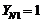 .
.
Для колеса 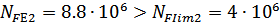
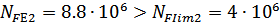 и в данном случае также
коэффициент долговечности
и в данном случае также
коэффициент долговечности 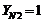 .
.
Допускаемые напряжения
изгиба 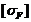 :
:
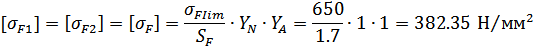
11. Проверочный расчет
передачи на сопротивление усталости зубьев при изгибе.
Коэффициент концентрации
нагрузки 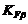 при
расчете по напряжениям изгиба для кривой 5 при Н1>350HB и Н2<350НВ для
при
расчете по напряжениям изгиба для кривой 5 при Н1>350HB и Н2<350НВ для 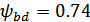
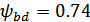 ;
; 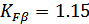
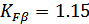
Коэффициент 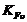 ,
учитывающий внутреннюю динамическую нагрузку передачи при расчете по
напряжениям изгиба, для:
,
учитывающий внутреннюю динамическую нагрузку передачи при расчете по
напряжениям изгиба, для: 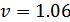
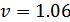 ;
; 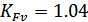
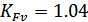 ;
; 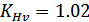
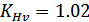 .
.
Число зубьев
эквивалентного прямозубого зубчатого колеса (эквивалентное число зубьев)  :
:
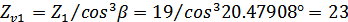
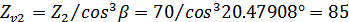
Коэффициент формы зуба и
концентрации напряжений 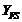 в
зависимости от
в
зависимости от  при
коэффициенте смещения исходного контура
при
коэффициенте смещения исходного контура  : для шестерни
: для шестерни 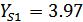
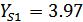 ; для колеса
; для колеса 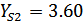
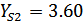 .
.
Т.к. 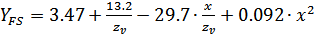
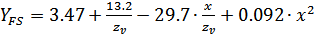
Коэффициент
неравномерности нагрузки одновременно зацепляющихся пар зубьев при расчете на
изгиб 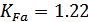
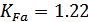 .
.
Коэффициент, учитывающий
повышение изгибной прочности вследствие наклона контактной линии к основанию
зуба в косозубой передаче и неравномерного распределения нагрузки:
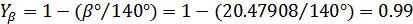
3. Расчет конической
зубчатой передачи с круговыми зубьями
Исходные данные:
а) передаточное
отношение передачи 
 (здесь индекс
(здесь индекс 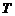 -
тихоходная ступень);
-
тихоходная ступень);
б) частота вращения
шестерни ступени 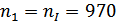
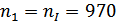
 ;
;
в) частота вращения
колеса ступени 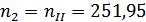
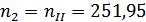
 ;
;
г) вращающий момент на
колесе ступени 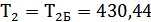
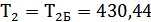
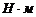 ;
;
д) остальные данные
указаны в техническом задании.
Порядок расчета
. Выбор варианта
термообработки зубчатых колес и определение допускаемых контактных напряжений 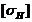 при
расчете зубчатой передачи на сопротивление контактной усталости активных
поверхностей зубьев.
при
расчете зубчатой передачи на сопротивление контактной усталости активных
поверхностей зубьев.
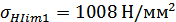

Коэффициент безопасности
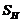 :
:
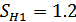
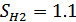

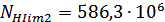
Изменились при этом
значения эквивалентного числа цикла нагружений:
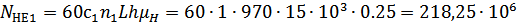

Для определения
коэффициента долговечности 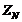 при расчёте на
сопротивление контактной усталости сопоставляем полученные величины
при расчёте на
сопротивление контактной усталости сопоставляем полученные величины 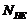 и
и
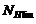 .
.
Для шестерни:
Т.к 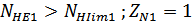
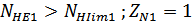
Для колеса:
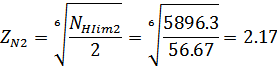
Тогда допускаемые
контактные напряжения 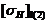 согласно
формуле для принятого варианта т.о. II:
согласно
формуле для принятого варианта т.о. II:
Для шестерни:
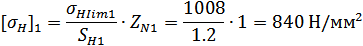
Для колеса:

Проектирование передачи
проводим по допускаемому контактному напряжению:
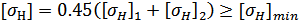

2. Основные параметры
передачи.
В конической передаче
коэффициент 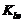 ширины
ширины
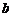 зубчатого
венца относительно внешнего конусного расстояния
зубчатого
венца относительно внешнего конусного расстояния 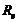 рекомендуется:
рекомендуется: 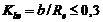 .
Принимаем наиболее распространенное значение
.
Принимаем наиболее распространенное значение 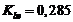 . Передаточное число
. Передаточное число 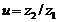 для
понижающей передачи:
для
понижающей передачи: 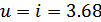
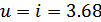 .
.
С целью повышения
жесткости опор конической зубчатой передачи предполагаем использование конических
роликоподшипников (т.е. опоры роликовые).
Определяем величину
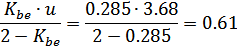
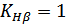
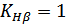 .
.
Зададимся коэффициентом 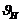 ,
учитывающим влияние вида зубьев конической передачи при расчёте её на
контактную усталость:
,
учитывающим влияние вида зубьев конической передачи при расчёте её на
контактную усталость:
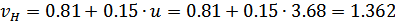
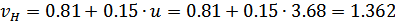 .
.
При приведённом модуле
упругости для стали 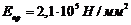 и
вращающем моменте на коническом колесе ступени
и
вращающем моменте на коническом колесе ступени 
 внешний делительный
диаметр колеса рассчитываемой конической передачи:
внешний делительный
диаметр колеса рассчитываемой конической передачи:
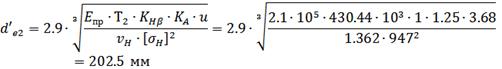
Внешний делительный
диаметр шестерни
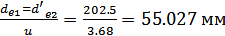
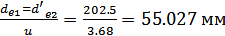 .
.
Принимаем число зубьев
шестерни с круговыми зубьями 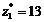 .
.
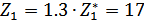
При этом выполняется
условие:
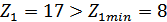
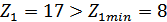 ,
,
где 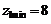 для
круговых зубьев при
для
круговых зубьев при 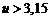 .
.
Тогда число зубьев
колеса

 .
.
Фактическое передаточное
число передачи
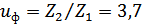
Отклонение 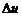 передаточного
числа
передаточного
числа 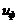 от
от
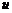 :
:
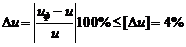 .
.
Внешний окружной модуль
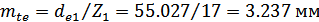
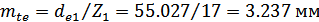 .
.
До стандартного значения
модуль 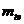 не
округляют.
не
округляют.
Уточняем внешний
делительный диаметр колеса:
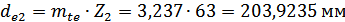
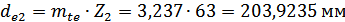 .
.
Углы делительных конусов
шестерни 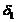 и
колеса
и
колеса 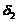 :
:
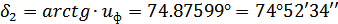
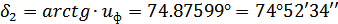 ;
;
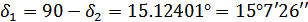
Внешнее делительное
конусное расстояние при 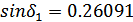
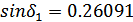 :
:
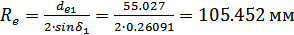
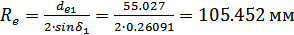 .
.
Ширина зубчатого венца
шестерни и колеса
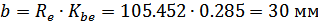
При этом величина 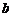 не
должна превосходить значения
не
должна превосходить значения 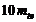 . Т.к нашем примере.
. Т.к нашем примере.
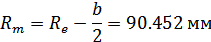
Средний окружной модуль:

 .
.
Средний нормальный
модуль при 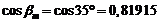 :
:
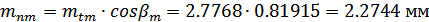
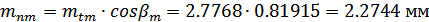 .
.
Средние делительные
диаметры шестерни и колеса:
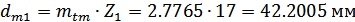
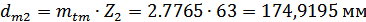
3. Смещение в конической
передаче с круговыми зубьями.
Для конических зубчатых
колес с круговыми зубьями расчётным является среднее нормальное сечение в
середине зубчатого венца, и коэффициенты радиального (высотного) смещения 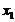 и
и
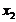 обозначают
соответственно
обозначают
соответственно 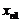 и
и
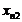 .
При этом в нашем случае:
.
При этом в нашем случае:
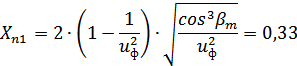
Для понижающей
конической передачи с круговыми зубьями коэффициенты тангенциального смещения 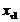 и
и
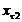 :
:
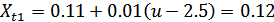
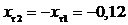 .
.
4. Проверочный расчёт
передачи на сопротивление контактной усталости активных поверхностей зубьев.
Уточняем коэффициент 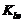 :
:
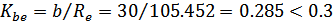
что допустимо.
Тогда величина
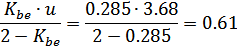
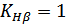
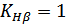 .
.
Средняя окружная
скорость зубчатых колес передачи
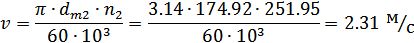
Принимаем 9-ю степень
точности передачи с круговыми зубьями.
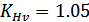
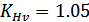 .
.
Окружная сила в
зацеплении при 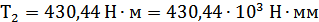
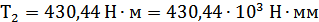 :
:
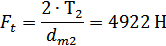
Тогда расчетные
контактные напряжения

Сопротивление контактной
усталости активных поверхностей зубьев обеспечивается, так как выполняется
условие:

5. Допускаемые
напряжения изгиба 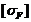 при
расчете на сопротивление усталости зубьев при изгибе.
при
расчете на сопротивление усталости зубьев при изгибе.
Для принятого варианта
термообработки II:
а) предел выносливости
зубьев по напряжениям изгиба 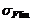 , соответствующий
абсциссе точки перелома кривой усталости для напряжений изгиба:
, соответствующий
абсциссе точки перелома кривой усталости для напряжений изгиба:
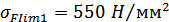
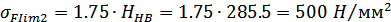
б) коэффициент
безопасности 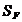 :
:

Коэффициент приведения  :
:
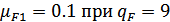
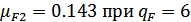
Эквивалентное число
циклов нагружения 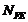 для
шестерни и колеса при числе зацеплений за один оборот зуба конической шестерни
для
шестерни и колеса при числе зацеплений за один оборот зуба конической шестерни 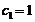 и
зуба колеса
и
зуба колеса 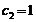 :
:
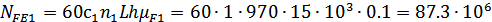
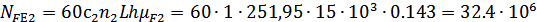
Базовое число циклов
нагружения  (абсцисса
точки перелома кривой усталости для напряжений изгиба) для всех видов
термообработки:
(абсцисса
точки перелома кривой усталости для напряжений изгиба) для всех видов
термообработки:
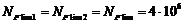 .
.
Для определения
коэффициента долговечности 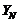 сопоставляем полученные
величины
сопоставляем полученные
величины 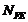 и
и
 :
:
а) для шестерни 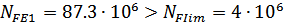
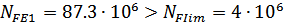 и коэффициент
долговечности
и коэффициент
долговечности 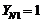 ;
;
б) для колеса 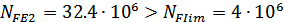
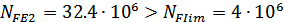 и коэффициент
долговечности
и коэффициент
долговечности 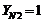 .
.
Lопускаемые
напряжения изгиба 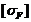 для
варианта т.о.II при
для
варианта т.о.II при 
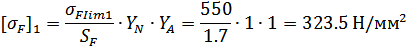
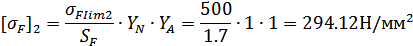
6. Проверочный расчёт
передачи на сопротивление усталости зубьев при изгибе.
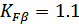
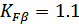 ;
; 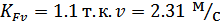
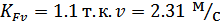
Коэффициент 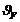 ,
учитывающий влияние вида зубьев конической передачи при расчете их на
сопротивление усталости при изгибе:
,
учитывающий влияние вида зубьев конической передачи при расчете их на
сопротивление усталости при изгибе:
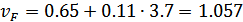
Числа зубьев
эквивалентных цилиндрических прямозубых зубчатых колес (эквивалентное число
зубьев)  :
:
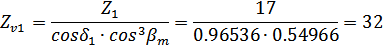
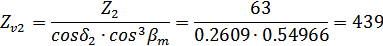
Коэффициент формы зуба и
концентрации напряжений 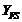 для
конических передач с круговыми зубьями принимают:
для
конических передач с круговыми зубьями принимают:
а) для шестерни 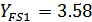
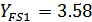 при
при 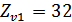
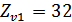 и
и 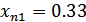
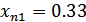 ;
;
б) для колеса 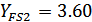
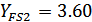 при
при 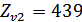
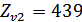 и
и 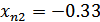
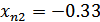 .
.
Тогда расчетные
напряжения при изгибе в опасном сечении зуба шестерни и колеса:
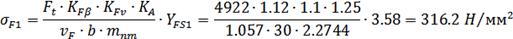
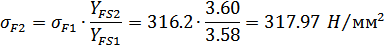
Расчетные напряжения при
изгибе должны быть 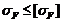 .
.
В нашем примере
сопротивление усталости зубьев при изгибе обеспечивается, так как для шестерни
и колеса выполняется условие:
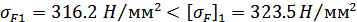

7. Геометрический расчет
конической передачи с круговыми зубьями.
Осевая форма зуба II. При данной форме зубьев вершины конусов делительного и впадин не
совпадают. Вершина конуса впадин располагается так, что ширина дна впадины
зубчатого колеса постоянна, а толщина зуба по делительному конусу растет с
увеличением расстояния от вершины.
Значения 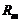 ,
,
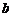 и
и
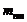 ,
при которых применяют осевую форму зуба II,
приведены в таблице
,
при которых применяют осевую форму зуба II,
приведены в таблице 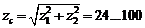 .
.
Изготовление конических
зубчатых колес с осевой формой зубьев II
производится простым двусторонним способом или двойным двусторонним способом,
при котором на шестерне и колесе образуются одновременно обе стороны зубьев.
Двойной двусторонний способ изготовления зубчатых колес осевой формы II является наиболее производительным из всех существующих и
является основным в крупносерийном и массовом производстве.
В качестве исходных
данных для выполнения геометрического расчета конической передачи с
круговыми зубьями принимаем величины, полученные ранее при прочностном расчете:
внешние делительные диаметры 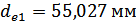
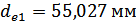 и
и 
 ; средние делительные
диаметры
; средние делительные
диаметры 
 и
и 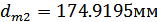
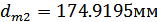 ; внешнее делительное
конусное расстояние
; внешнее делительное
конусное расстояние 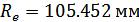
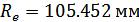 ; среднее делительное
конусное расстояние
; среднее делительное
конусное расстояние 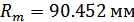
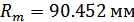 ; ширина венца шестерни
и колеса
; ширина венца шестерни
и колеса 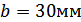
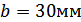 ; числа зубьев
; числа зубьев 
 и
и 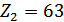
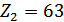 ; средний угол наклона
линии зуба
; средний угол наклона
линии зуба 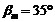 ;
коэффициенты радиального (высотного) смещения
;
коэффициенты радиального (высотного) смещения 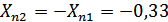
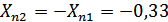 ; коэффициенты
тангенциального смещения
; коэффициенты
тангенциального смещения 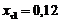 и
и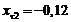 ;
средний нормальный модуль
;
средний нормальный модуль 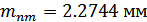
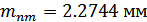 ; углы делительных
конусов
; углы делительных
конусов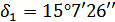
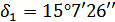
и 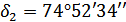
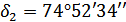 ; число зубьев плоского
колеса
; число зубьев плоского
колеса 
 ; номинальный диаметр
зуборезной головки
; номинальный диаметр
зуборезной головки 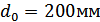
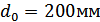 .
.
Так как для конических
зубчатых колес с круговыми зубьями расчетным является среднее нормальное
сечение в середине зубчатого венца, то при геометрическом расчете зацепления
вначале определяют размеры зуба в рас-четном сечении и только после этого
переходят на внешний торец зубчатого колеса. При этом в соответствии с ГОСТ 16202-81
параметры среднего нормального исходного контура: угол профиля 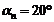 ;
коэффициент высоты головки исходного контура
;
коэффициент высоты головки исходного контура 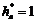 ; коэффициент
радиального зазора
; коэффициент
радиального зазора 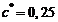 .
.
5. Расчёт подшипников
качения тихоходного вала редуктора на заданный ресурс
Общие сведения
Частота вращения вала:
тихоходного n = nIII
= 68 мин-1.
Требуемый ресурс
(долговечность) подшипников Lh
= 15·103ч. Типовой режим нагружения - 2 (средний равновероятный).
Условия эксплуатации подшипников - обычные. Рабочая температура подшипников t< 100˚ C.
Для тихоходного вала
предварительно был выбран шарико-радиальный однорядный подшипник лёгкой серии
211, для которого:
а) размеры:
d=
55 мм; D= 100 мм; В=21 мм.
б) грузоподъемность:
динамическая Сr= 43,6 кН;
статическая C0r=
25,0 кН.
Схема установки
подшипников - враспор (схема 1). Для данной схемы установки при d =55 мм расстояние между подшипниками должно быть не более lmax= =4·d
= 4·55 = 220 мм. В проектируемом редукторе расстояние между подшипниками l = l2Т
+ l3Т= 160 мм, что меньше lmax.
На опоры вала действуют
силы:
радиальные реакции опорRrA= 13657 H,
RrB= 7225 H;
осевая сила на колесе
косозубой цилиндрической передачи Fa2Т
= 3860,64 Н.
Таким образом на вал
действует только одна внешняя сила Fa2Т
= 3860,64 Н, которая в соответствии со схемой нагружения вала,
направлена в сторону опоры А, то её воспринимает подшипник данной опоры. Ввиду
того, что осевые составляющие от действия радиальных нагрузок в шариковых
подшипниках отсутствуют, то осевые нагрузки:
опора А: Ra1
= 0;
опора В: Ra2
= Fa2Т
= 3860,64H.
Определяем отношения i·Ra / C0r = 1·3860,64 / 25·103 = 0,1544
где iчисло рядов тел качения;
Ra
=Ra2.
Принимаем коэффициент
осевого нагружения e = 0,43.
Для подшипника опоры А,
воспринимаемый осевую силу Fa2Топределяем
отношения Ra2 /
VRr2 =
3860,64 / 1·7225 = 0,53
где V = 1;
Rr2 =RrВ = 7225H.
Т.к. Ra2 / VRr2 = 0,53, что больше e = 0,43 принимаем коэффициенты Х =
0,56 и Y = 1,00.
Таким образом подшипники будем
рассчитывать с учётом радиальных нагрузок Rr1 =RrA и Rr2 =RrВ, но т.к. Rr1>Rr2, то дальнейший расчёт будем производить для более нагруженного
подшипника опоры 1.
Принимаем коэффициенты: КНЕ
= 0,25, a23 = 0,8, Kб = 1,4, Kт = 1.
Эквивалентная динамическая нагрузка:
Pr1= (VXRr1+ YRa1) KБ КТ =(1·0,56·13657+ 1,00·3582,54) ·1,4·1 = 15722 Н.
Определим расчётную динамическую
грузоподъёмность Сr расчподшипника опоры 1:
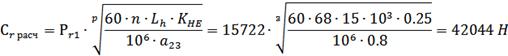
Т.к. Сr расч = 42044 Н <Сr = 43600 Н, то предварительно принятый подшипник лёгкой серии 211
подходит.
6. Выбор компенсирующей
упругой муфты
Конец тихоходного вала редуктора
диаметром d1 = 55 мм, длиной l = 54 мм. Расчётный вращающий момент
для выбора муфты при коэффициенте режима нагрузки Кр = 1,5;
вращающий момент на валу муфты Тм =430,44:
Тр = Кр· Тм
=1,5 · 430,44 =645,66 Н·м <T = 710 Н·м.
С учётом полученных значений
принимаем:
Муфта упругая втулочно-пальцевая
-55-4УЗ ГОСТ 21424-93.
Список источников
кинематический привод редуктор
зубчатый
1. Санюкевич Ф.М. Детали машин курсовое проектирование, Брест:
БГТУ 2004.
2. Анурьев В.И. Справочник конструктора-машиностроителя. М.:
Машиностроение, 1982.
. Васильцов С.В., Винокуров В.А., Земзин В.Н.
Проектирование сварных конструкций в машиностроении/ Под ред. С.А. Куркина. М.:
Машиностроение, 1974.
. Дунаев П.Ф. Конструирование узлов и деталей машин. -
Учебное пособие для ВУЗов, М.: Высшая школа, 1985.
. Иванов М.Н. Детали машин курсовое проектирование. -
Учебное пособие для машиностроительных ВУЗов, М.: Высшая школа, 1975.