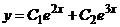Методы нахождения неопределенных интегралов
Контрольная
работа по высшей математике
Ситуационная (практическая) задача №
1
Написать три первых
члена степенного ряда по заданному общему члену 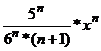 , найти интервал
сходимости ряда и исследовать его сходимость на концах этого интервала.
, найти интервал
сходимости ряда и исследовать его сходимость на концах этого интервала.
Решение.
Подставив
последовательно 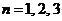 ,
запишем данный ряд в виде:
,
запишем данный ряд в виде:
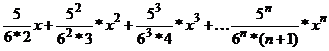
Так как среди
коэффициентов ряда нет коэффициентов равных нулю, находим радиус сходимости
ряда по формуле
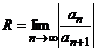 , где
, где 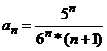 ,
,
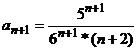
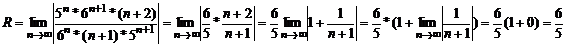
Следовательно, ряд
сходится при 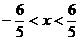
Исследуем сходимость
ряда на концах полученного интервала.
При 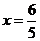 данный
ряд принимает вид
данный
ряд принимает вид 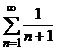 .
Сравним ряд
.
Сравним ряд 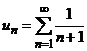 с
гармоническим рядом
с
гармоническим рядом 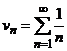 .
Применим второй признак сравнения.
.
Применим второй признак сравнения.
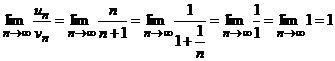
Так как полученный
предел конечен и не равен нулю, а гармонический ряд 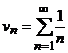 расходится,
то ряд
расходится,
то ряд 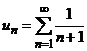 также
расходится по второму признаку сравнения положительных рядов.
также
расходится по второму признаку сравнения положительных рядов.
При 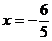 данный
ряд принимает вид
данный
ряд принимает вид 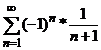 .
.
Последний ряд является
знакочередующим рядом. По признаку Лейбница знакопеременный ряд сходится, если
выполняются два условия:
. 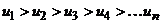 2.
2.
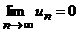
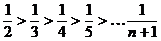 , т.е.
, т.е. 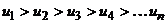
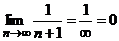
Выполняются два условия
сходимости знакочередующего ряда, т.е. по признаку Лейбница ряд 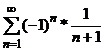 сходится.
Но знакопеременный ряд
сходится.
Но знакопеременный ряд 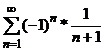 сходится
условно, так как расходится ряд, составленный из абсолютных величин этого ряда
сходится
условно, так как расходится ряд, составленный из абсолютных величин этого ряда 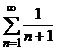 .
.
Ситуационная (практическая) задача №
2
Найти общее решение
дифференциального уравнения 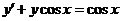 и частное решение,
удовлетворяющее начальному условию
и частное решение,
удовлетворяющее начальному условию 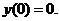
Решение.
Дано дифференциальное уравнение 1
порядка. Решаем его по методу Бернулли.
Заменим функцию 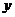 произведением
двух неизвестных функций
произведением
двух неизвестных функций 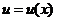 и
и
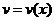 ,
положим
,
положим 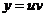 .
Тогда
.
Тогда 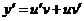 .
Подстановка
.
Подстановка 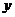 и
и
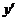 в
уравнение дает
в
уравнение дает 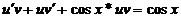 .
.
Преобразуем это
уравнение: 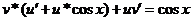
Положим 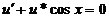 ,
и тогда
,
и тогда 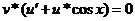 при
любом значении
при
любом значении 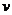 .
Из уравнения
.
Из уравнения 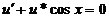 находим:
находим:
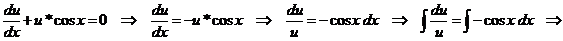
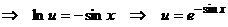
При найденном значении 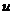 линейное
уравнение принимает вид:
линейное
уравнение принимает вид: 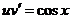 .
Подставляем значение
.
Подставляем значение 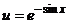 в
уравнение
в
уравнение 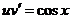 ,
получим
,
получим
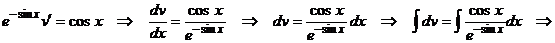
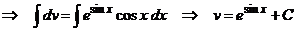
Зная, что 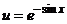 и
и
 ,
находим
,
находим
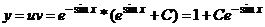
Проверка.
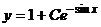 ,
, 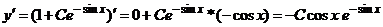
Подставим значения 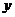 и
и
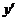 в
заданное уравнение
в
заданное уравнение 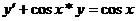
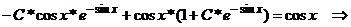
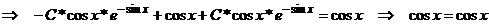
Получили тождество,
следовательно, найденное решение уравнения правильно.
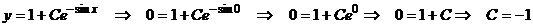
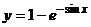 - частное решение при
- частное решение при 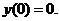
Ответ: 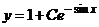 -
общее решение уравнения.
-
общее решение уравнения.
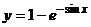 - частное решение при
- частное решение при 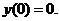
Тестовые задания
1. Применяя таблицу
интегралов и метод замены переменных, найти неопределённый интеграл 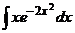
А. 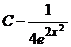 ,
Б.
,
Б. 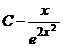 ,
В.
,
В. 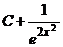 ,
Г.
,
Г. 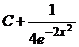 .
.
Ответ. А. 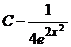
. Применяя метод
интегрирования по частям, найти неопределённый интеграл 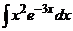
А.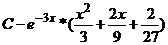 ,
Б.
,
Б. 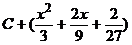 ,
,
В. 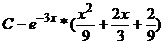 Г.
Г.
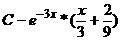
Ответ. А.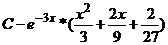
. Применяя метод
интегрирования рациональных алгебраических функций, найти неопределённый
интеграл 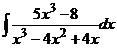
А.  ,
Б.
,
Б. 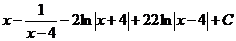
В. 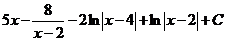 Г.
Г.
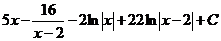
неопределенный интеграл
дифференциальный
Ответ. Г. 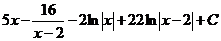
. Вычислить площадь
фигуры, ограниченной графиками функций
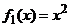 ,
, 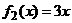 .
.
А. 3/2; Б. 125/6; В.
9/2; Г. 9
. Вычислить 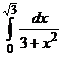
А. 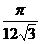 ,
Б.
,
Б. 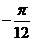 ,
В.
,
В. 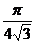 ,
Г.
,
Г. 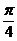
Ответ. В. 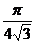
6. Выберите сходящийся ряд
А. 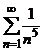 ,
Б.
,
Б. 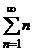 ,
В.
,
В. 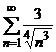 ,
Г.
,
Г. 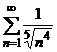
Ответ. А. 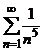 ,
,
7. Выберите абсолютно сходящийся
ряд.
А.  ,
Б.
,
Б.  ,
В.
,
В. 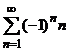 ,
Г.
,
Г. 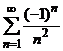
Ответ. Г. 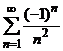
. В точке 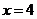 ряд
ряд
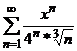
А. расходится, Б.
сходится абсолютно, В. сходится условно, Г. может, как сходиться, так и
расходиться.
Ответ. А. расходится
. При каком значении
параметра 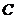 функция
функция
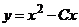 является
решением уравнения
является
решением уравнения 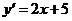
А. 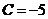 ,
Б.
,
Б.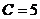 ,
В.
,
В.  ,
Г.
,
Г. 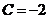
Ответ. А. 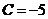
. Найти общее решение
уравнения 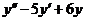
А. 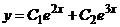 ,
Б.
,
Б. 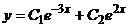 ,
В.
,
В.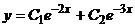 ,
Г.
,
Г. 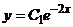 .
.
Ответ. А.