Термодинамика и основы теплотехники
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахский
национальный технический университет имени К.И. Сатпаева
Кафедра
«Машины и оборудование нефтяной и газовой промышленности»
К.Т. Тулеуов, С.А. Абдукаримов.
ТЕРМОДИНАМИКА
И ОСНОВЫ ТЕПЛОТЕХНИКИ
Методические
указания к лабораторным работам
(для
студентов специальностей 050724, 050729, 050708)
Издание
третье, переработанное
Алматы
2010
УДК 621.536.016(18)
СОСТАВИТЕЛИ: К.Т. Тулеуов, С.А. Абдукаримов.
Термодинамика и основы теплотехники. Издание третье, переработанное.
Методические указания к лабораторным работам. - Алматы: КазНТУ имени К.И.
Сатпаева, 2010, с.1-46
Методические указания составлены согласно
типовой учебной программе в соответствии с требованиями ГОСО специальностей, учебно-методических
комплексов, государственных стандартов, педагогико-психологических основ
организации и проведения лабораторных занятий. Они направляют студентов на
самостоятельную активизацию учебного процесса и содержит описание пяти
лабораторных работ, общие методические указания к лабораторным занятиям,
оформлению и защите отчетов.
Описание каждой лабораторной работы включает
цель работы, задание, основные краткие теоретические сведения, описание и
принцип работы экспериментальной установки, методику и порядок выполнения
работы и обработки опытных данных и перечень контрольных вопросов.
Методические указания предназначены для
студентов специальностей 050724, 050729, 050708. Они могут быть использованы
студентами других специальностей, изучающих курс теплотехники.
Ил.6. Табл.9. Прилож.3. Список лит. - 9 назв.
Рецензент А.Г. Танирбергенов, канд. физ.-мат.
наук, доцент
Печатается по типовой учебной программе
утвержденной Министерством образования и науки Республики Казахстан - 2010 год.
© КазНТУ имени К.И. Сатпаева, 2010 г.
ВВЕДЕНИЕ
Настоящий сборник содержит методические указания
по проведению пяти лабораторных работ по дисциплине «Термодинамика и основы
теплотехники»
Выполнение студентами этих лабораторных работ
позволит углубить теоретические знания по теплотехнике, усвоить основы
эксперимента по исследованию термодинамических свойств веществ, параметров
состояния, термодинамических процессов и физических основ переноса теплоты, а
также соответствующие методики.
Цель настоящих методических указаний - дать
студенту необходимые методические указания по организации и выполнению
лабораторных занятий в период учебного процесса.
Проведению каждой лабораторной работы
предшествует контроль и подготовка к ней. Для этого по рекомендуемым учебным
пособиям [1-9], лекциям и настоящему сборнику следует разобраться в содержании
заданной лабораторной работы, усвоить основные положения, необходимые для ее
выполнения.
Студенты должны проявлять научный и практический
интерес к лабораторным занятиям, строго выполнять учебный график, ставить
поисковые вопросы и задачи. Кроме того, студент должен самостоятельно работать
с литературой и УМК, а также кратко и четко выражать свои мысли при защите
отчета.
Методические указания по выполнению лабораторных
работ составлены по единой схеме и содержат: цель работы; задание; краткие
теоретические сведения; методика проведения работы и описание экспериментальной
установки включая схему измерений и общий вид установки с указанием
характеристик используемых средств измерения и контроля; порядок проведения
опыта и обработки результатов измерений; оценку погрешностей измерений и
контрольные вопросы
Настоящие методические указания переработаны и
написаны заново Тулеуовым К.Т., Абдукаримовым С.А.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
На первом лабораторном занятии студенты должны
знакомиться с лабораторной базой и пройти инструктаж по технике безопасности.
Студенты обязаны строго соблюдать требования техники безопасности и правила
внутреннего распорядка, установленные в лаборатории.
Получив от преподавателя задание на выполнение
лабораторной работы, студент обязан самостоятельно ознакомиться с описанием в
настоящем сборнике и подготовиться к коллоквиуму, которому отводиться 10….15
минут перед выполнением работы. Проведению лабораторной работы предшествует контроль
и подготовка к ней. Для этого каждый студент должен к началу лабораторного
занятия по рекомендуемым учебным пособиям [1-9], лекциям и настоящему сборнику
изучить теоретическую предпосылку, целью, заданию, методику и порядок
выполнения эксперимента предстоящей лабораторной работы и составить краткий
конспект, включающий все необходимые расчетно-графические и табличные материалы
для выполнения и защиты отчета по выполняемой работе, т.е. следует разобраться
в содержании данной лабораторной работы, усвоить основные положения,
необходимые для выполнения.
В течение аудиторного времени студент должен
успеть получить допуск, провести опыт, обработать его результаты и защитить
отчет по ранее выполненной работе. Для получения допуска к работе необходимо
знать краткие теории, целью работы, заданию, методику опыта, порядок выполнения
и обработки данных эксперимента.
По окончании работы студенту необходимо обсудить
с преподавателем полученные экспериментальные данные, занести их в таблицу
наблюдений, произвести необходимые расчеты, т.ч. построить, если это требуется,
графики и сделать выводы по работе. Результаты лабораторной работы
представляются в виде письменного отчета и защищаются студентом до начала
выполнения следующей работы.
Отчет по выполненной работе составляется
индивидуально в форме пояснительной записки на одной стороне листа бумаги
формата А4 (210*297), и титульный лист оформляется по СТ РГП 38944979-09-2009
(см. приложение В) с указанием темы (названия) и номер работы, индекс группы и
специальности, фамилии и инициалов студента и преподавателя, названия города и
даты выполнения, названия учебного заведения кафедры.
Отчет по каждой выполненной лабораторной работе
включает:
1) цель и задание лабораторной работы;
2) краткое описание работы с указанием основного
положения теории и эксперимента;
) количественные (расчетные и табличные)
и графические работы;
) принципиальная схема экспериментальной
установки с указанием характеристик используемых средств измерения;
) протокол испытания, подписанным
преподавателем;
) оценку ошибок определяемых величин и
выводы;
) список использованной литературы.
Результаты обработки экспериментальных данных
должны быть представлены в системе СИ. На защиту отчета выносится основные
теоретические положения, методика, порядок и результаты экспериментального
исследования, выводы студенты по работе. Кроме того, каждый студент при защите
лабораторной работе должен ответить на все приведенные контрольные вопросы,
содержащиеся в конце лабораторной работы. Графики, таблицы, рисунки, диаграммы
и т.п. оформляются по государственным стандартам или по стандартам организации
(КазНТУ имени К.И, Сатпаева) СТ РГП 38944979-09-2009
При неправильных оформлениях и результатах
работы преподаватель бракует лабораторную работу и она подлежит повторному
выполнению студентами во внеучебное время.
К экзамену по изучаемому курсу допускаются лишь
те студенты, которые выполнили и защитили предусмотренные лабораторные работы.
. ЛАБОРАТОРНАЯ РАБОТА №1. ОПРЕДЕЛЕНИЕ ГАЗОВОЙ
ПОСТОЯННОЙ ВОЗДУХА
1.1 Цель работы
Цель работы - экспериментальное определение
газовой постоянной воздуха, получение навыков проведения эксперимента по
определению параметров состояния идеального газа (воздуха)
1.2 Задание
) Экспериментальным путем найти значение газовой
постоянной воздуха.
) Расчетным путем по формуле (1.6) найти
расчетное значение газовой постоянной воздуха.
3) Сравнить экспериментальное
значение газовой постоянной воздуха 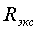 (1.12) с его расчетным
(1.12) с его расчетным 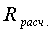 по формуле
(1.14) и литературным
по формуле
(1.14) и литературным 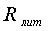 =287Дж/(кг*К)
значениями по формуле (1.15).
=287Дж/(кг*К)
значениями по формуле (1.15).
) Определить погрешность
эксперимента по формуле (1.16).
) Составить и защитить отчет по
выполненной работе.
1.3 Краткие
теоретические сведения
Воздух представляет собой газовую
смесь, состоящую из кислорода 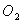 , азота
, азота 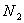 ,
углекислого газа
,
углекислого газа 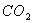 , аргона
, аргона 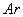 , водяных
паров и одноатомных газов. Объемные доли r этих газов в воздухе соответственно
равны:
, водяных
паров и одноатомных газов. Объемные доли r этих газов в воздухе соответственно
равны: 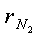 =0,7803;
=0,7803; 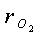 =0,21;
=0,21; 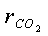 =0,0003;
=0,0003; 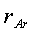 = 0,0093.
= 0,0093.
При давлениях, близких к
атмосферному, и комнатной температуре воздух обладает свойствами идеального
газа. Под идеальным газом понимают воображаемый газ, в котором отсутствуют силы
взаимодействия между молекулами, а объемом самих молекул можно пренебречь по
сравнению с объемом газом. Все реальные газы при высоких температурах и малых
давлениях по своим свойствам практически не отличаются от идеального газа.
Характеристическое уравнение или
уравнение состояния идеального газа связывает между собой основные параметры
состояния - давление, объем и температуру - и может бать представлено
уравнением Клапейрона (для 1 кг идеального газа)
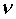 =RT или P=ρRT, (1.1)
=RT или P=ρRT, (1.1)
где Р,Т - абсолютные давления, Па, и
температура, К; ρ=1/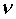 =m/V -
плотность газа
=m/V -
плотность газа 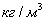 ;
; 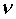 =V/m -
удельный объем,
=V/m -
удельный объем, 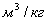 ; R -
(индивидуальная) газовая постоянная для 1 кг газа, Дж/(кг*К); V,m - объем,
; R -
(индивидуальная) газовая постоянная для 1 кг газа, Дж/(кг*К); V,m - объем, 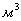 и масса
воздуха, кг.
и масса
воздуха, кг.
Для произвольной массы (m, кг) газа
уравнение состояния идеального газа можно получить путем умножения обеих частей
(1.1) на массу m:
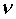 m=mRT или PV=mRT. (1.2)
m=mRT или PV=mRT. (1.2)
Для 1 кмоль газа уравнение состояния
(уравнение Клапейрона-Менделеева) можно получить путем умножения обеих частей
(1.1) на молярную массу газа μ
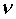 μ= μRT или P
μ= μRT или P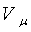 =μRT=
=μRT=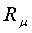 T , (1.3)
T , (1.3)
где 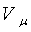 =μ
=μ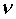 - объем 1 кмоля газа,
- объем 1 кмоля газа, 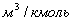 . При
нормальных условиях физических условиях (
. При
нормальных условиях физических условиях (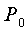 =1,01325*
=1,01325*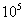 Па;
Па; 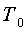 =273,15 К)
для всех газов
=273,15 К)
для всех газов 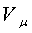 =22,41
=22,41 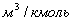 ;
; 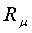 =μR
=μR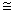 8314,2
Дж/(кмоль*К) - универсальная газовая постоянная для 1 кмоль газа, одинаковая
для всех газов; μ
- молярная
масса газа, кг/кмоль.
8314,2
Дж/(кмоль*К) - универсальная газовая постоянная для 1 кмоль газа, одинаковая
для всех газов; μ
- молярная
масса газа, кг/кмоль.
Численное значение 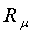 можно
получить из уравнения (1.3), записав его, например, для нормальных условий:
можно
получить из уравнения (1.3), записав его, например, для нормальных условий:
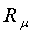 =
=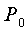
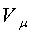 /
/ 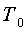 =1,01325*
=1,01325*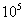 *22,41/273,15=8314,2
Дж/(кмоль*К) (1.4)
*22,41/273,15=8314,2
Дж/(кмоль*К) (1.4)
Универсальное уравнение состояния,
отнесенное к 1 кмоль газа (1.3) может быть переписано в виде
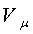 =8314,2*Т. (1.5)
=8314,2*Т. (1.5)
Индивидуальная газовая постоянная
(R) есть работа 1 кг идеального газа в процессе при постоянном давлении и при
изменении температуры на один градус (°С или К).
Газовую постоянную (воздуха) смеси
идеальных газов, если заданы массовые доли 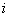 -x компонентов смеси
-x компонентов смеси 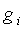 можно
определить по формуле
можно
определить по формуле
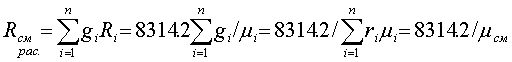 . (1.6)
. (1.6)
Среднюю молярную массу смеси можно
выразить через молекулярные массы компонентов и их объемные доли формулой
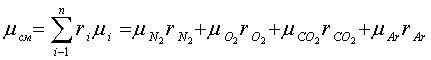 . (1.7)
. (1.7)
Согласно закону Амага для идеального
газа молярная доля 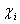 равна
объемной доле
равна
объемной доле 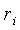
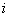 -й
компоненты газа. Молярные массы газов берут из приложения А.
-й
компоненты газа. Молярные массы газов берут из приложения А.
Если абсолютное давление 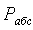 в сосуде
больше барометрического (атмосферного)
в сосуде
больше барометрического (атмосферного) 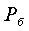 , то
, то 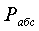 определяется по формуле
определяется по формуле
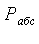 =
=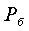 +
+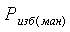 , (1.8) а если меньше, то по формуле
, (1.8) а если меньше, то по формуле
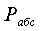 =
=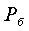 -
-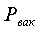 . (1.9)
. (1.9)
В уравнениях (1.8) и (1.9) 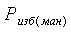 и
и 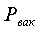 -
избыточное (манометрическое) и вакуумметрическое (разрежение) давления, Па,
измеряемые соответственно манометром и вакуумметром.
-
избыточное (манометрическое) и вакуумметрическое (разрежение) давления, Па,
измеряемые соответственно манометром и вакуумметром.
1.4
Методика проведения работы и описание экспериментальной установки
В данной работе экспериментальное
определение газовой постоянной воздуха 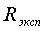 осуществляется следующим образом.
осуществляется следующим образом.
В сосуде 7 в соответствии с рисунком
1.1 с неизменным объемом V содержится воздух массой 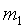 при
атмосферном давлении
при
атмосферном давлении 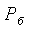 и
температуре помещения
и
температуре помещения 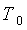 . Начальные
параметры его состояния связаны уравнением состояния
. Начальные
параметры его состояния связаны уравнением состояния
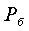 V=
V=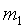
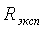
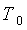 . (1.10)
. (1.10)
После откачки части воздуха из
сосуда и закрытие крана 6, его давление станет 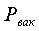 , масса
, масса 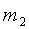 , а новое
состояние будет описываться уравнением
, а новое
состояние будет описываться уравнением
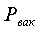 V=
V=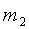
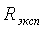
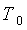 . (1.11)
. (1.11)
Если экспериментально определить
параметры этих равновесных состояний воздуха, то вычтя (1.11) из (1.10), можно
определить газовую постоянную 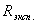
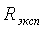 =
=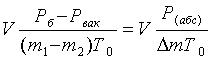 , Дж/(кг*К) (1.12)
, Дж/(кг*К) (1.12)
где 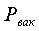 - разрежение (или вакуум) в сосуде,
измеряемое вакуумметром в Па,
- разрежение (или вакуум) в сосуде,
измеряемое вакуумметром в Па, 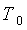 - температура окружающей среды
измеренная лабораторным термометром в К.
- температура окружающей среды
измеренная лабораторным термометром в К.
Объем сосуда V показан на стенде.
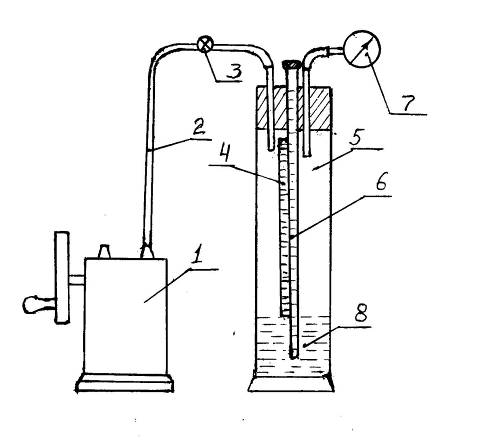
Схема экспериментальной установки показана на рис. 1.1.
Экспериментальная установка состоит
из точного электронного веса 8, на которой находится опытный сосуд 7, имеющий
кран 6. Последний с помощью металлических (стеклянных) 4 и резиновых трубок 5
соединяется с вакуум-насосом 1 и вакуумметром 3. Между вакуум-насосом 1 и
сосудом 7 подключен ресивер 2 для сглаживания пульсации давления при откачке
воздуха.
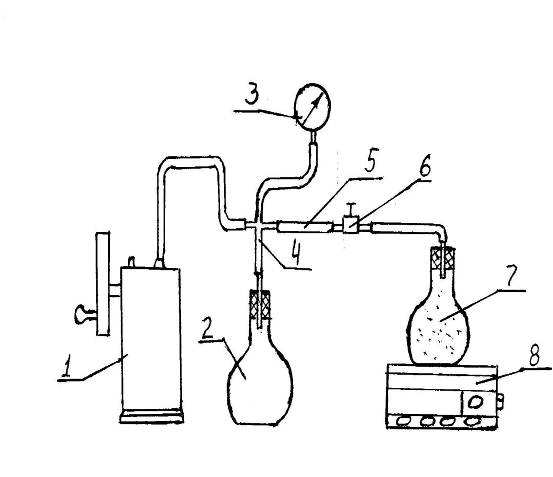
-вакуум-насос; 2-ресивер;
3-вакуумметр; 4-металлические (стеклянные) трубки; 6-кран (зажим); 7-опытный
сосуд; 8-лабораторный электронный вес.
Рисунок 1.1 - Схема
экспериментальной установки
1.5 Порядок
проведения работы и обработка результатов эксперимента
С помощью резиновой или (стеклянной)
трубки 5 отсоединяем опытный сосуд 7 от вакуумной системы. Открыв кран 6
необходимо подождать 2…3 минуты и проверить равенство весов сосуда 7, т.е. с
помощью электронного веса 8 определить первоначальный вес опытного сосуда 7
заполненный воздухом  . При этом
давление и температура воздуха в сосуде 7, очевидно будут равны давлению
. При этом
давление и температура воздуха в сосуде 7, очевидно будут равны давлению 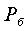 и
температуре окружающего лабораторного помещения
и
температуре окружающего лабораторного помещения 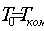 , которые определяются с помощью
барометра - анероида и термометра. Затем сосуд 7 с помощью резиновой (или
стеклянной) трубки 5, крана 6 подключается к вакуум-насосу 1, вакуумметру 3,
ресиверу 2 и проводится откачка части воздуха их сосуда 7, наблюдая за
величиной разрежения по вакуумметру 3. После откачки части воздуха до заданной
преподавателем величины
, которые определяются с помощью
барометра - анероида и термометра. Затем сосуд 7 с помощью резиновой (или
стеклянной) трубки 5, крана 6 подключается к вакуум-насосу 1, вакуумметру 3,
ресиверу 2 и проводится откачка части воздуха их сосуда 7, наблюдая за
величиной разрежения по вакуумметру 3. После откачки части воздуха до заданной
преподавателем величины 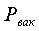 выждать 2…3
мин. и в этом состоянии необходимо измерить вакуумметром разрежение
выждать 2…3
мин. и в этом состоянии необходимо измерить вакуумметром разрежение 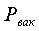 в сосуде 7.
За это время обычно устанавливается тепловое состояние сосуда с окружающей
средой. Затем кран 6 закрывается, отсоединяются резиновые трубки 5 и с помощью
лабораторного электронного веса 8 определяется вес (масса) сосуда 7 с учетом
откаченного воздуха
в сосуде 7.
За это время обычно устанавливается тепловое состояние сосуда с окружающей
средой. Затем кран 6 закрывается, отсоединяются резиновые трубки 5 и с помощью
лабораторного электронного веса 8 определяется вес (масса) сосуда 7 с учетом
откаченного воздуха 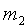 . При этом
мы имеем меньшую массу сосуда
. При этом
мы имеем меньшую массу сосуда 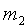 . Тогда вес откаченного воздуха
. Тогда вес откаченного воздуха 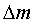 дает
величину
дает
величину
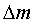 =
=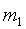 -
-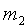 , (1.13)
, (1.13)
где 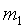 - масса сосуда с краном и резиновой
(или стеклянной) трубкой до начала опыта;
- масса сосуда с краном и резиновой
(или стеклянной) трубкой до начала опыта; 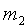 - масса сосуда с краном и резиновой
(или стеклянной) трубкой в конце опыта. Опыт повторяется при трех значениях
разрежения
- масса сосуда с краном и резиновой
(или стеклянной) трубкой в конце опыта. Опыт повторяется при трех значениях
разрежения 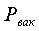 . До начала
опыта необходимо заготовить таблицу наблюдений (таблица 1.1).
. До начала
опыта необходимо заготовить таблицу наблюдений (таблица 1.1).
Объем опытного сосуда 7: V=….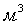 . Измерить
температуру окружающей среды
. Измерить
температуру окружающей среды 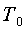 лабораторным термометром, а
давление барометром
лабораторным термометром, а
давление барометром 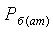
Таблица 1.1
Результаты измерений и обработки
результатов эксперимента.
Измеренные значения величин,
необходимые для расчета газовой постоянной воздуха, нужно выразить в системе СИ
(см. приложение Б), затем по формуле (1.12) найти 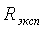 и
среднеарифметическое значение
и
среднеарифметическое значение 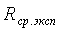 по данным трех опытов. Полученное
среднее значение
по данным трех опытов. Полученное
среднее значение 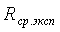 надо
сравнить соответственно с расчетным по формуле (1.6) и литературными данными (
надо
сравнить соответственно с расчетным по формуле (1.6) и литературными данными (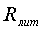 =287
Дж/(кг·К)) по формулам:
=287
Дж/(кг·К)) по формулам:
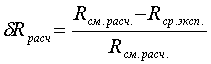 ; (1.14)
; (1.14)
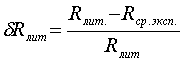 . (1.15)
. (1.15)
Максимальная относительная
(приборная) погрешность в определении газового постоянного воздуха находится
при использовании уравнения (1.12) с учетом применяемых в работе средств
измерения по формуле
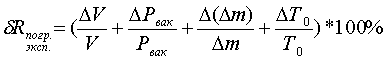 , (1.16)
, (1.16)
где 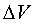 - абсолютная погрешность измерения
объема опытного сосуда, (
- абсолютная погрешность измерения
объема опытного сосуда, (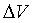
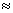 5*
5*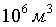 );
); 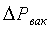 - абсолютная погрешность измерения
давления
- абсолютная погрешность измерения
давления 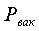 (определяется
классом точности прибора);
(определяется
классом точности прибора); 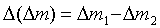 - абсолютная погрешность измерения
массы выкаченного воздуха (определяется классом точности прибора
- абсолютная погрешность измерения
массы выкаченного воздуха (определяется классом точности прибора  г);
г);  - абсолютная
погрешность измерения температуры окружающего воздуха (
- абсолютная
погрешность измерения температуры окружающего воздуха (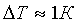 ).
).
Эксперимент считается проведенным
удовлетворительным, если 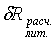 меньше или
равно
меньше или
равно 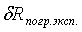
Литература: 1[стр. 6-11]; 2[стр.
10-32]; 5[стр.11-14].
Контрольные
вопросы
1) Чем отличается индивидуальная газовая и
универсальная газовая постоянные, связь между ними, их размерности?
2) Что такое абсолютное, барометрическое,
избыточное и вакуумметрическое давления? Какими приборами они измеряются? Какое
из давлений является параметром состояния и почему?
) Что такое термический параметр
состояния? Какие параметры приняты в технической термодинамике за основные и
почему?
) Какие уравнения состояния идеального
газа вы знаете, размерности величин, входящих в эти уравнения?
) Что такое рабочее тело, термодинамическая
система, равновесное и неравновесное состояние, равновесный и неравновесный
термодинамические процессы, обратимый и необратимые процессы?
) Чем отличается идеальный газ от
реального? Дать их определение?
) Что называется термодинамическим
процессом?
) Какие параметры определяют тепловое
состояние тела и в каких единицах они измеряются?
) Укажите погрешность измерения, какой
величины составляет максимальную долю погрешности определения газовой
постоянной воздуха?
) Дайте формулировку и напишите первый
закон термодинамики в дифференциальном и аналитическом видах.
2. ЛАБОРАТОРНАЯ РАБОТА №2. ИЗОТЕРМИЧЕСКОЕ СЖАТИЕ
ВОЗДУХА
2.1 Цель работы
Цель работы - изучение закономерностей изменения
параметров состояния идеального газа (воздуха) при изотермическом процессе,
расчет работы процесса и изменений калорических функций (энтропии).
2.2 Задание
1) Получить экспериментальную и
расчетную (теоретическую) зависимость объема газа (воздуха) от давления в
изотермическом процессе V=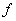 (P) при Т=
(P) при Т=
) Сравнить экспериментальную
зависимость V=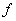 (P)
(изотерму(кривую)) с теоретической рассчитанной по формуле (2.2).
(P)
(изотерму(кривую)) с теоретической рассчитанной по формуле (2.2).
) Рассчитать экспериментальную и
теоретическую работу изотермического сжатия в процессе двумя заданными
состояниями по формуле (2.3) или (2.4).
) Определить (экспериментально)
показатель политропы процесса n в процессе двумя заданными состояниями по
формуле (2.12).
) Рассчитать (экспериментально)
изменения энтропии в процессе между двумя заданными состояниями по формуле
(2.7) или (2.9).
) Вычислить относительную величину
расхождения между значениями работы сжатия и давления, рассчитанную по
экспериментальной и расчетной кривой по формулам (2.2) и (2.4).
2.3 Краткие
теоретические сведения
Сухой воздух при давлениях, близких
к атмосферному с достаточной степенью точности может считаться идеальным газом.
В идеальных газах отсутствуют силы взаимного притяжения и отталкивания между
молекулами, а объем самих молекул пренебрежимо мал по сравнению с объемом газа.
Связь между параметрами в двух состояниях 1 и 2 равновесного изотермического
процесса идеального газа характеризуются уравнением Бойля-Мариотта
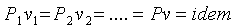 (2.1)
(2.1)
или для m кг газа
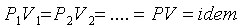 , (2.2)
, (2.2)
где 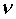 идеальный объем газа,
идеальный объем газа, 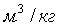 ; V=m
; V=m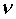 - объем
газа,
- объем
газа, 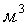 .
.
Экспериментальная работа изменения
объема газа в изотермическом процессе между состояниями 1 и 2 определяется по
формуле (для 1 кг газа)
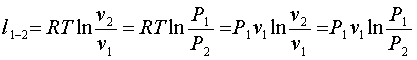 , Дж/кг (2.3)
, Дж/кг (2.3)
или для m кг газа
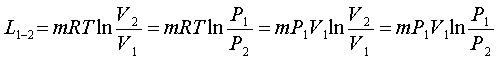 , Дж (2.4)
, Дж (2.4)
где m (кг) масса рабочего тела в
каждом опыте в бюретке 6, кг. Ее можно найти по уравнению состояния идеального
газа:
m=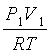 , кг (2.5)
, кг (2.5)
где R =287 Дж/(кг·К)- газовая
постоянная воздуха.
Внутренняя энергия и энтальпия газа
в изотермическом процессе не меняется, поэтому из первого закона термодинамики
(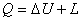 ) работа
изменения объема и количество теплоты, полученное телом, равны между собой.
) работа
изменения объема и количество теплоты, полученное телом, равны между собой.
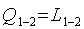 , Дж. (2.6)
, Дж. (2.6)
Изменение экспериментальной энтропии
в изотермическом процессе, т.е. разность энтропии, соответствующих состояниям
1и 2 вычисляется следующим образом
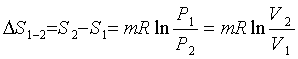 Дж/К . (2.7)
Дж/К . (2.7)
Формула (2.7) может быть приведена к
другому виду. Из уравнения состояния идеального газа имеем
=PV/T . (2.8)
С учетом этого соотношения (2.6)
приобретает вид
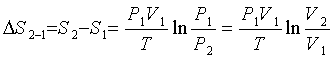 Дж/К. (2.9)
Дж/К. (2.9)
Теплоемкость в изотермическом
процессе
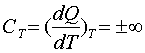 . (2.10)
. (2.10)
Показатель политропы n любого
политропного процесса 1-2 (из уравнения политропного процесса)
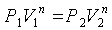 , (2.11)
, (2.11)
рассчитывается по формуле
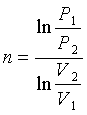 . (2.12)
. (2.12)
2.4
Методика проведения работы и описание экспериментальной установки
Изотермический процесс практически
может быть осуществлен за счет организации интенсивного теплообмена
термодинамической системы со средой, имеющей постоянную температуру. При этом
протекающий процесс можно рассматривать как квазиравномерный, если температура
во всех точках системы в каждый момент времени будет одинаковой. Поэтому
изотермический процесс технически может быть осуществить, строго говоря, ряд
дискретных равновесных состояний термодинамической системы, имеющей одинаковую
температуру.
Равновесный изотермический процесс
сжатия воздуха реализуется на экспериментальной установке, схема которой
показана на рис 2.1, путем дискретного перевода рабочего тела (воздуха) из
состояния равновесия с окружающей средой «1» в заданные состояние «2» через ряд
промежуточных равновесных состояний при комнатной температуре Т=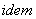
Исследуемое вещество (атмосферный
воздух) находится в тонкостенной стеклянной трубке 6, расположенной в сосуде 4,
верхний конец которой герметично закрыт, и нижний - открыт - конец погружен в
жидкость (трансформаторное масло) 8. Сосуд 4 соединен с манометром 7 и
вакуум-насосом 1.
Изменение давления воздуха в трубке
6 производится ручным вакуум-насосом 1 и краном 3 и измеряется манометром 7.
Изменение давления воздуха в бюретке 6 вызывает соответствующее изменение
объема, которое фиксируется по уровню жидкости в бюретке (трубке) 6 с помощью
шкалы 5.
- вакуум-насос; 2- резиновые трубки;
3- кран (зажим); 4- стеклянный сосуд; 5- шкала; 6- бюретка (рабочая трубка); 7-
манометр; 8- жидкость.
Рисунок 2.1- Схема экспериментальной
установки.
2.5 Порядок
проведения работы и обработка результатов эксперимента
Опыт состоит в измерении давлений и
объемов воздуха, соответствующих ряд равновесных состояний при одинаковой
температуре.
В начале опыта фиксируется
температура воздуха в помещении по ртутному термометру. После этого при
открытом кране 3 нужно записать давление 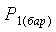 в первом равновесном состоянии по
показаниям манометра 7 (или барометра) и объем воздуха
в первом равновесном состоянии по
показаниям манометра 7 (или барометра) и объем воздуха 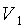 в условных
единицах (
в условных
единицах (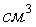 ) шкалы 5.
Далее вакуум-насосом 1 накачать воздух в сосуд 4 до заданного преподавателем
значения избыточного давления
) шкалы 5.
Далее вакуум-насосом 1 накачать воздух в сосуд 4 до заданного преподавателем
значения избыточного давления 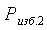 , фиксируя по манометру 7 и шкале 5
давление и объем
, фиксируя по манометру 7 и шкале 5
давление и объем 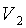 воздуха в
бюретке 6 в пяти-шести промежуточных между «1» и «2» равновесных состояниях
рабочего тела. При этом следует зафиксировать ряд равновесных состояний (не
менее 5…6) до максимального давления (приблизительно до 0,5 кгс/
воздуха в
бюретке 6 в пяти-шести промежуточных между «1» и «2» равновесных состояниях
рабочего тела. При этом следует зафиксировать ряд равновесных состояний (не
менее 5…6) до максимального давления (приблизительно до 0,5 кгс/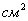 ).
Необходимо учитывать, что при сжатии температура воздуха несколько повышается,
поэтому после каждого изменения давления нужно выждать некоторое время (1…2
минуты) для того, чтобы температура воздуха вновь стала равной температуре в
сосуде 4. В это время давление и объем воздуха мало изменяются. Поэтому
измерять давление и объем надо после того, как эти величины установятся.
).
Необходимо учитывать, что при сжатии температура воздуха несколько повышается,
поэтому после каждого изменения давления нужно выждать некоторое время (1…2
минуты) для того, чтобы температура воздуха вновь стала равной температуре в
сосуде 4. В это время давление и объем воздуха мало изменяются. Поэтому
измерять давление и объем надо после того, как эти величины установятся.
В состоянии «1» абсолютное давление
рабочего тела равно барометрическому 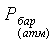 , а в остальных состояниях
, а в остальных состояниях
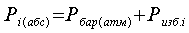 , Па (2.13)
, Па (2.13)
где 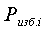 - избыточное давление рабочего тела,
фиксируемое манометром в каждом опыте;
- избыточное давление рабочего тела,
фиксируемое манометром в каждом опыте; 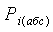 - абсолютное давление при различных
равновесных состояниях рабочего тела.
- абсолютное давление при различных
равновесных состояниях рабочего тела.
В термодинамике параметром состояния
рабочего тела является только абсолютное давление.
До подстановки величины 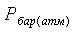 и
и 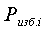 в (2.13) их
следует перевести в Па по приложению Б.
в (2.13) их
следует перевести в Па по приложению Б.
Данные измерения давлений и объемов
ряда равновесных изотермических состояний представляется в виде таблицы 2.1 и
P,V- диаграмме. В P,V- диаграмме строят экспериментальную (по данным таблицы
2.1) и теоретическую (расчетную) изотермы рассчитанную по формуле (2.2), или
(по данным таблицы 2.2), принимая за их общую начальную точки «1» с параметрами
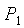 и
и 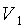 , т.е.
используя уравнение изотермического процесса идеального газа (2.2), необходимо
построить расчетную изотерму, проходящую через начальное состояние в каждом
опыте. Теоретическая (расчетная) изотерма строится по формуле (2.2). При этом,
давая значения объема V, определить соответствующие им давления Р.
, т.е.
используя уравнение изотермического процесса идеального газа (2.2), необходимо
построить расчетную изотерму, проходящую через начальное состояние в каждом
опыте. Теоретическая (расчетная) изотерма строится по формуле (2.2). При этом,
давая значения объема V, определить соответствующие им давления Р.
Ошибка эксперимента может быть оценена
по расхождению давлений на экспериментальной и теоретической (расчетной)
изотермах (кривых) в месте их максимального удаления друг от друга:
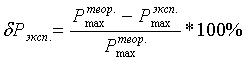 . (2.14)
. (2.14)
Величина 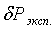 должна быть
сопоставлена с приборной погрешностью:
должна быть
сопоставлена с приборной погрешностью:
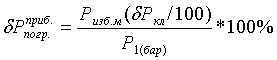 , (2.15)
, (2.15)
где 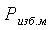 - максимальное избыточное давление,
измеряемое данным манометром;
- максимальное избыточное давление,
измеряемое данным манометром; 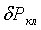 - класс точности прибора
(манометра);
- класс точности прибора
(манометра); 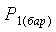 - начальное
барометрическое давление по показаниям барометра.
- начальное
барометрическое давление по показаниям барометра.
Если 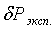 меньше или равно
меньше или равно 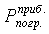 , то опыт
выполнен с достаточной точностью; если
, то опыт
выполнен с достаточной точностью; если 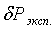 больше
больше 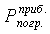 , необходимо
искать источник погрешности в эксперименте.
, необходимо
искать источник погрешности в эксперименте.
Далее, используя экспериментальную
кривую изотермического процесса (или по таблице 2.1), по соотношению (2.3) или
(2.4) определить экспериментальную работу изотермического сжатия рабочего тела
и экспериментальное изменение энтропии системы по формуле (2.7) или (2.9).
Максимальная относительная ошибка
определения работы и изменения энтропии в изотермическом процессе
рассчитываются соответственно по формулам:
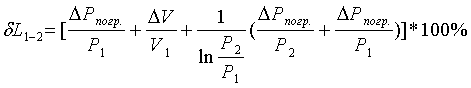 . (2.16)
. (2.16)
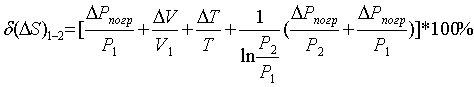 , (2.17)
, (2.17)
где 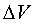 - абсолютная погрешность изменения
объема воздуха, соответствующая половине деления шкалы 5;
- абсолютная погрешность изменения
объема воздуха, соответствующая половине деления шкалы 5; 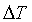 - абсолютная
погрешность измерения температуры воздуха;
- абсолютная
погрешность измерения температуры воздуха; 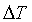 =1К или соответствующая половине
деления шкалы ртутного термометра;
=1К или соответствующая половине
деления шкалы ртутного термометра; 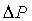 - абсолютная погрешность измерения Р
(определяется классом точности прибора).
- абсолютная погрешность измерения Р
(определяется классом точности прибора).
Далее нужно вычислить расчетную
работу сжатия системы по формулам (2.3) или (2.4), вычислить относительную
величину расхождения между значениями работы сжатия, рассчитанных по
экспериментальной и расчетной кривой по формуле
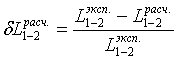 . (2.18)
. (2.18)
Полученную относительную величину
расхождения сравнить с максимальной относительной ошибкой определения,
вычисленной по формуле (2.16)
Далее нужно вычислить
экспериментальный показатель политропы n в процессе между двумя заданными
состояниями по формуле (2.12) и найти среднеарифметическое значение 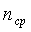
Таблица 2.1
Экспериментальные данные
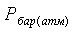 =…., Па; Т=…., К
=…., Па; Т=…., К
|
№
опыта
|
Давление
|
Объем
|
|
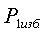 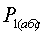 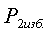 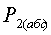 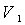 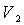
|
|
|
|
|
|
|
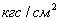 ПаПа ПаПа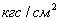 ПаПа ПаПа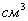 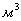 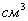 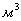
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
Расчетные данные заносятся в таблицу 2.2
Таблица 2.2
Расчетные данные
|
№
расчета
|
Давление
|
Объем
|
Работа
|
Изменение
энтропии
|
Показатель
политропы
|
|
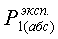 , Па , Па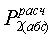 , Па , Па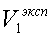 , , 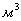 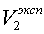 , , 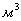 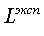 , Дж , Дж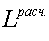 , Дж , Дж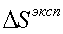 , Дж/К , Дж/К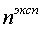 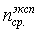
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
Литература: 1 [стр. 30-34]; 3 [стр.63-68]; 5,6
[стр.22-26].
Контрольные вопросы
1) Какой процесс называется изотермическим?
Соотношение между параметрами в изотермическом процессе.
2) Что называется равновесным состоянием и
равновесным процессом?
) Почему изменения внутренней энергии и
энтальпии идеального газа в изотермическом процессе равны нулю?
) Чему равна теплоемкость изотермического
процесса?
) Вывести формулы работы изменения объема
в изотермическом процессе?
) Как реализуется изотермический процесс
в данной работе?
) Каково взаимное расположение изотермы и
адиабаты на Р,V- диаграмме, проведенной из одной точки при сжатии и расширении
газа?
) Докажите, что в изотермическом процессе
работа, совершаемая идеальным газом, равна количеству тепла, подведенного в
данном процессе.
) Написать (два вида) уравнения первого
закона термодинамики для изотермического процесса.
) Как связаны между собой теплота, работа
и изменение внутренней энергии термодинамической системы и как называется эта
зависимость?
) Каково расположение изотермы в Р,V и
Т,S- координатах?
) При каких условиях политропный процесс
переходит в изотермический?
) Способы определения показателя
политропы.
) По каким уравнениям вычисляется
изменение энтропии в изотермическом процессе?
) Написать уравнение теплоемкости
политропного процесса и показать, что из данного уравнения можно получить
теплоемкости изотермического процесса.
) Что такое энтропия и энтальпия?
) Сформулируйте цель настоящей работы.
3. ЛАБОРАТОРНАЯ РАБОТА №3. АДИАБАТНОЕ РАСШИРЕНИЕ
ВОЗДУХА
3.1 Цель работы
Цель работы- изучение закономерностей изменения
параметров состояния воздуха при адиабатном расширении, расчет работы процесса
и показателя адиабаты, и получение навыков экспериментального
термодинамического исследования.
3.2 Задание
) Получить экспериментальную и расчетную
(теоретическую) зависимости объема газа (воздуха) от давления в адиабатном
процессе.
2) Сравнить экспериментальную
адиабату (кривую 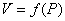 ) с
теоретической рассчитанной по формуле (3.8).
) с
теоретической рассчитанной по формуле (3.8).
) Определить (экспериментально)
показатель адиабаты К в процессе двумя заданными состояниями по формуле (3.18)
и сравнить его с литературным значением 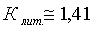 .
.
) Рассчитать экспериментальную и
расчетную работу адиабатного расширения в процессе двумя заданными состояниями
по формуле (3.13).
) Рассчитать экспериментальную
располагаемую работу в адиабатном процессе между двумя заданными состояниями по
формуле (3.14).
) Вычислить относительную величину
расхождения между значениями работы расширения, давления и показателя адиабаты,
рассчитанную по экспериментальной и расчетной величине по формулам (3.17) и
(3.20).
) Определить максимальную
относительную погрешность (эксперимента) определения работы расширения
адиабатного процесса по формуле (3.22).
) Составить и защитить отчет по
выполненной работе.
3.3 Краткие
теоретические сведения
Адиабатным процессом называется
такой процесс, в котором к термодинамической системе не подводится и от
термодинамической системы не отводится тепло, т.е. 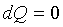 .
.
В реальных условиях процесс является
адиабатным в тех случаях, когда система снабжена хорошей теплоизоляцией или
когда процесс расширения (сжатия) системы происходит настолько быстро, что не
успевает произойти сколько-нибудь заметный теплообмен рабочего тела с
окружающей средой. Для получения адиабатного процесса необходимым и
обязательным условием является 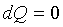 и, следовательно, Q=0.
и, следовательно, Q=0.
Для обратимого адиабатного процесса 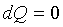 , но
поскольку на основании уравнения второго закона термодинамики для этого
процесса dQ=TdS, то dS=0 и изменение энтропии
, но
поскольку на основании уравнения второго закона термодинамики для этого
процесса dQ=TdS, то dS=0 и изменение энтропии 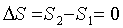 , т.е.
, т.е. 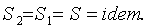 Следовательно,
обратимый адиабатный процесс является процессом при постоянной энтропии, или
изоэнтропным.
Следовательно,
обратимый адиабатный процесс является процессом при постоянной энтропии, или
изоэнтропным.
Дифференциальным уравнением
изоэнтропного (адиабатного) процесса является выражение
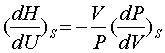 . (3.1)
. (3.1)
В термодинамике внутренняя энергия
U, энтальпия H, теплоемкость С называются калориметрическими свойствами
(параметрами) вещества, а объем V, давление Р, температура Т- термическими
свойствами (параметрами). Уравнение (3.1) показывает, как связан изменение
калорических свойств системы (Н,U) с изменением ее термических свойств (Р,V) в
изоэнтропном процессе.
В уравнении (3.1) обозначим 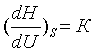 . (3.2)
. (3.2)
Величину К называют показателем
изоэнтропного (адиабатного) процесса.
Связь между параметрами в
адиабатическом процессе можно получить при 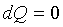 и двух форм записи первого закона
термодинамики.
и двух форм записи первого закона
термодинамики.
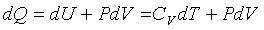 ; (3.3)
; (3.3)
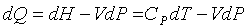 ; (3.4)
; (3.4)
разделив (3.4) на (3.3) и обозначив 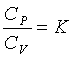 , получим
, получим
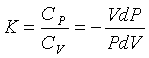 , (3.5)
, (3.5)
откуда, разделяя переменные,
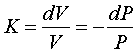 . (3.6)
. (3.6)
Тогда интегрируя (3.6) от 1-го до
2-го состояния уравнение адиабаты в дифференциальной форме
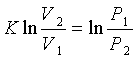 ; (3.7)
; (3.7)
откуда
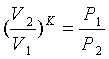 или
или 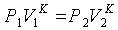 , (3.8)
, (3.8)
откуда уравнение адиабаты
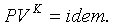 (3.9)
(3.9)
Кроме того, с учетом уравнения
состояния 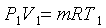 и
и 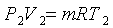 можно
получить связь между V и Т, Р и Т в адиабатическом процессе:
можно
получить связь между V и Т, Р и Т в адиабатическом процессе:
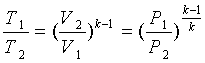 . (3.10)
. (3.10)
Здесь 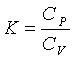 - показатель адиабаты;
- показатель адиабаты; 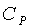 и
и 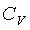 - массовая
изобарная и изохорная теплоемкость, Дж/К; Т, Р и V- абсолютная температура, К,
давление, Па, и объем,
- массовая
изобарная и изохорная теплоемкость, Дж/К; Т, Р и V- абсолютная температура, К,
давление, Па, и объем, 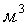 .
.
Теплоемкость адиабатного процесса
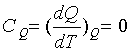 . (3.11)
. (3.11)
Показатель адиабаты К может
изменятся с изменением состоянием рабочего тела. При переменной К обычно при
технических расчетах берут среднее значение 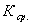 в рассматриваемом интервале
параметров. С учетом (3.9) и (3.10) можно получить:
в рассматриваемом интервале
параметров. С учетом (3.9) и (3.10) можно получить:
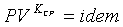 и
и 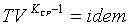 . (3.12)
. (3.12)
Для многих газов и паров величина
показателя изоэнтропы (адиабаты) К с изменением температуры изменяется
относительно слабо, причем для большинства газов значение К лежат в интервале
1,3….1,7. Для воздуха К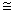 1,41.
1,41.
Работа расширения L и располагаемая
работа 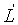 системы в
адиабатном процессе между состояниями 1 и 2 определяются по формулам:
системы в
адиабатном процессе между состояниями 1 и 2 определяются по формулам:
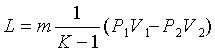 Дж. (3.13)
Дж. (3.13)
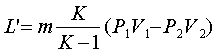 Дж. (3.14)
Дж. (3.14)
В адиабатическом процессе работа
расширения системы совершается за счет убыли внутренней энергии системы
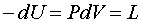 (3.15)
(3.15)
Следует подчеркнуть, что уравнения
(3.13) и (3.14) пригодны для расчетов  и
и  в том случае, если в интервале
параметров между точками 1 и 2 показатель адиабаты К сохраняется постоянным.
Если же К изменяется, то при расчете по уравнениям (3.13) и (3.14) следует
пользоваться средним значением
в том случае, если в интервале
параметров между точками 1 и 2 показатель адиабаты К сохраняется постоянным.
Если же К изменяется, то при расчете по уравнениям (3.13) и (3.14) следует
пользоваться средним значением 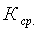 в данном интервале параметров.
в данном интервале параметров.
3.4
Методика проведения работы и описание экспериментальной установки
Работа выполняется на установке,
приведенной на рис. 2.1 (см.стр.14). Основным элементом экспериментальной
установки является сосуд 4 (стеклянный цилиндр), который соединен с манометром
7 и вакуум-насосом 1. В сосуд до определенного уровня залита жидкость 8.
Рабочая трубка 6 расположена внутри сосуда 4. Нижний конец ее открыт и
находится в жидкости, а верхний конец герметично закрыт.
Первоначально воздух (жидкость) в
трубке 6 сжимается до давления 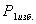 и объема
и объема 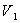 нагнетанием
воздуха в сосуд 1. Нагнетание воздуха производится вакуум-насосом 1 через кран
3. Затем кран закрывается, после чего необходимо выждать определенное время
(2…3 минуты) для установления температуры в системе. После установления
равновесного состояния рабочего тела (воздуха) необходимо измерить и записать значение
избыточного давления и объема в рабочей трубке 6. Избыточное давление жидкости,
а следовательно, и давление воздуха в трубке 6 измеряется манометром 7.
Измерение объема рабочего тела осуществляется по уровню жидкости в бюретке 6 с
помощью шкалы 5. Если открыт кран 3, то воздух в сосуде 4 будет истекать в
окружающую среду и воздух в трубке 6 практически адиабатно расширяется до
какого-то конечного состояния. Опыт необходимо повторить 5…6 раз при различных
начальных значениях начального давления и объема. При этом адиабатический
процесс обеспечивается высокой скоростью расширения воздуха и наличием
теплоизоляции объема, в котором происходит процесс (воздушная прослойка между
бюреткой 6 и сосудом 4).
нагнетанием
воздуха в сосуд 1. Нагнетание воздуха производится вакуум-насосом 1 через кран
3. Затем кран закрывается, после чего необходимо выждать определенное время
(2…3 минуты) для установления температуры в системе. После установления
равновесного состояния рабочего тела (воздуха) необходимо измерить и записать значение
избыточного давления и объема в рабочей трубке 6. Избыточное давление жидкости,
а следовательно, и давление воздуха в трубке 6 измеряется манометром 7.
Измерение объема рабочего тела осуществляется по уровню жидкости в бюретке 6 с
помощью шкалы 5. Если открыт кран 3, то воздух в сосуде 4 будет истекать в
окружающую среду и воздух в трубке 6 практически адиабатно расширяется до
какого-то конечного состояния. Опыт необходимо повторить 5…6 раз при различных
начальных значениях начального давления и объема. При этом адиабатический
процесс обеспечивается высокой скоростью расширения воздуха и наличием
теплоизоляции объема, в котором происходит процесс (воздушная прослойка между
бюреткой 6 и сосудом 4).
3.5 Порядок
проведения работы и обработка результатов эксперимента
Опыт состоит в измерении давлений и
объемов воздуха, соответствующих конечным равновесным состояниям ряда
адиабатных процессов расширения. С помощью вакуум насоса 1 давление в рабочем
теле довести до некоторого заданного преподавателя значения. Выдержать систему
в заданном состоянии 2…3 минуты и зафиксировать параметры начального состояния:
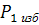
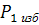 ,
,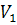
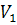 и
и 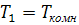
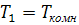 . Открыть кран 3, затем закрыть его,
не давая давлению в системе упасть до атмосферного, и в момент закрытия крана
зафиксировать значения объема
. Открыть кран 3, затем закрыть его,
не давая давлению в системе упасть до атмосферного, и в момент закрытия крана
зафиксировать значения объема 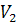
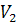 и давления
и давления 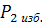
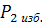 по шкале 5 и манометру 7
соответственно. Опыт повторить 5...6 раз.
по шкале 5 и манометру 7
соответственно. Опыт повторить 5...6 раз.
Абсолютное давление 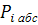
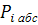 при различных равновесных
состояниях рабочего тела рассчитывается по опытным данным по формуле
при различных равновесных
состояниях рабочего тела рассчитывается по опытным данным по формуле
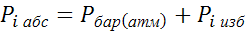
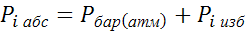 ,Па (3.16)
,Па (3.16)
где 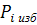
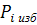 - избыточное давление рабочего
тела, измеренное манометром в каждом опыте, Па ;
- избыточное давление рабочего
тела, измеренное манометром в каждом опыте, Па ; 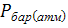
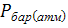 - давление окружающей среды (атмосферы),
Па.
- давление окружающей среды (атмосферы),
Па.
Результаты представить в виде
таблицы 3.1 и P,V - диаграмме, в которой построить экспериментальную и
теоретическую адиабаты, принимая за общую начальную точку 1 с параметрами 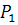
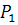 и
и 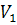
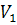 . Экспериментальная адиабата
строится по данным опыта (через точки 1 и 2), а теоретическая - из точки 1 -
как гипербола в соответствии с уравнением (3.9), в котором K=
. Экспериментальная адиабата
строится по данным опыта (через точки 1 и 2), а теоретическая - из точки 1 -
как гипербола в соответствии с уравнением (3.9), в котором K=
 =1,41. При этом, задаваясь
значениями объема V (в соответствии с таблицой 3.1), определить соответствующее
им давления P. Теоретическая (расчетная) адиабата должна походить через
начальное состояние
=1,41. При этом, задаваясь
значениями объема V (в соответствии с таблицой 3.1), определить соответствующее
им давления P. Теоретическая (расчетная) адиабата должна походить через
начальное состояние 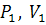
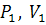 в каждом опыте.
в каждом опыте.
Ошибка эксперимента может быть
оценена по расхождению давлений на экспериментальной и теоретической адиабатах
в месте их максимального удаления друг от друга:
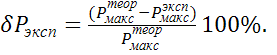
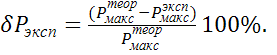 (3.17)
(3.17)
Опытный показатель адиабаты 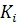
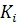 для n - опытов следует определить
по уравнению (3.7)в виде
для n - опытов следует определить
по уравнению (3.7)в виде
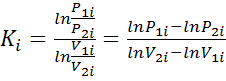
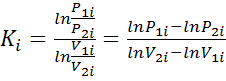 . (3.18)
. (3.18)
По этим значениям находят среднее
значение показателя адиабаты 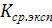
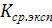 :
:
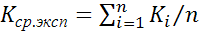
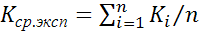 . (3.19)
. (3.19)
Значения среднего показателя 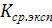
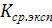 , полученные в опыте, следует
сравнить с литературным значением
, полученные в опыте, следует
сравнить с литературным значением 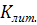
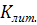 для воздуха и вычислить
относительную величину расхождения между ними в виде
для воздуха и вычислить
относительную величину расхождения между ними в виде
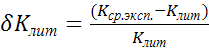
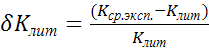 100%. (3.20)
100%. (3.20)
Работу расширения L и располагаемую
работу в каждом опыте рассчитать по (3.13) и(3.14), в которых m - масса
рабочего тела в бюретке 6, кг. Её можно найти по уравнению состояния идеального
газа:
=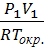
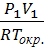 , кг (3.21)
, кг (3.21)
где R=287 Дж/(кгК) - газовая
постоянная воздуха.
Максимальная относительная
погрешность определения работы расширения адиабатного процесса рассчитывается
по формуле
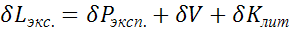
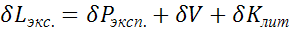 . (3.22)
. (3.22)
в которой 
 - относительная погрешность
определения объема в эксперименте;
- относительная погрешность
определения объема в эксперименте; 
 - абсолютная погрешность
определения объема,
- абсолютная погрешность
определения объема, 
 , соответствующая половине
минимального деления шкалы 5.
, соответствующая половине
минимального деления шкалы 5.
Таблица 3.1
Экспериментальные данные

 , Па;
, Па; 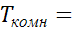
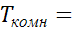 , К.
, К.
|
Номер
опыта
|
Давление
|
Объем
|
|
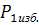
|
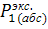
|
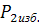
|
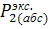
|
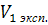
|
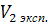
|
|
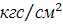
|
Па
|
Па
|
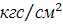
|
Па
|
Па
|
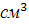
|

|
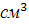
|

|
|
1
2 3 4 5 6
|
|
|
|
|
|
|
|
|
|
|
Расчетные данные заносятся в таблицу 3.2
Таблица 3.2
Расчетные данные
|
№
расчета
|
Давление
|
Объем
|
Работа
расширения
|
Располагаемая
Работа
|
Показатель
адиабаты
|
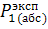 ,
,
Па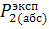
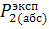 ,
,
Па
 ,
,
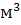
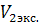
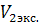 ,
,
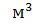
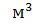 L,
L,
Дж
 ,
,
|
|
|
|
|
|
|
|
1
2 3 4 5 6
|
|
|
|
|
|
|
|
Литература: 1 стр[32-33]; 3 стр.[66-68]; 5,6[стр
24-25].
Контрольные вопросы
)Какой процесс называется адиабатным?
)Что называется изоэнтропным процессом?
)Как создается адиабатный процесс в данной
работе?
)За счет чего совершается работа в процессе
адиабатного расширения?
)Почему энтропия в адиабатном процессе не
меняется?
)Вывести одну из расчетных формул работы
расширения для адиабатного процесса?
)Напишите уравнение адиабатного процесса в Р, V
и Т, S - диаграммах.
)Напишите уравнение первого закона термодинамики
для адиабатного процесса.
)Напишите аналитическое выражение второго закона
термодинамики для обратимых и необратимых процессов и циклов через энтропию для
адиабатного процесса.
)Получите соотношение между параметрами Р и V, Т
и V, Р и Т в адиабатном процессе.
)Как называется процесс, в котором работа
совершается лишь за счет уменьшения внутренней энергии?
)Написать уравнение теплоемкости политропного
процесса и показать, что из данного уравнения можно получить теплоемкости
адиабатного процесса.
)Почему в адиабатном процессе расширения тела
температура убывает, а при сжатии увеличивается?
)Каково расположение адиабаты в Р, V и T, S -
диаграммах.
)Охарактеризовать источники погрешностей в
эксперименте?
4. ЛАБОРАТОРНАЯ РАБОТА №4. ИЗМЕРЕНИЕ
ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ
.1 Цель работы
Цель работы - экспериментальное исследование
(определение) температурной зависимости удельной массовой теплоемкости твердых
тел в режиме монотонного нагрева, ознакомление с методикой исследования и
получение навыков в проведении эксперимента.
4.2 Задание
) Ознакомиться с работой прибора “Измеритель
теплоемкости ИТ - с - 400”.
) Определить температурную зависимость удельной
массовой теплоемкости твердого механически обработанного (твердого) материала в
пределах интервала температуры от 25° до 150°С.
) Обработать результаты эксперимента по формуле
(4.14).
) Определить погрешность эксперимента по формуле
(4.15).
) Построить зависимость удельной массовой
теплоемкости испытуемого материала от температуры нагрева C=f(t).
) Составить и защитить отчет по выполненной
работе.
4.3 Краткие
теоретические сведения
Теплоемкостью называется количество теплоты,
которое нужно подвести к телу или отнять от него для изменения температуры тела
на градус (1° С или 1 К). Полная теплоемкость в данном процессе (Х)
определяется по формуле
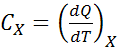
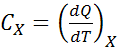 Дж/К. (4.1)
Дж/К. (4.1)
Обычно величину теплоемкости 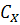
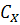 относят к единице количества
вещества и называют удельной теплоемкостью
относят к единице количества
вещества и называют удельной теплоемкостью 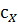
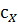 .
.
В зависимости от количественной
единицы вещества, к которому подводится теплота, различают: удельную массовую
теплоемкость (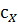
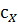 =
=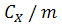
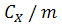 , Дж/(кг*К); удельную объемную
теплоемкость
, Дж/(кг*К); удельную объемную
теплоемкость  Дж/(
Дж/(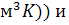
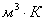 ) удельную мольную (молярную)
теплоемкость (
) удельную мольную (молярную)
теплоемкость (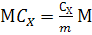
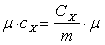 , Дж/(моль·К).
, Дж/(моль·К).
Названные удельные теплоемкости
связаны между собой следующими зависимостями:
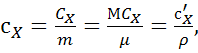
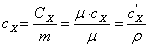

 , (4.2)
, (4.2)
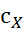
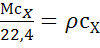
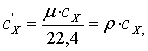
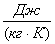 , (4.3)
, (4.3)
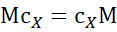
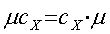 ,
, 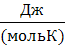
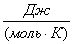 , (4.4)
, (4.4)
где индекс “X” в (4.1)…(4.4)
характеризует параметр, (P,V,T,n,q) которые остается постоянным в данном
термодинамическом процессе; 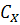
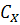 - полная теплоемкость в Дж/К;
- полная теплоемкость в Дж/К; 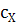
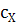 ,
,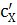
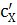 ,
,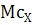
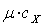 - удельные теплоемкости для единицы
количества вещества.
- удельные теплоемкости для единицы
количества вещества.
Для идеального газа между
теплоемкостями при постоянном давлении и постоянном объеме существует следующая
зависимость:
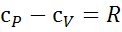
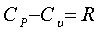 ,
,
или
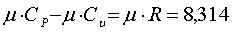
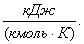 (4.5)
(4.5)
Теплоемкость является параметром
процесса и в общем случае величина переменная, зависит от температуры,
давления, вида вещества и от характера термодинамического процесса, в котором
подводится или отводится теплота.
В основу работы измерителя
теплоемкости положен сравнительный метод динамического с - калориметра с
тепломером и адиабатической оболочкой. Теоретическое обоснование метода
монотонного режима измерения изложено в [9].
На рисунке 4.1 показана тепловая
схема метода динамического с - калориметра. Образец (материал) испытуемый 1
размещают внутри металлической ампулы 2 и монотонно разогревают вместе с ней за
счет непрерывно поступающего к ампуле 2 через тепломе р 3 теплового потка
Q. Тепловая связь ампулы 2 и образца 1 с внешней средой допускается только
через тепломер 3, поэтому участки поверхности ампулы отделены от среды
оболочкой адиабатической 4.
Тепловой поток 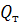
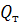 , проходящий через среднее значение
тепломера 3, идет на разогрев образца испытуемого 1 и ампулы 2 и определяется
по формуле
, проходящий через среднее значение
тепломера 3, идет на разогрев образца испытуемого 1 и ампулы 2 и определяется
по формуле
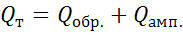
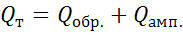 , (4.6)
, (4.6)
где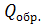
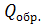 - тепловой поток, идущий на
разогрев испытуемого образца 1, Вт;
- тепловой поток, идущий на
разогрев испытуемого образца 1, Вт; 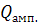
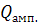 - тепловой поток идущий на разогрев
ампулы 2, Вт.
- тепловой поток идущий на разогрев
ампулы 2, Вт.
Тепловой поток, идущий на разогрев
испытуемого образца, определяется по формуле
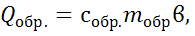
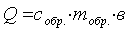 (4.7)
(4.7)
где 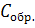
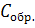 - удельная массовая теплоемкость
образца, Дж/(кг*К);
- удельная массовая теплоемкость
образца, Дж/(кг*К); 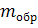
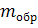 - масса образца, кг;
- масса образца, кг; 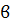
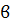 - скорость разогрева, К/с.
- скорость разогрева, К/с.
Тепловой поток, идущий на разогрев
ампулы, определяется по формуле
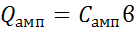
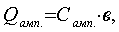 (4.8)
(4.8)
где 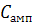
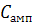 - полная теплоемкость ампулы, Дж/К.
- полная теплоемкость ампулы, Дж/К.
О величине теплового потока,
проходящего через тепломер 3 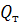
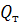 , можно судить по величине перепада
температуры на тепломере ∆
, можно судить по величине перепада
температуры на тепломере ∆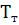
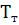 и тепловом проводимости
и тепловом проводимости 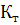
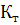 , определенной, из независимых
градуировочных экспериментов
, определенной, из независимых
градуировочных экспериментов
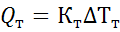
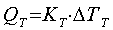 , (4.9)
, (4.9)
Параметр (тепловой проводимости
тепломера) 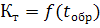
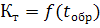 является постоянной прибора и
зависит только от температурного уровня образца
является постоянной прибора и
зависит только от температурного уровня образца 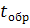
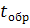 и приведен в таблице 4.1.
и приведен в таблице 4.1.
Градуировка измерителя заключается в
экспериментальном определении тепловой проводимости тепломера 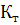
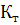 в зависимости от температуры
в зависимости от температуры 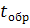
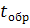 . Для этого необходимо проводить
пять экспериментов с эталонным образцом (медным М1 - ГОСТ 859 - 78 или
кварцевым стеклом КВ - ГОСТ 15130 - 86) и столько же с пустой ампулой в
соответствии со специальной методикой. При этом тепловая проводимость тепломера
определяется по следующей формуле:
. Для этого необходимо проводить
пять экспериментов с эталонным образцом (медным М1 - ГОСТ 859 - 78 или
кварцевым стеклом КВ - ГОСТ 15130 - 86) и столько же с пустой ампулой в
соответствии со специальной методикой. При этом тепловая проводимость тепломера
определяется по следующей формуле:
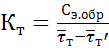
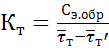 , Вт/К (4.10)
, Вт/К (4.10)
где 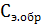
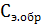 - полная теплоемкость эталонного
образца, Дж/К;
- полная теплоемкость эталонного
образца, Дж/К; 
 - среднее значение времени
запаздывания на тепломере в экспериментах с эталонным образцом, с;
- среднее значение времени
запаздывания на тепломере в экспериментах с эталонным образцом, с; 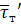
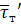 - среднее значение времени на
тепломере в экспериментах с пустой ампулой, с.
- среднее значение времени на
тепломере в экспериментах с пустой ампулой, с.
Полная теплоемкость эталонного
образца вычисляется по формуле
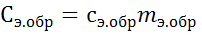
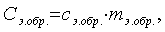 Дж/К (4.11)
Дж/К (4.11)
где 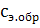
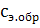 - табличное значение удельной
массовой теплоемкости эталонного образца, Дж/(кгК);
- табличное значение удельной
массовой теплоемкости эталонного образца, Дж/(кгК); 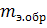
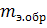 - масса эталонного образца, кг.
- масса эталонного образца, кг.
Вычисленные значения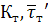
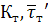 для медного (эталонного) образца
соответственно по (4.10) и
для медного (эталонного) образца
соответственно по (4.10) и 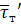
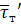 заносятся в таблицу 4.1 и их можно
использовать как постоянные приборы при определении удельной массовой
теплоемкости по формуле (4.14).
заносятся в таблицу 4.1 и их можно
использовать как постоянные приборы при определении удельной массовой
теплоемкости по формуле (4.14).
Расчетная формула удельной
теплоемкости испытуемого образца с учетом (4.6), (4.7), (4.8), (4.9) имеет
следующий вид:
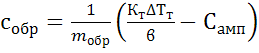
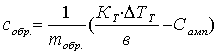 , (4.12)
, (4.12)
При малых перепадах температур на
тепломере можно перейти к измерению времени запаздывания температуры на
тепломере, учитывая, что
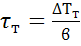
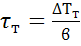 , (4.13)
, (4.13)
где 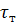
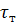 - время запаздывания температуры на
тепломере, с (определяется экспериментальным путем)
- время запаздывания температуры на
тепломере, с (определяется экспериментальным путем)
Тогда рабочая расчетная формула
удельной массовой теплоемкости испытуемого образца примет вид
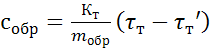
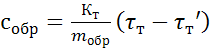 , (4.14)
, (4.14)
где 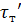
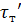 - время запаздывания температуры на
тепломере в экспериментах с пустой ампулой, с. Величина
- время запаздывания температуры на
тепломере в экспериментах с пустой ампулой, с. Величина 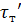
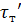 =
=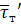
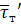 является постоянной прибора и
приведена в таблице 5.1
является постоянной прибора и
приведена в таблице 5.1
4.4
Методика проведения работы, описание и принцип работы прибора ИТ - с - 400
Измеритель теплоемкости ИТ - с - 400
предназначен для исследования температурной зависимости удельной теплоемкости
твердых тел, сыпучих, волокнистых материалов, жидкостей. Он рассчитан на
проведение массовых теплофизических исследований в лабораторных и заводских
условиях.
Ячейки измерительной (рисунок 4.2)
является важнейшей частью блока измерительного и состоит из корпуса 6,
разъемной оболочки теплоизоляционной 8 и металлического ядра (детали 1, 2, 4,
10, 11). Блок питания и регулирования обеспечивает нагрев ядра ячейки
измерительной (рисунок 4.2) с заданной скоростью - 0,1 К/с и автоматическое
регулирование температуры. Скорость разогрева определяется величиной начального
напряжения на нагревателе и скоростью его изменения. Обе эти величины строго
фиксированы. Для определения теплоемкости в эксперименте в процессе
непрерывного разогрева на фиксированных уровнях температуры используется прибор
микровольт амперметр Ш136. Он используется как нуль - прибор в потенциометре.
Прибор Ш136 рассчитан на определенные значения термо - эдс, соответствующие
фиксированным уровням температур от минус 125 до плюс 400°С через 25°С.
Для регулирования работы в
нагревателе и температурных измерений в приборе (в ампуле 2 и колпаке 4)
используются хромель - алюмелевые термопары 12 с диаметром электродов 0,2 мм.
Переключатель термопар
измерительного блока имеет три положения 
 , УСТ.О. В положениях
, УСТ.О. В положениях 
 измеряется температура основания 10
и испытуемого образца 9. В положении УСТ.О проверяется механический нуль
прибора Ш136. В эксперименте в процессе непрерывного разогрева на различных
уровнях температуры (через 25°С) с помощью прибора Ш136 и секундомера
измеряется временное запаздывание температуры ампулы по отношению к температуре
основания.
измеряется температура основания 10
и испытуемого образца 9. В положении УСТ.О проверяется механический нуль
прибора Ш136. В эксперименте в процессе непрерывного разогрева на различных
уровнях температуры (через 25°С) с помощью прибора Ш136 и секундомера
измеряется временное запаздывание температуры ампулы по отношению к температуре
основания.
Испытуемый образец 9 помещается в
ампулу 2, которая закрывается крышкой 3. Отпускается верхняя половина корпуса
измерительной ячейки. Подается напряжение на нагреватель 7, и ядро
измерительной ячейки начинает, плавно, монотонно разогреваться до верхней,
предельной для каждого образца 9, температуры. Во время разогрева с помощью
нагревателя 11, расположенного в охранном колпаке 4, поддерживаются
адиабатические условия (нулевая разность температур) между ампулой 2 и охранным
колпаком 4. Тепломер 1 смонтирован в медном основании 10. Рабочим слоем
тепломера является кольцо 1 из нержавеющей стали 12Х18Н9Т. Основание, кольцо 1
и ампула 2 спаяны друг с другом серебряным припоем.
Измерение удельной теплоемкости
производится на образцах диаметром 15±0,1 мм и высотой 10±0,5 мм.
Для улучшения теплового контакта
образцов используется смазка ПШМС - 4 ТУ6 - 02 - 917 - 74. Для образцов,
впитывающих смазку, используется графитовый порошок (ГОСТ 8295 - 73) или
алюминиевая пудра (ГОСТ 5494 - 71Е). В случае изменения смазки или начала
температурного диапазона необходима новая градуировка с измененными условиями.
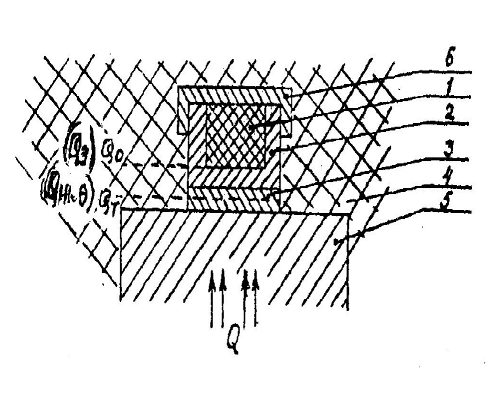
- образец испытуемый; 2 - ампула; 3
- тепломер; 4 - оболочка адиабатическая; 5 - основание; 6 - крышка.
Рисунок 4.1- Тепловая схема метода
динамического с - калориметра.
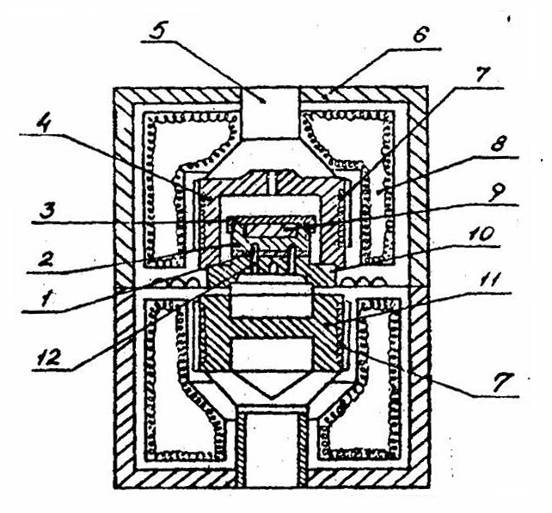
- тепломер; 2 - ампула; 3 - крышка;
4 - колпак охранный (адиабатическая оболочка); 5 - патрубок; 6 - корпус; 7 -
спираль нагревателей; 8 - оболочка теплоизоляционная; 9 - образец испытуемый;
10 - основание; 11 - блок нагревателей; 12 - термопары.
Рисунок 4.2 - Схема измерительной
ячейки.
4.5 Порядок
проведения работы и обработка результатов эксперимента
) Переводить переключатель “СЕТЬ” и
“НАГРЕВ” в положение “ВЫКЛ”.
) Подключить блок питания и
регулирования прибора Ш136 к сети 220 В, 50 Гц.
) Установить переключатель “ИЗМЕРЕНИЕ”
в положение “УСТ.О” и переключатель “ТЕМПЕРАТУРА” - в положение 25°С.
) Замкнуть входные штеккерны прибора
Ш136 и произвести коррекцию нуля.
) Взвесить испытуемый образец с
точностью ±0,001 г и занести полученное значение 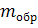
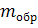 в таблицу 4.1.
в таблицу 4.1.
) Поднимать верхнюю часть ячейки
измерительной.
) Протереть бензином и нанести
тонкий слой смазки ПШМС - 4 на контактные поверхности образцов, ампулы и
крышки.
) В ампулу 2 установить испытуемый образец
9 и закрыть ампулу крышкой 3.
) Отпустить верхнюю часть ячейки
измерительной.
) Включить блок питания и
регулирования, нажав кнопку “СЕТЬ”
) Выведить по вольтметру блока
питания и регулирования напряжения до нуля.
) Установить переключатель “ИЗМЕРЕНИЕ”
в положение 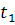
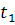 .
.
) Включить кнопку “НАГРЕВ”, основной
нагреватель и установить по вольтметру блока и регулирования начальное
напряжение 40±2 В при работе от плюса 25°С.
) Включить секундомер при достижении
температуры плюс 25°С (при положении светового указателя прибора Ш136 через
нуль шкалы) и переводить переключатель “ИЗМЕРЕНИЕ” в положение 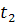
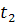 . Выключить секундомер при
прохождении светового указателя через нуль шкалы.
. Выключить секундомер при
прохождении светового указателя через нуль шкалы.
) Записать показания секундомера в
графу “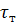
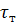 ” таблицы,4.1
” таблицы,4.1
) Повторить измерение 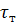
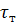 при всех значениях температур,
указанных в таблице 4.1.
при всех значениях температур,
указанных в таблице 4.1.
)Выключить нагреватель при
достижении желаемого уровня температуры или предельной температуры разогрева
образца.
) Заретируйте прибор Ш136 (полностью
отключить прибор Ш136).
) Установить переключатель
“ИЗМЕРЕНИЕ” в положение “УСТ.О”.
) Выключить блок питания и
регулирования.
) Поднимать верхнюю часть корпуса
ячейки измерительной.
) Охладить ячейку измерительной.
) Проводить расчет удельной массовой
теплоемкости по формуле (4.14).
) Построить зависимость удельной
массовой теплоемкости испытуемого образца 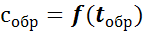
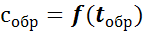 .
.
) Максимальная относительная
погрешность измерения удельной теплоемкости 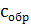
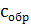 , оценивается по формуле
, оценивается по формуле
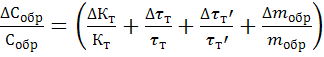
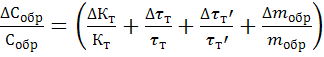 100%, (4.15)
100%, (4.15)
где 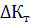
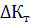 - абсолютная погрешность тепловой
проводимости тепломера (
- абсолютная погрешность тепловой
проводимости тепломера (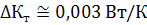
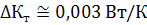 );
); 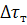
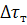 - абсолютная погрешность время
запаздывания температуры на тепломере в эксперименте с эталонным образцом,
соответствующая половине деления шкалы секундомера, с;
- абсолютная погрешность время
запаздывания температуры на тепломере в эксперименте с эталонным образцом,
соответствующая половине деления шкалы секундомера, с; 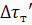
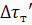 - абсолютная погрешность время
запаздывания температуры на тепломере в эксперименте с пустой ампулой, с (
- абсолютная погрешность время
запаздывания температуры на тепломере в эксперименте с пустой ампулой, с (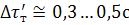
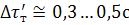 ) или соответствующая половине
деления шкалы секундомера;
) или соответствующая половине
деления шкалы секундомера; 
 абсолютная погрешность измерения
массы испытуемого образца (определяется классом точности прибора
абсолютная погрешность измерения
массы испытуемого образца (определяется классом точности прибора 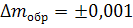
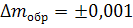 г). Общий предел допускаемой
погрешности определения
г). Общий предел допускаемой
погрешности определения 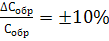
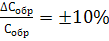 .
.
Результаты измерений и обработки
результатов эксперимента заносят в таблицу 4.1
Таблица 4.1
Результаты измерений и обработки
результатов эксперимента
Испытуемый образец
Масса испытуемого образца 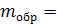
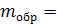 , кг
, кг
|
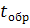 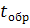 ,°С ,°С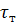 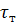 , с , с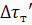 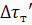 , с , с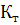 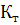 , Вт/К , Вт/К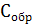 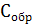 , Дж/(кгК) , Дж/(кгК)
|
|
|
|
|
|
25
|
|
12,4
|
0,483
|
|
|
50
|
|
12,4
|
0,501
|
|
|
75
|
|
12,3
|
0,513
|
|
|
100
|
|
11,9
|
0,532
|
|
|
125
|
|
11,5
|
0,541
|
|
|
150
|
|
11,0
|
0,552
|
|
Литература: 1
 .
.
Контрольные
вопросы
) Что называется теплоемкостью?
) Что такое полная и удельная
теплоемкость?
) Виды удельных теплоемкостей и
связь между ними?
) В каких единицах выражаются теплоемкости?
) Какие факторы влияют на
теплоемкость?
) В чем сущность метода
динамического с - калориметра?
) Что такое время запаздывания
температуры на тепломере 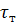
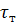 и метод ее определения?
и метод ее определения?
) Что такое время запаздывания
температуры на тепломере 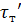
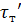 и метод определения?
и метод определения?
) Что такое тепловая проводимость
тепломера 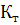
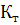 и метод ее определения?
и метод ее определения?
) Напишите первый закон
термодинамики в дифференциальном и интегральном видах?
) Что такое истинная и средняя
теплоемкость?
) Написать уравнение количество
теплоты через теплоемкость?
) Почему теплоемкость газа при
постоянном давлении 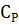
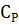 всегда больше теплоемкости при
постоянном объеме
всегда больше теплоемкости при
постоянном объеме 
 ?
?
5.ЛАБОРАТОРНАЯ РАБОТА №5. ИЗМЕРЕНИЕ
ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ТЕЛ
5.1 Цель
работы
Цель работы - экспериментальное
исследование определение температурной зависимости теплопроводность твердых
механически обработанных материалов в режиме монотонного нагрева, ознакомление
с методикой исследования и получение навыков в проведении эксперимента.
5.2 Задание
) Ознакомиться с раборой прибора
“Измеритель теплопроводимости ИТ - λ - 400”
2) Определить температурную
зависимость коэффицента теплопроводности λ твердого механически
обработанного материала в пределах интервала температуры от 25°С до 150°С.
) Обработать результаты
эксперимента.
) Определить погрешность
эксперимента по формуле (5.17)
) Построить график зависимости
коэффициента теплопроводности испытуемого образца λ от средней
температуры 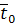
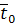 , т.е.
, т.е. 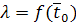
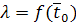 .
.
) Составить и защитить отчет по
выполненной работе.
5.3 Краткие
теоретические сведения
Коэффициент теплопроводности λ (Вт/(мК))
является физическим параметром, характеризующим способность тела проводить
теплоту или интенсивность переноса теплопроводности в веществе и в общем случае
зависит от температуры, количества подводимого или отводимого теплоты, давления,
пористости, влажности и рода вещества. Численно он равен плотности теплового
потока q (Вт/м2) при единичном температурном градиенте 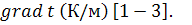
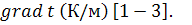
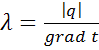
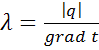 Вт/(мК) (5.1)
Вт/(мК) (5.1)
Значения коэффициента
теплопроводности вещества необходимо для аналитического описания процесса
теплопроводности в нем.
Для измерения теплопроводности в
измерителе теплопроводности использован метод динамического λ - калориметра,
теоретическое обоснование которого подробно изложено в [9].
На рисунке 5.1 показана тепловая
схема метода динамического 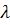
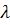 - калориметра. Испытуемый образец
4, пластина контактная 3 и стержень 5 монотонно разогреваются тепловым потоком
Q (τ),
поступающим
от основания 1. Боковые поверхности стержня 5, образца4, пластины 2 и 3
адиабатически изолированы. Стержень 5 и контактная пластина 3 изготовлены из
меди, обладающей высокой теплопроводностью, поэтому перепады температур на них
незначительны.
- калориметра. Испытуемый образец
4, пластина контактная 3 и стержень 5 монотонно разогреваются тепловым потоком
Q (τ),
поступающим
от основания 1. Боковые поверхности стержня 5, образца4, пластины 2 и 3
адиабатически изолированы. Стержень 5 и контактная пластина 3 изготовлены из
меди, обладающей высокой теплопроводностью, поэтому перепады температур на них
незначительны.
Тепловой поток Q (τ),проходящий
через пластину 2, частично поглощается ее и далее идет на разогрев пластины 3,
испытуемого образца 4 и стержня5. Размеры системы выбрали таким образом, чтобы
потоки, аккумулируемые испытуемым образцом и пластиной, были по крайне мере в 5
… 10 раз меньше поглощаемых стержнем. В этом случае температурное поле образца
4 и пластины 2 оказывается близким к линейному и стационарному.
Тепловые потоки, проходящие через
испытуемый образец 4 и поглощаемые стержнем 5 Qо(τ), и среднее
сечение пластины (тепломера) Qт (τ) определяются по формулам:
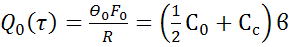
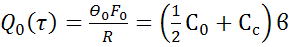 , Вт (5.2)
, Вт (5.2)
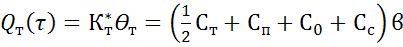
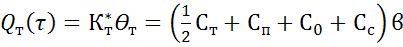 , Вт (5.3)
, Вт (5.3)
где ϴ0 - перепад
температуры на испытуемого образца 4, К; Fо - площадь поперечного сечения образца,
м2; R - тепловое сопротивление между стержнем 5 и контактной пластиной 3, м2
 К/Вт; Со- полная теплоемкость
образца 4, Дж/К; Сс - полная теплоемкость стержня 5, Дж/К; в- скорость
разогрева измерительной ячейки, К/с; Кт*- коэффициент пропорциональности,
характеризующий тепловую проводимость пластины (тепломера) 2, Вт/К; ϴт - перепад
температуры на пластине тепломера 2, К; Ст - полная теплоемкость пластины
тепломера 2, Дж/К; Сп - полная теплоемкость контактной пластины 3,Дж/К.
К/Вт; Со- полная теплоемкость
образца 4, Дж/К; Сс - полная теплоемкость стержня 5, Дж/К; в- скорость
разогрева измерительной ячейки, К/с; Кт*- коэффициент пропорциональности,
характеризующий тепловую проводимость пластины (тепломера) 2, Вт/К; ϴт - перепад
температуры на пластине тепломера 2, К; Ст - полная теплоемкость пластины
тепломера 2, Дж/К; Сп - полная теплоемкость контактной пластины 3,Дж/К.
Тепловое (термическое) сопротивление
между стержнем 5 и контактной пластиной 3 определяются по формуле
=Ro+Rк , (5.4)
где Ro- тепловое сопротивление
образца, м2
 К/Вт; Rк - поправка, учитывающая
тепловое сопротивление контакта, неидентичность и тепловое сопротивление
заделки термопар, м2
К/Вт; Rк - поправка, учитывающая
тепловое сопротивление контакта, неидентичность и тепловое сопротивление
заделки термопар, м2
 К/Вт.
К/Вт.
Тепловое сопротивление образца
определяется по формуле
= 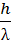
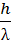 , (5.5)
, (5.5)
где h- высота исследуемого образца,
м; λ
- коэффициент
теплопроводности образца, Вт/(мК).
На основании формулы (5.2), (5.3),
(5.4), (5.5) получены рабочие расчетные формулы для теплового сопротивления
образца и его теплопроводности:
= 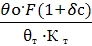
 - Rк, (5.6)
- Rк, (5.6)
где 
 с - поправка, учитывающая
теплоемкость образца
с - поправка, учитывающая
теплоемкость образца
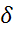
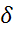 с =
с = 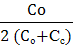
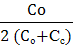 , (5.7) здесь Со=С(t) · mо,
(5.8)
, (5.7) здесь Со=С(t) · mо,
(5.8)
Сс=См(t) · mс,
(5.9)
здесь Со(t), См(t) -
ориентирововочное значение удельной теплоемкости образца и удельная
теплоемкость меди, Дж/(кг·К); mо, mс - масса образца и стержня, кг.
Значения См(t) и Со(t), даны в таблице 5.2.
Коэффициент теплопроводности образца
равен из (6.5)
λ= 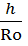
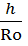 · (5.10)
· (5.10)
Вычисление значения λ образца
следует относить к средней температуре образца 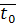
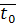 , которая определяется по формуле
, которая определяется по формуле
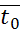
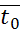 =tc(o)+0,5 ·At·По.
(5.11)
=tc(o)+0,5 ·At·По.
(5.11)
где tc(o) - температура, при которой
проводилось измерение теплопроводности, оС;At - чувствительность термопары
хромель-алюмель, К/мВ (таблица 5.2); По- перепад температуры на образце, мВ
(таблица 5.3).
Параметры Кт и Rк не зависят от
свойств испытуемого образца, является «постоянным» измерителя. Значение Rк
обычно дается для материалов С λ = 2 … 5 Вт/(м·К) и не превышает
(10…20%) теплового сопротивления образца Ro. Для определения Кт и Rк производят
градуировку измерителя с образцовой мерой из кварцевого стекла марки КВ (ГОСТ
15130-86) и образцом из меди М1 (ГОСТ 859-78), и показания записывают в таблицу
5.3.
Для определения теплопроводности
испытуемого образца в эксперименте необходимо на различных уровнях температуры
измерять перепады температуры на тепломере 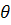
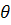 т и образца
т и образца 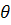
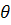 о в микровольтах, мкВ, Пт и По
(таблица 5.3). Значение термо - эдс(мкВ) необходимо перевести в мВ и
температуру Кельвина (мкВ·10-3 = мВ - таблица 5.3).
о в микровольтах, мкВ, Пт и По
(таблица 5.3). Значение термо - эдс(мкВ) необходимо перевести в мВ и
температуру Кельвина (мкВ·10-3 = мВ - таблица 5.3).
Тогда
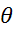
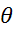 т= At· Пт, К и
т= At· Пт, К и 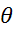
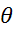 о=At· По, К, (5.12)
о=At· По, К, (5.12)
где Пт , По - перепады температуры
на пластине тепломера 2 и образце 4, мВ.
Градуировка измерителя теплопроводности
заключается в экспериментальном определении тепловой проводимости тепломера Кт
и поправки Rк, которая учитывает контактное сопротивление образца - заделки
термопар, динамические погрешности и неидентичность градуировки термопар. При
определении Кт проводит пять эксперимента, в которых в качестве образца
используют образцовую меру теплопроводности из плавленого кварца марки КВ ГОСТ
15130-86. Экспериментальные данные заносятся в таблицу 5.3 с учетом таблицы
5.2. Расчет Кт проводится без учета поправки Rк по формуле
Кт = 
 ·
· 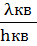
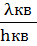 · F (1+
· F (1+
 с), (5.13)
с), (5.13)
где По- перепад температуры на
образце в микровольтах, мкВ; Пt - перепад температуры на рабочем слое термопара
в микровольтах, мкВ.
При определении теплового
сопротивления Rк проводят серию экспериментов с образцом из меди М1 (ГОСТ
859-78) (диаметр образца 15мм, высота - 5мм).
Экспериментальные данные заносят в
таблицу 5.3. Расчет Rк проводят по формуле
к = 
 ·
· 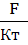
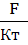 · (1+
· (1+
 с) -
с) - 
 , (5.14)
, (5.14)
где 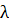
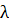 м- теплопроводность медного
образца, Вт/(м·К);
м- теплопроводность медного
образца, Вт/(м·К); 
 м - высота медного образца (
м - высота медного образца (
 м=5 · 10-3, м),м.
м=5 · 10-3, м),м.
Значения теплопроводности 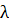
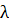 м в зависимости от температуры
приведены в таблице 5.2.
м в зависимости от температуры
приведены в таблице 5.2.
Приводят уточненный расчет Кт с
учетом среднего значения Rк по формуле
Кт =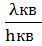
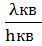
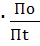
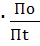 · F (1-
· F (1-
 к+
к+
 с), (5.15)
с), (5.15)
где
 кв - теплопроводность кварцевого
стекла марки КВ, Вт/(м·К) (приведены в таблице 5.2).
кв - теплопроводность кварцевого
стекла марки КВ, Вт/(м·К) (приведены в таблице 5.2). 
 кв - высота образца из кварцевого
стекла марки КВ (
кв - высота образца из кварцевого
стекла марки КВ (
 кв=4
кв=4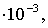 м),м; F - площадь поперечного
сечения образца из кварцевого стекла марки КВ, м2;
м),м; F - площадь поперечного
сечения образца из кварцевого стекла марки КВ, м2; 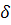
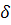 с - поправка, учитывающая
теплоемкость образца из кварца марки КВ;
с - поправка, учитывающая
теплоемкость образца из кварца марки КВ; 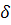
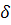 к- поправка, учитывающая тепловое
сопротивление Rк.
к- поправка, учитывающая тепловое
сопротивление Rк.
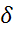
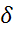 к= Rк·
к= Rк· 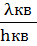
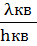 · (5.16)
· (5.16)
Среднее из вычисленных значений Кт
используют при дальнейшей работе.
Погрешности определения Кт и Rк
являются случайными. Величина их зависит от квалификации и опыта
экспериментатора и не должна превышать соответственно 5 и 10%.
5.4
Методика проведения работы, описание и принцип работы прибора ИТ - λ - 400
Измеритель теплопроводности
предназначен для исследования температурной зависимости теплопроводности
твердых, механически обработанных материалов в режиме монотонного нагрева.
Диапазон измерения теплопроводности измерителя от 0,1 до 5 Вт/(м · К).
Белок питания и регулирования
обеспечивает нагрев ядра измерительной ячейки со средней скорости 0,1 К/с и
автоматическое регулирование температуры. Для определения теплопроводности в
эксперименте в процессе непрерывного разогрева на фиксированных уровнях
температуры с помощью прибора (микроамперметра) 
 195 (в микровольтах) измеряется
перепад температуры на образце
195 (в микровольтах) измеряется
перепад температуры на образце 
 о и пластине П t- тепломера.
о и пластине П t- тепломера.
Ячейка измерительная (рисунок 5.2)
является важнейшей частью измерительного блока и состоит из корпуса 9,
разъемной теплозащитной оболочки 10 и металлического ядра (детали 1, 2, 3, 5,
7, 8).
На медном основании 1 размещены
термопары 7, пластина (тепломер) 2, контактная пластина 3, составляющие
тепломер и испытуемый образец 4. Для температурных измерений использованы
хромель - алюмелевые термопары с диаметром электродов 0,2 мм.
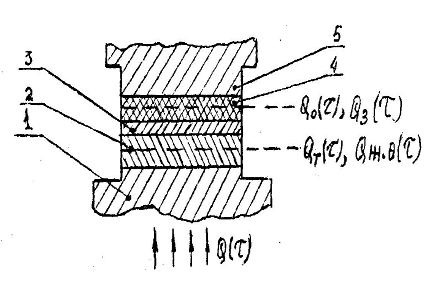
- основание; 2 - пластина тепломера;
3 - пластина контактная; 4 - испытуемый образец; 5 - стержень.
Рисунок 5.1 - Тепловая схема метода
динамического λ
- калориметра.
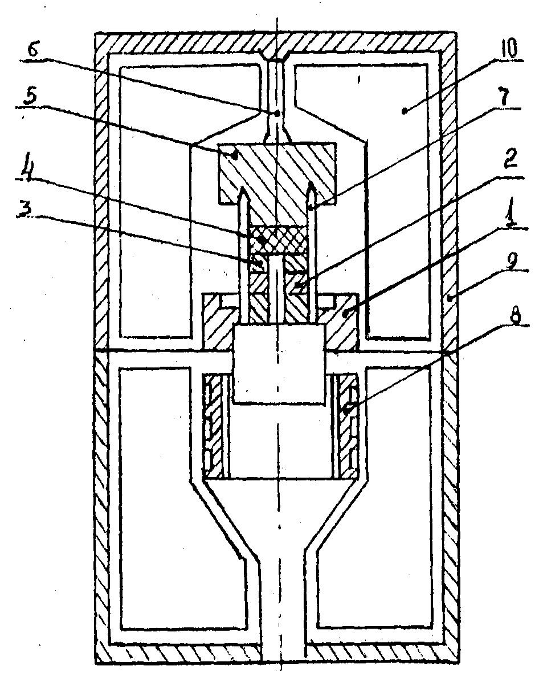
- основание; 2 - пластина тепломера;
3 - пластина контактная; 4 - испытуемый образец; 5 - стержень; 6 - прижим; 7 -
термопара; 8 - нагревательный блок; 9- корпус; 10 - теплозащитная оболочка.
Рисунок 5.2 - Схема измерительной
ячейки.
Используемый образец 4
устанавливается на контактную пластину 3 и сверху поджимается стержнем5,
прижимом 6. На медном основании 1 размещены термопары 7. Рабочем слоем
термопара является пластина 2 из нержавеющей стали. Основание 1 и блок
нагревателей 8 соединен винтами и специальной деталью.
Прибор 
 195 используется непосредственно
для измерения сигналов дифференциальных термопар, а также как нуль - прибор в
потенциометре. Прибор
195 используется непосредственно
для измерения сигналов дифференциальных термопар, а также как нуль - прибор в
потенциометре. Прибор 
 195 (потенциометр) рассчитан на
определенные значения термо - эдс, соответствующие фиксированным уровням
температур от - 125 до 400 оС. Температурный переключатель В1 прибора
195 (потенциометр) рассчитан на
определенные значения термо - эдс, соответствующие фиксированным уровням
температур от - 125 до 400 оС. Температурный переключатель В1 прибора 
 195 имеет четыре положения tc, По ,
Пt , УСТ.О. В положениях По и Пt измеряются перепады температуры на образце 4 и
рабочем слое тепломера 2 (в микровольтах, мкВ). В положении tc потенциометром
измеряется температура стержня 5. А в положении УСТ.О проверяется механический
нуль прибора
195 имеет четыре положения tc, По ,
Пt , УСТ.О. В положениях По и Пt измеряются перепады температуры на образце 4 и
рабочем слое тепломера 2 (в микровольтах, мкВ). В положении tc потенциометром
измеряется температура стержня 5. А в положении УСТ.О проверяется механический
нуль прибора 
 195.
195.
Измерение теплопроводности
производится на образцах (на твердых, механически обработанных материалов),
изготовленных в соответствии с диаметром 
 15
15 
 0,1 мм и высотой h - 0,5…5мм
(таблица 5.1). Lля улучшения теплового контакта образца используется
теплостойкая смазка ПФМС-4 ТУ6-02-917-74. Для образцов, впитывающих смазку,
можно использовать графитовый порошок (ГОСТ8295-73) или алюминиевую пудру
(ГОСТ5494-71Е).
0,1 мм и высотой h - 0,5…5мм
(таблица 5.1). Lля улучшения теплового контакта образца используется
теплостойкая смазка ПФМС-4 ТУ6-02-917-74. Для образцов, впитывающих смазку,
можно использовать графитовый порошок (ГОСТ8295-73) или алюминиевую пудру
(ГОСТ5494-71Е).
Таблица 5.1
Выбор высоты испытуемого образца h в
зависимости от ожидаемого значения коэффициента теплопроводности λ.
|
λ,
Вт/(м·К)
|
0,1-0,3
|
0,3-0,5
|
0,5-1,0
|
1,0-2
|
более
2
|
|
h·10-3,
м
|
0,5-1,0
|
1,0-2
|
2-3
|
3-5
|
5
|
5.5 Порядок проведения
работы и обработка результатов эксперимента
1) Соединить блок питания и
регулирования с измерительным блоком жгутом, прибор 
 195 с измерительным блоком шнуром в
соответствии со схемой электрических соединений.
195 с измерительным блоком шнуром в
соответствии со схемой электрических соединений.
) Переводить кнопки «СЕТЬ», «НАГРЕВ»
в положение «ВЫКЛ.».
) Подключить блок питания и
регулирования и прибор 
 195 к сети 220 В, 50 Гц.
195 к сети 220 В, 50 Гц.
) Установить переключатель
«ИЗМЕРЕНИЕ» в положение «УСТ.О» и переключить «ТЕМПЕРАТУРА» в положение 25 оС.
) Произвести подготовку
микроамперметра 
 195 к работе согласно инструкции по
эксплуатации прибора
195 к работе согласно инструкции по
эксплуатации прибора 
 195 (замкнуть входные штеккерны
прибора и произвести коррекцию нуля).
195 (замкнуть входные штеккерны
прибора и произвести коррекцию нуля).
) Замерить высоту и диаметр
испытуемого образца с точностью 
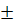 0,01 мм и взвесить испытуемый
образец с точность
0,01 мм и взвесить испытуемый
образец с точность 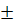
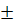 0,001г и занести полученные данные в
таблицу 5.3.
0,001г и занести полученные данные в
таблицу 5.3.
) Поднимать верхнюю половину корпуса
измерительной ячейки.
) Протереть бензином и нанести
тонкий слой смазки ПФМС - 4 на контактные поверхности стержня5, образца 4,
контактной пластины тепломера 3.
) Образец 4 установить на контактную
пластину тепломера 3, стержень 5 - на иглы термопары.
) Опустить верхнюю половину корпуса
измерительной ячейки.
) Включить блок питания и
регулирования кнопкой «СЕТЬ».
) Установить по вольтметру блока
питания и регулирования начальное напряжение 40 В при работе от плюс 25 оС.
) Установить переключатель
«ИМЕРЕНИЕ» в положение tc.
) Включить кнопкой «НАГРЕВ» основной
нагреватель.
) Снимать показания прибора 
 195 По и Пt при достижении каждой
из температур, указанных в таблице 5.3. Температура стержня достигает
ожидаемого значения при прохождении светового указателя прибора
195 По и Пt при достижении каждой
из температур, указанных в таблице 5.3. Температура стержня достигает
ожидаемого значения при прохождении светового указателя прибора 
 195 через нулевую отметку. Проводя
переключения рукояткой переключателя «ИЗМЕРЕНИЕ», занести значение По и Пt в
таблицу 5.3 и перевести переключатель «ИЗМЕРЕНИЕ» в положение tc.
195 через нулевую отметку. Проводя
переключения рукояткой переключателя «ИЗМЕРЕНИЕ», занести значение По и Пt в
таблицу 5.3 и перевести переключатель «ИЗМЕРЕНИЕ» в положение tc.
) Выключить кнопкой «НАГРЕВ»
основной нагреватель при достижении верхнего уровня температуры испытаний.
) Установить переключатель
«ИЗМЕРЕНИЕ» в положение «УСТ.О».
) Зааретируйте прибор 
 195.
195.
) Выключить блок питания и
регулирования.
) Проводить расчет теплопроводности
в следующей последовательности:
а) рассчитать поправку на
теплоемкость образца 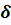
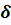 с по формуле (5.7);
с по формуле (5.7);
б) рассчитать тепловое сопротивление
образца по формуле (5.6);
в) рассчитать теплопроводность
испытуемого образца λ
по
формуле (5.10);
г) рассчитать температуру отнесения
измерительного значения теплопроводности 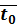
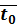 по формуле (5.11).
по формуле (5.11).
) Построить график зависимости
коэффициента теплопроводности λ испытуемого образца от температуры 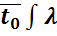
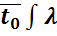 =
= 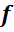
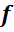 (
(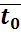
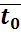 ).
).
) Максимальная относительная
погрешность измерения коэффициента теплопроводности λ оценивается
с помощью уравнения
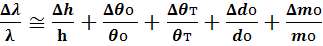
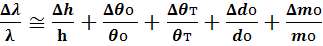 · (5.17)
· (5.17)
Примечание: Общий предел допускаемой
погрешности определения 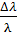
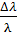 =
= 
 10% · Высота испытуемого
образца h замеряется с точность
10% · Высота испытуемого
образца h замеряется с точность 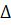
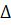 h =
h = 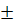
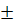 0,01 мм, масса образца с точностью
mо=
0,01 мм, масса образца с точностью
mо=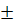
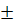 0,001г, диаметр образца
0,001г, диаметр образца 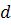
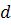 о- с точностью
о- с точностью 
 о=
о=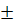
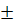 0,1мм. Предел допускаемой основной
погрешности
0,1мм. Предел допускаемой основной
погрешности 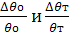
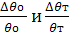 - 1,5%.
- 1,5%.
Значения Кт и Rк являются
постоянными прибора и определяются при их градуировке. Величина их погрешности
определения не должна превышать соответственно 5 и 10%.
Таблица 5.2
Данные, необходимые при определении
теплопроводности испытуемого образца λ и эксплуатации (градуировки)
измерителя теплопроводности.
|
t,
°С
|
С0(t)=Cр
кв(t), Дж/(кг·К)
|
См(t),
Вт/(кг·К)
|
A(t),
К/мВ
|
λм,
Вт/(м·К)
|
λкв,
Вт/(м·К)
|
|
25
|
730
|
385
|
24,8
|
384
|
1,342
|
|
50
|
770
|
392
|
24,5
|
381
|
1,413
|
|
75
|
820
|
396
|
24,6
|
379
|
1,426
|
|
100
|
840
|
400
|
24,7
|
377
|
1,461
|
|
125
|
870
|
403
|
24,8
|
376
|
1,492
|
|
150
|
895
|
405
|
25,5
|
375
|
1,527
|
|
175
|
925
|
406
|
25,0
|
374
|
1,571
|
|
200
|
950
|
408
|
25,0
|
373
|
1,617
|
|
225
|
975
|
410
|
24,9
|
373
|
1,665
|
Полученные данные свести в таблицу 5.3
Таблица 5.3
Основные параметры образца и результаты
эксперимента (если образец кварц - hобр=2·10-3, м; dобр=15·10-3, м,
тогда F0=1,767·10-4 , м2, m0=1,276·10-3); mс=42,028·10-3, кг
tс=tобр, °С П0, мкВ·
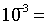 =мВПt,
=мВПt,
мкВ·
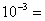 =мВϴ0,Кϴt,ККт,
=мВϴ0,Кϴt,ККт,
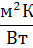 Rк·10-6,
Rк·10-6,
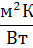 С0,
С0,
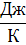 Сс,
Сс,
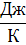 R0,
R0,
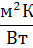 λ,
λ,
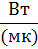
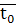
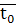 ,
,
|
°С
|
|
|
|
|
|
|
|
|
|
|
|
|
25
|
|
|
|
|
|
|
|
|
|
|
|
|
50
|
|
|
|
|
|
|
|
|
|
|
|
|
75
|
|
|
|
|
|
|
|
|
|
|
|
|
100
|
|
|
|
|
|
|
|
|
|
|
|
|
125
|
|
|
|
|
|
|
|
|
|
|
|
|
150
Контрольные вопросы
) Что такое теплопроводности?
) Какие факторы влияют на коэффициент
теплопроводности?
) Каков механизм передачи теплоты
теплопроводности?
) Что такое температурное поле и градиент
температуры?
) Основной закон теплопроводности (Закон Фурье).
) Что такое тепловой поток и плотность теплового
потока?
) Дифференциальное уравнение теплопроводности и
его физический смысл?
) Какое практическое значение имеет
экспериментальное определение коэффициента теплопроводности различных вещества?
) Сравните интервалы изменения коэффициента
теплопроводности различных веществ?
) В чем сущность метода динамического
калориметра?
) Уравнение теплового потока для однослойной
плоской стенки и понятие термического сопротивления стенок?
) Рассказать методику эксперимента и обработки
экспериментальных данных?
) Что такое тепловая проводимость тепломера Кт и
контактного теплового (термического) сопротивления Rк и методы их определения?
) Что являются постоянными прибора?
) Что такое средняя температура образца и способ
её вычисления?
) Теплопроводность через цилиндрическую стенку и
уравнение теплового потока?
)Чем отличается теплопроводность однослойных
стенок от многослойных?
СПИСОК ЛИТЕРАТУРЫ
1
Теплотехника: Учебник для вузов/А.П.Баскаков, Б.В.Берг, О.К.Витт и др.;
Под
ред. А.П.Баскакова - 2 - е изд. перераб. - М. : Энергоатомиздат, 1991. - 224с.
Нащокин
В.В Техническая термодинамика и теплопередача - 3 - е изд., испр. и доп. - М.:
Высш. школа, 1980. - 469с.
Теплотехника
: Учеб. для вузов/В. Н. Луканин, М. Г. Шатров, Г.М. Камфер и др.; Под ред. В.Н.
Луканина - М.: Высш. шк., 1999, 2002. - 671с.
Лабораторный
практикум по термодинамике и теплопередаче: Учеб. пособие для
энергомашиностроит. спец. вузов/В.Н. Афанасьев, А.А. Афонин, С.И. Исаев и др.;
Под ред. В.И. Крутова, Е.В. Шишова. - М.: Высш. шк., 1988. - 216с.
Тулеуов
К.Т. Учебно - методический комплекс дисциплины студента по дисциплине “Основы
теплотехники” для специальностей 050724 и 050729. - Алматы.: КазНТУ 2005 - 84с.
Тулеуов
К.Т. учебно-методический комплекс дисциплины студента по дисциплине
“Термодинамика и теплотехника” для специальности 050708. - Алматы.: КазНТУ,
2005.- 85с.
Тулеуов
К.Т., Мырзахметов Б.А. Основы теплопередачи. Учебное пособие - Алматы: КазНТУ,
2006. - 109с.
Тулеуов
К.Т. Техническая термодинамика. Лабораторных практикум по курсу “Термодинамика,
теплопередача и теплосиловые установки”. Издание второе, переработанное. - Алма
- Ата: КазПТИ, 1992. - 33с.
Платунов
Е.С. Теплофизические измерения в монотонном режиме. - М.: Издательство энергия,
1972.
Приложение А
Основные параметры некоторых газов при
нормальных условиях
|
Газы
|
Химическое
обозначение
|
Молярная
масса μ, кг/кмоль
|
Плотность
ρ,
кг/м3
|
Объем
киломоля μυ,м3/кмоль
|
Газовая
постоянная R, Дж/(кг*К)
|
|
Воздух
|
-
|
28.96
|
1.293
|
22.40
|
287.0
|
|
Кислород
|
O2
|
32.00
|
1.429
|
22.39
|
259.8
|
|
Азот
|
N2
|
28.026
|
1.251
|
22.40
|
296.8
|
|
Двуокись
углерода
|
CO2
|
44.01
|
1.977
|
22.26
|
188.9
|
|
Аргон
|
Ar
|
39.994
|
1.783
|
22.39
|
208.2
|
|
Водород
|
H2
|
2.016
|
0.090
|
22.43
|
4124.0
|
|
Метан
|
CH4
|
16.032
|
0.717
|
22.39
|
518.8
|
|
Водяной
пар
|
H2O
|
18.016
|
(0.804)
|
(22.4)
|
(461.0)
|
Приложение Б
газовый теплопроводность
теплоемкость твердый
Соотношение между единицами давления
|
Единица
|
Бар
|
Паскаль.
Па (н/м2)
|
Физическая
атмосфера, ат (кгс/см2)
|
Техническая
атмосфера, ат (кгс/см2)
|
Миллиметр
ртутного столба, мм.рт.ст.
|
Миллиметр
водяного столба, мм.вод.ст.
|
|
1
кгс/см2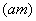 9,81*10-59,8070,968*10-410-4735,6*10-41 9,81*10-59,8070,968*10-410-4735,6*10-41
|
|
|
|
|
|
|
|
1
Па
|
10-5
|
1
|
0,987*10-5
|
0,102*10-4
|
750,1*10-5
|
0,102
|
|
1
ат
|
0,981
|
9,81*104
|
0,9678
|
1
|
735,6
|
104
|
|
1
атм
|
1,013
|
1,012*105
|
1
|
1,033
|
760
|
1,033*104
|
|
1
Бар
|
1
|
105
|
1,0197
|
1,0197
|
750,1
|
10197,2
|
|
1
мм рт.ст
|
0,00133
|
133,32
|
13,16*10-4
|
13,56*10-4
|
1
|
13,595
|
|
1
мм вод.ст.
|
0,981*10-4
|
9,807
|
0,968*10-4
|
10-4
|
735,6*10-4
|
1
|
Приложение В
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахский
национальный технический университет имени К.И. Сатпаева
Кафедра
«Машины и оборудование нефтяной и газовой промышленности»
ЛАБОРОТОРНАЯ
РАБОТА №
На
тему_________________________________________
_________________________________________
______________________________
(шифр и наименование специальности)
Выполнил:_____________________
Ф.И.О.
Преподаватель
______________________________
(должность, уч. степень, звание)
______________________________
И.О.Ф.
«___»__________________20___год
Алматы
20__
Св.план 20010….Поз….
Калдыбай Тулеуович Тулеуов
Садридин Абдукаримович Абдукаримов
ТЕРМОДИНАМИКА И ОСНОВЫ ТЕПЛОТЕХНИКИ
Методические указания к лабораторным работам.
Издание третье, переработанное
Редактор
Техн.редактор
УТВЕРЖДЕНЫ - Председателем учебно-методического
совета института
нефти и газа
Н.У. Алиевым
«______»_________________________2009 г.
СОГЛАСОВАНЫ - Руководителем службы
стандартизации
Г.А. Бейсебековой
«_____»______________________2009г.
Подписано в печать………2009 г.
Тираж 200 экз. Формат 60 84 1/16.
Бумага типографская №1. 84 1/16.
Бумага типографская №1.
Объем 4 п.л. Заказ №…… Цена
договорная
Издание Казахского национального
технического университета
имени К.И. Сатпаева
Научно-технический издательский
центр Каз.НТУ
г. Алматы, ул. Ладыгина 32
Похожие работы на - Термодинамика и основы теплотехники
|