Ряды Фурье
Задача 1
. Запишите формулы для расчета спектральных
коэффициентов ряда Фурье в тригонометрической форме.
. Вычислите спектральные коэффициенты для
сигнала, приведенного на рис. 1. Интервал разложения равен [-τ/2;
τ/2].
Число спектральных коэффициентов n = 5.
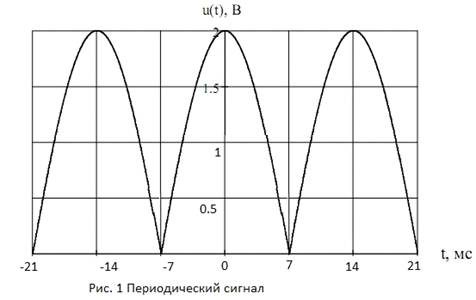
Рис. 1
Исходные данные:
длительность импульса τ=14
мс,
аналитическое выражение для сигнала на рис. 1: 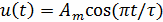
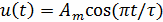
амплитуда сигнала 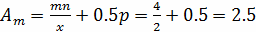
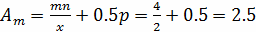
Решение:
. Любую периодическую функцию u(t)=u(t+nT),
удовлетворяющую в пределах периода условиям Дирихле, можно представить в виде
ряда Фурье:
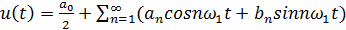
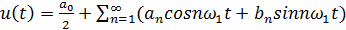
где 
 ;
;

 ;
;
В выражениях (1) и (2) T - период сигнала (здесь
Т=τ),
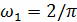
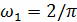 - частота первой
гармоники, n - номер гармоники.
- частота первой
гармоники, n - номер гармоники.
Ряд (1) можно записать в другой форме:
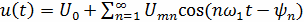
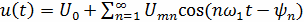 (3)
(3)
Отдельные составляющие этой функции называют
гармониками. Коэффициенты
ряда определяют по следующим формулам:
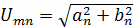
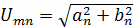 - амлитуды
гармоник; (4)
- амлитуды
гармоник; (4)
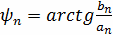
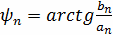 -начальные фазы
гармоник. (5)
-начальные фазы
гармоник. (5)
Величина U0 называется постоянной составляющей.
Она равна среднему значению функции за период:
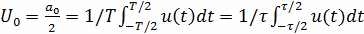
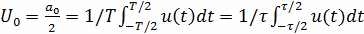 (6)
(6)
Зависимость амплитуд гармоник от частоты ω
или от номера гармоник n называют амплитудным спектром (АС) сигнала.
Зависимость начальных фаз гармоник от частоты или от номера гармоник называют
фазовым спектром (ФС) сигнала. АС и ФС периодических сигналов - дискретные.
2. Определим частоту первой гармоники. Она равна
частоте повторения импульсов:
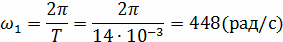
Определим постоянную составляющую по формуле
(6):
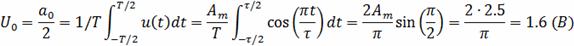
По формулам (2) определим коэффициенты an и bn
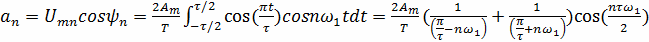
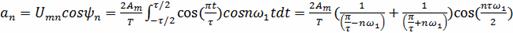
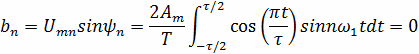
По формуле (4) определим амплитуды гармоник
входного сигнала. Рассчитанные значения для 5-ти гармоник запишем в таблицу 1.
Таблица 1
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
|
an,мВ
|
3183
|
1066
|
-213
|
91
|
-50
|
32
|
|
bn,мВ
|
0
|
0
|
0
|
0
|
0
|
0
|
|
Unm,мВ
|
3183
|
1066
|
213
|
91
|
50
|
32
|
Теперь по значениям таблицы 1 построим график АС
сигнала (рисунок 2).
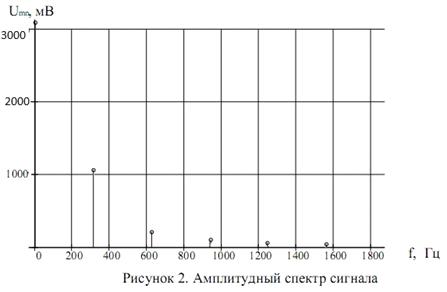
Рис. 2
Задача 2
. Для сигнала 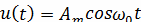
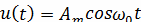 с параметрами:
с параметрами:
циклическая частота f0=25
амплитуда Am=mn/2+0.5p=4/2+0.5=2.5 (B)
найти спектральную плотность и амплитудный
спектр сигнала.
Решение:
. Для разложения в спектр непериодического
сигнала используется прямое преобразование Фурье (интеграл Фурье)
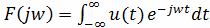
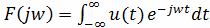 (7)
(7)
где u(t)- функция, описывающая сигнал.
Одним из условий применимости преобразования
Фурье к функции u(t) является её абсолютная интегрируемость:
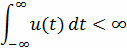
Это условие существенно ограничивает класс
сигналов, для которых существует спектр Фурье, выражаемый обычными функциями.
Например, гармоническое колебание, заданное при -∞<t<∞, не
отвечает выше приведённому условию.
Рассмотрим заданный сигнал 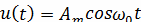
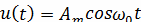 не обращая на то,
что такой сигнал не является абсолютно интегрируемым, выражение для
спектральной плотности запишем в форме (7)
не обращая на то,
что такой сигнал не является абсолютно интегрируемым, выражение для
спектральной плотности запишем в форме (7)
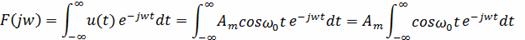
Воспользуемся формулой 

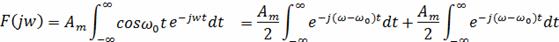
Т.к. 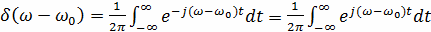
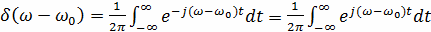
То 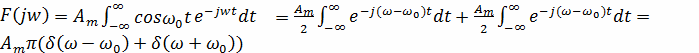
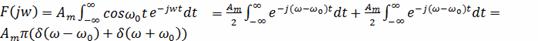
Подставим исходные данные. Для этого рассчитаем
частоту
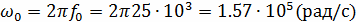
Тогда выражение для спектральной плотности имеет
вид
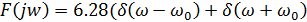
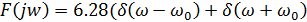 (В/Гц) (8)
(В/Гц) (8)
или модуль спектральной плотности
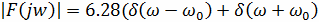
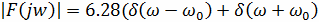 (В/Гц) (9)
(В/Гц) (9)
Эта функция равна нулю для всех частот, кроме ω=ω0
и
ω=-ω0,
при
которых F(ω) обращается в
бесконечность. Гармоническому колебанию с конечной амплитудой соответствует
бесконечно большая спектральная плотность при дискретных частотах ω=ω0
и
ω=-ω0.
3. Построим временную и спектральную диаграммы
сигнала. Выражение для сигнала имеет вид
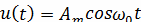
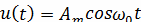 =2.5cos
=2.5cos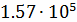
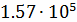 t
t
Временная диаграмма сигнала представлена на
рисунке 4.
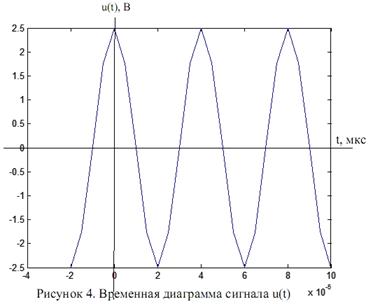
Рис. 3
Спектральная диаграмма сигнала, рассчитанная по
формуле (9), представлена на рисунке 5.

Рис. 4
Задача 3
. Дайте определение автокорреляционной функции
(АКФ) сигнала и запишите формулу для её расчета.
. Для заданного сигнала u(t) (рис. 5) с
параметрами:
Длительность импульса τи=1
мс,
Амплитуда A=mn/2-p/4=2-0.25=1.75 (B)
определить АКФ аналитическим и графическим
способами.
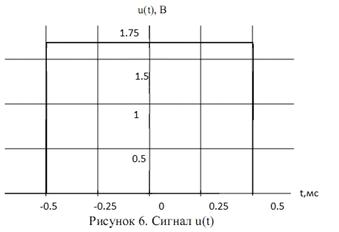
Рис. 5
Решение:
. Автокорреляционной функцией сигнала называется
скалярное произведение сигнала на его сдвинутую копию. Для детерминированного
сигнала конечной длительности АКФ определяется следующим выражением
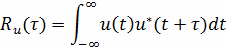
где τ - временной
сдвиг сигнала.
Для сигналов, являющихся вещественными функциями
времени, обозначение комплексного сопряжения можно опустить
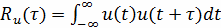
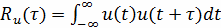 (10)
(10)
Из выражения (10) видно, что Ru(τ)
характеризует
степень связи (корреляции) сигнала u(t) со своей копией, сдвинутой на величину τ
по
оси времени. Ясно, что функция Ru(τ)
достигает максимума при τ=0, так как
любой сигнал полностью коррелирован с сами собой. При этом
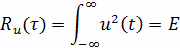
т.е. максимальное значение корреляционной
функции равно энергии сигнала.
С увеличением τ функция
Ru(τ)
убывает
(не обязательно монотонно) и при относительном сдвиге сигналов u(t) и u(t+τ)
на
время, превышающее длительность сигнала, обращается в нуль.
Автокорреляционная функция сигнала является
четной функцией. Эта функция сигнала связана с энергетическим спектром сигнала
парой преобразований Фурье.
Автокорреляционная функция сигнала с
неограниченной энергией связана преобразованиями Фурье со спектральной
плотностью мощности и ее максимальное значение определяется не энергией, а
средней мощностью сигнала. Неограниченную энергию имеют периодические сигналы,
неограниченные во времени.
. Определим АКФ аналитически.
Для расчёта АКФ аналитическим способом
используем выражение (10)
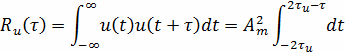
Верхний предел учитывает сдвиг начала сигнала.
Тогда
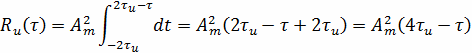
Данное выражение получено для τ>0.
Для
сдвига τ<0
аналогично
может быть получено выражение
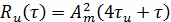
Объединяя полученные выражения, АКФ заданного
сигнала описывается выражением
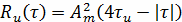
Сдвинутый на τ
(в сторону опережения) импульс u(t+τ) показан
на рисунке 7, б. Произведение u(t)u(t+τ) показано
на рисунке 7, в. При увеличении сдвига τ
произведение u(t)u(t+τ) будет уменьшаться и
при τ=τи
u(t)u(t+τи)=0.
При этом площадь закрашенного треугольника равна нулю. Очевидно, что уменьшение
u(t)u(t+τ)
будет
проходить линейно. При дальнейшем увеличении τ АКФ
всегда будет равна нулю.
В случае отрицательного τ
(сдвиг в сторону запаздывания) алгоритм построения аналогичен. Это показывает,
что АКФ Ru (τ) - чётная функция. АКФ
сигнала изображена ни рисунке 6, г.
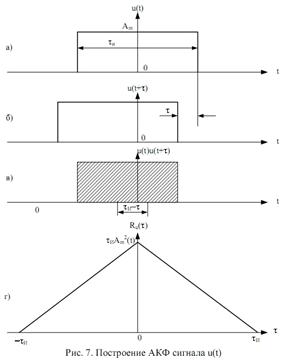
Рис. 6
Максимальное значение максимума равно энергии
импульса:
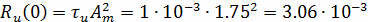
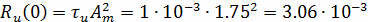 (В/Гц)
(В/Гц)
Задача 4
. Приведите формулу для определения энергии.
. Определите энергию сигнала
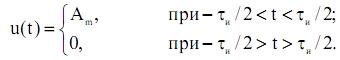
амплитуда
Am=mn/2-p=2-1=1(B)
длительность импульса τи=
(не указано)мс.
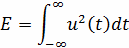
Если сигнал имеет конечную длительность Т, т.е.
не равен нулю на отрезке времени [-T/2,T/2], то его энергия равна
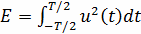
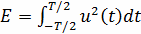 (11)
(11)
Другое выражение, которое может быть применено
для вычисления энергии сигнала, имеет вид
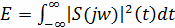
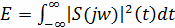 (12)
(12)
где S(jω) - спектральная
плотность сигнала.
Равенство (12) называют равенством Парсеваля.
Оно определяет энергию сигнала через спектральную плотность энергии, которая
равна 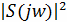
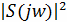
. Согласно 11, энергия заданного сигнала равна
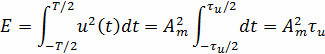
Подставляя числовые значения, получаем
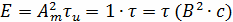
τ -небыл указан в
задании.
Задача 5
Составить структурную электрическую схему
модулятора шумоподобного сигнала (ШПС). Описать работу модулятора. В ячейках
регистра сдвига генератора ШПС до подачи тактовых импульсов хранится кодовая
комбинация 1,0,0,1,1 (“Б”).
Электронный ключ модулятора подключен к ячейке №
1 регистра.
Определите кодовую комбинацию на выходе
генератора после поступления n=10-1=9 тактовых импульсов и период М -
последовательности, если длительность каждого импульса шумоподобной
последовательности на выходе генератора 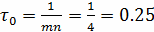
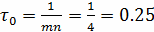 мкс Рассчитать
ширину спектра сигнала на выходе генератора ШПС.
мкс Рассчитать
ширину спектра сигнала на выходе генератора ШПС.
Решение:
Рассмотрим амплитудный модулятор ШС. Структурная
схема представлена на рисунке 7.
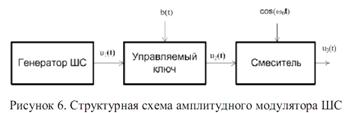
Рис. 7
Генератор шумоподобного сигнала формирует
М-последовательность. Формируются М-последовательности с помощью линейных
переключательных схем на основе сдвигающих регистров. По заданию сдвигающий
регистр состоит из пяти триггерных ячеек, которые выполняют роль дискретных
элементов задержек, и сумматора. На триггеры поступают сдвигающие импульсы. Они
следуют с тактовой частотой 1/τ0.
Каждый тактовый импульс вызывает изменение состояний (напряжения на выходе)
всех триггеров. При этом напряжение на выходе каждого триггера (символ)
становится равным напряжению (символу) на его входе для предыдущего такта.
Символы могут принимать два значения (0 и 1). При суммировании любых комбинаций
входных символов на выходе сумматора получаются только символы 0 и 1.
Поясним работу модулятора временными
диаграммами.
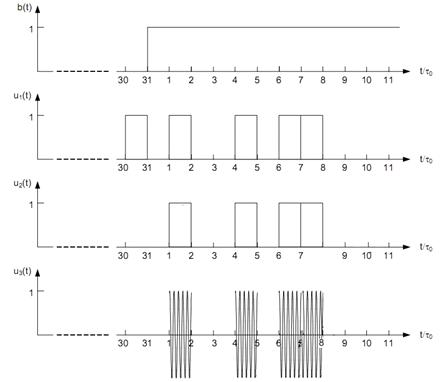
Рис. 8
Генератор шумоподобного сигнала формирует
М-последовательность. Формируются М-последовательности с помощью линейных
переключательных схем на основе сдвигающих регистров. По заданию сдвигающий
регистр состоит из пяти триггерных ячеек, которые выполняют роль дискретных
элементов задержек, и сумматора. На триггеры поступают сдвигающие импульсы. Они
следуют с тактовой частотой 1/τ0.
Каждый тактовый импульс вызывает изменение состояний (напряжения на выходе)
всех триггеров. При этом напряжение на выходе каждого триггера (символ)
становится равным напряжению (символу) на его входе для предыдущего такта.
Символы могут принимать два значения (0 и 1). При суммировании любых комбинаций
входных символов на выходе сумматора получаются только символы 0 и 1.
Для определения структуры цифрового автомата
необходимо знать характеристический многочлен степени k=5, порождающий
М-последовательность. Так как такой многочлен не задан, выберем его сами ([3],
таблица 3.9)
А=a0a1a2a3a4a5=100101. (13)
Знание коэффициентов аn позволяет однозначно
построить цифровой автомат формирования М-последовательности. Если an=1, то
выход n-го триггера подключён к сумматору mod2, если an=0, то выход n-го
триггера к сумматору mod2 не подключён. При этом коэффициент а0=1 всегда по
определению. Поясним функционирование сумматору mod2:
Следует сказать, что выходом генератора ШП может
служить выход любой из триггерной ячейки. Согласно заданию, электронный ключ
модулятора подключен к триггеру 1 регистра.
На основании (13) функциональная схема
генератора ШС приведена на рисунке 10.
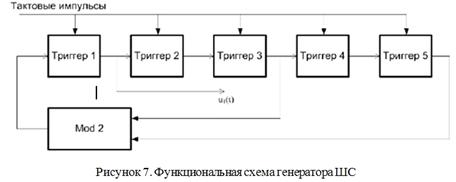
Рис. 9
В ячейках регистра сдвига генератора ШПС до
подачи тактовых импульсов хранится кодовая комбинация 1,0,0,1,1 (“Б”).
Первоначально в регистре записана комбинация 10011. На выходе схемы mod2
присутствует сигнал, определяемый состояниями триггеров 3 и 5. Так как эти
состояния различны, то на выходе схемы mod2 присутствует 1. После прихода
тактового импульса происходит смена состояний триггеров, а именно в триггеры со
второго по пятый записываются значения впереди стоящих триггеров, в триггер 1 записывается
сигнал с выхода схемы mod2, т.е. 1. Данное состояние соответствует второй
строке таблицы 2. Значение выходного сигнала определяется состоянием триггера
1. После прихода первого тактового импульса Q1=1, поэтому U1=1. Далее приходит
следующий тактовый импульс и работа повторяется. Определим кодовую комбинацию
на выходе генератора после поступления n=9 тактовых импульсов. Для удобства все
состояния схемы сведём в таблицу 2.
Таблица 2
|
№
|
Состояние
триггеров
|
Выход
Mod2
|
U1(t)
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
1
|
0
|
0
|
1
|
1
|
1
|
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
|
2
|
1
|
1
|
1
|
0
|
1
|
1
|
|
3
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
|
4
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
|
5
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
|
6
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
|
7
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
|
8
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
|
9
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
Из таблицы 2 определим, что за время подачи n=9
тактовых импульсов на выходе генератора сформировалась следующая
последовательность:
=111100011 .
Период М-последовательность равен:
N=2k-1=25-1=31 импульс,
или по времени
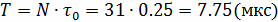
Спектр М-последовательности соответствует
спектру одиночного импульса, из которых состоит последовательность. Поэтому и
ширина спектра всей последовательности равна ширине спектра одиночного
импульса. Так как импульсы имеют прямоугольную огибающую, то
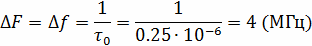
Задача 6
Для заданного конечного числа выборочных
значений сигнала и числа выборочных значений импульсной характеристики
линейного дискретного фильтра
|
Входной
сигнал
|
импульсная
характеристика
|
10111
|
найти:
коэффициенты дискретного преобразования Фурье;
коэффициенты передачи линейного дискретного
фильтра;
z - преобразование выборочных значений на входе
фильтра и на выходе фильтра;
z - преобразование выборочных значений импульсной
характеристики.
Решение:
Последовательность коэффициентов, образующих
дискретное преобразование Фурье (ДПФ) сигнала, рассчитывается по формуле
сигнал фурье дискретный фильтр
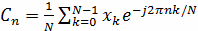
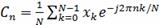 , (14)
, (14)
где N- количество отсчётов.
Отметим некоторые свойства ДПФ:
. Дискретное преобразование Фурье есть линейное
преобразование, т. с сумме сигналов отвечает сумма их ДПФ.
. Число различных коэффициентов С0, С1,… СN-1,
вычисляемых по формуле (14), равно числу N отсчетов за период; при п = N
коэффициент CN = С0.
. Коэффициент С0 (постоянная составляющая)
является средним значением всех отсчетов:
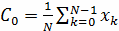
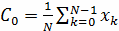 ,
,
. Если N - чётное, то 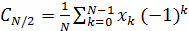
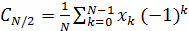
. Пусть отсчетные значения хk - вещественные
числа. Тогда коэффициенты ДПФ, номера которых располагаются симметрично
относительно N/2, образуют сопряженные пары:
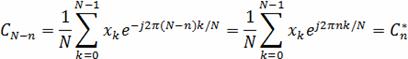
Поэтому можно считать, что коэффициенты
CN/2+1,…., CN-1 отвечают отрицательным частотам. При изучении амплитудного
спектра сигнала они не дают новых сведений.
Используя формулу (14) и используя свойства ДПФ,
непосредственно вычисляем коэффициенты:
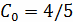
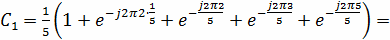
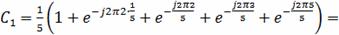 0.138 - j0.190
0.138 - j0.190
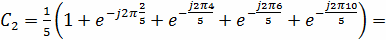
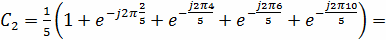 0.361 - j0.117
0.361 - j0.117
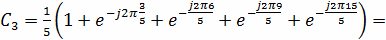
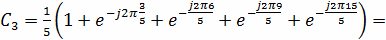 0.361+ j0.117
0.361+ j0.117

 0.138+ j0.190
0.138+ j0.190
Линейный цифровой фильтр, по определению, есть
дискретная система (физическое устройство или программа для ЭВМ), которая
преобразует последовательность{xk} числовых отсчётов входного сигнала в
последовательность {yk} числовых отсчётов выходного сигнала.
В частотной области ЦФ характеризуется
коэффициентом передачи:

 (15)
(15)
где hn - коэффициенты импульсной характеристики,
Δ
- интервал
дискретизации.
Подставляя в (15) отсчёты импульсной
характеристики, получим комплексную передаточную функцию:
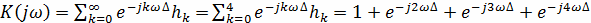
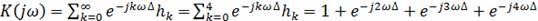
преобразованием последовательности {xk}
называется сумма ряда
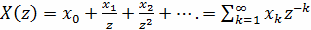
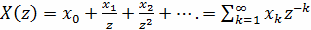 (16)
(16)
На основании (16) можно непосредственно найти
z-преобразование входногодискретного сигнала:
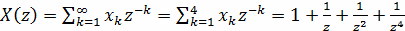
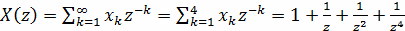 .
.
На основании рассчитанной комплексной
передаточной функции определим системную функцию H(z) (является
z-преобразованием импульсной характеристики).
Данная функция получается из К(jω)
заменой
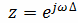
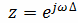 .
.
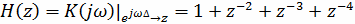
Теперь определим z-преобразование Y(z) выходного
дискретного сигнала {yk}
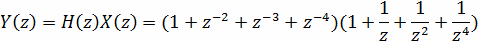
Литература
1. Клюев
Л.Л. ”Теория электрической связи” - Минск, 1998 г.
2. Гоноровский
И.И. “Радиотехнические цепи и сигналы”, Москва, Радио и связь, 1986 г.
. Варакин
Л.Е. “Системы связи с шумоподобными сигналами”, Москва, Радио и связь, 1985 г.
. Баскаков
С.И. “Радиотехнические цепи и сигналы”, Москва, Высшая школа, 1988 г.
. Чёрная
И.И. ”Теория электрической связи” - Минск. Ч.1, 2004 г.