Непрерывная зависимость решений от начальных данных и параметров
Оглавление
Непрерывная зависимость решений от
начальных данных и параметров
. Дифференциальное уравнение
с начальными данными
. Свойства предельных
множеств автономных систем
. Приближенное решение
дифференциальных уравнений
Список использованных источников
Непрерывная зависимость решений от начальных
данных и параметров
дифференциальное
уравнение множество
1. Дифференциальное уравнение с начальными
данными
Рассмотрим дифференциальное уравнение, зависящее
от параметра:
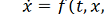
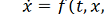


где f: 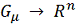
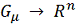 ,
, 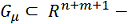
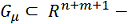 область. Предположим, что в области
область. Предположим, что в области
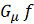
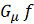 удовлетворяет условию Липшица по x локально:
удовлетворяет условию Липшица по x локально:
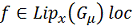
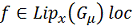 .
.
По теореме (существования и
единственности) G =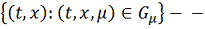
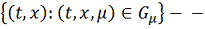 область единственности для системы
область единственности для системы 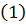
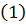 при каждом фиксированном μ. Рассмотрим
функцию
при каждом фиксированном μ. Рассмотрим
функцию 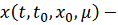
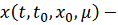 решение системы
решение системы 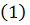
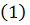 с начальными данными
с начальными данными 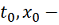
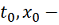 определенную на множестве
определенную на множестве
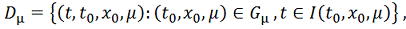
где 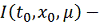
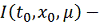 максимальный интервал
существования.
максимальный интервал
существования.
Теорема 1. При сделанных
предположениях 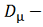
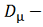 область и
область и 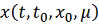
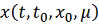 непрерывна в
непрерывна в 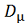
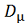 .
.
Д о к а з а т е л ь с т в о. Прежде
всего покажем, что 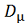
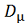 связно. Пусть
связно. Пусть 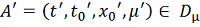
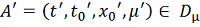 ,
, 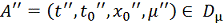
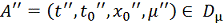 . Построим путь γ, лежащий в
. Построим путь γ, лежащий в 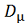
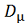 и соединяющий
и соединяющий 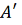
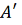 и
и 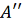
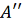 . Из определения
. Из определения 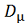
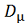 следует, что
следует, что 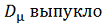
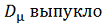 по
по 
 . Кроме того, так как по смыслу
понятия максимального интервала существования
. Кроме того, так как по смыслу
понятия максимального интервала существования 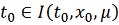
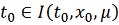 , то множество
, то множество
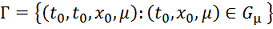
область гиперплоскости 
 , лежащая в
, лежащая в 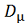
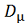 . Отсюда получаем следующий способ
построения γ:
точки
. Отсюда получаем следующий способ
построения γ:
точки
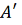
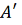 и
и 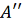
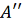 соединяем отрезками прямых с
точками
соединяем отрезками прямых с
точками 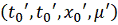
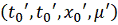 и
и 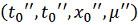
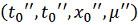 соответственно, а эти последние
точки соединяем любым путем, лежащим в
соответственно, а эти последние
точки соединяем любым путем, лежащим в 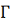
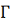 .
.
Теперь нужно доказать, что
существует 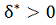
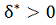 такое, что если
такое, что если 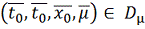
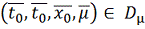 , то и ее
, то и ее 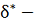
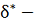 окрестность
окрестность 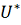
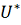 также принадлежит
также принадлежит 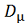
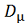 и
и 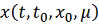
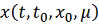 непрерывна в
непрерывна в 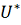
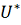 . Пусть
. Пусть 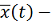
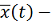 решение с начальными данными
решение с начальными данными 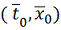
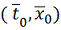 , соответствующее
, соответствующее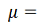
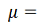
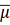
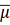 . По определению
. По определению 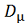
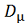 оно определенно при
оно определенно при 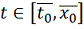
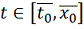 . Образуем
. Образуем 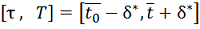
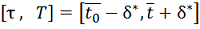 при
при 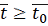
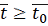 и
и 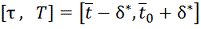
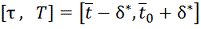 при
при 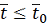
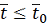 . Продолжая
. Продолжая 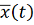
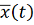 было определено на
было определено на 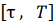
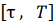 .
.
Отсюда следует, что достаточно
доказать следующее утверждение, равносильное теореме 1.
Теорема 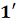
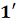 . Пусть в предположениях теоремы 1
дифференциальное уравнение
. Пусть в предположениях теоремы 1
дифференциальное уравнение 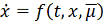
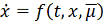 имеет решение
имеет решение 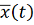
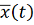 , определенное на отрезке
, определенное на отрезке 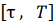
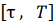 . Тогда существует
. Тогда существует 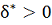
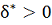 такое, что решение
такое, что решение 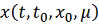
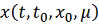 при
при 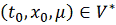
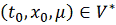 :
:
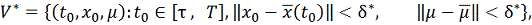
определено при 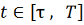
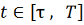 и функция
и функция 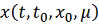
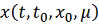 непрерывна на множестве
непрерывна на множестве 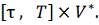
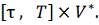
Д о к а з а т е л ь с т в о. Выберем
и зафиксируем столь малое 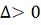
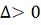 , чтобы замкнутая область
, чтобы замкнутая область
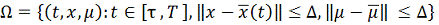
принадлежала 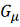
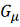 . Поскольку
. Поскольку 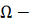
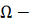 компакт в силу леммы f
компакт в силу леммы f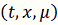
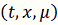 удовлетворяет на
удовлетворяет на 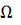
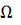 условию Липшица по
условию Липшица по 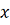
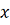 ( глобально) с некоторой постоянной
Липшица L. Далее, так как f непрерывна в области
( глобально) с некоторой постоянной
Липшица L. Далее, так как f непрерывна в области 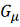
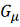 , то она равномерно непрерывна на
, то она равномерно непрерывна на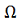
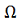 . Следовательно, любому
. Следовательно, любому 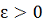
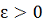 соответствует множество чисел
соответствует множество чисел 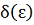
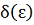 , обладающих свойством
, обладающих свойством
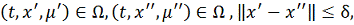
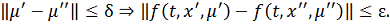
Пусть теперь 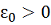
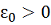 удовлетворяет неравенству
удовлетворяет неравенству
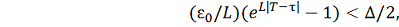
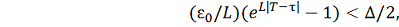
а 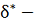
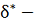 любое число из множества
любое число из множества 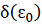
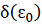 такое, что
такое, что


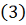
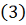
Покажем, что выбранное таким образом
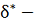
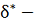 искомое. Пусть
искомое. Пусть 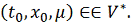
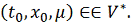 Решение
Решение 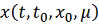
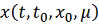 будем строить методом
последовательных приближений Пикара. За нулевое приближение
будем строить методом
последовательных приближений Пикара. За нулевое приближение 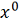
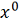 возьмем
возьмем
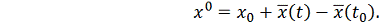
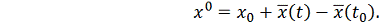
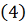
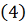
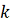
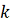 -e приближение
-e приближение 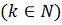
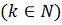 определяется рекуррентным
соотношение
определяется рекуррентным
соотношение
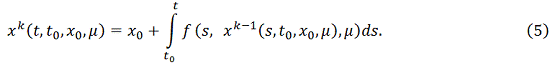
Лемма 1. При всех 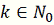
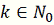 последовательные приближения
последовательные приближения 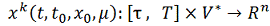
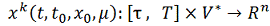 , определяемые формулами
, определяемые формулами 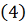
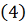 ,
, 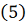
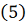 , обладают следующими свойствами:
, обладают следующими свойствами:
1) 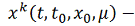
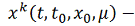 непрерывная функция.
непрерывная функция.
) 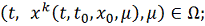
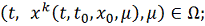
) 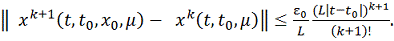
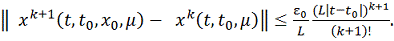
Лемму 1 докажем индукцией по 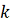
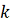 . Сначала докажем 1), 2), 3) при
. Сначала докажем 1), 2), 3) при 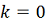
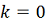 . Справедливость 1) при
. Справедливость 1) при 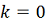
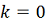 вытекает из
вытекает из 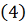
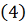 . Справедливость 2) при
. Справедливость 2) при 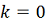
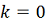 следует из
следует из 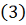
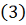 и
и 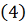
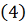 , так как
, так как
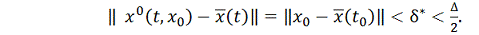
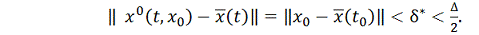
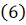
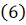
Докажем справедливость 3) при 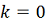
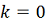 . В силу
. В силу 
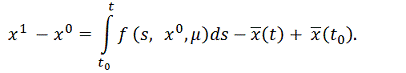
Учитывая, что 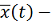
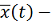 решение уравнения
решение уравнения 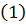
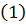 при
при 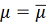
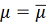 , имеем
, имеем
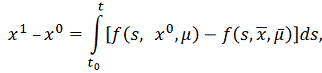
следовательно,
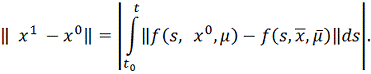
Очевидно, что 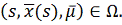
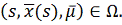 Кроме, того в силу справедливости
2) при
Кроме, того в силу справедливости
2) при 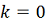
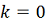
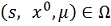
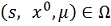 . Используя определение
. Используя определение 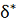
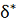 , получаем, что при
, получаем, что при 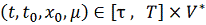
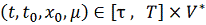
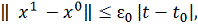
откуда и вытекает 3) при 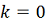
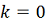 .
.
Предположим теперь, что утверждения
1) - 3) леммы 1
Справедливы для приближений с
номерами 0, 1, … , 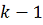
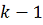 . Докажем их справедливость для -го
приближения.
. Докажем их справедливость для -го
приближения.
а) Согласно п.2) индукционного
предположения аргумент подынтегральной функции в 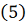
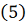 принадлежит
принадлежит 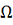
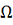 , согласно п.1) функция
, согласно п.1) функция 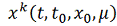
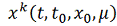 непрерывна, следовательно,
подынтегральной функция непрерывна как суперпозиция непрерывных функций, откуда
и следует непрерывность
непрерывна, следовательно,
подынтегральной функция непрерывна как суперпозиция непрерывных функций, откуда
и следует непрерывность 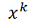
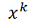 .
.
б) Достаточно доказать, что
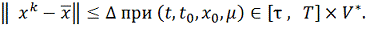
Имеем
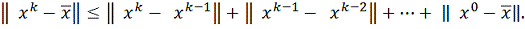
Отсюда, используя п.3) индукционного
предположения , 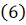
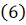 ,
,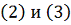
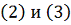 , получаем оценку
, получаем оценку
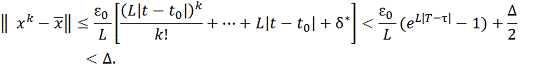
в) В силу 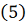
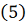
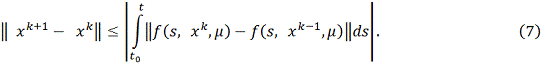
Используя утверждение п.2) леммы для
приближений с номерами 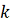
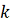 и
и 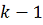
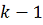 и учитывая, что
и учитывая, что 
 удовлетворяет на
удовлетворяет на 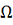
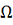 условию Липшица с постоянной
условию Липшица с постоянной 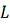
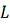 , из
, из 
 имеем
имеем
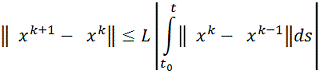
при 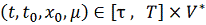
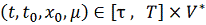 . В силу п.3) индуцированного
предположения
. В силу п.3) индуцированного
предположения
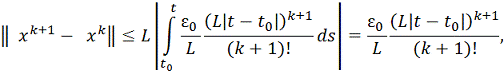
что и доказывает справедливость п.в)
для приближений с номером 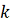
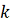 . Лемма 1 доказана.
. Лемма 1 доказана.
Вопрос о сходимости
последовательности заменяем эквивалентным вопросом о сходимости ряда
где 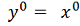
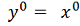 ,
, 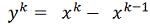
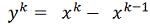
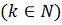
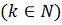 . В силу п.3) леммы 1 ряд
. В силу п.3) леммы 1 ряд 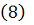
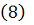 сходится равномерно относительно
сходится равномерно относительно 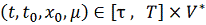
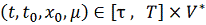 к предельной функции
к предельной функции 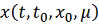
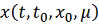 . Так как
. Так как 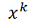
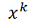 непрерывны, то и
непрерывны, то и 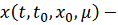
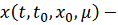 непрерывная функция. Далее, так как
f
непрерывная функция. Далее, так как
f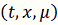
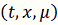 удовлетворяет на
удовлетворяет на 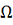
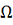 условию Липшица по
условию Липшица по 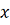
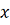 , то
, то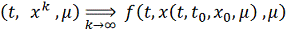
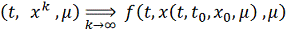 .
.
Следовательно, в 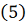
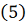 можно перейти к пределу под знаком
интеграла. Имеем
можно перейти к пределу под знаком
интеграла. Имеем
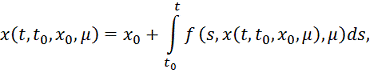
т. е. 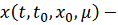
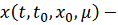 решение уравнения
решение уравнения 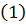
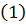 с начальными данными
с начальными данными 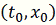
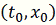 . Теорема 1 доказана.
. Теорема 1 доказана.
Следствие. Если 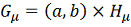
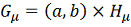 , где
, где 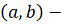
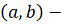 временный интервал,
временный интервал,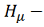
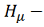 область пространства
область пространства 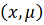
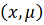 , и все решения продолжим на
интервал
, и все решения продолжим на
интервал 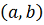
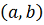 , то функция
, то функция 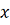
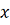 непрерывна в области
непрерывна в области 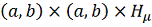
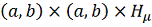 .
.
В частности, для линейной системы
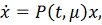
где 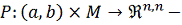
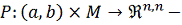 непрерывная функция,
фундаментальная матрица Φ
непрерывная функция,
фундаментальная матрица Φ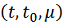
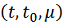 , нормированная при
, нормированная при 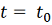
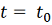 , непрерывна в области
, непрерывна в области 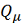
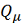 .
.
2. Свойства предельных множеств
автономных систем
Рассмотрим автономную систему
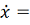
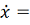 f
f

где 

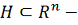
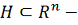 область фазового пространства.
область фазового пространства.
Переформулируем теорему 1 на языке
траекторий.
Теорема 2. Пусть 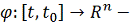
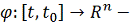 решение системы
решение системы 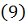
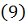 , причем
, причем 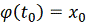
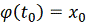 ,
,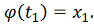
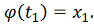 Для любого
Для любого 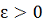
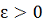 можно указать
можно указать 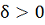
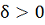 , обладающее следующим свойством:
любая траектория
, обладающее следующим свойством:
любая траектория 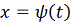
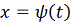 системы
системы 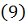
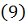 , проходящая при
, проходящая при 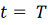
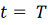 через точку из
через точку из 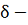
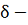 окрестности точки
окрестности точки 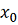
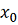 , определена на промежутке
, определена на промежутке 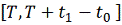
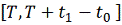 и расстояние
и расстояние 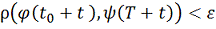
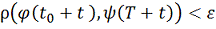 при
при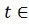
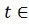
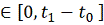
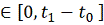 . В частности, точка
. В частности, точка 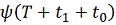
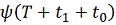 принадлежит
принадлежит 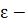
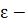 окрестности точки
окрестности точки 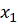
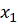 . Если
. Если 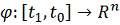
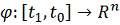 , то аналогичное утверждение
справедливо при
, то аналогичное утверждение
справедливо при 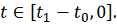
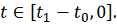
С помощью теоремы 2 можно установить
еще одно свойство предельных множеств автономных систем.
Теорема 3. Предельные множества
траекторий автономных систем состоят из целых траекторий.
Доказательство проведем для случая 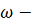
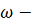 предельного множества. Пусть
предельного множества. Пусть 
 есть
есть 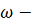
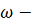 предельное множество траектории
предельное множество траектории 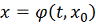
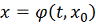 системы
системы 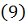
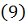 и q
и q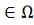
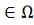 . Пусть
. Пусть 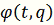
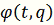 определена как функция
определена как функция 
 на
на 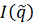
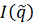 . По теореме 2 для любых
. По теореме 2 для любых 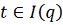
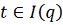 и
и 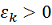
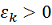 можно указать
можно указать 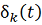
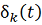 такое , что
такое , что
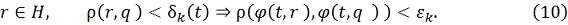
Пусть 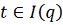
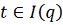 фиксировано,
фиксировано, 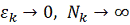
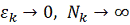 при
при 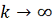
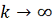 . Так как
. Так как 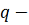
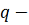
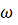
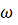 - предельная точка траектории
- предельная точка траектории 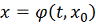
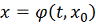 , то для каждого можно указать
, то для каждого можно указать 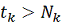
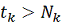 такое, что
такое, что 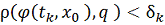
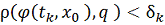 . Отсюда и из
. Отсюда и из 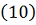
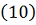 имеем
имеем
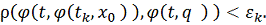
Так как 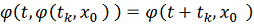
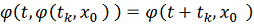 , следовательно,
, следовательно,
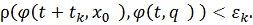
Это означает, что 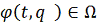
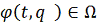 , так как
, так как 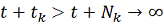
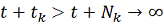 при
при 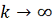
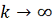 .
.
Теорема доказана.
Свойство предельного множества,
выраженное теоремой 3, называется его инвариантностью. Такое название
объясняется тем, что в силу теоремы 3 предельное множество инвариантно
относительно преобразования 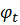
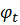 . Из теоремы 2 вытекает также, что
. Из теоремы 2 вытекает также, что 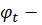
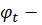 гомеоморфизм области
гомеоморфизм области 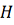
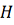 .
.
3. Приближенное
решение дифференциальных уравнений
Рассмотри систему в векторной записи

где 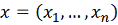
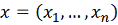 ,
, 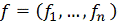
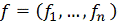 . Пусть в рассмотренной области
вектор-функция
. Пусть в рассмотренной области
вектор-функция 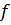
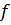 непрерывна по
непрерывна по 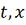
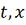 и удовлетворяет условию Липшица по
и удовлетворяет условию Липшица по 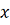
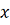
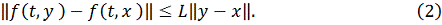 Через
Через 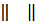
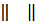 обозначается любая из обычно
применяемых норм вектора:
обозначается любая из обычно
применяемых норм вектора:
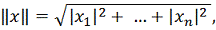
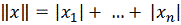
или
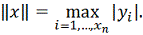
Пусть 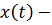
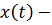 решение системы
решение системы 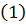
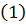 , а
, а 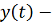
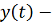 вектор-функция, удовлетворяющая
неравенствам
вектор-функция, удовлетворяющая
неравенствам
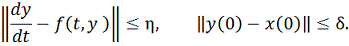
Тогда имеет место оценка
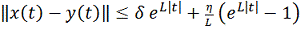
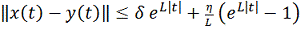 .
. 
Это неравенство можно принять для
грубой оценки ошибки приближенного решения 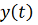
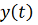 системы
системы 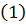
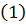 , а так же для оценки сверху
разности решения
, а так же для оценки сверху
разности решения 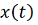
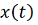 системы
системы 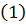
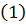 и решения
и решения 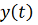
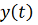 системы
системы 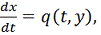
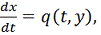 если
если 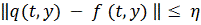
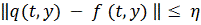 .
.
Пример. Оценим ошибку приближенного
решения на указанном отрезке.
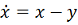
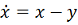 ,
, 
 t
t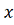
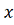 ,
, 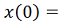
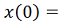 1,
1, 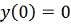
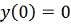 ,
, 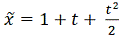
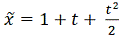 ,
, 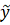
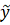 =
= 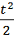
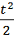 ,
, 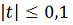
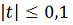 .
.
Пусть 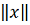
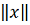 =
= 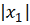
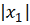
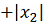
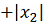
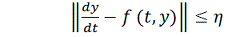
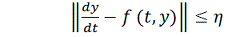 ,
, 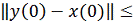
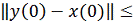 δ ,
δ , 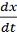
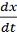 = f(t,
= f(t, 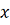
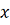 ).
).
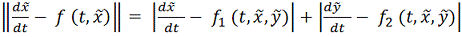
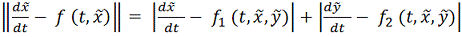
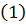
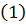

 =
= 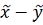
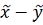 ,
, 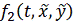
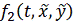 = t
= t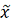
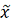
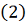
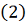
Следовательно, по формуле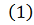
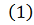 , получим
, получим
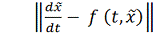
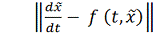 =
= 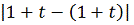
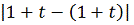 +
+ 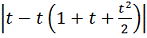
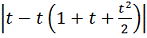 =
=
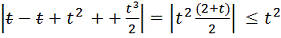
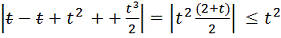
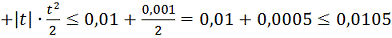
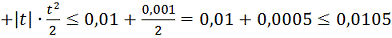 .
.
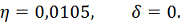
Используя формулы 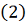
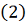 , получим
, получим
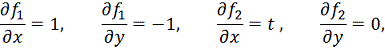
то постоянная Липшица 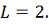
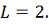
Рассчитывая по формуле
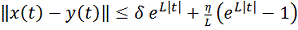
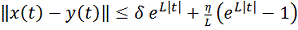 ,
,
получим
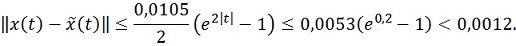
Тогда ответом будет являться данное
неравенство
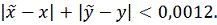
Список использованных источников
1. Бибиков Ю. Н. Курс обыкновенных
дифференциальных уравнений.- М.:Высшая школа, 1991.
2. Филиппов А. Ф. Сборник
задач по дифференциальным уравнениям.- Москва-Ижевск: НИЦ « Регулярная и
хаотическая динамика», 2004
. Филиппов А. Ф. Введение в
теорию дифференциальных уравнений.-
М.: КомКнига, 2007
. Зайцев В.Ф., Полянин А.Д.
Справочник по обыкновенным дифференциальным уравнениям. - М.: ФИЗМАТЛИТ, 2001